
The French version of this document is no longer maintained: be sure to check the more up-to-date English version.
Lexique
A CLASSER
Mixtures
Comment se ramener à des distributions normales ?
Que faire si les données ne sont vraiment pas normales ?
A CLASSER
Exemples, à utiliser un peu plus haut
Données goégraphiques
Divers
A CLASSER : Le livre de F.E.Harrell, Regression modelling strategies
A CLASSER
Simulations
A CLASSER
R for psychologists
Exemples fabriqués
********
Divers
Types de données
Régression
A CLASSER
Manipulation des données
Programmation
A FAIRE
Distributions statistiques
A CLASSER
EN COURS
A CLASSER
A CLASSER (exemples divers)
A FAIRE
Plan de la nouvelle version de ce document
A CLASSER...
Autre graphiques pour repérer ces problèmes
Divers
Plan d'analyse
Divers
A CLASSER
Quelques exemples
A FAIRE
Graphical models (modèles graphiques ?)
Distance de Kullback-Leibler
A FAIRE
Tentative de prédiction d'une variable statistique en fonction d'autres variables. Il s'agit donc d'étudier le lien entre plusieurs variables statistiques, mais de manière asymétrique : certaines variables sont << prédictives >> (ou indépendantes), d'autres << à prédire >> (ou dépendantes).
Variable que l'on cherche à prédire lors d'une régression.
Variables utilisée pour prédire les valeurs d'une autre variable lors d'une régression. Variable prédictive.
Variable indépendante.
Variable qui n'a qu'un nombre fini de valeurs possibles (exemples : vivant/mort, sain/infecté/malade, rouge/vert/bleu, des numéros de département, etc.).
Variable catégorique
Variable à valeurs numériques (exemples : un salaire, une vitesse, une durée, une distance, un poids, etc.)
Etude de la liaison entre un groupe de variables (généralement quantitatives) et une variable quantitative. Il s'agit plus précisément de prédire les valeurs de cette variable.
C'est une régression multiple dans laquelle on cherche à écrire la variable à prédire comme une combinaison linéaire des autres variables. Pour tenter de simplifier le modèle ainsi obtenu, en se débarassant des variables prédictives non nécessaires, on s'amuse à faire plein de tests statistiques du genre "H0 : tel coefficient est nul".
Régression sur les composantes principales (et non pas sur l'espace tout entier). De manière générale, c'est une bonne idée de tenter de se limiter à un nombre réduit de variables.
Cela pose un léger problème : on choisit les variables que seront utilisées pour la prédiction sans tenir compte de la variable à prédire.
A FAIRE : comment contourne-t-on ce problème ???
Régression quand toutes les variables prédictives sont qualitatives.
Plus précisément, on cherche à écrire (dans le cas de deux variables prédictives u et v)
y = qqch qui dépend de la valeur de u
+ qqch qui dépend de la valeur de v
+ qqch qui dépend de la valeur de (u,v)
+ bruitOn évalue les différents coefficients qui apparaissent dans cette écriture et on fait plein de tests pour regarder si certains des coefficients sont nuls (par exemple, les coefficients qui correspondent aux valeurs de (u,v), et qui correspondent à une interaction entre u et v).
Régression quand certaines des variables prédictives sont qualitatives et d'autres quantitatives (ces dernières sont alors qualifiées de covariables).
On procède comme pour l'analyse de la variance, toujours avec plein de tests.
Variable indépendante quantitative dans une régression, quand il y a aussi des variables indépendantes qualitatives (i.e., lors d'une analyse de la covariance).
Etude de la liaison entre un groupe de variables et une variable qualitative.
A FAIRE
Etude de la liaison entre des variables qualitatives.
Voir Modèle linéaire
On cherche à écrire une variable y comme combinaison linéaire d'autres variables x1, x2,... xn :
E(y) = a0 + a1 x1 + a2 x2 + ... + an xn.
Cela revient en fait à écrire
y = a0 + a1 x1 + a2 x2 + ... + an xn + bruit
où << bruit >> est un terme d'erreur (généralement normal, d'espérance nulle). On estimes les paramètres à l'aide de la méthode des moindres carrés (si le bruit est normal, c'est en fait équivalent à la méthode du maximum de vraissemblance, mais les calculs se réduisent à un peu d'algèbre linéaire).
Le modèle linéaire regroupe la régression simple (n=1), la régression multiple (n>1), l'analyse de la variance (si toutes les variables prédictives sont qualitatives) et l'analyse de la covariance (si certaines variables prédictives sont qualitatives et d'autres quantitatives).
Cette fois-ci, on écrit plutôt
g( E(y) ) = a0 + a1 x1 + a2 x2 + ... + an xn
où g est une certaine fonction. De plus, y ne suit pas nécessairement une loi normale, mais simplement une loi de la famille exponentielle (par exemple, normale, binomiale, Poisson, gamma). Pour trouver la valeur des paramètres, on utilise la méthode du maximum de vraissemblance (dans le cas d'une loi normale, on retombe sur les moindres carrés).
C'est en particulier ce que l'on utilise si Y est qualitative. Dans ce cas, on peut chercher P(y=0) ; mais comme une probabilité est toujours comprise entre 0 et 1, on n'arrivera pas à l'exprimer comme combinaison linéaire de variables quantitatives auxquelles on ajoute du bruit. On applique alors à cette probabilité une bijection g entre l'intervalle [0;1] et la droite réelle (on dit que g est un lien). On essaye alors d'exprimer g(P(y=0)) comme combinaison linéaire des variables prédictives.
La fonction g, dans la définition du modèle linéaire généralisé ou dans la régression logistique, qui permet de passer de l'intervalle [0,1] à la droite réelle entière, s'appelle un lien. Il a souvent une forme sigmoïdale.
Les principaux exemples de liens sont la fonction logistique (ou logit), la fonction probit.
Voir Fonction logistique.
C'est un exemple de lien.
p
logit(p) = log -------
1 - pOn peut donc écrire
P(gagner)
logit( P(gagner) ) = log -----------.
P(perdre)Le quotient P(gagner)/P(perdre) s'appelle la cote (vous avez surement déjà entendu l'expression << la cote est à ... contre 1 >>).
Voici le graphe de cette fonction.
x <- seq(0,1, length=100)
x <- x[2:(length(x)-1)]
logit <- function (t) {
log( t / (1-t) )
}
plot(logit(x) ~ x, type='l')
C'est un autre exemple de lien : c'est la fonction inverse de la fonction de répartition de la loi normale standard.
curve(logit(x), col='blue', add=F)
curve(qnorm(x), col='red', add=T)
a <- par("usr")
legend( a[1], a[4], c("logit","probit"), col=c("blue","red"), lty=1)
On suppose ici que les variables observées sont des combinaisons linéaires de "facteurs" (variables non observées, en nombre plus réduit). Cela revient en fait à faire une analyse en composantes principales.
A FAIRE
A FAIRE
Il s'agit de prédire la valeur d'une variables qualitative, i.e., de mettre les individus dans des classes. (Par exemple : aide au diagnostic médical, reconnaissance des mauvais payeurs par une banque, etc.) On cherche des "fonctions linéaires discirminantes (des combinaisons linéaires dea variables, qui maximisent la variance interclasse et minimisent la variance intraclasse)
Ils rendent à peu près les mêmes services que l'analyse discriminante.
A FAIRE
%%%%%%%%%%%%%%%% A FAIRE %%%%%%%%%%%% Relire tout ce qui suit...
On étudie les liaisons entre des variables qualitatives, sans qu'une variable joue un rôle particulier (il n'y a pas de variable à prévoir). Les données sont représentées par un tableau de contingence. On commence par formuler une hypothèse sur ce tableau, qui donne un certain modèle et certaines valeurs pour les fréquences. Par exemple, s'il y a deux variables, si on suppose qu'elles sont indépendantes, le modèle implique que
t(i,j) = t(i,*) t(*,j)
On utilise alors un test du Chi2 pour comparer cette distribution avec celle effectivement observée. Ce modèle peut s'écrire sous forme linéaire
ln t(i,j) = a1(i) + a2(j).
S'il ne convient pas, on peut essayer de rajouter un terme traduisant l'interaction entre les deux variables.
ln t(i,j) = a1(i) + a2(j) + a12(i,j)
Plus généralement, on pourra essayer
ln t(i,j,k) = a0 + a1(i) + a2(j) + a3(k)
+ a12(i,j) + a13(i,k) + a23(j,k)
+ a123(i,j).Ici encore, on pourrait s'amuser à faire plein de tests pour regarder si certains de ces coefficients sont nuls. Mais généralement, on commence par essayer les modèles les plus simples, et on les complexifie au fur et à mesure : on s'arrête quand le modèle convient.
Le modèle log-linéaire est pertinent si on a peu de variables (pas plus de 5 : sinon, on préfèrera l'analyse des correspondances) et beaucoup d'individus.
C'est un cas particulier du modèle linéaire généralisé, dans lequel le lien est la fonction logit.
On cherche à relier des variables qualitatives x1, x2,..., xn et une variable qualitative y qui prend deux valeurs (on parle de variable binaire ou dichotomoque). Pn cherche à estimer la probabilité
pi(x) = P ( y=1 | x ).
on considère le modèle
logit pi(x) = a0 + a1 x1 + ... + an xn
où
logit(t) = ln( t/(1-t) ).
Comme d'habitude, on estime les coefficients à l'aide de la méthode du maximum de vraissemblance et on fait plein de tests du genre "H0: a_i = 0".
Anova simple
Anova avec une seule variable qualitative.
Anova double
Anova avec deux variables qualitatives.
Supposons pour l'instant que ces variables n'interagissent pas. Le modèle est le suivant.
Y(i,j) = mu + A(i) + B(j) + Erreur(i,j)
On dit que A(i) est l'effet traitement et que B(j) est l'effet bloc.
S'il y a interaction, le modèle est :
Y(i,j) = mu + A(i) + B(j) + C(i,j) + Erreur(i,j).
Dans une anova double,
Y(i,j) = mu + A(i) + B(j) + C(i,j) + Erreur(i,j).
on dit que A(i) est l'effet traitement et que B(j) est l'effet bloc.
Dans une anova double,
Y(i,j) = mu + A(i) + B(j) + C(i,j) + Erreur(i,j).
on dit que A(i) est l'effet traitement et que B(j) est l'effet bloc.
(A FAIRE -- il doit y avoir d'autres morceaux sur le sujet ailleurs dans ce document...)
Comment trouver le nombre d'éléments d'une "mixture" ? Par exemple par des méthodes bayesiennes :
http://www.maths.soton.ac.uk/staff/Sahu/utrecht/adv.pdf
Il n'est pas toujours possible ou (raisonnable) de se ramener à une distribution normale : il arrive par exemple que la distribution présente plusieurs pics...
Pour analyser les données, il faut préalablement les vérifier (s'assurer qu'il n'y a pas d'erreurs, ni de données incohérentes : a priori ces erreurs sont rares, donc on les voit facilement, par exemple avec des boutes à moustaches ou d'autres représentations graphiques) et éventuellement les remplacer par des données plus symétriques.
En effet, beaucoup de traitements statistiques (par exemple : le calcul de la moyenne) sont très sensibles à des données (rares) qui s'éloignent beaucoup de la « norme », à des situations non symétriques et à des distributions avec des « queues épaisses » (beaucoup de données qui s'éloignent de la norme).
À l'aide d'une boite à moustaches ou à l'aide d'un test U de Wilcoxon, comme nous l'avons déjà vu plus haut.
A l'aide d'un graphe de symétrie.
Une première solution consiste à faire un test de Shapiro.
?shapiro.test
> shapiro.test(rnorm(100))
Shapiro-Wilk normality test
data: rnorm(100)
W = 0.9809, p-value = 0.1564
> shapiro.test(rnorm(100)^2)
Shapiro-Wilk normality test
data: rnorm(100)^2
W = 0.6976, p-value = 4.74e-13Le test de Kolmogorov--Smirnov est plus général : il marche avec des distributions autres que la distribution normale , et permet aussi de savoir si deux échantillons sont distribués suivant la même loi.
?ks.test
Une seconde méthode consiste à utiliser un QQplot.
Certaines données ne sont pas normales, mais on peut souvent s'y ramener par des transformations, comme prendre la racine carrée ou le logarithme.
On prend la racine carrée si la distribution ressemble à une distribution normale un peu deséquilibrée

par exemple


On applique le logarithme quand la distribution ressemble à une distribution lognormale

par exemple


A FAIRE : choisir une transformation en s'aidant du test de Shapiro.
A FAIRE
?boxcox
(Donne la meilleure valeur de lambda pour que y = a x^lambda + b ???)
data(trees)
boxcox(Volume ~ log(Height) + log(Girth), data = trees,
lambda = seq(-0.25, 0.25, length = 10))
data(quine)
boxcox(Days+1 ~ Eth*Sex*Age*Lrn, data = quine,
lambda = seq(-0.05, 0.45, len = 20))
Transforming non-normal data into normal data. The box.cox.powers
function in the car package does unconditional univariate and
multivariate Box-Cox transformations.
(Cette bibliothèque n'est pas installée...)
A FAIRE : exemple (des distributions à 2 pics, par exemple faithful, les premières notes de mes élèves, ou une somme de deux distributions normales).
x <- c( 2+rnorm(100), 6+rnorm(100) ) hist(x)
Nous avons vu certains tests non paramétriques : rappelons-les.
Pour la moyenne, on peut remplacer le test T de Student par le test U de Wincoxon. Dans le cas de plus de deux échantillons, on peut remplacer l'analyse de la variance par le test de Kruskal--Wallis.
Pour la variance, on peut remplacer le test F de Fisher ou celui de Bartlett par les tests d'Ansari, Mood ou Fligner.
On se donne deux échantillons de taille n, et on veut savoir si leur moyennes sont significativement différentes. Pour cela, on commence par calculer les moyennes et leur différences. Ensuite on recommence, mais en prenant deux échantillons de taille n au hasard dans nos 2n valeurs. Et on continue jusqu'à avoir une bonne estimation de la distribution de ces différences. Ensuite, on regarde où notre différence initiale se trouve dans cette distribution : on rejette l'hypothèse d'égalité si elle semble trop marginale.
Condition d'application : équivariance (i.e., les deux échantillons ont la même variance, ce que l'on vérifie à l'aide d'un test de F).
A FAIRE : comment appelle-t-on cela en anglais ? resampling ???
A FAIRE : un exemple pratique (reprendre les données du T-test ?)
Intégration numérique :
?integrate
Penalized Regression
library(Design) ?ols
Cp de Mallow : dans le cas gaussien, avec variance connue, il équivaut à l'AIC.
Dimension de Vapnik--Chernovenkis.
Définir la log-vraissemblance. On peut utiliser les quotients de vraissemblance pour faire des tests.
Likelihood ratio test: see the esample in ?loglm
scatterplot in the car package
Ellipses in the car package.
The Florida data set in the car package
"outlier" se traduit par "point atypique". "dummy variable" se traduit par "variable indicatrice".
Coefficient de détermination : corrélation entre y et \hat y. On peut donc le voir en représentant \hat y ~ y.
do.call
# The example comes from Rtips
plot(2:10,type="n")
do.call("rect",c(as.list(par("usr")[c(1,3,2,4)]),list(col="pink")))
points(2:10)
# équivalent à :
plot(2:10,type="n")
rect( par("usr")[1], par("usr")[2], par("usr")[3], par("usr")[4], col="pink" )
points(2:10)?signif
# Pour avoir plein de petits histogrammes latex(describe(df))
Contrastes (Dans les tests post-hoc ? Dans les tests de la régression multiple ?). On aimerait savoir si A,C>=A. On peut regarder si la moyenne de 2A-B-C est significativement non nulle. Les contrastes permettent (presque) de faire plusieurs tests en un seul.
Définir : corrélation avec les rangs de Spearman ; Corrélation avec les rangs de Kendal.
Parler de
http://dssm.unipa.it/R-php/
?termplot
Calcul parallèle :
library(help=Rpmi) http://www.mpi-forum.org/ Par exemple, pour les clusters Beowulf A FAIRE : URL library(help=rpvm) A FAIRE : URL pour PVM...
?tsSmooth ?monthplot ?decompose # classical decomposition of a time-series
Débugging:
?browser ?trace ?recover ?warning ?stop
Changements :
library(pastecs) ?turnpoints (à utiliser par exemple après loess, sur le spectre d'une série de Fourrier, pour avoir une idée de la période)
On peut directement récupérer des données boursières sur le Web :
library(tseries) ?get.hist.quote
Voir aussi :
?download.file
Modèle hiérarchisé. Modéle à effets croisés = modéne non hiérarchisé. Facteur à effet fixe (ou plan factoriel complet) : il y a qualque chose dans chaque case du tableau. Facteur à effet aléatoire : il n'y a pas nécessairement quelque chose dans chaque case du tableau.
Blocs. Il y a plein de variables qu'on ne connait pas, mais qui peuvent influencer le résultat. On fait donc plusieurs fois la même expérience dans les mêmes conditions (par exemple, sur le même individu, dans le même champ, etc.) : cela s'appelle un bloc. Pour pouvoir tirer des conclusions indépendemment des blocs, on refait la même expérience dans d'autres blocs. En gros, les blocs, ce sont les variables qualitatives dont on voudrait se débarasser.
Revoir la notion de M-estimateur. Quelles sont ces fonction rho et psi ?
qqplots stratified by the quantiles of Xi.
Many quantitative variables: draw a dendogram (for the variables, not the observations).
Compute and plot (dotplot(sort(...))) the adjsuted R-squared for each variable (lm(y~x[-i])).
two-way table. 2 variables qualitatives X1, X2, une variable quantitative, Y. Pour chaque couple de valeurs de (X1,X2), un seul individu. Modèle: Yij = mu + ai + bj + eij.
Median polish. Take a 2-way table. Substract its median from each row. Substract its median from each column. Iterate. (With the mean, we need not iterate). (Keep track of what you substract: these are the looked for ai and bj.)
n <- 3
p <- 5
m <- matrix( rpois(n*p,10), nr=n, nc=p )
my.median.polish <- function (m, median=median) {
a <- rep(0, dim(m)[1])
b <- rep(0, dim(m)[2])
c <- median(m)
m <- m-c
for (i in 1:10) {
print(paste("itération",i))
print(m)
a <- a + apply(m,1,median)
m <- m - a
b <- b + apply(m,2,median)
m <- t(t(m)-b)
}
print(a)
print(b)
print(c)
}
my.median.polish(m, median=mean)
A FAIRE : ça ne marche pas...
HairEyeColor : 3 variables quantitatives
InsectSprays : 1 variable quantitative, 1 qualitative
LifeCycleSavings : 5 variables quantitatives
Titanic : 4 variables qualitatives
ToothGrowth : 2 variables quantitatives, 1 qualitative
UCBAdmissions : 3 variables qualitatives
airmiles : time series
airquality : 4 variables quantitatives (bon pour une régression non linéaire)
anscombe : très bon exemple (construit) de régression linéaire
attenu: coplot?
chickwts: une variable quantitative, une qualitative (prédictive)
chickwts: bon exemple de boxplots avec des intervalles de confiance sur la médiane
co2: time series (looks like at+sin(bt+c))
eurodist: dist object
faithful: 1 quantitative variable
freeny: 5 variables quantitatives, régression bien linéaire
(est-ce un bon exemple pour comparer des modèles ?)
infert: régression logistique
longley: régression linéaire (6 variables)
mtcars: une dizaine de variables, tantôt qualitatives, tantôt quantitatives
nhtemp: time series
phones: 6 séries temporelles (exemple d'utilisation de matplot)
presidents: time series
pressure: deux variables quantitatives (exemple de régression non linéaire, ou exemple d'échelle logarithmique).
quakes: pairplot avec beaucoup de points (on doit pouvoir réutiliser cet exemple pour faire un peu d'algèbre linéaire, d'ACP et de dessins en 3D).
randu: mauvais nombres aléatoires
rivers: longueur de rivières (exemple pour la loi de Benford)
sleep: deux variables, une numérique, une qualitative (prédictive)
data(state)
state.area: pour la loi de Benford ?
state.x77: plein de variables quantitatives (régression pas claire)
sunspots: time series (irregular sines)
swiss: plein de variables quantitatives, une qualitatives (pairplot avec des couleurs)
trees: 3 variables quantitatives, coplot
volcano: contour plot
warpbreaks: une donnée numérique, deux données qualitatives (prédictives)
boxplot avec plusieures données qualitativesA FAIRE:
data(package=MASS)
coplot(..., show.given=F) xyplot (in the lattice library) supercedes the coplot command.
Variogramme:
library(geoR)
D <- matrix(scan("file.dat", n=530*3), 530,3, byrow=TRUE)
B <- as.geodata(D, coords.col=1:2, data.col=3)
variog(B, option = "cloud", max.dist = 1)
Superposer deux graphiques
x<-c(1,1,NA,2,2,NA,3,3) y<-c(2,4,NA,3,5,NA,1,4) par(fig=c(0,2/3,0,1)) plot(x,y) par(fig=c(2/3,1,0,1), new=F) qqnorm(x)
Start-up:
% cat ~/.Rprofile
cat("Running my .Rprofile...");
library(modreg)
cat("Running my .Rprofile...done");regression and 3D graphs:
library(akima) plan <- interp.old(x,y.z) image(plan)
Option pricing, etc.
library(RQuantLib)
Nomogram :
library(Design)
Bootstrap : derivation of distribution-free confidence intervals; estimation of optimism.
Bias: Variance often deminates bias. Biased methods are useful. eg: Penalized Maximum Likelyhood.
Deux utilisations
?update
?step
# Que signifie le point dans les podèles suivants ?
data(trees)
pairs(trees, panel = panel.smooth, main = "trees data")
plot(Volume ~ Girth, data = trees, log = "xy")
coplot(log(Volume) ~ log(Girth) | Height, data = trees,
panel = panel.smooth)
summary(fm1 <- lm(log(Volume) ~ log(Girth), data = trees))
summary(fm2 <- update(fm1, ~ . + log(Height), data = trees))
step(fm2)
## i.e. Volume ~= c * Height * Girth^2 seems reasonable
A FAIRE
Différentes manières de fabriquer des tables
?table ?ave ?by (quand on étudie une variable quantitative par rapport à une/des variables(s) quantitative(s))
matplot
sines <- outer(1:20, 1:4, function(x, y) sin(x / 20 * pi * y)) matplot(sines, pch = 1:4, type = "o", col = rainbow(ncol(sines)))
Aussi pour des nuages de points :
data(iris) # is data.frame with `Species' factor
table(iris$Species)
iS <- iris$Species == "setosa"
iV <- iris$Species == "versicolor"
op <- par(bg = "bisque")
matplot(c(1, 8), c(0, 4.5), type= "n", xlab = "Length", ylab = "Width",
main = "Petal and Sepal Dimensions in Iris Blossoms")
matpoints(iris[iS,c(1,3)], iris[iS,c(2,4)], pch = "sS", col = c(2,4))
matpoints(iris[iV,c(1,3)], iris[iV,c(2,4)], pch = "vV", col = c(2,4))
legend(1, 4, c(" Setosa Petals", " Setosa Sepals",
"Versicolor Petals", "Versicolor Sepals"),
pch = "sSvV", col = rep(c(2,4), 2))Ne pas oublier de parler de
par(mfcol=c(3,2))
sink("foo.result")Paired t-test
t.test(a1,b1,paired=TRUE) plot(a1,b1) abline(0,1) # Other plot matplot(t(cbind(a1,b1)),type="l")
Observe-t-on A plus souvent que B ?
prop.test(sum(a1>b1), sum(a1>b1)+sum(a1<b1)).
Chi-test
a1 <- c(1,1,1,1,1,1,1,0,0,0,0,0,0) b1 <- c(1,1,1,1,1,1,0,0,0,0,0,0,1) chisq.test(a1,b1)
On rappelle que ce test n'est qu'une approximation (d'ailleurs, R nous le dit). Pour une table 2x2, on peut utiliser le test (exact) de Fisher.
fisher.test(a1,b1)
Voir aussi :
?loglin library(MASS) ?logml
Corrélation ???
cor.test(a1,b1)
Partial correlation is the correlation of the residuals.
cor(lm(x1~z1)$resid,lm(y1~z1)$resid)
Factor Analysis ???
factanal(m1,factors=3)
???
v1 <- kmeans(x1,3)$cluster matplot(t(v1),t="l")
Standardize :
?scale
On ne peut pas comparer des modèles en les regardant séparémént.
summary(lm(y ~ x1 + x2)) summary(lm(y1 ~ x1 + x2 + x3 + x4)) model1 <- lm(y1 ~ x1 + x2) model2 <- lm(y1 ~ x1 + x2 + x3 + x4) anova(model1,model2) A FAIRE : comparaison de modèles library(MASS) ?addterm data(quine) quine.hi <- aov(log(Days + 2.5) ~ .^4, quine) quine.lo <- aov(log(Days+2.5) ~ 1, quine) addterm(quine.lo, quine.hi, test="F")
Simulations
v1 <- matrix(sample(c(1, 2, 3, 4, 5), size=1000, replace=T), ncol=10)
Une autre manière de remplir des matrices ou des vecteurs.
nsub1 <- nrow(q1) cors1 <- rep(NA,ns) for (i in 1:nsub1) cors1[i] <- cor(m1[i,],m2[i,])
AOV (within-subject) :
data1<-c(
49,47,46,47,48,47,41,46,43,47,46,45,
48,46,47,45,49,44,44,45,42,45,45,40,
49,46,47,45,49,45,41,43,44,46,45,40,
45,43,44,45,48,46,40,45,40,45,47,40) # across subjects then conditions
matrix(data1, ncol= 4,
dimnames = list(paste("subj", 1:12), c("Shape1.Color1", "Shape2.Color1",
"Shape1.Color2", "Shape2.Color2")))
Hays.df <- data.frame(rt = data1,
subj = factor(rep(paste("subj", 1:12, sep=""), 4)),
shape = factor(rep(rep(c("shape1", "shape2"), c(12, 12)), 2)),
color = factor(rep(c("color1", "color2"), c(24, 24))))
aov(rt ~ shape * color + Error(subj/(shape+color)), data=Hays.df)
aov(rt ~ shape * color + Error(subj + subj:shape + subj:color), data=Hays.df)
What goes inside the Error() statement, and the order in which they
are arranged, are very important in ensuring correct statistical
tests.
Here we show you two examples of common errors. The first mistakenly
computes the repeated measure design as if it was a randomized,
between-subject design. The second only separates the subject error
stratum. The aov() function will not prevent you from fitting these
models because they are legitimate. But the tests are not what we
want.
summary(aov(rt ~ (shape * color) * subj, data=Hays.df))
summary(aov(rt ~ shape * color + Error(subj), data=Hays.df))Autre exemple (tiré du même document, à ne pas reprendre directement)
MD497.dat <- matrix(c(
420, 420, 480, 480, 600, 780,
420, 480, 480, 360, 480, 600,
480, 480, 540, 660, 780, 780,
420, 540, 540, 480, 780, 900,
540, 660, 540, 480, 660, 720,
360, 420, 360, 360, 480, 540,
480, 480, 600, 540, 720, 840,
480, 600, 660, 540, 720, 900,
540, 600, 540, 480, 720, 780,
480, 420, 540, 540, 660, 780),
ncol = 6, byrow = T) # byrow=T so the matrix's layout is exactly like this
MD497.df <- data.frame(
rt = as.vector(MD497.dat),
subj = factor(rep(paste("s", 1:10, sep=""), 6)),
deg = factor(rep(rep(c(0,4,8), c(10, 10, 10)), 2)),
noise = factor(rep(c("no.noise", "noise"), c(30, 30))))
taov <- aov(rt ~ deg * noise + Error(subj / (deg + noise)), data=MD497.df)
summary(taov)...
summary(aov(rt ~ drug + Error(subj/drug), data = Stv.df)) summary(aov(rt ~ drug, data = Stv.df))
Un exemple assez long (un graphique fait à la main).
Ela.mat <-matrix(c(
19,22,28,16,26,22,
11,19,30,12,18,28,
20,24,24,24,22,29,
21,25,25,15,10,26,
18,24,29,19,26,28,
17,23,28,15,23,22,
20,23,23,26,21,28,
14,20,29,25,29,29,
16,20,24,30,34,36,
26,26,26,24,30,32,
22,27,23,33,36,45,
16,18,29,27,26,34,
19,21,20,22,22,21,
20,25,25,29,29,33,
21,22,23,27,26,35,
17,20,22,23,26,28), nrow = 16, byrow = T)
Ela.mul <- cbind.data.frame(subj=1:16, gp=factor(rep(1:2,rep(8,2))), Ela.mat)
dimnames(Ela.mul)[[2]] <-
c("subj","gp","d11","d12","d13","d21","d22","d23") # d12 = drug 1, dose 2
Ela.uni <- data.frame(effect = as.vector(Ela.mat),
subj = factor(paste("s", rep(1:16, 6), sep="")),
gp = factor(paste("gp", rep(rep(c(1, 2), c(8,8)), 6), sep="")),
drug = factor(paste("dr", rep(c(1, 2), c(48, 48)), sep="")),
dose=factor(paste("do", rep(rep(c(1,2,3), rep(16, 3)), 2), sep="")),
row.names = NULL)
attach(Ela.uni)
tmean <- tapply(effect, IND = list(gp, drug, dose), mean)
tse <- tapply(effect, IND = list(gp, drug, dose), se)
tbarHeight <- matrix(tmean, ncol=3)
dimnames(tbarHeight) <- list(c("gp1dr1","gp2dr1","gp1dr2","gp2dr2"),
c("dose1","dose2" ,"dose3"))
tn <- tapply(effect, IND = list(gp, drug, dose), length)
tu <- tmean + qt(.975, df=tn-1) * tse # upper bound of 95% confidence int.
tl <- tmean + qt(.025, df=tn-1) * tse # lower bound
tcol <- c("blue", "darkblue", "yellow", "orange") # color of the bars
tbars <- barplot(height=tbarHeight, beside=T, space=c(0, 0.5),
ylab="", xlab="", axes=F, names.arg=NULL, ylim=c(-15, 40),
col=tcol)
segments(x0=tbars, x1=tbars, y0=tl, y1=tu)
segments(x0=tbars-.1, x1=tbars+0.1, y0=tl, y1=tl) # lower whiskers
segments(x0=tbars-.1, x1=tbars+0.1, y0=tu, y1=tu) # upper whiskers
axis(2, at = seq(0, 40, by=10), labels = rep("", 5), las=1)
tx <- apply(tbars, 2, mean) # center positions for 3 clusters of bars
segments(x0=0, x1=max(tbars)+1.0, y0=0, y1=0, lty=1, lwd = 2)
text(c("Dose 1", "Dose 2", "Dose 3"), x = tx, y = -1.5, cex =1.5)
mtext(text=seq(0,40,by=10), side = 2, at = seq(0,40,by=10),
line = 1.5, cex =1.5, las=1)
mtext(text="Drug Effectiveness", side = 2, line = 2.5, at = 20, cex =1.8)
tx1 <- c(0, 1, 1, 0)
ty1 <- c(-15, -15, -13, -13)
polygon(x=tx1, y=ty1, col=tcol[1])
polygon(x=tx1, y=ty1 + 2.5, col=tcol[2]) # 2nd, moved 2.5 points up
polygon(x=tx1, y=ty1 + 5, col=tcol[3]) # 3rd
polygon(x=tx1, y=ty1 + 7.5, col=tcol[4]) # last
text(x = 2.0, y = -14, labels="group 1, drug 1", cex = 1.5, adj = 0)
text(x = 2.0, y = -11.5, labels="group 2, drug 1", cex = 1.5, adj = 0)
text(x = 2.0, y = -9, labels="group 1, drug 2", cex = 1.5, adj = 0)
text(x = 2.0, y = -6.5, labels="group 2, drug 2", cex = 1.5, adj = 0)A la fin, il y a une explication sur l'argument Error de la commande aov.
A FAIRE : A LIRE
Régression logistique. Il s'agit maintenant de prédire la valeur d'une variable qualitative à deux valeurs à l'aide de variables quantitatives. Pour une seule variable, on part de
P( Y=1 ) = exp(X) / (1 + exp(X) )
qui s'écrit encore
ln( P(Y) / (1-P(Y)) ) = X.
On essaye donc d'écrire
ln( P(Y) / (1-P(Y)) ) = a0 + a1 X1 + a2 X2 + ...
Sous R la fonction est glm (Generalized Linear Model). L'argument "binomial" dit quelle transformation il faut utiliser.
summary(glm(y ~ x1 + x2 + x3, family=binomial))
On a aussi souvent besoin de connaitre la pertinence du modèle.
glm1 <- glm(y ~ x1 + x2 + x3, family=binomial) glm0 <- glm(y ~ 1, family=binomial) anova(glm0,glm1,test="Chisq")
Modèles log-linéaires
?glm
(c'est moi qui les fabrique)
x <- sample( c(rep(0,3),rep(1,7)), 10, replace=T ) y <- sample( c(0,1), 10, replace=T )
La commande table permet d'avoir le résultat sous forme de tableau de contingence.
> table(x,y) y x 0 1 0 2 0 1 6 2
On peut faire un test d'indépendance en utilisant le Chi2.
> chisq.test(x,y, correct=T)
Pearson's Chi-squared test with Yates' continuity correction
data: x and y
X-squared = 0.0391, df = 1, p-value = 0.8433
Warning message:
Chi-squared approximation may be incorrect in: chisq.test(x, y, correct = T)R nous rappelle à juste titre que le Chi2 n'est qu'une approximation : dans ce cas précis, elle n'est probablement pas valable (si on a plus de 30 individus et si chaque case du tableau de contingence contient un nombre au moins égal à 5, on peut y aller les yeux fermés, mais ici...). On peut alors faire un test plus exact, celui de Fisher.
> fisher.test(t)
Fisher's Exact Test for Count Data
data: t
p-value = 1
alternative hypothesis: true odds ratio is not equal to 1
95 percent confidence interval:
0.03845334 Inf
sample estimates:
odds ratio
InfJe ne comprends pas pourquoi il donne souvent (prés d'une fois sur deux, d'après le graphique suivant) une p-valeur égale à 1.
N <- 10000
f <- NULL
c <- NULL
for (i in 1:N) {
x <- sample( c(rep(0,3),rep(1,7)), 10, replace=T )
y <- sample( c(0,1), 10, replace=T )
x <- factor(x, levels=c(0,1))
y <- factor(y, levels=c(0,1))
t <- table(x,y)
f <- append(f, fisher.test(t)$p.value)
c <- append(c, chisq.test(t)$p.value)
}
plot(sort(f), type='l')
points(sort(c), type='l', col='red')

Voici néanmoins un exemple où on n'a pas 1.
> x <- sample( c(rep(0,3),rep(1,7)), 10, replace=T )
> y <- sample( c(0,1), 10, replace=T )
> t <- table(x,y)
> t
y
x 0 1
0 4 1
1 1 4
> chisq.test(t)
Pearson's Chi-squared test with Yates' continuity correction
data: t
X-squared = 1.6, df = 1, p-value = 0.2059
Warning message:
Chi-squared approximation may be incorrect in: chisq.test(t)
> fisher.test(t)
Fisher's Exact Test for Count Data
data: t
p-value = 0.2063
alternative hypothesis: true odds ratio is not equal to 1
95 percent confidence interval:
0.45474 968.76176
sample estimates:
odds ratio
10.9072Calculons notre propre p-valeur à l'aide d'une simulation.
x <- sample( c(rep(0,3),rep(1,7)), 10, replace=T )
y <- sample( c(0,1), 10, replace=T )
x <- factor(x, levels=c(0,1))
y <- factor(y, levels=c(0,1))
pValeur <- function (x,y, N=1000) {
x <- factor(x)
y <- factor(y)
s <- numeric(N)
for (i in 1:N) {
xx <- sample( x, length(x), replace=T )
yy <- sample( y, length(y), replace=T )
s[i] <- as.numeric(chisq.test(table(xx,yy))$statistic)
}
t <- table(x,y)
p <- sum( chisq.test(t)$statistic > s )/length(s)
if( p>.5 ) p <- 1-p
p
}
t <- table(x,y)
c( ChiSq = chisq.test(t)$p.value, Fisher = fisher.test(t)$p.value, MonteCarlo = pValeur(x,y) )
#Représentons maintenant nos trois p-valeurs sur un même graphique.
N <- 100
f <- NULL
c <- NULL
s <- NULL
for (i in 1:N) {
x <- sample( c(rep(0,3),rep(1,7)), 10, replace=T )
y <- sample( c(0,1), 10, replace=T )
x <- factor(x, levels=c(0,1))
y <- factor(y, levels=c(0,1))
t <- table(x,y)
f <- append(f, fisher.test(t)$p.value)
c <- append(c, chisq.test(t)$p.value)
s <- append(s, pValeur(x,y,100))
}
plot(sort(f), type='l')
points(sort(c), type='l', col='green')
points(sort(s), type='l', col='red')
# J'ai de TRÈS gros doutes sur la pertinence de mes calculs...
# A FAIRE
library(MASS) data(anorexia) A FAIRE : dessin coplot(Postwt ~ Prewt | Treat, data=anorexia) plot(Postwt ~ Prewt, col=(2:10)[Treat]) plot( Postwt - Prewt ~ Treat) A FAIRE : les traitements ont-ils la même efficacité ? ?aov A FAIRE : comprendre les exemples de ?bacteria
Avec une dizaine de variables :
data(biopsy)
Comprendre des formules du genre :
data(nlschools)
library(nlme)
nl1 <- nlschools
attach(nl1)
classMeans <- tapply(IQ, class, mean)
nl1$IQave <- classMeans[as.character(class)]
nl1$IQ <- nl1$IQ - nl1$IQave
detach()
cen <- c("IQ", "IQave", "SES")
nl1[cen] <- scale(nl1[cen], center = TRUE, scale = FALSE)
nl.lme <- lme(lang ~ IQ*COMB + IQave + SES,
random = ~ IQ | class, data = nl1)
summary(nl.lme)Test non paramétrique de la médiane
a <- runif(10, 0,1)
b <- runif(10, 0,5)
# On range les données dans un Data Frame
d <- data.frame( value = c(a,b),
type = c( rep("A",10),rep("B",10) ),
block = factor( c(1:10,1:10) ))
# test non paramétrique
t <- table( d$value > mean(d$value), d$type )
chisq.test(t) # p-value = 0.005
# Test paramétrique
anova(lm(value~type, data=d), test="F") # p-value = 0.0002
# Test non paramétrique
wilcox.test(d$value[d$type=="A"], d$value[d$type=="B"]) # p-value = 0.0001
# Kruskal--Wallis
kruskal.test(d$value ~ d$type)
friedman.test(d$value, d$type, d$block)
#
anova(lm(value~type+other, data=d), test="F")
Régression affine
summary(lm(y~x))
Régression vraiment linéaire (ou test sur l'annulation du coefficient)
summary(lm(y~-1+x))
Graphiques (attention, il y en a plusieurs !!!)
plot( lm(y~x), ask=T )
ou
op=par(mfrow=c(3,2)) plot( lm(y~x) ) par(op)
(les trois premiers sont faciles à comprendre ; le troisième est un QQplot des résidus, pour vérifier leur normalité ; le quatrième permet de comparer la variance expliquée et la variance résiduelle ; le dernier donne la distance de Cook, ie, la distance entre les paramètres estimés avec ou sans le point, afin de repérer les points aberrants).
Régression et analyse de la variance ???
anova(lm( y ~ x )) anova(lm( y ~ x+z )) anova(lm( y ~ x+z+w ))
Régression polynomiale, recherche du degré du polynôme.
anova(lm( y ~ x + poly(z,2) + w ), lm( y ~ x + poly(z,3) + w ) )
Ecriture du modèle : on utilise des << + >> quand il n'y a pas d'interaction et des << * >> quand (on pense qu') il y en a. Un point signifie "toutes les autres variables du data frame" :
y~.
Lecture des résultats
?anova ?aov # idem, avec une interface différente ?summary ?plot(..., ask=T) ?effects ?predict ?lm.influence ?glm
Comparaison de moyennes à l'aide de permutations.
x <- c(40,40,41)
y <- c(42,43,45)
t.test(x,y)
N <- 10000
mx <- NULL
my <- NULL
for (i in 1:N) {
v <- sample( c(x,y), replace=F )
x1 <- v[1:length(x)]
y1 <- v[length(x)+1:length(y)]
mx <- append(mx, mean(x1))
my <- append(my, mean(y1))
}
pValue <- function (x, m) {
p <- sum(x<=m)/length(x)
if( p>.5 ) p <- sum(x>=m)/length(x)
2*p
}On trouve :
> pValue( mx, mean(x) ) [1] 0.0934 > pValue( my, mean(y) ) [1] 0.0934
Alors qu'en faisant des permutations avec remplacement, (A FAIRE : comprendre quelle est la différence, au niveau de l'interprétation du résultat) on obtiendrait :
> pValue( mx, mean(x) ) [1] 0.1834 > pValue( my, mean(y) ) [1] 0.2432
On peut représenter cela graphiquement
myPlot <- function (x,m) {
x <- sort(x)
plot( x ~ seq(0,1,length=length(x)), type="l", lwd=3 )
confidence <- .05
xx <- x[ (N*confidence/2) : (N - N*confidence/2) ]
points( xx ~ seq(confidence/2, 1-confidence/2, length=length(xx)), type="l", col="green", lwd=3)
abline(m,0, col="red")
p <- sum(x<=m)/length(x)
if( p>.5 ) p <- sum(x<m)/length(x)
points( p,m, col='red', pch=4, lwd=2 )
}
myPlot( mx, mean(x) )
*Voici le graphique que l'on obtiendrait avec des échantillons normaux standard de 50 individus chacun.
*
A titre de comparaison, le test de Student nous donne :
> t.test(x,y)
Welch Two Sample t-test
data: x and y
t = -3.182, df = 2.56, p-value = 0.06215
alternative hypothesis: true difference in means is not equal to 0
95 percent confidence interval:
-6.3143919 0.3143919
sample estimates:
mean of x mean of y
40.33333 43.33333Dans tous les cas, la conclusion est la même : on ne rejette pas l'hypothèse nulle << les deux moyennes sont égales >>.
----------------------
vocabulaire
Factorial design : on a variables qualitatives et on représente le sésultat de l'expérience par un tableau de contingences. On parle de << factorial design >> si aucune des cases de ce tableau n'est vide. On examine toutes ces cases, i.e., on ne se contente pas de regarder les effectgifs marginaux.
voici mes premières notes sur R
A FAIRE : les intégrer à celles ci-dessus.
Une suite d'objets, tous de même type (nombre, booléen, chaine de caractères).
Un tableau, avec plusieures colonnes ; chaque colonne est un vecteur et porte un titre, les colonnes peuvent être de types différents.
Régression linéaire
lm(y ~ x)
Régression résistante (il peut y avoir des données fausses).
rlm(y ~ x)
curve Tracer une courbe à l'aide de son équation
Regarder des données catégoriques.
> table(a>5) FALSE TRUE 10 7 > table(a) a 0 1 3 4 5 6 7 8 9 1 2 2 4 1 3 1 1 2
Histogramme (l'unité verticale est le nombre d'éléments).
> hist(a)
Histogramme (l'unité verticale est la proportion des éléments -- utile pour comparer deux histogrammes réalisés avec des populations différentes).
> hist(a, probability=TRUE)
Histogramme avec des choses en plus sur l'axe horizontal (???)
> hist(a) > rug(jitter(a))
Histogramme (on spécifie le nombre de classes).
> hist(a, breaks=10)
Histogramme (on spécifie les classes).
> hist(a, breaks=c(0,3,5,7,max(a)))
Frequency polygon
> tmp = hist(a)
> lines( c(min(tmp$breaks),tmp$mids,max(tmp$breaks)),
c(0,tmp$counts,0),
type="l")Densités
> density(a)
Call:
density(x = a)
Data: a (17 obs.); Bandwidth 'bw' = 1.143
x y
Min. :-3.430 Min. :0.0002538
1st Qu.: 0.535 1st Qu.:0.0165095
Median : 4.500 Median :0.0653932
Mean : 4.500 Mean :0.0629752
3rd Qu.: 8.465 3rd Qu.:0.1003278
Max. :12.430 Max. :0.1404533
> hist(a, probability=TRUE)
> points(density(a),type='l')
> points(density(a,bw=.1),type='l')Bar plots
> data(package='MASS')
> library("MASS")
> ?biopsy
> data(biopsy)
> barplot(table(biopsy$class, biopsy$V7), beside=TRUE)> barplot(table(biopsy$V7, biopsy$class))
Side-by-side boxplots
> boxplot( biopsy$V7 [biopsy$class == 'benign'],
biopsy$V7 [biopsy$class == 'malignant'])
> boxplot( biopsy$V7 ~ biopsy$class )Boxplots to compare different data.
> data(crabs) > boxplot( crabs$RW, crabs$CW)
We may have to scale them (so that they have mean 0 and standard deviation 1).
> boxplot( as.data.frame(scale(data.frame( crabs$RW, crabs$CW ))))
Strip charts : an alternative to box plots
> stripchart(crabs$RW[1:20])
Side by side strip charts (hint: put the data in a data frame?)
> stripchart(data.frame(crabs$RW, crabs$CW)) > stripchart(crabs)
Scatter Plot
> plot(crabs$CL, crabs$CW) DESSIN
Scatter plot with linear regression
> plot(crabs$CL, crabs$CW)
> lm( crabs$CL ~ crabs$CW )
Call:
lm(formula = crabs$CL ~ crabs$CW)
Coefficients:
(Intercept) crabs$CW
-0.6619 0.8998
> summary(lm( crabs$CL ~ crabs$CW ))
Call:
lm(formula = crabs$CL ~ crabs$CW)
Residuals:
Min 1Q Median 3Q Max
-1.6732 -0.4943 -0.1069 0.5915 1.6396
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) -0.661948 0.238574 -2.775 0.00606 **
crabs$CW 0.899846 0.006404 140.504 < 2e-16 ***
---
Signif. codes: 0 `***' 0.001 `**' 0.01 `*' 0.05 `.' 0.1 ` ' 1
Residual standard error: 0.7112 on 198 degrees of freedom
Multiple R-Squared: 0.9901, Adjusted R-squared: 0.99
F-statistic: 1.974e+04 on 1 and 198 DF, p-value: < 2.2e-16
> abline(lm( crabs$CL ~ crabs$CW ))Histogram of residuals
> lm.res = lm(crabs$CL ~ crabs$CW) > plot(residuals(lm.res)) # Non > hist(residuals(lm.res))
Residual plot : on fait une régression, puis on fait un "scatter plot" avec en abscisse les valeurs théoriques et en ordonnées les valeurs réelles.
A FAIRE DESSIN
On peut aussi représenter les valeurs calculées en abscisse et les valeurs résiduelles en ordonnée.
> ?lm > plot(lm.res$fitted.values, lm.res$residuals) > abline(0,0) DESSIN
Paired scatter plot
A FAIRE
Normal plot : en abscisse, les quantiles d'une distribution normale, en ordonnée, les quatiles effectivement observées. Si c'est une droite, les données sont normales.
> qqnorm(a); qqline(a)
> qqnorm(crabs$CL); qqline(crabs$CL)
> x = rnorm(100); qqnorm(x); qqline(x)
> x = runif(100); qqnorm(x); qqline(x)
Normal plot of residuals : do a regression and check if the residuals are normal.
> lm.res = lm(crabs$CL ~ crabs$CW) > qqnorm(residuals(lm.res)); qqline(residuals(lm.res))
> x = rnorm(1000) > y = exp(x) > qqnorm(y); qqline(y)
> y = x[x>0] > qqnorm(y); qqline(y)
> y = rexp(1000) > qqnorm(y); qqline(y)
Extraire un ou plusieurs éléments d'un vecteur :
> a[1] [1] 1 > a[1:3] [1] 1 4 9 > a[1,3,5] Error in a[1, 3, 5] : incorrect number of dimensions > a[c(1,3,5)] [1] 1 9 8
Extraire un ou plusieurs éléments d'un vecteur à l'aide de conditions booléennes.
> a>5 [1] FALSE FALSE TRUE TRUE TRUE TRUE FALSE FALSE TRUE FALSE FALSE TRUE [13] FALSE FALSE TRUE FALSE FALSE > a[a>5] [1] 9 6 8 6 6 9 7
Attention aux connecteurs logiques : ce sont & et |.
> a[a>3 & a<7] [1] 4 6 6 4 6 4 5 4 > a[a<3 | a>7] [1] 1 9 8 9 0 1
Pour la négation, c'est bien !
> a[!is.na(x)]
Compter le nombre d'éléments qui vérifient une condition.
> sum(a>5) [1] 7
Tri des données
> sort(a) [1] 0 1 1 3 3 4 4 4 4 5 6 6 6 7 8 9 9
Transformer des données numériques en données catégoriques. (voir aussi le paramètre break de la fonction hist)
> b = cut(a, breaks=c(0, 3, 7, 10))
> b
[1] (0,3] (3,7] (7,10] (3,7] (7,10] (3,7] (0,3] (3,7] (3,7] (3,7]
[11] (3,7] (7,10] <NA> (0,3] (3,7] (0,3] (3,7]
Levels: (0,3] (3,7] (7,10]
> table(b)
b
(0,3] (3,7] (7,10]
4 9 3
> ?factorMise à l'échelle des données pour les comparer : si le Data Frame foo contient deux colonnes numériques, on peut les mettre à la même échelle pour les comparer :
bar = as.data.frame(scale(bar))
Boucle
> for ( i in 1:100 ) { ... }Définition d'une fonction
> f = function(x) sqrt(var(x)) > f(a); sd(a) [1] 2.687115 [1] 2.687115
Définition d'une fonction plus longue : on ajoute des accolades ; la dernière valeur calculée est renvoyée.
foo = function(x) {
a = fivenum(x)
a[4] - a[2]
}On peut voir le code d'une fonction en tapant son nom, sans parenthèses.
> abline
function (a = NULL, b = NULL, h = NULL, v = NULL, reg = NULL,
coef = NULL, untf = FALSE, col = par("col"), lty = par("lty"),
lwd = NULL, ...)
{
if (!is.null(reg))
a <- reg
if (!is.null(a) && is.list(a)) {
temp <- as.vector(coefficients(a))
if (length(temp) == 1) {
a <- 0
b <- temp
}
else {
a <- temp[1]
b <- temp[2]
}
}
if (!is.null(coef)) {
a <- coef[1]
b <- coef[2]
}
.Internal(abline(a, b, h, v, untf, col, lty, lwd, ...))
invisible()
}
A FAIRE : les fonctions pnorm, qnorm. page 47
------------
Exemples de données
Données numériques univariées
data(aircondit)
Données numériques bivariées
data(cars)
plot(cars, xlab = "Speed (mph)", ylab = "Stopping distance (ft)",
las = 1)
lines(lowess(cars$speed, cars$dist, f = 2/3, iter = 3), col = "red")
title(main = "cars data")
plot(cars, xlab = "Speed (mph)", ylab = "Stopping distance (ft)",
las = 1, log = "xy")
title(main = "cars data (logarithmic scales)")
lines(lowess(cars$speed, cars$dist, f = 2/3, iter = 3), col = "red")
Autre exemple: trees
Autre exemple:
data(longley)
pairs(longley)Données catégoriques bivariées.
Autre exemple: Titanic
Données multivariées en partie numériques en partie catégoriques
?ToothGrotwth The Effect of Vitamin C on Tooth Growth in Guinea Pigs data(ToothGrowth)
Time series
data(nhtemp)
plot(nhtemp, main = "nhtemp data",
ylab = "Mean annual temperature in New Haven, CT (deg. F)")------------
Exemples
data(ToothGrowth)
coplot(len ~ dose | supp, data = ToothGrowth, panel = panel.smooth,
xlab = "ToothGrowth data: given is supplement type")
data(HairEyeColor)
## Full mosaic
mosaicplot(HairEyeColor)
## Aggregate over sex:
x <- apply(HairEyeColor, c(1, 2), sum)
x
mosaicplot(x, main = "Relation between hair and eye color")
data(cars)
plot(cars, xlab = "Speed (mph)", ylab = "Stopping distance (ft)",
las = 1)
lines(lowess(cars$speed, cars$dist, f = 2/3, iter = 3), col = "red")
title(main = "cars data")
plot(cars, xlab = "Speed (mph)", ylab = "Stopping distance (ft)",
las = 1, log = "xy")
title(main = "cars data (logarithmic scales)")
lines(lowess(cars$speed, cars$dist, f = 2/3, iter = 3), col = "red")
summary(fm1 <- lm(log(dist) ~ log(speed), data = cars))
opar <- par(mfrow = c(2, 2), oma = c(0, 0, 1.1, 0),
mar = c(4.1, 4.1, 2.1, 1.1))
plot(fm1)
par(opar)
## An example of polynomial regression
plot(cars, xlab = "Speed (mph)", ylab = "Stopping distance (ft)",
las = 1, xlim = c(0, 25))
d <- seq(0, 25, len = 200)
for(degree in 1:4) {
fm <- lm(dist ~ poly(speed, degree), data = cars)
assign(paste("cars", degree, sep="."), fm)
lines(d, predict(fm, data.frame(speed=d)), col = degree)
}
anova(cars.1, cars.2, cars.3, cars.4)
data(Titanic)
mosaicplot(Titanic, main = "Survival on the Titanic")
## Higher survival rates in children?
apply(Titanic, c(3, 4), sum)
## Higher survival rates in females?
apply(Titanic, c(2, 4), sum)
## Use loglm() in package `MASS' for further analysis ...
data(trees)
pairs(trees, panel = panel.smooth, main = "trees data")
plot(Volume ~ Girth, data = trees, log = "xy")
coplot(log(Volume) ~ log(Girth) | Height, data = trees,
panel = panel.smooth)
summary(fm1 <- lm(log(Volume) ~ log(Girth), data = trees))
summary(fm2 <- update(fm1, ~ . + log(Height), data = trees))
step(fm2)
## i.e. Volume ~= c * Height * Girth^2 seems reasonable
data(faithful)
f.tit <- "faithful data: Eruptions of Old Faithful"
ne60 <- round(e60 <- 60 * faithful$eruptions)
all.equal(e60, ne60) # relative diff. ~ 1/10000
table(zapsmall(abs(e60 - ne60))) # 0, 0.02 or 0.04
faithful$better.eruptions <- ne60 / 60
te <- table(ne60)
te[te >= 4] # (too) many multiples of 5 !
plot(names(te), te, type="h", main = f.tit, xlab = "Eruption time (sec)")
plot(faithful[, -3], main = f.tit,
xlab = "Eruption time (min)",
ylab = "Waiting time to next eruption (min)")
lines(lowess(faithful$eruptions, faithful$waiting, f = 2/3, iter = 3),
col = "red")
data(longley)
longley.x <- data.matrix(longley[, 1:6])
longley.y <- longley[, "Employed"]
pairs(longley, main = "longley data")
summary(fm1 <- lm(Employed ~ ., data = longley))
opar <- par(mfrow = c(2, 2), oma = c(0, 0, 1.1, 0),
mar = c(4.1, 4.1, 2.1, 1.1))
plot(fm1)
par(opar)
data(precip)
dotchart(precip[order(precip)], main = "precip data")
title(sub = "Average annual precipitation (in.)")
data(iris3)
dni3 <- dimnames(iris3)
ii <- data.frame(matrix(aperm(iris3, c(1,3,2)), ncol=4,
dimnames=list(NULL, sub(" L.",".Length",
sub(" W.",".Width", dni3[[2]])))),
Species = gl(3,50,lab=sub("S","s",sub("V","v",dni3[[3]]))))
data(iris)
all.equal(ii, iris) # TRUE
matplot((-4:5)^2, main = "Quadratic") # almost identical to plot(*)
sines <- outer(1:20, 1:4, function(x, y) sin(x / 20 * pi * y))
matplot(sines, pch = 1:4, type = "o", col = rainbow(ncol(sines)))
x <- 0:50/50
matplot(x, outer(x, 1:8, function(x, k) sin(k*pi * x)),
ylim = c(-2,2), type = "plobcsSh",
main= "matplot(,type = \"plobcsSh\" )")
## pch & type = vector of 1-chars :
matplot(x, outer(x, 1:4, function(x, k) sin(k*pi * x)),
pch = letters[1:4], type = c("b","p","o"))
data(iris) # is data.frame with `Species' factor
table(iris$Species)
iS <- iris$Species == "setosa"
iV <- iris$Species == "versicolor"
op <- par(bg = "bisque")
matplot(c(1, 8), c(0, 4.5), type= "n", xlab = "Length", ylab = "Width",
main = "Petal and Sepal Dimensions in Iris Blossoms")
matpoints(iris[iS,c(1,3)], iris[iS,c(2,4)], pch = "sS", col = c(2,4))
matpoints(iris[iV,c(1,3)], iris[iV,c(2,4)], pch = "vV", col = c(2,4))
legend(1, 4, c(" Setosa Petals", " Setosa Sepals",
"Versicolor Petals", "Versicolor Sepals"),
pch = "sSvV", col = rep(c(2,4), 2))
nam.var <- colnames(iris)[-5]
nam.spec <- as.character(iris[1+50*0:2, "Species"])
iris.S <- array(NA, dim = c(50,4,3), dimnames = list(NULL, nam.var, nam.spec))
for(i in 1:3) iris.S[,,i] <- data.matrix(iris[1:50+50*(i-1), -5])
matplot(iris.S[,"Petal.Length",], iris.S[,"Petal.Width",], pch="SCV",
col = rainbow(3, start = .8, end = .1),
sub = paste(c("S", "C", "V"), dimnames(iris.S)[[3]],
sep = "=", collapse= ", "),
main = "Fisher's Iris Data")------------
for(fn in methods("predict"))
cat(fn,":\n\t",deparse(args(get(fn))),"\n")revoir les histoires de conversion, à partir de la page 38. factor stack split unstack t rbind
outer paste
Je suis arrivé page 38.
loi multinomiale
(plusieures catégories d'évènements)
loi hypergéométrique loi binomiale Poisson
(tirage sans remise) (2 catégories d'évènements) (p=0 ou 1)
Loi normale
(chi2, student, fisher)
Chi_n^2 = somme des carrés de n lois normales
Pour n grand, Chi_n^2 ~ N(n, sqrt(2n))
Application : intervalle de confiance de l'écart-type.
Dessiner le graphe de la densité du Chi2, pour différents degrés de liberté.
Fisher
F_{n,m} = (Chi_n^2 / n) / (Chi_m^2 / m)
(test F de rapport de variances,
analyse de variance)
Student
T_n = N(0,1)/sqrt( Chi_n^2 / n )
= sqrt( F_{1,n} )
(test de comparaison de moyenne,
probabilité d'observer un écart donné à la moyenne,
estimation des paramètres d'une population)
C'est la distribution de la moyenne empirique d'un
échantillon de n individus d'une population de N>>n individus.
(moyenne empirique - moyenne réelle)/(variance empirique/sqrt(n)) ~ T_n
Pour n>1000, T_n ~ N(0,1)
Application : calcul d'intervalle de confiance pour
la moyenne.
/home/zoonek/spool/WWW/DOC/STAT/biol10.biol.umontreal.ca/BIO2041/pdf/Cours_05-Int_confiance.pdf
text affiche du texte à un endrot du dessin mtext affiche du texte dans la marge
Analyse en composantes principales.
a <- Seconde13[3:7] a <- as.matrix(a) a[is.na(a)]=10 cov(a) b <- eigen(cov(a), symmetric=TRUE) x <- b$vectors[,1] y <- b$vectors[,2] Il faut projeter orthogonalement sur Vect(x,y)
C'est déjà là...
library(mva) a <- Seconde13[3:7] a <- as.matrix(a) a[is.na(a)]=10 p <- princomp(a) p p$scores plot( p$scores[,2] ~ p$score[,1], pch=" " ) text( p$score[,1], p$score[,2], as.vector(Seconde13[,1]) ) plot(p$sdev, type="h")
EFFACER CE QUI PRECEDE
a <- Seconde13[3:7] a <- a - t( array( apply(a, 2, mean, na.rm=T), dim(t(a)) )) apply(a, 2, mean, na.rm=T) a <- as.matrix(a) a[is.na(a)]=0 a <- a / t( array( apply(a, 2, sd), dim(t(a)) )) apply(a, 2, sd) library(mva) p <- princomp(a)
# ACP : plot( p$scores[,2] ~ p$score[,1], pch=" " ) text( p$score[,1], p$score[,2], as.vector(Seconde13[,1]) )
# Les valeurs propres plot(p$sdev, type="h")
# Le cercle des covariances A FAIRE
A FAIRE : la même chose, mais à la main.
A FAIRE : comprendre les fonctions :
princomp prcomp factanal kmeans hclust plot.agnes Plots of an Agglomerative Hierarchical Clustering plot.diana Plots of a Divisive Hierarchical Clustering plot.mona Banner of Monothetic Divisive Hierarchical Clusterings plot.partition Plot of a Partition of the Data Set
MASS : Modern Applied Statistics with S (avec plein de jeux de données)
library(help=MASS) library(MASS) ...
Réseaux de neurones
library(help=nnet) library(nnet) ...
Séries temporelles
library(help=ts) library(ts) ...
Trois types de tableaux de nombres : valeurs d'une variable quatitative, tableau de contingence, tableau de présence-absence contenant des 0 et des 1 (sous R, ce dernier type de tableau est plutôt un tableau dont les colonnes sont des facteurs).
A FAIRE : différence entre corrélation et covariance (la covariance a une unité, pas la corrélation).
Le zoo des tests statistiques : A FAIRE
A FAIRE : le vocabulaire de la statistique est très mal conçu. Des méthodes similaires (au niveau technique ou au niveau des applications) portent des noms complètement différents. Essayer de résumer ce vocabulaire à l'aide d'un tableau.
Gauss-Markov Theorem: Least squares estimates of beta have the smallest variance among all linear unbiased estimates. (But it is not a good idea to restrict oneself to unbiased estimates...)
?by
Legend under the graph (not over...)
par("mar") # borders, see ?par
# [1] 5.1 4.1 4.1 2.1
# Now increase size of the bottom-border:
par(mar=c(10.1, 4.1, 4.1, 2.1))
# And set cpd=TRUE, so all plotting is clipped to the figure
# (not the plot) region:
par(xpd=TRUE)
# Your barplot:
bp <- barplot(1:3)
# Text for the legend:
legend.text <- c("cats", "dogs", "cows")
# And plot the legend below the existing plot:
legend(1,-0.5, legend.text, fill=heat.colors(length(legend.text)))
# Or much nicer, center the legend:
legend(mean(range(b)), -0.5, legend.text, xjust = 0.5,
fill=heat.colors(length(legend.text)))Same, horizontal.
## increase size of the bottom-border:
par(mar= c(6, 4, 4, 2) + .1)
## Set xpd=TRUE, so all plotting is clipped to the figure
## (not the plot) region:
par(xpd=TRUE)
## Your barplot:
bp <- barplot(1:3)
## Text for the legend:
legend.text <- c("cats", "dogs", "cows")
## And plot the legend below the existing plot -- centering it
legend(mean(range(bp)), -0.3, legend.text, xjust = 0.5,
fill=heat.colors(length(legend.text)), horiz = TRUE)Search for outliers, Mahalanobis distance
As I want to do some multivariate calibration using these data, I checked whether some multivariate outliers existed. I calculated Mahalanobis distances and did a qqplot(qchisq(ppoints(382),169),XMaha) where XMaha contained my Mahalanobis distances. The points on my QQ plot were nicely aligned onto a y=x line, so no outliers.
Beaux exemples de graphiques :
http://www.visualmining.com/examples/index.html
?plotmath
Les symboles mathématiques dans les graphiques
Mon problème avec outer() est décrit dans la FAQ : If you have a
function that cannot handle two vectors but can handle two scalars,
then you can still use outer() but you will need to wrap your
function up first, to simulate vectorized behavior. Suppose your
function is
foo <- function(x, y, happy) {
stopifnot(length(x) == 1, length(y) == 1) # scalars only!
(x + y) * happy
}
If you define the general function
wrapper <- function(x, y, my.fun, ...) {
sapply(seq(along=x), FUN = function(i) my.fun(x[i], y[i], ...))
}
then you can use outer() by writing, e.g.,
outer(1:4, 1:2, FUN = wrapper, my.fun = foo, happy = 10)
GAM (from the FAQ):
7.17 Are GAMs implemented in R?
There is a gam() function for Generalized Additive Models in package
mgcv, but it is not an exact clone of what is described in the White
Book (no lo() for example). Package gss can fit spline-based GAMs
too. And if you can accept regression splines you can use glm(). For
gaussian GAMs you can use bruto() from package mda.
mixtures
CART
library(help=rparts)
GAM
EDA: Exploratory Data Analysis
OLS: Ordinary Least Squares
RSS: Residual Sum of Squares (la quantité que l'on cherche à minimiser avec les OLS)
Comment mentir avec des statistiques
ex: faire plein de tests afin d'augmenter le risque d'erreur de type 1
ex: prendre des hypothèses non symétriques par ce qu'on veut que le
résultat soit dans un sens.
Vérifier l'indépendance de deux variables à l'aide d'un chi-plot.
Andrew curve ???
?image
(to plot a matrix, in image analysis)
?read.pnm
(to read it from a file)
Fitting a distribution to a given law, and finding the parameters.
library(MASS)
?fitdistr
Calculs numériques
Minimiser une fonction :
?optim
?lnm
Trouver une racine (une seule variable)
?uniroot
A FAIRE : modifier plot.lm
pour ajouter qqline au qqplot des résidus
et ajouter un lissage des résidus.
Clustering (variante de l'ACP?)
library(cluster)
clusplot(a, pam(a, 3)$clustering, diss = FALSE, plotchar = TRUE, color = TRUE)
data(votes.repub)
votes.diss <- daisy(votes.repub)
votes.clus <- pam(votes.diss, 2, diss = TRUE)$clustering
clusplot(votes.diss, votes.clus, diss = TRUE, shade = TRUE)
data(iris)
iris.x <- iris[, 1:4]
clusplot(iris.x, pam(iris.x, 3)$clustering, diss = FALSE,
plotchar = TRUE, color = TRUE)
mentionner refcard.pdf
Pour les graphiques, renvoyer au document en espagnol (même si on ne parle pas cette langue -- je n'en comprends pas un mot, mais j'ai trouvé le document très instructif)
séries temporelles
fréquences cumulées
Intervalle de confiance pour les paramètres d'une régression
ANOVA et régression :
quand on fait une régression,
variance de Y = variance expliquée par X + variance résiduelle
Le Chi2 est un test courant filtrant, pour prévenir que l'on a collecté assez de données pour rejeter H0
Le Chi2 d'indépendance (deux variables qualitatives)
Parler aussi de processus (Markov, Poisson)
file:///home/zoonek/spool/WWW/DOC/STAT/rfv.insa-lyon.fr/%257Ejolion/STAT/poly.html
Séries temporelles : représenter les points de coordonnées (x_n, x_{n+k}), où k est un entier fixé. Par exemple, avec un mauvais générateur aléatoire. Ca sert à repérer de l'ordre dans le chaos apparent.
Tests fishériens ou tests de permutations
Exemple : analyse d'image
Exemple : analyse de son
Réseaux de neurones
ACP après avoir remplacé les variables par le rang (de Pearson)
Tracer des suites, ou des fonctions de distribution discrètes :
lines(..., type='b')
conditional logistic regression
library(nlme)
Contrasts in linear models
weibull survival analysis
Mixture Analysis: les données proviennent de deux modèles (ou plus), mais on ne sait pas à quel modèle se ratachent les individus (typiquement : l'histogramme des données a deux pics).
Classification à l'aide d'une droite (on a deux variables
quantitatives, un variable qualitative à deux valeurs, on fait un
diagramme de dispersion sur les deux premières variables, on
représente les individus par un symbole différent selon la valeur de
la dernière variable, on cherche un droite qui sépare le plan en
deux, selon la valeur de ce paramètre.
Contour plot / surface représentant la densité d'une v.a. bivariée.
KalmanLike(ts) Kalman Filtering
(c'est une régression linéaire incrémentale).
> From <@uconnvm.uconn.edu:kent@darwin.eeb.uconn.edu> Wed Jan 7 12:51 GMT 1998 > To: ripley@stats.ox.ac.uk (Prof Brian Ripley) > Cc: s-news@utstat.toronto.edu > Subject: Re: Summary of Robust Regression Algorithms > From: kent@darwin.eeb.uconn.edu (Kent E. Holsinger) > > >>>>> "Brian" == Prof Brian Ripley <ripley@stats.ox.ac.uk> writes: > > Brian> My best example of this not knowing the literature is the > Brian> Hauck-Donner (1977) phenomenon: a small t-value in a > Brian> logistic regression indicates either an insignificant OR a > Brian> very significant effect, but step.glm assumes the first, > Brian> and I bet few users of glm() stop to think. > > All right I confess. This is a new one for me. Could some one explain > the Hauck-Donner effect to me? I understand that the t-values from > glm() are a Wald approximation and may not be terribly reliable, but I > don't understand how a small t-value could indicate "either an > insignificant OR a very significant effect." > > Thanks for the help. It's finding gems like these that make this group > so extraordinarily valuable.
There is a description in V&R2, pp. 237-8., given below. I guess I was teasing people to look up Hauck-Donner phenomenon in our index. (I seem to remember this was new to my co-author too, so you were in good company. This is why it is such a good example of a fact which would be useful to know but hardly anyone does. Don't ask me how I knew: I only know that I first saw this in about 1980.)
There is a little-known phenomenon for binomial GLMs that was pointed out by Hauck & Donner (1977: JASA 72:851-3). The standard errors and t values derive from the Wald approximation to the log-likelihood, obtained by expanding the log-likelihood in a second-order Taylor expansion at the maximum likelihood estimates. If there are some \hat\beta_i which are large, the curvature of the log-likelihood at \hat{\vec{\beta}} can be much less than near \beta_i = 0, and so the Wald approximation underestimates the change in log-likelihood on setting \beta_i = 0. This happens in such a way that as |\hat\beta_i| \to \infty, the t statistic tends to zero. Thus highly significant coefficients according to the likelihood ratio test may have non-significant t ratios.
To expand a little, if |t| is small it can EITHER mean than the Taylor expansion works and hence the likelihood ratio statistic is small OR that |\hat\beta_i| is very large, the approximation is poor and the likelihood ratio statistic is large. (I was using `significant' as meaning practically important.) But we can only tell if |\hat\beta_i| is large by looking at the curvature at \beta_i=0, not at |\hat\beta_i|. This really does happen: from later on in V&R2:
There is one fairly common circumstance in which both convergence problems and the Hauck-Donner phenomenon (and trouble with \sfn{step}) can occur. This is when the fitted probabilities are extremely close to zero or one. Consider a medical diagnosis problem with thousands of cases and around fifty binary explanatory variables (which may arise from coding fewer categorical factors); one of these indicators is rarely true but always indicates that the disease is present. Then the fitted probabilities of cases with that indicator should be one, which can only be achieved by taking \hat\beta_i = \infty. The result from \sfn{glm} will be warnings and an estimated coefficient of around +/- 10 [and an insignificant t value].
That was based on a real-life example, which prompted me to write what is now stepAIC. Once I had that to try, I found lots of examples.
Brian Ripley
Voir aussi :
http://www.r-project.org/nocvs/mail/r-help/2002/1487.html
NA
Missing values: use CART or logistic regression to investigate and impute. Do not discard missing data.
Do not categorize continuous variables during data collection.
Dummy variables for categorical predictors.
Model validation
data splitting leave-out-one cross-validation (jackknife): take all the observations but one fit the model predict the missing value and compare with the actual one iterate Cross-validation: idem, but split the data into 10 groups, fit the model with all the groups but one, predict its values, compare. Iterate with the other nine groups. Iterate, with other groups. Bootstrap: fit the model on a bootstrap sample You get an idea of the bias/variance of the parameters. The optimism (=bias) is overestimated: multiply bay .0632 (rule of thumb)
Interpretation
The model gives associations, not causal relations
Pour les données cartographiques, on peut aussi utiliser GMT (qui n'a rien à voir avec R).
http://gmt.soest.hawaii.edu/
AIC
library(MASS); ?stepAIC
Interfaçage avec des bases de données
Estimation d'un paramètre à l'aide d'un estimateur/test/intervalle de confiance
?str
data(LifeCycleSavings)
summary(lm.SR <- lm(sr ~ pop15 + pop75 + dpi + ddpi,
data = LifeCycleSavings),
corr = TRUE)
str(lmI <- lm.influence(lm.SR))Hachures:
m <- matrix(runif(30), ncol=5)
barplot(m, beside=FALSE, col=rep(c("white", "light green", "pink"), 2),
border=rep(c("white", "red"), 3), horiz=TRUE,
xlim=c(0, 6), axes=FALSE)
par(new=TRUE)
barplot(m, beside=FALSE, col="blue",
density=rep(c(10, 5, -1), 2),
angle=rep(c(45, -45, 0), 2), horiz=TRUE,
xlim=c(0, 6))
par(fg='white', bg='black', col='white', col.axis='white', col.lab='white', col.main='white', col.sub='white');plot(0,0)
SPC: Statistics Process Control
On peut faire ses propres QQplots pour comparer deux distributions.
x <- rexp(100)
qqplot( qexp(ppoints(100)), sort(x) )
abline(0,1)
qqplot : expliquer comment lire un QQplot.
En particulier : distribution décentrée,
distribution plus dispersée qu'une normale, moins dispersée, etc.
?split
?lapply
?by
Comparer (graphiquement) la loi de Student avec la loi normale.
Donner un exemple d'utilisation de la commande legend
(c'est une commande séparée).
(par exemple quand il y a plusieurs courbes, de couleurs différentes)
?persp
?contour
Pour représenter une loi normale multivariée
Estimateurs/Tests/Intervalles de confiance
Régression: estimation des corfficients/tests sur les coefs/IC des coefs/IC des valeurs prédites/comparaison de modèles
Histogramme avec des barres coloriées (ou hachurées)
Avec des ombres
Colorier entre deux courbes (écrire une fonction pour ça).
x <- runif(20)
y <- 1-2*x+.1*rnorm(20)
res <- lm(y~x)
plot(y~x)
new <- data.frame( x=seq(0,1,length=21) )
p <- predict(res, new, interval='prediction')
for (l in seq(0,1,length=100)){
points( (l*p[,2]+(1-l)*p[,3]) ~ new$x, type='l', col="red" )
}
p <- predict(res, new, interval='confidence')
for (l in seq(0,1,length=100)){
points( (l*p[,2]+(1-l)*p[,3]) ~ new$x, type='l', col="green" )
}
points(y~x)
p <- predict(res, new)
points( p ~ new$x, type='l' )
?rug
(en dessous d'un histogramme ou d'un boxplot)vcd: Visualization if categorical data.
Andrew curve
Chiplot
ftable : table de contingence en dim >2.
Libraries: VR complements MASS wave* (wavelets) ade4 MVA.
Comment mentir avec des chiffres
ne pas mettre de 0 sur le graphique confusion longueur/aire.
RFS plot : side by side, sort(yhat)~index and sort(y)~index (donner un exemple où y est quantitatif mais discret).
Rgraphviz (dans bioconductor)
?cancor
Syntaxe de R
RTFM/Documentation (?, help.search, exampl, demo, library(), library(help=...), data)
Les différents types de données
Saisie des données
Manipulations des types de données
Matrices et algèbre linéaire
Structures de contrôle
Fonctions (elles n'ont pas d'effet de bord : en clair, il n'y a pas de variables globales)
Persistance
library
R CMD ...
Objets
ESS
sweave
Graphiques avec R
Commandes de base
Options (détailler)
Mise en garde : je suis incompétent
Le Zoo des lois de probabilités
Données univariées
paramètres statistiques (mean, var, sd, median, quartiles, mad, etc.)
dotplot
scatterplot
boxplot
stem-and-leaf plot
histogramme
rug
symetry plot (mentionner le test de Wilcoxon)
qqplot (mentionner le test de Shapiro)
ces quatre graphiques sur une seule figure
Transformations des données, boxcox
(données ordonnées)
barplot : données qualitatives
pie
Tests statistiques : théorie
Zoo des tests statistiques
(dans un premier paragraphe, lister tous les tests,
si possible dans un tableau)
Méthodes non paramétriques
robustesse
résistance
breakdown (la proportion d'individus que l'on peut modifier sans parvenir à envoyer les estimateurs à l'infini).
Représentation graphiques de données multivariées (sans la régression)
deux variables quantitatives
une variable quantitative, une qualitative
deux variables qualitatives
Plusieurs variables quantitatives : pairs
Plusieurs variables quantitatives : treillis
Trois variables quantitatives : ternary plot
Plus de deux variables : découpage en tranches (treillis)
starplots
Représentation graphiques de données multivariées (suite)
ACP
Analyse en composantes robustes
Aggrégation autour des centres mobiles
Classification hiérarchique (dendogramme)
A FAIRE : une ou plusieurs des variables sont qualitatives
(analyse factorielle discriminante, des correspondances simples/multiples, etc.)
Régression : PLAN A REVOIR
Régression
Avant de commencer la régression : lissage, quelques méthodes robustes
Avant de commencer la régression : transformations
Régression linéaire : définition
Comparaison avec l'ACP
Résidus : graphiques pour explorer une régression
(les résidus vus comme une seule variable (boxplot, hist, etc.)
(les résidus en fonction de la prédiction, en fonction d'une variable indépendante (très mauvaise idée: prendre l'exemple d'un modèle constant y~1), de la variable indépendante)
Résidus non normaux
Hétéroscédasticité des résidus
Influence, leverage (?), distance de Cook
Autocorrélation
Régression multiple
Graphiques pour explorer une régression multiple
Multicolinéarité
Régression curvilinéaire
Régression non linéaire
Exemple : un problème de classification (régression linéaire, curvilinéaire, plus proches voisins)
Tests statistiques sur une régression
Lecture du résultat d'une régression : première présentation de l'Anova
A FAIRE :
Régression robuste (WLS,IRLS)
Modèle linéaire généralisé
Régression logistique
Anova
Motivation
Calculs détaillés sur un exemple, à la main
Calculs détaillés sur un exemple, avec R
Régression et sommes de carrés : une autre motivation de l'Anova
Anova et comparaison de modèles
Séries temporellesA FAIRE:
Nulle part je n'ai parlé de processus (mais j'utilise parfois le terme...) La malédiction de la dimension
A FAIRE Lack of fit: if there are several Y-values for a given X-value, compare y~x with y~factor(x)
A FAIRE
(how to ensure symetry, equal spread, straightness, additive structure)
(a power plot which is a straight line with slope m suggests a power transformation whose exponent is 1-m.)
1. Transformation for equal spread. (Location/spread plot) Deux variables, une quantitative, une qualitative. Cela revient à répartir les individus dans différentes classes. On représente log(IQR) en fonction de log(median).
2. Transformation plot for symetry. (xU+xL)/2-M en fonction de ((xU-M)^2+(M-xL)^2)/(4M), où M est la médiane et xU, xL des quartiles (inférieurs et supérieurs).
3. Transformation plot for straightness. y-My-C(x-Mx) en fonction de C^2(x-Mx)^2/(2My) où Mx, My sont les médianes de x et y, C pente de la régression (que l'on ne connait pas).
4. Transformation for additivity (diagnostic plot). Two-way table. Par des DL, on remarque que si y_ij^p = m + a_i + b_j, alors y_ij = D + A_j + B_j + (1-p) A_i A_i / D. On trace donc y_ij-(m+a_i+b_j) en fonction de a_i b_j / m où y_ij=m+a_i+b_j est un un modèle additif (qui ne convient donc pas).
(Il faudra faire une partie entière sur les transformations) Transformations: boxcox (in MASS), choose a simple exponent from the graph, such as 1/2, 1/3, 1/4, etc. (If 1 is in the confidence interval, there is no good reason to transform the data) (very sensitive to outliers) (The transformation should not be extreme: if you get 5, blame the outliers) Other transformations: logit (for proportions, percentages), Fisher's Z transform (for correlations) Do not remove the intercept: it acts as a sink for the effect of unincluded variables Do not remove lower order terms even if they are not statistically significant: the prevent against additive modifications
Voici comment on peut procéder pour faire une régression (à des fins de prédiction), face à un exemple réel.
1. Regarder les variables une par une, regarder s'il y a des valeurs atypiques (si elles résultent d'erreurs, les corriger), transformer éventuellement les variables pour les rapprocher de la normalité.
2. Regarder s'il y a des valeurs manquantes, regarder si elles apparaissent par hasard ou si elles obéissent à un motif, essayer de les inférer.
3. Regarder les variables dans leur ensemble (pairs, xgobi, princomp), deux par deux (partial effect plots), avec des treillis (Y ~ X1 | X2) rpart).
4. Choisir le modèle. C'est le point le plus délicat : faut-il utiliser toutes les variables ? Les dépendances entre les variables sont-elles linéaires ? Faut-il des termes d'interaction ?
5. Faire différents tests, tant numériques que graphiques : résidus, observations influentes, tests divers (annulation des coefficients, anova pour comparer des modèles). On prendra garde à ne pas faire trop de tests : plus on en fait, plus le risque d'erreur est grand... Modifier le modèle en conséquence.
6. Interpréter les résultats, à l'aide des coefficients et de tous les graphiques précédents.
A FAIRE : partial effect plots.
n <- 100 x1 <- rnorm(n) x2 <- rnorm(n) x3 <- rnorm(n) y <- x1 - x2*x2 + 2*x3 + rnorm(n) pairs(cbind(y,x1,x2))

y3 <- lm(y~x3)$residuals
x13 <- lm(x1~x3)$residuals
x23 <- lm(x2~x3)$residuals
plot( y3 ~ x13,
xlab="x1 sans les effets linéaires de x3",
ylab="y sans les effets linéaires de x3" )
library(lattice) bwplot( ~ y3 | equal.count(x13), layout=c(1,6) )

bwplot( ~ y3 | equal.count(x13) + equal.count(x23) )

Missing values : CART or logistic regression Imputing missing values : transcan
Risk of overfitting : use the bootstrap to estimate the optimism (=bias) and substract it from R^2.
Regression trees MARS neural networks (For small data sets or high noise level, complex methods are not justified: stick to LS.)
ST Support Trees SOTA Self Organizing Tree Algorithm RN Relevance Networks CAST Clustering Affinity Search Technique SOM Self Organizing Maps FOM Figures Of Merit RELAGGS (relational learning algorithms) ROC ROC curve (Receiver Operating Characteristic) Prob(detection)~Prob(false alarm) area under curve Les courbes ROC sont utilisées pour examiner la sensibilité d'un classificateur qui renvoie une réponse qualitative après avoir comparé une pré-réponse quantitative avec un seuil. On trace la proportion de bonnes réponses en fonction du seuil (???) AUC: Area Under Curve. C'est ce que l'on mesure sur une courbe ROC.
On tire à pile ou face 1000 fois et on regarde comment évolue la fréquence de « pile ». On constate qu'elle « tend » vers 0.5.
n <- 1000 x <- runif(n) x <- x>.5 x <- cumsum(x)/(1:n) plot(x, ylim=c(0,1), type="l")

Idem, sur une échelle logarithmique
plot(x, ylim=c(0,1), type="l", log="x")
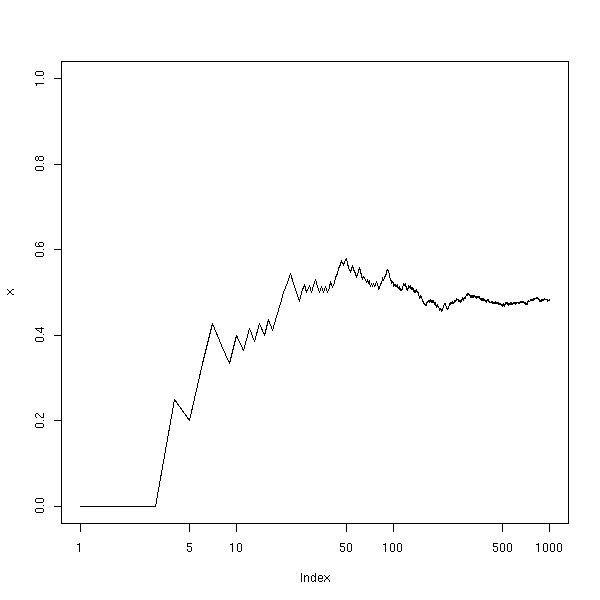
Simulation de 20 séries de 10 tirages aléatoires d'une variable normale.
N <- 10 n <- 20 x <- rnorm(n*N) y <- rep(1:n, N) boxplot(x ~ y)

par( mfrow = c(4,5) )
for (i in 1:n) {
hist(x[ y==i ])
}
Maintenant, 20 séries de 100 tirages.
N <- 100 n <- 20 x <- rnorm(n*N) y <- rep(1:n, N) boxplot(x ~ y)

par( mfrow = c(4,5) )
for (i in 1:n) {
hist(x[ y==i ])
}
20 séries de 3 tirages ; on met en évidence les séries pour lesquelles la moyenne réelle n'est pas entre les valeurs extrèmes.
N <- 3 n <- 20 x <- rnorm(n*N) y <- rep(1:n, N) m <- matrix(x, nrow=N, byrow=T) c <- apply(m,2,min)>0 | apply(m,2,max)<0 boxplot(x ~ y, col=c(0,6)[1+c])

Echantillons gaussiens de taille de plus en plus grande.
x <- rnorm(10+100+1000+10000+100000) y <- c( rep(5,10), rep(4,100), rep(3,1000), rep(2,10000), rep(1,100000)) boxplot(x~y, horizontal=T, axes=F) axis(1) axis(2, 1:5, c(10,100,1000,10000,100000) )

Si on prend des données numériques << réelles >>, leur premier chiffre suit une loi de Benford.
x <- 1:9 y <- log(1+1/x)/log(10) plot(y~x, type="h")

Vérifions-le à l'aide de données boursières. Commençons par récupérer des cours de bourse et des volumes échangés de quelques 130 titres.
rm A for i in AB C DE FI JN OR S TZ do GET 'http://fr.finance.yahoo.com/q?s=@SRD_'$i'.PA&f=snlcvi' >> A done perl -n -l -e 'm#e.gif[^>]*>([0-9,]+)<# && print$1' A | perl -p -e 's/\.//g; s/,/./g' > Cours.txt perl -n -l -e 'm#.*>([0-9.]*?)</font.*Graphique# && print "$1"' A | perl -p -e 's/\.//g' > Volume.txt
Récupérons les données sous R
a <- read.table("Cours.txt")
a <- a[a>0]
a <- as.vector(a)
a <- floor(a*10^-floor(log(a)/log(10)))
hist(a, probability=T)
points((x+.5), y, type='h', col='red', lwd=3)
chisq.test(table(factor(a)), p=y) # p-value = 0.06
a <- read.table("Volume.txt")
a <- a[a>0]
a <- as.vector(a)
a <- floor(a*10^-floor(log(a)/log(10)))
hist(a, probability=T)
points((x+.5), y, type='h', col='red', lwd=3)
chisq.test(table(factor(a)), p=y) # p-value = 0.85
Voici une justification théorique de ce fait :
http://www.math-info.univ-paris5.fr/smel/articles/benford/cadre_benford.html
On se donne deux vaiid normales X et Y de moyenne 0 et de variance 1 et on essaye de trouver a, b et c de sorte que (aX, bY+cX) ait la bonne variance.
> rnorm2 <- function(n, mean=c(0,0), cov=c(1,1,0)) {
a <- sqrt(cov[1])
c <- cov[3]/a
b <- sqrt(cov[2]-c^2)
x <- rnorm(n)
y <- rnorm(n)
print(a); print(b); print(c);
cbind( mean[1]+a*x, mean[2]+b*y+c*x )
}
> cov(rnorm2(10000, cov=c(1,5,2)))
[1] 1
[1] 1
[1] 2
[,1] [,2]
[1,] 1.015107 2.034396
[2,] 2.034396 5.069416Voir aussi :
library(MASS) ?mvrnorm library(help=mvtnorm) library(combinat) ?rmultinomial library(normix) ?rmultinom
plot(sort(runif(100)))
for (i in 1:1000) {
lines( sort(runif(100)) )
}
On peut tracer les bornes sup et inf de ces choses-là.
n <- 1000 m <- 200 a <- matrix( runif(n*m), c(n,m) ) b <- apply(a, 1, sort) c <- apply(b, 1, range) plot( c[1,], type="l" ) lines( c[2,] ) n <- 10 m <- 200 a <- matrix( runif(n*m), c(n,m) ) b <- apply(a, 1, sort) c <- apply(b, 1, range) lines( c[1,] ) lines( c[2,] )

Test de Mantel : mesure la corrélation de deux matrices de distances (par exemple, une distance génétique et une distance géographique). On procède ainsi : on calcule le coefficient de corrélation entre les deux matrices (qui n'a pas grand sens, car les valeurs d'une même matrice ne sont pas indépendantes), on applique une permutation sur les lignes et les colonnes d'une des matrices et on recalcule le coefficient, on recommence plusieurs centaines de fois, on regarde enfin où se trouve la valeur initiale par rapport aux valeurs ultérieures.
Muticolinéarité : calculer le R^2 de x~. pour chaque x, s'il est supérieur à 95%, c'est inquiétant.
Quand on manipule plusieurs variables statistiques, disons X, Y, Z, T, on essaye souvent d'exprimer leur distribution conjointe comme un produit de distributions plus simples. Dans le cas le plus trivial,
P(X,Y,Z,T) = P(X) * P(Y) * P(Z) * P(T).
Mais, on général, on a des relations de dépendance entre ces variables, par exemple
P(X,Y,Z,T) = P(X) * P(Y) * P(Z|X,Y) * P(T|Z).
On peut représenter de telles relations par un un graphe orienté (DAG : Directed Acyclic Graph).
X Y
\ /
\ /
\ /
Z
|
|
|
T
(si je savais mieux dessiner, il y aurait des flèches vers le bas).
C'est une mesure de la dissimilarité de deux distributions de probabilité.
D(f,g) = Intégrale( log(f/g) * f ).
On remarquera que ça n'est pas symétrique.
08_tests.txt : LR test
Vincent Zoonekynd
<zoonek@math.jussieu.fr>
latest modification on Wed Oct 13 22:33:29 BST 2004