
The French version of this document is no longer maintained: be sure to check the more up-to-date English version.
Ondelettes
Graphes
Chaines de Markov
MCMC : simulation de Monte-Carlo à l'aide de chaines de Markov
Données géographiques (GIS)
Génétique
A CLASSER
(Ce chapitre regroupe tous les sujets que je n'ai pas évoqués et sur lesquels je ne connais rien : n'en attendez rien d'autre qu'une liste de titres, sans aucune explication).
A FAIRE
(c'est important)
wavethresh
waveslim
Rwave
URL: li.pdf
Survey on Wavelet Applications in Data Mining
SIGKDD Explorations
Idée de base : analyse de Fourrier.
Décomposer une fonction périodique en une somme de fonctions
sinusoïdales, chacune indiquant ce qui se passe à une échelle
donnée.
Problème : cela suppose que le signal étudié est stationnaire.
On voudrait en fait décomposer le signal le long de deux échelles :
d'une part la fréquence, d'autre part la localisation.
Une idée consiste à découper le signal en petits morceaux, supposer
que le signal sur chacun de ces morceaux est stationnaire, et en
faire une décomposition de Fourrier.
Les ondelettes proposent une autre solution.
De même que l'analyse de Fourrier consistait à partir d'une fonction
(le sinus), la changer d'échelle (sin(x), sin(2x), sin(3x), etc.),
remarquer qu'on obtient une base orthonormale d'un certain espace de
fonctions, et décomposer les fonctions selon cette base ; de même,
on peut partir d'une fonction, la changer d'échelle et de
localisation (on lui applique à la fois des homothéties et des
translations, on obtient donc une famille de fonctions dépendant de
deux paramètres), regarder si c'est une base ortonormale (ça n'est
pas automatique) et, si c'est le cas, décomposer la fonction à
étudier selon cette base.
Plus précisément, on cherche une fonction psi telle que la famille
( psi(2^j x - k), j, k \in Z )
forme une base orthonormale de L^2(R).
Voici quelques exemples de telles fonctions :
L'ondelette de Haar:
H(x) = 1 dans [0,.5]
-1 dans [.5,1]
0 ailleurs
A FAIRE : les ondelettes de Daubechies
(Il y en a tout une famille.)
(Il existe une recette pour fabriquer de telles ondelettes,
consistant à partir d'une fonction "auto-similaire", i.e., vérifiant
une équation de la forme phi(x) = Somme( a_k phi(2x-k) ), puis à
considérer psi(x) = Somme( \bar a_{1-k} phi(2x-k) ) : pour certaines
valeurs des a_k, psi convient (convergence, orthogonalité, etc.).
C'est cette condition d'auto-similarité qui explique l'aspect
accidenté des ondelettes.
On dit que phi est l'ondelette père et psi l'ondelette mère.
Si on n'utilise pas cette construction, on peut n'avoir qu'une
ondelette mère et pas d'ondelette père.)
DWT: Discrete Wavelet Transform
MRA: Multi-Resolution Analysis
On ne travaille pas toujours dans L^2(R), mais dans des espaces plus
petits. En particulier, étant donnée une ondelette père phi, on peut
construire une filtration de L^2(R) (i.e., une suite croissante de
sous-espaces de L^2(R))
... V(-2) \subset V(-1) \subset V(0) \subset V(1) \subset V(2) ...
telle que
f(x) \in V(n) \ssi f(2x) \in V(n+1)
en prenant pour V(0) le sous-espace engendré par les
phi(x-k), k \in Z.
En termes d'ondelettes mères, V(1) est engendré par les
psi(2^j x - k), j <= 1, k \in Z.
On considère aussi souvent les espaces W(n), engendrés par les
psi(2^n x - k), k \in Z.
On a
V(1) = V(0) \oplus W(1)
= \bigoplus _{ j \leq 1 } W(j).
Exemple de décomposition en ondelettes de Haar de la fonction (7 5 1 9)
("algorithme pyramidal")
Resolution Approximations Detail coefficients
----------------------------------------------
4 7 5 1 9
2 6 5 -1 4
1 5.5 -0.5
Haar(7 5 1 9) = (5.5, -.5, -1, 4)
Complexité : O(n log n) pour la FFT contre O(n) pour les ondelettes.
Applications statistiques :
Gestion des données à l'aide de la structure arborescente des
transformées en ondelettes, en particulier pour accélérer la
recherche de changement de tendance dans des séries temporelles
sans qu'il soit nécessaire de récupérer la série entière (TSA,
Trend and Surprise Abstraction)
On peut utiliser la même idée pour indexer des images ou des
fichiers audio.
Plus simplement, on peut choisir de retenir les k premiers
coefficients et les utiliser pour indexer les données.
On peut appliquer une décomposition en composantes principales
aux coefficients de résolution "moyenne" d'images (on oubie les
autres coefficients, ce qui accélère beaucoup les calculs), afin
de les classer.
On peut utiliser les ondelettes pour le nettoyage des données
(retrait du bruit et réduction de la dimension) en ne gardant que
les coefficients les plus élevés -- c'est le principe de la
compression d'images, JPEG ou ondelettes.
WaveShrink: effectuer la transformée en ondelettes, réduire les
coefficients (en appliquant un seuil (dont le choix est délicat)
-- ou quelque chose de plus lisse), prendre la transformée
inverse.
On peut aussi les utiliser pour réduire la dimension des données :
après transformation en ondelettes, ne garder que les coefficients
les plus importants (c'est juste un changement de base, comme
l'analyse en composantes principales) ; après transformation en
ondelettes, séparer les coefficients (par exemple selon la
fréquence), faire une analyse en composantes principales dans
chacune de ces bandes (on pourra retenir un nombre différent de
dimensions dans certaines bandes, voire en oublier certaines).
Les ondelettes permettent aussi de transformer un problème de
régression non paramétrique en une régression paramétrique, dont
la résolution sera affinée de manière itérative. En fait,
généralement, les coefficients les plus important correspondent au
signal que l'on cherche à reconstruire et les moins importants au
bruit : on peut ne retenir que les premiers (comme pour le
nettoyage des données ou la compression).
Autres applications, en vrac : clustering (WaveCluster),
classification (exemple : classification des pixels dans une
image).
Les ondelettes son aussi adaptées au calcul distribué, très à la
mode avec les Clusters.
A FAIRE : terminer de lire li.pdf (je suis arrivé page 13).
Les bibliothèques suivantes permettent de manipuler des graphes :
graph Construction de graphes, lecture/écriture de fichiers GXL Rgraphviz Dessin de graphes sna Sociologie ergm
Exemples de graphes : les arbres phylogénétiques, les citations qui relient des articles de recherche, voies métaboliques, régulations entre protéines/gènes, réseaux sociaux (connaissances, échanges de seringues, relations amoureuses, appels téléphoniques, etc.).
Pour un problème donné, on peut considérer plusieurs graphes différents. Prenons l'exemple du web.
1. Sommets : pages web
Arrête d'un sommet A vers sun sommet B s'il y a un lien de A à B.
2. Sommets : pages web
Arrête de A à B si A est un préfixe de B
(ce graphe est un arbre, qui montre la structure des sites)
3. Sommets : pages web
Arrête entre A et B s'il existe un document C avec des liens vers
A et B.
On peut pondérer les arrêtes en fonction du nombre de tels documents C.
4. Sommets : pages web
Arrête entre A et B si A et B contiennent un lien vers un même
document C.
On peut pondérer les arrêtes en fonction du nombre de tels documents C.
5. Sommets : {pages web}x{1,2}
Arrête de (A,1) à (B,2) si A contient un lien vers B.
C'est un graphe bipartite.Toujours pour le Web, on peut exprimer la rang d'une page à l'aide des valeurs propres ou des vecteurs propres de la matrice d'adjacence ou de la matrice de Markov de certains de ces graphes.
Quelques documents qui détaillent tout cela :
http://www.research.att.com/%7Evolinsky/Graphs/program.html
Exemples de graphes :
# L'un des graphes est trop gros...
library(Rgraphviz)
data(graphExamples)
op <- par(mfrow=c(6,3))
for (g in graphExamples) {
try( plot(g) )
}
par(op)Quelques graphes au hasard :
library(Rgraphviz)
data(graphExamples)
op <- par(mfrow=c(3,3))
set.seed(2)
for (i in 1:9) {
try( plot(randomGraph(LETTERS[1:10], 1, .3)) )
}
par(op)
op <- par(mfrow=c(3,3))
for (i in 1:9) {
try( plot(randomGraph(LETTERS[1:10], 1, .5)) )
}
par(op)
op <- par(mfrow=c(3,3))
for (i in 1:9) {
try( plot(randomGraph(LETTERS[1:10], 1, .8)) )
}
par(op)
Quelques méthodes :
> g <- randomGraph(LETTERS[1:10], 1, .8)
> g
A graph with undirected edges
Number of Nodes = 10
Number of Edges = 28
> edgeMatrix(g)
A1 A2 A3 A4 A5 A6 A7 C2 C3 C4 C5 C6 C7 E3 E4 E5 E6 E7 F4 F5 F6 F7 G5 G6 G7 H6 H7 I7
from 1 1 1 1 1 1 1 3 3 3 3 3 3 5 5 5 5 5 6 6 6 6 7 7 7 8 8 9
to 3 5 6 7 8 9 10 5 6 7 8 9 10 6 7 8 9 10 7 8 9 10 8 9 10 9 10 10
> numNodes(g)
[1] 10
> isConnected(g)
[1] FALSE
> connComp(g)
[[1]]
[1] "A" "C" "E" "F" "G" "H" "I" "J"
[[2]]
[1] "B"
[[3]]
[1] "D"
> acc(g, "A")
C E F G H I J
1 1 1 1 1 1 1
> acc(g, "B")
named numeric(0)
> degree(g)
A B C D E F G H I J
7 0 7 0 7 7 7 7 7 7
> edges(g)
$A
[1] "C" "E" "F" "G" "H" "I" "J"
$B
character(0)
$C
[1] "A" "E" "F" "G" "H" "I" "J"
$D
character(0)
$E
[1] "A" "C" "F" "G" "H" "I" "J"
$F
[1] "A" "C" "E" "G" "H" "I" "J"
$G
[1] "A" "C" "E" "F" "H" "I" "J"
$H
[1] "A" "C" "E" "F" "G" "I" "J"
$I
[1] "A" "C" "E" "F" "G" "H" "J"
$J
[1] "A" "C" "E" "F" "G" "H" "I"
> complement(g)
A graph with undirected edges
Number of Nodes = 10
Number of Edges = 17La documentation :
?"graph-class" ?"graphNEL-class"
La matrice d'incidence d'un tel graphe :
n <- numNodes(g)
m <- matrix(0, nr=n, nc=n, dimnames=list(nodes(g),nodes(g)))
e <- edges(g)
for(i in nodes(g)) {
for (j in e[[i]]) {
m[i,j] <- 1
}
}
mConstruction d'un graphe à l'aide de sa matrice d'incidence :
op <- par(mfrow=c(2,2))
for (a in 1:4) {
n <- 10
V <- LETTERS[1:n]
m <- matrix(sample(0:1,n*n,replace=T,prob=c(.8,.2)), nr=n, nc=n, dimnames=list(V,V))
m <- m + t(m)
m <- 1 - (m-1)*(m-2)/2
m <- m - diag(diag(m))
e <- vector("list", length=n)
names(e) <- V
for (i in 1:n) {
e[[i]] <- list( edges = which(m[i,]==1) ) # Les numéros des sommets, pas leurs noms
}
g <- new("graphNEL", nodes=V, edgeL=e)
plot(g)
}
par(op)
A FAIRE
Sur la notion de graphe aléatoire d'Erdos-Renyi (il y a une arrête entre les sommets A et B avec une probabilité p ; ces graphes présentent un changement de phase : (quand le nombre de sonnets est grand) quand le nombre moyen d'arrêtes qui part d'un sommet est inférieur à 1, il y a beaucoup de petites composantes connexes, quand ce nombre est supérieur à 1, il y en a une énorme) et ses défauts (le coefficient de transitivité (clustering coefficient), i.e., la probabilité que A et C soient liés sachant que A,B et B,C le sont, est plus élevée dans les réseaux réels ; la distribution de la valence des sommets n'est pas poissonienne).
arXiv:cond-mat/0202208
A FAIRE (reprendre l'exemple de l'araignée)
Très souvent, on constate que le vecteur de probabilité à l'instant t se stabilise quand t devient grand et ne dépend pas du point de départ.
A FAIRE : exemple
En fait, la distribution stationnaire n'est pas toujours unique. Par exemple, quand on peut séparer les états en deux classes et qu'il est impossible de passer de l'une à l'autre : on aura alors une distribution stationnaire différente pour chaque classe.
A FAIRE : un exemple graphique
Au niveau de la matrice de transitions, cela signifie qu'on peut changer l'ordre des états afin qu'elle soit diagonale par blocs.
A FAIRE : un exemple de matrice. (une situation dans laquelle il est nécessaire de réordonner les états)
On dit qu'une chaine de Markov est irréductible quand, étant donnés deux états a et b, il est toujours possible d'aller de a à b, éventuellement en plusieurs étapes.
Un temps de retour à un état e, c'est un entier t tel que
P( X(t)=e | X(0)=e ).
Une chaine de Markov est apériodique si, pour tout état, le pgcd de ses temps de retour est égal à un.
Par exemple, si on peut séparer les états en deux classes, et si les transitions vont toujours d'une classe vers l'autre, les temps de retour sont toujours pairs : une telle chaine n'est pas apériodique.
Si une chaine est irréductible et apériodique, alors elle possède une unique distribution stationnaire et on peut utiliser la chaine de Markov pour intégrer par rapport à cette distribution.
1/N * Somme( f(X_n), n=1..N ) ---> Intégrale( f * p )
A FAIRE : comprendre
Une chaine de Markov de matrice de transition P et de distribution stationnaire p est inversible (en anglais : reversible) si
P(y|x)p(x) = P(x|y)p(y)
L'algorithme est décrit très clairement ici :
http://students.washington.edu/~fkrogsta/bayes/stat538.pdf
Pour plus de détails, demander "MCMC metropolis hastings" à Google.
Motivations Tirages au hasard Calculs d'intégrales (espérance : moyenne, variance, etc.) Méthodes bayesiennes Exemples d'espaces Algorithme de Métropolis, implémentation Généralisations et variantes Correction de Hastings Echantilloneur de Gibbs Métropolis-Hastings-Green Applications Phylogénie Alignement multiple
On cherche à tirer au hasard un élément parmi la population (x1,x2,...,xn) selon la distribution (p1,p2,...,pn). Une manière compliquée de procéder consiste à construire une chaine de Markov dont c'est la distribution limite.
Pour des exemples simplistes, ça semble vraiment tordu, mais on se retrouve parfois face à des espaces (ou univers) finis de taille gigantesque : par exemple, lors d'une étude phylogénétique, on peut vouloir faire des tirages dans l'ensemble des arbres à 1000 feuilles.
Si on voulait un tirage selon une distribution équiprobable, on pourrait s'en tirer plus facilement : mais, afin de faire des simulations, on aimerait que les arbres qui décrivent assez bien l'évolution des espèces étudiées aient une probabilité plus importante.
Mais il y a encore pire : en général, on ne sait pas calculer cette probabilité. Pour chaque arbre a, on sait calculer un score S(a) et la probabilité d'un arbre a0 est
score(a0)
P(a0) = ----------------
Somme score(a)
aOr, cette somme est beaucoup trop grande pour être calculée.
Les chaines de Markov vont nous permettre de nous promener dans l'espace des arbres, en passant d'un arbre à un arbre "voisin" (pour une notion de voisinage qui reste à définir). Les échantillons qu'on obtiendra ainsi ne seront bien évidemment pas indépendants, mais ils suffiront néanmoins pour effectuer quelques simulations et calculer certaines quantités associées à la distribution de probabilité sur notre espace d'arbres.
On rencontre ces mesures de probabilité non équiprobables quand on applique des méthodes bayesiennes : quand on cherche à calculer la valeur d'un paramètre d'un modèle qui décrive le mieux les données observées, on veut souvent un seul résultat. Mais ça n'est pas très naturel, car ce résultat sera, par nature, imprécis : on le complète donc par un intervalle de confiance ou une variance. Mais cette variance n'est directement interprétable que si la distribution du paramètre estimé est normale -- ce qui n'est probablement pas le cas. Une manière de préciser le résultat consiste à donner, non pas une valeur du paramètre, mais toute sa distribution : si on veut une seule valeur, on prendra le mode (MLE) ou la moyenne de cette distribution ; si on veut des intervalles de confiance, on pourra facilement les calculer, quel que soit le risque. Cette distribution de probabilité est dite "a posteriori".
Si l'univers est complexe (par exemple, un ensemble d'arbres ou de graphes), on peut difficilement décrire cette distribution de probabilité. Mais ça n'est pas grave, car on n'a pas besoin de la décrire : si on peut faire des tirages aléatoires selon cette distribution, on pourra en déduire ce qui nous intéresse (le mode, la moyenne, des "intervalles" de confiance, etc.). Les méthodes que nous allons présenter (simulation de Monte Carlo à l'aide de chaines de Markov, MCMC) permettent justement d'effectuer ces tirages.
La méthode de Monte-Carlo permet de calculer une intégrale
Intégrale( f(x), x \in I )
de la manière suivante : prendre x1, x2, ..., xn au hasard dans I et calculer
1 --- Somme f(X_k) N k=1..N
Si l'ensemble d'intégration I est un intervalle fermé de la droite réelle, on prendra les x1 au hasard suivant une loi uniforme. Par contre, s'il s'agit de la droite réelle tout entière, ça n'est plus possible (il n'y a pas de loi de probabilité uniforme sur R tout entier) ; on essaiera d'écrire la fonction à intégrer sous la forme f(x) = g(x) p(x) où p est la densité d'une mesure de probabilité sur R. Il suffira alors de prendre les xi au hasard suivant la loi de p et de calculer
1 --- Somme g(X_k) N k=1..N
Si on compare avec les méthodes d'intégration numérique auxquelles on est habitué (rectangles, trapèzes, etc.), ça n'a pas l'air très efficace -- en particulier en dimension un, i.e., sur la droite réelle. C'est en dimension élevée que l'intégration de Monte-Carlo devient plus intéressante. Imaginons que l'on veuille calculer l'intégrale d'une fonction f de 1000 variables dans l'hypercube [0,1]^1000. La généralisation de la méthode des rectangles suggère d'évaluer la fonction f en chacun des coins de cet hypercube et de faire la moyenne. Le problème, c'est que cet hypercube a 2^1000 coins. C'est trop. L'intégration de Monte-Carlo se contentera d'évaluer f en quelques centaines de points au hasard dans cet hypercube et de faire la moyenne : c'est un peu moins précis, mais on a un résultat avant que le Soleil ne s'éteigne...
Cet exemple peut sembler tirer par les cheveux : rencontre-t-on vraiment des fonction de 1000 variables dans la vie de tous les jours ? Est-on réellement amené à calculer des intégrales sur de tels espaces dans des problèmes concrets ?
Eh bien oui. Face à un arbre phylogénétique retraçant l'évolution d'un millier d'espèces, on peut chercher le nombre de mutation sur chacune des branches, i.e., la longueur de ces branches. L'ensemble de ces longueurs (il y en a quelques milliers) est un point dans un espace de dimension élevée. En fait, l'espace est bien pire que ça, car on voudra considérer tous les arbres...
Mais veut-on réellement calculer des intégrales sur de tels espaces ? Eh bien oui : moyenne (espérance), variance, probabilités peuvent s'écrire sous forme d'intégrale. Par exemple, la probabilité que l'on soit dans un certain ensemble H0 d'hypothèses, sachant qu'on a observé O s'écrit
P(H \in H0) = intégrale( P(H|O), H \in H0 )
P(O|H) P(H)
= intégrale( ------------- , H \in H0 )
P(O)Autre exemple, la probabilité d'observer O' sachant qu'on a déjà observé O s'écrit
P(O'|O) = Intégrale( P(O'|H) * P(H|O), H )
Voici un algorithme un peu trop simpliste (c'est juste l'intégration de Monte-Carlo) :
Pour i = 1 à N: Choisir Xi au hasard suivant p
Le problème, c'est que p peut être arbitraire et, en particulier, difficile à calculer. Dans les exemples qui vont nous intéresser, l'univers sera fini mais très grand et les probabilités seront de la forme
w(a)
P(X=a) = ------------------
Somme( w(b), b )On peut calculer le numérateur, mais le dénominateur, somme sur tous les élements de l'univers, ne se calcule pas.
Au lieu de cela, on peut essayer :
Choisir X0 au hasard. Pour i = 1 à N: Choisir Xi parmi les voisins de X(i-1)
Cela revient en fait à mettre une chaine de Markov sur notre espace, qui permet de passer d'un élément x(i) à un élément voisin x(i-1). Cette manière de choisir un point voisin s'appelle un noyau de transition.
Il y a un "léger" problème, c'est qu'on n'utilise plus p : réintroduisons-le.
Choisir X0 au hasard. Pour i = 1 à N: Choisir X' parmi les voisins de X(i-1) Poser Xi = X(i-1) ou Xi = X' (choisir selon p).
Mais comment fait-on pour "choisir selon p" ? D'après la forme de p mentionnée plus haut, on ne sait pas calculer la probabilité d'un élément, mais par contre, on sait calculer le quotient de deux probabilités. On peut donc procéder ainsi.
# Algorithme de Métropolis
Choisir X0 au hasard.
Pour i = 1 à N:
Choisir X' parmi les voisins de X(i-1)
Choisir un nombre u au hasard dans [0,1]
P(X')
Si u < -----------
P(X(i-1))
Alors
X(i) = X'
Sinon
X(i) = X(i-1)Cet algorithme convient (i.e., la chaine de Markov a bien la distribution limite souhaitée -- modulo quelques hypothèses sur le noyau de transition) si la chaine de Markov est symétrique, i.e., si la probabilité de passer de X à Y est la même que celle de passer de Y à X. Si ce n'est pas le cas, il convient de corriger l'algorithme.
# Algorithme de Métropolis-Hastings
Choisir X0 au hasard.
Pour i = 1 à N:
Choisir X' parmi les voisins de X(i-1)
Choisir un nombre u au hasard dans [0,1]
P( X(i-1) | X' ) P(X')
Si u < ------------------ -----------
P( X' | X(i-1) ) P(X(i-1))
Alors
X(i) = X'
Sinon
X(i) = X(i-1)On peut aussi avoir quelques scrupules, car les Xi ne sont pas indépendants -- en fait, ça n'est pas grave.
P(X | X') ne dépend que de la distance entre X et X'.
Dans l'algorithme, on peut changer
Choisir X' parmi les voisins de X(i-1)
en
Choisir X' au hasard.
Si la distribution selon laquelle on choisit X' a des queues plus épaisses que la distribution cible, ça marchera très bien -- mais en cas contraire, ça marchera vraiment très mal...
Dans un espace de dimension n, on peut traiter les coordonnées une à une : à chaque étape, on ne chage qu'une seule des coordonnées.
La littérature affirme souvent que c'est plus simple, plus rudimentaire que l'algorithme de Metropolis-Hastings : ça me semble plus complexe, et ça suppose qu'on connait somme toute beaucoup de choses sur la distribution.
L'échantilloneur de Gibbs est un cas particulier de la méthode précédente, qui traitait les coondonnées une à une : on impose que le noyau de transition soit la probabilité conditionnelle
P(xi | xj, j!=i)
Ca veut dire qu'il faut connaitre ces probabilités conditionnelles...
Considérons par exemple deux variables X1, X2, normales, de moyenne nulle, de variance 1, de covariance r. On a alors
X1|X2 ~ N(r*X2, 1-r^2)
et de même pour X2. A chaque étape de l'algorithme, on modifie soit X1, soit X2. Le chemin est donc "manhattanien".
my.gibbs <- function (x0=c(0,0), N=20, r=.5, plot.it=T) {
res <- matrix(NA, nr=N, nc=2)
res[1,] <- c(0,0)
for (i in seq(2,N-1,by=2)) {
x1 <- res[i-1,1]
x2 <- res[i-1,2]
res[i,2] <- x2
# Normalement, on devrait prendre un nouveau point n'importe comment
# et l'accepter ou le rejeter -- pour simplifier, j'en prend directement
# un suivant la probabilité marginale.
x1 <- rnorm(1, r*x2, sd=sqrt(1-r^2))
res[i,1] <- x1
res[i+1,1] <- x1
x2 <- rnorm(1, r*x1, sd=sqrt(1-r^2))
res[i+1,2] <- x2
}
if (plot.it) {
plot(res, type='l', xlab="x1", ylab="x2", main="Gibbs sampler")
points(res, pch=16)
invisible(res)
} else {
res
}
}
my.gibbs()
my.gibbs(N=1000)
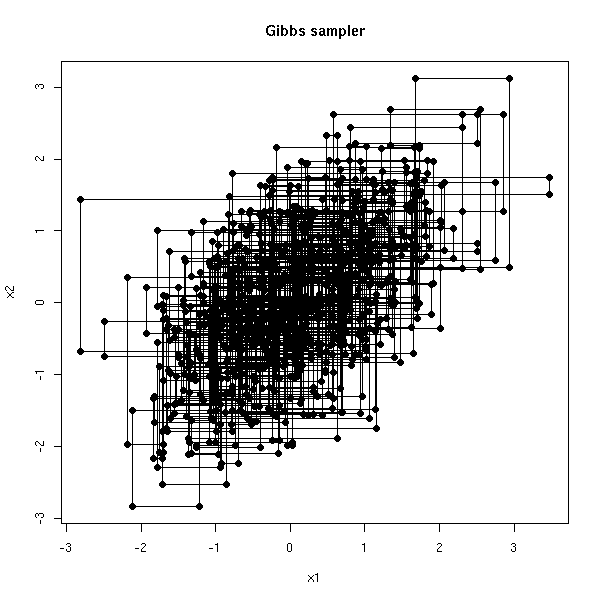
Avec l'algorithme de Métropolis-Hastings, une trajectoire ressemblerait plutôt à
r <- my.gibbs(N=40,plot.it=F)[2*(1:20),]
plot(r, type='l', xlab="x1", ylab="x2",
main="Trajectoire d'une simulation de Métropolis (presque)")
points(r, pch=16)
r <- my.gibbs(N=2000,plot.it=F)[2*(1:1000),]
plot(r, type='l', xlab="x1", ylab="x2",
main="Trajectoire d'une simulation de Métropolis (presque)")
points(r, pch=16)
A FAIRE : un exemple qui montre que l'allure globale des trajectoires ne dépend pas du point de départ (dessiner deux trajectoires, avec des départs complètement différents, de couleurs différentes).
On étudie une famille de protéines (une protéine, c'est une suite d'acides aminés, i.e., une chaine de caractères écrites à l'aide d'un alphabet de 20 lettres) et on cherche un "motif" commun à cette famille, présent dans chacune des séquences.
Pour simplifier, on suppose qu'on cherche un motif de longueur fixée a priori L. On commence par prendre un segment de longueur L sur chacune des séquences : l'ensemble de ces segments forme une première approximation, très mauvaise, de notre motif.
Ensuite, à chaque itération, on choisit l'une des séquences et on regarde toutes les positions possibles pour la fenêtre de largeur L : on choisit la meilleure (variante : en choisir une au hasard, avec une probabilité proportionnelle à son score ; variante : recuit simulé).
Quelques problèmes peuvent se poser : il faut choisir la largeur de la fenêtre ; en lançant l'algorithme plusieurs fois, on n'obtient pas toujours la même chose : s'agit-il de motifs semblables ? complètement différents ? qui se chevauchent ?
Voir :
http://www.msci.memphis.edu/%7Egiri/compbio/papers/gibbs2.pdf
On se place en dimension deux ; le modèle s'écrit
X = f(Y1,Y2)
où Y1 et Y2 sont indépendants. On a observé X et on cherche à prédire Y1 à partir de X. Par exemple :
Y1 = l'étalon est porteur d'un gène certain gène Y2 = la jument est porteuse de ce gène X = la progéniture est porteuse de ce gène
On va utiliser l'échantilloneur de Gibbs pour prédire à la fois Y1 et Y2.
Ici, Y1 et Y2 sont les paramètres du modèle : dans ces méthodes, paramètres et variables aléatoires jouent des rôles similaires.
On commence par fixer des valeurs aléatoires de Y1 et Y2. On calcule ensuite
P(X | Y1,Y2) * P(Y1 | Y2)
P(Y1 | X,Y2) = ---------------------------
P(X | Y2)
P(X | Y1,Y2) * P(Y1)
= ---------------------- (car Y1 et Y2 sont indépendants)
P(X | Y2)(c'est possible, car on connait le modèle), ce qui permet de tirer au hasard une nouvelle valeur de Y1.
On recommence avec Y2.
On itère de nombreuses fois : au bout d'un certain moment, on a atteint une phase stationnaire et les valeurs de Y1 et Y2 qu'on obtient correspondent à la distribution a posteriori de ces paramètres : on peut en déduire le mode (ou la moyenne, ou la médiane, on n'importe quelle autre information intéressante) de Y1.
A FAIRE : donner un exemple de calcul, sous R.
Exercice : implémenter un échantilloneur de Gibbs pour trouver la moyenne et la variance d'un échantillon sensé suivre une loi normale.
A FAIRE P(moyenne | X, variance) = ... P(variance | X, moyenne) = ...
C'est une généralisation de Métropolis-Hastings dans laquelle on remplace les densités par des mesures de probabilité : cela généralise toutes les variantes précédentes, y compris l'échantilloneur de Gibbs.
Le choix du noyau de transition (i.e., du "voisinage") est délicat.
D'une part, il faut que le taux d'acceptation soit suffisemment élevé pour ne pas rester coincé en un point. Pour cela, il fait que les "voisins" soient assez "proches".
D'autre part, il faut pouvoir atteindre assez rapidement des états assez éloignés : pour cela, il faut que les "voisins" ne soient pas trop "proches".
Pour voir si ces problèmes apparaissent ou pas, pour choisir ou paramétrer le noyau de transition, il convient de faire des dessins (en dimension un : série temporelle et ACF (ou PACF)). Un coup d'oeil à l'ACF permet aussi de construire des variables indépendantes, en prenant X(n), X(n+k), X(n+2k), X(n+3k), etc., avec k suffisemment grand pour que l'autocorrélation cor(X(n),X(n+k)) soit suffisemment faible.
Il convient aussi de faire plusieurs simulations, avec des points de départ différents, afin de voir si ça converge ou pas, et surtout au bout de combien de temps ça converge. On peut aussi faire une simulation beaucoup plus longue, afin de vérifier que ça a bien convergé.
N <- 200
K <- 5
res <- matrix(NA, nr=N, nc=K)
for (i in 1:K) {
r <- my.gibbs(x0=runif(2,-1,1), N=N, plot.it=F)
res[,i] <- apply(r,1,cumsum)[1,] / 1:N
}
matplot(res, type='l', lty=1,
ylab="Estimateur", xlab="Longueur de la simulation",
main="Gibbs sampler")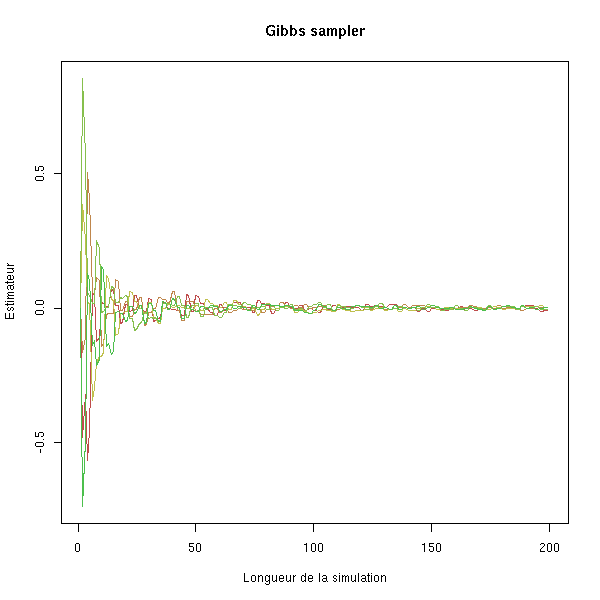
Généralement, on retire le début de la série temporelle, jusqu'à ce que la chaine de Markov ait atteint sa distribution stationnaire.
A FAIRE : ça porte un nom En anglais : burn-in
En R :
library(ts)
MH <- function (N = 1000,
voisin = function (x) { rnorm(1,x,1) },
p = dnorm, # Distribution de probabilité à simuler
q = function (x,y) { 1 } # Correction de Hastings
) {
res <- rep(NA,N)
x <- 0
for (i in 1:N) {
y <- voisin(x)
u <- runif(1)
if ( u < q(x,y)/q(y,x) * p(y)/p(x) ) {
x <- y
}
res[i] <- x
}
ts(res)
}
x1 <- ts(rnorm(1000))
x2 <- MH()
x3 <- MH(voisin = function (x) { rnorm(1,x,.01) })
x4 <- MH(voisin = function (x) { rnorm(1,x,50) })
op <- par(mfrow=c(4,1))
plot(x1, main="Hasard")
plot(x2, main="MCMC")
plot(x3, main="MCMC, voisins trop proches")
plot(x4, main="MCMC, voisins trop lointains")
par(op)
op <- par(mfrow=c(2,2)) qqnorm(x1, main="Hasard"); qqline(x1); qqnorm(x2, main="MCMC"); qqline(x2); qqnorm(x3, main="MCMC, voisins trop proches"); qqline(x3); qqnorm(x4, main="MCMC, voisins trop lointains"); qqline(x4) par(op)

op <- par(mfrow=c(2,2)) hist(x1, col='light blue', probability=T, main="Hasard") curve(dnorm(x),col='red',lwd=3, add=T) hist(x2, col='light blue', probability=T, main="MCMC") curve(dnorm(x),col='red',lwd=3, add=T) hist(x3, col='light blue', probability=T, main="MCMC, voisins trop proches") curve(dnorm(x),col='red',lwd=3, add=T) hist(x4, col='light blue', probability=T, main="MCMC, voisins trop lointains") curve(dnorm(x),col='red',lwd=3, add=T) par(op)

op <- par(mfrow=c(4,1)) acf(x1, main="Hasard") acf(x2, main="MCMC") acf(x3, main="MCMC, voisins trop proches") acf(x4, main="MCMC, voisins trop lointains") par(op)

op <- par(mfrow=c(4,1)) pacf(x1, main="Hasard") pacf(x2, main="MCMC") pacf(x3, main="MCMC, voisins trop proches") pacf(x4, main="MCMC, voisins trop lointains") par(op)

(Pour une chaine de Markov d'ordre 1, c'est normal : il n'y a que la première autocorrélation à regarder)
Exemple d'application à des calculs d'intégrales (on devrait trouver 1 : c'est la variance d'une loi normale standard) :
> mean(x1^2) [1] 0.960904 > mean(x2^2) [1] 1.004407 > mean(x3^2) [1] 0.01575253 > mean(x4^2) [1] 0.9143307
Autre exemple : on peut utiliser cette chaine de Markov pour avoir des vaiid suivant la loi en question. On ne peut pas prendre directement les valeurs obtenues car, justement, elles ne sont pas indépendantes (c'est l'idée générale des chaines de Markov).
N <- 3000 x <- MH(N=N) plot(x[2:N]~x[2:N-1],xlab='x(i)',ylab='x(i+1)') abline(0,1,col='red')

(La ligne horizontale provient du rejet de certaines des valeurs : on se retrouve alors avec deux valeurs identiques successives.)
Par contre, si on prend une valeur sur 10 ou 100, ça a vraiment l'air aléatoire.
N <- 100000 x <- MH(N=N) x <- x[100:length(x)] # burn-in x <- x[seq(1,length(x),by=50)] N <- length(x) plot(x[2:N]~x[2:N-1],xlab='x(i)',ylab='x(i+1)') abline(0,1,col='red')

op <- par(mfrow=c(4,1)) plot(ts(x)) acf(x) pacf(x) spectrum(x) par(op)

Dans les algorithmes MCMC, on peut modifier la probabilité d'acceptation d'un nouvel état au cours du temps : au début, on est très tolérant et on accepte des état qu'on ne devrait pas accepter et, progressivement, on se rapproche de la probabilité d'acceptation de Métropolis-Hastings.
Cela permet d'éviter certaines pathologies de la chaine de Markov (irréductibilité, etc.).
On peut détourner cette méthode pour un but complètement différent : maximiser (ou minimiser) une certaine quantité, par exemple une log-vraissemblance. L'algorithme (qu'on appelle le "recuit simulé") est le suivant :
1. Prendre une valeur au hasard.
2. Prendre une nouvelle valeur "proche" de l'ancienne
3. Si c'est mieux
Alors
garder la nouvelle valeur
Sinon
garder l'ancienne valeur, avec une certaine probabilité
4. Recommencer en 2.Il y a très, très longtemps, j'ai écrit un mémoire sur quelques méthodes d'optimisation, dont le recuit simulé :
http://zoonek.free.fr/Ecrits/1994_recuit_simulé.ps.gz
Pour estimer un paramètre d'un modèle statistique par la méthode du maximum de vraissemblance, on est amené à calculer une log-vraissemblance, qui s'écrit comme une somme (ou une intégrale, c'est pareil). Si cette somme est trop grande, on peut utiliser une simulation de Monte-Carlo pour l'estimer.
A FAIRE
Pour calculer
I = Intégrale( f(x) p(x), x \in I )
quand on ne sait pas prendre des éléments au hasard en suivant la distribution définie par p, on peut essayer d'écrire
p(x)
I = Intégrale( f(x) * ------ * q(x), x \in I )
q(x)où q définit une distribution pour laquelle on peut facilement faire des tirages.
On utilise cette méthode même quand on connait p, car en choisissant bien q, on peut faire baisser la variance de I.
http://galton.uchicago.edu/%7Eeichler/stat24600/Handouts/l9.pdf
Quelques bibliothèques permettant de manipuler des données spaciales :
geoR (voir plutôt geoRglm) geoRglm spatstat fields grasper pastecs spatial splancs GRASS (devel)
Pour plus de détails, voir par exemple :
http://freegis.org/index.en.html
Pour l'instant, je ne détaille pas : je me contente de mentionner quelques paquetages liés à la génétique.
qtl (quantitative traits loci) bqtl GeneSOM Clustering genes using Self-Organizing Maps (SOMs). ape Analyses of Phylogenetics and Evolution sma micro-array analysis permax (DNA array) genetics PHYLOGR (devel)
Voir aussi le projet Bioconductor, qui s'intéresse essentiellement aux puces à ADN (microarrays) :
http://www.bioconductor.org/packages/devel/html/
sparseM
brlr Bias-reduced logistic regression: fits logistic regression models by maximum penalized likelihood.
Apprentissage non supervisé :
cclust Convex clustering methods, including k-means algorithm, on-line update algorithm (Hard Competitive Learning) and Neural Gas algorithm (Soft Competitive Learning) and calculation of several indexes for finding the number of clusters in a data set. maptree Functions with example data for graphing and mapping models from hierarchical clustering and classification and regression trees. mclust
Apprentissage supervisé :
class Functions for classification (k-nearest neighbor and LVQ). Contained in the VR bundle.
Réseaux bayesiens :
deal Bayesian networks with continuous and/or discrete variables can be learned and compared from data. knnTree Construct or predict with k-nearest-neighbor classifiers, using cross-validation to select k, choose variables (by forward or backwards selection), and choose scaling (from among no scaling, scaling each column by its SD, or scaling each column by its MAD). The finished classifier will consist of a classification tree with one such k-nn classifier in each leaf.
Markov:
MCMC: coda Output analysis and diagnostics for Markov Chain Monte Carlo (MCMC) simulations. Multi-state Markov model: msm VLMC Functions, classes & methods for estimation, prediction, and simulation (bootstrap) of VLMC (Variable Length Markov Chain) models.
mixtures:
moc
pixmap
Variable selection:
subselect
CORBA (devel)
Vincent Zoonekynd
<zoonek@math.jussieu.fr>
latest modification on Wed Oct 13 22:33:23 BST 2004