
The French version of this document is no longer maintained: be sure to check the more up-to-date English version.
Introduction
Modélisation simple d'une série temporelle
Analyse spectrale
ARIMA
********************
Divers
Validation d'un modèle
Modèles non linéaires : ARCH et GARCH (Generalized AutoRegressive Conditionnal Heteroscedasticity)
State-Space Models, Kalman filtering
Sujets non traités
A EFFACER
A FAIRE : A CLASSER
[Ce chapitre est encore à l'état de brouillon (bien plus que les autres) et sa structure risque de changer.]
A FAIRE
Plan provisoire
Introduction Où rencontre-t-on des séries temporelles ? Exemples Le problème fondamental : on dispose d'une seule réalisation du processus Quelques graphiques : ACF Analyse spectrale, Périodogramme, TTF Processus AR, MA, ARMA, ARIMA, SARIMA, Box-Jenkins Processus ARCH, GARCG, EGARCH SSM Divers Chaines de Markov, chaines de Markov cachées SDE, Série temporelles irrégulières
En probabilités, une série temporelle (on parle aussi parfois de processus stochastique -- c'est presque la même chose) est une suite de variables aléatoires. En statistiques, c'est une variable qui dépend du temps : par exemple, des cours de bourse jour après jour, des températures (des précipitations, etc.) au cours de l'année, le rythme cardiaque d'un patient au fil du temps, etc.
library(ts) data(LakeHuron) x <- LakeHuron plot(x)

Si on ne voit pas grand chose, on peut lisser la courbe.
data(sunspots) x <- window(sunspots, start=1750, end=1800) plot(x) plot(x, type='p') k <- 20 lines(filter(x, rep(1/k,k)), col='red', lwd=3)

On peut mettre la périodicité en évidence, graphiquement, avec des barres verticales.
data(UKgas)
plot.band <- function (x, ...) {
plot(x, ...)
a <- time(x)
i1 <- floor(min(a))
i2 <- ceiling(max(a))
y1 <- par('usr')[3]
y2 <- par('usr')[4]
if( par("ylog") ){
y1 <- 10^y1
y2 <- 10^y2
}
for (i in seq(from=i1, to=i2-1, by=2)) {
polygon( c(i,i+1,i+1,i), c(y1,y1,y2,y2), col='grey', border=NA )
}
par(new=T)
plot(x, ...)
}
plot.band(UKgas, log='y')
Comme toujours, avant d'analyser la série, on la regarde (évolution par rapport au temps, recherche de changements brusques, valeurs atypiques (plus les données sont volumineuses, plus elles sont sales : ainsi, dans des données boursières, on peut trouver des valeurs anormalement élevées (fautes de frappe), nulles (quelqu'un a pu décider que les valeurs manquantes seraient remplacées par des zéros), dans le desordre (si on dispose à la fois des valeurs et de l'instant auquel elles ont été mesurées, on peut les remettre dans l'ordre), ou associées à des temps aberrants (valeurs boursières en dehors des heures d'ouverture de la bourse)), distribution des valeurs (histogramme), y[i+1]~y[i], etc.).
data(LakeHuron) x <- LakeHuron op <- par(mfrow=c(1,2)) hist(x) qqnorm(x) qqline(x, col='red') par(op)

boxplot(x, horizontal=T)

plot(x)

n <- length(x)
k <- 5
m <- matrix(nr=n+k-1, nc=k)
for (i in 1:k) {
m[,i] <- c(rep(NA,i-1), x, rep(NA, k-i))
}
pairs(m, lower.panel = panel.smooth,
upper.panel = function (x,y) {
panel.smooth(x,y)
par(usr = c(0, 1, 0, 1))
a <- cor(x,y, use='pairwise.complete.obs')
text(.1,.9,
adj=c(0,1),
round(a, digits=2),
col='blue',
cex=2*a)
})
Nous verrons aussi d'autres graphiques, propres aux séries temporelles.
op <- par(mfrow=c(3,1)) acf(x) pacf(x) spectrum(x) par(op)

Voici, en vrac, quelques exemples de simulations.
La première série est juste un bruit gaussien ; la seconde est un "bruit gaussien intégré". On peut ensuite élaborer, en ajoutant du bruit, en intégrant plusieurs fois, en ajoutant une tendance linéaire ou périodique, etc.
op <- par(mfrow=c(3,3))
n <- 100
k <- 5
N <- k*n
x <- (1:N)/n
y1 <- rnorm(N)
plot(ts(y1))
y2 <- cumsum(rnorm(N))
plot(ts(y2))
y3 <- cumsum(rnorm(N))+rnorm(N)
plot(ts(y3))
y4 <- cumsum(cumsum(rnorm(N)))
plot(ts(y4))
y5 <- cumsum(cumsum(rnorm(N))+rnorm(N))+rnorm(N)
plot(ts(y5))
# With a trend
y6 <- 1 - x + cumsum(rnorm(N)) + .2 * rnorm(N)
plot(ts(y6))
y7 <- 1 - x - .2*x^2 + cumsum(rnorm(N)) + .2 * rnorm(N)
plot(ts(y7))
# With a seasonnal component
y8 <- .3 + .5*cos(2*pi*x) - 1.2*sin(2*pi*x) +
.6*cos(2*2*pi*x) + .2*sin(2*2*pi*x) +
-.5*cos(3*2*pi*x) + .8*sin(3*2*pi*x)
plot(ts(y8+ .2*rnorm(N)))
lines(y8, type='l', lty=3, lwd=3, col='red')
y9 <- y8 + cumsum(rnorm(N)) + .2*rnorm(N)
plot(ts(y9))
par(op)
En statistiques, on aime bien avoir des valeurs indépendantes -- or les séries temporelles ont des valeurs naturellement corrélées. Le but de l'étude des séries temporelles sera donc de les ramener à une série de valeurs indépendantes, généralement en donnant une "recette" (un modèle) permettant de construire une série ressemblant à la série étudiée à partir de bruit (i.e., à partir de valeurs aléatoires indépendantes identiquement distribuées). C'est une extension de l'idée sous-jacente
On peut présenter ce problème sous un autre angle : quand on étudie un phénomène statistique, on dispose généralement de plusieurs réalisations de ce phénomène. Avec les séries temporelles, on n'en a qu'une seule. Pour étudier une série temporelle, on remplace donc l'étude en un instant donné de réalisations multiples par l'étude en des instant multiples d'une réalisation unique. Selon la nature de la série temporelle, ces deux points de vue peuvent être équivalents -- ou non. C'est le problème de l'ergodicité, sur lequel nous reviendrons.
Comme les observations d'une série temporelle ne sont généralement pas indépendantes, on peut regarder leur corrélation : la fonction d'auto-corrélation ou ACF (on parle de fonction d'auto-corrélation de l'échantillon, SACF (Sample AutoCorrelation Function), si elle est estimée à partir d'un échantillon) est la corrélation entre l'observation numéro n et l'observation n-k. Pour pouvoir la calculer à l'aide d'un échantillon, on est contraint de supposer qu'elle ne dépend pas de n.
On pourrait le faire à la main (exercice : essayez !),
my.acf <- function (x, lag.max = ceiling(5*log(length(x)))) {
m <- matrix(
c( NA,
rep( c(rep(NA, lag.max-1), x),
lag.max ),
rep(NA,, lag.max-1)
),
byrow=T,
nr=lag.max)
x0 <- m[1,]
apply(m,1,cor, x0, use="complete")
}
n <- 200
x <- rnorm(n)
plot(my.acf(x), type='h')
abline(h=0)
mais il y a déjà une fonction, qui le fait plus efficacement.
op <- par(mfrow=c(2,1)) acf(x, main="fonction d'autocorrélation d'un bruit blanc") x <- LakeHuron acf(x, main="fonction d'autocorrélation d'une série temporelle") par(op)

Voici les fonctions d'autocorrélation des exemples de l'introduction, dans le desordre : sauriez-vous les remettre dans l'ordre ? A défaut, que remarque-t-on ? Peut-on classer ces séries dans différents groupes ?
op <- par(mfrow=c(3,3))
for (y in sample(list(y1,y2,y3,y4,y5,y6,y7,y8,y9))) {
acf(y)
}
par(op)
Personnellement, je vois trois groupes : l'ACF qui est presque nulle correspond à des données non corrélées, l'ACF tantôt positive, tantôt négative à dees données pérriodiques, les autres à des données corrélées.
Un bruit blanc est une suite de variables aléatoires d'espérance nulle, de variance constante et non-corrélées, i.e., des "vaiid au second ordre".
On rencontrera du bruit blanc lors de la modélisation des séries temporelles : on tentera de décrire la série comme somme d'un terme que l'on peut interpréter et d'un terme de bruit.
Par exemple, une suite de vaiid normales.
op <- par() layout( matrix(c(1,2),nr=1,nc=2), widths=c(3,1) ) n <- 100 x <- ts(rnorm(n)) plot(x) abline(h=0, lty=3) title(main="Bruit iid normal") hist(x, main='') par(op)

Par exemple, une suite de vaiid non normales.
op <- par() layout( matrix(c(1,2),nr=1,nc=2), widths=c(3,1) ) n <- 100 x <- ts(runif(n,-1,1)) plot(x) abline(h=0, lty=3) title(main="Bruit iid non normal") hist(x, main='') par(op)

plot(ts(rnorm(100)^3)) abline(h=0, lty=3) title(main="Bruit iid non normal")

Mais on peut aussi avoir des suites de variables aléatoires non corrélées mais non indépendantes (la définition demande en fait qu'elles soient << indépendantes jusqu'au second ordre >>).
n <- 100
x <- rep(0,n)
z <- rnorm(n)
for (i in 2:n) {
x[i] <- z[i] * sqrt( 1 + .5 * x[i-1]^2 )
}
plot(ts(x))
abline(h=0, lty=3)
title("Bruit non iid")
Certaines suites parfaitement déterministes ressemblent beaucoup à du bruit blanc.
n <- 100
x <- rep(.7, n)
for (i in 2:n) {
x[i] <- 4 * x[i-1] * ( 1 - x[i-1] )
}
x <- x - mean(x)
plot(ts(x))
abline(h=0, lty=3)
title(main="Une suite déterministe")
n <- 1000
tn <- cumsum(rexp(n))
# Une fonction, de classe C^infini, définie comme une somme de
# densités gaussiennes.
f <- function (x) {
# si x est un seul nombre : sum(dnorm(x-tn))
apply( dnorm( outer(x,rep(1,length(tn))) - outer(rep(1,length(x)),tn) ),
1,
sum )
}
op <- par(mfrow=c(2,1))
curve( f(x), xlim=c(1,500),
n=1000,
main="De loin, ça a l'air aléatoire..." )
curve( f(x), xlim=c(1,10),
n=1000,
main="...mais pas de près (c'est une fonction C^infini)" )
par(op)
On dispose de quelques tests pour vérifier si une série temporelle est bien du bruit blanc, que nous allons maintenant présenter.
L'analyse d'une série temporelle consistera essentiellement à l'exprimer en fonction d'un bruit blanc (comme les simulations que nous avons faites dans l'introduction) : pour vérifier que l'analyse est pertinente, il faudra s'assurer que les résidus sont bien du bruit blanc (comme pour la régression). Pour cela, on peut regarder l'ACF (en moyenne 5% des valeurs doivent être entre les pointillés),
z <- rnorm(200) op <- par(mfrow=c(2,1)) plot(ts(z)) acf(z) par(op)

data(co2) x <- diff(co2) y <- diff(x,lag=12) op <- par(mfrow=c(2,1)) plot(ts(y)) acf(y) par(op)

Pour avoir un résultat numérique (une p-valeur), on peut faire les tests de Box--Pierce ou Ljung--Box (on parle de "portmanteau statistics") : il s'agit de considérer des sommes (pondérées) des premiers coefficients d'auto-corrélation -- ces sommes suivent, asymptotiquement, une distribution du Chi^2 (le test de Ljung-Box est une variante de celui de Box-Pierce, qui ressemble un peu plus à une distribution du Chi^2 pour des petits échantillons).
> Box.test(z) # Box-Pierce
Box-Pierce test
X-squared = 0.014, df = 1, p-value = 0.9059
> Box.test(z, type="Ljung-Box")
Box-Ljung test
X-squared = 0.0142, df = 1, p-value = 0.9051
> Box.test(y)
Box-Pierce test
X-squared = 41.5007, df = 1, p-value = 1.178e-10
> Box.test(y, type='Ljung')
Box-Ljung test
X-squared = 41.7749, df = 1, p-value = 1.024e-10
op <- par(mfrow=c(2,1))
plot.box.ljung <- function (z, k=15, main="p-valeur du test de Ljung-Box") {
p <- rep(NA, k)
for (i in 1:k) {
p[i] <- Box.test(z, i, type = "Ljung-Box")$p.value
}
plot(p, type='h', ylim=c(0,1), lwd=3, main=main)
abline(h=c(0,.05),lty=3)
}
plot.box.ljung(z, main="Données aléatoires")
plot.box.ljung(y, main="diff(diff(co2),lag=12)")
par(op)
Il y a d'autres tests, que je ne mentionne pas (McLeod-Li, Turning-point, difference-sign, rank test).
On peut aussi mentionner le test de Durbin-Watson, dont nous avons déjà parlé dans le cadre de la régression.
A FAIRE : il faut en parler dans l'un des chapitres sur la régression. library(car) ?durbin.watson library(lmtest) ?dwtest
Ici :
> dwtest(LakeHuron ~ 1)
Durbin-Watson test
data: LakeHuron ~ 1
DW = 0.3195, p-value = < 2.2e-16
alternative hypothesis: true autocorrelation is greater than 0
op <- par(mfrow=c(2,1))
library(lmtest)
plot(LakeHuron, main="Lake Huron")
acf(LakeHuron, main=paste("p =", signif(dwtest(LakeHuron~1)$p.value)))
par(op)
n <- 200
x <- rnorm(n)
op <- par(mfrow=c(2,1))
x <- ts(x)
plot(x, main="Bruit blanc")
acf(x, main=paste("p =", signif(dwtest(x~1)$p.value)))
par(op)
n <- 200
x <- rnorm(n)
op <- par(mfrow=c(2,1))
y <- filter(x,.8,method="recursive")
plot(y, main="AR(1)")
acf(y, main=paste("p =", signif(dwtest(y~1)$p.value)))
par(op)
Attention, ce test passe à côté de choses évidentes...
(A FAIRE : si quelqu'un comprends pourquoi la p-valeur n'est pas significative...)
n <- 200
x <- rnorm(n)
y <- filter(x, c(0,1), method="recursive")
op <- par(mfrow=c(3,1))
plot(y, main=paste("p =",dwtest(y~1)$p.value))
acf(y)
pacf(y)
par(op)
Détails :
> dwtest(y~1)
Durbin-Watson test
data: y ~ 1
DW = 3.4316, p-value = 1
alternative hypothesis: true autocorrelation is greater than 0
> dwtest(abs(y)~1)
Durbin-Watson test
data: abs(y) ~ 1
DW = 1.0476, p-value = 6.525e-12
alternative hypothesis: true autocorrelation is greater than 0On peut aussi aussi regarder l'histogramme ou le qqplot des résidus.
op <- par(mfcol=c(2,2)) hist(z) qqnorm(z) qqline(z,col='red') hist(y) qqnorm(y) qqline(y, col='red') par(op)

Il y a d'autres tests, comme le test du nombre de suites
A FAIRE
ou le test de Cowles-Jones.
A FAIRE
A sequence is a pair of consecutive returns of the same sign; a
reversal is a pair of consecutive returns of opposite signs.
Their ratio, the Cowles-Jones ratio,
number of sequences
CJ = ---------------------
number of reversals
should be around one IF the drift is zero.
En fait, il y a déjà une fonction, tsdiag, qui fait quelques tests sur la modélisation d'une série temporelle (graphique des résidus, ACF et tests de Ljung-Box).
data(co2) r <- arima(co2, order = c(0, 1, 1), seasonal = list(order = c(0, 1, 1), period = 12)) tsdiag(r)

Classiquement, on tente de décomposer les séries temporelles en une somme de trois termes : une tendance (souvent une fonction affine), une composante saisonnière (une fonction périodique) et du bruit.
Dans cette partie, nous allons tenter d'analyser les séries temporelles à l'aide de cette idée, en utilisant les méthodes statistiques classiques (essentiellement la régression) que nous avons déjà présentées. Ces explorations setont parfois pertinentes, mais pas toujours : prenez garde !
A FAIRE : compléter cette introduction en donnant le plan de cette section.
data(co2) plot(co2)

Commençons par essayer d'estimer les données par la somme d'une fonction affine et d'une fonction sinusoïdale.
y <- as.vector(co2) x <- as.vector(time(co2)) r <- lm( y ~ poly(x,1) + cos(2*pi*x) + sin(2*pi*x) ) plot(y~x, type='l') lines(predict(r)~x, lty=3, col='red', lwd=3)

C'est insuffisant. Si ça n'est pas clair sur le graphique, on peut regarder les résidus.
plot( y-predict(r) )

On complique donc un peu le modèle : un polynôme de degré 2 plus une fonction sinusoïdale (si ça ne suffisait pas, on remplacerait le polynôme par des splines).
r <- lm( y ~ poly(x,2) + cos(2*pi*x) + sin(2*pi*x) ) plot(y~x, type='l') lines(predict(r)~x, lty=3, col='red', lwd=3)

C'est mieux.
plot( y-predict(r) )

On pourrait essayer de compliquer la composante périodique, mais ça n'apporterait pas grand chose de plus.
r <- lm( y ~ poly(x,2) + cos(2*pi*x) + sin(2*pi*x)
+ cos(4*pi*x) + sin(4*pi*x) )
plot(y~x, type='l')
lines(predict(r)~x, lty=3, col='red', lwd=3)
plot( y-predict(r), type='l' )

Néanmoins, l'ACF suggère que ces modèles ne conviennent pas vraiment : si les résidus étaient vraiment du bruit, on n'aurait très peu (1/20) de valeurs en dehors des pointillés...
op <- par(mfrow=c(2,1))
acf(y - predict(lm( y ~ poly(x,2) + cos(2*pi*x) + sin(2*pi*x) )))
acf(y - predict(lm( y ~ poly(x,2) + cos(2*pi*x)
+ sin(2*pi*x) + cos(4*pi*x) + sin(4*pi*x) )))
par(op)
Ces graphiques nous disent deux choses : d'une part, il était quand-même utile de compliquer la composante périodique, d'autre part, nous ne sommes pas parvenus à nous débarasser des problèmes d'autocorrélation.
Pour estimer la composante périodique, on pourrait faire la moyenne de tous les mois de janvier, etc.,
m <- tapply(co2, gl(12,1,length(co2)), mean) m <- rep(m, ceiling(length(co2)/12)) [1:length(co2)] m <- ts(m, start=start(co2), frequency=frequency(co2)) op <- par(mfrow=c(3,1)) plot(co2) plot(m) plot(co2-m) r <- lm(co2-m ~ poly(as.vector(time(m)),2)) lines(predict(r) ~ as.vector(time(m)), col='red') par(op)

Néanmoins, les résidus nous signalent que la composante périodique est toujours là...
op <- par(mfrow=c(4,1))
plot(r$res)
acf(r$res)
pacf(r$res)
spectrum(r$res, col=par('fg'))
abline(v=1:6, lty=3)
par(op)
Utiliser la moyenne comme ci-dessus pour obtenir la composante périodique n'est valable que si le modèle est de la forme
y ~ a + b x + composante périodique
(ici, on a un terme quadratique, donc ça ne marche pas). Néanmoins, on peut reprendre la même idée avec une seule régression (on utilise cette régression pour trouver à la fois la partie périodique (au lieu de calculer des moyennes) et la tendance. La parie périodique est ici absolument quelconque : on cherche 12 coefficients.
k <- 12 m <- matrix( as.vector(diag(k)), nr=length(co2), nc=k, byrow=T) m <- cbind(m, poly(as.vector(time(co2)),2)) r <- lm(co2~m-1) summary(r) b <- r$coef y1 <- m[,1:k] %*% b[1:k] y1 <- ts(y1, start=start(co2), frequency=frequency(co2)) y2 <- m[,k+1:2] %*% b[k+1:2] y2 <- ts(y2, start=start(co2), frequency=frequency(co2)) res <- co2 - y1 - y2 op <- par(mfrow=c(3,1)) plot(co2) lines(y2+mean(b[1:k]) ~ as.vector(time(co2)), col='red') plot(y1) plot(res) par(op)

Ici, l'analyse n'est pas terminée : il reste à étudier le bruit qu'on a finalement obtenu (mais contrairement à la situation précédente, on s'est bien débarassé de la composante périodique).
op <- par(mfrow=c(3,1))
acf(res)
pacf(res)
spectrum(res, col=par('fg'))
abline(v=1:10, lty=3)
par(op)
Dans l'exemple précédent, si la période était plus longue, on utiliserait des splines pour trouver une partie périodique plus lisse (et aussi pour avoir un modèle avec moins de paramètres : 14, pour le précédent, c'était déjà beaucoup).
Exercice laissé au lecteur A FAIRE
Pour trouver la tendance d'une série temporelle, on peut simplement la << lisser >>, par exemple avec une moyenne mobile (Moving Average ou MA, en anglais),
x <- co2 n <- length(x) k <- 12 m <- matrix( c(x, rep(NA,k)), nr=n+k-1, nc=k ) y <- apply(m, 1, mean, na.rm=T) y <- y[1:n + round(k/2)] y <- ts(y, start=start(x), frequency=frequency(x)) y <- y[round(k/4):(n-round(k/4))] yt <- time(x)[ round(k/4):(n-round(k/4)) ] plot(x) lines(y~yt, col='red')

(si on choisit bien les coefficients, la moyenne mobile laisse invariantes certaines fonctions, par exemples, les polynômes de degré 3). La fonction "filter" permet d'effectuer ce lissage plus simplement :
x <- co2 plot(x) k <- 12 lines( filter(x, rep(1/k,k)), col='red')

A FAIRE :
Prendre des données boursières (sur yahoo ou boursorama) Faire une moyenne mobile à 20 et 50 jours. Quand les deux courbes se coupent, on recommande de vendre/acheter. Idem avec un lissage exponentiel.
Il y a aussi le lissage exponentiel : au lieu de prendre les N dernières valeurs en leur donnant la même importance, on prend toutes les valeurs précédentes en donnant plus d'importance aux valeurs récentes.
lissage.exponentiel <- function (x, a) {
m <- x
for (i in 2:n) {
# Définition du lissage exponentiel :
m[i] <- a * x[i] + (1-a)*m[i-1]
}
m <- ts(m, start=start(x), frequency=frequency(x))
m
}
plot.lissage.exponentiel <- function (x, a=.9) {
plot(lissage.exponentiel(x,a))
par(usr=c(0,1,0,1))
text(.02,.9, a, adj=c(0,1), cex=3)
}
op <- par(mfrow=c(4,1))
plot(x, main="Lissages exponentiels")
plot.lissage.exponentiel(x)
plot.lissage.exponentiel(x,.1)
plot.lissage.exponentiel(x,.02)
par(op)
r <- x - lissage.exponentiel(x,.02) op <- par(mfrow=c(4,1)) plot(r, main="Résidus du lissage exponentiel") acf(r) pacf(r) spectrum(r) abline(v=1:10,lty=3) par(op)

En fait, il y a déjà une fonction pour faire ça (c'est un cas particulier du filtrage de Holt-Winters -- nous verrons le cas général un peu plus loin) :
x <- co2 m <- HoltWinters(x, alpha=.1, beta=0, gamma=0) p <- predict(m, n.ahead=240, prediction.interval=T) plot(m, predicted.values=p)

A FAIRE : enlever les hautes fréquences
A FAIRE
Si une série temporelle possède une tendance qu'on peut estimer par un polynôme de degré n, on peut la transformer en une série sans tendance en la dérivant (discrètement) n fois.
A FAIRE : un exemple A FAIRE : comment retrouver la série initiale à partir du bruit qu'on a obtenu ? -- Facile : en intégrant (intégration discrète, i.e., sommes cumulées). Comment exprimer la tendance ? Tendance --> série non stationnaire On peut estimer la tendance par un polynôme de degré n En dérivant n fois, on se débarasse de la tendance. A FAIRE : expliquer le lien entre tendance, stationarité, intégration, dérivation
A FAIRE : prendre une ou deux séries et leurs appliquer toutes les méthodes précédentes, afin de les comparer.
Pour décomposer une série temporelle en une tendance, une composante périodique et une composante irrégulière :
op <- par(mfrow=c(3,1)) r <- stl(co2, s.window="periodic")$time.series plot(co2) lines(r[,2], col='blue') lines(r[,2]+r[,1], col='red') plot(r[,3]) acf(r[,3], main="résidus") par(op)
La fonction "decompose" fait la même chose, de manière un peu plus rudimentaire.
A FAIRE
C'est une généralisation du filtrage exponentiel (ce dernier suppose qu'il n'y a pas de tendance ni de composante saisonnière). Il présente les mêmes intérêts : il est peu sensible aux changements structurels pas trop brusques.
Le modèle du filtrage exponentiel est
a(t) = alpha * Y(t) + (1-alpha) * a(t-1).
Cela revient à supposer que la série est localement constante. Voici un exemple.
data(LakeHuron) x <- LakeHuron avant <- window(x, end=1935) apres <- window(x, start=1935) a <- .2 b <- 0 g <- 0 modèle <- HoltWinters(avant, alpha=a, beta=b, gamma=g) prévisions <- predict(modèle, n.ahead=37, prediction.interval=T) plot(modèle, predicted.values=prévisions) lines(apres)

On peut rajouter une tendance : il s'agit alors de modéliser les données par une droite, à l'aide des valeurs précédentes, les valeurs les plus récentes comptant beaucoup plus que les valeurs les plus vieilles.
data(LakeHuron) x <- LakeHuron avant <- window(x, end=1935) apres <- window(x, start=1935) a <- .2 b <- .2 g <- 0 modèle <- HoltWinters(avant, alpha=a, beta=b, gamma=g) prévisions <- predict(modèle, n.ahead=37, prediction.interval=T) plot(modèle, predicted.values=prévisions) lines(apres)

Selon le choix de béta, les prédictions peuvent être très différentes...
data(LakeHuron)
x <- LakeHuron
op <- par(mfrow=c(2,2))
avant <- window(x, end=1935)
apres <- window(x, start=1935)
a <- .2
b <- .5
g <- 0
for (b in c(.02, .04, .1, .5)) {
modèle <- HoltWinters(avant, alpha=a, beta=b, gamma=g)
prévisions <- predict(modèle, n.ahead=37, prediction.interval=T)
par(mar=c(0,0,0,0))
plot(modèle, predicted.values=prévisions, axes=F, xlab='', ylab='', main='')
box()
text( (4*par('usr')[1]+par('usr')[2])/5,
(par('usr')[3]+5*par('usr')[4])/6,
paste("béta =",b),
cex=3, col='blue' )
lines(apres)
}
par(op)
On peut aussi ajouter une composante saisonnière (qui peut être additive ou multiplicative).
A FAIRE : un exemple additif A FAIRE un exemple multiplicatif
Avant de présenter des modèles généraux mais dont l'interprétation n'est pas immédiate (ARIMA, SARIMA), arrétons-nous sur les modèles structuraux, qui en sont des cas particuliers, directement compréhensibles.
Une marche aléatoire, avec du bruit (en fait, un cas particulier d'ARIMA(0,1,1)) :
X(t) = mu(t) + bruit1 mu(t+1) = mu(t) + bruit2 n <- 200 plot(ts(cumsum(rnorm(n)) + rnorm(n)))

Une marche aléatoire, c'est simplement du bruit intégré (comme l'intégration est discrète, on utilise la commande cumsum).
On peut aussi changer la variance des bruits.
op <- par(mfrow=c(2,1)) plot(ts(cumsum(rnorm(n, sd=1))+rnorm(n,sd=.1))) plot(ts(cumsum(rnorm(n, sd=.1))+rnorm(n,sd=1))) par(op)
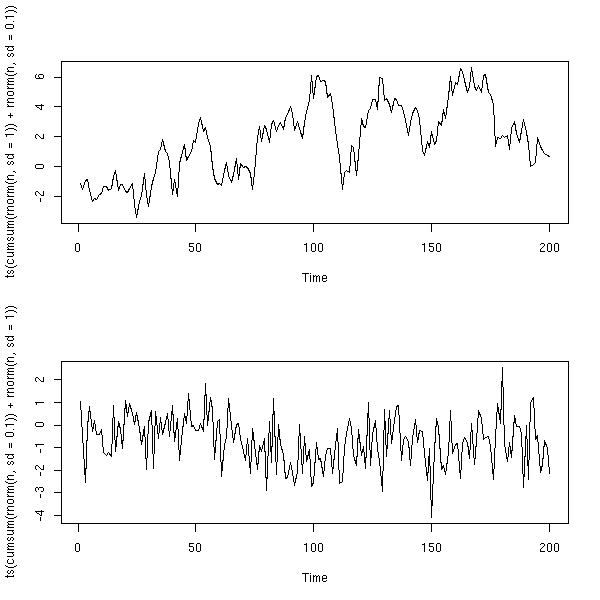
Une marche aléatoire bruitée, intégrée avec du bruit (un cas particulier d'ARIMA(0,2,2)) :
X(t) = mu(t) + bruit1 mu(t+1) = mu(t) + nu(t) + bruit2 (niveau) nu(t+1) = nu(t) + bruit 3 (pente) n <- 200 plot(ts( cumsum( cumsum(rnorm(n))+rnorm(n) ) + rnorm(n) ))

Ici, encore, on peut changer la variance des bruits.
n <- 200 op <- par(mfrow=c(3,1)) plot(ts( cumsum( cumsum(rnorm(n,sd=1))+rnorm(n,sd=1) ) + rnorm(n,sd=.1) )) plot(ts( cumsum( cumsum(rnorm(n,sd=1))+rnorm(n,sd=.1) ) + rnorm(n,sd=1) )) plot(ts( cumsum( cumsum(rnorm(n,sd=.1))+rnorm(n,sd=1) ) + rnorm(n,sd=1) )) par(op)

Une marche aléatoire bruitée, intégrée avec du bruit, à laquelle on ajoute une composante saisonnière variable.
X(t) = mu(t) + gamma(t) + bruit1
mu(t+1) = mu(t) + nu(t) + bruit2 (niveau)
nu(t+1) = nu(t) + bruit 3 (pente)
gamma(t+1) = -(gamma(t) + gamma(t-1) + gamma(t-2)) + bruit 4 (composante saisonnière)
# je ne sais pas le faire sans boucle...
structural.model <- function (n=200, sd1=1, sd2=1, sd3=1, sd4=1, sd5=200) {
sd1 <- 1
sd2 <- 2
sd3 <- 3
sd4 <- 4
mu <- rep(rnorm(1),n)
nu <- rep(rnorm(1),n)
g <- rep(rnorm(1,sd=sd5),n)
x <- mu + g + rnorm(1,sd=sd1)
for (i in 2:n) {
if (i>3) {
g[i] <- -(g[i-1]+g[i-2]+g[i-3]) + rnorm(1,sd=sd4)
} else {
g[i] <- rnorm(1,sd=sd5)
}
nu[i] <- nu[i-1] + rnorm(1,sd=sd3)
mu[i] <- mu[i-1] + nu[i-1] + rnorm(1,sd=sd2)
x[i] <- mu[i] + g[i] + rnorm(1,sd=sd1)
}
ts(x)
}
n <- 200
op <- par(mfrow=c(3,1))
plot(structural.model(n))
plot(structural.model(n))
plot(structural.model(n))
par(op)
Ici aussi, on peut changer la variance du bruit : si la composante saisonnière n'est pas bruitée, elle est constante (mais arbitraire).
n <- 200 op <- par(mfrow=c(3,1)) plot(structural.model(n,sd4=0)) plot(structural.model(n,sd4=0)) plot(structural.model(n,sd4=0)) par(op)

On peut modéliser une série temporelle à l'aide de ces modèles, avec la commande StructTS.
data(AirPassengers) plot(AirPassengers)

plot(log(AirPassengers))

x <- log(AirPassengers) r <- StructTS(x) plot(x) f <- apply(fitted(r), 1, sum) f <- ts(f, frequency=frequency(x), start=start(x)) lines(f, col='red', lty=3, lwd=3)

Ici, le fait que la pente soit (presque) nulle est assez étrange.
> r
Call:
StructTS(x = x)
Variances:
level slope seas epsilon
0.0007718 0.0000000 0.0013969 0.0000000
> summary(r$fitted[,"slope"])
Min. 1st Qu. Median Mean 3rd Qu. Max.
0.000000 0.009101 0.010210 0.009420 0.010560 0.011040
matplot( (StructTS(x-min(x)))$fitted, type='l')
Il est aussi possible de faire des prédictions (mais elles ne me semblent pas très fiables...).
l <- 1956 x <- log(AirPassengers) x1 <- window(x, end=l) x2 <- window(x, start=l) r <- StructTS(x1) plot(x) f <- apply(fitted(r), 1, sum) f <- ts(f, frequency=frequency(x), start=start(x)) lines(f, col='red') p <- predict(r, n.ahead=100) lines(p$pred, col='red') lines(p$pred + qnorm(.025) * p$se, col='red', lty=2) lines(p$pred + qnorm(.975) * p$se, col='red', lty=2) title(main="Prédictions avec un modèle structurel")

A FAIRE : mettre àa à la fin de l'introduction ?
Voici une fonction pour tracer certains des graphiques associés à une série temporelle (nous ne les avons pas encore tous vus).
# Une fonction pour regarder une série temporelle
eda.ts <- function (x, bands=FALSE) {
# Calcul des p-valeurs du test de Ljung-Box
# (on le les affiche que si leur examen est nécessaire, i.e.,
# si on peut penser que c'est du bruit blanc)
p.min <- .05
k <- 15
p <- rep(NA, k)
for (i in 1:k) {
p[i] <- Box.test(x, i, type = "Ljung-Box")$p.value
}
if( max(p)>p.min ) {
op <- par(mfrow=c(5,1))
} else {
op <- par(mfrow=c(4,1))
}
if(!is.ts(x))
x <- ts(x)
plot(x)
if(bands) {
a <- time(x)
i1 <- floor(min(a))
i2 <- ceiling(max(a))
y1 <- par('usr')[3]
y2 <- par('usr')[4]
if( par("ylog") ){
y1 <- 10^y1
y2 <- 10^y2
}
for (i in seq(from=i1, to=i2-1, by=2)) {
polygon( c(i,i+1,i+1,i), c(y1,y1,y2,y2), col='grey', border=NA )
}
lines(x)
}
acf(x)
pacf(x)
spectrum(x, col=par('fg'))
if( max(p)>p.min ) {
main <- "p-valeur du test de Ljung-Box"
plot(p, type='h', ylim=c(0,1), lwd=3, main=main)
abline(h=c(0,.05),lty=3)
}
par(op)
}
data(co2)
eda.ts(co2, bands=T)
Certaines séries temporelles comportent une composante temporelle difficile à repérer : on peut alors utiliser un périodogramme (c'est juste une transformée de Fourrier discrète) pour trouver la période. Dans l'exemple suivant, on retrouve la période 1 an, avec ses harmoniques (2 ans, 3 ans, 4 ans). (Les harmoniques sont présentes quand la fonction périodique n'est pas exactement sinusoïdale.)
spectrum(co2) abline(v=1:10, lty=3)

Prenons un exemple plus compliqué.
data(sunspots) plot(sunspots)

On pourrait trouver la période sans le périodogramme :
a <- locator() # cliquer sur les maximaux locaux b <- a$x - a$x[1] bb <- outer(b, 9:13, '/') apply(abs(bb - round(bb)), 2, mean)
Il vient :
[1] 0.2278710 0.1606527 0.1545937 0.1979566 0.2106840
i.e., la période la plus probable est 11.
C'est néanmoins plus simple avec un périodogramme.
spectrum(sunspots)

Pour l'insant, on ne voir rien : on demande à R de lisser un peu le périodogramme.
spectrum(sunspots, spans=10)

On voit maintenant un sommet proche de zéro. On peut estimer sa valeur à l'aide de la fonction locator, comme tout-à-l'heure, puis grossir le dessin.
spectrum(sunspots, spans=10, xlim=c(0,1)) abline(v=1:3/11, lty=3) # une seule harmonique

Pour décomposer cette série, on peut commencer par la transformer (j'ai envie de la transformer, mais je ne suis pas du tout convaincu que ce soit utile : les valeurs de la série ont l'air << un peu plus normales >>, certes, mais elle est toujours aussi irrégulière). A FAIRE
library(car) box.cox.powers(3+sunspots) y <- box.cox(sunspots,.3) spectrum(y, spans=10, xlim=c(0,1)) abline(v=1:3/11, lty=3) # une seule harmonique

x <- as.vector(time(y))
y <- as.vector(y)
r1 <- lm( y ~ sin(2*pi*x/11) + cos(2*pi*x/11) )
r2 <- lm( y ~ sin(2*pi*x/11) + cos(2*pi*x/11)
+ sin(2* 2*pi*x/11) + cos(2* 2*pi*x/11)
+ sin(3* 2*pi*x/11) + cos(3* 2*pi*x/11)
+ sin(4* 2*pi*x/11) + cos(4* 2*pi*x/11)
)
plot(y~x, type='l')
lines(predict(r1)~x, col='red')
lines(predict(r2)~x, col='green', lty=3, lwd=3)
Les termes supplémentaires n'apportent pas grand-chose.
> summary(r2)
...
Estimate Std. Error t value Pr(>|t|)
(Intercept) 6.854723 0.045404 150.973 < 2e-16 ***
sin(2 * pi * x/11) 1.696287 0.064100 26.463 < 2e-16 ***
cos(2 * pi * x/11) 1.213098 0.064319 18.860 < 2e-16 ***
sin(2 * 2 * pi * x/11) 0.056443 0.064238 0.879 0.380
cos(2 * 2 * pi * x/11) 0.343087 0.064182 5.346 9.74e-08 ***
sin(3 * 2 * pi * x/11) 0.025019 0.064249 0.389 0.697
cos(3 * 2 * pi * x/11) 0.003333 0.064169 0.052 0.959
sin(4 * 2 * pi * x/11) 0.039955 0.064191 0.622 0.534
cos(4 * 2 * pi * x/11) -0.046268 0.064216 -0.721 0.471Pour autant l'analyse n'est pas terminée : les résidus ne ressemblent pas du tout à du bruit blanc (on pourra par exemple utiliser un modèle ARMA).
z <- y - predict(r1) op <- par(mfrows=c(2,2)) hist(z) qqnorm(z) acf(z) pacf(z) par(op)

Ils sont liés :
+infini
f(oméga) = Somme( rho(k) * exp(- i k oméga ) )
k=-infiniA FAIRE :
spectre de : n <- 200 a <- rnorm(n) b <- rnorm(n) x <- 1:n y <- a*cos(x) + b*sin(x) + rnorm(n) y <- ts(y) spectrum(y) ??? Le spectre théorique est infini pour oméga=1. A FAIRE : periodogram = sample spectrum A FAIRE : Un filtre linéaire agit linéairement sur le spectre. (c'est pour ça qu'on utilise beaucoup la transformée de Fourier : elle transforme des dérivations en multiplications) A FAIRE : le périodogramme "brut" contient énormément de bruit : il est nécessaire de le lisser.
Dans cette section, nous revenons plus en détail sur la notion de périodogramme.
L'idée de la transformée de Fourier est d'écrire une fonction (périodique) comme une somme de sinus et de cosinus.
f(t) = a0 + a1 cos(t) + b1 sin(t) + a2 cos(2t) + b2 sin(2t) + ...
C'est plus simple à écrire avec des exponentielles complexes :
f(t) = ... + c(-2) e^(-2it) + c(-1) e^-it + c(0) + c1 e^it + c2 e^2it + ...
Plus précisément, il s'agit d'une série de Fourier.
A FAIRE : effacer ce qui suit ???
A FAIRE : dire comment on trouve les coefficients
A FAIRE : parler de la transformation de Fourier
A FAIRE : expliquer la TTF
A FAIRE : mentionner quelques applications de la FFT.
A FAIRE : expliquer à quoi correspondent les résultats donnés par R.
(et commenter le graphique suivant).
La FFT de certaines fonctions (une couleur pour chaque fonction)
(la commande mvfft calcule la FFT de chaque colonne)
n <- 8
x <- 1:n/n*2*pi
k <- 0
y <- cbind( rep(1,n),
1 + exp(1i *x),
1 + exp(1i *x) + exp(-1i),
1 + exp(1i *x) + exp(-1i) + exp(2i),
1 + exp(1i *x) + exp(-1i) + exp(2i) + exp(-2i)
)
z <- mvfft(y)
op <- par(mfrow=c(2,1))
barplot(Re(t(z)), beside=T, col=rainbow(dim(y)[2]))
barplot(Im(t(z)), beside=T, col=rainbow(dim(y)[2]))
par(op)
A FAIRE : effacer ce qui précède ?
Si on part d'une fonction réelle, c'est beaucoup plus clair.
n <- 8
x <- 1:n/n*2*pi
k <- 0
y <- cbind( rep(1,n),
1 + cos(x),
1 + cos(x) + sin(x),
1 + cos(x) + sin(x) + cos(2*x),
1 + cos(x) + sin(x) + cos(2*x) + sin(2*x)
)
z <- mvfft(y)
op <- par(mfrow=c(2,1))
barplot(Re(t(z)), beside=T, col=rainbow(dim(y)[2]), main="Partie réelle de la FFT")
barplot(Im(t(z)), beside=T, col=rainbow(dim(y)[2]), main="Partie imaginaire de la FFT")
par(op)
Le premier coefficient correspond au terme constant, les deuxième et dernier coefficients (qui sont conjugués) correspondent aux coefficients en cos(t) et sin(t), les troisième et avant-dernier aux coefficients en cos(2t) et sin(2t), etc.
Comme le signal que l'on étudie est réel, les derniers coefficients sont les conjugués des premiers : il n'est pas nécessaire de les représenter. Par ailleurs, si on ne s'intéresse pas aux histoires de déphasage, il suffit de représenter le module de la FFT.
Voici quelques exemples de FFT.
x <- rep(0,256) x[129:256] <- 1 op <- par(mfrow=c(2,1)) plot(x, type='l') plot(Mod(fft(x)[1: ceiling((length(x)+1)/2) ]), type='l') par(op)

x <- rep(0,256) x[33:64] <- 1 x[64+33:64] <- 1 x[128+33:64] <- 1 x[128+64+33:64] <- 1 op <- par(mfrow=c(2,1)) plot(x, type='l') plot(Mod(fft(x)[1: ceiling((length(x)+1)/2) ]), type='l') par(op)

x <- rep( 1:32/32, 8 ) op <- par(mfrow=c(2,1)) plot(x, type='l') plot(Mod(fft(x)[1: ceiling((length(x)+1)/2) ]), type='l') par(op)

x <- 1:256/256 op <- par(mfrow=c(2,1)) plot(x, type='l') plot(Mod(fft(x)[1: ceiling((length(x)+1)/2) ]), type='l') par(op)

x <- abs(1:256-128) op <- par(mfrow=c(2,1)) plot(x, type='l') plot(Mod(fft(x)[1: ceiling((length(x)+1)/2) ]), type='l') par(op)

x <- 1:256/256 x <- sin(2*pi*x) + cos(3*pi*x) + sin(4*pi*x+pi/3) op <- par(mfrow=c(2,1)) plot(x, type='l') plot(Mod(fft(x)[1: ceiling((length(x)+1)/2) ]), type='l') par(op)

x <- 1:256/256 x <- sin(16*pi*x) op <- par(mfrow=c(2,1)) plot(x, type='l') plot(Mod(fft(x)[1: ceiling((length(x)+1)/2) ]), type='l') par(op)

x <- 1:256/256 x <- sin(16*pi*x) + .3*cos(56*pi*x) op <- par(mfrow=c(2,1)) plot(x, type='l') plot(Mod(fft(x)[1: ceiling((length(x)+1)/2) ]), type='l') par(op)

On peut donc utiliser la FFT pour filtrer un signal, en en enlevant les hautes ou les basses fréquences.
n <- 1000 x <- cumsum(rnorm(n))+rnorm(n) y <- fft(x) y[20:(length(y)-19)] <- 0 y <- Re(fft(y, inverse=T)/length(y)) op <- par(mfrow=c(3,1)) plot(x, type='l') lines(y, col='red', lwd=3) plot(Mod(fft(x)[1: ceiling((length(x)+1)/2) ]), type='l') plot(Mod(fft(y)[1: ceiling((length(y)+1)/2) ]), type='l') par(op)

n <- 1000
x <- cumsum(rnorm(n))+rnorm(n)
plot(x, type='l')
for (i in 1:10) {
y <- fft(x)
y[(1+i):(length(y)-i)] <- 0
y <- Re(fft(y, inverse=T)/length(y))
lines(y, col=rainbow(10)[i])
}
n <- 1000 x <- c(129:256,1:128)/256 y <- fft(x) y[20:(length(y)-19)] <- 0 y <- Re(fft(y, inverse=T)/length(y)) plot(x, type='l', ylim=c(-.2,1.2)) lines(y, col='red', lwd=3)

A FAIRE : reprendre l'exemple concret de série temporelle qui m'a conduit ici.
A FAIRE : Montrer comment utiliser la FFT pour filtrer une série temporelle.
A FAIRE : récupérer la tendance
x <- co2 y <- fft(x) y[20:(length(y)-19)] <- 0 y <- Re(fft(y, inverse=T)/length(y)) plot(x, type='l') lines(y, col='red', lwd=3)

A FAIRE : Problème : le résultat est une fonction continue périodique, ce qui ne correspond pas du tout à ce qu'on voulait... A FAIRE : pour que la valeur au début égale celle à la fin, on peut faire une régression linéaire. p <- predict(lm(co2~time(co2))) x <- co2 - p y <- fft(x) y[20:(length(y)-19)] <- 0 y <- Re(fft(y, inverse=T)/length(y)) plot(x+p, type='l') lines(y+p, col='red', lwd=3) lines(x-y+mean(x+p), col='green', lwd=3)

A FAIRE : Même problème si on essaye de faire le contraire et de récupérer la composante périodique sans la tendance.
x <- co2 y <- fft(x) k <- 20 n <- length(y) y[1:(k+1)] <- 0 y[(n-k):n] <- 0 y <- Re(fft(y, inverse=T)/length(y)) plot(x, type='l') lines(y+mean(x), col='red', lwd=3)

(et ici, on a encore un autre problème, avec la période, qui n'est pas la bonne -- 40 ans au lieu d'un an) A FAIRE
A FAIRE : déplacer cette partie ???
library(sound)
x <- loadSample("sample.wav")
plot(x)
n <- length(x$sound) n <- round(n/3) y <- x$sound[ n:(n+2000) ] n <- length(y) op <- par(mfrow=c(2,1)) plot(y, type='l') #plot(Mod(fft(y)[1: ceiling((length(y)+1)/2) ]), type='l') plot(Mod(fft(y)[1:100]), type='l')

A FAIRE : Donner un exemple de transformation de Fourier sur un signal sonore. (faire un graphique en 2D qui indique les changements de cette FFT quand on déplace une fenêtre (comment choisir sa largeur ?) le long de l'échantillon). (prendre un échantillon pour tracker, avec plusieurs notes) A FAIRE : Donner des exemples de filtrage sur des signaux sonores (donner le fichier *.wav initial, ainsi que le résultat) A FAIRE : Regrouper ces exemples sonores dans une partie bien séparée.
La principale différence entre les séries temporelles et les suites de vaiid que nous rencontrions précédemment, c'est justement le défaut d'indépendance. La corrélation est un moyen (imprécis en cas de non normalité) de mesurer ce défaut d'indépendance.
La fonction d'autocorrélation (ACF) est la corrélation entre un terme et le i-ième terme précédent (si, dans un modèle donné, cette corrélation ne dépend pas de la position du terme, on dit que le processus est faiblement stationnaire -- il est fortement stationnaire si pout tous t, h, (X(t),X(t+1),...,X(t+n)) et (X(t+h),X(t+h+1),...,X(t+h+n)) ont la même distribution). Dans le graphique suivant, à part la première, la plupart (1/20) des valeurs de l'ACF doivent être entre les pointillés. (En toute rigueur, il convient de distinguer l'ACF, associée à un modèle, et la SACF (ACF de l'échantillon), que l'on calcule à l'aide d'une réalisation de ce modèle : ici, il s'agit de SACF.)
op <- par(mfrow=c(2,1)) x <- ts(rnorm(200)) plot(x, main="vaiid normales") acf(x) par(op)

Sur un exemple réel, c'est loin d'être le cas.
op <- par(mfrow=c(2,1)) data(BJsales) plot(BJsales) acf(BJsales) par(op)

A FAIRE (il manque une phrase)
f <- 24 x <- seq(0,10, by=1/f) y <- sin(2*pi*x) y <- ts(y, start=0, frequency=f) op <- par(mfrow=c(4,1)) plot(y) acf(y) pacf(y) spectrum(y) par(op)

A FAIRE : effacer l'exemple suivant s'il duplique le précédent.
f <- 24 x <- seq(0,10, by=1/f) y <- x + sin(2*pi*x) + rnorm(10*f) y <- ts(y, start=0, frequency=f) op <- par(mfrow=c(4,1)) plot(y) acf(y) pacf(y) spectrum(y) par(op)

A FAIRE : le graphe de l'ACF s'appelle corrélogramme. Dans le cas où les observations ne sont pas régulièrement espacées, on peut tracer le variogramme : (y(t_i)-y(t_j))^2 en fonction de t_i-t_j.
A FAIRE : graphique avec des données espacées aléatoirement. A FAIRE : lisser ce graphique.
Souvent, il s'agit de séries temporelles régulièrement espacées auxquelles il manque certains termes. Dans ce cas, pour une abscisse donnée de k=t_i-t_j, on a plusieurs points : on les remplacera par leur moyenne.
A FAIRE : exemple (prendre une série temporelle, enlever certaines valeurs, comparer corrélogramme, variogramme de la série entière, variogramme de la série amputée)
Voici une manière simple de construire une série temporelle à partir d'un bruit : si X est un bruit blanc, on peut obtenir une version "lissée" de X en en faisant une moyenne mobile (en anglais : Moving Average ou MA).
n <- 200 x <- rnorm(n) y <- ( x[2:n] + x[2:n-1] ) / 2 op <- par(mfrow=c(3,1)) plot(ts(x), main="buit blanc") plot(ts(y), main="MA(1)") acf(y) par(op)

n <- 200 x <- rnorm(n) y <- ( x[1:(n-3)] + x[2:(n-2)] + x[3:(n-1)] + x[4:n] )/4 op <- par(mfrow=c(3,1)) plot(ts(x), main="bruit blanc") plot(ts(y), main="MA(3)") acf(y) par(op)

On peut aussi faire un moyenne mobile avec d'autres coefficients.
n <- 200 x <- rnorm(n) y <- x[2:n] - x[1:(n-1)] op <- par(mfrow=c(3,1)) plot(ts(x), main="bruit blanc") plot(ts(y), main="MA(1)") acf(y) par(op)

n <- 200 x <- rnorm(n) y <- x[3:n] - 2 * x[2:(n-1)] + x[1:(n-2)] op <- par(mfrow=c(3,1)) plot(ts(x), main="bruit blanc") plot(ts(y), main="MA(2)") acf(y) par(op)

Plutôt que d'effectuer la moyenne mobile à la main, on peut utiliser la commande filter.
n <- 200 x <- rnorm(n) y <- filter(x, c(1,-2,1)) op <- par(mfrow=c(3,1)) plot(ts(x), main="bruit blanc") plot(ts(y), main="MA(2)") acf(y, na.action=na.pass) par(op)

Une autre manière de construire des séries temporelles, c'est de construire chaque terme à partir du précédent en lui ajoutant une valeur aléatoire : c'est une marche aléatoire.
Par exemple,
n <- 200
x <- rep(0,n)
for (i in 2:n) {
x[i] <- x[i-1] + rnorm(1)
}Ce que l'on peut écrire plus simplement
n <- 200 x <- rnorm(n) y <- cumsum(x) op <- par(mfrow=c(3,1)) plot(ts(x)) plot(ts(y), main="AR(1)") acf(y) par(op)

Plus généralement, on peut considérer
X(n+1) = a X(n) + bruit.
On appelle ça un modèle auto-régressif, car on peut obtenir le coefficients en faisant une régression de x sur lag(x,1).
n <- 200
a <- .7
x <- rep(0,n)
for (i in 2:n) {
x[i] <- a*x[i-1] + rnorm(1)
}
y <- x[-1]
x <- x[-n]
r <- lm( y ~ x -1)
plot(y~x)
abline(r, col='red')
abline(0, .7, lty=2)
Plus généralement, un processus AR(q) est un processus dans lequel un terme est la somme d'une combinaison linéaire (à coefficients constants) des q termes précédents et d'un bruit blanc.
n <- 200
x <- rep(0,n)
for (i in 4:n) {
x[i] <- .3*x[i-1] -.7*x[i-2] + .5*x[i-3] + rnorm(1)
}
op <- par(mfrow=c(3,1))
plot(ts(x), main="AR(3)")
acf(x)
pacf(x)
par(op)
On peut aussi simuler ces modèles à l'aide de la commande arima.sim.
n <- 200 x <- arima.sim(list(ar=c(.3,-.7,.5)), n) op <- par(mfrow=c(3,1)) plot(ts(x), main="AR(3)") acf(x) pacf(x) par(op)

La Fonction d'AutoCorrélation Partielle (PACF) est un estimateur des coefficients d'un modèle AR(infini) : on l'a vue sur les exemples précédents. Elle se calcule simplement (à l'aide des "équations de Yule-Walker") à partir de l'autocorrélation.
A FAIRE : je crois que ce n'est pas ça, les équations de Yule-Walker...
Pour calculer la fonction d'autocorrélation d'un processus AR(p) dont on connait les coefficients,
(1 - a1 B - a2 B^2 - ... - ap B^p) Y = Z
il suffit de calculer les premières autocorrélations r1, r2, etc., puis d'utiliser les équations de Yule-Walker :
r(j) = a1 r(j-1) + a2 r(j-2) + ... + ap r(j-p).
On peut aussi les utiliser dans l'autre sens, pour trouver les coefficients du processus AR à partir de ses autocorrélations.
Une série temporelle est faiblement stationnaire si l'espérance de X(t) ne dépend pas de t et si la covariance de X(t) et X(s) ne dépend que de abs(t-s). (On dit qu'elle est stationnaire si les X(t) ont tous la même distribution et si les (X(t),X(s)) ont tous la même distribution : faiblement stationnaire signifie donc "stationnaire au second ordre".)
Par exemple, s'il y a une tendance, i.e., si l'espérance de X(t) n'est pas constante, la série n'est pas stationnaire.
n <- 200 x <- seq(0,2,length=n) tendance <- ts(sin(x)) plot(tendance, ylim=c(-.5,1.5), lty=2, lwd=3, col='red', ylab='') r <- arima.sim(list(ar = c(0.5,-.3), ma = c(.7,.1)), n, sd=.1 ) lines(tendance+r)

Autre exemple : une marche aléatoire n'est pas stationnaire, car la variance de X(t) augmente avec t.
n <- 200
k <- 10
x <- 1:n
r <- matrix(nr=n,nc=k)
for (i in 1:k) {
r[,i] <- cumsum(rnorm(n))
}
matplot(x,r,type='l',lty=1,col=par('fg'))
abline(h=0,lty=3)
Ergodicité et stationarité sont deux notions voisines mais distinctes.
Etant donné un processus stochastique X(n), n entier, pour calculer la moyenne de X(1), on peut procéder de deux manières différentes : soit on prend plusieurs réalisations de ce processus, qui donnent chacune une valeur de X(1), et on fait la moyenne de ces valeurs ; soit on prend un seul processus, et on fait la moyenne de X(1), X(2), X(3), etc. Le résultat que l'on veut est le premier, mais dans certains cas, les deux coïncident : on dit alors que le processus est ergodique.
Les processus ergodiques sont intéressants, car généralement, on ne dispose que d'une seule réalisation.
A FAIRE : bien comprendre les différences. (Exemple : un processus stationnaire n'est pas nécessairement ergodique.)
Dans un processus autorégressif (AR), il est raisonnable de demander que les observations antérieures aient d'autant moins d'influence qu'elles soient lointaines. C'est pourquoi on demande, dans le modèle AR(1),
Y(t+1) = a * Y(t) + Z(t) (où Z est un bruit blanc)
que abs(a)<1. Cela peut aussi s'écrire :
Y(t+1) - a Y(t) = Z(t)
ou encore
phi(B) Y = Z (où phi(u) = 1 - a u )
et on demande que toutes les racines de phi soient de module strictement supérieur à 1.
Plus généralement, un procesus AR
phi(B) Y = Z où phi(u) = 1 - a_1 u - a_2 u^2 - ... - a_p u^p
est stationnaire si les racines de phi sont toutes de module strictement supérieur à 1.
On peut vérifier que ces processus sont MA(infini).
Par symétrie, pour les moyennes mobiles, définies par
Y = psi(B) Z où psi(u) = 1 + b_1 u + b_2 u^3 + ... + b_q u^q
on demandera aussi que les racines de psi soient toutes de module strictement supérieur à un (on dit alors que le processus est inversible). Sans cette hypothèse, la fonction d'autocorrélation de définit pas uniquement les coefficients de la moyenne mobile. Par exemple, pour un processus MA(1),
Y(t+1) = Z(t+1) + a Z(t),
on peut remplacer a par 1/a sans changer la fonction d'autocorrélation.
n <- 200 ma <- 2 mai <- 1/ma op <- par(mfrow=c(4,1)) x <- arima.sim(list(ma=ma),n) plot(x) acf(x) lines(0:n, ARMAacf(ma=ma, lag.max=n), lty=2, lwd=3, col='red') x <- arima.sim(list(ma=mai),n) plot(x) acf(x) lines(0:n, ARMAacf(ma=mai, lag.max=n), lty=2, lwd=3, col='red') par(op)

A FAIRE : un exemple en degré plus élevé (je pensais qu'il suffisait d'inverser les racines du polynôme, mais visiblement, ce n'est pas ça...)
sym.poly <- function (z,k) {
# Somme des produits de k éléments distincts du vecteur z
if (k==0) {
r <- 1
} else if (k==1) {
r <- sum(z)
} else {
r <- 0
for (i in 1:length(z)) {
r <- r + z[i]*sym.poly(z[-i],k-1)
}
r <- r/k # chaque terme a été compté k fois...
}
r
}
sym.poly( c(1,2,3), 1 ) # 6
sym.poly( c(1,2,3), 2 ) # 11
sym.poly( c(1,2,3), 3 ) # 6
roots.to.poly <- function (z) {
n <- length(z)
p <- rep(1,n)
for (k in 1:n) {
p[n-k+1] <- (-1)^k * sym.poly(z,k)
}
p <- c(p,1)
p
}
roots.to.poly(c(1,2)) # 2 -3 1
round(Re( polyroot( roots.to.poly(c(1,2,3)) ) ), digits=1)
# Après ce léger interlude, on peut enfin inverser construire
# un processus MA et son inverse
n <- 200
k <- 3
ma <- runif(k,-1,1)
# On calcule les racines
z <- polyroot(c(1,-ma))
# On les inverse
zi <- 1/z
# On reconstruit le polynôme
p <- roots.to.poly(zi)
# Le résultat doit être réel, mais à cause des erreurs d'arrondi il ne l'est pas
p <- Re(p)
# On veut que le terme constant égale 1
p <- p/p[1]
mai <- -p[-1]
op <- par(mfrow=c(4,1))
x <- arima.sim(list(ma=ma),n)
plot(x)
acf(x)
lines(0:n, ARMAacf(ma=ma, lag.max=n), lty=2, lwd=3, col='red')
x <- arima.sim(list(ma=mai),n)
plot(x)
acf(x)
lines(0:n, ARMAacf(ma=mai, lag.max=n), lty=2, lwd=3, col='red')
par(op)
Le processus MA(p) inversibles ont un autre avantage : ce sont des processus AR(infini).
A FAIRE : sur un exemple (un résultat de modélisation), représenter graphiquement les racines de ces deux polynômes.
A FAIRE :
# Pour vérifier si la série qu'on étudie a des racines de l'unité library(tseries) ?adf.test ?pp.tests
On peut bien sûr mélanger les modèles MA et AR, pour obtenir un modèle ARMA (dans les formules suivantes, z représente un bruit blanc et x la série qui nous intéresse).
MA(p) : x(i) = a1 z(i-1) + a2 z(i-2) + ... + ap z(i-p) AR(q) : x(i) - b1 x(i-1) - b2 x(i-2) - ... - bq x(i-q) = z(i) ARMA(p,q) : x(i) - b1 x(i-1) - ... - bq x(i-q) = a1 z(i-1) + ... + ap z(i-p)
Remarque : on peut montrer que les processus AR(q) sont aussi des processus MA(infini).
Remarque : Le théorème de Wold affirme que tout processus stationnaire peut se décomposer comme une somme d'un processus MA(infini) et d'un processus déterministe (A FAIRE : définir la notion de processus déterministe).
Remarque : Si on note B l'opérateur de décalage (de sorte que l'opérateur de dérivation s'écrive 1-B), on peut écrire un processus ARMA ainsi :
phi(B) X(t) = theta(B) Z(t) où theta(B) = 1 + a1 B + a2 B^2 + ... + ap B^p phi(B) = 1 - b1 B - b2 B^2 - ... - bq B^q Z est un bruit blanc
Les processus ARMA donne une bonne approximation au second ordre des propriétés de la plupart des processus stationnaires. On peut donc utiliser les coefficients du processus ARMA le plus proche (au sens des MLE) comme un résumé statistique du processus étudié, exactement comme la moyenne et les quantile pour les séries univariées. S'ils permettent d'effectuer des prédictions, il donnent généralement peu d'information sur les mécanismes sous-jacents qui ont produit la série étudiée.
Un processus ARMA(p,q)
phi(B) Y = theta(B) Z
dans lequel phi et theta ont une racine en commun peut se simplifier en un processus ARMA(p-1,q-1).
Pour modéliser une série à l'aide d'un modèle ARMA, il faut qu'elle soit soit stationnaire. Pour s'y ramener (en gros, pour se débarasser de la tendance), on peut tenter de la dériver.
Le fait que la série n'est pas stationnaire se voit généralement sur le graphique. Sinon, on peut regarder sur l'ACF : pour une série stationnaire, elle décroit rapidement (exponentiellement) vers zéro.
data(Nile) op <- par(mfrow=c(2,1)) plot(Nile, main="Il n'y a pas de tendance") acf(Nile) par(op)

data(BJsales) op <- par(mfrow=c(3,1)) plot(BJsales, main="il y a une tendance") acf(BJsales) acf(BJsales, main="Elle disparait si on dérive") par(op)

n <- 2000 x <- arima.sim(model=list(ar=c(.3,.6), ma=c(.8,-.5,.2), order=c(2,1,3)), n) x <- ts(x) op <- par(mfrow=c(3,1)) plot(x, main="Dériver une fois suffit") acf(x) acf(diff(x)) par(op)

n <- 10000 x <- arima.sim(model=list(ar=c(.3,.6), ma=c(.8,-.5,.2), order=c(2,2,3)), n) x <- ts(x) op <- par(mfrow=c(4,1)) plot(x, main="Dériver deux fois fois suffit") acf(x) acf(diff(x)) acf(diff(x,differences=2)) par(op)

Pour voir un peu plus précisément si la décroissance est exponentielle, on peut faire une régression.
acf.exp <- function (x, lag.max=NULL, lag.max.reg=lag.max, ...) {
a <- acf(x, lag.max=lag.max.reg, plot=F)
b <- acf(x, lag.max=lag.max, ...)
r <- lm( log(a$acf) ~ a$lag -1)
lines( exp( b$lag * r$coef[1] ) ~ b$lag, lty=2 )
}
op <- par(mfrow=c(2,1))
data(BJsales)
acf.exp(BJsales)
acf.exp(BJsales, lag.max=40)
par(op)
data(Nile) acf.exp(Nile, lag.max.reg=10)

On peut aussi se débarasser de la composante saisonnière en dérivant, mais avec un décalage : au lieu de regarder les mesures effectuées chaque mois, on regarde la différence avec le même mois de l'année précédente.
x <- diff(co2, lag=12)
op <- par(mfrow=c(4,1))
plot(x)
acf(x)
pacf(x)
spectrum(x, col=par('fg'))
par(op)
y <- diff(x)
op <- par(mfrow=c(4,1))
plot(y)
acf(y)
pacf(y)
spectrum(y, col=par('fg'))
par(op)
Les processus ARIMA sont simplement des processus ARMA intégrés. En d'autres termes, un processus est ARIMA d'ordre d si sa d-ième dérivée est ARMA. Le modèle peut s'écrire
phi(B) (1-B)^d X(t) = theta(B) Z(t)
Les processus ARIMA ne sont pas des processus stationnaires (par exemple, la variance d'un bruit blanc intégré augmente). A FAIRE : Comprendre
A FAIRE : montrer sur un exemple qu'un processus ARIMA(0,1,0) n'est pas stationnaire. Y a-t-il des tests pour vérifier si c'est stationnaire ??? (sinon, on peut en faire un rapidement à la main : on découpe les données en deux, au milieu,et on compare la première autocorrélation des deux morceaux).
Pour avoir une idée de l'ordre d'un processus ARIMA, on le dérive jusqu'à ce que son ACF décroisse rapidement.
n <- 200 x <- arima.sim(list(order=c(2,1,2), ar=c(.5,-.8), ma=c(.9,.6)), n) op <- par(mfrow=c(3,1)) acf(x, main="Il faudra dériver une fois") acf(diff(x)) acf(diff(x, differences=2)) par(op)

n <- 200 x <- arima.sim(list(order=c(2,2,2), ar=c(.5,-.8), ma=c(.9,.6)), n) op <- par(mfrow=c(3,1)) acf(x, main="Il faudra dériver deux fois") acf(diff(x)) acf(diff(x, differences=2)) par(op)

Voici un exemple concret dans lequel on est tenté de dériver.
#data(sunspot, package=ts) # moved into stats data(sunspot) op <- par(mfrow=c(4,1)) plot(sunspot.month) acf(sunspot.month) plot(diff(sunspot.month)) acf(diff(sunspot.month)) par(op)

Dans l'exemple suivant aussi (mais en fait, la dérivation se contente de faire disparaitre la tendance, affine).
data(JohnsonJohnson) x <- log(JohnsonJohnson) op <- par(mfrow=c(4,1)) plot(x) acf(x) plot(diff(x)) acf(diff(x)) par(op)

Voici quelques exemples concrets dans lesquels on peut être tenté de dériver deux fois. Mais ça n'est pas toujours une bonne idée : si l'ACF décroit exponentiellement, on arrête de dérivée.
data(BJsales) x <- BJsales op <- par(mfrow=c(6,1)) plot(x) acf(x) plot(diff(x)) acf(diff(x)) plot(diff(x, difference=2)) acf(diff(x, difference=2)) par(op)

data(austres) x <- austres op <- par(mfrow=c(6,1)) plot(x) acf(x) plot(diff(x)) acf(diff(x)) plot(diff(x, difference=2)) acf(diff(x, difference=2)) par(op)

# Dans l'exemple précédent, il y avait clairement une tendance # linéaire : extrayons-la. data(austres) x <- lm(austres ~ time(austres))$res op <- par(mfrow=c(6,1)) plot(x) acf(x) plot(diff(x)) acf(diff(x)) plot(diff(x, difference=2)) acf(diff(x, difference=2)) par(op)

Ce sont des processus ARIMA saisonniers (l'intégration, la moyenne mobile ou la partie auto-régressive peuvent être saisonnières). On les note
(p,d,q) \times (P,D,Q) _s
et ils sont décrits par le modèle :
phi(B) Phi(B^s) (1-B)^d (1-B^s)^D X(t) = theta(B) Theta(B^s) Z(t) où theta(B) = 1 + a1 B + a2 B^2 + ... + ap B^p phi(B) = 1 - b1 B - b2 B^2 - ... - bq B^q Theta(B^s) = 1 + A1 B^s + A2 B^2s + ... + AP B^(P*s) Phi(B^s) = 1 - B1 B^s - B2 B^2s - ... - BQ B^(Q*s) Z est un bruit blanc
Il n'y a pas de fonction prévue pour simuler des processus SARIMA (mais pour la modélisation, c'est bon).
my.sarima.sim <- function (n=20, period=12, model, seasonal) {
x <- arima.sim( model, n*period )
x <- x[1:(n*period)]
for (i in 1:period) {
xx <- arima.sim( seasonal, n )
xx <- xx[1:n]
x[i + period * 0:(n-1)] <- x[i + period * 0:(n-1)] + xx
}
x <- ts(x, frequency=period)
x
}
op <- par(mfrow=c(3,1))
x <- my.sarima.sim(20, 12,
list(ar=.6, ma=.3, order=c(1,0,1)),
list(ar=c(.5), ma=c(1,2), order=c(1,0,2))
)
eda.ts(x, bands=T)
x <- my.sarima.sim(20, 12,
list(ar=c(.5,-.3), ma=c(-.8,.5,-.3), order=c(2,1,3)),
list(ar=c(.5), ma=c(1,2), order=c(1,0,2))
)
eda.ts(x, bands=T)
x <- my.sarima.sim(20, 12,
list(ar=c(.5,-.3), ma=c(-.8,.5,-.3), order=c(2,1,3)),
list(ar=c(.5), ma=c(1,2), order=c(1,1,2))
)
eda.ts(x, bands=T)
L'exemple co2 (un peu plus haut), doit bien se modéliser comme un processus SARIMA.
Pour trouver l'ordre du modèle, on peut tatonner ainsi.
x <- co2 eda.ts(x)

On commence par remarquer qu'il y a une tendance : on dérive pour s'en débarasser.
eda.ts(diff(x))

On remarque ensuite qu'il y a une composante périodique, de période 12 mois : on dérive, avec un décalage de 12 mois, pour s'en débarasser.
eda.ts(diff(diff(x),lag=12))

On regarde ensuite l'ACF et le PACF, qui suggèrent un modèle ARMA(1,1)(2,1) ou ARMA(1,2)(2,1).
Calculons les coefficients de ce modèle :
r1 <- arima( co2,
order=c(1,1,1),
list(order=c(2,1,1), period=12)
)
r2 <- arima( co2,
order=c(1,1,2),
list(order=c(2,1,1), period=12)
)Il vient :
> r1
Call:
arima(x = co2, order = c(1, 1, 1), seasonal = list(order = c(2, 1, 1), period = 12))
Coefficients:
ar1 ma1 sar1 sar2 sma1
0.2595 -0.5902 0.0113 -0.0869 -0.8369
s.e. 0.1390 0.1186 0.0558 0.0539 0.0332
sigma^2 estimated as 0.08163: log likelihood = -83.6, aic = 179.2
> r2
Call:
arima(x = co2, order = c(1, 1, 2), seasonal = list(order = c(2, 1, 1), period = 12))
Coefficients:
ar1 ma1 ma2 sar1 sar2 sma1
0.5935 -0.929 0.1412 0.0141 -0.0870 -0.8398
s.e. 0.2325 0.237 0.1084 0.0557 0.0538 0.0328
sigma^2 estimated as 0.08132: log likelihood = -82.85, aic = 179.7Regardons leur p-valeur
> round(pnorm(-abs(r1$coef), sd=sqrt(diag(r1$var.coef))),5)
ar1 ma1 sar1 sar2 sma1
0.03094 0.00000 0.42007 0.05341 0.00000
> round(pnorm(-abs(r1$coef), sd=sqrt(diag(r1$var.coef))),5)
ar1 ma1 ma2 sar1 sar2 sma1
0.00535 0.00004 0.09635 0.39989 0.05275 0.00000Ce qui suggère un modèle SARIMA(1,1,1)(0,1,1).
r3 <- arima( co2,
order=c(1,1,1),
list(order=c(0,1,1), period=12)
)Il vient :
> r3
Call:
arima(x = co2, order = c(1, 1, 1), seasonal = list(order = c(0, 1, 1), period = 12))
Coefficients:
ar1 ma1 sma1
0.2399 -0.5710 -0.8516
s.e. 0.1430 0.1237 0.0256
sigma^2 estimated as 0.0822: log likelihood = -85.03, aic = 178.07
> round(pnorm(-abs(r3$coef), sd=sqrt(diag(r3$var.coef))),5)
ar1 ma1 sma1
0.04676 0.00000 0.00000On regarde maintenant les résidus.
r3 <- arima(co2, order = c(1, 1, 1), seasonal = list(order = c(0, 1, 1), period = 12)) eda.ts(r3$res)

C'est bon, on peut faire des prédictions. Pour avoir une idée de la qualité de ces prédictions, on peut utiliser le début des données pour faire la modélisation, prédire la suite et comparer avec les valeurs réelles.
x1 <- window(co2,end=1990) r <- arima(x1, order = c(1, 1, 1), seasonal = list(order = c(0, 1, 1), period = 12)) plot(co2) p <- predict(r, n.ahead=100) lines(p$pred, col='red') lines(p$pred+qnorm(.025)*p$se, col='red', lty=3) lines(p$pred+qnorm(.975)*p$se, col='red', lty=3)

# Par contre, je ne sais pas quoi penser de ce graphique # (on dirait du bruit intégré) : eda.ts(co2-p$pred)

On dira que ça a l'air fiable : on peut faire des prédictions.
r <- arima(co2, order = c(1, 1, 1), seasonal = list(order = c(0, 1, 1), period = 12)) p <- predict(r, n.ahead=150) plot(co2, xlim=c(1959,2010), ylim=range(c(co2,p$pred))) lines(p$pred, col='red') lines(p$pred+qnorm(.025)*p$se, col='red', lty=3) lines(p$pred+qnorm(.975)*p$se, col='red', lty=3)
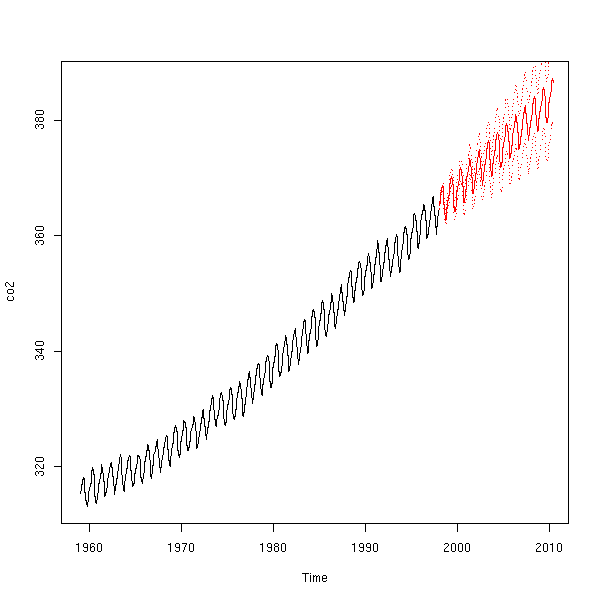
Ce que l'on vient de faire s'appelle la méthode de Box et Jenkins. En toute généralité, ça peut être un peu plus compliqué : si les résidus ne conviennent pas, il faut retourner en arrière et essayer de trouver un autre modèle.
0. Différencier pour avoir un processus stationnaire (S'il y a une tendance, il n'est pas stationnaire. Si l'ACF décroit lentement, essayer de dériver une fois -- rarement plus.) 1. Identifier le modèle ARMA(1,0): ACF: décroissance exponentielle ; PACF: un seul pic ARMA(2,0): ACF: décroissance exponentielle ou vagues ; PACF: deux pics ARMA(0,1): ACF: un seul pic ; PACF: décroissance exponentielle ARMA(0,2): ACF: deux pics ; PACF: décroissance exponentielle ou vagues ARMA(1,1): ACF&PACF: décroissance exponentielle 2. Calculer les coefficients 3. Diagnostics (repartir en 1 si ça ne convient pas) (calculer les p-valeurs, essayer d'enlever les paramètres inutiles) Regarder les résidus. 4. Prévisions
Voici quelques exemples de processus ARMA (en rouge : l'ACF et la PACF théoriques).
Un modèle ARMA(1,0) se reconnait à la décroissance exponentielle de son ACF et au pic unique de sa PACF.
op <- par(mfrow=c(4,2))
n <- 200
for (i in 1:4) {
x <- NULL
while(is.null(x)) {
model <- list(ar=rnorm(1))
try( x <- arima.sim(model, n) )
}
acf(x, main=paste("ARMA(1,0)","AR:",round(model$ar,digits=1)))
points(0:50, ARMAacf(ar=model$ar, lag.max=50), col='red')
pacf(x)
points(1:50, ARMAacf(ar=model$ar, lag.max=50, pacf=T), col='red')
}
par(op)
Un modèle ARMA(2,0) se reconnait aux deux pics de sa PACF et à la décroissance exponentielle de (ou à la présence de vagues dans) son ACF.
op <- par(mfrow=c(4,2))
n <- 200
for (i in 1:4) {
x <- NULL
while(is.null(x)) {
model <- list(ar=rnorm(2))
try( x <- arima.sim(model, n) )
}
acf(x,
main=paste("ARMA(2,0)","AR:",
round(model$ar[1],digits=1),
round(model$ar[2],digits=1)
))
points(0:50, ARMAacf(ar=model$ar, lag.max=50), col='red')
pacf(x)
points(1:50, ARMAacf(ar=model$ar, lag.max=50, pacf=T), col='red')
}
par(op)
Un modèle ARMA(0,1) se reconnait au pic unique de son ACF et à la décroissance exponentielle de sa PACF.
op <- par(mfrow=c(4,2))
n <- 200
for (i in 1:4) {
x <- NULL
while(is.null(x)) {
model <- list(ma=rnorm(1))
try( x <- arima.sim(model, n) )
}
acf(x, main=paste("ARMA(0,1)","MA:",round(model$ma,digits=1)))
points(0:50, ARMAacf(ma=model$ma, lag.max=50), col='red')
pacf(x)
points(1:50, ARMAacf(ma=model$ma, lag.max=50, pacf=T), col='red')
}
par(op)
Un modèle ARMA(0,2) se reconnait aux deux pics de son ACF et à la décroissance exponentielle (ou à la présence de vagues) de sa PACF.
op <- par(mfrow=c(4,2))
n <- 200
for (i in 1:4) {
x <- NULL
while(is.null(x)) {
model <- list(ma=rnorm(2))
try( x <- arima.sim(model, n) )
}
acf(x, main=paste("ARMA(0,2)","MA:",
round(model$ma[1],digits=1),
round(model$ma[2],digits=1)
))
points(0:50, ARMAacf(ma=model$ma, lag.max=50), col='red')
pacf(x)
points(1:50, ARMAacf(ma=model$ma, lag.max=50, pacf=T), col='red')
}
par(op)
Un modèle ARMA(1,1) se reconnait à la décroissance exponentielle de son ACF et de sa PACF.
op <- par(mfrow=c(4,2))
n <- 200
for (i in 1:4) {
x <- NULL
while(is.null(x)) {
model <- list(ma=rnorm(1),ar=rnorm(1))
try( x <- arima.sim(model, n) )
}
acf(x, main=paste("ARMA(1,1)",
"AR:", round(model$ar,digits=1),
"AR:", round(model$ma,digits=1)
))
points(0:50, ARMAacf(ar=model$ar, ma=model$ma, lag.max=50), col='red')
pacf(x)
points(1:50, ARMAacf(ar=model$ar, ma=model$ma, lag.max=50, pacf=T), col='red')
}
par(op)
Au lieu de tatonner à la main comme on vient de le faire, on aurait pu tatonner beaucoup plus violemment, en regardant l'AIC de tous les modèles d'une complexité raisonnable et en retenant ceux dont l'AIC est le plus faible (comme cela revient en fait à faire d'innombrables tests, on ne prend pas le seul modèle dont l'AIC est le plus bas, mais on en prend plusieurs : on en choisira un qui soit à la fois simple et dont les résidus aient l'air corrects). (Je ne suis pas sûr que l'AIC soit une bonne idée pour comparer des modèles avec un nombre de dérivées différent.)
a <- array(NA, dim=c(2,2,2,2,2,2))
for (p in 0:2) {
for (d in 0:2) {
for (q in 0:2) {
for (P in 0:2) {
for (D in 0:2) {
for (Q in 0:2) {
r <- list(aic=NA)
try(
r <- arima( co2,
order=c(p,d,q),
list(order=c(P,D,Q), period=12)
)
)
a[p,d,q,P,D,Q] <- r$aic
cat(r$aic); cat("\n")
}
}
}
}
}
}
# Pour exploiter les résultats, j'ai besoin de connaitre les
# valeurs pour lesquelles l'AIC est le plus faible.
argmin.vector <- function (v) {
(1:length(v)) [ v == min(v) ]
}
x <- sample(1:10)
x
argmin.vector(x)
x <- sample(1:5, 20, replace=T)
x
argmin.vector(x)
x <- array(x, dim=c(5,2,2))
index.from.vector <- function (i,d) {
res <- NULL
n <- prod(d)
i <- i-1
for (k in length(d):1) {
n <- n/d[k]
res <- c( i %/% n, res )
i <- i %% n
}
res+1
}
index.from.vector(7, c(2,2,2))
index.from.vector(29, c(5,3,2))
argmin <- function (a) {
a <- as.array(a)
d <- dim(a)
a <- as.vector(a)
res <- matrix(nr=0, nc=length(d))
for (i in (1:length(a))[ a == min(a) ]) {
j <- index.from.vector(i,d)
res <- rbind(res, j)
}
res
}
x <- array( sample(1:10,30, replace=T), dim=c(5,3,2) )
argmin(x)Après deux ou trois heures de calculs (je m'inquiète peut-être pour rien, mais l'ordinateur emmet un drôle de sifflement quand je lance ces calculs...), il vient :
1 1 1 2 1 2
Ce sont des modèles un peu trop compliqués. Regardons quels sont les modèles dont l'AIC est proche de celui-ci.
x <- as.vector(a)
d <- dim(a)
o <- order(x)
res <- matrix(nr=0, nc=6+2)
for (i in 1:30) {
p <- index.from.vector(o[i],d)
res <- rbind( res, c(p, sum(p), x[o[i]]))
}
colnames(res) <- c("p","d","q", "P","D","Q", "n", "AIC")
resIl vient :
p d q P D Q n AIC
[1,] 1 1 1 2 1 2 8 172.7083
[2,] 1 1 2 2 1 2 9 173.3215
[3,] 0 1 1 2 1 2 7 173.5009
[4,] 2 1 2 2 1 2 10 173.8748
[5,] 0 1 2 2 1 2 8 174.0323
[6,] 2 1 1 0 1 1 6 177.8278
[7,] 1 1 1 0 1 1 5 178.0672
[8,] 0 1 1 0 1 1 4 178.1557
[9,] 2 1 1 2 1 1 8 178.9373
[10,] 2 1 2 0 1 1 7 179.0768
[11,] 2 1 0 2 1 2 8 179.0776
[12,] 0 1 2 0 1 1 5 179.0924
[13,] 1 1 1 2 1 1 7 179.2043
[14,] 2 1 1 0 1 2 7 179.3557
[15,] 2 1 1 1 1 1 7 179.4335
[16,] 1 1 2 2 1 1 8 179.6950
[17,] 1 1 1 0 1 2 6 179.6995
[18,] 0 1 1 2 1 1 6 179.7224
[19,] 1 1 1 1 1 1 6 179.7612
[20,] 0 1 1 0 1 2 5 179.8808
[21,] 0 1 1 1 1 1 5 179.9235
[22,] 1 1 2 0 1 1 6 180.1146
[23,] 1 1 0 2 1 2 7 180.1713
[24,] 2 1 2 2 1 1 9 180.2019
[25,] 1 1 2 1 1 1 7 180.2686
[26,] 0 1 2 2 1 1 7 180.4483
[27,] 2 1 2 0 1 2 8 180.4797
[28,] 2 1 2 1 1 1 8 180.5757
[29,] 1 1 1 1 1 2 7 180.7777
[30,] 0 1 2 0 1 2 6 180.8024
[31,] 0 1 2 1 1 1 6 180.8495
[32,] 0 1 1 1 1 2 6 181.1830
[33,] 1 1 2 1 1 2 8 181.3127
[34,] 2 1 2 1 1 2 9 181.6425
[35,] 1 1 2 0 1 2 7 181.7322
[36,] 0 1 2 1 1 2 7 181.9859
[37,] 2 1 0 0 1 1 5 183.4687
[38,] 1 1 0 0 1 1 4 184.1817
[39,] 2 1 0 2 1 1 7 185.1404
[40,] 2 1 0 0 1 2 6 185.1918
[41,] 2 1 0 1 1 1 6 185.2337
[42,] 1 1 0 0 1 2 5 185.7290
[43,] 1 1 0 1 1 1 5 185.7909
[44,] 1 1 0 2 1 1 6 186.0117
[45,] 2 1 0 1 1 2 7 186.5521
[46,] 1 1 0 1 1 2 6 187.1703En regardant la répartition des AIC,
plot(sort(as.vector(a))[1:100])
on constate que le premier paquet de valeurs se situe en dessous de 200 : parmi tous ces cas, on choisit les plus simples :
p d q P D Q n AIC 0 1 1 0 1 1 4 178.1557 1 1 0 0 1 1 4 184.1817 1 1 1 0 1 1 5 178.0672 0 1 2 0 1 1 5 179.0924 0 1 1 0 1 2 5 179.8808 0 1 1 1 1 1 5 179.9235 2 1 0 0 1 1 5 183.4687 1 1 0 0 1 2 5 185.7290 1 1 0 1 1 1 5 185.7909
Je serais tenté de choisir le premier.
0 1 1 0 1 1
ou le troisième (celui que nous avait donné la méthode de Box et Jenkins)
1 1 1 0 1 1
Faisons les calculs.
> r <- arima(co2, order=c(0,1,1), list(order=c(0,1,1), period=12 ) )
> r
Call:
arima(x = co2, order = c(0, 1, 1), seasonal = list(order = c(0, 1, 1), period = T))
Coefficients:
ma1 sma1
0.1436 0.1436
s.e. 0.1068 0.1068
sigma^2 estimated as 0.7821: log likelihood = -604.01, aic = 1214.02
> r$var.coef
ma1 sma1
ma1 0.01140545 -0.01048563
sma1 -0.01048563 0.01140545
> pnorm(-abs(r$coef), sd=sqrt(diag(r$var.coef)))
ma1 sma1
0.08940721 0.08940721Regardons les résidus.
r <- arima(co2, order=c(0,1,1), list(order=c(0,1,1), period=12 ) ) eda.ts(r$res)

C'est bon, on garde ce modèle (si les résidus n'avaient pas convenu, on aurait pris un modèle un peu plus compliqué, jusqu'à ce qu'ils aient l'air convenables).
Comme précédemment, on peut valider le modèle et faire des prédictions.
x1 <- window(co2,end=1990) r <- arima(x1, order = c(0, 1, 1), seasonal = list(order = c(0, 1, 1), period = 12)) plot(co2) p <- predict(r, n.ahead=100) lines(p$pred, col='red') lines(p$pred+qnorm(.025)*p$se, col='red', lty=3) lines(p$pred+qnorm(.975)*p$se, col='red', lty=3)

eda.ts(co2-p$pred)

r <- arima(co2, order = c(0, 1, 1), seasonal = list(order = c(0, 1, 1), period = 12)) p <- predict(r, n.ahead=150) plot(co2, xlim=c(1959,2010), ylim=range(c(co2,p$pred))) lines(p$pred, col='red') lines(p$pred+qnorm(.025)*p$se, col='red', lty=3) lines(p$pred+qnorm(.975)*p$se, col='red', lty=3)

Les prédictions sont les mêmes que celles du modèle précédent.
r1 <- arima(co2, order = c(0, 1, 1), seasonal = list(order = c(0, 1, 1), period = 12)) r2 <- arima(co2, order = c(1, 1, 1), seasonal = list(order = c(0, 1, 1), period = 12)) p1 <- predict(r1, n.ahead=150) p2 <- predict(r2, n.ahead=150) plot(co2, xlim=c(1959,2010), ylim=range(c(co2,p$pred))) lines(p1$pred, col='red') lines(p2$pred, col='green', lty=3, lwd=4)

Comme pour la régression, on transforme préalablement les données pour qu'elles soient "plus gentilles" (pour cela, on peut commenter par les tracer : histogramme, densité, qqplot, etc., puis chercher une transformation de Box-Cox). Par exemple, si on remarque que les variations de la série sont d'autant plus grande que la valeur est grande, i.e., si on pense que le modèle est de la forme << quelque chose de déterministe >> multiplié par du bruit, on prendra le logarithme, pour se ramener à un modèle additif.
A FAIRE : mettre de l'ordre dans l'exemple suivant.
Exemples
data(AirPassengers) x <- AirPassengers plot(x)

plot(x) abline(lm(x~time(x)), col='red')

Les résidus ou la première dérivée discrète montrent que l'amplitude des variations augmente.
plot(lm(x~time(x))$res)

plot(diff(x))

On prend donc le logarithme.
x <- log(x) plot(x) abline(lm(x~time(x)),col='red')

plot(lm(x~time(x))$res)

plot(diff(x))

On peut aussi regarder les différences suivantes.
op <- par(mfrow=c(3,1)) plot(diff(x,1,2)) plot(diff(x,1,3)) plot(diff(x,1,4)) par(op)

La nature de la série suggère une composante de période 12 mois.
op <- par(mfrow=c(3,1)) plot(x) abline(h=0, v=1950:1962, lty=3) y <- diff(x) plot(y) abline(h=0, v=1950:1962, lty=3) plot(diff(y, 12,1)) abline(h=0, v=1950:1962, lty=3) par(op)

La régression permet plus facilement de se débarasser de la tendance haussière.
op <- par(mfrow=c(3,1)) plot(x) abline(lm(x~time(x)), col='red', lty=2) abline(h=0, v=1950:1962, lty=3) y <- x - predict(lm(x~time(x))) plot(y) abline(h=0, v=1950:1962, lty=3) plot(diff(y, 12,1)) abline(h=0, v=1950:1962, lty=3) par(op)

On regarde maintenant le reste, et on le différencie.
z <- diff(y,12,1) op <- par(mfrow=c(3,1)) plot(z) abline(h=0,lty=3) plot(diff(z)) abline(h=0,lty=3) plot(diff(z,1,2)) abline(h=0,lty=3) par(op)

Pour savoir combien de fois il faut différencier, on peut regarder la corrélation entre x(i) et x(i-1) après chaque différentiation.
k <- 3
n <- 2*k
op <- par(mfrow=c(k,2))
zz <- z
for(i in 1:n) {
acf(zz, main=i-1)
zz <- diff(zz)
}
par(op)
A FAIRE : calculer la première corrélation à la main.
NON : il arrive que la première corrélation soit significativement non nulle
sans qu'il faille dériver (par exemple, MA(1)).
n <- 20
a <- rep(NA,n)
zz <- z
for(i in 1:n) {
a[i] <- acf(zz, plot=F)$acf[2]
zz <- diff(zz)
}
plot(a,type='h')
abline(h=0,lty=3)
Quelques exemples de ce genre de graphique
(qui n'est peut-être pas très facile à lire, donc peut-être pas très utile...)
op <- par(mfrow=c(2,2))
n <- 20
for (k in 1:4) {
zz <- rnorm(100)
for (l in 1:k) {
zz <- cumsum(zz)+rnorm(100)
}
a <- rep(NA,n)
for(i in 1:n) {
a[i] <- acf(zz, plot=F)$acf[2]
zz <- diff(zz)
}
plot(a,type='h', main=paste("Il faut dériver",k,"fois"))
abline(h=c(0,.5,-.5),lty=3)
}
par(op)
Autre idée : faire une régression de x(i) sur x(i-1), x(i-2), etc.
Pour avoir des résultats fiables, on peut orthogonaliser les
variables prédictives.
A FAIRE
A FAIRE : Lien avec la PACF ?
data(sunspots)
op <- par(mfrow=c(5,1))
for (i in 10+1:5) {
plot(diff(sunspots,i))
}
par(op)
A FAIRE
A FAIRE : cross-validation (c'est un peut limité, parce que, a priori, on ne peut faire qu'une seule validation : on choisit un modèle avec toutes les données, on calcule ses coefficients avec le début et on vérifie sur la fin -- si ça concorde, on accepte le modèle et on calcule ses coefficients à l'aide de toute la série).
A FAIRE : bootstrap et séries temporelles (on construit une nouvelle série en mettant bout-à-bout des morceaux de la série de départ (on coupe n'importe où, des morceaux de n'importe quelle longueur). C'est déjà prévu dans le paquetage boot. Pour plus d'explications, voir le numéro ***A FAIRE*** (A FAIRE : URL) de RNews.)
De même que les modèles AR(I)MA étudient les séries temporelles en modélisant leur autocorrélation, les modèles (G)ARCH les étudient en modélisant leur variance.
Il est utile de rappeler le statut de la variance dans les modèles que nous avons rencontrés jusqu'à présent : on la supposait toujours constante. C'était le cas pour la régression, où il fallait bien vérifier (graphiquement) que les résidus ne présentaient pas d'hétéroscédasticité. C'était aussi le cas pour les modèles ARIMA : on s'efforçait de dériver suffisemment pour avoir une série stationnaire, que l'on modélisait alors par un processus ARMA.
A FAIRE : est-ce que la stationnarité implique que la variance est constante ??? La stationnarité dit que les autocorrélations cor(X(t),X(t-n)) ne dépendent pas de n. Mais ce sont des corrélations, pas des covariances...
On rencontre souvent les modèles (G)ARCH en finance, où ils permettent de modéliser la volatilité : en effet, on a remarqué que des changements importants dans le cours d'une action sont suivis d'autres changements importants (dans un sens quelconque : on peut avoir une hausse importante suivie d'une baisse importante, ou une hausse importante suivie d'une autre hausse importante). On pas de "volatility clustering".
data(EuStockMarkets) x <- EuStockMarkets[,1] x <- diff(log(x)) i <- abs(x)>median(abs(x))
Regardons si les valeurs élevées ont tendance à se suivre :
> library(tseries)
> runs.test(factor(i))
Runs Test
data: factor(i)
Standard Normal = -2.2039, p-value = 0.02753
alternative hypothesis: two.sidedC'est le test du "nombre de suites" : on regarde le nombre de suites de valeurs élevées qui se suivent, le nombre de suites de valeurs faibles qui se suivent, on les transforme pour avoir quelque-chose qui suive (asymptotiquement) une loi normale. Ici, on obtient une valeur négative, ce qui signifie qu'on a moins de suites qu'on pouvait s'y attendre, i.e., que ces suites sont plus longues, et la p-valeur est inférieure à 5% : cette différence est statistiquement significativement.
Voici une autre implémentation de ce test :
nombre.de.suites <- function (x) {
1+sum(abs(diff(as.numeric(x))))
}
test.du.nombre.de.suites <- function (x, R=999) {
if( is.numeric(x) )
x <- factor(sign(x), levels=c(-1,1))
if( is.logical(x) )
x <- factor(x, levels=c(FALSE,TRUE))
if(!is.factor(x))
stop("x should be a factor")
# Test non paramétrique, basé sur le
# rééchantillonage
n <- length(x)
res <- rep(NA, R)
for (i in 1:R) {
res[i] <- nombre.de.suites(
x[sample(1:n,n,replace=F)]
)
}
t0 <- nombre.de.suites(x)
n1 <- 1+sum(t0<=res)
n2 <- 1+sum(t0>=res)
p <- min( n1/R, n2/R )*2
p <- min(1,p) # On peut avoir des problèmes
# si plus de la moitié des
# valeurs sont identiques...
# Test paramétrique, basé sur une formule
# trouvée sur Internet... On admet que Z
# suit à peu près une loi normale (on peut
# vérifier, par des simulations, que c'est
# complètement faux avec des évènements assez
# rares -- comme les mutations qui nous
# intéressent).
n1 <- sum(x==levels(x)[1])
n2 <- sum(x==levels(x)[2])
r <- nombre.de.suites(x)
mr <- 2*n1*n2/(n1+n2) + 1
sr <- sqrt( 2*n1*n2*(2*n1*n2-n1-n2)/
(n1+n2)^2/(n1+n2-1) )
z <- (r-mr)/sr
pp <- 2*min(pnorm(z), 1-pnorm(z))
r <- list(t0=t0, t=res, R=R,
p.value.boot=p,
n1=n1, n2=n2, r=r, mr=mr, sr=sr, z=z,
p.value.formula=pp)
class(r) <- "nstest"
r
}
print.nstest <- function (d) {
cat("Test du nombre de suites\n");
cat(" NS = ")
cat(d$t0)
cat("\n p-valeur (")
cat(d$R)
cat(" rééchantillonages) = ")
cat(round(d$p.value.boot,digits=3))
cat("\n")
cat(" p-valeur théorique = ")
cat(d$p.value.formula)
cat("\n")
}
plot.statistic <- function (t0, t, ...) {
xlim <- range(c(t,t0))
hist(t, col='light blue', xlim=xlim, ...)
points(t0, par("usr")[4]*.8,
type='h', col='red', lwd=5)
text(t0, par("usr")[4]*.85, signif(t0,3))
}
plot.nstest <- function (
d, main="Test du nombre de suites",
ylab="effectif", ...
) {
plot.statistic(d$t0, d$t, main=main,
xlab=paste("Nombre de suites, p =",signif(d$p.value.boot,3)),
...)
}
# Exemple
data(EuStockMarkets)
x <- EuStockMarkets[,1]
x <- diff(log(x))
i <- abs(x)>median(abs(x))
plot(test.du.nombre.de.suites(i))
On obtient la même p-valeur :
> test.du.nombre.de.suites(i) Test du nombre de suites NS = 883 p-valeur (999 rééchantillonages) = 0.024 p-valeur théorique = 0.02752902
On peut répéter cette expérience avec d'autres séries boursières :
op <- par(mfrow=c(2,2))
for (k in 1:4) {
x <- EuStockMarkets[,k]
x <- diff(log(x))
i <- abs(x)>median(abs(x))
plot(test.du.nombre.de.suites(i))
}
par(op)
A FAIRE : reprendre ces calculs avec beaucoup plus de séries...
Voici quelques exemples de modélisations de séries temporelles rencontrées en finance. Les notations sont les suivantes.
S la quantité modélisée t le temps dX le bruit gaussien, de variance dt s volatilité m dérive n une autre constante
Une marche aléatoire :
dS = s dX
Une marche aléatoire avec une dérive :
dS = m dt + s dX
Une marche aléatoire logarithmique :
dS = m S dt + s S dX
A mean-reverting random walk (utilisée pour modéliser une valeur qui ne va nulle part, par exemple un taux d'intérêt) :
dS = (n - m S) dt + s dX
Another mean-reverting random walk :
dS = (n - m S) dt + s S^.5 dX
On peut les simuler ainsi :
sde.sim <- function (t, f, ...) {
n <- length(t)
S <- rep(NA,n)
S[1] <- 1
for (i in 2:n) {
S[i] <- S[i-1] + f(S[i-1], t[i]-t[i-1], sqrt(t[i]-t[i-1])*rnorm(1), ...)
}
S
}
a <- 0
b <- 10
N <- 1000
x <- sde.sim(seq(a,b,length=N),
function (S,dt,dX,m=1,s=1) { m * S * dt + s * S * dX })
x <- ts(x, start=a, end=b, freq=(N-1)/(b-a))
op <- par(mfrow=c(4,1))
plot(x)
plot(log(x))
plot(diff(log(x)))
acf(diff(log(x)))
par(op)
Revoici des simulations des exemples précédents.
A FAIRE : plusieurs exemples pour chaque modèle
N <- 1000
a <- 0
b <- 3
op <- par(mfrow=c(3,1))
for (i in 1:3) {
x <- sde.sim(seq(a,b,length=N),
function (S,dt,dX,m=1,s=1) { s * dX })
x <- ts(x, start=a, end=b, freq=(N-1)/(b-a))
plot(x, main="Marche aléatoire")
}
par(op)
op <- par(mfrow=c(3,1))
for (i in 1:3) {
x <- sde.sim(seq(a,b,length=N),
function (S,dt,dX,m=1,s=1) { m * dt + s * dX })
x <- ts(x, start=a, end=b, freq=(N-1)/(b-a))
plot(x, main="Marche aléatoire avec dérive")
}
par(op)
op <- par(mfrow=c(3,1))
for (i in 1:3) {
x <- sde.sim(seq(a,b,length=N),
function (S,dt,dX,m=1,s=1) { m * S * dt + s * S * dX })
x <- ts(x, start=a, end=b, freq=(N-1)/(b-a))
plot(x, main="Marche aléatoire lognormale")
}
par(op)
b <- 10
op <- par(mfrow=c(3,1))
for (i in 1:3) {
x <- sde.sim(seq(a,b,length=N),
function (S,dt,dX,m=3,s=1,n=3) { (n - m*S) * dt + s * dX })
x <- ts(x, start=a, end=b, freq=(N-1)/(b-a))
plot(x, main="Mean-reverting random walk")
abline(h=1,lty=3)
}
par(op)
op <- par(mfrow=c(3,1))
for (i in 1:3) {
x <- sde.sim(seq(a,b,length=N),
function (S,dt,dX,m=3,s=1,n=3) { (n - m*S) * dt + s * sqrt(S) * dX })
x <- ts(x, start=a, end=b, freq=(N-1)/(b-a))
plot(x, main="Mean-reverting random walk")
abline(h=1,lty=3)
}
par(op)
A FAIRE :
regarder la volatilité sur ces exemples.
(préalablement, définir la volatilité)
op <- par(mfrow=c(2,1))
x <- sde.sim(seq(a,b,length=N),
function (S,dt,dX,m=1,s=1) { m * S * dt + s * S * dX })
x <- ts(x, start=a, end=b, freq=(N-1)/(b-a))
plot(x, main="Marche aléatoire lognormale")
return <- diff(x) / x[ -length(x) ]
y <- return^2
plot(y)
lines(predict(loess(y~time(y))) ~ as.vector(time(y)), col='red', lwd=3)
par(op)
Eh bien non, ça n'a visiblement rien à faire dans la section sur les modèles GARCH...
A FAIRE : mettre ça ailleurs...
Une série ARCH est une suite de variables aléatoires normales, centrées, indépendantes, mais pas de même variance.
u(n) ~ N(0, var=h(n)) h(n) = a0 + a1 u(n-1)^2 + a2 u(n-2)^2 + ... + aq u(n-q)^2
Exemple :
n <- 200
a <- c(1,.2,.8,.5)
a0 <- a[1]
a <- a[-1]
k <- length(a)
u <- rep(NA,n)
u[1:k] <- a0 * rnorm(k)
for (i in (k+1):n) {
u[i] <- sqrt( a0 + sum(a * u[(i-1):(i-k) ]^2 )) * rnorm(1)
}
u <- ts(u)
eda.ts(u)
Les graphiques que nous faisons ne permettent pas vraiment de voir l'hétéroscédasticité, même dans des cas plus extrèmes : ça ressemble vraiment à du bruit.
h <- rnorm(1000)^2 x <- filter(h, rep(1,50)) x <- x[!is.na(x)] eda.ts(x)

y <- rnorm(length(x),0,sqrt(x)) eda.ts(y)

h <- c(rep(1,100), rep(2,100)) y <- ts(rnorm(length(h), 0, sd=h)) eda.ts(y)
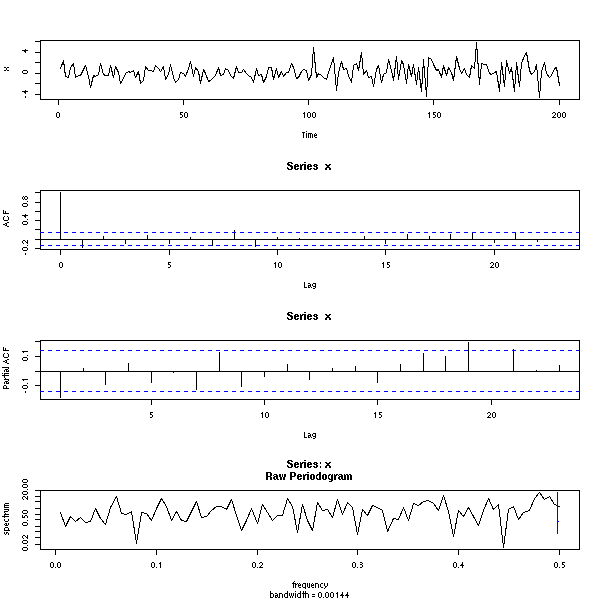
Comment s'appercevoir de l'hétéroscédasticité ?
Si elle est flagrante, comme dans le dernier, exemple, on peut faire une régression polynomiale (ou autre) sur la valeur absolue de la série.
plot(abs(y)) lines(predict(loess(abs(y)~time(y))), col='red', lwd=3) k <- 20 lines(filter(abs(y), rep(1/k,k)), col='blue', lwd=3, lty=2)

Avec notre modèle ARCH initial :
plot.ma <- function (x, k=20, ...) {
plot(abs(x), ...)
a <- time(x)
b <- predict(loess(abs(x) ~ a))
lines(b ~ as.vector(a), col='red', lwd=3)
k <- 20
lines(filter(abs(x), rep(1/k,k)), col='blue', lwd=3)
}
plot.ma(u)
Les séries que nous étudions précédemment étaient effectivement différentes.
n <- 1000 op <- par(mfrow=c(4,1)) plot.ma(ts(rnorm(n))) plot.ma(arima.sim(list(ar = c(.8,.1)), n)) plot.ma(arima.sim(list(ma = c(.8,.1)), n)) plot.ma(arima.sim(list(ma = c(.8,.4,.1), ar = c(.8,.1)), n)) par(op)

Dans tous ces modèles, on modèlise la variance d'une série temporelle (une série qui ressemble à du bruit : par exemple, ce qui reste après une régression, ou ce qui reste après s'être débarassé de la tendance et des composantes periodiques).
La série est définie par
u(n) ~ N(0, var=h(n))
et la variance, h(n), s'exprime en fonction des u(k) précédents.
ARCH :
h(n) = a0 + a1 u(n-1)^2 + a2 u(n-2)^2 + ... + aq u(n-q)^2
GARCH :
h(n) = a0 + a1 u(n-1)^2 + a2 u(n-2)^2 + ... + aq u(n-q)^2
+ b1 h(n-1) + ... + bq h(n-q)Dans ces modèles, le signe de u n'intervient pas. Néanmoins, dans des données boursières, on constate que ce signe est important.
Enfin, la littérature nous dit qu'il en est ainsi, moi je constate le contraire.
A FAIRE : vérifier que je n'ai pas confondu + et -...
op <- par(mfrow=c(1,4))
data(EuStockMarkets)
for (a in 1:4) {
x <- EuStockMarkets[,a]
x <- diff(log(x))
n <- length(x)
s <- rep(NA, n+1)
s[ which(x>0) + 1 ] <- "+"
s[ which(x<0) + 1 ] <- "-"
i <- which( !is.na(s) )
s <- factor(s[i])
x <- x[i]
boxplot(log(abs(x))~s, col='light blue')
}
par(op)
A FAIRE : prendre d'autres données boursières...
Certains modèles reflètent cette asymétrie (vous en trouverez probablement bien d'autres dans la littérature -- et vous pouvez d'ailleurs inventer les vôtres) :
AGARCH1 (effets symétriques autour de A, pas autour de 0) :
h(n) = a0 + a1 (A + u(n-1))^2 + ... + aq (A + u(n-q))^2
+ b1 h(n-1) + ... + bq h(n-q)AGARCH2 (coefficients plus grands quand u>0) :
h(n) = a0 + a1 (abs(u(n-1)) + A*u(n-1))^2 + ... + aq (abs(u(n-q)) + A*u(n-q))^2
+ b1 h(n-1) + ... + bq h(n-q)GJR-GARCH (idem) :
h(n) = a0 + (a1 + A * (u(n-1)>0)) * u(n-1))^2 + ... + (aq + A*(u(n-q)>0)) * u(n-q))^2
+ b1 h(n-1) + ... + bq h(n-q)EGARCH :
A FAIRE A FAIRE
On peut utiliser un modèles (G)ARCH pour modéliser le bruit dans une régression (dont on constate que les résidus sont hétéroscédastiques).
A FAIRE : un exemple, qui met en évidence les effets de l'hétéroscédasticité (biais ? distribution non normale des résidus ? erreur dans les intervales de confiance ?)
Attention : je n'ai pas encore compris ce qui suit. Il n'y a aucune raison pour que ce soit correct.
On considère le prix d'une action, donné par un modèle de la forme
x(t) = m + erreur
où le terme d'erreur n'a pas une variance constante. Cela peut s'écrire
x(t) = m + sqrt( v(t) ) * epsilon(t)
où epsilon(t) est une suite de vaiid de variance 1.
On s'intéresse avant tout à la variance ou à la volatilité et pas vraiment au prix de l'action : la série qu'on modélise n'est pas le prix de l'action, mais sa volatilité. Il est assez naturel de modéliser le cours de l'action comme un processus AR(1) avec une erreur multiplicative :
x(t+1) = x(t) * erreur
où l'erreur pourratit être log-normale, de variance variable. Pour avoir un terme d'erreur additif et normal, on prend le logarithme puis on différencie.
data(EuStockMarkets)
x <- EuStockMarkets[,1]
op <- par(mfrow=c(3,1))
plot(x, main="Un indice boursier")
y <- diff(log(x))
plot(abs(y), main="volatilité")
k <- 30
z <- filter(abs(y),rep(1,k)/k)
plot(z, ylim=c(0,max(z,na.rm=T)), col='red', type='l',
main="volatilité lissée (30 jours)")
par(op)
Une simulation :
n <- 200
v <- function (t) { .1*(.5 + sin(t/50)^2) }
x <- 1:n
y <- rnorm(n) * v(x)
y <- ts(y)
op <- par(mfrow=c(3,1))
plot(ts(cumsum(y)), main="Une simulation")
plot(abs(y), main="volatilité")
plot(v(x)~x,
ylim=c(0,.3),
type='l', lty=2, main="volatilité lissée")
k <- c(5,10,20,50)
col <- rainbow(length(k))
for (i in 1:length(k)) {
z <- filter(abs(y),rep(1,k[i])/k[i])
lines(z, col=col[i])
}
par(op)
A FAIRE : variante simple : EWMA (exponentially weighted moving average)
v[i] <- lambda * v[i-1] + (1-lambda) * u[i-1]^2 (c'est plus simple, il n'y a qu'un seul paramètre...) (on peut choisir, empiriquement, lambda=0.94) A FAIRE : simulation et modélisation (à la main) A FAIRE : ma vraissemblance est FAUSSE. Il doit juste y avoir des gaussiennes, pas de Chi2.
On peut essayer d'estimer cette variance v(t+1) en faisant une moyenne pondérée de : la variance moyenne V (obtenue par exemple par un lissage exponentiel) ; la prévision de la veille v(t) ; le carré du taux d'accroissement de la valeur de l'action u(t) = (x(t)-x(t-1))/x(t-1).
v(t+1) = gamma V + alpha v(t) + béta u(t)^2.
Plutôt que de choisir les coefficients alpha, béta, gamma soi-même, on peut les évaluer par la méthode du maximum de vraissemblance.
A FAIRE : exemple (à la main : écrire explicitement la vraissemblance...)
ll <- function (u, gammaV, alpha, beta) {
n <- length(u)
v <- rep(NA,n)
v[1] <- u[1]^2
for (i in 2:n) {
v[i] <- gammaV + alpha * v[i-1] + beta*u[i-1]^2
}
sum(log(dchisq(u^2 / v, df=1)))
}
lll <- function (p) {
ll(y,p[1],p[2],p[3])
}
r <- nlm(lll, c(.4*mean(diff(y)^2),.3,.3))
r$estimate
res <- NULL
for (i in 1:20) {
p <- diff(c(0,sort(runif(2)),1)) *
c( mean((diff(y)/y)^2), 1, 1 )
r <- NULL
try( r <- nlm(lll, p) )
if(!is.null(r)){
res <- rbind(res, c(r$minimum, r$estimate))
print(res)
}
}
colnames(res) = c("minimum", "gammaV", "alpha", "beta")
res
A FAIRE :
je n'ai jamais le même résultat
gammaV est toujours négatif : ça me gène beaucoup...
minimum gammaV alpha beta
[1,] -473.3557 -2.489084e-05 0.31610437 0.23202868
[2,] -280.1692 -4.024827e-05 0.09674672 0.73230780
[3,] -266.3034 -5.859300e-05 0.23999115 0.59694235
[4,] -506.3229 -5.244953e-05 0.51160110 0.16128155
[5,] -228.9716 6.530461e-06 0.97200115 0.02253152
[6,] -516.4043 -5.520438e-05 0.85418375 0.06408601
[7,] -415.7290 -2.314525e-05 0.14884342 0.37617978
[8,] -291.3665 -1.223586e-04 0.50715120 0.36927627
[9,] -278.2773 -7.733857e-05 0.35255591 0.45927997
[10,] -310.3256 -5.888580e-05 0.17611217 0.69979118
[11,] -288.9966 -3.312234e-05 0.07831422 0.72978797
[12,] -259.3784 -1.318697e-04 0.43313467 0.46553856
[13,] -314.1510 -9.033081e-05 0.58692361 0.24131744
[14,] -210.2558 -1.020534e-05 0.22237139 0.77719951
[15,] -407.7668 -2.849821e-05 0.11921529 0.42430838
[16,] -505.7438 -1.841478e-05 0.27421749 0.22635609
[17,] -193.4423 -1.266605e-05 0.79456866 0.19993238
[18,] -426.6810 -3.046373e-05 0.26306608 0.29960224
[19,] -929.4232 -7.528851e-06 0.09520649 0.13700275Nous venons de présenter le modèle GARCH(1,1) ; le modèle GARCH(p,q) le généralise ainsi :
v(t+1) = gamma V + alpha1 v(t) + alpha2 v(t-1) + ... + alphaq v(t-q+1)
+ béta1 u(t) + ... + bétap u(t-p+1).
A FAIRE : autre motivation : on ne veut pas uniquement des prédictions
des valeurs de la variable étudiée, mais aussi une estimation de l'erreur
de ces prédictions.
Question: parmi les diagnostics d'une modélisation de série
temporelle, ai-je mentionné la possible hétéroscédasticité des
résidus ? (on peut la voir graphiquement, par lissage du carré des
résidus ou à l'aide des tests dans lmtest)
A FAIRE : une simulation
A FAIRE : vérifier que c'est bien ça...
garch.sim <- function (n, gammaV, p=NULL, q=NULL) {
if(gammaV<0){ stop("gammaV should be positive") }
if (any(p)<0 || any(p)>1) {
stop("The coefficients in p should be in [0,1]")
}
if (any(q)<0 || any(q)>1 ){
stop("The coefficients in q should be in [0,1]")
}
if (sum(c(p,q))>1) {
stop("The coefficients (including gamma) should sum up to 1")
}
gamma <- 1-sum(p)-sum(q)
V <- gammaV/gamma
v <- ( sqrt(V)*rnorm(n) )^2
u <- sqrt(V)*rnorm(n)
# A FAIRE : initialisation
k <- max(length(p),length(q)+1)
for (i in k:n) {
v[i] <- gammaV
for (j in 1:length(q)) {
v[i] <- v[i] + q[j]*v[i-j]
}
for (j in 1:length(p)) {
v[i] <- v[i] + p[j]*u[i-j]^2
}
u[i] <- sqrt(v[i]) * rnorm(1)
}
ts(u)
}
res <- NULL
for (i in 1:20) {
x <- garch.sim(200,1,c(.3,.2),c(.2,.1))
r <- garch(x, order=c(2,2))
res <- rbind(res, r$coef)
}
res
res <- NULL
for (i in 1:200) {
x <- garch.sim(200,1,.5,.3)
r <- garch(x, order=c(1,1))
res <- rbind(res, r$coef)
}
res
apply(res, 2, mean)Sous R, les fonctions pour manipuler des modèles GARCH (et pour faire de la finance) sont dans la bibliothèque tseries.
library(tseries) x <- EuStockMarkets[,1] y <- diff(x)/x r <- garch(y) # plot(r) La fonction plot ne marche qu'en interactif... op <- par(mfrow=c(2,1)) plot(y, main = r$series, ylab = "Series") plot(r$residuals, main = "Residuals", ylab = "Series")

hist(y, main = paste("Histogram of", r$series), xlab = "Series")
hist(r$residuals, main = "Histogram of Residuals", xlab = "Series")
qqnorm(y, main = paste("Q-Q Plot of", r$series), xlab = "Normal Quantiles")
qqnorm(r$residuals, main = "Q-Q Plot of Residuals", xlab = "Normal Quantiles")
acf(y^2, main = paste("ACF of Squared", r$series))
acf(r$residuals^2, main = "ACF of Squared Residuals", na.action = na.remove)
par(op)
On obtient (le test de Jarque Bera est un test de normalité) :
> r
Call:
garch(x = y)
Coefficient(s):
a0 a1 b1
5.054e-06 6.921e-02 8.847e-01
> summary(r)
Call:
garch(x = y)
Model:
GARCH(1,1)
Residuals:
Min 1Q Median 3Q Max
-12.66546 -0.47970 0.04895 0.65193 4.39506
Coefficient(s):
Estimate Std. Error t value Pr(>|t|)
a0 5.054e-06 8.103e-07 6.237 4.45e-10 ***
a1 6.921e-02 1.151e-02 6.014 1.81e-09 ***
b1 8.847e-01 1.720e-02 51.439 < 2e-16 ***
---
Signif. codes: 0 `***' 0.001 `**' 0.01 `*' 0.05 `.' 0.1 ` ' 1
Diagnostic Tests:
Jarque Bera Test
data: Residuals
X-squared = 17279.64, df = 2, p-value = < 2.2e-16
Box-Ljung test
data: Squared.Residuals
X-squared = 0.1291, df = 1, p-value = 0.7194A FAIRE
A FAIRE : diagnostics (regarder les résidus : ils sont censés être de moyenne nulle (ou au moins constante), de variance constante et sans auto-corrélation (test de Ljung-Box avec des décalages jusqu'à 15 jours)). A FAIRE : disgnostics autocorrélation autocorrélation de u/sqrt(v) A FAIRE : prédiction des valeurs de l'action ??? (à l'aide de la variance, on peut représenter des intervalles de prédiction à 95% pour les trajectoires ; on peut aussi tracer quelques trajectoires simulées ; ou encore estimer ces intervalles de prédiction à l'aide de nombreuses prédictions) A FAIRE : généralisations TARCH (Threshold ARCH) EGARCH http://marshallinside.usc.edu/simrohoroglu/teaching/543/spring2002/garch101.pdf A FAIRE : regression with GARCH error terms ? no (not yet in R)
A FAIRE : comment dit-on "state space model" en français ? (Dans la suite, j'utilise SSM).
A FAIRE : rédiger cette partie
A FAIRE : SSM et modèles classiques
Lors de la présentation du modèle classique (tendance, composante saisonnière, bruit), n'avais-je pas présenté des modèles à l'aide de plusieurs équations, qui en faisaient des SSM ? (ça donnerait une bonne motivation des SSM ?)
A FAIRE : SSM et BUGS...
Un document assez clair : lecture10.pdf google: bayesian modelling of time series Kyrre drgrad Timeseries 031022
A FAIRE A FAIRE : autre motivation : la volatilité, en finance. Initialement, c'était un paramètre du modèle décrivant l'évolution du prix des actions, mais ce paramètre n'est pas mesurable. Des modèles plus récents considèrent la volatilité comme une variable aléatoire : on modélise donc l'évolution de deux quantités, le prix de l'action et sa volatilité -- la première est directement mesurable, la seconde non.
Considérons un processus, S, autorégressif
S(t+1) = f( S(t) ) + bruit_1
que l'on n'observe pas directement : on observe simplement une certaine fonction de S, avec du bruit :
X = g(S) + bruit_2.
On dit que
S est l'état non observé X sont les données observées g est la fonction de transition f est la fonction de mesure bruit_1 est le bruit de l'état bruit_2 est le bruit de la mesure
Très souvent, on demandera que f et g soient linéaires, mais on acceptera qu'elles dépendent du temps.
On peut s'intéresser à différents problèmes :
1. Connaissant g, f, la variance des deux bruits et les premières valeurs de X, prédire les valeurs passées et futures de S -- c'est le filtre de Kalman.
2. Connaissant les premières valeurs de X, trouver f, g, la variance des deux bruits. Pour ce problème, on supposera que f et g sont linéaires et même qu'elles ont une certaine forme.
Le processus suivant
S(n) = a S(n-1) + u(n) X(n) = S(n) + v(n)
est un processus ARMA(1,1) (exercice laissé au lecteur).
Tous les processus ARMA(1,1) sont en fait des SSM : si
X(n) = a X(n-1) + u(n) + b u(n-1),
alors, en posant
/ X(n-1) \
| |
S(n) = | u(n) |
| |
\ u(n-1) /on a :
X = ( a 1 b ) * S
/ a 1 0 \ / 0 \
| | | |
S(n) = | 0 0 0 | * S(n-1) + | u(n) |
| | | |
\ 0 0 1 / \ 0 /Cela se généralise : tous les processus ARMA(p,q) sont des SSM.
Ils sont généraux : ils englobent les modèles ARMA, et les modèles ARMA avec des coefficients qui changent avec le temps.
Ils permettent d'étudier des données multivariées : quand on dispose de plusieurs séries temporelles, on peut les étudier séparément, mais on risque de perdre l'information relative à leur corrélation. Les State Space Models permettent de considérer ces séries temporelles entre elles.
A FAIRE :
Il y a un lien entre les State Space Models et les méthodes bayesiennes.
A FAIRE : ARMA, VARMA, VARMAX ???
A FAIRE :
State-space models: library(dse) library(dse1) library(dse2) library(dseplus) library(tseries) (econometrics) Kalman filtering ARAR Intervention analysis (at some moment in time, the model changes) Transfer function models (?)
Valeurs manquantes : Rnews 2 2 (June 2002) library(fracdiff ) Maximum likelihood estimation of the parameters of a fractionally differenced ARIMA(p,d,q) model (Haslett and Raftery, Applied Statistics, 1989).
A FAIRE : si on a deux séries temporelles : corrélogramme
data(EuStockMarkets) x <- EuStockMarkets[,1] y <- EuStockMarkets[,2] acf(ts.union(x,y),lag.max=100)

x <- diff(x) y <- diff(y) acf(ts.union(x,y),lag.max=100)

A FAIRE : exemple avec deux composantes périodiques (dont le rapport des périodes n'est pas rationnel).
n <- 2000
x <- 1:n
y <- sin(x/10) + cos(pi*x/20) + rnorm(n)
op <- par(mfrow=c(4,1))
plot(ts(y))
acf(y)
pacf(y)
spectrum(y, col=par('fg'))
abline(v=c(1/40,1/20/pi), lty=3)
par(op)
A FAIRE
# AR, MA, ARMA, ARIMA, etc. library(nlme) ?gls
Lancer la commande plot sur tous les exemples.
doit <- function (d) {
name <- deparse(substitute(d))
cat(paste(name,"\n"))
png(filename=paste(name,".png",sep=''), width=600, height=600, pointsize=12, bg="white")
try(plot(d, main=name))
dev.off()
}
source("ALL.R")
find -size 0 -exec rm {} \;
find -name "*.png" -size 444c -exec rm {} \;
(
echo '<html><head><title>R</title></head><body>'
for i in *.png
do
echo '<p>'$i'</p>'
echo '<img src="'$i'"><hr>'
done
echo '</body></html>'
) > all.htmlA FAIRE : On s'efforce de régler la hauteur du graphique pour que la courbe ait des pentes assez douces, aux alentours de 45 degrés. Donner un exemple, avec un graphique trop haut, sur lequel on ne voit rien, et un graphique tout petit mais très clair.
?filter (Exercice : compute Centered Moving Averages with it) library(ts) help(filter) filter(y,rep(1,12),method="convolution",sides=1)[-(1:11)]
Various libraries:
Only ts has full handling of ARIMA models. It's changed a lot in R-devel. It also provides basic function on which all the others rely. tseries contains other models primarily of interest in economics, and GARCH models (which are better models of stock prices). It also has arma, which is subsumed by arima (and arima0) in R-devel. fracdiff handles fractionally differenced models, a very specialized topic.
(GARCH models variance, i.e., volatility)
Une chaîne de Markov d'ordre 1, c'est une série temporelle à valeurs discrètes dans laquelle
P( X(n+1)=a | X(n)=b )
ne dépend pas de n. La matrice de ces probabilités s'appelle la matrice de transition. (Les chaines de Markov d'ordre supérieur se ramènent aisément à des chaines de Markov d'ordre 1.)
A FAIRE Chaine de Markov : simulation, estimation de la matrice de transition library(help=dse1) library(help=dse2) library(help=VLMC) # Variable-length Markov Chains
Hidden Markov model
(We do not directly observe the states of the Markov chain,
but other states, probabilistically related to them (by a "confusion matrix"))
Forward algorithm: probability of observing a given (sequence of) state(s).
Viterbo algorithm : to get an estimation of the hidden state transitions knowing the observable state transitions
Forward-backward algorithm: to get an estimation of the transition matrix, the confusion matrix, and the initial probability vector
http://www.comp.leeds.ac.uk/roger/HiddenMarkovModels/html_dev/main.html
library(msm) # Multi-state Markov models in continuous time
library(qtl) # Tools for analyzing QTL experiments --
# Analysis of experimental crosses to identify genes
# (called quantitative trait loci, QTLs) contributing
# to variation in quantitative traits -- see
# http://www.biostat.jhsph.edu/~kbroman/qtl
Replicated time series
see.ts <- function (name, ma=NULL, ar=NULL, d=0, n=2000) {
order=c(length(ar), d, length(ma))
x <- arima.sim(list(ma=ma, ar=ar, order=order), n)
op <- par(mfrow=c(4,1))
plot(x, main=name)
acf(x)
pacf(x)
spectrum(x, spans=10, col=par('fg'))
par(op)
}
n <- 200
see.ts("MA(1) theta_1=.9", .9)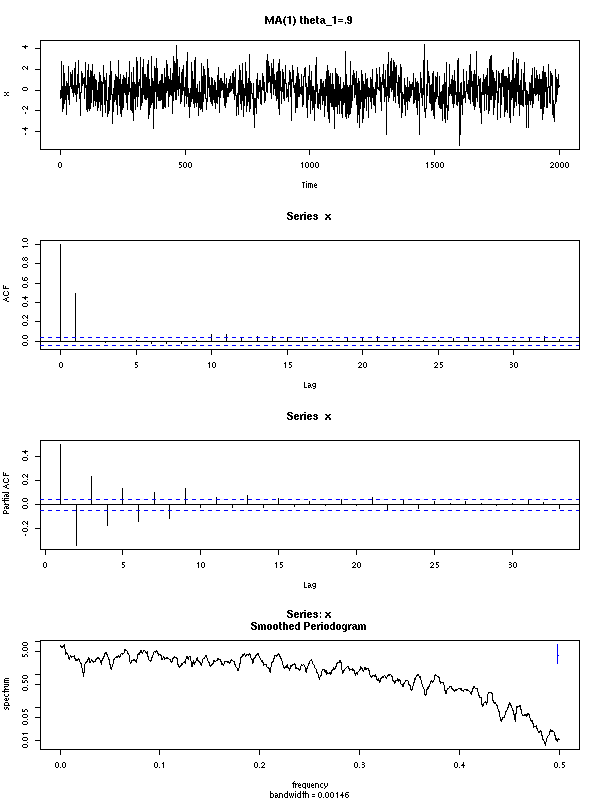
see.ts("MA(1) theta_1=.5", .5)
see.ts("MA(1) theta_1=.1", .1)
see.ts("MA(1) theta_1=-.9", -.9)
see.ts("AR(1) phi_1=.9", 0, .9)
see.ts("AR(1) phi_1=.8", 0, .9)
see.ts("AR(1) phi_1=.5", 0, .5)
see.ts("AR(1) phi_1=.1", 0, .1)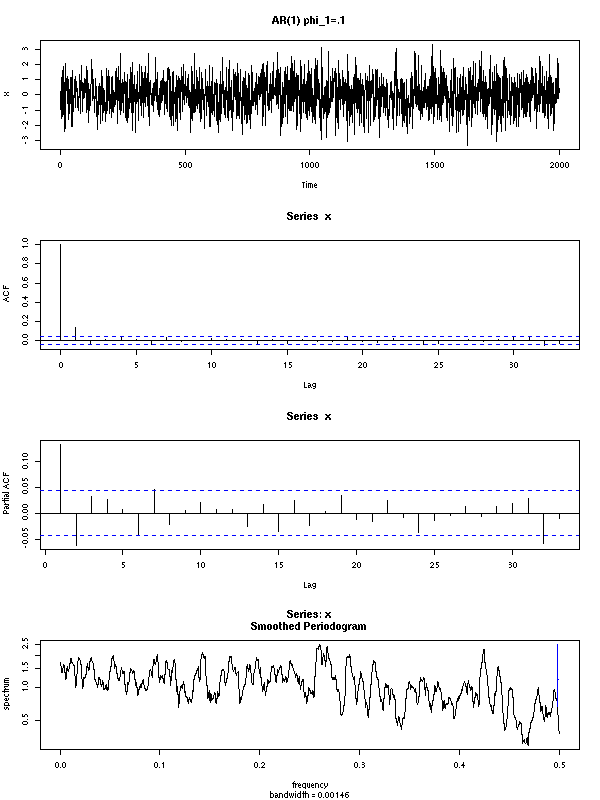
see.ts("AR(1) phi_1=-.9", 0, -.9)
see.ts("AR(1) phi_1=-.8", 0, -.8)
see.ts("ARMA(1,1) theta_1=.9 phi_1=.9", .9, .9)
see.ts("ARMA(1,1) theta_1=.9 phi_1=-.9", .9, -.9)
see.ts("ARMA(1,1) theta_1=-.9 phi_1=.9", -.9, .9)
see.ts("ARMA(1,1) theta_1=-.9 phi_1=-.9", -.9, -.9)
A FAIRE : exemples du manuel
op <- par(mfrow=c(4,1)) data(AirPassengers) plot(AirPassengers) acf(AirPassengers) pacf(AirPassengers) spectrum(AirPassengers); par(op)

op <- par(mfrow=c(4,1)) data(austres) plot(austres) acf(austres) pacf(austres) spectrum(austres); par(op)

op <- par(mfrow=c(4,1)) data(beavers) plot(ts(beaver1$temp)) acf(beaver1$temp) pacf(beaver1$temp) spectrum(beaver1$temp); par(op)

op <- par(mfrow=c(4,1)) data(BJsales) plot(BJsales) acf(BJsales) pacf(BJsales) spectrum(BJsales); par(op)

op <- par(mfrow=c(4,1)) data(EuStockMarkets) plot(EuStockMarkets[,1]) acf(EuStockMarkets[,1]) pacf(EuStockMarkets[,1]) spectrum(EuStockMarkets[,1]); par(op)

op <- par(mfrow=c(4,1)) data(JohnsonJohnson) plot(JohnsonJohnson) acf(JohnsonJohnson) pacf(JohnsonJohnson) spectrum(JohnsonJohnson); par(op)

op <- par(mfrow=c(4,1)) data(LakeHuron) plot(LakeHuron) acf(LakeHuron) pacf(LakeHuron) spectrum(LakeHuron); par(op)

op <- par(mfrow=c(4,1)) data(lh) plot(lh) acf(lh) pacf(lh) spectrum(lh); par(op)

op <- par(mfrow=c(4,1)) data(lynx) plot(lynx) acf(lynx) pacf(lynx) spectrum(lynx); par(op)

op <- par(mfrow=c(4,1)) data(Nile) plot(Nile) acf(Nile) pacf(Nile) spectrum(Nile); par(op)

op <- par(mfrow=c(4,1)) data(nottem) plot(nottem) acf(nottem) pacf(nottem) spectrum(nottem); par(op)

op <- par(mfrow=c(4,1)) #data(sunspot, package=ts) # Il y en a aussi dans "boot"... data(sunspot) plot(sunspot.month) acf(sunspot.month) pacf(sunspot.month) spectrum(sunspot.month); par(op)
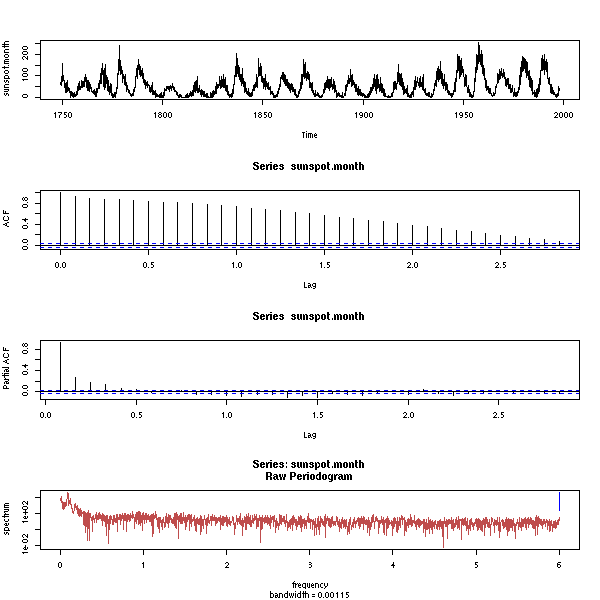
op <- par(mfrow=c(4,1)) data(treering) plot(treering) acf(treering) pacf(treering) spectrum(treering); par(op)

op <- par(mfrow=c(4,1)) data(UKDriverDeaths) plot(UKDriverDeaths) acf(UKDriverDeaths) pacf(UKDriverDeaths) spectrum(UKDriverDeaths); par(op)

op <- par(mfrow=c(4,1)) data(UKLungDeaths) plot(ldeaths) acf(ldeaths) pacf(ldeaths) spectrum(ldeaths); par(op)

op <- par(mfrow=c(4,1)) data(UKgas) plot(UKgas) acf(UKgas) pacf(UKgas) spectrum(UKgas); par(op)

op <- par(mfrow=c(4,1)) data(USAccDeaths) plot(USAccDeaths) acf(USAccDeaths) pacf(USAccDeaths) spectrum(USAccDeaths); par(op)
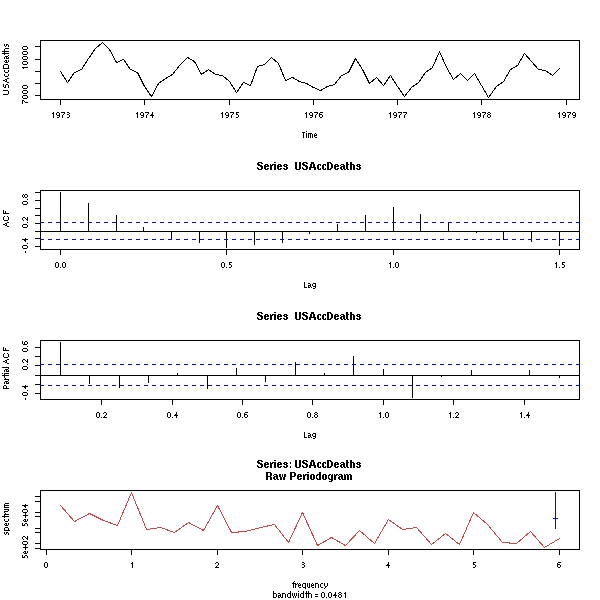
op <- par(mfrow=c(4,1)) data(WWWusage) plot(WWWusage) acf(WWWusage) pacf(WWWusage) spectrum(WWWusage); par(op)

Théorème de Nyquist : il faut échantilloner le processus suffisemment souvent, sinon on ne verra pas les fréquences les plus élevées et on observera des artefacts.
Fréquence d'échantillonage > 2 * fréquence maximale A FAIRE : dessin
Autre manière de représenter une série temporelle : y(i+1)~y(i) (tracer les segments)
Exemple : une sinusoïde
Exemple : une somme de deux sinusoïdes
Exemple : une série temporelle déterministe
x(n+1) = 4 * x(n) * ( 1 - x(n) )
Exemple : AR(1)
Exemple : quelque chose de complètement aléatoire
etc.
L'attracteur précédent pouvait s'écrire
x(n+1) = f( x(n) )
Comme on représente les points dans un espace de dimension deux, on peut aussi écrire
x(n+1) = y(n) y(n+1) = f(y(n))
Si on note X = (x,y), cela devient
X = f(X).
On peut ainsi considérer des séries temporelles à valeurs vectorielles. Dans certains cas, on dispose de toutes les coordonnées de ces vecteurs, dans d'autres, on a qu'une seule des coordonnées. On a donc un modèle avec des "variables cachées".
A FAIRE :
Phase space analysis, correlation dimension
nombre de i<j tq abs(xi-xj)<r
C(r) = -------------------------------
nombre de i<j (i.e., n(n-1))
En dimension d, C(r) est proportionnel à r^d
On en déduit la dimension de l'attracteur.
(Mais la présence de bruit perturbe ce calcul.)Vincent Zoonekynd
<zoonek@math.jussieu.fr>
latest modification on Wed Oct 13 22:33:21 BST 2004