
The French version of this document is no longer maintained: be sure to check the more up-to-date English version.
Introduction
Quelques distributions
Estimation de Kaplan-Meier
Modèles à temps discret
Modèle de régression paramétrique
Proportional Hazard (PH) models
Accelerated Failure Time (AFT) models
Autres modèles
Cox Proportional Hazard model
A FAIRE
A FAIRE : terminer d'écrire cette partie (il me reste encore à comprendre la régression de Cox...)
A FAIRE : plan de cette partie
Analyse de la survie sans variables prédictives Fonction de survie, de risque, de risque cumulé Quelques distributions Méthodes non paramétriques : estimation de Kaplan-Meier Méthodes paramétriques : A FAIRE Modèles discrets Analyse de la survie avec variables prédictives A FAIRE
A FAIRE :
Il convient de distinguer les données de survie discrète des données de survie continues. Très souvent, on ne parle que des données continues et on traite les données discrètes comme si elles étaient continues -- ça n'est pas une très bonne idée.
A FAIRE :
Les données de survie son assez difficiles à manipuler : on les remplacera par la fonction de survie, ou le taux de survie cumulé ou le taux de survie. Ce sont des fonctions, c'est plus facile.
A FAIRE :
Insuffisance de la régression classique : elle ne permet pas de traiter la censure des données, ni de prendre en compte des variables prédictives qui dépendent du temps.
A FAIRE :
Pas de variables prédictives : - méthodes paramétriques (MLE, avec les modèles exposés ci-après) - méthodes non paramétriques (Kaplan-Meier (cas continu) ou LifeTable (cas discret) Avec des variables prédictives : - méthodes paramétriques - méthodes semi-paramétriques (régression de Cox : paramétrique pour la partie qui dépend des variables prédictives, non paramétriques pour le reste).
A FAIRE : frailty = unobserved heterogeneity.
A FAIRE : quelle différence entre données de survie et données longitudinales ?
On s'intéresse ici à des variables de survie : une variable de survie, c'est à peu près comme une variable quantitative, mais elle peut prendre des valeurs numériques précises, comme "13 ans", mais aussi des valeurs moins précises, du genre "plus de 15 ans".
On qualifie de "valeurs censurées" ces valeurs moins précises. On les note généralement ainsi :
10+ Plus de 10 (donnée censurée à droite) 5- Moins de 5 (censurée à gauche) [5,10] Entre 5 et 10
On les rencontre par exemple quand on regarde la durée de survie après un cancer : si l'étude dure 10 ans, on pourra donner la durée de survie de tous les patients qui sont morts, mais pour les autres, on pourra juste dire que leur durée de survie est supérieure à 10 ans. La censure à gauche correspond à des évènements qui ont eu lieu avant le début de l'étude (mais tous les individus ne rentrent pas dans l'étude en même temps). A FAIRE : donner un exemple concret de censure à gauche. La censure par intervalle se rencontre par exemple quand on constate l'apparition d'un symptome lors d'une visite médicale : il est apparu depuis la visite précédente, mais on ne sait pas exactement quand.
Voici d'autres exemples : durée de survie d'un patient, durée de survie d'un mariage, durée de survie d'une entreprise, durée de fonctionnement sans panne d'un produit manufacturé, durée pendant laquelle un produit reste suffisemment populaire pour continuer à être produit, durée de survie d'un enseignant en lycée (jusqu'à sa démission, son internement en hopital psychiatrique, son suicide), durée jusqu'à l'arret de prise d'un médicament, etc.
On peut aussi voir les variables de survie comme des variables qualitatives binaires (celles qu'on cherche à prédire dans la régression logistique) indiquant la survenue ou non d'un évènement, auxquelles on a ajouté l'instant de survenue de cet évènement. Les valeurs censurées correspondent à << l'évènement ne s'est pas produit >> : dans les exemples précédents, cela revient à remplacer les valeurs << Vivant / Mort >> par << Vivant / Date de la mort >>.
Les variables de survie peuvent avoir plusieurs valeurs : par exemple sain, malade et mort (si un patient guérit entre deux maladies, ça devient encore plus compliqué). Dans ces situations plus complexes, on parle parfois de données transitionnelles (car on s'intéresse à la transition d'un état vers un autre) ou de "spell duration data".
On peut aussi voir une donnée de survie comme une série temporelle qualitative, dans laquelle on s'intéresse aux transitions d'un état à l'autre.
A FAIRE :
Competing risk models Un état de départ et plusieurs états absorbants (exemple : passage du chomage à un emploi ou du chomage à une sortie du marché de l'emploi ; autre exemple : concurrence entre mort du cancer et mort de maladie cardiovasculaire).
Si T est une variable de survie, sa fonction de survie est
S(t) = P(T>t) = 1-F(t).
Par exemple, si T désigne le nombre d'années de survie après la diagnostic d'un cancer, S(t) est la probabilité de survivre au moins t années.
Sa "hazard function", ou "hazard rate" (je ne sais pas comment on dit en français : fonction de risque ?) est
P( t < T <= t + u | T > t )
lambda(t) = lim -----------------------------
u -> 0 u
dF/dt
= -------
S
d ln S
= - --------
dtLa formule ressemble beaucoup à la définition de la densité, mais on a ajouté la condition "T>t".
A la différenciation près, c'est très semblable à la différence entre l'espérance de vie à la naissance et l'espérance de vie à 60 ans, ou la différence entre la probabilité de mourir entre 12 et 13 ans et la probabilité de mourir entre 12 et 13 ans sachant que le patient a déjà survécu 12 ans.
On rencontre aussi parfois la "cumulative hazard function", primitive de la précédente, qui représente le risque cumulé.
Lambda(t) = - ln S(t)
Elle correspond à une "hazard function" constante,
lambda(t) = lambda Lambda(t) = lambda t S(t) = exp( - lambda t ) op <- par(mfrow=c(3,1)) n <- 20 lambda <- rep(2,n) x <- seq(0,2,length=n) plot(lambda ~ x, type='l', main=expression(lambda)) plot(lambda*x ~ x, type='l', main=expression(Lambda)) plot(exp(-lambda*x) ~ x, type='l', main="S") par(op)

Elle correspond à une "hazard function" de la forme
Lambda(t) = a * t ^ gamma S(t) = exp( - a * t ^ gamma ) op <- par(mfrow=c(3,1)) n <- 20 alpha <- 1 g <- rep(2,n) x <- seq(0,2,length=n) plot(g * alpha * x^(g-1) ~ x, type='l', main=expression(lambda (gamma==2))) plot(alpha * x^g ~ x, type='l', main=expression(Lambda)) plot(exp(-alpha*x^g) ~ x, type='l', main="S") par(op)

op <- par(mfrow=c(3,1)) n <- 20 alpha <- 1 g <- rep(.5,n) x <- seq(0,2,length=n) plot(g * alpha * x^(g-1) ~ x, type='l', main=expression(lambda (gamma==.5))) plot(alpha * x^g ~ x, type='l', main=expression(Lambda)) plot(exp(-alpha*x^g) ~ x, type='l', main="S") par(op)

C'est par exemple ce qu'on utilise pour modéliser la durée de fonctionnement sans panne d'une machine : plus la machine est vieille, plus le risque de panne est grand ; le risque de panne dépend de l'âge de la machine.
Considérons une machine très fiable : elle possède des circuits de secours. Pour qu'elle tombre réellement en panne, il faut que plusieurs circuits tombent en panne. Le temps d'attente avant une panne de cette machine est le temps d'attente de trois pannes de ces circuits.
A FAIRE : distribution Gamma
A FAIRE : expliquer
op <- par(mfrow=c(3,1))
n <- 200
x <- seq(0,5,length=n)
plot(1-plnorm(x) ~ x, type='l', main="S")
L <- function (x) { -log(1-plnorm(x)) }
plot(L(x) ~ x, type='l', main=expression(Lambda))
h <- .001
plot( (L(x+h)-L(x))/h ~ x, type='l', main=expression(lambda))
par(op)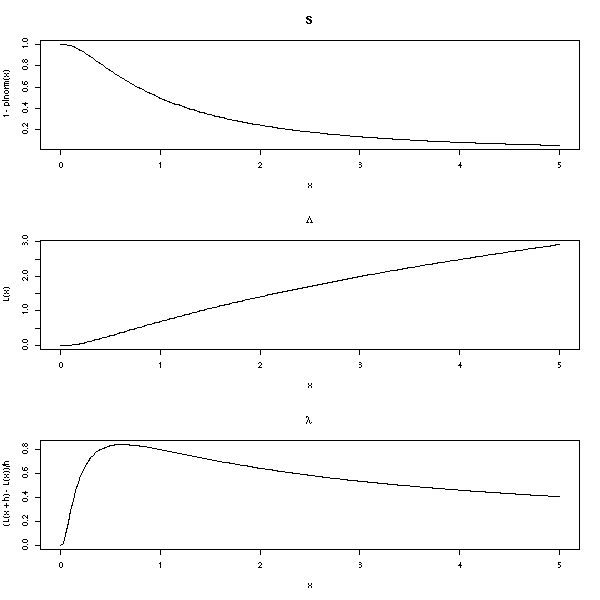
Weibul: lambda = alpha * t^(alpha-1) * exp(+X béta)
???
A FAIRE : il y a une variable prédictive, qui n'a pas encore sa
place ici...
log-logistic model:
1
S(t) = -------------------------- with lambda = exp(- X béta)
1 + (lambda t)^(1/gamma)
Gompertz: lambda = exp( exp(+X béta) + gamma t )
(important)
Generalized Gamma
(généralise les modèles précédents: kappa=1:Weibul,
kappa=0:lognormal, kappa=sigma:gamma)Il y a aussi des modèles à temps discret :
logistic complementary log-log
S'il n'y a pas de censure, on peut estimer la fonction de survie ainsi :
Card( i : T_i>t )
S(t) = -------------------
nEn présence de censure, on tient compte des données censurées jusqu'à ce qu'on arrive à leur valeur, et après on les oublie. Plus précisément, si le temps est discret :
S(t0) = P(vivant à t=t0 | vivant à t=t0-1) * P(vivant à t=t0-1)
Par exemple, la fonction de survie de la série
1 2 2 2+ 3+ 3+ 3+ 4 4 4 4 ... (100 individus)
se calcule ainsi :
temps sujets morts censures p1 p2 S=p1*p2 ------------------------------------------------------ 1 100 1 0 99/100 1 .99 2 99 2 1 97/100 .99 .9603 3 96 0 3 96/100 .9603 .9219 4 93 3 0 90/100 .9219 .8297
Les valeurs de S sont des produits de plus en plus gros :
S(0) = 1 S(1) = 1 * 99/100 S(2) = 1 * 99/100 * 97/100 S(3) = 1 * 99/100 * 97/100 * 96/100 S(4) = 1 * 99/100 * 97/100 * 96/100 * 90/100 etc.
On peut donner une formule générale :
di
S(t) = Produit ( 1 - ---- )
i tel que ti<t niOn peut calculer des intervalles de confiance en supposant que Lambda (qui vaut -log(S)) est normale.
A FAIRE : comment a-t-on la variance de Lambda ???
Il existe d'autres estimateurs de la fonction de survie, par exemple celui d'Altschuler--Nelson--Aalen--Flemming--Harrington :
di
Lambda(t) = Somme ------.
i tel que ti<t niCes estimateurs ont une variance élevée : si on a un modèle raisonnable, il vaut mieux préférer un estimateur paramétrique obtenu par le maximum de vraissemblance (on peut signaler que l'estimateur de Kaplan--Meier correspond à un maximum de vraissemblance (non paramétrique)).
La plupart des fonctions sont dans le paquetage "survival".
La commande Surv permet de créer des variables de survie.
> Surv(c(1,2,2,2,3,3,3,4,4,4,4), + c(1,1,1,0,0,0,0,1,1,1,1)) [1] 1 2 2 2+ 3+ 3+ 3+ 4 4 4 4
La commande survfit permet de calculer la fonction de survie.
> x <- Surv(c(1,2,2,2,3,3,3,4,4,4,4),
+ c(1,1,1,0,0,0,0,1,1,1,1))
> survfit(x)
Call: survfit(formula = x)
n events rmean se(rmean) median 0.95LCL 0.95UCL
11.000 7.000 3.364 0.322 4.000 Inf Inf
> summary(survfit(x))
Call: survfit(formula = x)
time n.risk n.event survival std.err lower 95% CI upper 95% CI
1 11 1 0.909 0.0867 0.754 1
2 10 2 0.727 0.1343 0.506 1
4 4 4 0.000 NA NA NAou de la tracer
set.seed(87638) library(survival) n <- 200 x <- rweibull(n,.5) y <- rexp(n,1/mean(x)) s <- Surv(ifelse(x<y,x,y), x<=y) plot(s) # peu informatif
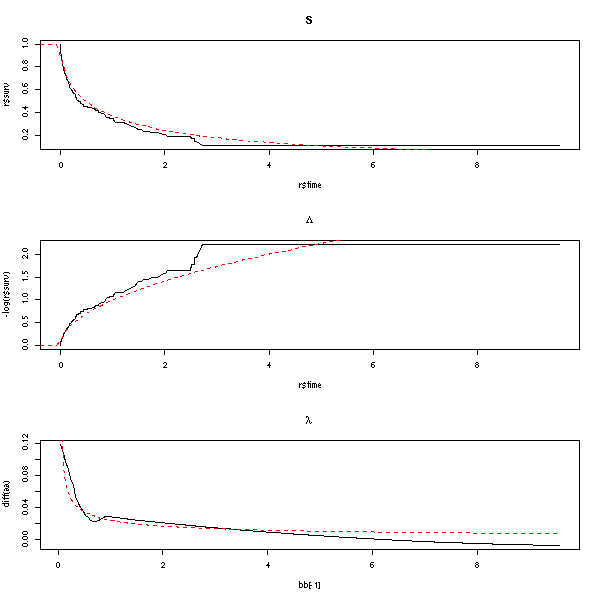
plot(survfit(s))
lines(survfit(s, type='fleming-harrington'), col='red')
r <- survfit(s)
lines( 1-pweibull( r$time, .5 ) ~ r$time, lty=3, lwd=3, col='blue' )
legend( par("usr")[2], par("usr")[4], yjust=1, xjust=1,
c("Kaplan-Meier", "Fleming-Harrington", "Fonction de survie théorique"),
lwd=c(1,1,3), lty=c(1,1,3),
col=c(par("fg"), 'red', 'blue'))
title(main="Fonction de survie (estimation de Kaplan-Meier)")
op <- par(mfrow=c(3,1)) r <- survfit(s) plot(r$surv ~ r$time, type='l', main="S") curve( 1-pweibull(x,.5,1), col='red', lty=2, add=T ) plot(-log(r$surv) ~ r$time, type='l', main=expression(Lambda)) curve( -log(1-pweibull(x,.5,1)), col='red', lty=2, add=T ) # Avant de dériver, on commence par lisser Lambda a <- -log(r$surv) b <- r$time library(modreg) l <- loess(a~b) bb <- seq(min(b),max(b),length=200) aa <- predict(l, data.frame(b=bb)) plot( diff(aa) ~ bb[-1], type='l', main=expression(lambda) ) aa <- -log(1-pweibull(bb,.5,1)) lines( diff(aa) ~ bb[-1], col='red', lty=2 ) par(op)
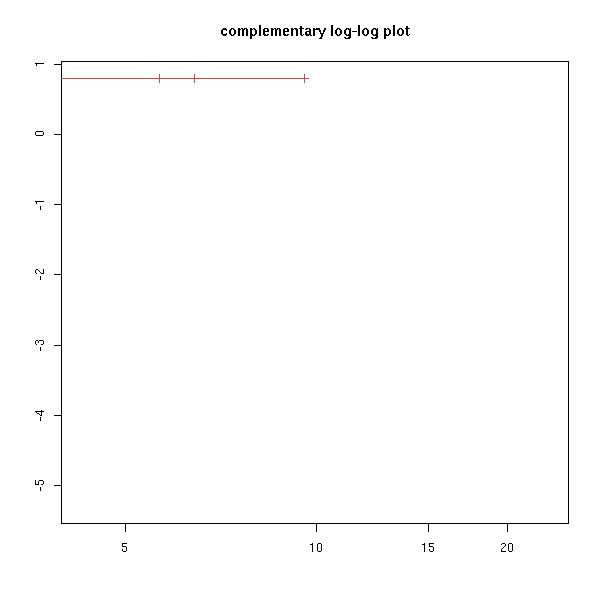
Remarque : on peut obtenir certains des graphiques ci-dessus en modifiant l'option "fun".
plot(r, fun="log", main="log-survival curve")

plot(r, fun="event", main="cumulative events: f(y)=1-y")

plot(r, fun="cumhaz", main="cumulative hazard: f(y)=-log(y)=Lambda")

try( plot(r, fun="cloglog", main="complementary log-log plot") ) # f(y)=log(-log(y)), log-scale on the x-axis
On peut aussi avoir un (ou plusieurs) facteurs -- nous en reparlerons plus loin.
n <- 200 x1 <- rweibull(n,.5) x2 <- rweibull(n,1.2) f <- factor( sample(1:2, n, replace=T), levels=1:2 ) x <- ifelse(f==1,x1,x2) y <- rexp(n,1/mean(x)) s <- Surv(ifelse(x<y,x,y), x<=y) plot(s, col=as.numeric(f))
plot( density(s[,1][ s[,2] == 1 & f == 1]), lwd=3,
main="Analyse de la survie, un facteur" )
lines( density(s[,1][ s[,2] == 0 & f == 1]), lty=2, lwd=3 )
lines( density(s[,1][ s[,2] == 1 & f == 2]), col='red', lwd=3 )
lines( density(s[,1][ s[,2] == 0 & f == 2]), lty=2, col='red', lwd=3 )
legend( par("usr")[2], par("usr")[4], yjust=1, xjust=1,
c("non censored, f = 1", "censored, f = 1",
"non censored, f = 2", "censored, f = 2"),
lty=c(1,2,1,2),
lwd=1,
col=c(par('fg'), par('fg'), 'red', 'red') )
plot(survfit(s ~ f), col=as.numeric(levels(f)))
A FAIRE : avec deux facteurs survfit(s~f1+f2)
A FAIRE : et si f n'est pas un facteur ??? (mettre ça un peu plus loin, quand on parlera de régression d'une variable de survie).
A FAIRE : choisir deux exemples, l'un avec l'autre sans covariables, que l'on utilisera jusqu'à la fin de ce chapitre.
data(lung) x <- Surv(lung$time, lung$status) plot(x)

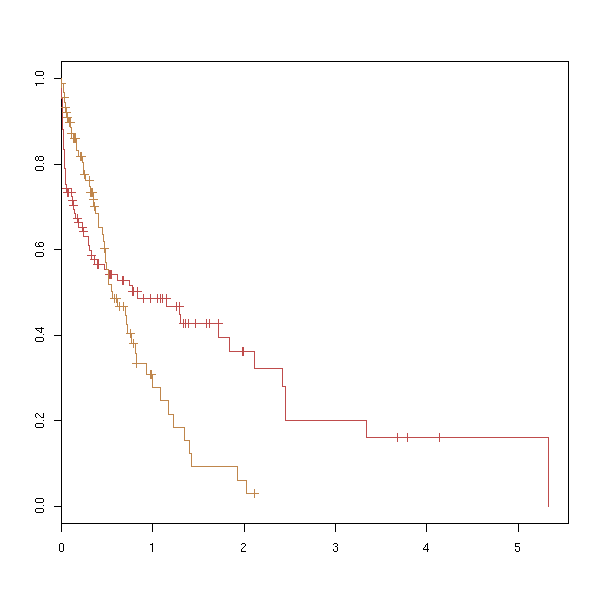
plot(survfit(x))

On peut demander si une variable de survie dépend d'un facteur.
data(lung) y <- Surv(lung$time, lung$status) x <- lung$sex summary(coxph(y~x)) Rsquare= 0.046 (max possible= 0.999 ) Likelihood ratio test= 10.6 on 1 df, p=0.00111 Wald test = 10.1 on 1 df, p=0.00149 Score (logrank) test = 10.3 on 1 df, p=0.00131
A FAIRE Discrete hazard rate : h(aj) = P[ a(j-1) < T <= a(j) | T > a(j-1) ] A FAIRE : exprimer la fonction de survie en fonction de h. A FAIRE LifeTable : c'est l'équivalent discret de l'estimateur de Kaplan-Meier
A FAIRE : Introduction
Nous allons maintenant ajouter des variables prédictives. Certaines ne dépendent pas du sujet (mais dépendent du temps) : inflation, faux de chomage, température extérieure, etc. D'autres dépendent du sujet et peuvent dépendre du temps (CSP, age, pression artérielle) ou pas (sexe). Méthodes : - paramétrique - semi-paramétrique (régression de Cox) : paramétrique pour la partie qui dépend des variables prédictives, non paramétrique (Kaplan-Meier) pour le reste.
A FAIRE : classification des différents modèles
Continu : exponentielle (PH et AFT), Weibull (PH et AFT), Gompertz (PH), lognormal (AFT), loglogistic (AFT), gamma généralisée (AFT) discret : logistic (proportionnal odds), cloglog (PH) PH (Proportionnal Hazards) : lambda = lambda0(t) * exp(X béta) AFT (Accelerated Failure Time) : T = exp(-X béta) * exp(z)
A FAIRE : que fait la fonction survreg ???
On peut tout d'abord effectuer ces calculs à la main, en écrivant explicitement la log-vraissemblance
Prod( f(b,x_i) où i non censuré ) * Prod( S(b,x_i) où i censuré )
(il manque des termes correspondant à la probabilité de censure, mais on suppose que la censure est indépendante du résultat de l'expérience, donc on peut l'oublier) à l'aide de la commande optim. Le seul point délicat est le choix des paramètres initiaux : s'il sont mal choisis (j'avais commencé par prendre c(1,1)), la vraissemblance est nulle...
Pour vérifier graphiquement que c'est bien un minimum, on peut faire un dessin (ici, il y a deux paramètres à estimer : s'il n'y en avait qu'un, on ferait un dessin en dimension un (on en a déjà fait), s'il y en avait plus, on aurait plus de problèmes (on pourrait s'en tirer avec une animation ou un treillis))
data(lung)
x <- Surv(lung$time, lung$status)
f <- function (p,t) { dweibull(t,p[1],p[2]) }
S <- function (p,t) { 1-pweibull(t,p[1],p[2]) }
ll <- function (p) {
time <- x[,1]
status <- x[,2]
censored <- 0
dead <- 1
# cat(p); cat("\n"); str(time); cat("\n");
-2*( sum(log(f(p,time[status==dead]))) + sum(log(S(p,time[status==censored]))) )
}
# Quelques estimations du second paramètre
m <- 1 # Ne marche pas
m <- 100
s <- survfit(x)
m <- mean(s$time)
m <- max(s$time[s$surv>.5])
r <- optim( c(1,m), ll )
# Dessinons la log-vraissemblance
myOuter <- function (x,y,f) {
r <- matrix(nrow=length(x), ncol=length(y))
for (i in 1:length(x)) {
for (j in 1:length(y)) {
r[i,j] <- f(x[i],y[j])
}
}
r
}
lll <- function (u,v) {
r <- ll(c(u,v))
if(r==Inf) r <- NA
r
}
a <- seq(1,1.6,length=50)
b <- seq(100,700,length=50)
ab <- myOuter(a,b,lll)
persp(a,b,ab)
op <- par(mfrow=c(3,3))
for (i in seq(0,360,length=10)[-10]) {
persp(a,b,ab,theta=i)
}
par(op)
On pourrait aussi utiliser xgobi :
xgobi(data.frame( x=rep(a,1,each=length(b)), y=rep(b,length(a)), z=as.vector(ab)) )
Mais on voit peut-être mieux en restant en dimension deux :
image(a,b,ab) points(r$par[1],r$par[2],lwd=3,cex=3)

Avec les couleurs par défaut, on ne voit rien :
n <- 255 image(a,b,ab, col=topo.colors(n), breaks=quantile(ab,(0:n)/n, na.rm=T)) points(r$par[1],r$par[2],lwd=3,cex=3)

Voire même, pour souligner les différences au voisinage du minimum :
image(a,b,ab, col=topo.colors(n), breaks=quantile(ab,((0:n)/n)^2,na.rm=T)) points(r$par[1],r$par[2],lwd=3,cex=3)

On pourrait faire les mêmes dessins avec la bibliothèque "lattice".
A FAIRE library(lattice) ?levelplot ?contourplot
On peut comparer la courbe de Kaplan-Meier avec la courbe théorique :
plot(survfit(x)) curve( 1-pweibull(x,r$par[1],r$par[2]), add=T, col='red', lwd=3, lty=2 )

Prenons un exemple et essayons de le modéliser à l'aide d'une distribution exponentielle, de Weibull et Gamma.
ph.mle.weibull <- function (x) {
f <- function (p,t) { dweibull(t,p[1],p[2]) }
S <- function (p,t) { 1-pweibull(t,p[1],p[2]) }
m <- mean(survfit(x)$time)
ph.mle.optim(x,f,S,c(1,m))
}
ph.mle.exp <- function (x) {
f <- function (p,t) { dexp(t,p) }
S <- function (p,t) { 1-pexp(t,p) }
m <- mean(survfit(x)$time)
ph.mle.optim(x,f,S,1/m)
}
ph.mle.gamma <- function (x) {
f <- function (p,t) { dgamma(t,p[1],p[2]) }
S <- function (p,t) { 1-pgamma(t,p[1],p[2]) }
m <- mean(survfit(x)$time)
ph.mle.optim(x,f,S,c(1,1/m))
}
ph.mle.optim <- function (x,f,S,m) {
ll <- function (p) {
time <- x[,1]
status <- x[,2]
censored <- 0
dead <- 1
-2*( sum(log(f(p,time[status==dead]))) + sum(log(S(p,time[status==censored]))) )
}
optim(m,ll)
}
eda.surv <- function (x) {
r <- survfit(x)
plot(r)
a1 <- ph.mle.exp(x)$par
lines( 1-pexp(r$time,a1) ~ r$time, col='red' )
a2 <- ph.mle.weibull(x)$par
lines( 1-pweibull(r$time,a2[1],a2[2]) ~ r$time, col='green' )
a3 <- ph.mle.gamma(x)$par
lines( 1-pgamma(r$time,a3[1],a3[2]) ~ r$time, col='blue' )
legend( par("usr")[2], par("usr")[4], yjust=1, xjust=1,
c(paste("Exponentielle(", signif(a1,2), ")", sep=''),
paste("Weibull(", signif(a2[1],2), ", ", signif(a2[2],2), ")", sep=''),
paste("Gamma(", signif(a3[1],2), ", ", signif(a3[2],2), ")", sep='')
),
lwd=1, lty=1,
col=c('red', 'green', 'blue'))
title(main="Parametric estimation of PH models")
}
data(lung)
x <- Surv(lung$time, lung$status)
eda.surv(x)
Pour regarder la qualité de l'estimation, on peut aussi adapter le qqplot.
x <- Surv(lung$time, lung$status)
r <- survfit(x)
a1 <- ph.mle.exp(x)$par
t1 = 1-pexp(r$time,a1)
a2 <- ph.mle.weibull(x)$par
t2 <- 1-pweibull(r$time,a2[1],a2[2])
a3 <- ph.mle.gamma(x)$par
t3 <- 1-pgamma(r$time,a3[1],a3[2])
plot( t1 ~ r$surv, col='red', xlab='sample', ylab='model')
points( t2 ~ r$surv, col='green')
points( t3 ~ r$surv, col='blue' )
abline(0,1)
legend( par("usr")[1], par("usr")[4], yjust=1, xjust=0,
c(paste("Exponentielle(", signif(a1,2), ")", sep=''),
paste("Weibull(", signif(a2[1],2), ", ", signif(a2[2],2), ")", sep=''),
paste("Gamma(", signif(a3[1],2), ", ", signif(a3[2],2), ")", sep='')
),
lwd=1, lty=1,
col=c('red', 'green', 'blue'))
title(main="Parametric estimation of PH models")
On peut aussi représenter les résidus (la différence entre l'estimation non paramétrique (Kaplan-Meier) et l'estimation paramétrique de la fonction de survie.
plot( t1 - r$surv ~ t1, col='red', xlab='predicted values', ylab='residuals')
points( t2 - r$surv ~ t2, col='green')
points( t3 - r$surv ~ t3, col='blue' )
abline(h=0, lty=3)
legend( par("usr")[2], par("usr")[4], yjust=1, xjust=1,
c(paste("Exponentielle(", signif(a1,2), ")", sep=''),
paste("Weibull(", signif(a2[1],2), ", ", signif(a2[2],2), ")", sep=''),
paste("Gamma(", signif(a3[1],2), ", ", signif(a3[2],2), ")", sep='')
),
lwd=1, lty=1,
col=c('red', 'green', 'blue'))
title(main="Parametric estimation of PH models")
plot( abs(t1 - r$surv) ~ t1, col='red',
xlab='predicted values', ylab=expression( abs(residuals) ))
points( abs(t2 - r$surv) ~ t2, col='green')
points( abs(t3 - r$surv) ~ t3, col='blue' )
abline(h=0, lty=3)
legend( par("usr")[2], par("usr")[4], yjust=1, xjust=1,
c(paste("Exponentielle(", signif(a1,2), ")", sep=''),
paste("Weibull(", signif(a2[1],2), ", ", signif(a2[2],2), ")", sep=''),
paste("Gamma(", signif(a3[1],2), ", ", signif(a3[2],2), ")", sep='')
),
lwd=1, lty=1,
col=c('red', 'green', 'blue'))
title(main="Parametric estimation of PH models")
A FAIRE : ajouter un test pour vérifier si, sous l'hypothèse d'un modèle de Weibull, les données sont vraiment différentes d'un modèle exponentiel (ie, tester si le premier paramètre est vraiment différent de un). (mettre ce test dans eda.surv et afficher le résultat sur le dessin)
Si on reprend l'exemple simulé utilisé plus haut (Weibull de paramètres .5 et 1), on obtient des valeurs proches des valeurs attendues.
> n <- 200 > x <- rweibull(n,.5) > y <- rexp(n,1/mean(x)) > s <- Surv(ifelse(x<y,x,y), x<=y) > ph.mle.weibull(s)$par [1] 0.4891810 0.9924432
A FAIRE : tests...
A FAIRE : diagnostic plots
Si on cherche à prédire une variable de survie à l'aide d'une autre variable, X, on peut utiliser le modèle suivant
lambda(t|X) = lambda(t) * exp(X*b)
où lambda est une Hazard function sous-jacente (correspondant par exemple à un modèle de Weibull) et b un paramètre à estimer. Pour trouver b et les paramètres du modèle sous-jacent, on utilise toujours le maximum de raissemblance.
A FAIRE : exemple
data(lung)
y <- Surv(lung$time, lung$status)
x1 <- lung$age
x2 <- lung$meal.cal
A FAIRE : ajouter b dans le code suivant...
Je n'arrive pas à obtenir d'expression simple et générale de la
log-vraissemblance (j'ai une intégrale de lambda qui apparait...)
f <- function (p,t) { dweibull(t,p[1],p[2]) }
S <- function (p,t) { 1-pweibull(t,p[1],p[2]) }
m <- mean(survfit(y)$time)
ll <- function (p) {
time <- y[,1]
status <- y[,2]
censored <- 0
dead <- 1
-2*( sum(log(f(p,time[status==dead]))) + sum(log(S(p,time[status==censored]))) )
}
optim(m,ll)En fait, la fonction survreg nous donne ce résultat.
A FAIRE : comprendre.
Expliquer en quoi c'est le même résultat.
> summary(survreg(y~x1+x2))
Call:
survreg(formula = y ~ x1 + x2)
Value Std. Error z p
(Intercept) 6.82e+00 0.57891 11.785 4.64e-32
x1 -1.35e-02 0.00809 -1.667 9.55e-02
x2 2.37e-05 0.00018 0.131 8.95e-01
Log(scale) -2.54e-01 0.06973 -3.641 2.71e-04
Scale= 0.776
Weibull distribution
Loglik(model)= -930.6 Loglik(intercept only)= -932.2
Chisq= 3.17 on 2 degrees of freedom, p= 0.21
Number of Newton-Raphson Iterations: 4
n=181 (47 observations deleted due to missing)
A FAIRE : pour vérifier aue je comprends bien le sens de ce résultat,
il faudrait faire une simulation (Weibul de paramètres .5 et 3, b=c(1 2 -1))
et la donner à survreg.
A FAIRE : un exemple avec des variables prédictives qui ne dépendent pas du temps
???
A FAIRE : un exemple avec des variables prédictives qui dépendent du temps ???
???
On suppose que la variable de survie T est donnée par :
ln(T) = béta X + erreur
où le terme d'erreur suit une certaine distribution (par exemple, si c'est une distribution normale, T est log-normale)
A FAIRE : extreme value distribution with 2 parameters (this yields the Weibul distribution)
On peut aussi écrire ces modèles :
ln(psi * T) = erreur psi = exp(-béta X)
On remarquera que psi ne dépend pas de T ; de plus, si psi>1, on meurt plus vite, alors que si psi<1, on meurt plus lentement -- d'où le nom "Accelerated Failure Time".
Ce sont simplement des modèles linéaires généralisés.
A FAIRE ?glm A FAIRE
C'est un modèle PH dans lequel lambda (la Hazard function sous-jacente) est constante par morceaux (c'est l'expérimentateur qui choisit les instants en lesquels la constante change).
C'est une première analyse, un peu simpliste, que l'on peut faire quand les prédicteurs dépendent du temps.
A FAIRE : traiter un exemple
Dans un "Proportional Hazard Model",
lambda = lambda0 * exp(b * X)
on peut en fait estimer les coefficients de régression b sans tenir compte de la forme de lambda0, à l'aide d'une vraissemblance partielle.
A FAIRE (pas tout de suite) : je n'ai pas compris d'où vient la vraissemblance partielle.
library(survival) ?survfit ?survreg ?coxph Proportionnal hazard: lambda(t|X) = lambda(t) exp(X beta) Cox proportional hazard model A popular semi-parametric model for survival analysis -- as efficient as parametric models, even when those apply. The model is still lambda(t|X) = lambda(t) exp(X beta), but we do not assign a prescribed form to lambda. Variables prédictives : elles peuvent dépendre du temps (ça complique beaucoup les choses). A FAIRE : différence entre PH: Proportional Hazard models AFT: Accelerated Failure Time models
On peut avoir plusieurs évènements dans la série, par exemple plusieurs types de mort, ou un évènement final (mort) éventuellement précédé d'autres évènements non léthaux (AVC, infarctus, diagnostic d'HTA, opération, etc.).
A FAIRE : exemple S'il y a deux types d'évènements léthaux indépendants, on peut les traiter séparément. Mort accidentelle : 1 1 1 3 Mort non accidentelle : 1 2 4 5 5 6 Vie : 7+ 7+ 7+ Pour étudier les morts accidentelles : 1 1 1 3 1+ 2+ 4+ 5+ 5+ 6+ 7+ 7+ 7+ Pour étudier les morts non accidentelles : 1+ 1+ 1+ 3+ 1 2 4 5 5 6 7+ 7+ 7+ Si les évènements ne sont pas indépendants (par exemple, mort par cancer ou par infarctus, qui peuvent avoir ue cause commune (tabac)), les résultats seront biaisés.
A FAIRE : est-ce le bon endroit ?
On peut aussi imaginer la situation suivante : tous les patients ont une fonction de risque qui a la même forme, à un facteur multiplicatif près. Si on disposait de suffisemment de variables prédictives, on essaierait de prédire ce facteur à l'aide de ces variables. Mais si on n'en a pas, ou pas suffisemment, on ne peut pas bien prédire ce facteur. On s'intéresse alors à des modèles de la forme
lambda(t) = lambda0(t) * u
où u est une variable aléatoire, positive, de moyenne 1. Comme la valeur de u change d'un sujet à l'autre, on ne pourra pas la prédire, mais on pourra au moins estimer sa variance.
A FAIRE : comment fait-on ?
A FAIRE : et sous R ?
frail.fit(eha) Fits a frailty proportional hazards model
frailty(survival) (Approximate) Frailty models
mlefrailty.fit(survrec)
Survival function estimator for correlated
recurrence time data under a Gamma Frailty
Model
Recurrent failure times library(survrec) Penalized maximum likelihood ?pspline ?frailty ?ridge The Kaplan-Meier curves should not cross: it indicates that the PH model does NOT hold. On peut utiliser l'analyse de la survie même si les observations ne sont pas censurées : les notions (hazard function) et les graphiques que l'on manipule peuvent être pertinents. Frailty models (c'est important)
Vincent Zoonekynd
<zoonek@math.jussieu.fr>
latest modification on Wed Oct 13 22:33:13 BST 2004