The French version of this document is no longer maintained: be sure to check the more up-to-date English version.
Exemple : un problème de classification
Classificateur bayesien naïf
Analyse discriminante
Régression logistique
A FAIRE
Variantes de la régression logistique
Nous nous intéressons maintenant à la régression avec une variable à prédire qualitative.
A FAIRE : dans ce chapitre, je parle d'analyse discriminante, déjà évoquée dans le chapitre sur l'anamyse en composantes principales. Choisir à quel endroit développer cette notion.
Pour l'instant, nous n'avons vu que la régression pour prédire une variable quantitative continue. Cela nous permet néanmoins d'examiner certaines situations dans lesquelles des variables qualitatives apparaissent : en voici un exemple.
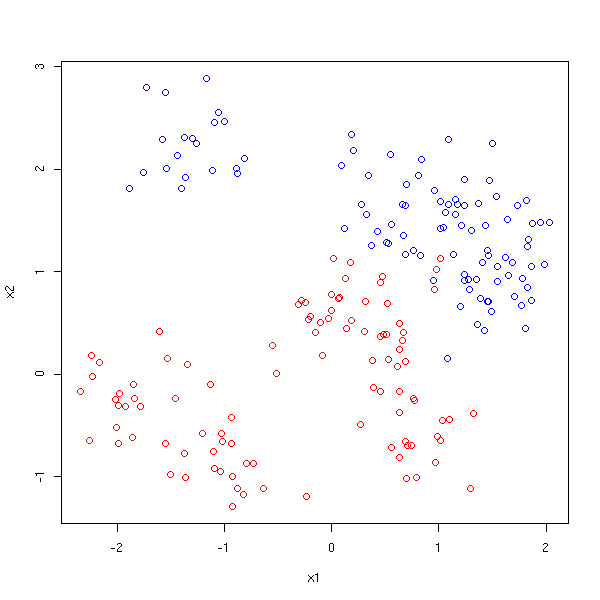
On dispose de trois variables, deux quantitatives, X1 et X2, et une qualitative, Y, à deux valeurs, que l'on cherche à prédire.
n <- 10
N <- 10
s <- .3
m1 <- rnorm(n, c(0,0))
a <- rnorm(2*N*n, m1, sd=s)
m2 <- rnorm(n, c(1,1))
b <- rnorm(2*N*n, m2, sd=s)
x1 <- c( a[2*(1:(N*n))], b[2*(1:(N*n))] )
x2 <- c( a[2*(1:(N*n))-1], b[2*(1:(N*n))-1] )
y <- c(rep(0,N*n), rep(1,N*n))
plot( x1, x2, col=c('red','blue')[1+y] )
On peut considérer la variable qualitative comme une variable numérique, à deux valeurs, 0 et 1, et procéder à un régression linéaire par rapport aux deux autres. On otient une expression du genre
Y = b0 + b1 X1 + x2 X2.
On peut alors séparer le plan (X1,X2) en deux, le long de la droite d'équation b0 + b1 X1 + x2 X2 = 1/2.
plot( x1, x2, col=c('red','blue')[1+y] )
r <- lm(y~x1+x2)
abline( (.5-coef(r)[1])/coef(r)[3], -coef(r)[2]/coef(r)[3] )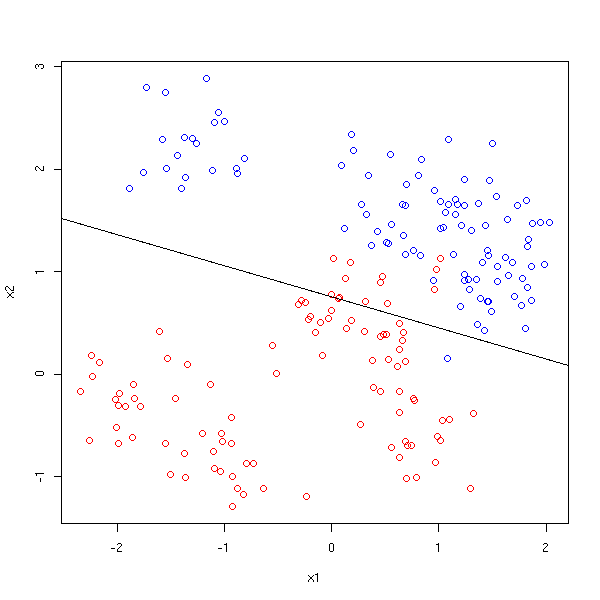
La situation est la même que précédemment, mais on fait une régression de Y par rapport aux variables X1, X2, X1X2, X1^2, X2^2.
# J'ai besoin d'une fonction pour tracer des côniques
conic.plot <- function (a,b,c,d,e,f, xlim=c(-2,2), ylim=c(-2,2), n=20, ...) {
x0 <- seq(xlim[1], xlim[2], length=n)
y0 <- seq(ylim[1], ylim[2], length=n)
x <- matrix( x0, nr=n, nc=n )
y <- matrix( y0, nr=n, nc=n, byrow=T )
z <- a*x^2 + b*x*y + c*y^2 + d*x + e*y + f
contour(x0,y0,z, nlevels=1, levels=0, drawlabels=F, ...)
}
r <- lm(y~x1+x2+I(x1^2)+I(x1*x2)+I(x2^2))$coef
plot( x1, x2, col=c('red','blue')[1+y] )
conic.plot(r[4], r[5], r[6], r[2], r[3], r[1]-.5,
xlim=par('usr')[1:2], ylim=par('usr')[3:4], add=T)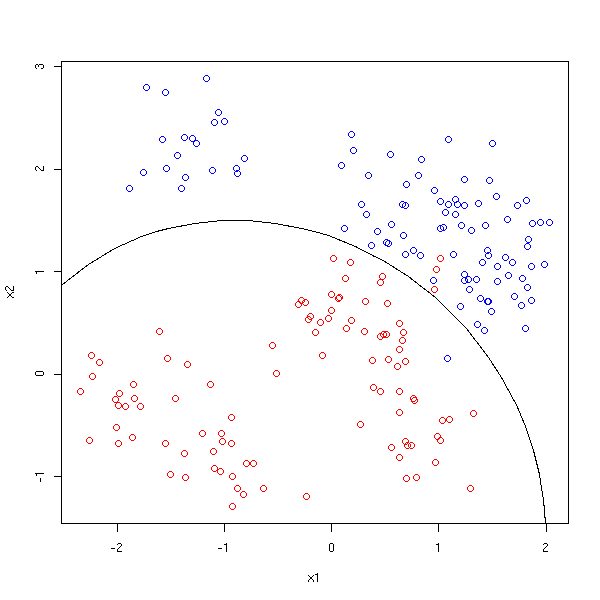
La situation est encore la même que précédemment. Cette fois-ci, pour trouver la valeur de Y à l'aide de celles de X1 et X2, on va regarder les 10 points de l'échantillon les plus proches de (X1,X2), faire la moyenne des valeurs de Y correspondantes et arrondir à 0 ou 1.
M <- 100
d <- function (a,b, N=10) {
mean( y[ order( (x1-a)^2 + (x2-b)^2 )[1:N] ] )
}
myOuter <- function (x,y,f) {
r <- matrix(nrow=length(x), ncol=length(y))
for (i in 1:length(x)) {
for (j in 1:length(y)) {
r[i,j] <- f(x[i],y[j])
}
}
r
}
cx1 <- seq(from=min(x1), to=max(x1), length=M)
cx2 <- seq(from=min(x2), to=max(x2), length=M)
plot( x1, x2, col=c('red','blue')[1+y] )
contour(cx1, cx2, myOuter(cx1,cx2,d), levels=.5, add=T)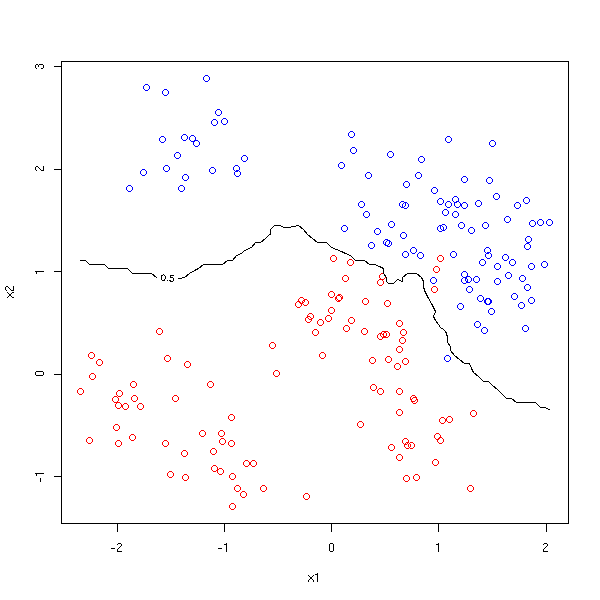
Le problème de la fonction outer est mentionné dans la FAQ où ils proposent une autre solution, plus parallèle que la mienne...
wrapper <- function(x, y, my.fun, ...) {
sapply(seq(along=x), FUN = function(i) my.fun(x[i], y[i], ...))
}
outer(cx1,cx2, FUN = wrapper, my.fun = d)Voici une autre situation, dans laquelle cette méthode se révèle plus pertinente que la précédente.
n <- 20
N <- 10
s <- .1
m1 <- rnorm(n, c(0,0))
a <- rnorm(2*N*n, m1, sd=s)
m2 <- rnorm(n, c(0,0))
b <- rnorm(2*N*n, m2, sd=s)
x1 <- c( a[2*(1:(N*n))], b[2*(1:(N*n))] )
x2 <- c( a[2*(1:(N*n))-1], b[2*(1:(N*n))-1] )
y <- c(rep(0,N*n), rep(1,N*n))
plot( x1, x2, col=c('red','blue')[1+y] )
M <- 100
cx1 <- seq(from=min(x1), to=max(x1), length=M)
cx2 <- seq(from=min(x2), to=max(x2), length=M)
#text(outer(cx1,rep(1,length(cx2))),
# outer(rep(1,length(cx1)), cx2),
# as.character(myOuter(cx1,cx2,d)))
contour(cx1, cx2, myOuter(cx1,cx2,d), levels=.5, add=T)
# On colorie les différentes zones
points(matrix(cx1, nr=M, nc=M),
matrix(cx2, nr=M, nc=M, byrow=T),
pch='.',
col=c("red", "blue")[ as.numeric( myOuter(cx1,cx2,d) >.5 )+1])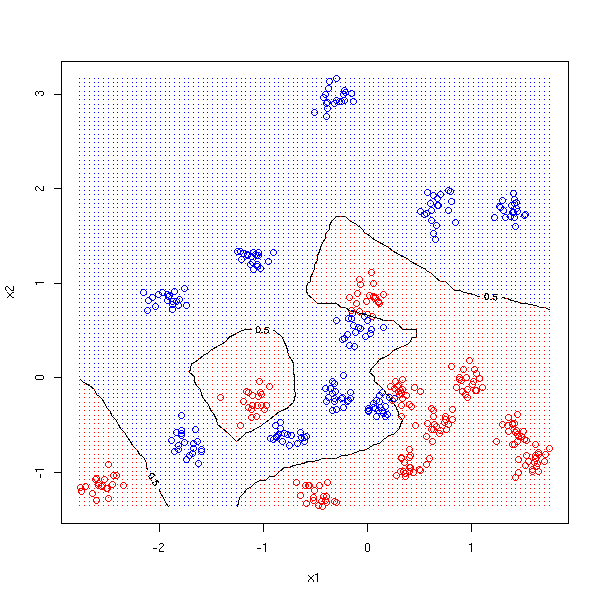
pastel <- .9
plot( x1, x2, col=c('red','blue')[1+y] )
points(matrix(cx1, nr=M, nc=M),
matrix(cx2, nr=M, nc=M, byrow=T),
pch=16,
col=c(rgb(1,pastel,pastel), rgb(pastel,pastel,1))
[ as.numeric( myOuter(cx1,cx2,d) >.5 )+1])
points(x1, x2, col=c('red','blue')[1+y] )
contour(cx1, cx2, myOuter(cx1,cx2,d), levels=.5, add=T)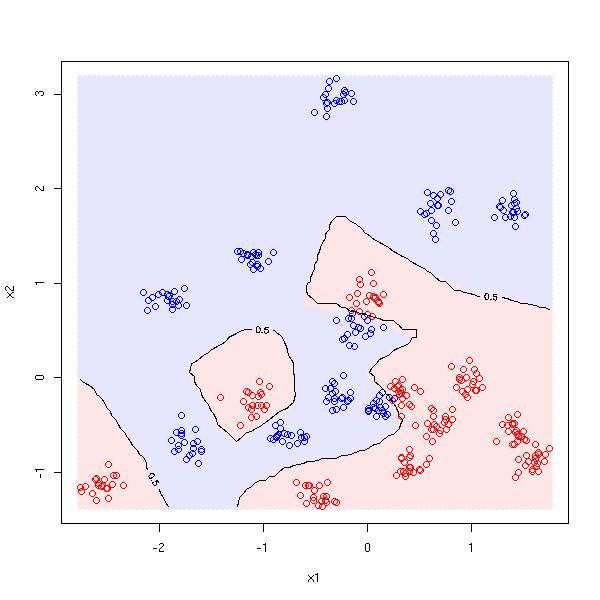
Comparons avec ce qu'on obtient en faisant varier le nombre de voisins.
plot( x1, x2, col=c('red','blue')[1+y] )
v <- c(3,10,50)
for (i in 1:length(v)) {
contour(cx1, cx2,
myOuter(cx1,cx2, function(a,b){d(a,b,v[i])}),
levels=.5, add=T, drawlabels=F, col=i+1)
}
legend(min(x1),max(x2),as.character(v),col=1+(1:length(v)), lty=1)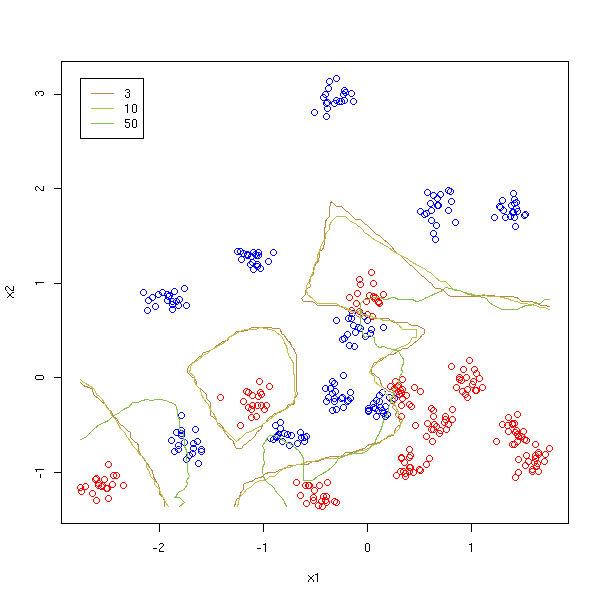
On constate qu'il ne faut pas prendre trop de points.
Dans le cas où on ne prend pas les 10 points les plus proches mais simplement le point le plus proche, on obtient un diagramme de Voronoï.
http://www.perlmonks.org/index.pl?node_id=189941

Il existe des variantes de cette méthode : au lieu de faire la moyenne sur les 10 voisins les plus proches, on peut prendre tous les points, mais en les pondérant selon leur distance (une telle pondération s'appelle un noyau) ; au lieu de prendre la distance euclidienne, on peut prendre une distance qui donne plus d'importance à certaines coordonnées ; etc.
La régression est beaucoup plus stable, elle fonctionne correctement avec des observations peu nombreuses, mais ses résultats sont imprécis. Par ailleurs, elle suppose que les données ont une structure simple.
Par contre, la méthode des plus proches voisins est plus précise, elle ne fait pas d'hypothèse sur la structure des données, mais elle est peu stable et n'est pertinente que si les observations sont nombreuses.
De plus, la méthode des plus proches voisins est victime de la malédiction de la dimension : en dimension élevée, les voisins sont généralement très loin...
A FAIRE : prendre deux échantillons, un petit (100 ou 200 observations) pour faire les calculs et un autre, plus gros (1e4 observations) pour les valider. Représenter le taux d'erreur en fonction du nombre de voisins. A FAIRE : vérifier que ça marche.
get.model <- function (n=10, m=2, s=.1) {
list( n=n, m=m, x=runif(n), y=runif(n), z=sample(1:m,n,replace=T), s=s )
}
get.sample <- function (model, n=200) {
i <- sample( 1:model$n, n, replace=T )
data.frame( x=rnorm(n, model$x[i], model$s),
y=rnorm(n, model$y[i], model$s),
z=model$z[i] )
}
nearest.neighbour.predict <- function (x, y, d, k=10) {
o <- order( (d$x-x)^2 + (d$y-y)^2 )[1:k]
s <- apply(outer(d[o,]$z, 1:max(d$z), '=='), 2, sum)
order(s, decreasing=T)[1]
}
m <- get.model()
d <- get.sample(m)
N <- 1000
d.test <- get.sample(m,N)
n <- 50
r <- rep(0, n)
# Très lent
for (k in 1:n) {
for(i in 1:N) {
r[k] <- r[k] +
(nearest.neighbour.predict(d.test$x[i], d.test$y[i], d, k) != d.test$z[i] )
}
}
plot(r/N, ylim=c(0,1), type='l', xlab="Taux d'erreurs")
abline(h=c(0,.5,1), lty=3)
rm(d.test)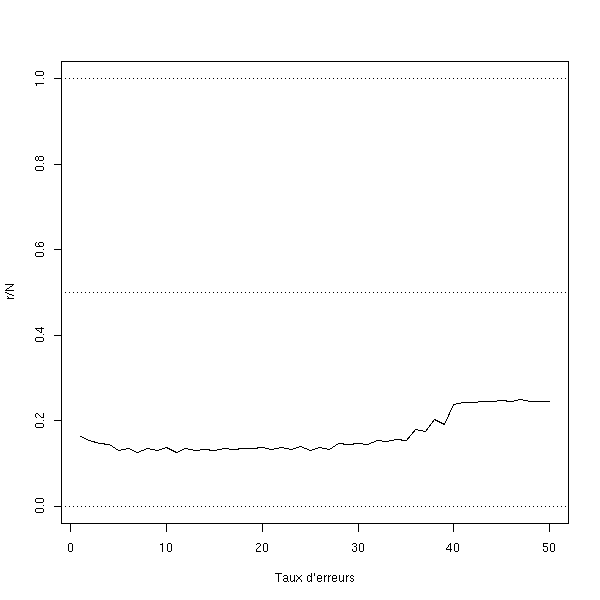
Avec un échantillon plus petit :
m <- get.model()
d <- get.sample(m, 20)
N <- 1000
d.test <- get.sample(m,N)
n <- 50
r <- rep(0, n)
# Très lent
for (k in 1:n) {
for(i in 1:N) {
r[k] <- r[k] +
(nearest.neighbour.predict(d.test$x[i], d.test$y[i], d, k) != d.test$z[i] )
}
}
plot(r/N, ylim=c(0,1), type='l', xlab="Taux d'erreurs")
abline(h=c(0,.5,1), lty=3)
rm(d.test)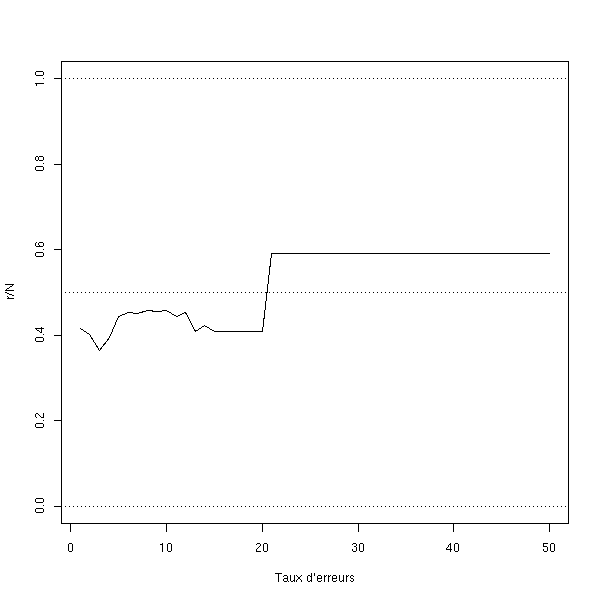
Cette méthode reste valable même s'il y a plus de deux classes.
nearest.neighbour.plot <- function (d, k=10, model=NULL) {
col <- rainbow(max(d$z))
plot( d$x, d$y, col=col )
cx <- seq(min(d$x), max(d$x), length=100)
cy <- seq(min(d$y), max(d$y), length=100)
pastel <- .8
colp <- round(pastel*255 + (1-pastel)*col2rgb(col))
colp <- rgb(colp[1,], colp[2,], colp[3,], max=255)
points(matrix(cx,nr=100,nc=100),
matrix(cy,nr=100,nc=100,byrow=T),
col = colp[
myOuter(cx,cy, function(a,b){
nearest.neighbour.predict(a,b,d,k)
})
],
pch=16
)
points( d$x, d$y, col=col )
if(!is.null(model)){
points(model$x,model$y,pch='+',cex=3,lwd=3,col=col[model$z])
}
}
m <- get.model(n=10, m=4)
d <- get.sample(m)
nearest.neighbour.plot(d, model=m)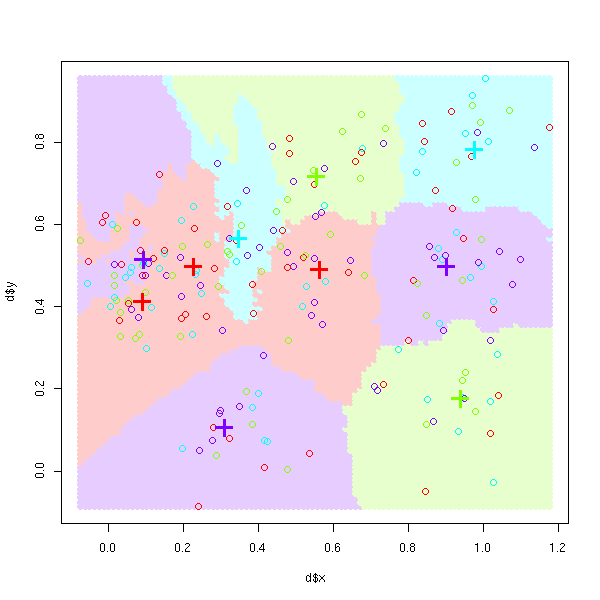
A FAIRE : tracer la limite théorique.
A FAIRE : il y a déjà une bibliothèque pour ça...
library(help=knnTree)
Au lieu d'utiliser uniquement les plus proches voisins, on peut utiliser un noyau, i.e., tenir compte de toutes les observations de l'échantillon, les observations proches comptant plus que les observations lointaines.
(laissé en exercice au lecteur)
A FAIRE : lire le chapitre 4 de "The Elements of Statistical Learning"
Mixture discriminant analysis
library(mda) ?mda
Flexible discriminant analysis
library(mda) ?fda
On considère deux variables aléatoires qualitatives binaires X et Y et on cherche à prédire Y à partir de X.
Par exemple, on cherche le nom d'un fruit à l'aide de sa forme.
X = "rond" ou "long" Y = "pomme" ou "non pomme" (par exemple : banane, orange)
On dispose d'un ensemble de fruits pour apprendre à les reconnaître : on connait leur forme et on sait s'ils sont ou non une pomme. Par exemple :
| pomme | pas une pomme
-----+---------+-----------------
rond | |
-----+---------+-----------------
long | |
A FAIRE : prendre des nombres...Si on observe un nouveau fruit, on peut tenter de deviner s'il s'agit d'une pomme ou non de la manière suivante : on calcule les probabilités conditionnelles
P( Y = pomme et X = rond )
P( Y = pomme | X = rond ) = ----------------------------
P( X = rond )
P( Y = non-pomme et X = rond )
P( Y = non-pomme | X = rond ) = --------------------------------
P( X = rond )et on les compare. Si la première est la plus grande, on dit que c'est une pomme, si c'est la seconde, on dit que ce n'est pas une pomme.
Avec nos valeurs :
A FAIRE
Toutes les présentations du classificateur de Bayes naïf reposent sur la formule de Bayes. En effet, la formule que nous avons utilisée,
P( Y = pomme et X = rond )
P( Y = pomme | X = rond ) = ----------------------------
P( X = rond )peut aussi s'écrire
P( X = rond | Y = pomme ) * P( Y = Pomme )
P( Y = pomme | X = rond ) = --------------------------------------------
P( X = rond )C'est ça, la formule de Bayes.
Quand on n'avait qu'une variable prédictive, elle ne servait pas à grand-chose, mais nous allons voir qu'avec plusieurs variables prédictives, elle permet de faire des prédiction.
Ce raisonnement se généralise facilement si on a plusieurs variables prédictives qualitatives (forme du fruit, couleur du fruit, présence de pépins ou de noyaux, etc.).
P(X1=b1 et ... et Xn=bn et Y=a)
P(Y=a|X=(b1,b2,...,bn)) = ---------------------------------
P(X1=b1 et ... et Xn=bn)Mais, si les variables prédictives sont nombreuses, certains problèmes peuvent apparaître : il est possible qu'on n'ait pas observé b1, b2,..., bn ensembles. Que faire ?
C'est ici que l'on va voir l'utilité d'écrire la formule à l'aide de probabilités conditionnelles.
P(X=(b1,...,bn)|Y=a) * P(Y=a)
P(Y=a|X=(b1,b2,...,bn)) = -------------------------------
P(X=(b1,...,bn))Si les Xi sont indépendantes (c'est une hypothèse raisonnable : sinon, il faudrait savoir quelle est la relation de dépendance entre les Xi -- cela demanderait beaucoup plus de données), ça s'écrit
P(X1=b1|Y=a) * ... * P(Xn=bn|Y=a) * P(Y=a)
= --------------------------------------------
P(X=(b1,...,bn))Ce qui nous intéresse, c'est la valeur de a qui maximise cette quantité. Comme a n'apparait pas au dénominateur, on peut s'en débarasser et se contenter de trouver la valeur de a qui maximise le numerateur
P(X1=b1|Y=a) * ... * P(Xn=bn|Y=a) * P(Y=a)
Un prédicteur baysien naïf s'utilisera donc en deux étapes : tout d'abord calculer les probabilités conditionnelles
P(Xi=bj|Y=a)
pour toutes les valeurs de i, j et a et les probabilités a priori
P(Y=a)
à l'aide du jeu de données d'apprentissage, puis, dans un deuxième temps, étant données les valeurs des variables prédictives Xi, trouver la valeur de a qui maximise
P(X1=b1|Y=a) * ... * P(Xn=bn|Y=a) * P(Y=a).
On a dû supposer que les variables prédictives étaient indépendantes (c'est là le sens du mot "naïf" dans l'expression "prédicteur bayesien naïf"). Cette hypothèse est généralement fausse ; néanmoins, les prédictions sont quand-même plus ou moins valables.
http://www.cs.washington.edu/homes/pedrod/mlj97.ps.gz A FAIRE : lire ce document
Comme le principe est relativement simple, on peut facilement implémenter soi-même un tel prédicteur : exercice.
my.bayes <- function (y, x, xp) {
# Il faudrait vérifier que y, les colonnes de x et de xp sont des facteurs,
# que xp et x ont le même nombre de colonnes, que les "levels" des colonnes
# de x et xp sont les mêmes (ou que les valeurs des colonnes de xp soient des
# valeurs des colonnes de x) -- je ne fais pas ces vérifications
na <- names(x)
m <- dim(x)[2]
# Calcul des probabilités conditionnelles
pc <- list()
for (i in 1:m) {
a <- table(data.frame(y,x=x[,i]))
a <- a / apply(a,1,sum)
pc[[ na[i] ]] <- a
}
# Calcul des probabilités a priori
pap <- table(y)
pap <- pap/sum(pap)
# Pour éviter les problèmes numériques, on prend des sommes de
# logarithmes de probabilités au lieu des produits de probabilités
pc <- lapply(pc,log)
pap <- log(pap)
# Calcul des P(X1=b1|Y=a) * ... * P(Xn=bn|Y=a) * P(Y=a)
papo <- matrix(0, nr=dim(xp)[1], nc=length(pap))
colnames(papo) <- names(pap)
# Il doit y avoir moyen de faire ça sans boucle...
for (i in 1:dim(xp)[1]) {
for (j in 1:length(pap)) {
papo[i,j] <- pap[j]
for (k in 1:dim(x)[2]) {
papo[i,j] <- papo[i,j] + pc[[ na[k] ]][j,xp[i,k]]
}
}
}
papo <- papo - apply(papo,1,mean)
papo <- exp(papo)
levels(y)[ apply(papo, 1, function (a) { which(a==max(a))[1] }) ]
}
# Des données
library(e1071)
data(HouseVotes84)
y <- HouseVotes84[,1]
x <- HouseVotes84[,-1]
# Je n'ai pas prévu de traitement des valeurs manquantes
i <- which(!apply( apply(x,1,is.na), 2, any ))
x <- x[i,]
y <- y[i]
# Calcul des prédictions : exactes dans près de 92% des cas.
yp <- my.bayes(y,x,x)
mean(y==yp)
En fait, c'est déjà implémenté sous R -- et la fonction tient compte d'éventuelles valeurs manquantes.
library(e1071) ?naiveBayes
Pour des exemples de données :
library(mlbench) data(package=mlbench)
A FAIRE : rappeler ce que c'est
Pour évaluer l'efficacité
library(mlbench) data(DNA) d <- DNA d$Class <- factor(ifelse(d$Class=='n','n','i')) library(e1071) r <- naiveBayes(Class~.,d) i <- sample(1:dim(d)[2],100) p <- predict(r, d[,-length(d)][i,]) # Long... A <- sum(p == 'i' & d$Class[i] == 'i') B <- sum(p == 'i' & d$Class[i] != 'i') C <- sum(p != 'i' & d$Class[i] == 'i') # Taux de précision 100 * A/(A+B) # Taux de rappel 100 * A/(A+C)
A FAIRE library(mlbench) data(DNA) d <- DNA d$Class <- factor(ifelse(d$Class=='n','n','i')) library(e1071) r <- naiveBayes(Class~.,d) p <- predict(r, d[,-length(d)], type='raw')
Depuis quelques années, la recrudescence du spam a amené les classificateurs bayesien sur le devant de la scène.
A FAIRE : URL http://www.xml.com/pub/a/2003/11/19/udell.html K. Williams, An Introduction to Machine Learning with Perl http://conferences.oreillynet.com/presentations/bio2003/williams_ken.ppt
La variable à prédire, y, a deux valeurs "spam", "non spam". Il y a une variable prédictive pour chaque mot (ça fait plusieurs milliers de mots), avec deux valeurs "présent" ou "absent".
L'apprentissage s'effectue avec des messages dont on connait la nature (par exemple, les messages que l'on a reçu en une semaine).
De manière plus générale, la classification de textes est l'une des principales applications des classificateurs de Bayes naïfs.
Il y a une autre notion de "classificateur de Bayes naïf", dans lequel les variables prédictives sont quantitatives : ce sont des variables de comptage (dans l'exemple du spam ou de la classification de texte, on ne se contente pas de regarder la présence ou l'absence de chaque mot, on regarde aussi le nombre d'occurrences) et pas des variables de présence-absence.
Si on tient à être très rigoureux sur la terminologie, le classificateur de Bayes naïf utilisant des variables de présence-absence est un "classificateur de Bayes naïf binomial" alors que celui qui utilise des variables de comptage est un "classificateur de Bayes naïf multinomial".
A. McCallum, K. Nigam A Comparison of Event Models for Naive Bayes Text Classification http://www-2.cs.cmu.edu/%7Eknigam/papers/multinomial-aaaiws98.pdf
Il existe des variantes du classificateur de Bayes naïf qui tentent de contourner ses hypothèses un peu trop naïves (l'indépendance des variables prédictives).
Les TAN (Tree-augmented Naïve Bayes) modélisent les relations de dépendance entre les variables prédictives par un arbre.
Les réseaux bayesiens (très à la mode depuis un ou deux ans, un peu comme les réseaux de neurones au débit des années 90) modélisent les relations de dépendance entre les variables prédictives par un graphe.
http://www.vision.ethz.ch/gm/bnclassifiers.pdf A FAIRE : d'autres liens, en particulier les exemples de Holmes & Watson...
De manière générale, tous les problèmes de classification...
1. On cherche à savoir si des patronymes sont originaires d'Asie du Sud ou pas. Pour cela, on regarde la présence ou l'absence des chaines de quatre lettres dans chaque nom.
http://dimax.rutgers.edu/%7Esguharay/newfinalpresentation.pdf
2. Reconnaissance de caractères manuscrits (sur un Palm).
3. Reconnaissance de la parole (sur un téléphone portable).
4. On dispose de plein de résumés d'articles de biologie et on cherche les phrases qui décrivent une interaction entre gènes. Pour ce faire, on commence par traiter à la main une centaine de résumés, que l'on découpe en phrase. Pour chaque phrase, on regarde d'une part si elle décrit une interaction de gènes ou non (c'est notre variable à prédire) d'autre part quels mots elle contient (ce sont nos variables prédictives). A l'aide de ces données d'apprentissage, on calcule les probabilités conditionnelles et les probabilités a priori. Etant donné une nouvelle phrase, le classificateur de Bayes nous donne la probabilité qu'elle décrive une interaction.
Nous l'avons déjà vue plus haut : on a une variable qualitative que l'on cherche à prédire à l'aide de plusieurs variables quantitatives. On cherche un plan (ou un sous-espace de dimension plus petite) dans lequel les différentes valeurs de la variable qualitative correspondent à des points les plus éloignés possibles.
library(MASS) n <- 100 k <- 5 x1 <- runif(k,-5,5) + rnorm(k*n) x2 <- runif(k,-5,5) + rnorm(k*n) x3 <- runif(k,-5,5) + rnorm(k*n) x4 <- runif(k,-5,5) + rnorm(k*n) x5 <- runif(k,-5,5) + rnorm(k*n) y <- factor(rep(1:5,n)) plot(lda(y~x1+x2+x3+x4+x5))
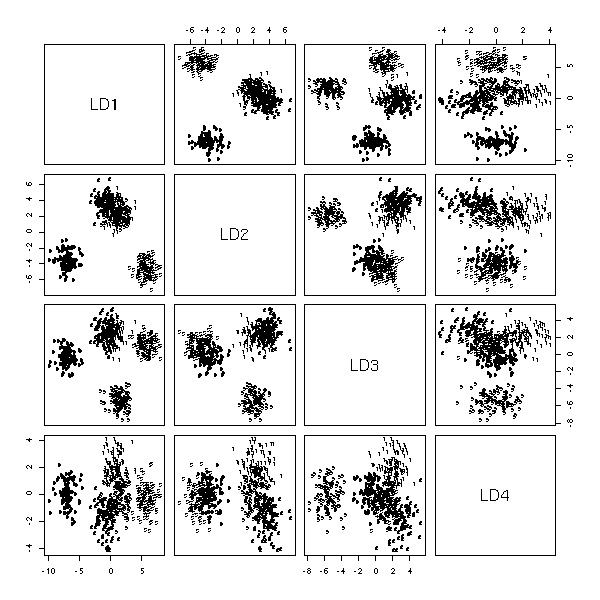
La régression avec des variables quantitatives consiste à écrire
E(Y) = a0 + a1 x1 + ... + an xn.
Mais si Y n'a qu'un nombre fini de valeurs, ce n'est plus pertinent : on peut certes remplacer les valeurs de y par des nombres (comme nous l'avons fait plus haut, dans l'exemple du problème de classification), mais le membre de gauche sera borné et pas celui de droite -- ça ne fait pas très propre, et c'est très génant si on veut prédire des valeurs...
n <- 100 x <- c(rnorm(n), 1+rnorm(n)) y <- c(rep(0,n), rep(1,n)) plot(y~x) abline(lm(y~x), col='red')
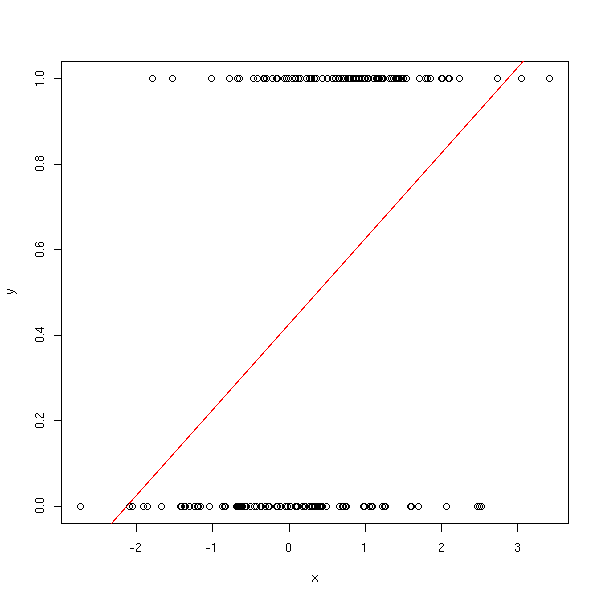
L'idée du modèle linéaire généralisé consiste à remplacer E(y) par autre chose.
Dans le cas de la régression logistique, on s'intéresse à une variable Y à deux valeurs, 0 et 1, et on regarde la probabilité qu'elle soit égale à 1.
P[ Y == 1 ] = a0 + a1 x1 + ... + an xn.
C'est exactement la même formule que précédemment (car E(Y)=P(Y==1)), et on a donc le même problème : le membre de gauche est borné, pas celui de droite. Pour contourner ce problème, on peut appliquer au membre de gauche une fonction qui établit une bijection entre l'intervalle [0,1] et la droite réelle -- une telle fonction s'appelle un lien.
On prend souvent la fonction logistique :
p
logit(p) = log -------
1 - pOn peut donc écrire
P(gagner)
logit( P(gagner) ) = log -----------.
P(perdre)Le quotient P(gagner)/P(perdre) s'appelle la cote ("odds", en anglais) -- vous avez surement déjà entendu l'expression << la cote est à ... contre 1 >>.
Voici le graphe de cette fonction.
x <- seq(0,1, length=100)
x <- x[2:(length(x)-1)]
logit <- function (t) {
log( t / (1-t) )
}
plot(logit(x) ~ x, type='l')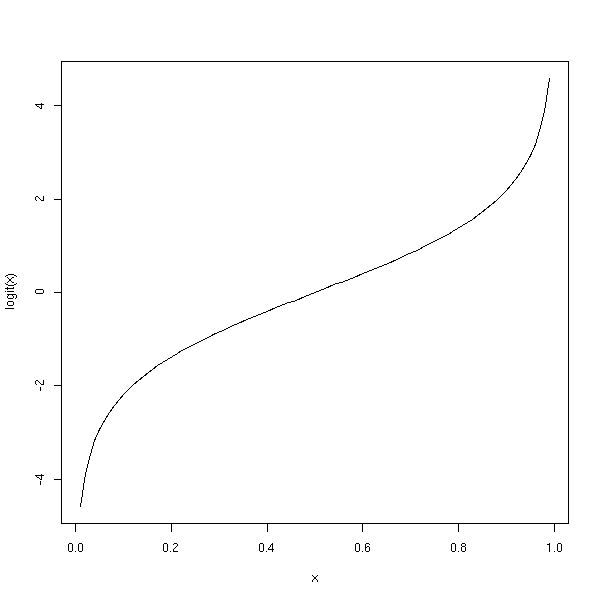
La fonction probit, la réciproque de la fonction de répartition de la loi normale standard, est un autre lien.
curve(logit(x), col='blue', add=F)
curve(qnorm(x), col='red', add=T)
a <- par("usr")
legend( a[1], a[4], c("logit","probit"), col=c("blue","red"), lty=1)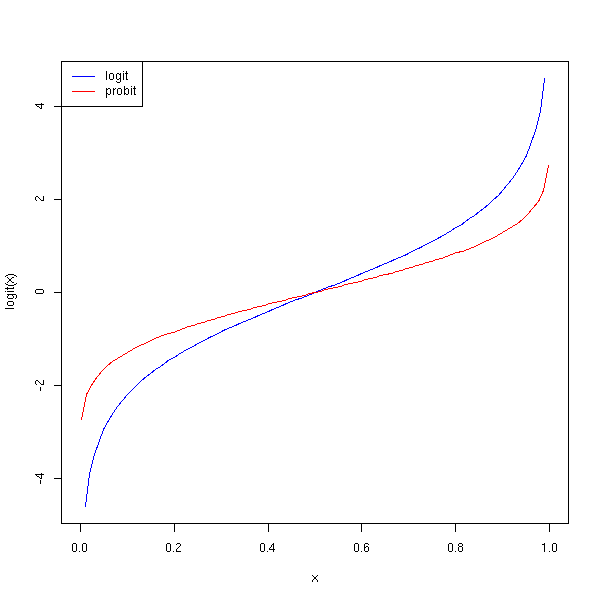
On rencontre aussi parfois la fonction log-log.
curve(logit(x), col='blue', add=F)
curve(qnorm(x), col='red', add=T)
curve(log(-log(1-x)), col='green', add=T)
abline(h=0, lty=3)
abline(v=0, lty=3)
a <- par("usr")
legend( a[1], a[4],
c("logit","probit", "log-log"),
col=c("blue","red","green"),
lty=1)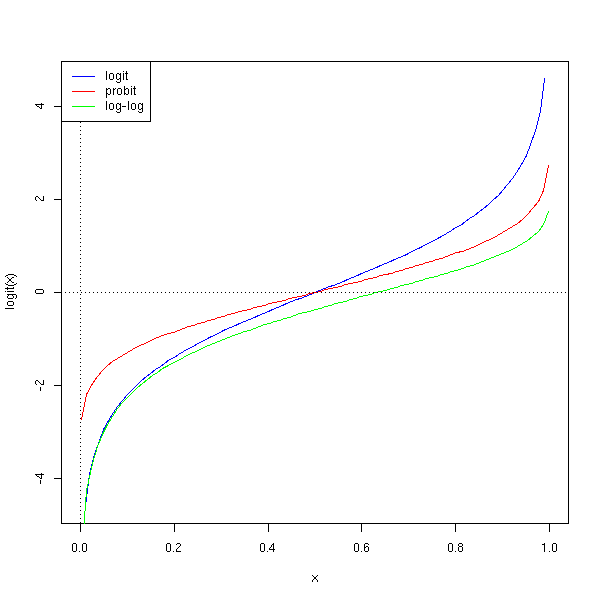
On pourrait penser transformer les données à l'aide de l'inverse du lien, faire une régression linéaire, et appliquer le lien : ça ne marche pas, car les données initiales sont soit 0, soit 1, qui donneraient plus ou moins l'infini après transformation.
A FAIRE : expliquer plus en détails cette erreur.
ilogit <- function (l) {
exp(l) / ( 1 + exp(l) )
}
fakelogit <- function (l) {
ifelse(l>.5, 1e6, -1e6)
}
n <- 100
x <- c(rnorm(n), 1+rnorm(n))
y <- c(rep(0,n), rep(1,n))
yy <- fakelogit(y)
xp <- seq(min(x),max(x),length=200)
yp <- ilogit(predict(lm(yy~x), data.frame(x=xp)))
yp[is.na(yp)] <- 1
plot(y~x)
lines(xp,yp, col='red', lwd=3)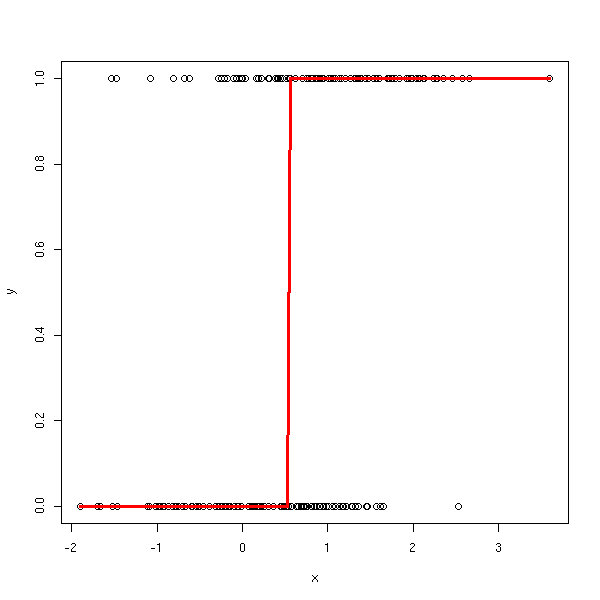
On abandonne donc les moindres carrés et on essaye d'utiliser la méthode du maximum de vraissemblance.
n <- 100
x <- c(rnorm(n), 1+rnorm(n))
y <- c(rep(0,n), rep(1,n))
f <- function (a) {
-sum(log(ilogit(a[1]+a[2]*x[y==1]))) - sum(log(1-ilogit(a[1]+a[2]*x[y==0])))
}
r <- optim(c(0,1),f)
a <- r$par[1]
b <- r$par[2]
plot(y~x)
curve( dnorm(x,1,1)*.5/(dnorm(x,1,1)*.5+dnorm(x,0,1)*(1-.5)), add=T, col='red')
curve( ilogit(a+b*x), add=T )
legend( .95*par('usr')[1]+.05*par('usr')[2],
.9,
c('courbe théorique', 'MLE'),
col=c('red', par('fg')),
lty=1, lwd=1)
title(main="Régression logistique à la main")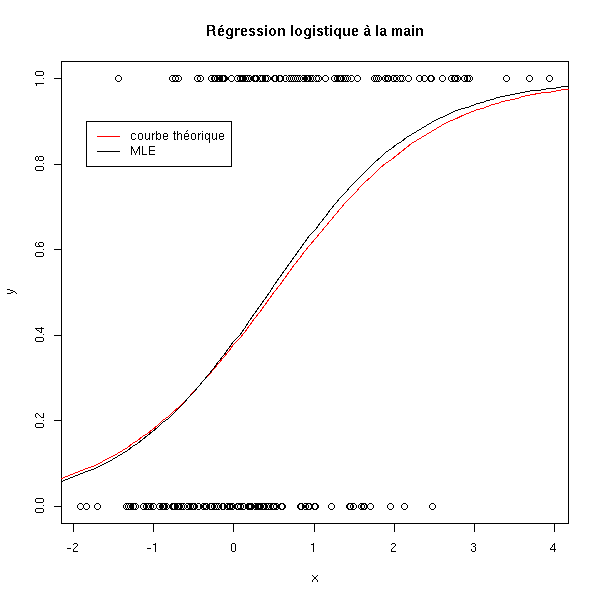
On peut faire ça directement à l'aide de la commande glm.
#
# ATTENTION !!!
# Surtout ne pas oublier l'argument "family" -- sinon, on fait une régression linéaire...
#
r <- glm(y~x, family=binomial)
plot(y~x)
abline(lm(y~x),col='red',lty=2)
xx <- seq(min(x), max(x), length=100)
yy <- predict(r, data.frame(x=xx), type='response')
lines(xx,yy, col='blue', lwd=5, lty=2)
lines(xx, ilogit(r$coef[1]+xx*r$coef[2]))
legend( .95*par('usr')[1]+.05*par('usr')[2],
.9,
c('régression linéaire',
"prédiction à l'aide de la commande predict",
"prédiction à l'aide des coefficients"),
col=c('red', 'blue', par('fg')),
lty=c(2,2,1), lwd=c(1,5,1))
title(main="Régression logistique avec la commande glm")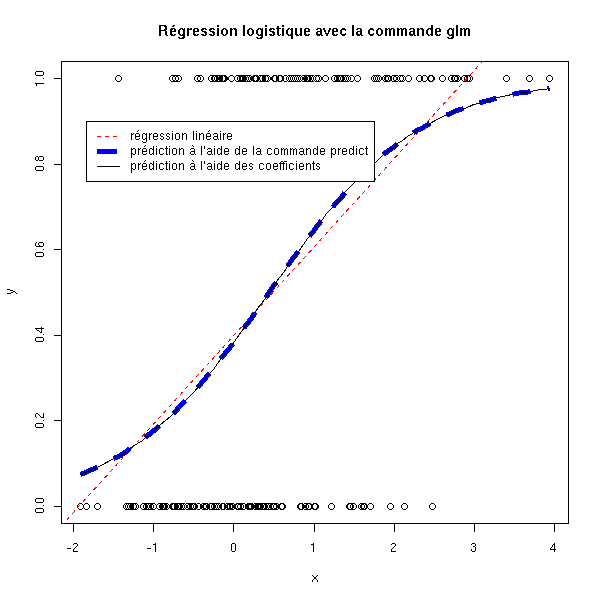
En particulier, on constate que les valeurs prédites, qui sont des probabilités, sont bien entre 0 et 1 -- alors qu'avec la régression linéaire, on avait des valeurs non bornées.
On peut comparer les différents types de régression : on constate que la régression logistique donne les résultats les plus proches de la courbe théorique.
n <- 100
x <- c(rnorm(n), 1+rnorm(n))
y <- c(rep(0,n), rep(1,n))
plot(y~x)
# prédiction brutale
m1 <- mean(x[y==0])
m2 <- mean(x[y==1])
m <- mean(c(m1,m2))
if(m1<m2) a <- 0
if(m1>m2) a <- 1
if(m1==m2) a <- .5
lines( c(min(x),m,m,max(x)),
c(a,a,1-a,1-a),
col='blue')
# régression linéaire
abline(lm(y~x), col='red')
# régression logistique
xp <- seq(min(x),max(x),length=200)
r <- glm(y~x, family=binomial)
yp <- predict(r, data.frame(x=xp), type='response')
lines(xp,yp, col='orange')
# Courbe théorique
curve( dnorm(x,1,1)*.5/(dnorm(x,1,1)*.5+dnorm(x,0,1)*(1-.5)), add=T, lty=3, lwd=3)
legend( .95*par('usr')[1]+.05*par('usr')[2],
.9, #par('usr')[4],
c('prédiction brutale', "régression linéaire", "régression logistique",
"courbe théorique"),
col=c('blue','red','orange', par('fg')),
lty=c(1,1,1,3),lwd=c(1,1,1,3))
title(main="Comparaison des régressions linéaire et logistique")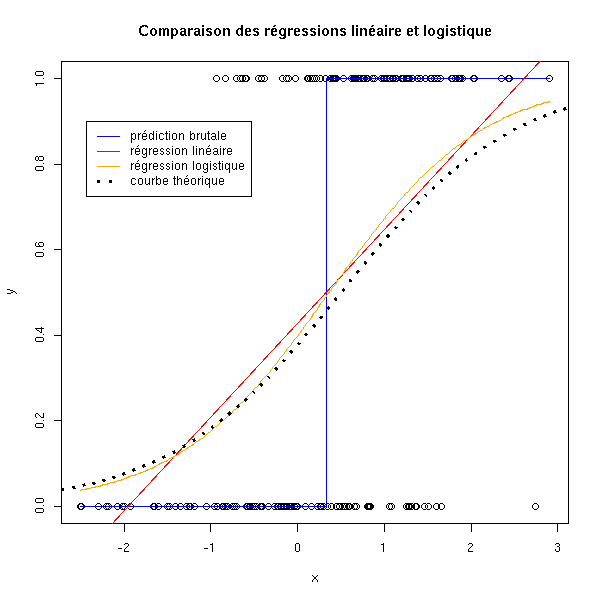
N'oubliez pas de regarder les exemples d'utilisation de la commande glm :
demo("lm.glm")
Comme pour la régression linéaire, on a trois manières d'afficher le résultat.
La commande print :
> r
Call: glm(formula = y ~ x, family = binomial)
Coefficients:
(Intercept) x
-0.4864 0.9039
Degrees of Freedom: 199 Total (i.e. Null); 198 Residual
Null Deviance: 277.3
Residual Deviance: 239.7 AIC: 243.7La commande summary :
> summary(r)
Call:
glm(formula = y ~ x, family = binomial)
Deviance Residuals:
Min 1Q Median 3Q Max
-1.94200 -0.99371 0.05564 0.97949 1.87198
Coefficients:
Estimate Std. Error z value Pr(>|z|)
(Intercept) -0.4864 0.1804 -2.696 0.00702 **
x 0.9039 0.1656 5.459 4.79e-08 ***
---
Signif. codes: 0 `***' 0.001 `**' 0.01 `*' 0.05 `.' 0.1 ` ' 1
(Dispersion parameter for binomial family taken to be 1)
Null deviance: 277.26 on 199 degrees of freedom
Residual deviance: 239.69 on 198 degrees of freedom
AIC: 243.69
Number of Fisher Scoring iterations: 3La commande anova :
> anova(r)
Analysis of Deviance Table
Model: binomial, link: logit
Response: y
Terms added sequentially (first to last)
Df Deviance Resid. Df Resid. Dev
NULL 199 277.259
x 1 37.566 198 239.693Il y a aussi la commande aov.
> aov(r)
Call:
aov(formula = r)
Terms:
x Residuals
Sum of Squares 9.13147 40.86853
Deg. of Freedom 1 198
Residual standard error: 0.45432
Estimated effects may be unbalancedMentionnons aussi la commande manova.
?summary.manova
On dispose aussi de graphiques pour examiner la qualité de la régression.
Les résidus de Pearson sont définis par
y_i - \hat y_i
r_i = ----------------
s_ioù s_i est l'estimation de l'écart-type du bruit. Il en existe aussi une version normalisée (c'est comme pour la régression linéaire : l'écart-type du bruit et l'écart-type des résidus diffèrent) et une version standardisée (on divise par une estimation de l'écart-type obtenue en ôtant l'observation i).
On remarquera que y_i vaut 0 ou 1, alors que \hat y_i est une probabilité (entre 0 et 1), ce qui explique la forme du graphique : on voit deux courbes, un e au dessus de l'axe, l'autre en dessous, qui correspondent aux deux valeurs possibles de y_i. L'une de ces courbes est décroissante et tend vers 0 en + l'infini, pour l'autre, c'est le contraire.
n <- 100 x <- c(rnorm(n), 1+rnorm(n)) y <- c(rep(0,n), rep(1,n)) r <- glm(y~x, family=binomial) plot(r, which=1)
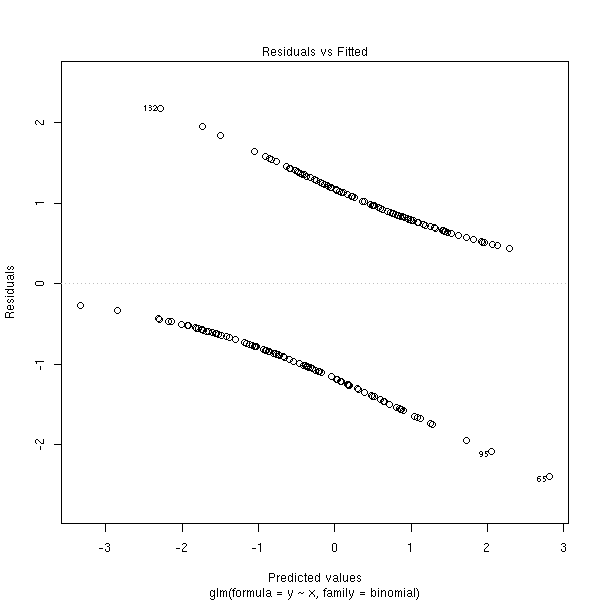
En fait, cette simulation ne correspond pas exactement au modèle de la régression logistique. Ce serait plutôt des choses comme ça :
n <- 1000 a <- -2 b <- 1 x <- runif(n, -4, 5) y <- exp(a*x+b + rnorm(n)) y <- y/(1+y) y <- rbinom(n,1,y) plot(y~x)
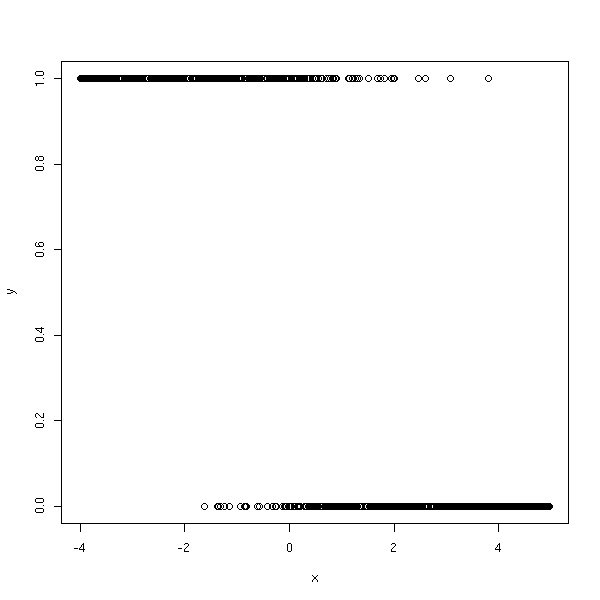
boxplot(x~y, horizontal=T)
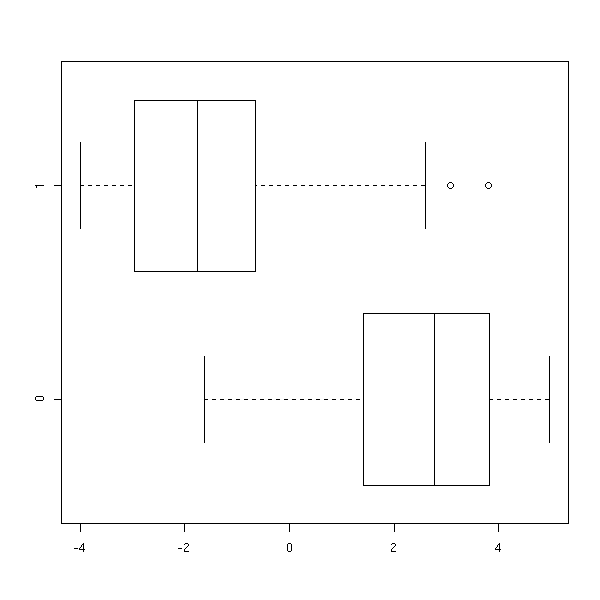
op <- par(mfrow=c(2,1)) hist(x[y==1], probability=T, col='light blue') lines(density(x[y==1]),col='red',lwd=3) hist(x[y==0], probability=T, col='light blue') lines(density(x[y==0]),col='red',lwd=3) par(op)
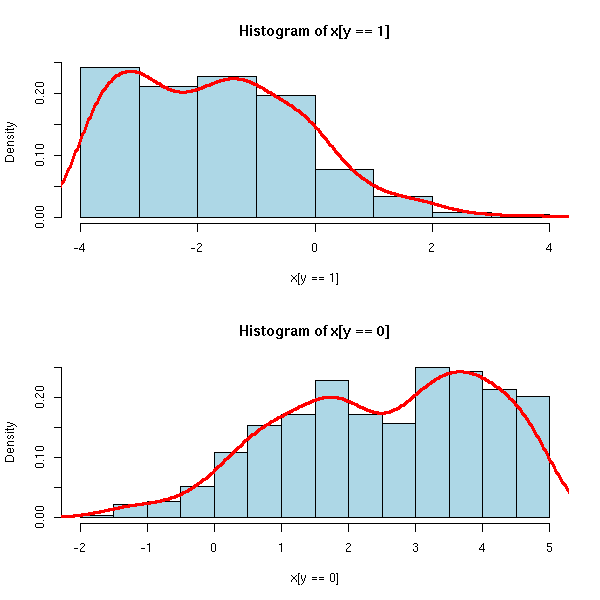
rt <- glm(y~x, family=binomial) plot(rt, which=1)
A FAIRE : donner des exemples concrets de pathologies.
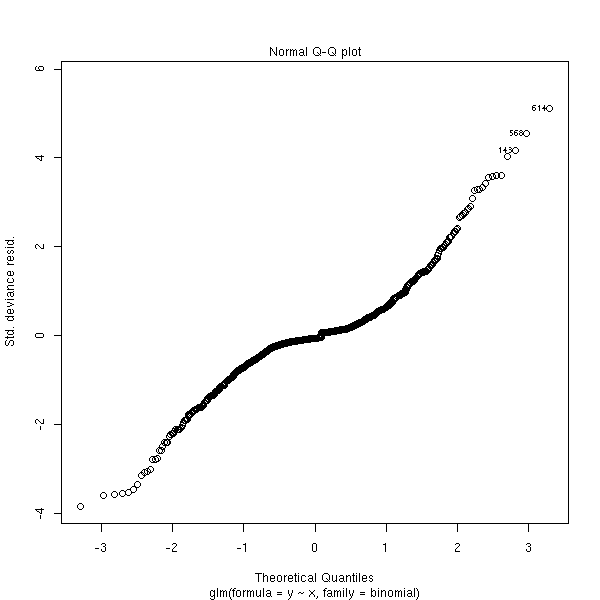
On nous propose aussi le QQplot des résidus : je ne comprends pas pourquoi, car les résidus ne suivent PAS une loi normale...
plot(rt, which=2)
hist(rt$residuals, breaks=seq(min(rt$residuals),max(rt$residuals)+1,by=.5),
xlim=c(-10,10),
probability=T, col='light blue')
points(density(rt$residuals, bw=.5), type='l', lwd=3, col='red')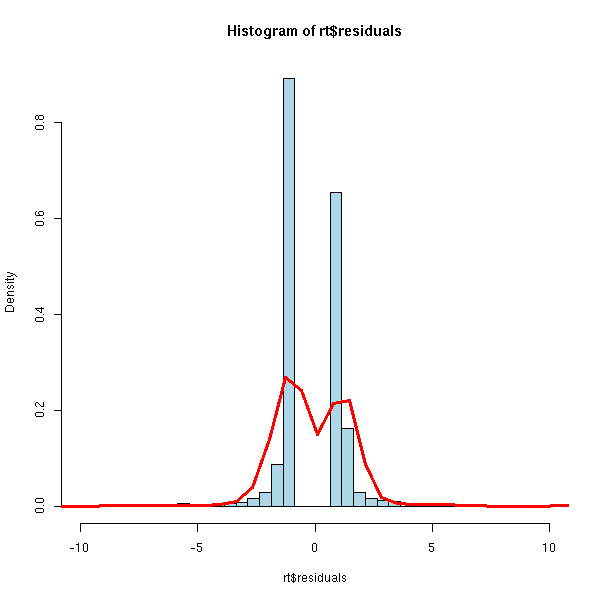
Néanmoins, on peut transformer ces résidus pour obtenir des résidus suivant une loi normale : ce sont les résidus d'Anscombe. Cette transformation est complexe et R ne semble pas la connaître...
Exercice : effectuer cette transformation, de manière approchée, à l'aide d'une simulation.
On a aussi la valeur absolue des résidus
plot(rt, which=3)
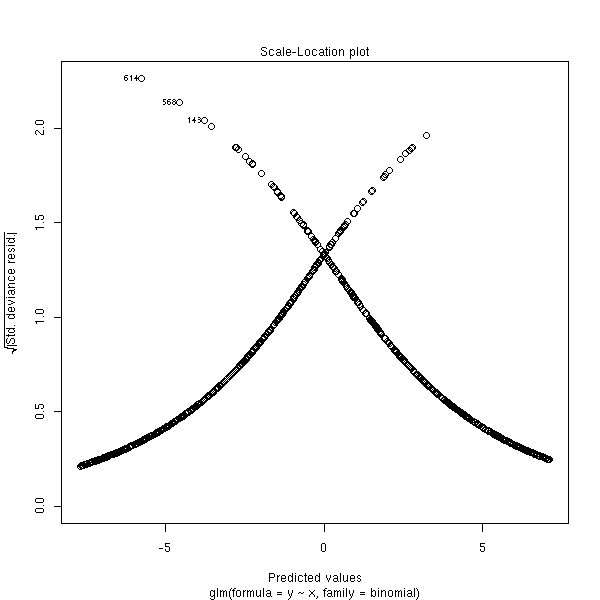
et les distances de Cook.
plot(rt, which=4)
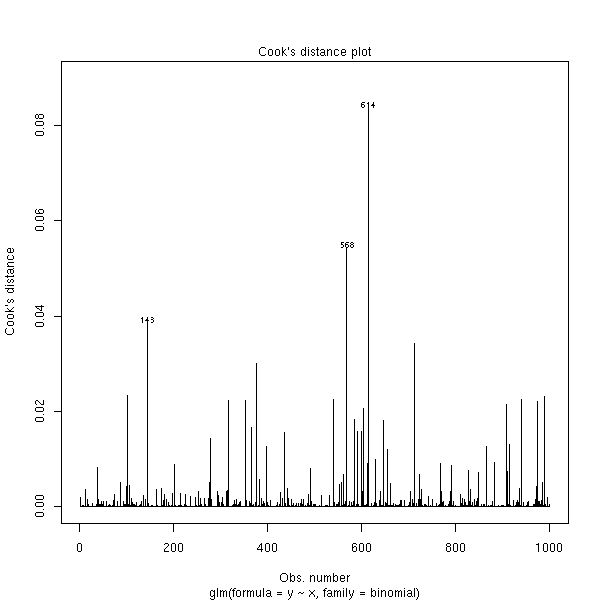
La déviance est définie par
D = -2(L-Lsat)
où L est la log-vraissemblance et Lsat la log-vraissemblance du modèle saturé (avec autant de variables que d'observations). On est content si D/ddl < 1.
> rt$deviance [1] 362.0677
On a aussi la déviance du modèle nul (correspondant à l'hypothèse << les variables prédictives n'ont aucun effet >>, i.e., la probabilité est constante et ne dépend pas des variables prédictives).
> rt$null.deviance [1] 1383.377
Le AIC (Akaike Information Criterion) est préférable à la déviance pour comparer des modèles, car il tient compte du nombre de paramètres de ces modèles.
> rt$aic [1] 366.0677
Il est défini par
- 2 * log-vraissemblance + 2 * nombre de paramètres.
Il en existe des variantes, comme le BIC,
- 2 * log-vraissemblance + ln(nombre d'observations) * nombre de paramètres.
Nous avons déjà vu les différents résidus. Résidus de Pearson (bruts, standardisés ou studentisés) :
y_i - \hat y_i
----------------
s_iRésidus de déviance : contribution de chaque observation à la déviance.
Résidus d'Anscombe : on transforme préalablement la variable pour que les résidus suivent une loi normale (la fonction t est compliquée) :
t(y_i) - t(\hat y_i)
----------------------
t'(y_i) s_iR ne semble pas connaitre les résidus d'Anscombe...
Comme dans le cas linéaire, on peut mesurer l'effet de levier, avec la << matrice chapeau >> (mais ce n'est pas exactement la même matrice que dans le cas linéaire).
A FAIRE : avec R
# C'est sensé ne pas être la même que dans le cas linéaire : là, c'est la même... plot(hat(x), type='h')
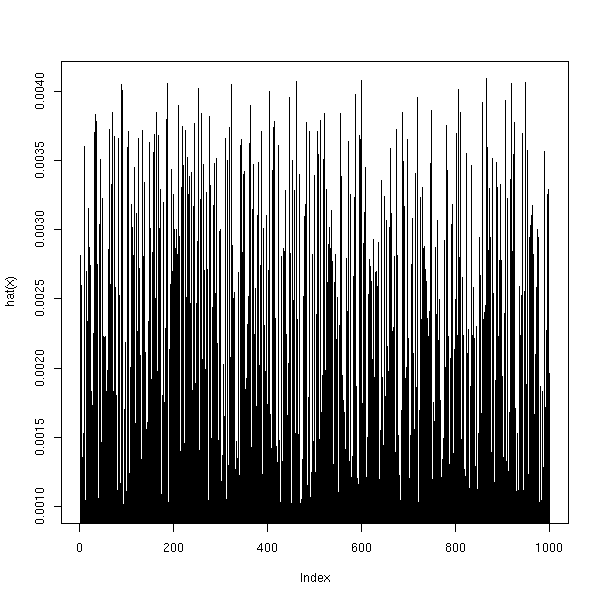
On dispose aussi de la distance de Cook, comme pour la régression linéaire.
plot(rt, which=4)
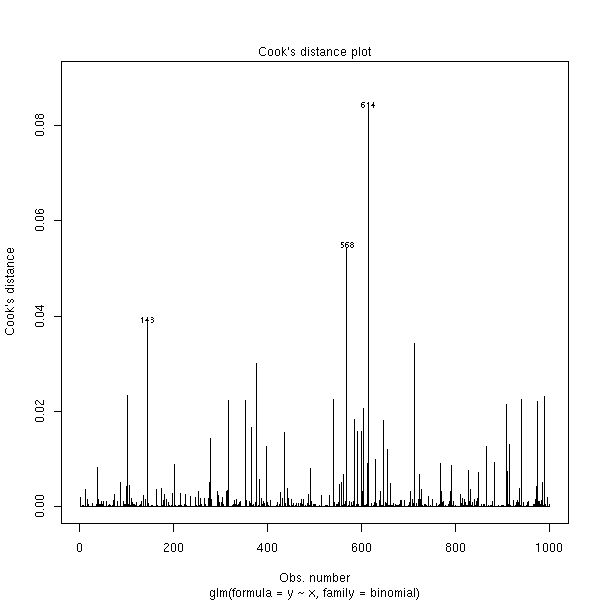
Test du rapport de vraissemblance : pour comparer deux modèles imbriqués à q1 et q2 paramètres, on regarde D2 - D1, qui suit asymptotiquement une loi du Chi^2 (dans le cas d'une loi binomiale ou de Poisson) ou de Fisher (dans le cas d'une loi gaussienne) à q2-q1 degrés de liberté.
A FAIRE
Test de Wald : c'est une approximation quadratique du test du rapport de vraissemblance.
library(car) ?linear.hypothesis
(ce qui suit est la réponse à un mai qu'on m'avait envoyé)
(Je rappelle que je ne suis pas du tout statisticien, mes explications sont donc peut-être parfois erronnées.)
Dans les lignes qui suivent, je prend un exemple de régression logistique (j'ai pris l'exemple au hasard, il n'est probablement pas pertinent) :
library(mlbench) data(BostonHousing) y <- BostonHousing[,1] y <- factor(y>median(y)) x1 <- BostonHousing[,2] x2 <- BostonHousing[,3]
On peut calculer la régression à l'aide de la fonction glm
glm(y~x1+x2, family=binomial)
ou à l'aide de la fonction lrm dans la bibliothèque Design, qui donne beaucoup plus d'information -- en particulier certains des tests dont vous parlez.
library(Design) lrm(y~x1+x2)
Il vient :
> lrm(y~x1+x2)
Logistic Regression Model
lrm(formula = y ~ x1 + x2)
Frequencies of Responses
FALSE TRUE
253 253
Obs Max Deriv Model L.R. d.f. P C Dxy
506 3e-06 234.13 2 0 0.862 0.724
Gamma Tau-a R2 Brier
0.725 0.363 0.494 0.145
Coef S.E. Wald Z P
Intercept -1.66990 0.27245 -6.13 0e+00
x1 -0.04954 0.01280 -3.87 1e-04
x2 0.17985 0.02084 8.63 0e+00> 1. dans une régression logistique comment savoir si le modèle est bon? > (l'équivalent du R² dans les régression linéaire)
Il y a plusieurs équivalents du R^2 pour la regression logistique, que je ne connais pas vraiment. Le plus immédiat ("pseudo-R^2" ou "R^2 de McFadden") consiste à calculer
(déviance du modèle) - (déviance du modèle nul)
-------------------------------------------------
(déviance du modèle nul)Je rappelle que la déviance, c'est -2*log(L) où L est la vraissemblance, et que le modèle nul, c'est y~1. De même que le R^2 de la régression linéaire s'interprète comme le pourcentage de variance expliqué par le modèle, celui-ci s'interprète comme le pourcentage de déviance expliqué par le modèle.
Mais ça ne dit pas si le modèle est bon : si le R^2 est faible, cela peut signifier qu'il y a beaucoup de bruit ou que le modèle est incomplet.
On pourrait penser à faire comme avec les modèles linéaires : des dessins. Pour apprendre à les lire, effectuons quelques simulations.
Données aléatoires :
n <- 1000 y <- factor(sample(0:1,n,replace=T)) x <- rnorm(n) r <- glm(y~x,family=binomial) op <- par(mfrow=c(2,2)) plot(r,ask=F) par(op)
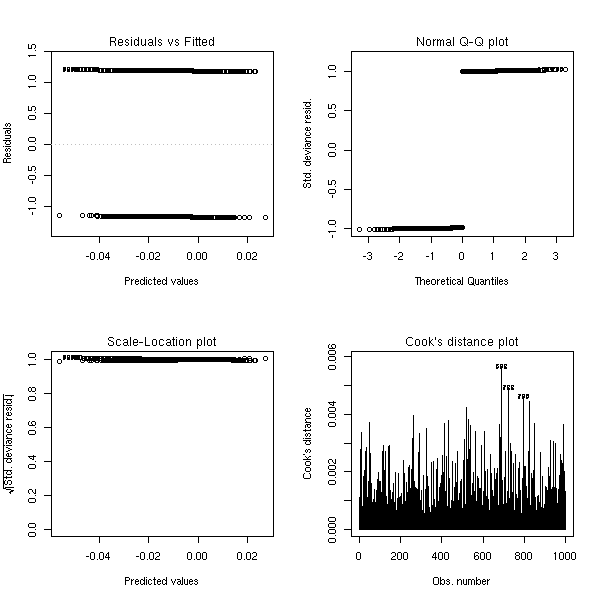
library(Design) r <- lrm(y~x,y=T,x=T) P <- resid(r,"gof")['P'] resid(r,"partial",pl=T) title(signif(P))
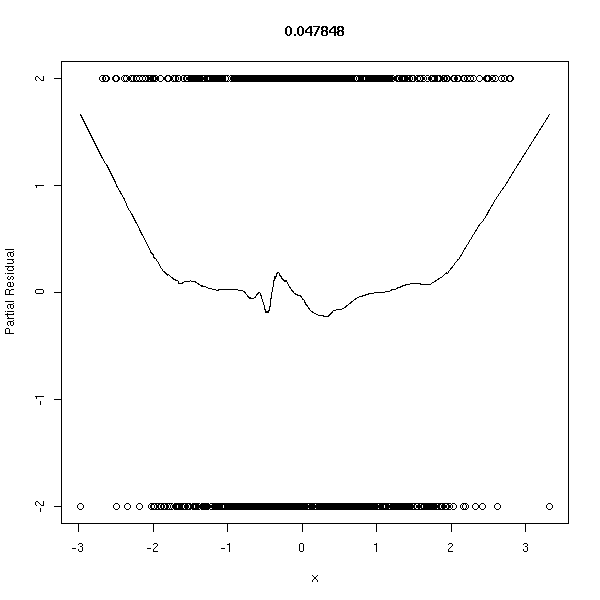
Données conformes au modèle :
n <- 1000 x <- rnorm(n) a <- 1 b <- -2 p <- exp(a+b*x)/(1+exp(a+b*x)) y <- factor(ifelse( runif(n)<p, 1, 0 ), levels=0:1) r <- glm(y~x,family=binomial) op <- par(mfrow=c(2,2)) plot(r,ask=F) par(op)
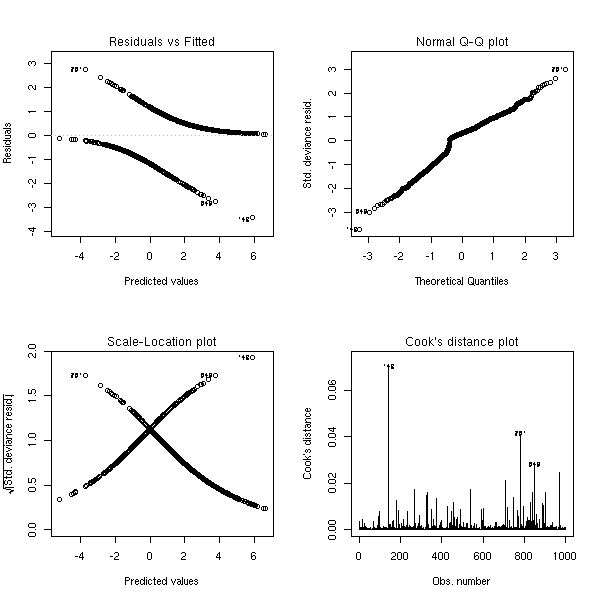
r <- lrm(y~x,y=T,x=T) P <- resid(r,"gof")['P'] resid(r,"partial",pl=T) title(signif(P))
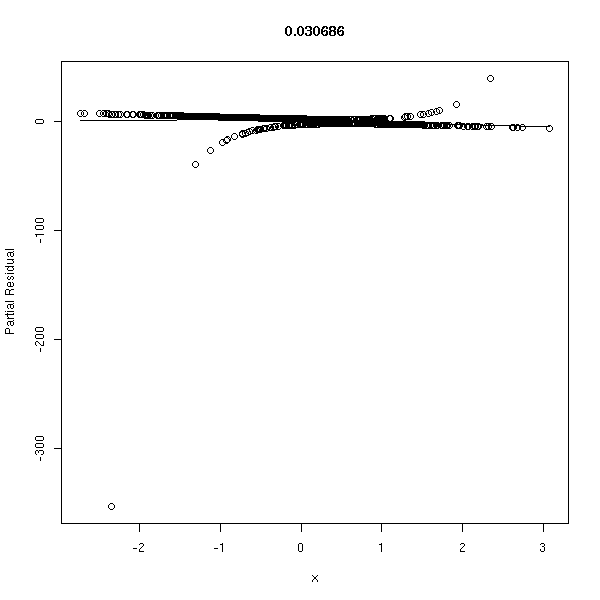
Données conformes au modèle, avec des erreurs aléatoires (je ne vois rien de remarquable sur les dessins -- mais les estimateurs de a et b sont biaisés vers zéro) :
n <- 1000
x <- rnorm(n)
a <- 1
b <- -2
p <- exp(a+b*x)/(1+exp(a+b*x))
y <- ifelse( runif(n)<p, 1, 0 )
i <- runif(n)<.1
y <- ifelse(i, 1-y, y)
y <- factor(y, levels=0:1)
col=c(par('fg'),'red')[1+as.numeric(i)]
r <- glm(y~x,family=binomial)
op <- par(mfrow=c(2,2))
plot(r,ask=F, col=col)
par(op)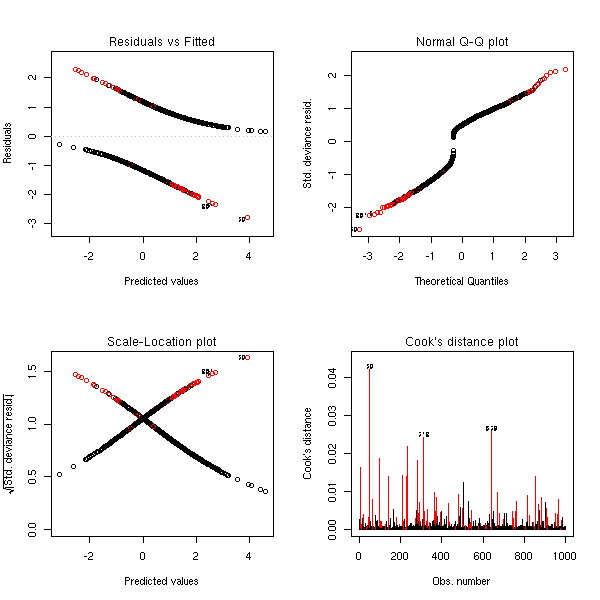
r <- lrm(y~x,y=T,x=T) P <- resid(r,"gof")['P'] resid(r,"partial",pl=T) title(signif(P))
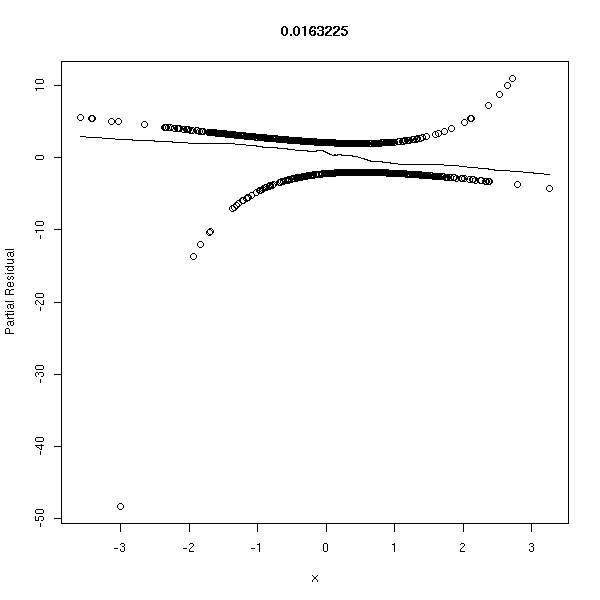
Données conformes au modèle avec des erreurs plus extrèmes :
n <- 1000
x <- rnorm(n)
a <- 1
b <- -2
p <- exp(a+b*x)/(1+exp(a+b*x))
y <- ifelse( runif(n)<p, 1, 0 )
i <- runif(n)<.5 & abs(x)>1
y <- ifelse(i, 1-y, y)
y <- factor(y, levels=0:1)
col=c(par('fg'),'red')[1+as.numeric(i)]
r <- glm(y~x,family=binomial)
op <- par(mfrow=c(2,2))
plot(r,ask=F, col=col)
par(op)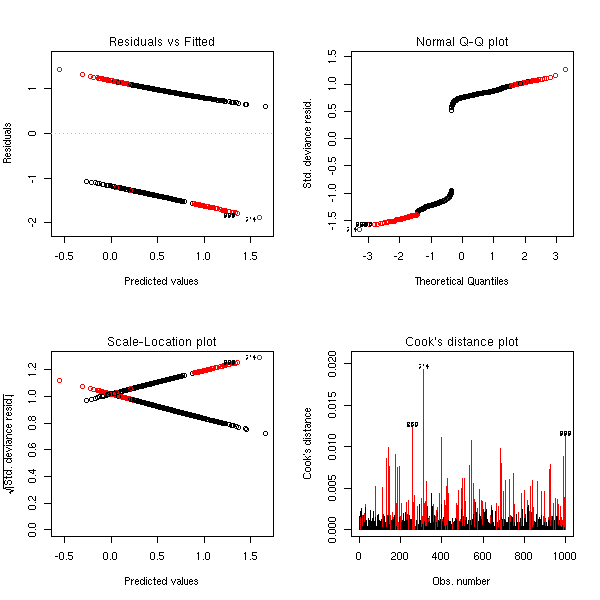
r <- lrm(y~x,y=T,x=T) P <- resid(r,"gof")['P'] resid(r,"partial",pl=T) title(signif(P))
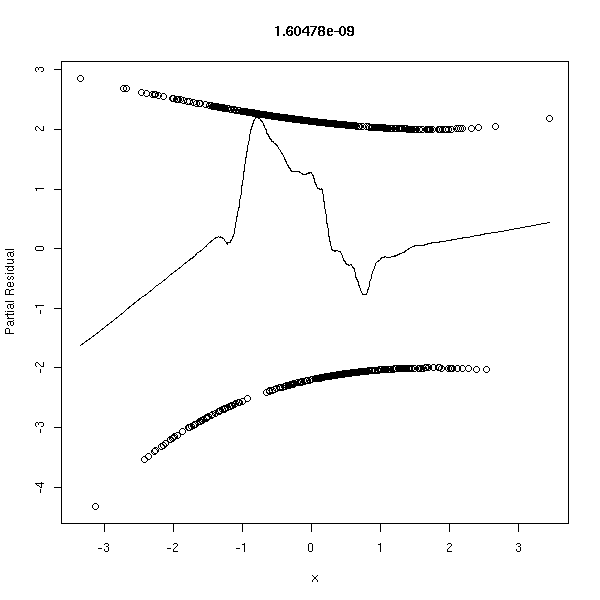
Une variable en trop :
n <- 1000 x1 <- rnorm(n) x2 <- rnorm(n) a <- 1 b <- -2 p <- exp(a+b*x1)/(1+exp(a+b*x1)) y <- factor(ifelse( runif(n)<p, 1, 0 ), levels=0:1) r <- glm(y~x1+x2,family=binomial) op <- par(mfrow=c(2,2)) plot(r,ask=F) par(op)
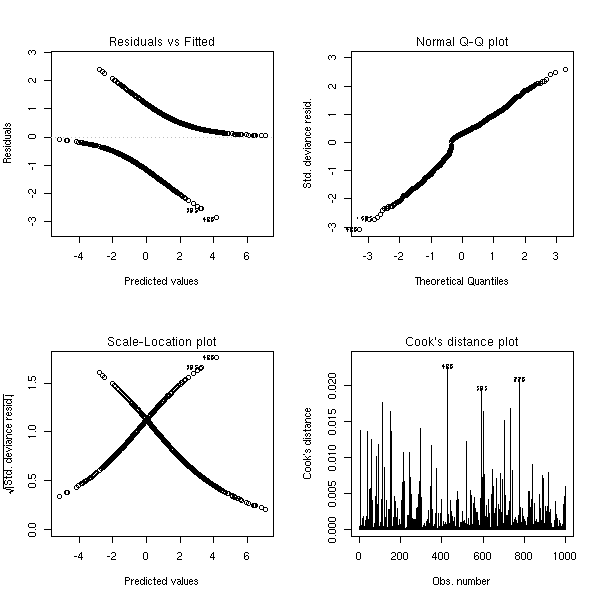
r <- lrm(y~x,y=T,x=T) P <- resid(r,"gof")['P'] resid(r,"partial",pl=T) title(signif(P))
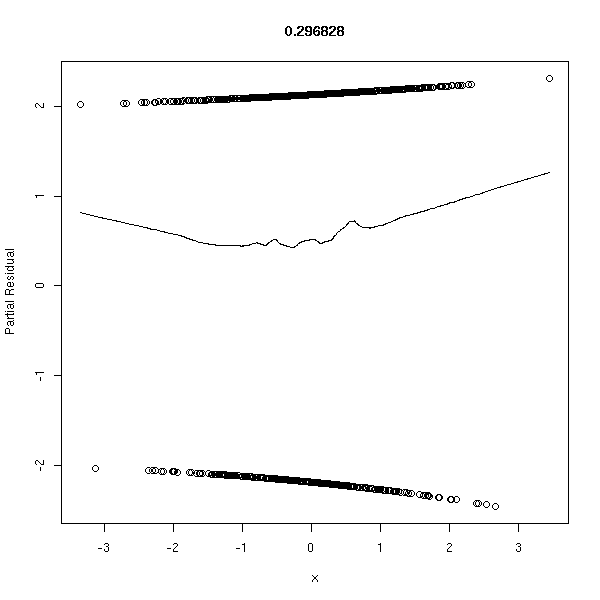
Modèle non linéaire :
n <- 1000 x <- rnorm(n) a <- 1 b1 <- -1 b2 <- -2 p <- 1/(1+exp(-(a+b1*x+b2*x^2))) y <- factor(ifelse( runif(n)<p, 1, 0 ), levels=0:1) r <- glm(y~x,family=binomial) op <- par(mfrow=c(2,2)) plot(r,ask=F) par(op)
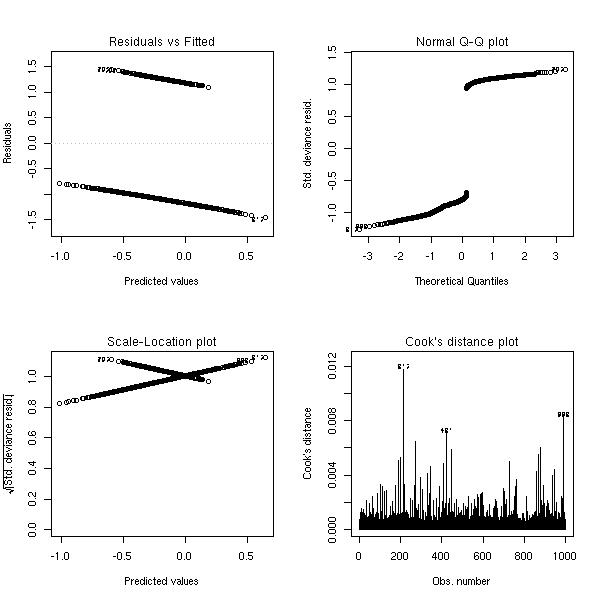
r <- lrm(y~x,y=T,x=T) P <- resid(r,"gof")['P'] resid(r,"partial",pl=T) title(signif(P))
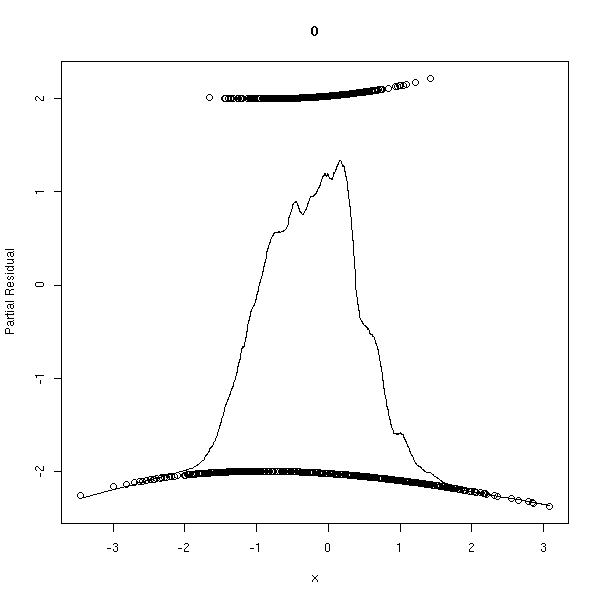
Réflexion faite, ces graphiques sont beaucoup moins utiles que pour la régression linéaire...
> 2. pourriez vous me donner des explications simples sur les test > de : Wald; Hosmer et Lemshow; D de Somer (à quoi servent ils et > comment les calculer et les interpréter?)
Sauf erreur de ma part, le test de Wald est une approximation du test du rapport de vraissemblance : autant faire ce dernier.
Le test du rapport de vraissemblance permet de comparer deux modèles imbriqués dont les paramètres ont été estimés par la méthode du maximum de vraissemblance. Sous R, on le calcule souvent avec la commande "anova". (Le "test de F" permettant de comparer un modèle linéaire au modèle trivial est un cas particulier du test de vraissemblance.)
On s'attendrait à pouvoir faire ce test exactement comme pour les modèles linéaires :
r <- glm(y~x1+x2, family=binomial()) anova(r)
mais non...
On peut faire ce test à la main : la différence des déviances des deux modèles imbriqués (ici, le modèle qui nous intéresse et le modèle null) suit, asymptotiquement, une distribution du Chi2 à p degrés de liberté, où p est le nombre de paramètres qu'on a fixé.
r <- glm(y~x1+x2, family=binomial()) pchisq(r$null.deviance - r$deviance, df=2, lower.tail=F)
On peut aussi utiliser ce test pour comparer deux modèles non triviaux (mais toujours imbriqués).
r0 <- glm(y~x1+x2, family=binomial)
r1 <- glm(y~x1, family=binomial)
r2 <- glm(y~x2, family=binomial)
lr.test <- function (r.petit,r.gros) {
pchisq(r.petit$deviance - r.gros$deviance, df=1, lower.tail=F)
}
lr.test(r1,r0)
lr.test(r2,r0)On trouve que le modèle y~x1+x2 est sensiblement meilleur que le modèle y~x1, avec un risque d'erreur inférieur à 10^-21 et que le modèle y~x1+x2 est sensiblement meilleur que le modèle y~x2 avec un risque d'erreur inférieur à 10^-6.
En fait, la commande lrm effectue le test du quotient des vraissemblances pour comparer le modèle étudié et le modèle trivial.
lrm(y~x1+x2)
Dans notre exemple,
Obs Max Deriv Model L.R. d.f. P C Dxy
506 3e-06 234.13 2 0 0.862 0.724
Gamma Tau-a R2 Brier
0.725 0.363 0.494 0.145p-valeur est nulle, donc le modèle est sensiblement meilleur que le modèle trivial, avec un risque d'erreur négligeable.
Je crois qu'on appelle aussi "test de Wald" le test regardant si l'un des coefficients de la régression est nul (sous l'hypothèse nulle que la vraie valeur de ce coefficient est nulle, le coefficient estimé, divisé par son écart-type, suit une loi normale ; si on élève le tout au carré, ça suit une loi du Chi2 à un degré de liberté). Ainsi, en regardant la dernière colonne du résultat de la commande précédente,
Coef S.E. Wald Z P
Intercept -1.66990 0.27245 -6.13 0e+00
x1 -0.04954 0.01280 -3.87 1e-04
x2 0.17985 0.02084 8.63 0e+00on peut affirmer que l'ordonnée à l'origine et le coefficient de x2 sont non nuls avec un risque d'erreur négligeable et on peut affirmer que le coefficient de x1 est non nul avec un risque d'erreur inférieur à 1 pour mille.
On avait en fait déjà ces résultats avec la commance glm :
> summary(r0)
Call:
glm(formula = y ~ x1 + x2, family = binomial)
Deviance Residuals:
Min 1Q Median 3Q Max
-2.5902 -0.7571 0.1312 0.6106 2.0397
Coefficients:
Estimate Std. Error z value Pr(>|z|)
(Intercept) -1.66990 0.27245 -6.129 8.84e-10 ***
x1 -0.04954 0.01280 -3.870 0.000109 ***
x2 0.17985 0.02084 8.632 < 2e-16 ***
(Dispersion parameter for binomial family taken to be 1)
Null deviance: 701.46 on 505 degrees of freedom
Residual deviance: 467.33 on 503 degrees of freedom
AIC: 473.33
Number of Fisher Scoring iterations: 6Je ne connais pas le test de Hosmer et Lemeshow, mais Google me renvoie à
http://www.biostat.wustl.edu/archives/html/s-news/1999-04/msg00147.html http://maths.newcastle.edu.au/~rking/R/help/03b/0735.html http://www.learnlink.mcmaster.ca/OpenForums/00031830-80000001/00040559-80000001/0045CA16-00977198-005B1B21
pages qui présentent ce test comme obsolète. La fonction residuals.lrm de la bibliothèque Design propose un test le remplaçant -- mais je ne sais pas ce qu'il y a derrière ni comment l'inerpréter.
library(Design) ?residuals.lrm
Pour notre exemple :
> resid( lrm(y~x1+x2, y=T, x=T), "gof" )
Sum of squared errors Expected value|H0 SD
7.328945e+01 7.632820e+01 5.739924e-01
Z P
-5.294060e+00 1.196300e-07Je ne connais pas non plus le D de Somers, mais quelques simulations permettent de l'interpréter :
> library(Design)
> somers2(x1,as.numeric(y)-1)
C Dxy n Missing
0.2846475 -0.4307051 506.0000000 0.0000000
> somers2(-x1,as.numeric(y)-1)
C Dxy n Missing
0.7153525 0.4307051 506.0000000 0.0000000
> somers2(x2,as.numeric(y)-1)
C Dxy n Missing
0.8551532 0.7103064 506.0000000 0.0000000
> somers2(-x2,as.numeric(y)-1)
C Dxy n Missing
0.1448468 -0.7103064 506.0000000 0.0000000
> somers2(rnorm(506),as.numeric(y)-1)
C Dxy n Missing
0.50564764 0.01129529 506.00000000 0.00000000Ca semble s'interprèter comme une corrélation, quand l'une des variable n'a que deux valeurs, 0 et 1.
Il y a donc les mêmes problèmes qu'avec la corrélation : ça ne repère que les relations linéaires. Ainsi, les calculs suivants donnent (approximativement) 1 et 0.
n <- 1000 a <- rnorm(n) b <- ifelse(a<0,0,1) somers2(a,b) b <- ifelse(abs(a)<.5,0,1) somers2(a,b)
# age age <- c(25.0, 32.5, 37.5, 42.5, 47.5, 52.5, 57.5, 65.0) # nombre de succès n <- c(100, 150, 120, 150, 130, 80, 170, 100) # variable explicative Y <- c(10, 20, 30, 50, 60, 50, 130, 80) f<-Y/n g<-log(f/(1-f)) # Transformation des données w<-n*f*(1-f) # Pondération des données r<-predict(lm(g~age,weights=w)) # Régression pondérée p<-exp(r)/(1+exp(r)) # Transformation inverse plot(age,f,ylim=c(0,1)) lines(age,p) symbols(age,f,circles=w,add=T) # On itère cette régression pondérée w<-n*p*(1-p) gu<-r+(f-p)/p/(1-p) r<-predict(lm(gu~age,weights=w)) # encore p<-exp(r)/(1+exp(r)) w<-n*p*(1-p) gu<-r+(f-p)/p/(1-p) r<-predict(lm(gu~age,weights=w))
On obtient en fait les résultats de
glm(cbind(Y,n-Y)~age,family=binomial)
La variable dépendante n'est plus une variable binaire, mais une variable de comptage. Pour effectuer cette régression de Poisson, on utilise toujours la commande glm, avec l'argument family=poisson.
Je ne donne pas d'exemple ici, je me contente de renvoyer à ceux du manuel.
library(MASS) ?epil ?housing
A FAIRE : donner un exemple (une simulation).
Voir aussi les fonctions loglm, multinom, gam.
?loglm library(nnet) ?multinom library(mgcv) ?gam library(survival) ?survexp
Si la variable quantitative a plus de deux valeurs, je ne sais pas comment faire...
# NON n <- 100 x <- c( rnorm(n), 1+rnorm(n), 2.5+rnorm(n) ) y <- factor(c( rep(0,n), rep(1,n), rep(2,n) )) r <- glm(y~x, family=binomial) plot(as.numeric(y)-1~x) xp <- seq(-5,5,length=200) yp <- predict(r,data.frame(x=xp), type='response') lines(xp,yp)
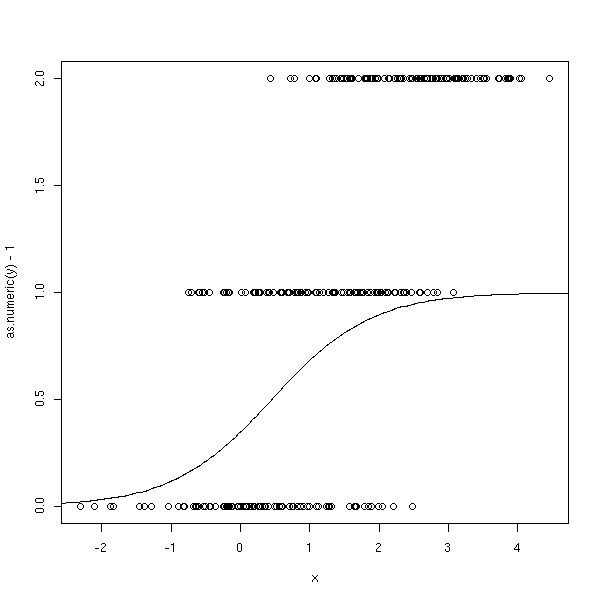
Essayons de coder la variable à prédire à l'aide de variables binaires, à la main.
Premier essai : on y va brutalement, sans réfléchir.
n <- 100 x <- c( rnorm(n), 10+rnorm(n), 25+rnorm(n), -7 + rnorm(n) ) y <- factor(c( rep(0,n), rep(1,n), rep(2,n), rep(3,n) )) y1 <- factor(c( rep(0,n), rep(0,n), rep(1,n), rep(1,n) )) y2 <- factor(c( rep(0,n), rep(1,n), rep(0,n), rep(1,n) )) r1 <- glm(y1~x, family=binomial) r2 <- glm(y2~x, family=binomial) xp <- seq(-50,50,length=500) y1p <- predict(r1,data.frame(x=xp), type='response') y2p <- predict(r2,data.frame(x=xp), type='response') plot(as.numeric(y)-1~x) lines(xp,y1p+2*y2p) lines(xp,y1p, col='red') lines(xp,y2p, col='blue')
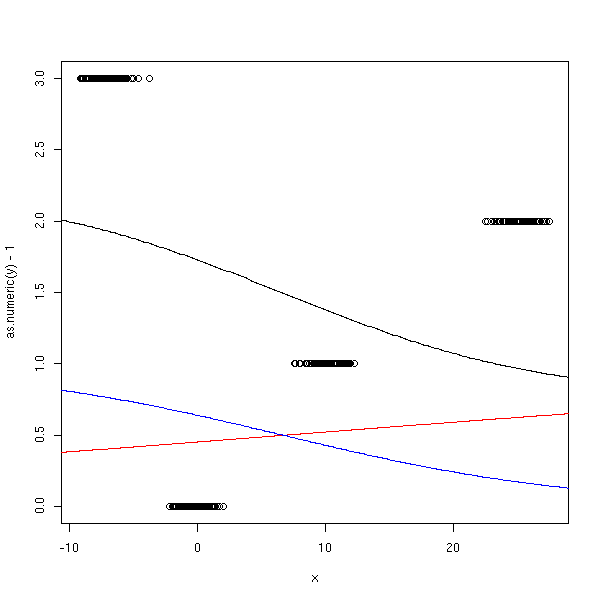
Ca ne marche pas, car Y1 et Y2 ne sont pas du tout décrites par le modèle logistique :
plot(as.numeric(y1)-1~x) lines(xp,y1p, col='red')
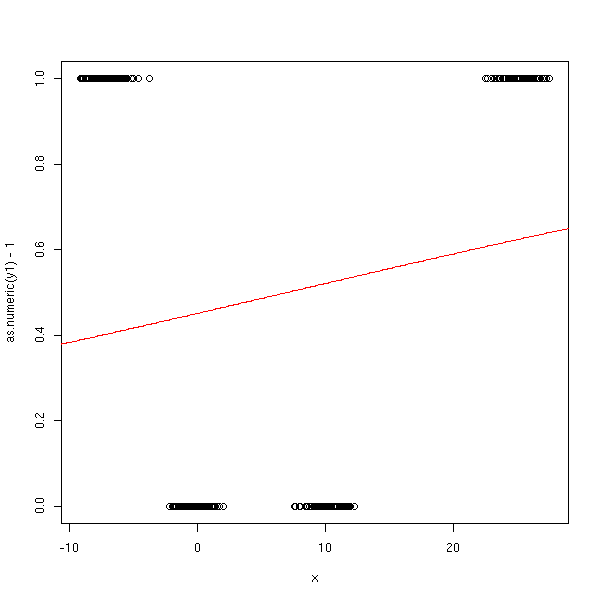
Deuxième essai.
n <- 100 x <- c( rnorm(n), 10+rnorm(n), 25+rnorm(n), -7 + rnorm(n) ) y <- factor(c( rep(0,n), rep(1,n), rep(2,n), rep(3,n) )) y1 <- factor(c( rep(0,n), rep(1,n), rep(1,n), rep(1,n) )) y2 <- factor(c( rep(0,n), rep(0,n), rep(1,n), rep(1,n) )) y3 <- factor(c( rep(0,n), rep(0,n), rep(0,n), rep(1,n) )) r1 <- glm(y1~x, family=binomial) r2 <- glm(y2~x, family=binomial) r3 <- glm(y3~x, family=binomial) xp <- seq(-50,50,length=500) y1p <- predict(r1,data.frame(x=xp), type='response') y2p <- predict(r2,data.frame(x=xp), type='response') y3p <- predict(r3,data.frame(x=xp), type='response') plot(as.numeric(y)-1~x) lines(xp,y1p+y2p+y3p)
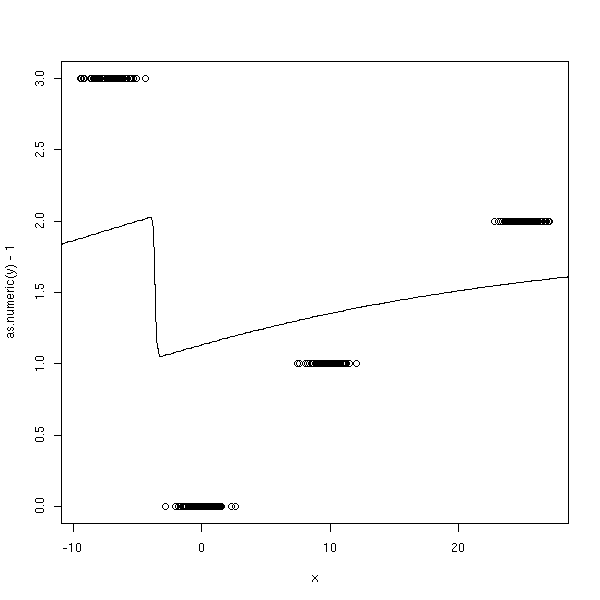
C'est le même problème...
plot(as.numeric(y1)-1~x) lines(xp,y1p, col='red')
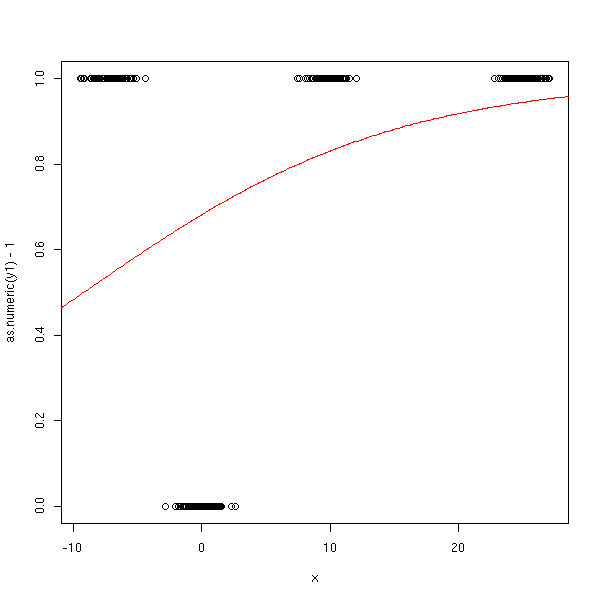
Troisième essai : avec des variables ordonnées.
n <- 100 x <- c( -7+rnorm(n), rnorm(n), 10+rnorm(n), 25+rnorm(n)) y <- factor(c( rep(0,n), rep(1,n), rep(2,n), rep(3,n) )) y1 <- factor(c( rep(0,n), rep(1,n), rep(1,n), rep(1,n) )) y2 <- factor(c( rep(0,n), rep(0,n), rep(1,n), rep(1,n) )) y3 <- factor(c( rep(0,n), rep(0,n), rep(0,n), rep(1,n) )) r1 <- glm(y1~x, family=binomial) r2 <- glm(y2~x, family=binomial) r3 <- glm(y3~x, family=binomial) xp <- seq(-50,50,length=500) y1p <- predict(r1,data.frame(x=xp), type='response') y2p <- predict(r2,data.frame(x=xp), type='response') y3p <- predict(r3,data.frame(x=xp), type='response') plot(as.numeric(y)-1~x) lines(xp,y1p+y2p+y3p)
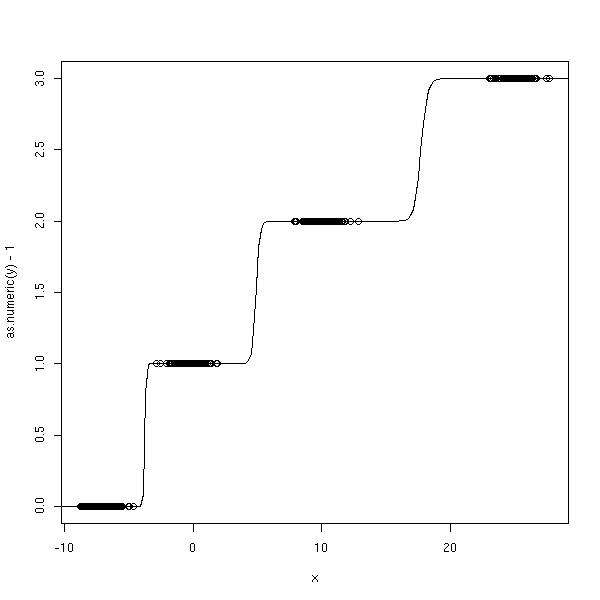
n <- 100 x <- c( -.7+rnorm(n), rnorm(n), 1+rnorm(n), 2.5+rnorm(n)) y <- factor(c( rep(0,n), rep(1,n), rep(2,n), rep(3,n) )) y1 <- factor(c( rep(0,n), rep(1,n), rep(1,n), rep(1,n) )) y2 <- factor(c( rep(0,n), rep(0,n), rep(1,n), rep(1,n) )) y3 <- factor(c( rep(0,n), rep(0,n), rep(0,n), rep(1,n) )) r1 <- glm(y1~x, family=binomial) r2 <- glm(y2~x, family=binomial) r3 <- glm(y3~x, family=binomial) xp <- seq(-5,5,length=500) y1p <- predict(r1,data.frame(x=xp), type='response') y2p <- predict(r2,data.frame(x=xp), type='response') y3p <- predict(r3,data.frame(x=xp), type='response') plot(as.numeric(y)-1~x) lines(xp,y1p+y2p+y3p) lines(xp,round(y1p+y2p+y3p, digits=0), col='red')

On peut aussi faire de la régression logistique pour prédire une variable qualitative ordonnée. Voici quelques uns des modèles dont on dispose.
Proportionnal odds model (les effets sont monotones par rapport à la variable quantitative) :
1
P[ Y >= j | X ] = -----------------------
- ( a_j + X b )
1 + eContinuation ratio model :
1
P [ Y = j | Y >= j, X ] = -----------------------
- ( a_j + X b )
1 + eLes raisonnements du paragraphe précédent nous ont en fait conduits au premier modèle.
n <- 100
x <- c( -.7+rnorm(n), rnorm(n), 1+rnorm(n), 2.5+rnorm(n))
y <- factor(c( rep(0,n), rep(1,n), rep(2,n), rep(3,n) ))
ordinal.regression.one <- function (y,x) {
xp <- seq(min(x),max(x), length=100)
yi <- matrix(nc=length(levels(y)), nr=length(y))
ri <- list();
ypi <- matrix(nc=length(levels(y)), nr=100)
for (i in 1:length(levels(y))) {
yi[,i] <- as.numeric(y) >= i
ri[[i]] <- glm(yi[,i] ~ x, family=binomial)
ypi[,i] <- predict(ri[[i]], data.frame(x=xp), type='response')
}
plot(as.numeric(y) ~ x)
lines(xp, apply(ypi,1,sum), col='red', lwd=3)
}
ordinal.regression.one(y,x)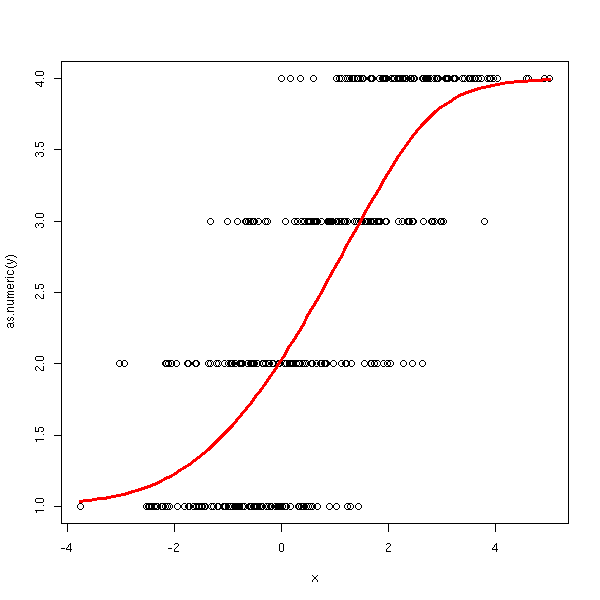
n <- 100 v <- .2 x <- c( -.7+v*rnorm(n), v*rnorm(n), 1+v*rnorm(n), 2.5+v*rnorm(n)) y <- factor(c( rep(0,n), rep(1,n), rep(2,n), rep(3,n) )) ordinal.regression.one(y,x)
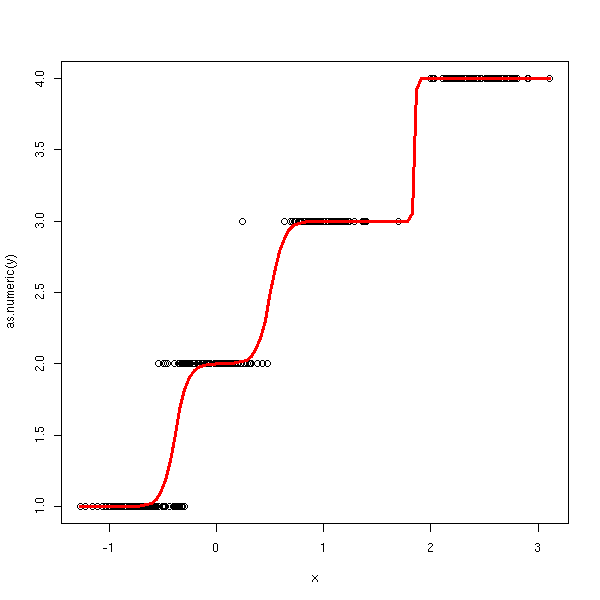
Voici le second modèle.
n <- 100
x <- c( -.7+rnorm(n), rnorm(n), 1+rnorm(n), 2.5+rnorm(n))
y <- factor(c( rep(0,n), rep(1,n), rep(2,n), rep(3,n) ))
ordinal.regression.two <- function (y,x) {
xp <- seq(min(x),max(x), length=100)
yi <- list();
ri <- list();
ypi <- matrix(nc=length(levels(y)), nr=100)
for (i in 1:length(levels(y))) {
ya <- as.numeric(y)
o <- ya >= i
ya <- ya[o]
xa <- x[o]
yi[[i]] <- ya == i
ri[[i]] <- glm(yi[[i]] ~ xa, family=binomial)
ypi[,i] <- predict(ri[[i]], data.frame(xa=xp), type='response')
}
# Le dessin est un peu plus compliqué à faire que tout-à-l'heure...
plot(as.numeric(y) ~ x)
p <- matrix(0, nc=length(levels(y)), nr=100)
for (i in 1:length(levels(y))) {
p[,i] = ypi[,i] * (1 - apply(p,1,sum))
}
for (i in 1:length(levels(y))) {
p[,i] = p[,i]*i
}
lines(xp, apply(p,1,sum), col='red', lwd=3)
}
ordinal.regression.two(y,x)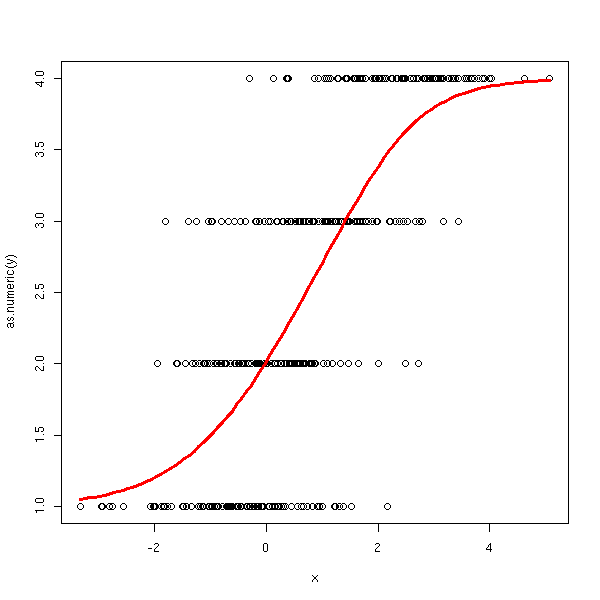
n <- 100 v <- .1 x <- c( -.7+v*rnorm(n), v*rnorm(n), 1+v*rnorm(n), 2.5+v*rnorm(n)) y <- factor(c( rep(0,n), rep(1,n), rep(2,n), rep(3,n) )) ordinal.regression.two(y,x)
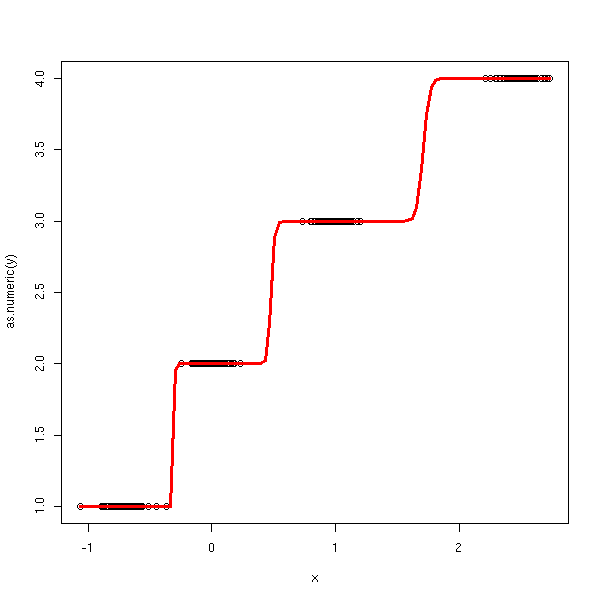
En fait, c'est déjà implémenté :
library(MASS) ?polr
A FAIRE
Modèle :
P( Y=1 | X=x )
log ---------------- = b_{1,0} + b_1 x
P( Y=k | X=x )
P( Y=2 | X=x )
log ---------------- = b_{2,0} + b_2 x
P( Y=k | X=x )
P( Y=k-1 | X=x )
log ------------------ = b_{k-1,0} + b_{k-1} x
P( Y=k | X=x )
(fit with MLE)
A FAIRE : re-rédiger après avoir lu la section précédente.
Voyons maintenant que faire si la variable à prédire a plusieurs valeurs, non ordonnées.
library(nnet) ?multinom A FAIRE A FAIRE (si la variable est binaire, on obtient les mêmes résultats qu'avec la régression logistique -- à vérifier). A FAIRE library(nnet) ?multinom
Vincent Zoonekynd
<zoonek@math.jussieu.fr>
latest modification on Wed Oct 13 22:33:12 BST 2004