
The French version of this document is no longer maintained: be sure to check the more up-to-date English version.
Régression avec des variables prédictives qualitatives
Analyse de la variance
Vocabulaire de l'ANOVA
Vocabulaire (suite)
Exemples divers -- à classer
Multilevel Analysis
Modèles mixtes, modèles hiérarchiques
A FAIRE : classer
Les dangers de l'Anova
A FAIRE : classer ce qui suit -- exemples d'analyse de variance
A FAIRE : Classer ce qui suit
L'analyse de la variance, c'est la régression quand les variables prédictives sont qualitatives -- plus précisément, il s'agit des tests qu'on effectue dans ce cadre.
L'analyse de la covariance, c'est la régression quand certaines des variables prédictives sont qualitatives et d'autres quantitatives (on appelle alors ces dernières covariables).
La manière la plus simple de voir l'analyse de la variance, c'est comme une généralisation du test de Student : elle permet de voir si la moyenne d'une variable quantitative est la même dans différents groupes ou, en d'autres termes, si une variable quantitative dépend d'une variable qualitative.
Une manière plus générale de voir l'analyse de la variance (et c'est le point de vue adopté par la commande "anova" sous R), c'est comme un test comparant deux modèles.
Nous présenterons les choses dans cet ordre : régression avec des variables prédictives qualitatives, généralisation du test de Student, comparaison de modèles. Dans un dernier temps, nous présenterons, plus rapidement, des généralisations de l'analyse de la variance : modèles mixtes, modèles hiérarchiques, modèles graphiques, réseaux bayesiens.
Avant de passer à l'anova proprement dite (i.e., les tests relatifs à une régression avec des variables prédictives qualitatives), nous nous intéressons à la régression avec des variables prédictives qualitatives. En fait, il n'y a pas grande différence avec la régression classique.
C'est très simple : on la code par 0 ou 1 et on fait une régression linéaire.
n <- 200 x <- sample(0:1, n, replace=T) y <- 2*(x==0) +rnorm(n) plot( y ~ factor(x), horizontal=T, xlab='y', ylab='x' )

plot(density(y[x==0]), lwd=3, xlim=c(-3,5), ylim=c(0,.5), col='blue') lines(density(y[x==1]), lwd=3, col='red')

plot(y~x) abline(lm(y~x), col='red')

Comme il n'y a que deux valeurs possibles, il n'y a que deux prédictions possibles (ce sont les moyennes des groupes correspondants).
> predict(lm(y~x), data.frame(x=c(0,1)))
1 2
2.0785496 -0.1654518
> tapply(y,x,mean)
0 1
2.0785496 -0.1654518On peut aussi se demander si les moyennes des deux groupes sont sensiblement différentes, à l'aide d'un test de Student,
> t.test(y[x==0], y[x==1])
Welch Two Sample t-test
data: y[x == 0] and y[x == 1]
t = 15.1062, df = 197.472, p-value = < 2.2e-16ou à l'aide d'une anova (l'anova, c'est la dernière ligne du résultat de la régression).
> summary(lm(y~x))
Call:
lm(formula = y ~ x)
Residuals:
Min 1Q Median 3Q Max
-3.7520 -0.5786 0.1071 0.6504 2.7427
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 2.1283 0.1068 19.93 <2e-16 ***
x1 -2.1218 0.1440 -14.73 <2e-16 ***
Residual standard error: 1.013 on 198 degrees of freedom
Multiple R-Squared: 0.523, Adjusted R-squared: 0.5206
F-statistic: 217.1 on 1 and 198 DF, p-value: < 2.2e-16On peut aussi demander explicitement une anova, i.e., explicitement comparer le modèle y~x avec le modèle trivial y~1.
> anova( lm(y~x), lm(y~1) ) Analysis of Variance Table Model 1: y ~ x Model 2: y ~ 1 Res.Df RSS Df Sum of Sq F Pr(>F) 1 198 203.27 2 199 426.11 -1 -222.84 217.07 < 2.2e-16 ***
(Je ne sais jamais dans quel sens il faut mettre les modèles ; ici, on constate que le nombre de degrés de liberté est négatif, ce que ne fait pas très sérieux -- il aurait mieux valu mettre le modèle trivial en premier.)
Cela peut sembler trivial : on n'a pas besoin de connaitre la régression pour calculer ou comparer des moyennes. Les choses deviennent légèrement moins triviales quand on a à la fois des variables prédictives discrètes et continues.
n <- 200
x1 <- sample(0:1, n, replace=T)
x2 <- rnorm(n)
y <- 1 - 2*(x1==0) + x2 +rnorm(n)
plot( y ~ x2, col=c(par('fg'), 'red')[1+x1] )
rc <- lm(y~x1+x2)$coef
abline(rc[1],rc[3])
abline(rc[1]+rc[2],rc[3], col='red')
Le modèle précédent, sans terme d'interaction, construisait des droites parallèles. Si on rajoute un terme d'interaction, les droites ne sont plus nécessairement parallèles.
n <- 200
x1 <- sample(0:1, n, replace=T)
x2 <- rnorm(n)
y <- 1 + x2 - (x1==1)*(2+3*x2) + rnorm(n)
plot( y ~ x2, col=c(par('fg'), 'red')[1+x1] )
# Sans interaction (en pointillés)
rc <- lm(y~x1+x2)$coef
abline(rc[1],rc[3], lty=3)
abline(rc[1]+rc[2],rc[3], col='red', lty=3)
# avec
rc <- lm(y~x1+x2+x1:x2)$coef
abline(rc[1],rc[3])
abline(rc[1]+rc[2],rc[3]+rc[4], col='red')
Il s'agit en fait de faire une régression linéaire pour chaque valeur de la variable qualitative.
A FAIRE : interaction plot (matrix plot) if the lines are parallel, there is no interaction.
A FAIRE
Imaginons que notre variable ait 4 valeurs : 0, 1, 2 et 3.
n <- 200 x <- sample(0:3, n, replace=T) y <- 2*(x==0) + 5*(x==2) -2*(x==3) +rnorm(n) plot( y ~ factor(x), horizontal=T, xlab='y', ylab='x' )

On ne peut pas la coder par ces quatre nombres : cela supposerait, entre autres, que ces quatre valeurs sont ordonnées, que leurs effets sont monotones et linéaires. On peut s'en tirer en rajoutant des variables indicatrices (dummy variables, en anglais), qui ne prennent que deux valeurs.
x1 <- as.numeric(x==1) x2 <- as.numeric(x==2) x3 <- as.numeric(x==3)
(Il y a d'autres codages possibles : ils donneront les mêmes prédictions, les mêmes statistiques (F, etc.), mais les coefficients s'interprèteront différemment.)
Et on fait ensuite une régression tout à fait normale.
> lm(y~x1+x2+x3)
Call:
lm(formula = y ~ x1 + x2 + x3)
Coefficients:
(Intercept) x1 x2 x3
2.178 -2.293 2.844 -4.110En fait, R fait cette transformation lui-même quand l'une des variables prédictives est un facteur.
> lm(y~factor(x))
Call:
lm(formula = y ~ factor(x))
Coefficients:
(Intercept) factor(x)1 factor(x)2 factor(x)3
2.178 -2.293 2.844 -4.110Comme il n'y a que quatre valeurs possibles, il n'y a que quatre valeurs à prédire, qui sont les moyennes des quatre groupes.
> predict(lm(y~factor(x)), data.frame(x=c(0,1,2,3)))
1 2 3 4
2.1778596 -0.1148520 5.0220615 -1.9325181
> tapply(y,x,mean)
0 1 2 3
2.1778596 -0.1148520 5.0220615 -1.9325181Comme précédemment, les choses ne sont intéressantes que s'il y a d'autres variables prédictibles quantitatives (mais ici encore, cela revient à faire une régression pour chaque valeur de la variable qualitative).
n <- 1000
x1 <- sample(1:4, n, replace=T)
x2 <- runif(n, min=-1, max=1)
y <- (x1==1) * (2 - 2*x2) +
(x1==2) * (1 + x2) +
(x1==3) * (-.5 + .5*x2) +
(x1==4) * (-1) +
rnorm(n)
cols <- c(par('fg'), 'red', 'blue', 'orange')
plot( y~x2, col=cols[x1] )
x1 <- factor(x1)
r <- lm(y~x1*x2)
xx <- seq( min(x2), max(x2), length=100 )
for (i in levels(x1)) {
yy <- predict(r, data.frame(x1=rep(i, length(xx)), x2=xx))
lines(xx,yy, col=cols[as.numeric(i)], lwd=3)
}
Si les variables ne sont pas binaires, R se charge tout seul de créer les variables indicatrices, sans qu'on ait à y penser. Expliquons néanmoins comment on peut faire.
Avec deux variables :
Deux variables qualitatives U et V à 3 valeurs (a, b et c). On remplace U par deux variables X1 et X2. Si U=a, on prend X1=1 et X2=0. Si U=b, on prend X1=0 et X2=1. Si U=c, on prend X1=X2=0. On remplace de même V par deux variables X3 et X4. Si on ne veut pas d'interaction, le modèle est Y ~ X1 + X2 + X3 + X4
Si on veut des interactions, on remplace U par deux variables V1, V2.
Si U=a, on prend V1=1, V2=0. Si U=b, on prend V1=0, V2=1. Si U=v, on prend V1=V2=-1. On remplace de même V par V3, V4. Le modèle est alors Y ~ V1 + V2 + V3 + V4 + V1V3 + V1V4 + V2V3 + V2V4 C'est plus général que la transformation précédente, mais plus difficile à interpréter...
Il est possible de demander à R d'utiliser un codage ou un autre.
> options()$contrasts
unordered ordered
"contr.treatment" "contr.poly"
> apropos("contr\\.")
[1] "contr.helmert" "contr.poly" "contr.sum" "contr.treatment"Il est à noter que par défaut, SPlus utilise les contrastes de Helmert (mais beaucoup pensent que c'est une mauvaise idée, car les résultats sont plus difficiles à interpréter).
n <- 100
l <- 1:4
x <- factor( sample(l, n, replace=T), levels=l )
y <- ifelse(x==1, rnorm(n),
ifelse(x==2, -4+rnorm(n),
ifelse(x==3, -2+rnorm(n), 4+rnorm(n))))On peut voir la matrice obtenue à l'aide de la fonction model.matrix.
> cbind(x,y)[1:5,]
x y
[1,] 3 -2.1962202
[2,] 4 3.9745616
[3,] 1 0.3440235
[4,] 4 2.7521184
[5,] 2 4.3539651
> model.matrix(y~x)[1:5,]
(Intercept) x2 x3 x4
1 1 0 1 0
2 1 0 0 1
3 1 0 0 0
4 1 0 0 1
5 1 1 0 0
> model.matrix(y~x, contrasts=list(x=contr.helmert))[1:5,]
(Intercept) x1 x2 x3
1 1 0 2 -1
2 1 0 0 3
3 1 -1 -1 -1
4 1 0 0 3
5 1 1 -1 -1
> model.matrix(y~x, contrasts=list(x=contr.poly))[1:5,]
(Intercept) x.L x.Q x.C
1 1 0.2236068 -0.5 -0.6708204
2 1 0.6708204 0.5 0.2236068
3 1 -0.6708204 0.5 -0.2236068
4 1 0.6708204 0.5 0.2236068
5 1 -0.2236068 -0.5 0.6708204
> model.matrix(y~x, contrasts=list(x=contr.sum))[1:5,]
(Intercept) x1 x2 x3
1 1 0 0 1
2 1 -1 -1 -1
3 1 1 0 0
4 1 -1 -1 -1
5 1 0 1 0Le codage contr.treatment (celui par défaut) n'est pas symétrique : l'une des valeurs joue le rôle de valeur de base. On peut préciser laquelle à l'aide de la commande relevel.
Voici ce que l'on obtient avec les contrastes contr.treatment (ceux utilisés par défaut).
> lm(y~x)
Call:
lm(formula = y ~ x)
Coefficients:
(Intercept) x2 x3 x4
-0.1659 -3.7780 -2.0133 3.8462Voici le résultat avec contr.helmert.
> a <- options()$contrasts > a[1] <- "contr.helmert" > options(contrasts=a) > lm(y~x) Call: lm(formula = y ~ x) Coefficients: (Intercept) x1 x2 x3 -0.65218 -1.88902 -0.04143 1.44416
Avec contr.sum
> a <- options()$contrasts
> a[1] <- "contr.sum"
> options(contrasts=a)
> lm(y~x)
Call:
lm(formula = y ~ x)
Coefficients:
(Intercept) x1 x2 x3
-0.6522 0.4863 -3.2918 -1.5270Et enfin avec contr.poly
> a <- options()$contrasts
> a[1] <- "contr.poly"
> options(contrasts=a)
> lm(y~x)
Call:
lm(formula = y ~ x)
Coefficients:
(Intercept) x.L x.Q x.C
-0.6522 2.9747 4.8188 -0.3238Résumons les résultats
contr.treatment -0.1659 -3.7780 -2.0133 3.8462 contr.helmert -0.65218 -1.88902 -0.04143 1.44416 contr.sum -0.6522 0.4863 -3.2918 -1.5270 contr.poly -0.6522 2.9747 4.8188 -0.3238
Regardons ce qui se passe en cas de monotonie :
n <- 100
v <- .3
l <- 1:4
x <- factor( sample(l, n, replace=T), levels=l )
y <- ifelse(x==1, -3+v*rnorm(n),
ifelse(x==2, -1+v*rnorm(n),
ifelse(x==3, 1+v*rnorm(n), 3+v*rnorm(n))))
a <- options()$contrasts
for (i in c("contr.treatment", "contr.helmert", "contr.sum", "contr.poly")) {
a[1] <- i
options(contrasts=a)
print(lm(y~x)$coef)
}on obtient :
contr.treatment -2.911686 1.887725 3.938457 5.914572 contr.helmert 0.02350254 0.94386256 0.99819831 0.99312780 contr.sum 0.02350254 -2.93518867 -1.04746355 1.00326881 contr.poly 0.02350254 4.42617327 0.04419473 -0.05313457
Il est possible que la moyenne ne dépende ni de X1 ni de X2, mais du couple (X1,X2). On peut par exemple avoir
E[ Y | X=(0,0) ] > E[ Y | X=(0,1) ] E[ Y | X=(1,0) ] < E[ Y | X=(1,1) ]
C'est ce que l'on voir sur le dessin suivant.
n <- 1000
l <- 0:1
v <- .5
x1 <- factor( sample(l, n, replace=T), levels=l )
x2 <- factor( sample(l, n, replace=T), levels=l )
y <- ifelse( x1==0,
ifelse( x2==0, 1+v*rnorm(n), v*rnorm(n) ),
ifelse( x2==0, v*rnorm(n), 1+v*rnorm(n) )
)
boxplot( y ~ x1, horizontal=T )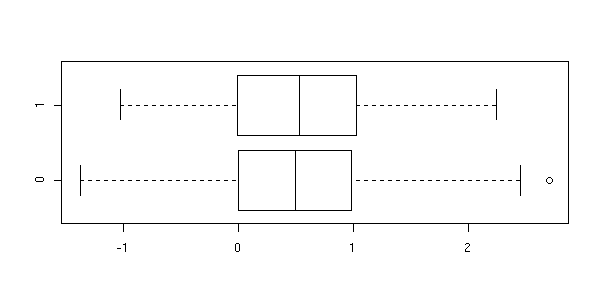
boxplot( y ~ x2, horizontal=T )

boxplot( y ~ x2, horizontal=T )

plot( as.numeric(x1)-1+.2*rnorm(n), y,
col=c("red","blue")[as.numeric(x2)],
xlab="x1 (jittered)" )
C'est un autre nom pour la régression avec des variables prédictives qualitatives, ou plus précisément pour les tests que l'on effectue dans ces conditions.
Nous avons vu que la régression en présence d'une variable quantitative se ramenait à des calculs de moyennes. On peut voir l'anova comme un test de comparaison des moyennes. C'est donc une généralisation du test T de Student, avec un nombre quelconque d'échantillons (et pas seulement deux).
Les conditions d'application sont les mêmes que pour le test de Student : les échantillons sont normaux et de même variance, les variables sont indépendantes.
En termes de régression, les choses se présentent ainsi : on dispose de deux variables, X et Y, la variable Y est quantitative (c'est la quantité dont la moyenne nous intéresse) et la variable X est qualitative (elle nous donne le numéro de la classe l'échantillon). On essaye de voir si Y dépend de X, i.e., on fait une régression en Y en fonction de X, qui nous donne
Y = a0 + a1*(X==1) + a2*(X==2) + a3*(X==3) + a4*(X==4)
et on compare ce modèle avec le modèle trivial
Y = b0.
Voici une simulation :
N <- 10 a <- rnorm(N) b <- rnorm(N) c <- rnorm(N) d <- rnorm(N) df <- data.frame( y=c(a,b,c,d), x=factor(c(rep(1,N),rep(2,N),rep(3,N),rep(4,N))) ) plot( y ~ x, data=df )

plot(density(df$y,bw=1), xlim=c(-6,6), ylim=c(0,.5), type='l') points(density(a,bw=1), type='l', col='red') points(density(b,bw=1), type='l', col='green') points(density(c,bw=1), type='l', col='blue') points(density(d,bw=1), type='l', col='orange')

Le graphique ci-dessous représente la valeur d'une variable statistique sur trois échantillons. On cherche à savoir si ces trois échantillons proviennent de la même population. Pour cela, on regarde la moyenne de notre variable statistique. Ces trois moyennes sont différentes, mais ces différences sont-elles suffisemment importantes pour être statistiquement significatives ? On constate que les différences entre les moyennes sont relativement importantes par rapport à la << largeur >> des courbes en cloche, qui ne se chevauchent presque pas. Pour cette raison, on rejettera l'hypothèse << les moyennes sont identiques >>.
curve( dnorm(x-2), from=-6, to=6, col='red' )
curve( dnorm(x+2), add=T, col='green')
curve( dnorm(x+2+.2), add=T, col='blue')
curve( dnorm(x+2-.3), add=T, col='orange')
x <- c(2, -2, -2.2, -1.7)
segments( x, c(0,0,0,0), x, rep(dnorm(0),4), col=c('red', 'green', 'blue', 'orange') )
C'est tout le contraire dans la figure suivante. Bien que les moyennes des échantillons soient exactement les mêmes que dans le cas précédent, les différences entre ces moyennes sont relativement petites par rapport à la largeur des courbes en cloche, qui se recoupent beaucoup. Pour cette raison, on ne rejettera pas l'hypothèse << les moyennes sont égales >>.
s <- 3
curve( dnorm(x-2, sd=s), from=-6, to=6, col='red' )
curve( dnorm(x+2, sd=s), add=T, col='green')
curve( dnorm(x+2+.2, sd=s), add=T, col='blue')
curve( dnorm(x+2-.3, sd=s), add=T, col='orange')
x <- c(2, -2, -2.2, -1.7)
segments( x, c(0,0,0,0), x, rep(dnorm(0, sd=s),4),
col=c('red', 'green', 'blue', 'orange') )
Pour quantifier ces raisonnements qualitatifs et graphiques, il nous faut une mesure de la largeur des courbes en cloche : on pourrait prendre la variance de chaque échantillon, mais comme on préfère n'avoir qu'un seul nombre, on prendra la moyenne de ces variances (si les trois échantillons proviennent de la même population, on obtient un estimateur sans biais de la variance de la population). Il nous faut aussi une mesure de la dispersion des moyennes : on pourrait prendre la variance des moyennes, mais pour comparer avec l'estimateur précédent, on va la transformer en un estimateur de la variance de la population, en la multipliant par la taille des échantillons.
Finalement, on est amené à considérer le quotient (n désigne la taille de chaque échantillon)
n * (variance des moyennes)
F = -----------------------------
moyenne des variancesA FAIRE : vérifier cette formule
Si F >> 1, on rejette l'hypothèse d'égalité des moyennes, si F est petit, on ne la rejette pas. C'est donc un test asymétrique. On démontre que si les moyennes sont égales, l'espérance de F est 1 ; si elles sont différentes, l'espérance est plus grande que 1. Il arrive bien sûr que F<1 : dans ce cas on ne rejette pas l'hypothèse.
Ce quotient, F, suit une loi de F à ********* et ********* degrés de liberté. Voici le graphe de la fonction de distribution de ces lois. Quand le premier paramètre croît, le maximum se déplace vers le bas à droite, quand le second croît, il se déplace vers le haut.
curve( df(x, 2, 2), from=0, to=4, ylim=c(0,1) ) curve( df(x, 2, 10), add=T, col='red' ) curve( df(x, 4, 2), add=T, col='green' ) curve( df(x, 4, 6), add=T, col='green' ) curve( df(x, 4, 10), add=T, col='green' ) curve( df(x, 4, 20), add=T, col='green' ) curve( df(x, 6, 2), add=T, col='blue' ) curve( df(x, 6, 6), add=T, col='blue' ) curve( df(x, 6, 10), add=T, col='blue' ) curve( df(x, 6, 20), add=T, col='blue' )

On pourrait suivre textuellement la définition.
n <- 10 a <- rnorm(n) b <- rnorm(n) c <- rnorm(n) d <- 1+rnorm(n) sx2 <- var(c( mean(a), mean(b), mean(c), mean(d) )) sp2 <- mean(c( var(a), var(b), var(c), var(d) )) MSbetween <- n * sx2 dlbetween <- 4-1 MSwithin <- sp2 dlwithin <- 4*(n-1) F <- MSbetween / MSwithin
On trouve :
> F [1] 5.137807
Mais généralement, on fait les calculs différemment, en se rappelant que la variance peut se calculer à l'aide de sommes de carrés :
Var(X) = E[ (X-EX)^2 ]
= E[X^2] - (EX)^2On présente alors les calculs ainsi.
# La somme des valeurs
sa <- sum(a)
sb <- sum(b)
sc <- sum(c)
sd <- sum(d)
s <- sa + sb + sc + sd
# La somme des carrés
ssa <- sum(a^2)
ssb <- sum(b^2)
ssc <- sum(c^2)
ssd <- sum(d^2)
ss <- ssa + ssb + ssc + ssd
# Les valeurs qui nous intéressent
# SS = Sum of Squares
# MS = Mean Square
# effect = between = variance expliquée
SSeffect <- (sa^2/n + sb^2/n + sc^2/n + sd^2/n) - s^2/(4*n)
dleffect <- 4-1
MSeffect <- SSeffect/dleffect
SStotal <- ss - s^2/(4*n) # ????
# error = within = residuals = variance résiduelle
SSerror = SStotal - SSeffect
dlerror <- 4*(n-1)
MSerror <- SSerror/dlerror
F <- MSeffect / MSerror
res <- matrix( nrow=3, ncol=5 )
rownames(res) <- c("Effect", "Error", "Total")
colnames(res) <- c("SS", "df", "MS", "F", "p-value")
res[,1] <- c(SSeffect, SSerror, SStotal)
res[,2] <- c(dleffect, dlerror, dleffect+dlerror)
res[,3] <- c(MSeffect, MSerror, NA)
res[,4] <- c(F, NA, NA)
res[,5] <- c(1-pf(F,dleffect,dlerror), NA, NA)
print(res, na.print="")On obtient :
SS df MS F p-value Effect 15.18513 3 5.0617083 5.137807 0.00463538 Error 35.46678 36 0.9851884 Total 50.65191 39
On définit le rapport de corrélation comme le quotient
> SSeffect/SStotal [1] 0.2997937
On dit alors que << 30% de la variation est expliquée par la variable explicative >>.
On comprend maintenant un peu mieux le résultat donné par R :
> df <- data.frame(y=c(a,b,c,d), x=factor(c(rep(1,n),rep(2,n),rep(3,n),rep(4,n))))
> anova(lm(y~x,data=df))
Analysis of Variance Table
Response: y
Df Sum Sq Mean Sq F value Pr(>F)
x 3 15.185 5.062 5.1378 0.004635 **
Residuals 36 35.467 0.985
---
Signif. codes: 0 `***' 0.001 `**' 0.01 `*' 0.05 `.' 0.1 ` ' 1Le seul nombre qui nous intéresse, c'est la p-valeur : ici, on peut rejeter l'hypothèse << les quatre moyennes sont égales >> avec un risque d'erreur inférieur à 1%.
Le modèle de l'analyse de la variance est le suivant ; on cherche à prédire une variable quantitative Y en fonction d'une variable qualitative X :
Y = a0 + a1*(X==1) + ... + an*(X==n) + bruit
ce que l'on peut aussi écrire
Y = a_0 + a_X + bruit
ou (en notant i (précédemment X) le groupe de l'observation j) :
Y_ij = a + b_i + c_ij
L'interprétation du test F est la même que pour la régression linéaire entre variables quantitatives (regarder quelle partie de la variance de Y est expliquée par X).
Le modèle peut contenir plusieurs variables
y = qqch qui dépend de la valeur de u
+ qqch qui dépend de la valeur de v
+ bruiti.e.,
Y_ijk = a + b_i + c_j + d_ijk
et même des termes d'interaction,
y = qqch qui dépend de la valeur de u
+ qqch qui dépend de la valeur de v
+ qqch qui dépend de la valeur de (u,v)
+ bruiti.e.,
Y_ijk = a + b_i + c_j + d_ij + e_ijk.
Quand certaines des variables prédictives sont quantitatives, on parle d'analyse de la covariance -- mais cela ne change alsolument rien aux calculs.
Donner un exemple (réel ?) avec deux variables prédictives.
Sous R, la commande anova est beaucoup plus générale : elle permet de comparer des modèles. L'Anova telle que nous venons de la présenter est en fait une comparaison du modèle qui nous intéresse avec le modèle trivial.
n <- 200 k <- 5 m <- sample(0:1, k, replace=T, p=c(.9,.1)) # Les moyennes (peut-être égales, peut-être pas) x <- factor(sample(1:k,n,replace=T)) y <- rnorm(n,m[x]) anova( lm(y~x), lm(y~1) )
Il vient :
Analysis of Variance Table Model 1: y ~ x Model 2: y ~ 1 Res.Df RSS Df Sum of Sq F Pr(>F) 1 195 184.366 2 199 226.197 -4 -41.831 11.061 4.177e-08 ***
Et en effet :
> m [1] 0 0 0 1 0
On peut en fait utiliser la commande anova pour comparer des modèles imbriqués quelconques : par exemple deux modèles non triviaux, ou plus de deux modèles. Mais il est important que les modèles soient imbriqués.
A FAIRE : donner un exemple réel. anova( lm(y~x1+x2), lm(y~x1), lm(y~1) ) anova( lm(y~x1+x2), lm(y~x2), lm(y~1) )
Bien sûr, on prendra garde à ne pas faire "trop" de tests : à force, on risquerait de voir quelque chose qui ne serait pas là...
A FAIRE : Est-ce le test des quotients de vraissemblance ou un cas particulier de ce test ?
L'une des choses qui m'ont le plus perturbé quand j'ai cherché à comprendre ce qu'était l'anova, c'est le vocabulaire utilisé : plein de mots très compliqués pour des choses, somme toute, très simples.
Anova avec une seule variable prédictive (i, dans le modèle suivant).
Y_ij = a + b_i + e_ij
Sous R, le modèle s'écrira
y ~ x
où y est la variable quantitative à prédire et x la variable qualitative prédictive.
Voici un exemple de données :
n <- 30 x <- sample(LETTERS[1:3],n,replace=T, p=c(3,2,1)/6) x <- factor(x) y <- rnorm(n) plot(y~x, col='pink')

L'analyse de la variance nous dit si les trois échantillons ont la même moyenne.
> summary(aov(y~x))
Df Sum Sq Mean Sq F value Pr(>F)
x 2 2.271 1.135 1.1193 0.3307
Residuals 97 98.391 1.014
Anova avec deux variables prédictives (i et j, dans l'exemple suivant).
Y_ijk = a + b_i + c_j + e_ijk
Sous R, cela s'écrirait
y ~ x + y
Dans cet exemple, les variables prédictives n'interagissent pas : on peut regarder si elles interagissent, i.e., comparer avec le modèle
Y_ijk = a + b_i + c_j + d_ij + e_ijk
Sous R, le modèle avec interaction s'écrirait
y ~ x + y + x:y
ou
y ~ x * y
Voici une autre simulation.
n <- 100 x1 <- sample(LETTERS[1:3],n,replace=T,p=c(3,2,1)/6) x1 <- factor(x1) x2 <- sample(LETTERS[1:2],n,replace=T,p=c(3,1)/4) x2 <- factor(x2) y <- rnorm(n) i <- which(x1=='A' & x2=='B') y[i] <- rnorm(length(i),.5) library(lattice) bwplot(~y|x1*x2, layout=c(1,6))

L'anova correspondante :
> summary(aov(y~x1*x2))
Df Sum Sq Mean Sq F value Pr(>F)
x1 2 2.855 1.427 1.4716 0.2348
x2 1 0.487 0.487 0.5021 0.4803
x1:x2 2 0.241 0.121 0.1243 0.8833
Residuals 94 91.175 0.970Quand les classes n'ont pas le même effectif, le résultat dépend de l'ordre dans lequel on a mis les variables prédictives.
> summary(aov(y~x2*x1))
Df Sum Sq Mean Sq F value Pr(>F)
x2 1 0.798 0.798 0.8230 0.3666
x1 2 2.544 1.272 1.3112 0.2744
x2:x1 2 0.241 0.121 0.1243 0.8833
Residuals 94 91.175 0.970
C'est un graphique qui permet de voir s'il faut un terme d'interaction dans un modèle avec deux variables prédictives.
Si on cherche à comparer y~x1+x2 avec y~x1*x2, on peut tracer y en fonction de x1 pour chaque valeur de x2 : on obtient une courbe pour chaque valeur de x2. On peut aussi intervertir le rôle de x1 et x2.
Des droites parallèles indiquent une absence d'interaction.
x1 <- gl(2,2,4,c(0,1))
x2 <- gl(2,1,4,c(0,1))
n <- function (x) {
as.numeric(as.vector(x))
}
y1 <- n(x1) + n(x2)
interaction.plot(x1,x2,y1, main="Pas d'interaction")
y2 <- n(x1) + n(x2) - 2*n(x1)*n(x2) interaction.plot(x1,x2,y2, main="Interaction")

On a plusieurs variables indépendantes, par exemple X1 et X2, et on a plusieurs individus pour chaque valeur de (X1,X2).
C'est un cas particulier de l'anova double.
On a plusieurs variables indépendantes, par exemple X1 et X2, et on a un seul individu pour chaque valeur de (X1,X2). Dans ce cas, on n'a pas suffisemment d'information pour étudier l'interaction des deux variables.
C'est un cas particulier de l'anova double.
On peut imaginer des modèles qui, bien qu'ils ressemblent aux précédents, ne se traitent pas de la même manière : il s'agit des modèles mixtes.
Avant de montrer comment les traiter, nous allons poursuivre notre présentation du vocabulaire.
C'est toujours une anova double, i.e., un modèle de la forme
Y_ijk = a + b_i + c_j + e_ijk
mais cette fois-ci, la valeur de i détermine entièrement celle de j. En d'autres termes, la variable j permet de regrouper les différentes valeurs de i. Par exemple
i = numéro de la feuille (de 1 à 100)
j = numéro de l'arbre (1 à 10 : les feuilles 1 à 10 sont sur l'arbre
1, les 10 suivantes sur l'arbre 2, etc.)Autre exemple :
i = numéro de l'élève j = numéro de sa classe
Voici une simulation
n <- 2000 # Nombre d'expériences k <- 20 # Nombre d'individus l <- 4 # Nombre de groupes kl <- sample(1:l, k, replace=T) # Groupe des individus x1 <- sample(1:k, n, replace=T) x2 <- kl[x1] A <- rnorm(1,sd=4) B <- rnorm(k,sd=4) C <- rnorm(l,sd=4) y <- A + B[x1] + C[x2] + rnorm(n) x1 <- factor(x1) x2 <- factor(x2) op <- par(mfrow=c(1,2)) plot(y~x1, col='pink') plot(y~x2, col='pink') par(op)
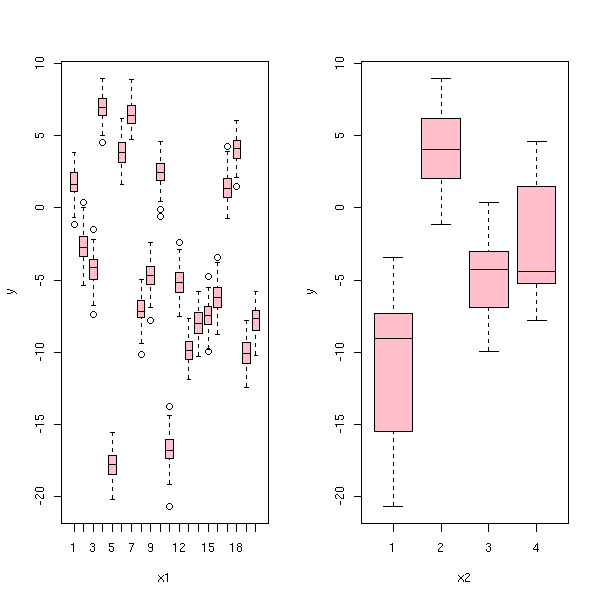
On peut faire la même chose en un seul dessin en assigant une couleur différente à chaque groupe
# If the data were real, we wouldn't know kl.
# One may recover it that way.
kl <- tapply(x2, x1, function (x) { a <- table(x); names(a)[which(a==max(a))[1]] } )
kl <- factor(kl, levels=levels(x2))
plot(y~x1, col=rainbow(l)[kl])
et en réordannant les individus.
x1 <- factor(x1, levels=order(kl)) kl <- sort(kl) plot(y~x1, col=rainbow(l)[kl])

J'ai affirmé plus haut que les méthodes précédentes ne marchaient pas directement sur ces exemples moins triviaux : vérifions-le.
> a <- x1
> b <- x2
> lm(y~a+b)
Call:
lm(formula = y ~ a + b)
Coefficients:
(Intercept) a11 a18 a19 a1 a2
10.0156 -2.7380 -2.6942 -0.7015 -15.9302 -11.5106
a8 a13 a14 a15 a3 a4
-13.3365 -3.0425 -10.6694 -10.7422 -15.2508 -20.9595
a9 a17 a20 a5 a7 a10
-21.8916 -19.5307 -19.9899 -11.1213 -7.5232 -10.9528
a12 a16 b2 b3 b4
-5.8704 -6.5261 NA NA NASi on lui demande ainsi, il est incapable d'estimer les coefficients de la variable correspondant aux groupe.
Pour chaque sujet.
Par exemple, si on a mesuré une quantité Y, pour chaque valeur d'une variable qualitative X, on peut calculer la variance des mesures faites par un sujet donné. Si X est quantitative, on peut faire une régression pour un sujet donné.
Moyenne (ou autre chose) sur tous les sujets.
Ainsi, dans l'exemple précédent, on peut calculer la moyenne des variances "within subject".
Dans bien des cas, on peut choisir les valeurs des variables prédictives, car on les fixe nous-même lors de l'expérience.
A FAIRE : comprendre ce qui suit. CRD: Completely Randomized Design RCBD: Randomized Block Design Latin Square: Randomized Block Design with two series of blocks BIB: Balanced incomplete Block Design Factorial Design
On considère qu'il n'y a pas de différence entre les individus.
On considère qu'il y a une différence entre les sujets. C'est souvent le cas dans les expériences de psychologie : on fait subir différentes expériences aux sujets. Mais c'est le même individu qui subit ces expériences.
Pratiquement, le tableau des résultats a une ligne de plus, correspondant aux sujets.
On parle alors d'Anova Within.
Une variable qualitative dont la valeur est entièrement déterminée une fois qu'on connait les autres. Par exemple : le groupe auquel le sujet appartient, quand chaque sujet appartient exactement à un groupe.
A FAIRE
Dans un in-subject design, il faut que les tests que l'on fait subir aux individus soient indépendants (par exemple, si on demande au sujet de réaliser une tache dans certaines conditions, puis ensuite dans d'autres conditions, il rique de se souvenir de ce qu'il a fait la première fois.
Ce sont les paramètres de la régression (i.e., les valeurs que l'on cherche).
Les effets sont des constantes.
Les effets ne sont pas des constantes mais des variables aléatoires
A FAIRE : expliquer, comprendre et donner un exemple. fixed, random and mixed effects models...
On mesure la même quantité sur chaque individu, plusieurs fois.
C'est très semblable à ce qu'on a vu lors de l'anova à facteurs hiérarchisés : le modèle s'écrit
Y_ij = a_i + b x_ij + c_ij
où
i est le numéro du sujet j est le numéro de la mesure effectuée sur ce sujet x est une variables quantitative prédictive
C'est comme une régression linéaire, mais l'ordonnée à l'origine dépend de l'individu -- par contre, la pente n'en dépend pas.
A FAIRE : une simulation et un dessin.
n <- 1000 k <- 9 sujet <- factor(sample(1:k,n,replace=T), levels=1:k) a <- rnorm(k,sd=4) b <- rnorm(1) x <- rnorm(n) y <- a[sujet] + b * x + rnorm(n) plot(y~x) abline(lm(y~x))

Mais on ne voit pas grand-chose... On a une droite, certes, mais les points ont quand-même l'air très éloignés de cette droite.
En fait, on a plusieurs droites (une pour chaque sujet) qui se superposent.
col <- rainbow(k)
plot(y~x)
for (i in 1:k) {
points(y[sujet==i] ~ x[sujet==i], col=col[i])
abline( lm(y~x, subset=sujet==i), col=col[i] )
}
Ce cas est très simple : les droites sont réellement parallèles. Dans ces situations réelles, elles ne le sont pas, ou ce ne sont pas des droites : sur un dessin sur lequel tout se superpose, on ne voit rien. On fait donc des dessins séparés.
library(lattice) xyplot(y~x|sujet)

Les sujets sont répartis en différents groupes et on effectue plusieurs mesures pour chaque sujet.
Idem, mais on a deux niveaux de regroupement : chaque individu est dans un groupe et chaque groupe est dans un sur-groupe.
A FAIRE : un tableau qui présente les différents types de modèles.
Modèle Nom
-----------------------------------------------------------------------------------
Y_ij = a + b_i + c_ij Anova à un facteur
i : variable prédictive qualitative
Y_ijk = a + b_i + c_j + d_ijk Anova à deux facteur, sans interaction
i : variable prédictive qualitative
j : autre variable prédictive qualitative
i et j sont indépendantes
Y_ijk = a + b_i + c_j + d_ij + e_ijk Anova à deux facteurs, avec interaction
Y_ijk = a + b_i + c_j + d_ijk Anova à facteurs hiérarchisés
i et j : variables prédictives, qualitatives
i : numéro de l'individu
j : numéro du groupe de l'individu
j est entièrement déterminé par i
A FAIRE : la suite
Ensuite, on ajoute des variables quantitatives...
On mesure la même quantité sur chaque individu, plusieurs fois.
n <- 30 k <- 10 sujet <- gl(k,n/k,n) x <- gl(n/k,1,n) y <- rnorm(k) y <- rnorm(n, y[sujet]) y[ x==2 ] <- y[ x==2 ] + 1 # On ne voit rien plot(y~x, col='pink')

interaction.plot(x,sujet,y)

Voici l'analyse de la variance :
> summary(aov(y~x+Error(sujet/x)))
Error: sujet
Df Sum Sq Mean Sq F value Pr(>F)
Residuals 9 40.000 4.444
Error: sujet:x
Df Sum Sq Mean Sq F value Pr(>F)
x 2 8.6491 4.3245 7.8876 0.003468 **
Residuals 18 9.8689 0.5483Ne pas considérer le terme d'erreur revient à considérer les boites à moustaches ci-dessus : on ne voit rien.
> summary(aov(y~x))
Df Sum Sq Mean Sq F value Pr(>F)
x 2 8.649 4.325 2.3414 0.1154
Residuals 27 49.869 1.847On aurait aussi pu imaginer prendre le numéro du sujet comme une autre variable prédictive : mais on estime alors beaucoup trop de paramètres par rapport aux données, il ne reste plus suffisemment d'information (on dit souvent : "de degrés de liberté") pour faire un test :
> summary(aov(y~x*sujet))
Df Sum Sq Mean Sq
x 2 8.649 4.325
sujet 9 40.000 4.444
x:sujet 18 9.869 0.548
Les sujets sont répartis en différents groupes et on effectue plusieurs mesures pour chaque sujet.
n <- 50 k <- 10 sujet <- gl(k,n/k,n) groupe <- sample(1:3, k, replace=T)[sujet] groupe <- factor(groupe) x <- gl(n/k,1,n) y <- rnorm(n) y[x==1] <- y[x==1] + 1 plot(y~x, col='pink')

Voici l'analyse de la variance (ici, x est le seul facteur intra-sujet, car chaque sujet appartient à un seul groupe) :
> summary(aov( y ~ x * groupe + Error(sujet/x) ))
Error: sujet
Df Sum Sq Mean Sq F value Pr(>F)
groupe 2 1.7068 0.8534 0.5958 0.5768
Residuals 7 10.0260 1.4323
Error: sujet:x
Df Sum Sq Mean Sq F value Pr(>F)
x 4 25.149 6.287 4.5296 0.00601 **
x:groupe 8 1.994 0.249 0.1795 0.99191
Residuals 28 38.865 1.388
Idem, mais on a deux niveaux de regroupement : chaque individu est dans un groupe et chaque groupe est dans un sur-groupe.
n <- 64 groupe <- gl(16,n/16,n) surgroupe <- gl(4,n/4,n) sujet <- gl(64,n/64,n) y <- rnorm(n) A FAIRE : dessin y ~ groupe, la couleur étant donnée par le surgroupe
Ici, chaque individu apparait une seule fois.
L'analyse de la variance s'écrit en deux temps : on regarde tout d'abord si le surgroupe a une importance :
> summary(aov( y ~ surgroupe + Error(groupe) ))
Error: groupe
Df Sum Sq Mean Sq F value Pr(>F)
surgroupe 3 0.8376 0.2792 0.2675 0.8475
Residuals 12 12.5227 1.0436
Error: Within
Df Sum Sq Mean Sq F value Pr(>F)
Residuals 48 50.131 1.044puis s'il y a des disparités à l'intérieur des surgroupes, dues aux groupes.
> summary(aov( y ~ surgroupe:groupe ))
Df Sum Sq Mean Sq F value Pr(>F)
surgroupe:groupe 15 13.360 0.891 0.8528 0.6173
Residuals 48 50.131 1.044
A FAIRE
Reprenons le même exemple, mais cette fois-ci, chaque individu apparait plusieurs fois.
n <- 256 groupe <- gl(16,n/16,n) surgroupe <- gl(4,n/4,n) sujet <- gl(64,n/64,n) y <- rnorm(n)
On commence par regarder si les surgroupes ont une influence :
summary(aov( y ~ surgroupe + Error(surgroupe/groupe*sujet) )) A FAIRE : je ne suis pas du tout sûr de ce qui précède De surcroît, R met très longtemps pour faire ces calculs...
y ~ variables prédictives + Error(
Sujet / (somme ou produit des variables prédictives dont
l'effet est suceptible de varier d'un sujet à l'autre)
)Cela permet de faire les tests :
Est-ce que ça varie sensiblement en fonction du sujet ? L'effet des variables prédictives en question dépend-il effectivement du sujet ?
On dit que les variables dont les effets sont suceptibles de dépendre du sujet sont des "within effects" ou "within-subject factor".
Variance de cette syntaxe :
sujet / v
est équivalent à
sujet + v %in% sujet
One-way analysis of variance: Y_ij = a + b_i + c_ij
Unbalanced anova: les groupes n'ont pas le même effectif (ça
complique un peu les calculs).
Nested design: Y_ijk = a + b_i + c_ij + d_ijk
Il n'y a pas de terme c_j
Exemple : i = numéro de l'arbre, j = numéro de la feuille
Exemple : i = numéro du père, j = numéro de la mère (en
agriculture, un même père sera utilisé plusieurs fois, mais la
mère une seule fois : il faut attendre qu'elle mette bas).
Nested unbalanced anova : les groupes n'ont pas le même effectif. Ca
complique beaucoup les calculs et les tests.
Voici un autre exemple de simulation : on regarde la durée d'un rhume chez des patients auxquels on a donné un médicament ou un placébo. Si on fait l'expérience avec des individus tous différents, les différences entres les patients sont plus importantes que celles provoquées par le médicament.
n <- 10 sujet <- gl(n,2) traitement <- gl(2,1,2*n, 0:1) duree <- ifelse( traitement==1, rpois(2*n,2), rpois(2*n,3) ) summary(lm( duree ~ traitement )) # Non significatif
Il n'y a pas d'effet significatif.
> summary(lm( duree ~ traitement )) # Non significatif
Call:
lm(formula = duree ~ traitement)
Residuals:
Min 1Q Median 3Q Max
-2.20 -1.20 -0.10 0.45 3.80
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 3.2000 0.5033 6.358 5.46e-06 ***
traitement1 -1.2000 0.7118 -1.686 0.109
---
Signif. codes: 0 `***' 0.001 `**' 0.01 `*' 0.05 `.' 0.1 ` ' 1
Residual standard error: 1.592 on 18 degrees of freedom
Multiple R-Squared: 0.1364, Adjusted R-squared: 0.08838
F-statistic: 2.842 on 1 and 18 DF, p-value: 0.1091Néanmoins, si on fait deux expériences avec chaque patient (qui doit donc contracter deux rhumes), une avec le placébo, l'autre avec le médicament, on constate que la durée du rhume est souvent réduite avec le médicament.
n <- 10 sujet <- gl(n,2) traitement <- gl(2,1,2*n, 0:1) duree <- ifelse( traitement==1, rpois(2*n,2), rpois(2*n,3) ) sans <- duree[2*(1:n)-1] avec <- duree[2*(1:n)] plot(sans+rnorm(n), avec+rnorm(n)) abline(0,1)

Proportion de candidats pour lesquels le médicaments est efficace :
> sum(sans>avec)/n [1] 0.8
D'après le tests de Wilcoxon, c'est significatif.
> wilcox.test(avec,sans, paired=T)
Wilcoxon signed rank test with continuity correction
data: avec and sans
V = 3.5, p-value = 0.02355
alternative hypothesis: true mu is not equal to 0On peut faire une régression en considérant la différence entre les deux expériences pour chaque candidat.
> summary( lm(I(sans-avec) ~ 1) )
Call:
lm(formula = I(sans - avec) ~ 1)
Residuals:
Min 1Q Median 3Q Max
-2.20 -0.20 -0.20 0.55 1.80
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 1.2000 0.3887 3.087 0.013 *
---
Signif. codes: 0 `***' 0.001 `**' 0.01 `*' 0.05 `.' 0.1 ` ' 1
Residual standard error: 1.229 on 9 degrees of freedomC'est en fait le résultat du test de Student.
> t.test(sans-avec)
One Sample t-test
data: sans - avec
t = 3.087, df = 9, p-value = 0.01299
alternative hypothesis: true mean is not equal to 0
95 percent confidence interval:
0.3206314 2.0793686
sample estimates:
mean of x
1.2On peut aussi le formuler sous forme d'une régression (cela présente un avantage : certains candidats peuvent avoir fait l'expérience plus de deux fois).
> summary(lm( duree ~ traitement + sujet )) # significatif
Call:
lm(formula = duree ~ traitement + sujet)
Residuals:
Min 1Q Median 3Q Max
-1.100e+00 -1.750e-01 9.714e-17 1.750e-01 1.100e+00
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 2.6000 0.6446 4.033 0.00296 **
traitement1 -1.2000 0.3887 -3.087 0.01299 *
sujet2 1.5000 0.8692 1.726 0.11849
sujet3 -0.5000 0.8692 -0.575 0.57923
sujet4 -1.0000 0.8692 -1.150 0.27961
sujet5 2.5000 0.8692 2.876 0.01829 *
sujet6 0.5000 0.8692 0.575 0.57923
sujet7 -0.5000 0.8692 -0.575 0.57923
sujet8 3.5000 0.8692 4.027 0.00299 **
sujet9 -0.5000 0.8692 -0.575 0.57923
sujet10 0.5000 0.8692 0.575 0.57923
---
Signif. codes: 0 `***' 0.001 `**' 0.01 `*' 0.05 `.' 0.1 ` ' 1
Residual standard error: 0.8692 on 9 degrees of freedom
Multiple R-Squared: 0.8712, Adjusted R-squared: 0.7281
F-statistic: 6.088 on 10 and 9 DF, p-value: 0.006023On retrouve la même valeur.
Voici encore une autre manière de présenter ces calculs :
> summary(aov(duree ~ traitement + Error(sujet/traitement)))
Error: sujet
Df Sum Sq Mean Sq F value Pr(>F)
Residuals 9 38.800 4.311
Error: sujet:traitement
Df Sum Sq Mean Sq F value Pr(>F)
traitement 1 7.2000 7.2000 9.5294 0.01299 *
Residuals 9 6.8000 0.7556
---
Signif. codes: 0 `***' 0.001 `**' 0.01 `*' 0.05 `.' 0.1 ` ' 1Attention toutefois à la manière de construire ces termes d'erreur : pour bien la comprendre, on peut se référer à
http://cran.r-project.org/doc/contrib/rpsych.html
De manière générale :
summary(aov( resultat ~ a1 * a2 * a3 * b1 * b2 + Error(subj/(a1+a2+a3)) ))
where a1, a2, a3 are within-subject factors and b1, b2 are between-subject factors.
Formule | Modèle
------------------------------------------------------
y ~ j | y = a_j + Erreur
y ~ j + Error(i) | y = a_j + b_i + Erreur
y ~ j + Error(i/j) | y = a_j + c_{i,j} + ErreurExercice : Dans l'exemple précédent, fallait-il prendre un terme d'erreur de la forme Error(sujet) ou Error(sujet/traitement) ?
La commande lme, dans la bibliothèque nlme semble faire des choses comparables (ça n'est pas le même exemple : sinon, on aurait exactement la même p-valeur).
> summary( lme(duree ~ traitement, random = ~ 1 | sujet) )
Linear mixed-effects model fit by REML
Data: NULL
AIC BIC logLik
67.44822 71.00971 -29.72411
Random effects:
Formula: ~1 | sujet
(Intercept) Residual
StdDev: 0.7601167 0.8850613
Fixed effects: duree ~ traitement
Value Std.Error DF t-value p-value
(Intercept) 3.2 0.3689324 9 8.673676 <.0001
traitement1 -1.3 0.3958114 9 -3.284392 0.0095
Correlation:
(Intr)
traitement1 -0.536
Standardized Within-Group Residuals:
Min Q1 Med Q3 Max
-0.98547570 -0.73238917 0.03706879 0.48334911 1.85051895
Number of Observations: 20
Number of Groups: 10A FAIRE : comprendre et expliquer la syntaxe du terme d'erreur pour la commande mle.
La commande nlme semble être un analogue non linéaire de lme (donc un mélange de lme et nls).
Parfois, tous les coefficients du modèle de l'anova ne nons intéressent pas. Par exemple, on peut étudier l'effet d'un médicament sur la performance à un certain test, suivant le modèle
Y_ij = a + b_i + c_j + e_ij
où i est la variable "traitement" (médicament ou placebo) et j le numéro du sujet. Ce qui nous intéresse, c'est b_i (l'effet du médicament) et pas du tout c_j (qui correspond au niveau du sujet).
C'est juste ça, un modèle mixte.
En termes matriciels, le modèle linéaire s'écrit
Y = X b + e
(X et Y sont connus, e est aléatoire, on cherche b) alors que le modèle mixte s'écrit
Y = X b + Z u + e
(X, Y et Z sont connus, u et e sont aléatoires, on cherche b). On dit que b représente les effets fixes et u les effets aléatoires.
Les variables prédictives auxquelles on s'intéresse, dans un modèle mixte.
Les variables prédictives auxquelles on ne s'intéresse pas, dans un modèle mixte. Elles sont généralement qualitatives, avec un nombre potentiellement infini de valeurs.
On pourrait être tenté de voir le modèle mixte comme un cas particulier du modèle linéaire (on peut mettre X et Z dans une même matrice, b et u dans un même vecteur, estimer b et u et oublier qu'on a estimé u). Il y a en fait quelques différences.
Dans le modèle mixte, on a moins de paramètres à estimer, on peut donc effectuer ces estimations avec moins de données.
Il y a aussi des différences au niveau des tests qu'on effectue sur ces estimations (pour utiliser un vocabulaire que je n'aime pas : on a plus de "degrés de liberté").
Rappelons que dans le modèle linéaire (moindres carrés ordinaires), la variance du terme de bruit est une matrice scalaire (i.e., les e_ijk sont non-corrélés et de même variance). Avec les moindres carrés généralisés, cette matrice de variance-covariance peut être quelconque.
C'est justement ce qu'on retrouve dans le modèle mixte
Y = X b + Z u + e.
Si on note R et G les matrice de variance-covariance de e et u, la variance de Y est
Var(Y) = ZGZ'+R.
Donc même si e et u sont des matrices scalaires, la variance de Y peut être plus complexe : le modèle mixte n'est pas un cas particulier du modèle linéaire dans lequel on ne s'intéresse pas à tous les coefficients, mais un cas particulier des moindres carrés généralisés.
HLM (Hierarchical Level Model) = Mixed Model = Random Coefficient Model = Multilevel Analysis = Grouped Data
Dans les modèles classiques, on dispose d'un univers (par exemple, la population française) dans lequel on tire, au hasard des individus (dans notre exemple, des français), sur lesquels on mesure les variables qui nous intéressent (salaire, sexe, âge, poids, etc.). On répète cela autant ce fois qu'on veut d'observations.
Dans les modèles hiérarchiques, ce tirage au sort s'effectue en deux étapes (ou plus). On dispose d'un premier univers (par exemple, l'ensemble des villes françaises), dans lequel on tire, au hasard, des éléments (des villes). Pour chacun de ces éléments, on mesure les variables qui nous intéressent (latitude, longitude, nombre d'habitants, impôts locaux, salaire moyen des habitants, etc.). A chacun de ces éléments (à chaque ville) est associé un univers (les habitants de cette ville), dans lequel on tire, à nouveau, au hasard, des éléments (des habitants), sur lesquels on mesure les variables qui nous intéressent (salaire, âge, etc.).
Si on met les données observées dans un tableau, on a deux tableaux.
Ville Superficie Nombre d'habitants ---------------------------------------- A 1 28000 B 7 50000 C 3 15000 Individu Ville salaire âge ----------------------------- Artaud A 30 32 Balzac A 50 38 Camus B 10 21 Descartes C 20 49 Etiemble C 27 36 Fénelon C 23 29 Gide B 15 56
Quitte à se répéter, on peut tout mettre dans un unique tableau.
Individu Ville Superficie Nombre d'habitants Salaire Âge ------------------------------------------------------------- Artaud A 1 28000 30 32 Balzac A 1 28000 50 38 Camus B 7 50000 10 21 Descartes C 3 15000 20 49 Etiemble C 3 15000 27 36 Fénelon C 3 15000 23 29 Gide B 7 50000 15 56
Dans cet exemple, il y a deux niveaux d'échantillonage (ville et individus) et il y a des variables définies à chacun de ces niveaux (superficie et nombre d'habitants sont définis pour les villes, i.e., sont les mêmes pour tous les habitants d'une même ville ; salaire et âge sont définis au niveau des individus).
Après avoir donné un exemple de données sous forme de tableau(x), passons aux simulations et aux graphiques.
# Il y a 12 villes n.villes <- 12 # La superficie des villes (plus raisonnablement, le logarithme de # leur superficie) sont des variables aléatoires indépendantes, # normales, de moyenne 5 et d'écart-type 1. superficie.moyenne <- 5 superficie.sd <- 1 superficie <- rnorm(n.villes, superficie.moyenne, superficie.sd) a <- rnorm(n.villes) b <- rnorm(n.villes) # Il y a 200 individus, 20 dans chaque ville n.individus <- 20 ville <- rep(1:n.villes, each=n.individus) # L'âge des individus sont des variables aléatoires indépendantes, # normales, de moyenne 40, d'écart-type 10. # On aurait pu choisir une loi différente pour chacune des villes # (soit de manière purement aléatoire, soit en tenant compte de leur # superficie). age <- rnorm(n.villes*n.individus, 40, 10) # Le salaire (la variable qu'on cherche à expliquer) est une # fonction affine de l'âge, mais les coefficients dépendent de la # ville. # Ici, ces coefficients sont pris au hasard, mais on aurait pu les # faire dépendre de la superficie de la ville. # Ici, ces coefficients sont indépendants -- c'est rarement le cas. a <- rnorm(n.villes, 20000, sd=2000) b <- rnorm(n.villes, sd=20) salaire <- 200*superficie[ville] + a[ville] + b[ville]*age + rnorm(n.villes*n.individus, sd=200) plot(salaire ~ age, col=rainbow(n.villes)[ville], pch=16)

On ve voit pas grand-chose, sur ce graphique. Une idée est de faire un graphique différent pour chaque ville : c'est ce que propose la bibliothèque "lattice" (dont l'idée générale est, rappelons-le, de couper les nuages de points en tranches). Retenez la syntaxe,
variable à prédire ~ variables prédictives | groupe
nous la retrouverons lors de l'estimation des coefficients des modèles mixtes (i.e., l'estimation de la moyenne et de la variance de a et b, la covariance de (a,b), ainsi que les tests pour savoir si a et b dépendent vraiment de la ville, i.e., pour savoir si leur variance est significativement non nulle).
library(lattice) xyplot(salaire ~ age | ville)

Dans cet exemple, a et b dépendaient tous deux de la ville. Il est possible que seul l'un d'entre eux, ou même aucun, n'en dépende.
a <- rnorm(n.villes, 20000, sd=2000) b <- rep(rnorm(1, sd=20), n.villes) salaire <- 200*superficie[ville] + a[ville] + b[ville]*age + rnorm(n.villes*n.individus, sd=200) xyplot(salaire ~ age | ville)

a <- rep( rnorm(1, 20000, sd=2000), n.villes ) b <- rnorm(n.villes, sd=20) salaire <- 200*superficie[ville] + a[ville] + b[ville]*age + rnorm(n.villes*n.individus, sd=200) xyplot(salaire ~ age | ville)

a <- rep( rnorm(1, 20000, sd=2000), n.villes ) b <- rep(rnorm(1, sd=20), n.villes) salaire <- 200*superficie[ville] + a[ville] + b[ville]*age + rnorm(n.villes*n.individus, sd=200) xyplot(salaire ~ age | ville)

Les modèles mixtes apparaissent quand les observations ne sont pas indépendantes : les individus appartiennent à des groupes (qu'on connait, mais qui sont éventuellement très nombreux) et les variables mesurées sur les individus d'un même groupe ont des valeurs proches.
A FAIRE : détailler Donner un exemple explicite ? Exemple : les résultats scolaires dépendent de la classe Exemple : cluster sampling
On peut avoir plus de deux niveaux :
élève/classe/enseignant/école/ville/académie A FAIRE : mettre d'autres exemples A FAIRE : mettre un exemple avec des données longitudinales
On peut déplacer certaines variables d'un niveau à l'autre : par exemple, on peut associer un salaire à chaque individu ou un salaire moyen à chaque ville.
A FAIRE : donner la syntaxe pour décrire ces modèles plus compliqués sous R.
Les différentes variables aléatoires qui interviennent ne sont pas nécessairement indépendantes : le modèle précise souvent la forme de la matrice de variance-covariance.
A FAIRE : détailler. Donner des exemples précis...
Il ne faut pas commettre l'erreur de faire une analyse à un niveau et d'en déduire des conséquences à un autre.
Exemple : si on constate une corrélation entre le taux d'illetrisme et la présence d'une certaine minorité, rien ne dit qu'on retrouve cette corrélation au niveau des individus.
(Mais rassurez-vous, on peut quand-même faire des analyse transversales, ou multiniveaux, par exemple en essayant de prédire une variable au niveau des individus à l'aide d'un mélange de variables au niveau des individus et des groupes)
A FAIRE : expliquer que les niveaux ne servent pas de variables prédictives. Par exemple, le nom de la ville. (Tout simplement par ce qu'on a fait un tirage au sort et qu'on n'a pas pris toutes les villes.)
La première idée, pour analyser des données groupées, consiste à effectuer une régression dans chaque groupe. Reprenons l'un de nos exemples simulés ci-dessus.
n.villes <- 12 superficie <- rnorm(n.villes, 5, 1) a <- rnorm(n.villes) b <- rnorm(n.villes) n.individus <- 20 ville <- rep(1:n.villes, each=n.individus) age <- rnorm(n.villes*n.individus, 40, 10) a <- rnorm(n.villes, 20000, sd=2000) b <- rep(rnorm(1, sd=20), n.villes) salaire <- 200*superficie[ville] + a[ville] + b[ville]*age + rnorm(n.villes*n.individus, sd=200) xyplot(salaire ~ age | ville)

La fonction lmList de la bibliothèque nlme effectue une régression dans chaque groupe.
library(nlme) d <- data.frame(salaire, age, ville, superficie=superficie[ville]) r <- lmList(salaire ~ age | ville, data=d)
Il vient :
> summary(r)
Call:
Model: salaire ~ age | ville
Data: d
Coefficients:
(Intercept)
Estimate Std. Error t value Pr(>|t|)
1 21479.14 162.7878 131.94565 0
2 24026.24 274.6432 87.48163 0
3 19633.32 169.5408 115.80292 0
4 17354.47 205.3334 84.51853 0
5 22675.63 207.5127 109.27345 0
6 22732.46 235.9244 96.35486 0
7 21292.20 178.5410 119.25666 0
8 20044.50 185.1989 108.23230 0
9 18924.25 136.4418 138.69835 0
10 20630.17 147.8031 139.57873 0
11 20572.80 170.0011 121.01566 0
12 18025.29 180.2910 99.97887 0
age
Estimate Std. Error t value Pr(>|t|)
1 -6.0190190 4.343643 -1.38570746 0.16726531
2 4.3642466 6.469611 0.67457638 0.50066630
3 5.1117531 4.252501 1.20205817 0.23065717
4 0.2409800 5.088937 0.04735370 0.96227508
5 0.2023943 5.150521 0.03929589 0.96869078
6 8.0885149 5.755782 1.40528515 0.16137312
7 7.9947740 4.245020 1.88333011 0.06099939
8 4.2547386 4.528523 0.93954232 0.34850184
9 2.9008258 3.713258 0.78120777 0.43553568
10 3.4318408 3.813179 0.89999457 0.36912542
11 -3.1825003 3.956591 -0.80435410 0.42207690
12 -1.3094108 4.573603 -0.28629742 0.77492474
Residual standard error: 195.6667 on 216 degrees of freedomOn voit donc que le coefficient a (l'ordonnée à l'origine) dépend de la ville, alors que le coefficient b (le coefficient directeur de la droite) n'en dépend pas. On dit que a est un coefficient aléatoire.
library(nlme) d <- data.frame(salaire, age, ville, superficie=superficie[ville]) r <- lmList(salaire ~ age | ville, data=d) plot(intervals(r))

A FAIRE : on n'a pas tenu compte de la superficie...
La suite
Plan de cette partie :
Introduction
Idée générale
Les observations dans un même groupe sont souvent corrélées.
Exemple 1 : Y_ijk = a_i + b_ij + c_ijk i=groupe, j=individu
Exemple 2 : Y_ij = a_i + b_i X_ij + c_ij
Exemples concrets : amova,
Une première simulation et un graphique
Vocabulaire
Longitudinal data, repeated measures data, longitudinal data, split-splot design,
aov, Error
rpsych, break the sum of squares into the pieces defined by the Error term
Treillis, nlme, groupedData, comparaison de la syntaxe avec aov/Error
modèles mixtes et matrice de variance-covariance
nlme : modèles mixtes non linéaires
Autres fonctions
glmmPQL (MASS)
GLMM (lme4)
lme (nlme)
nlme
aov
glm ???
Généralisations : modèles graphiques, réseaux bayesiens
Quelques exemples de nlme :
data(Orthodont); formula(Orthodont); attr(Orthodont,"outer"); plot(Orthodont) plot(Orthodont, outer=T) data(Machines); formula(Machines); plot(Machines) data(CO2); formula(CO2); attr(CO2,"outer"); plot(CO2) plot(CO2, outer=T) data(Pixel); formula(Pixel); attr(Pixel,"outer"); plot(Pixel) plot(Pixel, inner=~Side)
Mais ça ne correspond pas vraiment aux problèmes que j'ai mentionnés plus haut : j'avais des variables prédictives qualitatives...
y ~ x y ~ x | sujet y ~ x | sujet, outer = ~ groupe y ~ x | sujet, outer = ~ groupe1 * groupe2 m <- groupedData(...) lmList(m) # Calcule une régression pour chaque sujet Utilisation des modèles mixtes : commencer par écrire le modèle, sur papier Indiquer quels sont les effets fixes et les effets aléatoires. Ecrire le modèle sous R : lme(fixed = y ~ x | sujet, random= ~ x) Modèle fixed random ---------------------------------------------------------------------- Y = (a+a_i) + (b+b_i) x y ~ x ~ x Y = (a+a_i) + b x y ~ x ~ 1 Y = a + (b+b_i) x y ~ x ~ -1 + x Il est aussi possible de préciser le matrices de variance-covariance, mais je n'ai encore regardé. Expliquer comment lire les résultats. summary(...) anova(lme(...,methodd="ML")) fixed.effects(r) random.effects(r) Graphiques : plot(r, x ~ fitted(.) | g) ... resid(.) Prédictions : predict
Modèles mixtes :
glmmPQL (MASS) GLMM (lme4) lme (nlme) aov glm ???
Effets mixtes non linéaires :
nlme La documentation donne l'exemple suivant : Y = A_i ( 1 - exp( - B_i ( X - C_i ) + bruit_ij i : numéro de la plante j : numéro de l'observation Arguments de nlme : Y ~ f(X, A, B, C) fixed = A + B + C ~ 1 | plante random = A + B + C ~ 1 | plante Si on a d'autres variables qualitatives prédictives, on peut écrire : fixed = A + B + C ~ x1 * x2 | plante random = A + B + C ~ 1 | plante On peut aussi mettre des listes : fixed = list( A + B ~ x1 * x2, C ~ 1 ) Scatter plot matrix of the random effects : pairs(r, ranef(.)) Plot the fitted curves : r <- nlme(...) plot(augPred(r))
Vocabulaire :
Longitudinal data repeated measures data longitudinal data split-splot design mixed model, hierarchical analysis, multilevel analysis Les observations dans un même groupe sont souvent corrélées.
Autres exemples :
Theoph
Wafer 3 nested levels of grouping: Wafer, Site within Wafer, Device within Site
outer factor = it is constant for each level of the grouping factor
= it is entirely determined by the group (or subject)
inner factor = it varies
Pour décrire un modèle avec des groupes (éventuellement sur
plusieurs niveaux) et des facteurs internes et externes,
une seule formule du genre
y ~ x1 + x2 | g1/g2/g3
ne suffit pas.
On peut ajouter des arguments "inner" ou "outer" à la fonction groupedData.
y ~ x | sujet, outer = ~ x1 * x2
(ici, x est quantitative, sujet détermine x1 et x2)
In a plot: group=lines, outer=panels
grouping factor: the population from which we sample.
inner factor: can change within groups
In a plot: inner=lines, group=panels
Inner: changes within a group
Outer: does not change within a group
S'il y a plusieurs niveaux de groupage, le caractère interne/externe
peut varier :
current ~ voltage | Wafer/Site/Device
inner=list( Wafer = ~ Length, Site = ~ Length)
ou
current ~ voltage | Wafer/Site/Device
outer=list( Device = ~ Length )
Longitudinal data : c'est ce dont on parle; y~x, avec y et x
continues, des individus/groupes, quelques autres variables
qualitatives.
Affichage de données de type groupedData.
data(Pixel)
plot(Pixel)
Ici, il y a deux niveaux de groupage : on peut n'en mettre qu'un.
plot(Pixel, display=1)
Ca ressemble beaucoup aux arguments outer ou inner qu'on peut aussi
utiliser avec la méthode plot. Comparer avec
plot(Pixel, inner=~Side)
On peut se retrouver avec des graphiques peu lisibles, avec
d'innombrables courbes superposées. On peut demander à l'ordinateur
de fusionner ces courbes, à l'aide d'une fonction de notre choix.
Exemple (c'est la fonction par défaut) :
plot(Pixel, display=1, collapse=1, FUN=mean)
Si on veut examiner l'hétéroscédasticité :
plot(Pixel, display=1, collapse=1, FUN=sd)
Si on n'a que deux courbes dans chaque panel, très différentes, on
peut regarder leur différence :
plot(Pixel, display=1, collapse=1, FUN=diff)
On peut se retrouver avec un nombre de panels énorme et n'en vouloir
que quelques uns. On peut les sélectionner à l'aide de l'option
"subset".
plot(Pixel, subset=list(Dog=c(3,4)))
Mixed Models: les observations concernant un même individu sont
corrélées. Les modèles mixtes permettent d'en tenir compte.
Exemple de domaine utilisant des modèles hiérarchiques :
l'éducation. On mesure les résultats des élèves selon l'élève,
l'année, la classe, l'enseignant, l'école, les méthodes, les livres,
le district, le sexe, les CSP, etc. De plus, ces résultats évoluent
avec le temps.
Ainsi, certains constatent une inflation des notes : mais à quoi
est-elle due ? Pour un même niveau, met-on des notes plus élevées ?
Ou bien les notes sont-elles les mêmes, avec simplement une variance
plus élevée ?
Autre exemple de modèle hiérarchique : Amova ?
Autre exemple : élevage (groupe = étalon qui a servi de père)
HLM: Hiearchical Linear Modeling
Modèles linéaires : les observations sont sensées être indépendantes.
Modèles mixtes : les observations ne sont pas indépendantes.
Première présentation des modèles hiérarchiques :
y ~ x | Sujet, outer = ~ groupe
On commence par faire une régression y ~ x pour chaque sujet.
Ensuite, on prend les coefficients qu'on a obtenus (dans l'exemple
ci-dessus, a pour l'ordonnée à l'origine et b pour la pente) et on
regarde s'ils dépendent du groupe : a ~ groupe et b ~ groupe.
On peut faire la même chose avec une régression logistique.
Modèles mixtes et hiérarchiques : il y a plusieurs notions de
résidus. Mais les erreurs sur ces résidus sont d'autant plus
nombreuses que le modèle est complexe (dans la cadre classique, les
résidus sont une approximation des termes de bruit, mais ici, il y a
plusieurs termes de bruit, qui se mélangent tous un peu...).
Modèles hiérarchiques : Les observations sont "groupées" et on
connait ces groupes. (On pourrait aussi imaginer des situations dans
lesquelles on ne connaitrait pas les groupes...)
Autre introduction possible des modèles mixtes : on a effectué deux
ou trois observations sur quelques milliers de sujets. Notre modèle
suggère de faire une régression linéaire pour chaque sujet (ou une
régression un peu plus complexe) : ça n'est pas possible, car on a
trop peu d'observations par rapport au nombre de paramètre. On peut
se dépétrer de cette situation en supposant que ces paramètres,
qu'on cherchent, ont une certaine distribution. (C'est un point de
vue bayesien.) On ne s'intéresse alors plus aux paramètres de chaque
sujet, mais simplement aux paramètres de cette distribution.
HLM = Multilevel Analysis (je crois)
Voici un lexique de "Multilevel Analysis" :
http://www.paho.org/English/DD/AIS/be_v24n3-multilevel.htm
http://cran.r-project.org/doc/contrib/rpsych.html
On considère trois évènements, A,B et C. S'ils sont indépendants, on a
P(A, B, C) = P(A) * P(B) * P(C).
Mais ces évènements peuvent être liés, par exemple :
Si A est vrai, alors B a une probabilité plus forte. Si B est vrai, alors C a une probabilité plus forte.
Cela peut se modéliser ainsi :
P(A,B,C) = P(A) * P(B|A) * P(C|A).
Dans des situations plus complexes, ce serait plus difficile à lire : on peut représenter ces dépendances par un graphique :
A ---> B ---> C
Voici une autre situation possible :
Si A est vrai, Alors B est plus probable. Si C est vrai, Alors B est plus probable. P(A,B,C) = P(A) * P(C) * P(B|A,C) A ---> B <--- C
On peut représenter graphiquement les relations de dépendance entre des varaibles A, B, C, D, E de la manière suivante.
1. Choisir un ordre sur ces variables.
2. Simplifier le plus possible l'écriture
P(A,B,C,D,E) = P(A) * P(B|A) * P(C|A,B) * P(D|A,B,C) * P(E|A,B,C,D),
par exemple :
P(A,B,C,D,E) = P(A) * P(B|A) * P(C) * P(D|B,C) * P(E|A,C)
3. Dessiner le graphe dont les sommets sont les variables et avec une arrête x ---> y si P(y|...x...) apparaît dans la formule ci-dessus.
Dans notre exemple, on aurait :
E <--- A <--- B ^ | | | | V C ----------> D
Le problème, c'est que ça dépend de l'ordre qu'on a choisi au début. S'il est bien choisi, l'information sera concise et facilement interprétable. Sinon...
En particulier, si on connait certaines relations causales entre nos variables on choisira un ordre qui les respecte -- et si on n'en a oublié aucune, le réseau ne contiendra rien d'autre.
Ce graphe n'est pas encore utilisable : il faut encore lui ajouter des probabilités. Dans l'exemple précédent, il s'agit des distributions de A, B|A, C, D|BC et E|AC.
Un tel graphe permet alors de calculer toutes les probabilités conditionnelles qui font intervenir ces variables.
Par exemple :
P(A) P(A) P(A)
P(A|EB) = -------- = --------------------- = --------------------
P(ABE) P(B) P(A|B) P(E|AB) P(B) P(A|B) P(E|A)On peut formaliser les manipulations qu'on vient de faire, afin qu'un ordinateur puisse effectuer ces calculs ; on peut aussi recourrir à des algorithmes qui modifient le graphe pour faciliter le calcul (appliquer la formule de Bayes revient à changer le sens d'une des arrêtes).
Comme expliqué succintement dans le paragraphe sur l'anova within, il faut faire très attention au choix du modèle et aux termes d'erreur.
Dans un modèle du genre
Y(i,j,k) = mu + A(i) + B(j) + C(k) + Erreur(i,j,k)
l'ordre dans lequel on écrit les termes est important. Ainsi, dans l'exemple suivant,
n <- 100 a <- rnorm(n) b <- rnorm(n) y <- 1 -.2*a + .3*b + rnorm(n) anova(lm(y~a+b)) anova(lm(y~b+a))
les tables d'anova sont
Df Sum Sq Mean Sq F value Pr(>F) a 1 3.356 3.356 3.0749 0.08267 . b 1 21.165 21.165 19.3924 2.741e-05 *** Residuals 97 105.866 1.091
et
Df Sum Sq Mean Sq F value Pr(>F) b 1 19.753 19.753 18.0991 4.837e-05 *** a 1 4.767 4.767 4.3682 0.03923 *
Dans le premier cas, l'influence de a n'est pas significative (à 5%), mais elle l'est dans le second.
Je ne sais pas exactement ce que cela implique pour l'interprétation du résultat d'une analyse de la variance. Si les résultats sont vraiment très significatifs, il n'y a pas de problème, ils le resteront même si on change l'ordre des variables. Par contre, s'ils sont moyennement significatifs, on peut espérer pouvoir faire dire ce que l'on veut à l'analyse de la variance rien qu'en changement l'ordre -- c'est encore une autre idée d'utilisation des statistiques pour manipuler les gens.
L'analyse de la variance suppose que les variables sont normales et équivariantes (dans les exemples ci-dessus, les variables n'étaient pas toujours normales...). Si ce n'est pas le cas, on peut la remplacer par le test de Kruskal et Wallis.
?kruskal.test
Si l'analyse de la variance nous a dit que les moyennes n'étaient pas égales, il faut encore savoir lesquelles sont différentes. On pourrait penser à faire des tests de Student pour tous les couples de classes, afin de trouver quelles moyennes sont sensiblement différentes. Mais il y a un gros problème : cela fait grimper le risque d'erreur de type I...
Il y a d'innombrables méthodes pour faire ces tests en réduisant ce risque (Bonferroni, HSD de Tukey, LSD de Fisher, Scheffe), qui tournent quand même autour des tests de Student, mais on prend toute la population pour évaluer les variances, et on ne fait pas des tests à 95% -- en fait, je ne comprends pas les différences entre ces différentes méthodes.
A FAIRE :
1.
Si on prend la décision de faire certains tests avant de regarder
les données (peu réaliste, sauf, éventuellement si on décide de
faire tous les tests).
1a. Une seule comparaison : test T de student
1b. quelques comparaisons : ajustement de Bonferroni du test T de
Student : on fait un test T avec une valeur critique alpha/m au lieu
de alpha, où m est le nombre de tests.
A FAIRE : justifier et critiquer
Regarder expérimentalement min(p-valeurs de tests de Student) ~ p-valeur
de l'anova correspondantes.
On n'a pas p-valeur de l'anova = m * p-valeur de student.
(car des pourcentages, ça ne s'ajoute pas).
C'est pourtant l'ajustement de Bonferronni.
On a néanmoins : p-valeur de l'anova < m * p-valeur de student
Et, pour des p-valeurs faibles, c'est une bonne approximation.
Si les tests étaient indépendants, on pourrait multiplier :
p ---> 1 - (1-p)^m
Mais les tests ne sont pas indépendants.
C'est pourtant l'ajustement de ????
On a néanmoins : p-valeur de l'anova < 1 - (1-p)^m
On peut vérifier tout cela à l'aide de simulations
N <- 1000
n <- 20 # Taille des échantillons
k <- 4 # Nombre d'échantillons
res <- matrix(NA, nr=N, nc=2)
for (a in 1:N) {
x <- factor(rep(1:k,1,each=n))
y <- rnorm(k*n)
res[a,1] <- summary(aov(y~x))[[1]][1,5]
p <- 1
for (i in 1:(k-1)) {
for (j in (i+1):k) {
p <- min(c( p, t.test(y[x==i],y[x==j])$p.value ))
}
}
res[a,2] <- p
}
plot(res, xlab="p-valeur (anova)", ylab="p-valeur (tests de Student multiples)")
plot(sort(res[,1]), main="p-valeurs (anova)") abline(0,1/N, col='red')

plot(sort(res[,2]), main="p-valeurs (tests de Student multiples)") abline(0,1/N, col='red')

plot(sort(k*(k-1)/2*res[,2]), ylim=c(0,1), main="p-valeurs (Bonferronni)") abline(0,1/N, col='red')

plot(sort(1-(1-res[,2])^(k*(k-1)/2)), main="p-valeurs (correction de ???)") abline(0,1/N, col='red')

Regardons ce qui se passe si les tests sont beaucoup plus nombreux :
# Très, très long...
N <- 1000
n <- 20 # Taille des échantillons
k <- 20 # Nombre d'échantillons
res <- matrix(NA, nr=N, nc=2)
for (a in 1:N) {
x <- factor(rep(1:k,1,each=n))
y <- rnorm(k*n)
res[a,1] <- summary(aov(y~x))[[1]][1,5]
p <- 1
for (i in 1:(k-1)) {
for (j in (i+1):k) {
p <- min(c( p, t.test(y[x==i],y[x==j])$p.value ))
}
}
res[a,2] <- p
}
op <- par(mfrow=c(2,2))
plot(res, xlab="p-valeur (anova)", ylab="p-valeur (tests de Student multiples)")
# plot(sort(res[,1]), main="p-valeurs (anova)")
# abline(0,1/N, col='red')
plot(sort(res[,2]), ylim=c(0,1), main="p-valeurs (tests de Student multiples)")
abline(0,1/N, col='red')
abline(h=.05, lty=3)
plot(sort(k*(k-1)/2*res[,2]), ylim=c(0,1), main="p-valeurs (Bonferronni)")
abline(0,1/N, col='red')
abline(h=.05, lty=3)
plot(sort(1-(1-res[,2])^(k*(k-1)/2)), main="p-valeurs (correction de ???)")
abline(0,1/N, col='red')
abline(h=.05, lty=3)
par(op)
On pourrait essayer de tatonner pour trouver une transformation,
mais on n'est plus assuré que la p-valeur annoncée est supérieure à
la p-valeur réelle...
op <- par(mfrow=c(4,4))
for (i in seq(50,200,length=16)) {
plot(sort(1-(1-res[,2])^i), main=paste(
"p-valeurs (correction exposant = ",round(i),")", sep='') )
abline(0,1/N, col='red')
abline(h=.05, lty=3)
}
par(op)
2.
La plupart du temps, on décide de faire des tests après avoir
regardé les données et fait l'anova. On va par exemple vouloir
savoir si les valeurs des paramètres ai et aj sont significativement
différentes -- on ne fait pas ça pour tous les couples (i,j), mais
uniquement pour ceux pour lesquels la différence est importante.
2a. LSD de Tukey : on calcule un intervalle de confiance pour ai-aj :
ai-aj \pm t _{n-I} ^{alpha/2} \hat sigma (1/Ji-1/Jj)
où I est le nombre de niveaux de la variable prédictive,
Ji est le nombre d'observations avec X=i
Le problème, c'est que c'est très faux.
2b. LSD de Fisher
Idem, mais avant, on fait un test de F pour voir si tous les
coefficients sont égaux.
Le problème, c'est que c'est toujours faux : la distribution de la
différence entre le plus petit coefficient et le plus grand ne suit
pas une distribution de T.
2c. HSD de Tukey (Honest Significant Difference)
On utilise la bonne distribution.
TukeyHSD(aov(...))
A FAIRE
?qtukey
A FAIRE : relire le dernier chapitre du livre de Faraway.
Les commande p.adjust, pairwise.t.test (et même pairwise.*)
permettent de faire ce genre de chose.
A FAIRE :
library(help=multcomp)
Correction des p-valeurs :
library(multcomp)
rawp <- 2 * (1 - pnorm(abs(teststat)))
procs <- c("Bonferroni", "Holm", "Hochberg", "SidakSS", "SidakSD",
"BH", "BY")
res <- mt.rawp2adjp(rawp, procs)
adjp <- res$adjp[order(res$index), ]
adjp
A FAIRE : des graphiques qui comparent ces différentes corrections.
A FAIRE : donner des exemples de situations dans lesquelles on veut
réellement faire des tests très nombreux.
1. Cartographie du génome
2. Analyse de résultats de puces à ADN.
A FAIRE : comprendre
3. Contrastes
Un contraste, c'est une combinaison linéaire des effets
(=coefficients de la régression) dont la somme des coefficients est
nulle. Par exemple << a1 - a2 >> ou << (a1+a2)/2 - (a3+a4)/2 >>.
On peut être amené à poser des questions plus complexes que <<
est-ce que ai=aj >> (auxquelle on peut répondre par le HSD de Tukey)
: des questions du genre << tel contraste est-il nul ? >>. Cela
revient à comparer plus de deux effets en même temps.
Le théorème de Scheffé donne des intervalles de confiance pour ces
contrastes.
A FAIRE : expliquer comment
A FAIRE : donner une interprétation géométrique
(je crois avoir compris la chose suivante : un contraste définit un
hyperplan, l'intervalle de confiance s'obtient à l'aide de
l'ellipsoïde de confiance en le coupant par une droite orthogonale à
cet hyperplan).
A FAIRE
FWER: Family-Wise type-I Error Rate
FDR: False Discovery Rate
R: L'ordre dans les facteurs d'une Anova : il change les résultats si les classes n'ont pas toutes le même effectif. R: Anova ?reshape ?aggregate ?stack
A FAIRE longitudinal data repeated measures data, multilevel data split-plot designs
A FAIRE
Analyse de la variance à un facteur
Données : une variable quantitative, une variable qualitative (à beaucoup de valeurs)
Test préliminaire : les données ont-elles l'air normales ?
boxplot, histogrammes (lattice), qqnorm
Test préliminaire : équivariance (test.bartlett)
Analyse de la variance
S'il y a lieu : tests post-hoc
A FAIRE
REML: Restricted Maximum Likelihood
Exemples :
EM algorithm (first derivatives)
Fischer Scoring (2nd derivatives)
Derivative Free
Average Information algorithm
Design matrix: the matrix X in "Y = X b + e"
Mixed model: Y = X b + Z u + e
Fixed effects: the term "X b"
Random effects: the term "Z u"
Y, X et Z sont connus.
On cherche b.
On considère u et e comme du bruit (on peut bien sûr les estimer,
mais dans les tests on les considèrera comme du bruit).
Si on veut juste trouver b, sans chercher d'information sur u,
sans vouloir faire de test, on peut tout aussi bien faire une
régression linéaire usuelle : Y ~ cbind(X,Z)
Quand on regarde le modèle mixte, on s'intéresse aussi à la variance
(en fait, la matrice de variance-covariance) de u.
Mixed model: Y_ijk = a_i + (b_j + e_ijk) où le terme entre
parenthèses est considéré comme du bruit.
estimation: find b (the fixed effects)
prediction: find u (the random effects)
BLUE: Best Linear Unbiased Estimator
BLUP: Best Linear Unbiased Prediction
Mixed model:
library(nlme)
nlme(y~x1+x2, fixed=x1~1, random=x2~1)
A FAIRE : quelques simulations pour montrer que c'est réellement
différent de l'anova usuelle...
Il y a moins de paramètres à estimer.
Examples of grouped data (y~x|group, where x may be time, a factor, or a continuous variable) include
longitudinal data,
repeated measures data,
multilevel data,
split-plot designs.
Grouped data: something that looks like
library(nlme)
data(Orthodont)
formula(Orthodont)
plot(Orthodont)
plot(Orthodont, outer=T)

data(Machines) bwplot(score~Machine|Worker, data=Machines)

data(CO2) plot(CO2)

plot(CO2, outer=T)

Le type de données groupedData permet de mettre une formule avec les
données.
groupedData(y~x|z1, data=d, outer=~z2)
(ici, on a un plan d'expérience hiérarchique : la valeur de z2 est
entièrement déterminée par z1).
outer = ~z2*z3
outer = list(~z2, ~z3) (non testé)
Exemples de modèles mixtes :
1. On effectue plusieurs observations (x,y) pour chaque individu, on
constate, graphiquement, que y~x est linéaire pour chaque individu,
mais avec une pente et une ordonnée à l'origine différente. On
cherche la "pente moyenne" et l'"ordonnée à l'origine moyenne".
y_ij = (a + a_i) + (b + b_i) * x_ij + c_ij
i = numéro de l'individu
j = numéro de l'observation chez cet individu
a_i, b_i, c_ij sont les termes de bruit
a et b sont les quantités à estimer.
2. Variante : les individus sont regroupés en deux classes. On peut
calculer la pente moyenne et l'ordonnée à l'origine moyenne de
chacune de ces classes. Sont-elles sensiblement différentes ?
y_ijk = (a_k + a_ik) + (b_k + b_ik) * x_ijk + c_ijk
i = numéro de l'individu
j = numéro de l'observation chez cet individu
k = classe de cet individu (chaque individu appartient à une seule
classe, dont k est entièrement déterminé une fois qu'on
connait i)
a_ik, b_ik, c_ijk sont les termes de bruit
a_k, b_k sont les quantités à déterminer
H0: a_1=a_2 et b_1=b_2
H1: a_1 \neq a_2 et b_1 \neq b_2
A FAIRE : donner des exemples de modèles,
avec éventuellement des exercices.
test du quotient de vraissemblance
r1 <- lme(...)
r1 <- update(r1, method="ML") # Sinon, c'est REML, le test n'a pas de sens
...
anova(r1,r2)
Graphiques :
plot(r, resid(.,type="p") ~ fitted(.) | z)
predict
(un peu différent à cause des effets aléatoires)On commence par regarder les données (pour voir d'éventuelles erreurs).
data(InsectSprays) y <- InsectSprays$count x <- InsectSprays$spray boxplot(y~x, col='pink')

Regardons si elles sont normales.
library(lattice) histogram(~ y | x)

qqmath(~ y | x) # A FAIRE : ajouter qqmathline

On peut aussi effectuer des tests plus formels.
n <- length(levels(x))
res <- matrix(NA, nr=n, nc=2)
colnames(res) <- c('raw p-value', 'Bonferroni-corrected p-value')
rownames(res) <- levels(x)
for (i in 1:n) {
p <- shapiro.test(y[ x == levels(x)[i] ])$p.value
res[i,] <- c(p, min(c(1,n*p)))
}
resIl vient
raw p-value Bonferroni-corrected p-value A 0.749 1.000 B 0.641 1.000 C 0.048 0.286 D 0.003 0.016 E 0.297 1.000 F 0.101 0.605
L'échantillon D pose un léger problème :
> y[ x=='D' ] [1] 3 5 12 6 4 3 5 5 5 5 2 4
La valeur 12 semble très élevée par rapport aux autres :
> shapiro.test(y[ x=='D' ][-3])
Shapiro-Wilk normality test
data: y[x == "D"][-3]
W = 0.8978, p-value = 0.1735On effectuera donc l'analyse avec cette valeur et sans elle.
A FAIRE... i <- which( (x != 'D') | (y != 12) ) xx <- x[i] yy <- y[i]
Il convient aussi de vérifier que les échantillons ont la même variance.
> bartlett.test(y~x)
Bartlett test for homogeneity of variances
data: y by x
Bartlett's K-squared = 25.9598, df = 5, p-value = 9.085e-05
> bartlett.test(yy~xx)
Bartlett test for homogeneity of variances
data: yy by xx
Bartlett's K-squared = 36.8992, df = 5, p-value = 6.275e-07On a donc un gros problème...
A FAIRE : idée 1 : corriger les données ??? idée 2 : passer à une analyse de la variance non paramétrique idée 3 : ne rien faire et ignorer le problème (on aura les mêmes conclusions)
Passons maintenant à l'analyse de la variance : avec la fonction lm ou aov.
r1 <- anova(lm(y~x)) r2 <- summary(aov(y~x))
Les résultats sont les mêmes
> r1
Analysis of Variance Table
Response: y
Df Sum Sq Mean Sq F value Pr(>F)
x 5 2668.83 533.77 34.702 < 2.2e-16 ***
Residuals 66 1015.17 15.38
> r2
Df Sum Sq Mean Sq F value Pr(>F)
x 5 2668.83 533.77 34.702 < 2.2e-16 ***
Residuals 66 1015.17 15.38Cela nous dit que les moyennes dans les différents groupes sont effectivement différentes.
Pour savoir où sont les différences, on peut effectuer des tests de Student. Mais attention : comme il y en a beaucoup (15), il convient de corriger les p-valeurs.
n <- length(levels(x))
res <- matrix(NA, nr=n, nc=n)
rownames(res) <- levels(x)
colnames(res) <- levels(x)
for (i in 2:n) {
for (j in 1:(i-1)) {
res[i,j] <- t.test( y[ x == levels(x)[i] ], y[ x == levels(x)[j] ] )$p.value
}
}
#res <- res * n*(n-1)/2; res <- ifelse(res>1,1,res)
res <- 1 - (1-res)^n
image(res, col=topo.colors(255)) # A FAIRE : peu lisible
# Ecrire une fonction qui dessine des matrices
# de distance, de corrélation, de p-valeurs.
# Avec le nom des lignes/colonnes, avec une légende
# pour les couleurs
round(res,3)
Il vient :
A B C D E F A B 0.998 C 0.000 0.000 D 0.000 0.000 0.034 E 0.000 0.000 0.375 0.545 F 0.923 0.991 0.000 0.000 0
Cela suggère une partition en deux groupes : ABF et DCE.
On remarque que C et E ne sont pas significativement différents, E et D non plus, mais C et D si (enfin, pas trop : à 5%, mais pas à 1%).
On peut représenter cela graphiquement en transformant les p-valeurs en distances entre les groupes.
d <- 1-res d <- ifelse(is.na(d), t(d), d) diag(d) <- 0 p <- isoMDS(d)$points plot(p, pch=16) text(p, levels(x), pos=c(1,2,1,1,1,3))

Il existe déjà une fonction qui fait ces calculs :
TukeyHSD(aov(y~x))
Cela nous redonne les groupes ABF et CDE.
> TukeyHSD(aov(y~x))
Tukey multiple comparisons of means
95% family-wise confidence level
Fit: aov(formula = y ~ x)
$x
diff lwr upr
B-A 0.8333333 -3.866075 5.532742
C-A -12.4166667 -17.116075 -7.717258
D-A -9.5833333 -14.282742 -4.883925
E-A -11.0000000 -15.699409 -6.300591
F-A 2.1666667 -2.532742 6.866075
C-B -13.2500000 -17.949409 -8.550591
D-B -10.4166667 -15.116075 -5.717258
E-B -11.8333333 -16.532742 -7.133925
F-B 1.3333333 -3.366075 6.032742
D-C 2.8333333 -1.866075 7.532742
E-C 1.4166667 -3.282742 6.116075
F-C 14.5833333 9.883925 19.282742
E-D -1.4166667 -6.116075 3.282742
F-D 11.7500000 7.050591 16.449409
F-E 13.1666667 8.467258 17.866075A FAIRE : terminer ???
Notes prises en lisant le document
http://cran.r-project.org/doc/contrib/Fox-Companion/appendix-mixed-models.pdf
Le modèle linéaire suppose que les observations sont indépendantes ; mais parfois, les observations peuvent être regroupées : les observations de groupes différents sont effectivement indépendantes, mais par contre, les observations d'un même groupe sont corrélées.
A FAIRE : un exemple de simulation. A FAIRE : un exemple de situation réelle... L'influence des variables prédictives n'est pas la même dans les différents groupes. A FAIRE : quelques graphiques expliquant dans quelles situations il faut penser à un modèle mixte.
Fonctions sous R :
lme: modèles linéaires mixtes
nlme: modèles non linéaires mixtes
Pas encore de modèle linéaire mixte généralisé.
En attendant, utiliser glmmPQL dans MASS.On représente souvent les modèles mixtes sous une forme hiérarchique.
L'argument "panel" :
xyplot(mathach ~ ses | school, data=Pub.20, main="Public",
panel=function(x, y){
panel.xyplot(x, y)
panel.loess(x, y, span=1)
panel.lmline(x, y, lty=2)
}
)Première étape de l'analyse d'un modèle mixte : on fait une régression dans chaque groupe (en d'autres termes, on considère que tous les effets sont aléatoires).
A FAIRE : graphique (xyplot(y~x|g,...)) r <- lmList(y~x|g) plot(intervals(r))
On voit quels sont les effets constants et les effets aléatoires (i.e., quelles sont les variables prédictives dont l'effet est le même dans tous les groupes et celles dont l'effet change d'un groupe à l'autre).
On calcule la régression à l'aide de la commande lme :
r <- lme(y ~ effets constants,
random = ~ effets aléatoires | groupe,
)
r
summary(r)
intervals(r)
plot(r)???A FAIRE : détailler la manière dont ce résultat est affiché. (residual=écart-type, corrélations, etc.)
Questions qu'on peut se poser sur une telle régression :
1. (Comme pour une régression normale) Tel coefficient est-il significativement non nul ? Intervalle de confiance ? 2. Un effet aléatoire est-il réellement aléatoire ? En d'autres termes, une variable prédictive, dont on pense qu'elle a un effet différent dans les différent groupes, a-t-elle réellement un effet différent dans les différents groupes ? Pour cela, on regarde si la variance du coefficient qui lui correspond est significativement différente de zéro. On fait ça en comparant des modèles, à l'aide de la commande anova. A FAIRE : ils ont utilisé REML et ils comparent quand-même la vraissemblance ???
Comparaison de deux modèles mixtes : on demande qu'ils soient calculés à l'aide du maximum de vraissemblance (par défaut, c'est REML) et on les donne à la commande anova.
A FAIRE : différentes complications du modèle simpliste que j'ai présenté.
1. Plusieurs effets aléatoires : ils sont corrélés. Matrice de covariance. 2. Des groupes dans les groupes...
A FAIRE
A FAIRE : sous R ??? ?manova ?summary.manova
Il y a plusieurs variables quantitatives à expliquer à l'aide d'une (ou plusiseurs) variable(s) qualitative(s). La statistique du test correspondant est celle de Pillai-Bartlett (conseillé) ou le lambda de Wilks (multivariate F) (déconseillé mais populaire) ou celle de Hotelling-Lawley ou celle de Roy.
C'est une mauvaise idée de faire (directement) plusieurs analyses de la variance, d'une part car on effectuerait plusieurs tests, d'autre part car on ne tiendrait pas compte d'une éventuelle corrélation entre les variables à expliquer (mais il ne faut pas que les variables à expliquer soient trop corrélées : il serait plus simple d'oublier les variables superflues -- A FAIRE).
Le plan d'une analyse de la variance multiple serait :
1. Vérifier les hypothèses 2. Faire une Manova pour savoir s'il y a un effet 3. S'il y a un effet, regarder les variables à expliquer une par une (avec une anova classique). 4. Faire des tests post hoc et quantifier ces effets. A FAIRE : trouver (fabriquer ?) un exemple. A FAIRE : plusieurs variables prédictives A FAIRE : plusieurs variables prédictives dont certaines quantitatives.
Hypothèses de la manova : variables normales, homogénéité des variances, homogénéité des covariances.
library(car)
?Anova
options(contrasts=c("contr.sum", "contr.sum")) ????
r <- lme(y ~ x2, random = ~ 1 | x1 )
summary(r)
fixed.effects(r)
random.effects(r)Vincent Zoonekynd
<zoonek@math.jussieu.fr>
latest modification on Wed Oct 13 22:33:09 BST 2004