The French version of this document is no longer maintained: be sure to check the more up-to-date English version.
Exemple
A FAIRE : reprendre cet exemple, de manière plus complète. Fournir les données sous forme d'un fichier. Fournir les valeurs des xi pour Ajouter des données manquantes, des données aberrantes. Dans la modélisation, proposer plusieurs méthodes et expliquer comment les comparer (avec du bootstrap). (en particulier : régression avec ou sans transformation des données, en remplaçant les données manquantes par la moyenne/médiane ou en enlevant les observations, en prenant toutes les variables ou en effectuant une sélection, avec une régression linéaire ou avec des splines, avec des svm à la place de la régression, etc.)
Considérons les données suivantes
y x1 x2 x3 x4 x5 1 0.17737252 0.255593371 -0.01877868 55.041698 1.06486649 1.601552 2 0.12867410 0.960419271 -0.19436940 1.198466 1.29289552 1.746549 3 0.13069250 0.863139268 -1.75373604 1.235540 1.62006050 1.474043 4 0.24660910 0.545280691 0.77253952 1.729689 -0.96193294 1.819215 5 0.06068440 0.678051326 -0.52889122 6.262365 2.02333474 2.784879 6 0.01562173 0.751754458 -1.15476842 1.525834 3.45646388 1.621467 7 0.12855980 0.440126896 0.48876004 3.591808 0.93048007 2.760134 8 0.01311403 0.387135598 -1.14240969 2.416364 3.60703700 1.664418 9 0.12805800 0.084511305 -1.35014687 5.811351 1.44654008 2.129711 10 0.07289424 0.216225055 1.94773238 1.629576 1.66476647 1.243259 11 0.20015592 0.375460150 -0.10764990 33.271750 0.60030701 2.554126 12 0.00967752 0.420041527 -0.69493709 15.786367 3.91269188 2.943540 13 0.18532207 0.252310834 -0.16696766 1.652677 1.09072717 1.570431 14 0.14099584 0.666372093 0.76253962 1.060118 0.34173217 1.363799 15 0.07331360 0.048310076 0.04428767 1.743556 1.92284974 1.517609 16 0.39708878 0.323382935 0.95223442 2.270229 -0.41723736 1.550922 17 0.12408025 0.044613951 0.41033758 3.831911 1.31146354 1.636827 18 0.12769826 0.053085268 0.59687579 1.908977 1.10201039 1.550858 19 0.20857330 0.972532847 -0.90311733 1.290658 1.26966839 1.447662 20 0.15594300 0.081915355 -1.15742730 1.405443 1.05322479 2.940306 21 0.37840463 0.649070143 -0.35228245 1.917989 0.36974761 1.356612 22 0.66522777 0.260343743 -2.47825418 4.795896 0.54582777 1.162321 23 0.63918773 0.513310948 -0.14159619 1.332781 -0.26621952 2.991911 24 0.11260928 0.543954646 1.06146044 6.681447 1.07751157 2.989188 25 0.09960026 0.403813454 0.55095958 7.279781 1.50800580 1.611078 26 -0.61535539 0.706742991 -1.20051134 7.564472 -0.56472250 2.157740 27 0.24971773 0.748126270 -0.26498237 1.117801 0.73077297 2.904779 28 0.06268585 0.764109087 -2.05296785 1.218234 2.24522236 2.527298 29 0.22153778 0.402428063 1.43230181 2.624402 -0.52847371 2.189166 30 0.21088420 0.497645303 1.47542866 1.518825 -0.19523074 1.472104 31 0.13608028 0.291170579 -1.46970914 1.516058 1.34040053 1.863857 32 0.75431108 0.478386517 0.31657036 1.225444 -0.58215047 2.218527 33 0.05093748 0.331470089 -0.07112817 1.007887 2.24270617 2.430400 34 0.04495159 0.261359577 1.14768074 13.174180 2.27230911 1.753251 35 0.19566843 0.129011235 0.32604949 2.475796 0.66536288 2.146549 36 0.46863291 0.067206315 0.86525243 1.208705 -0.62951123 2.062168 37 -1.74756315 0.378743229 -1.25873494 1.179726 -0.85146758 2.799012 38 0.04493936 0.617941440 0.10186404 1.103134 2.36010564 1.245357 39 0.08532079 0.659343313 1.47558024 1.515066 1.19388336 1.649593 40 0.10020669 0.203460848 -0.44762778 3.175103 1.38946612 2.967908 41 -16.03253190 0.110310319 0.01567256 2.266611 -0.26535524 2.495451 42 0.14614080 0.009384898 -0.22534736 15.678337 1.06682652 2.379440 43 0.16193855 0.985065327 0.28556123 5.103220 0.16327102 1.808208 44 0.04025704 0.749261997 0.65743242 4.235644 2.39118753 2.013844 45 -0.49303230 0.664672238 -1.42673466 1.111907 -0.73723968 1.532473 46 0.15835584 0.149211494 -0.23719301 3.172205 0.86034783 2.481339 47 0.27790539 0.165996711 0.64921865 3.399877 -0.06153391 2.339315 48 0.12971347 0.387604755 0.38543904 4.045104 1.05940996 2.211520 49 0.04955036 0.417031078 0.43766860 5.399120 2.17897848 2.339830 50 0.41876667 0.131038313 0.48986874 4.725115 0.33483485 1.238809
et essayons de prédire y à partir de x1, x2, x3, x4 et x5.
m <- read.table("faraway")
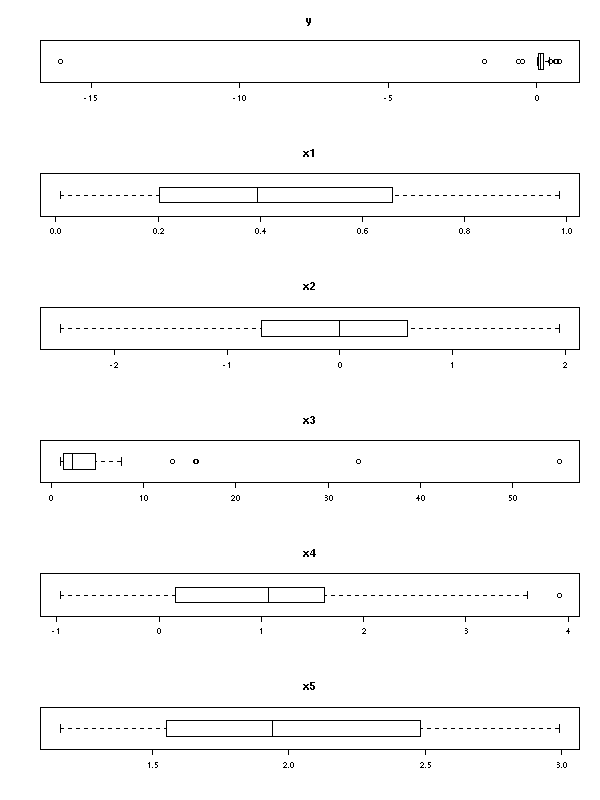
op <- par(mfrow=(c(6,1)))
for (i in 1:6) {
boxplot(m[,i], horizontal=T, main=names(m)[i])
}
par(op)
m <- read.table("faraway")
op <- par(mfrow=(c(3,2)))
for (i in 1:6) {
hist(m[,i], col='light blue', probability=T, xlab=names(m)[i])
lines(density(m[,i]), col='red', lwd=2)
}
par(op)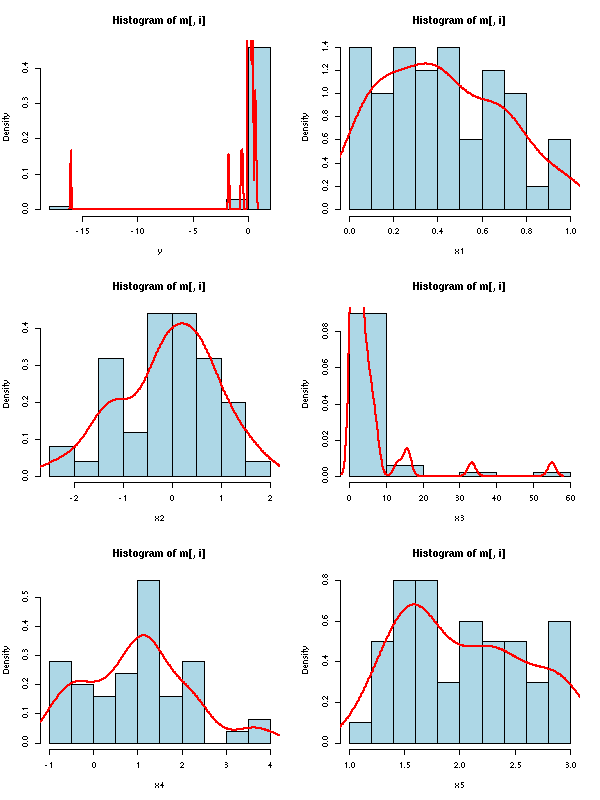
m <- read.table("faraway")
op <- par(mfrow=(c(3,2)))
for (i in 1:6) {
qqnorm(m[,i], main=names(m)[i])
qqline(m[,i], col='red')
}
par(op)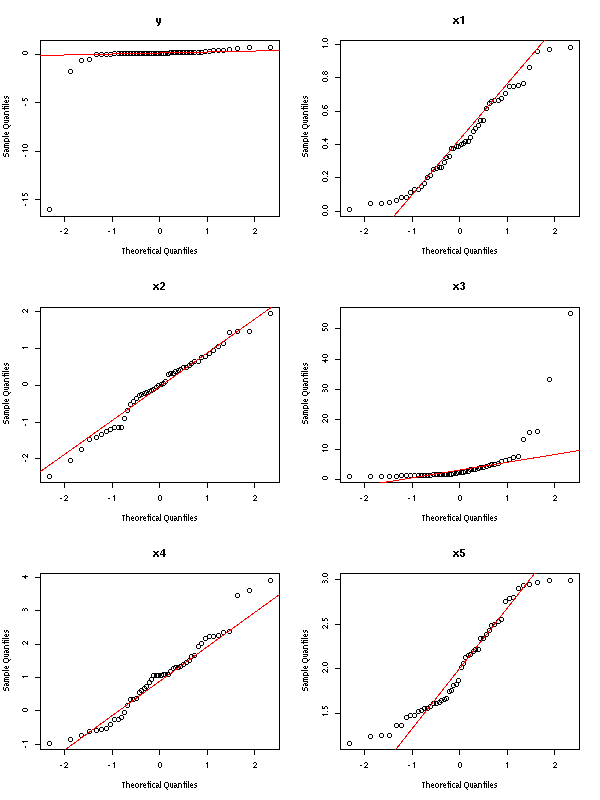
On constate que y et x3 ont besoin d'être transformées.
A FAIRE : trouver la transformation A FAIRE : refaire les graphiques précédents (juste pour y et x3) A FAIRE : regarder s'il reste des points atypiques -- si c'est le cas, les enlever. A FAIRE
J'ai repris cet exemple du livre de Faraway, qui dit l'avoir donné en exercice à ses étudiants et avoir constaté d'énormes différences entre leurs résultats. Le modèle est le suivant :
faraway.sample <- function (n=50) {
n <- 50
x1 <- runif(n)
x2 <- rnorm(n)
x3 <- 1/runif(n)
x4 <- rnorm(n,1,1)
x5 <- runif(n,1,3)
e <- rnorm(n)
y <- 1/(x1+.57*x1^2+4*x1*x2+2.1*exp(x4)+e)
data.frame(y,x1,x2,x3,x4,x5)
}
A FAIRE : regarder la qualité de mes prédictions, la comparer avec celles mentionnées dans le livre de Faraway.
Vincent Zoonekynd
<zoonek@math.jussieu.fr>
latest modification on Wed Oct 13 22:33:04 BST 2004