The French version of this document is no longer maintained: be sure to check the more up-to-date English version.
Introduction
Sélection des variables en classification non supervisée
A FAIRE
Sélection de variables et régression
Réduction de la dimension
SVM (Support Vector Machines)
GAM (Generatized Additive Model)
Classification et arbre de régression (CART (TM))
PRIM (Patient Rule Induction Method, aka Bump Hunting)
Bagging (bootstrap aggregation)
Boosting
Ensemble methods
Random Forest
Détection des valeurs atypiques
Réseaux de neurones
Réseaux bayesiens
MARS (Multivariate Adaptative Regression Splines)
HME (Hierarchical Mixture of Experts)
MART
A FAIRE : classer ce qui suit
A FAIRE : mettre cette partie après les autres formes de régression (logistique, Poisson, ordonnée, multilogistique).
A FAIRE : écrire cette partie
A FAIRE : je parle surtout de modèles non linéaires en dimension élevée, mais que faire quand il y a plus de variables que d'observations ??? Si, il y a les svm.
Nous avons déjà évoqué la malédiction de la dimension : que faire quand on a plus de variables que d'observations ? que faire quand on veut une régression non linéaire avec un nombre de variables démesuré ? Dans ces deux cas, si on tente de généraliser les méthodes valables en petite dimension, on se retrouve avec un nombre de paramètres à estimer (très) supérieur au nombre d'observations (ou même légèrement inférieur à) : les estimations de ces paramètres seront farfelues.
On peut contourner ce problème en cherchant d'autres modèles, plus simples, avec moins de paramètres à estimer, mais néanmoins suffisemment complexes pour décrire la situation.
Les méthodes de régression suivantes se situent entre la régression linéaire (pertinente quand il y a vraiment peu d'observations ou quand elles sont très bruitées) et la régression non linéaire multidimentionnelle (inutilisable car il y a trop de paramètres à estimer). Elles permettent de se débarasser de la malédiction de la dimension. Ainsi, nous parlerons de sélection des variables, de régression sur les composantes principales (ainsi que la ridge regression, le lasso, les moindres carrés partiels), les modèles additifs généralisés, les algorithmes à base d'arbres (CART, MARS).
A FAIRE : indiquer le plan de ce chapitre
plan possible de ce chapitre : Sélection de variables Modèles additifs généralisés : GAM, ACE? AVAS? Arbres: CART, MARS bootstrap: bagging, boosting
Remarque : toutes les méthodes que nous exposerons ne semblent pas implémentées sous R.
Face à des données réelles comportant un nombre de variables très élevé, on commencera généralement par réduire la dimension, par exemple en sélectionnant certaines des variables.
Mais je ne sais pas du tout comment on fait.
A FAIRE
Voici néanmoins quelques idées (Attention : elles ne sont peut-être pas pertinentes).
Faire une analyse en composantes principales et l'"arrondir". Prendre les dimensions une par une et essayer de voir s'il y a un amas ou plusieurs, par exemple en essayant de modéliser ces données (univariées) comme un mélange de deux gaussiennes et en se demandant si les moyennes sont significativement différentes. (Si les dimensions ne sont pas trop nombreuses, on peut aussi les regarder à l'oeil nu.) Pour l'apprentissage supervisé, on utiliserait un arbre de décision : adapter cette remarque à l'apprentissage non supervisé (mettre toutes les observations dans la même classe, ajouter d'autres observations, au hasard, dans une deuxième classe).
A CLASSER Sélection des variables pour la prédiction d'une variable qualitative. 1. Faire des anova pour ne retenir que les variables importantes (p-valeur>.05) n <- 100 k <- 5 x <- matrix(rnorm(n*k),nc=k) y <- x[,1] + x[,2] - sqrt(abs(x[,3]*x[,4])) y <- y-median(y) y <- factor(y>0) pairs(x, col=as.numeric(y)+1)

for (i in 1:k) {
f <- summary(lm(x[,i]~y))$fstatistic
f <- pf(f[1],f[2],f[3], lower.tail=F)
print(paste(i, "; p =", round(f, digits=3)))
}
2. Avec les variables retenues, calculer les corrélations avec une
p-valeur (correspondant au test H0:"cor=0").
A FAIRE : un exemple avec des variables colinéaires.
cor(x)
round(cor(x),digits=3)
m <- cor(x)
for (i in 1:k) {
for (j in 1:k) {
m[i,j] <- cor.test(x[,i],x[,j])$p.value
}
}
m
round(m,digits=3)
m<.05
Exercice : écrire une routine d'affichage de la matrice des
corrélation avec des étoiles à côté des corrélations
significativement non nulles.
Quand on a trop de variables prédictives dans une régression (par rapport au nombre d'observations) la première chose qui vient à l'esprit, c'est de se débarasser des variables "en trop". On peut procéder de plusieurs manières.
On peut commencer avec un modèle contenant toutes les variables, retirer celle qui apporte le moins à la régression (celle dont la p-valeur est la plus grande), et continuer jusqu'à ce que toutes les p-valeurs soient en dessous d'un seuil préalablement fixé. On retire les variables une par une, car quand on en a retiré une, les autres p-valeurs changent (nous avons déjà évoqué ce phénomène lors de la régression polynômiales : en général, les variables prédictives ne sont pas orthogonales).
On peut aussi faire le contraire : commencer avec un modèle vide et rajouter les variables les unes après les autres, en ajoutant celle qui a la p-aleur la plus faible.
Enfin, on peut mélanger ces deux méthodes : on commence par ajouter les variables les unes après les autres, puis on essaye d'en retirer, puis on essaye à nouveau d'en ajouter, etc. On arrête quand ça se stabilise ou quand on est fatigué.
Dans la discussion précédente, nous avons utilisé la p-valeur pour décider s'il fallait garder une variable : il existe d'autres critères.
On peut par exemple comparer différents modèles avec une log-vraissemblance pénalisée, par exemple l'AIC (Akaike Information Criterion),
AIC = -2log(vraissemblance) + 2 p
le BIC (Bayesian Information Criterion),
BIC = -2log(vraissemblance) + p ln n
Construisons un exemple.
library(nlme) # Pour la fonction BIC n <- 20 m <- 15 d <- as.data.frame(matrix(rnorm(n*m),nr=n,nc=m)) i <- sample(1:m, 3) d <- data.frame(y=apply(d[,i],1,sum)+rnorm(n), d) r <- lm(y~., data=d) AIC(r) BIC(r) summary(r)
Il vient :
Call:
lm(formula = y ~ ., data = d)
Residuals:
1 2 3 4 5 6 7 8
-0.715513 0.063803 0.233524 1.063999 -0.001007 -0.421912 0.712749 -1.188755
9 10 11 12 13 14 15 16
-1.686568 -0.907378 0.293071 -0.506539 0.644674 2.046780 0.236374 -0.110205
17 18 19 20
0.256414 0.397595 0.052581 -0.463687
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) -0.03322 0.86408 -0.038 0.971
V1 0.76079 1.23426 0.616 0.571
V2 0.60744 0.52034 1.167 0.308
V3 -0.18183 1.09441 -0.166 0.876
V4 0.49537 0.68360 0.725 0.509
V5 0.54538 1.72066 0.317 0.767
V6 -0.16841 0.89624 -0.188 0.860
V7 0.51331 1.25093 0.410 0.703
V8 0.25457 2.05536 0.124 0.907
V9 0.34990 0.82277 0.425 0.693
V10 0.72410 1.26269 0.573 0.597
V11 0.69057 1.84400 0.374 0.727
V12 0.64329 1.15298 0.558 0.607
V13 0.07364 0.79430 0.093 0.931
V14 -0.06518 0.53887 -0.121 0.910
V15 0.92515 1.18697 0.779 0.479
Residual standard error: 1.798 on 4 degrees of freedom
Multiple R-Squared: 0.7795, Adjusted R-squared: -0.04715
F-statistic: 0.943 on 15 and 4 DF, p-value: 0.5902La commande gls nous donne directement l'AIC et le BIC.
> r <- gls(y~., data=d)
> summary(r)
Generalized least squares fit by REML
Model: y ~ .
Data: d
AIC BIC logLik
86.43615 76.00316 -26.21808
...Néanmoins, ces quantités ne sont intéressantes que quand on compare des modèles avec un nombre de variables différent : on voit ici qu'AIC et BIC présentent un minimum si on prend les trois bonnes variables, alors que la log-vraissemblance continue de croître quand on ajoute des variables inutiles (c'est juste un exemple : dans une situation réelle, on n'ajouterait bien évidemment pas les variables dans l'ordre dans lequel elles arrivent).
library(nlme)
n <- 20
m <- 15
d <- as.data.frame(matrix(rnorm(n*m),nr=n,nc=m))
# i <- sample(1:m, 3)
i <- 1:3
d <- data.frame(y=apply(d[,i],1,sum)+rnorm(n), d)
k <- m
res <- matrix(nr=k, nc=5)
for (j in 1:k) {
r <- lm(d$y ~ as.matrix(d[,2:(j+1)]))
res[j,] <- c( logLik(r), AIC(r), BIC(r), summary(r)$r.squared, summary(r)$adj.r.squared )
}
colnames(res) <- c('logLik', 'AIC', 'BIC', "R squared", "adjusted R squared")
res <- t( t(res) - apply(res,2,mean) )
res <- t( t(res) / apply(res,2,sd) )
matplot(0:(k-1), res, type='l',
col=c(par('fg'),'blue','green', 'orange', 'red'), lty=1,
xlab="Nombre de variables")
legend(par('usr')[2], par('usr')[3], xjust=1, yjust=0,
c('log-vraissemblance', 'AIC', 'BIC',
"coefficient de détermination", "coefficient de détermination ajusté" ),
lwd=1, lty=1,
col=c(par('fg'), 'blue', 'green', "orange", "red") )
abline(v=3, lty=3)
(Dans certains cas, la simulation précédente nous montre un minimum local de AIC et BIC pour les 3 variables et un minimum global pour une douzaine de variables.)
Il y a d'autres critères, comme le coefficient de détermination ajusté (adjusted R-squared) ou le Cp de Mallow
> library(wle)
> r <- mle.cp(y~., data=d)
> summary(r)
Call:
mle.cp(formula = y ~ ., data = d)
Mallows Cp:
(Intercept) V1 V2 V3 V4 V5 V6 V7 V8 V9 V10 V11 V12 V13 V14 V15 cp
[1,] 0 0 0 0 0 0 0 1 0 0 1 0 0 0 1 0 -5.237
[2,] 0 1 0 0 0 0 0 1 0 0 1 0 0 0 1 0 -4.911
[3,] 0 0 1 0 0 0 0 1 0 0 1 0 0 0 1 0 -4.514
[4,] 0 0 0 0 0 0 0 1 0 0 1 0 1 0 1 0 -4.481
[5,] 0 0 0 0 0 0 1 1 0 0 1 0 0 0 1 0 -4.078
[6,] 0 1 1 0 0 0 0 1 0 0 1 0 0 0 1 0 -3.854
[7,] 0 0 0 1 0 0 0 1 0 0 1 0 0 0 1 0 -3.829
[8,] 0 1 0 0 0 0 1 1 0 0 1 0 0 0 1 0 -3.826
[9,] 1 0 0 0 0 0 0 1 0 0 1 0 0 0 1 0 -3.361
[10,] 0 0 0 0 0 0 1 1 0 0 1 0 1 0 1 0 -3.335
[11,] 0 0 0 0 1 0 0 1 0 0 1 0 1 0 1 0 -3.287
[12,] 0 0 0 0 0 0 0 1 1 0 1 0 0 0 1 0 -3.272
[13,] 0 0 0 0 0 0 0 1 0 0 1 0 0 0 1 1 -3.261
[14,] 0 0 0 0 1 0 0 1 0 0 1 0 0 0 1 0 -3.241
[15,] 0 0 0 0 0 0 0 1 0 0 1 1 0 0 1 0 -3.240
[16,] 0 1 0 1 0 0 0 1 0 0 1 0 0 0 1 0 -3.240
[17,] 0 0 0 0 0 0 0 1 0 1 1 0 0 0 1 0 -3.240
[18,] 0 0 0 0 0 1 0 1 0 0 1 0 0 0 1 0 -3.240
[19,] 0 0 0 0 0 0 0 1 0 0 1 0 0 1 1 0 -3.237
[20,] 0 1 0 0 0 0 0 1 0 0 1 0 1 0 1 0 -3.216
Printed the first 20 best models
> i
[1] 7 10 14
Construisons un exemple :
get.sample <- function () {
# Nombre d'observations
n <- 20
# Nombre de variables
m <- 10
# Numéro des variables qui interviennent vraiment
k <- sample(1:m, 5)
print(k)
# Coefficients
b <- rnorm(m); b <- round(sign(b)+b); b[-k] <- 0
x <- matrix(nr=n, nc=m, rnorm(n*m))
y <- x %*% b + rnorm(n)
data.frame(y=y, x)
}Sélectionnons les variables, en partant d'un modèle nul, et en ajoutant progressivement les variables dont la p-valeur est la plus faible.
my.variable.selection <- function (y,x, p=.05) {
nvar <- dim(x)[2]
nobs <- dim(x)[1]
v <- rep(FALSE, nvar)
done <- FALSE
while (!done) {
print(paste("Itération", sum(v)))
done <- TRUE
# On cherche si l'une des p-valeurs est inférieure à p
pmax <- 1
imax <- NA
for (i in 1:nvar) {
if(!v[i]){
# Calcul de la p-valeur
m <- cbind(x[,v], x[,i])
m <- as.matrix(m)
pv <- 1
try( pv <- summary(lm(y~m))$coefficients[ dim(m)[2]+1, 4 ] )
if( is.nan(pv) ) pv <- 1
if (pv<pmax) {
pmax <- pv
imax <- i
}
}
}
if (pmax<p) {
v[imax] <- TRUE
done <- FALSE
print(paste("Adding variable", imax, "with p-value", pmax))
}
}
v
}
d <- get.sample()
y <- d$y
x <- d[,-1]
k.exp <- my.variable.selection(y,x)Très souvent, on retrouve le même modèle, mais pas toujours.
> d <- get.sample() [1] 9 4 7 8 2 > y <- d$y > x <- d[,-1] > k.exp <- my.variable.selection(y,x) [1] "Itération 0" [1] "Adding variable 8 with p-value 0.00326788125893668" [1] "Itération 1" [1] "Adding variable 3 with p-value 0.0131774876254023" [1] "Itération 2" [1] "Adding variable 9 with p-value 0.0309234855260663" [1] "Itération 3" [1] "Adding variable 4 with p-value 0.00370166323917281" [1] "Itération 4"
Comparons le modèle théorique avec le modèle expérimental.
> x <- as.matrix(x)
> summary(lm(y~x[,c(9,4,7,8,2)]))
...
Estimate Std. Error t value Pr(>|t|)
(Intercept) 0.1471 0.3260 0.451 0.65870
x[, c(9, 4, 7, 8, 2)]X9 1.2269 0.3441 3.565 0.00311 **
x[, c(9, 4, 7, 8, 2)]X4 1.9826 0.3179 6.238 2.17e-05 ***
x[, c(9, 4, 7, 8, 2)]X7 1.2958 0.4149 3.123 0.00748 **
x[, c(9, 4, 7, 8, 2)]X8 2.6270 0.4089 6.425 1.59e-05 ***
x[, c(9, 4, 7, 8, 2)]X2 -0.9715 0.3086 -3.148 0.00712 **
Residual standard error: 1.287 on 14 degrees of freedom
Multiple R-Squared: 0.8859, Adjusted R-squared: 0.8451
F-statistic: 21.73 on 5 and 14 DF, p-value: 3.837e-06
> summary(lm(y~x[,k.exp]))
...
Estimate Std. Error t value Pr(>|t|)
(Intercept) -0.005379 0.360940 -0.015 0.98831
x[, k.exp]X3 -1.070913 0.443122 -2.417 0.02886 *
x[, k.exp]X4 1.292099 0.376419 3.433 0.00370 **
x[, k.exp]X8 2.863028 0.469379 6.100 2.03e-05 ***
x[, k.exp]X9 1.541648 0.388408 3.969 0.00123 **
Residual standard error: 1.537 on 15 degrees of freedom
Multiple R-Squared: 0.8254, Adjusted R-squared: 0.7788
F-statistic: 17.73 on 4 and 15 DF, p-value: 1.486e-05On constate que le modèle théorique a quand même l'air mieux...
On peut représenter les résidus en fonction de vhaque variable ajoutée (en noir, avant de la rajouter, en rouge,n après l'avoir ajoutée).
get.sample <- function () {
# Nombre d'observations
n <- 20
# Nombre de variables
m <- 10
# Numéro des variables qui interviennent vraiment
k <- sample(1:m, 5)
print(k)
# Coefficients
b <- rnorm(m); b <- round(sign(b)+b); b[-k] <- 0
x <- matrix(nr=n, nc=m, rnorm(n*m))
y <- x %*% b + rnorm(n)
data.frame(y=y, x)
}
my.variable.selection <- function (y,x, p=.05) {
nvar <- dim(x)[2]
nobs <- dim(x)[1]
v <- rep(FALSE, nvar)
p.values <- matrix(NA, nr=nvar, nc=nvar)
res1 <- list()
res2 <- list()
done <- FALSE
while (!done) {
print(paste("Itération", sum(v)))
done <- TRUE
# On cherche si l'une des p-valeurs est inférieure à p
pmax <- 1
imax <- NA
for (i in 1:nvar) {
if(!v[i]){
# Calcul de la p-valeur
m <- cbind(x[,v], x[,i])
m <- as.matrix(m)
pv <- 1
try( pv <- summary(lm(y~m))$coefficients[ dim(m)[2]+1, 4 ] )
if( is.nan(pv) ) pv <- 1
if (pv<pmax) {
pmax <- pv
imax <- i
}
p.values[i,sum(v)+1] <- pv
}
}
if (pmax<p) {
print(paste("Adding variable", imax, "with p-value", pmax))
m1 <- as.matrix(x[,v])
res1[[ length(res1)+1 ]] <- NULL
try( res1[[ length(res1)+1 ]] <- data.frame(res=lm(y~m1)$res,xi=x[,imax]) )
v[imax] <- TRUE
done <- FALSE
m2 <- as.matrix(cbind(x[,v], x[,imax]))
res2[[ length(res2)+1 ]] <- data.frame(res=lm(y~m2)$res,xi=x[,imax])
}
}
list(variables=v, p.values=p.values[,1:sum(v)], res1=res1, res2=res2)
}
d <- get.sample()
y <- d$y
x <- d[,-1]
res <- my.variable.selection(y,x)
k <- ceiling(length(res$res1)/3)
op <- par(mfrow=c(k,3))
for (i in 1:length(res$res1)) {
r1 <- res$res1[[i]]
r2 <- res$res2[[i]]
plot(r1[,1] ~ r1[,2], ylab="res", xlab=names(r1)[2])
points(r2[,1] ~ r2[,2], col='red')
}
par(op)
On peut aussi représenter l'évolution des p-valeurs (en gras, les variables qui ont été retenues).
matplot(t(res$p.values), type='l', lty=1, lwd=1+2*res$variables) abline(h=.05, lty=3)

Exercice : améliorer la fonction précédente : partir d'un ensemble de variables vide ; les ajouter une par une, quand leur p-valeur est inférieure à .05, en commençant par les variables dont la p-valeur est la plus basse ; quand on ne peut plus en ajouter, retirer celles dont la p-valeur est inférieure à 0.05, en commençant par celles dont la p-valeur est la plus haute ; quand on ne peut plus en retirer, essayer à nouveau d'en ajouter, etc.. Qu'est-ce que cela donne avec l'exemple précédent ? Et si on fait varier la valeur 0.05 choisie comme seuil ?
Exercice : Trouver, dans les données fournies avec R ou ses paquetages, des données avec beaucoup de variables par rapport au nombre d'observations et reprendre la discussion précédente. Que remarque-t-on ?
grep variable str_data | perl -p -e 's/^(.*\s)([0-9]+)(\s+variables:)/$2 $1$2$3/' | sort -n library(ade4) data(microsatt) x <- microsatt$tab # 18 observations, 112 variables, beaucoup de zéros y <- x[,3] x <- x[,-3] Avec cet exemple, on a 16 paramètres pour 18 observations : ça ne marche pas. On peut penser interpréter les choses ainsi : le vecteur que l'on cherchait à prédire est "presque" orthogonal aux autres vecteurs. Si on essaye de le vérifier, en normalisant y et les colonnes de x et en calculant les produits scalaires, on constate que c'est complètement faux... library(ade4) data(microsatt) x <- microsatt$tab # 18 observations, 112 variables, beaucoup de zéros y <- x[,3] x <- x[,-3] yn <- y/sqrt(sum(y*y)) xn <- t(t(x)/sqrt(apply(x*x, 2, sum))) plot( sort(as.vector(t(yn) %*% xn)), type='h')

En fait, de telles fonctions existent déjà :
leaps (dans la bibliothèque leaps), subset (dans la bibliothèque car), stepAIC (dans la bibliothèque MASS).
Essayons-les sur notre exemple construit.
d <- get.sample() y <- d[,1] x <- as.matrix(d[,-1]) library(leaps) a <- regsubsets(y~x) summary(a)
Il vient (les variables dans le modèle théorique sont 1, 3, 6, 7, 10) :
Selection Algorithm: exhaustive
X1 X2 X3 X4 X5 X6 X7 X8 X9 X10
1 ( 1 ) " " " " " " " " " " " " "*" " " " " " "
2 ( 1 ) " " " " "*" " " " " " " " " " " " " "*"
3 ( 1 ) " " " " "*" " " " " " " "*" " " " " "*"
4 ( 1 ) "*" " " "*" " " " " " " "*" " " " " "*"
5 ( 1 ) "*" " " "*" " " " " " " "*" "*" " " "*"
6 ( 1 ) "*" " " "*" " " " " " " "*" "*" "*" "*"
7 ( 1 ) "*" " " "*" " " " " "*" "*" "*" "*" "*"
8 ( 1 ) "*" " " "*" "*" " " "*" "*" "*" "*" "*"La fonction subsets de la bibliothèque car permet de représenter graphiquement ces résultats.
library(leaps)
library(car)
get.sample <- function () {
# Nombre d'observations
n <- 20
# Nombre de variables
m <- 10
# Numéro des variables qui interviennent vraiment
k <- sample(1:m, 5)
print(k)
# Coefficients
b <- rnorm(m); b <- round(sign(b)+b); b[-k] <- 0
x <- matrix(nr=n, nc=m, rnorm(n*m))
y <- x %*% b + rnorm(n)
list(y=y, x=x, k=k, b=b)
}
d <- get.sample()
x <- d$x
y <- d$y
k <- d$k
b <- d$b
subsets(regsubsets(x,y), statistic='bic', legend=F)
title(main=paste(sort(k),collapse=', '))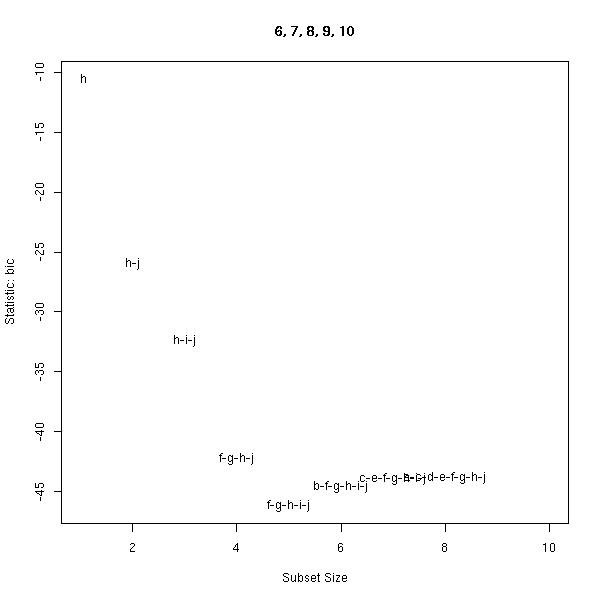
Mentionnons enfin la commande stepAIC, dans la bibliothèque MASS.
d <- data.frame(y=y,x) r <- stepAIC(lm(y~., data=d), trace = TRUE) r$anova > r$anova Stepwise Model Path Analysis of Deviance Table Initial Model: y ~ X1 + X2 + X3 + X4 + X5 + X6 + X7 + X8 + X9 + X10 Final Model: y ~ X1 + X3 + X4 + X5 + X7 + X10 Step Df Deviance Resid. Df Resid. Dev AIC 1 NA NA 9 18.62116 20.57133 2 - X9 1 0.007112768 10 18.62828 18.57897 3 - X6 1 0.037505223 11 18.66578 16.61919 4 - X2 1 0.017183580 12 18.68296 14.63760 5 - X8 1 0.098808619 13 18.78177 12.74309 > k [1] 5 10 3 7 4
Comparons avec le modèle théorique :
> summary(lm(y~x[,k]))
...
Estimate Std. Error t value Pr(>|t|)
(Intercept) 0.2473 0.3023 0.818 0.426930
x[, k]1 1.7478 0.3330 5.249 0.000123 ***
x[, k]2 1.4787 0.2647 5.587 6.7e-05 ***
x[, k]3 -1.5362 0.4903 -3.133 0.007334 **
x[, k]4 -1.1025 0.2795 -3.944 0.001470 **
x[, k]5 1.6863 0.4050 4.164 0.000956 ***
Residual standard error: 1.27 on 14 degrees of freedom
Multiple R-Squared: 0.8317, Adjusted R-squared: 0.7716
F-statistic: 13.84 on 5 and 14 DF, p-value: 5.356e-05
> AIC(lm(y~x[,k]))
[1] 73.1798
> b
[1] 0 0 -2 2 2 0 -1 0 0 2
> summary(lm(y~x[,c(1,3,4,5,7,10)]))
...
Estimate Std. Error t value Pr(>|t|)
(Intercept) 0.1862 0.2886 0.645 0.52992
x[, c(1, 3, 4, 5, 7, 10)]1 -0.4408 0.2720 -1.620 0.12915
x[, c(1, 3, 4, 5, 7, 10)]2 -1.6742 0.4719 -3.548 0.00357 **
x[, c(1, 3, 4, 5, 7, 10)]3 1.5300 0.3953 3.870 0.00193 **
x[, c(1, 3, 4, 5, 7, 10)]4 1.7813 0.3159 5.639 8.07e-05 ***
x[, c(1, 3, 4, 5, 7, 10)]5 -1.0521 0.2664 -3.949 0.00167 **
x[, c(1, 3, 4, 5, 7, 10)]6 1.4903 0.2506 5.946 4.85e-05 ***
Residual standard error: 1.202 on 13 degrees of freedom
Multiple R-Squared: 0.86, Adjusted R-squared: 0.7954
F-statistic: 13.31 on 6 and 13 DF, p-value: 6.933e-05
> AIC(lm(y~x[,c(1,3,4,5,7,10)]))
[1] 71.50063Si on regarde les p-valeurs, on a envie d'enlever X1, mais si on regarde l'AIC, on a envie de la garder...
La bibliothèque dr implémente plusieurs algorithmes de réduction de la dimension.
library(help=dr) xpdf /usr/lib/R/library/dr/doc/drdoc.pdf
A FAIRE : expliquer les algorithmes (sir, save, phd) (le document PDF ci-dessus est incompréhensible).
sir Sliced Inverse Regression save Sliced Average Variance Estimation phd Principal Hessian Direction
A FAIRE : un exemple, avec quelques dessins... (prendre un exemple autre que celui du manuel...)
# L'exemple du manuel
library(dr)
data(ais)
# Les données
op <- par(mfrow=c(3,3))
for (i in names(ais)) {
hist(ais[,i], col='light blue', probability=T, main=i)
lines(density(ais[,i]),col='red',lwd=3)
}
par(op)
# Leur logarithme
op <- par(mfrow=c(3,3))
for (i in names(ais)) {
x <- NA
try( x <- log(ais[,i]) )
if( is.na(x) | any(abs(x)==Inf) ){
plot.new()
} else {
hist(x, col='light blue', probability=T, main=i)
lines(density(x),col='red',lwd=3)
}
}
par(op)
# Réduction de la dimension
r <- dr(LBM ~ Ht + Wt + log(RCC) + WCC, data=ais, method="sir")
plot(r)
r
summary(r) # A FAIRE : parler des tests pour la dimension...
On rencontre les SVM, par exemple, dans le contexte suivant.
On peut utiliser la génétique pour faire des tests afin de savoir si des patients présentent tel ou tel risque. Si on connait bien le mécanisme de la pathologie en question, on sait quels sont les gènes concernés, quels sont les mutations possibles : on peut donc aisément faire des tests. Mais parfois, on ne comprend pas encore très bien les mécanismes : on peut néanmoins espérer aboutir à une conclusion en faisant des test "au hasard". Plus pr centaines de patients, dont on connait l'état (par des tests peut-être invasifs, comme une autopsie) et on leur fait subir une baterie de tests génétiques (on peut tester la présence de plusieurs dizaines de milliers de gènes en une seule fois, sur une petite plaque de verre appelée micro-chip ou microarray). On dispose donc de plusieurs dizaines de milliers de variables et de quelques centaines d'observations. On cherche à prédire la valeur d'une de ces variables (le patient présente la maladie donnée ou pas) à l'aide des autres.
Le problème, c'est qu'on a trop de variables.
Première idée : se limiter à 20 variables définies à l'avance.
Deuxième idée : se limiter à 20 variables (les 20 meilleures) : c'est la sélection des variables, que nous avons déjà présentée.
Troisième idée : dans le cas d'une variable dépendante qualitative (comme dans l'exemple), il s'agit de trouver un hyperplan qui sépare les deux nuages de points. Au lieu de trouver un hyperplan, i.e., une fonction affine f telle que f>0 ssi le patient est malade, on peut chercher un hyperplan épais, i.e., une fonction affine f telle que f>a ssi le patient est malade et f<-a ssi le patient est sain, avec a le plus grand possible (ou plutôt, avec a fixé à l'avance et avec une pénalité pour les observations mal classées).
En fait, la méthode des SVM est beaucoup plus générale : on peut partir d'un espace de dimension modeste, "ajouter des dimensions" (pour tenir compte de phénomènes non linéaires) et chercher un hyperplan séparateur épais.
L'algorithme est le suivant :
1. Maximiser l'épaisseur de l'hyperplan, en exigeant qu'il soit séparateur : c'est juste une histoire de diviseurs de Lagrange. On a un diviseur de Lagrange pour chaque point : si ce diviseur est nul, c'est que le point n'intervient pas (il est loin de l'hyperplan), s'il est non nul, on dit que le point est un vecteur support. Ces points vont toucher l'hyperplan épais -- et en fait, on peut oublier tous les autres points.
2. Si ça ne marche pas, essayer de passer en dimensions supérieures. On pourrait considérer des plongements, du genre (x,y) |---> (x,x^2,x*y,y^2), mais en fait, on va simplement changer l'équation de l'"hyperplan" (qui ne sera donc plus un hyperplan) en remplaçant le produit scalaire qui y apparaissait par quelque chose du genre K(x,y) = ( <x,y> + a )^b ou K(x,y) = exp( -a Norme(x-y)^2 ). Si on utilise des algorithmes ne faisant intervenir que des produits scalaires, cela permet d'augmenter la dimension sans avoir de coordonnées nombreuses à manipuler.
3. On acceptera aussi que certains points se trouvent du mauvais côté de l'hyperplan, avec une pénalit
n <- 200 x <- rnorm(n) y <- rnorm(n) u <- sqrt(x^2+y^2) u <- ifelse( u<.5*mean(u), 1, 2) plot(y~x, col=u, pch=15)

help.search("svm")
help.search("support vector machine")
library(e1071)
library(help=e1071)
?svm
library(e1071)
u <- factor(u)
r <- svm(u~x+y)
{
# La fonction plot.svm appelle browser() : pourquoi ???
# Et après, ça plante...
# (e1071 version 1.3-16, 1.3-16)
browser <- function () {}
try( plot(r, data.frame(x,y,u), y~x) )
}
n <- 200 x <- runif(n, -1,1) y <- runif(n, -1,1) u <- abs(x-y) u <- ifelse( u<.5*mean(u), 1, 2) plot(y~x, col=u, pch=15)

u <- factor(u)
r <- svm(u~x+y)
{
browser <- function () {}
try( plot(r, data.frame(x,y,u), y~x) )
}
Si on veut utiliser sérieusement les SVM, on essaiera différentes valeurs pour les paramètres cost et gamma et on demandera une validation croisée.
Les SVM se généralisent :
Pour distinguer entre plus de deux classes, on peut considérer les classes deux par deux, puis utiliser un vote pour prédire la classe d'une nouvelle observation.
On peut aussi utiliser les SVM pour distinguer entre une seule classe. Ça parrait un peu bizarre, mais ça permet de repérer les valeurs atypiques.
On peut aussi utiliser ces méthodes pour de la régression. La régression linéaire consiste à trouver un hyperplan de sorte que la plupart des points se trouvent près de cet hyperplan, i.e., on cherche un hyperplan épais dans lequel se trouvent la plupart des points. C'est le même problème que précédemment, mais avec toutes les inégalités à l'envers.
Il y a une autre manière (duale) d'interpréter ces méthodes : prendre l'hyperplan médiateur du segment joignant les points les plus proches dans l'enveloppe convexe de chacun des deux ensembles de points. Si les enveloppes convexes se coupent, on les remplace par des enveloppes convexes réduites (toujours définies comme des ensembles de barycentre, mais avec une restriction sur les coefficients : on demande qu'ils soient tous inférieurs à 0.5 (par exemple), de manière à ne pas donner trop d'importance à un point isolé).
Pour de plus amples détails, d'autres exemples et une comparaison des SVM et des arbres de régression, voir
/usr/lib/R/library/e1071/doc/svmdoc.pdf
Pour d'autres détails :
http://bioconductor.org/workshops/Heidelberg02/moldiag-svm.pdf http://www.kernel-machines.org/ http://www.csie.ntu.edu.tw/~cjlin/papers/ijcnn.ps.gz http://www.acm.org/sigs/sigkdd/explorations/issue2-2/bennett.pdf http://www.csie.ntu.edu.tw/~cjlin/papers/libsvm.ps.gz
Exercice : utiliser une SVM dans le cadre donné dans l'introduction, celui des microarrays.
A FAIRE : expliquer (comprendre ???) ce qui suit. Est-ce terminé ?
library(help=sma) library(help=pamr) library(e1071) library(sma) data(MouseArray) # Mice number 1, 2 and 3: control # Number 4, 5, 6: treatment m <- t(mouse.lratio$M) m <- data.frame( mouse=factor(c(1,1,1,2,2,2)), m) # r <- svm(mouse~., data=m, na.action=na.omit, kernel="linear") # Out of memory... m <- m[,1:500] r <- svm(mouse~., data=m, na.action=na.omit, kernel="linear") A FAIRE : terminer (en particulier, comment lit-on le résultat ???) Prédiction : m <- t(mouse.lratio$M) m <- m[,!is.na(apply(m,2,sum))] m <- data.frame( mouse=factor(c(1,1,1,2,2,2)), m) m <- m[,1:500] m6 <- m[6,] m <- m[1:5,] r <- svm(mouse~., data=m, na.action=na.omit, kernel="linear") predict(r,m6) # 1 au lieu de 2... r <- svm(mouse~., data=m, na.action=na.omit) predict(r,m6) # 1 au lieu de 2... # On pouvait s'attendre à ce genre d'erreur : library(cluster) m <- t(mouse.lratio$M) m <- m[,!is.na(apply(m,2,sum))] plot(hclust(dist(m))) rm(m,m6,r)
On rencontre les modèles additif généralisés quand on essaye de décrire une situation non linéaire avec un nombre de variables élevé (si le modèle était linéaire, ce nombre de variables serait tout à fait raisonnable, mais avec la non-linéarité, le nombre de paramètres à estimer explose).
Un modèle linéaire consisterait à écrire
Y = b0 + b1 x1 + b2 x2 + ... + bn xn.
où les bi sont des nombres.
Un modèle additif généralisé consiste à écrire
Y = a + f1(x1) + f2(x2) + ... + fn(xn)
où les fi sont des fonctions arbitraires (on les estimera comme on veut : splines, noyau, régression locale, etc.). L'important, c'est qu'il s'agit de fonctions d'une seule variable : elles ne sont pas trop complexes.
Bien sûr, toutes les fonctions R^n --> R ne peuvent pas se mettre sous cette forme : mais on en a déjà beaucoup et, la plupart du temps, ça suffira. Il y a toutefois un gros problème : on oublie complètement les éventuelles interactions entre les variables. Non linéarité ou interactions, il faut choisir.
L'algorithme utilisé pour trouver ces fonctions est itératif. Si on oubliait la constante, ce serait :
1. Prendre une estimation initiale des fi (par exemple, des constantes, à l'aide d'un modèle linéaire).
2. Pour tout k, définir fk comme la régression locale de
Y - Sum(fj(xj)) ~ Xk j!=k
3. Recommencer jusqu'à ce que ça converge.
Si on n'oublie pas la constante :
1. alpha <- mean(y)
f[k] <- 0
2. f[k] <- Smoother( Y - alpha - Sum(fj(xj)) )
j!=k
3. f[k] <- f[k] - 1/N * Sum fk(xik)
i
4. Goto 2 until the f[k] no longer change.On peut généraliser cet algorithme en ajoutant des termes d'ordre supérieur (quand c'est nécessaire) : fij(xi,xj), etc.
On peut aussi exiger que certaines de ces fonctions aient une forme particulière (par exemple, qu'elles soient linéaires).
On peut montrer que cela l'algorithme précédent minimise une somme de carrés pénalisée.
Variante : Cette méthode peut s'étende au cas de la régression logistique ou de Poisson (elle s'interprère alors avec une log-vraissemblance pénalisée), mais l'algorithme est un peu différent (un mélange de backfitting et de IRLS). Pour une régression multilogistique, c'est encore plus compliqué.
On peut interpréter le modèle additif généralisé comme la recherche de la meilleure transformation à faire subir aux variables prédictives pour que le modèle linéaire soit valable.
Remarque : comme souvent, on suppose que la variable à prédire suit une distribution normale --- si elle en est trop loin, on la transformera. Idem pour les variables prédictives : on s'arrangera au moins pour qu'elles aient le même ordre de grandeur.
Voyons maintenant comment modéliser des données à l'aide d'un GAM sous R.
A FAIRE : library(mgcv) ?gam n <- 200 x1 <- runif(n,-3,3) x2 <- runif(n,-3,3) x3 <- runif(n,-3,3) f1 <- sin; f2 <- cos; f3 <- abs; y <- f1(x1) + f2(x2) + f3(x3) + rnorm(n) pairs(cbind(y,x1,x2,x3)) # on ne voit pas grand-chose...

library(mgcv) r <- gam(y~s(x1)+s(x2)+s(x3)) x <- seq(-3,3,length=200) z <- rep(0,200) m.theorique <- cbind(f1(x),f2(x),f3(x)) m.experimentale <- cbind( predict(r, data.frame(x1=x,x2=z,x3=z)), predict(r, data.frame(x1=z,x2=x,x3=z)), predict(r, data.frame(x1=z,x2=z,x3=x)) ) matplot(m.theorique, type='l', lty=1) matplot(m.experimentale, type='l', lty=2, add=T)

On peut difficilement comparer, car les courbes sont décalées...
zero.mean <- function (m) {
t(t(m)-apply(m,2,mean))
}
matplot(zero.mean(m.theorique), type='l', lty=1)
matplot(zero.mean(m.experimentale), type='l', lty=2, add=T)
title(main="GAM")
legend(par('usr')[2], par('usr')[3], xjust=1, yjust=0,
c('courbes théoriques', 'courbes expérimentales'),
lty=c(1,2))
op <- par(mfrow=c(2,2))
for (i in 1:3) {
plot(r, select=i)
lines(zero.mean(m.theorique)[,i]~x, lwd=3, lty=3, col='red')
}
par(op)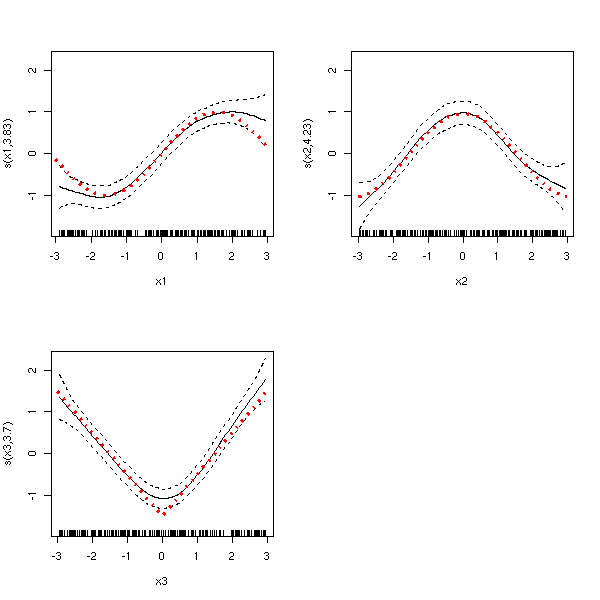
res <- residuals(r) op <- par(mfrow=c(2,2)) plot(res) plot(res~predict(r)) hist(res, col='light blue', probability=T) lines(density(res), col='red', lwd=3) rug(res) qqnorm(res) qqline(res) par(op)

op <- par(mfrow=c(2,2)) plot(res ~ x1) plot(res ~ x2) plot(res ~ x3) par(op)

A FAIRE : référence à d'autres documents, URLs... A FAIRE : que signifie "thin-plate regression spline" ???
A FAIRE : Other functions to fit GAMs:
library(mda) ?bruto # Gaussian GAM library(help=gss) ?glm # ???
A FAIRE : Quel est le critère utilisé ?
GCV ???
C'est une manière de prédire une variable qualitative binaire à l'aide de beaucoup de variables (quantitatives ou qualitatives), sans aucune hypothèse de linéarité.
L'algorithme est le suivant. Choisir l'une des variables et un point de coupure de manière à maximiser un certain critère statistique ; continuer jusqu'à ce qu'il n'y ait plus que quelques (20 à 50) observations dans chaque classe. Repr d'arbre. Elaguer (par exemple en comparant avec d'autres échantillons, ou : trouver le nombre de noeuds de sorte que l'arbre construit à partir de 90% des données donne les meilleurs résultats possible sur les 10% restants).
library(rpart) data(kyphosis) r <- rpart(Kyphosis ~ ., data=kyphosis) plot(r) text(r)

Une autre application, à part l'obtention d'un arbre de décision, c'est l'étude des données manquantes.
library(Hmisc) ?transcan
Il est très important d'élaguer l'arbre, car sinon, on a un arbre de décision qui décrit précisément l'échantillon, mais pas la population.
A FAIRE : dessin
La méthode se généralise à la prédiction d'une variable de comptage (régression de Poisson).
Cette méthode n'est pas très stable : on peut réduire la variance du résultat à l'aide du bagging. Voir aussi MART.
On cherche à prédire une variable binaire Y à l'aide de variables quantitatives, en cherchant des boites dans l'espace des variables prédictives dans lesquelles on a souvent Y=1. L'algorithme est le suivant.
1. Prendre une boite (toutes les données) 2. La réduire dans l'une des dimensions pour augmenter la proportion de points avec Y=1. 3. Reprendre en 2, jusqu'à ce qu'il y ait suffisemment peu de points mal classés dans la boite. 4. Regarder s'il n'est pas possible de faire à nouveau grandir la boite. 5. Enlever les points de la boite. 6. Recommencer.
On se retrouve alors avec des boites (toutes les dimensions n'apparaissent pas dans chaque boite, loin de là), que l'on peut voir comme des règles.
On peut voir cette méthode comme une variante des arbres de régression (CART).
Visiblement, il n'y a pas de fonction R qui implémente cet algorithme.
help.search('PRIM')
help.search('bump')
Pour améliorer la qualité d'un estimateur (non linéaire, instable : par exemple un arbre de régression), on calcule sa moyenne sur plusieurs échantillons de Bootstrap.
A FAIRE : comment traduit-on "bagging" et "bagged estimator" en français ?
Par exemple, le résultat d'une prédiction par un arbre de régression est généralement une classe (1, 2, 3, ... ou k) : on le remplace par un vecteur (0,0,...,0,1,0,...,0) et on fait la moyenne de ces vecteurs -- on obtient un vecteur de probabilités.
Le résultat de l'estimateur à améliorer déjà être un vecteur de probabilités : on fait alors la moyenne de ces vecteurs.
Remarque : la structure de l'estimateur est perdue (si on part d'un arbre de régression, on n'a plus d'arbre -- c'est plus dur à interpréter).
Remarque : ça n'a aucun effet sur les estimateurs linéaires (qui commuttent avec la moyenne).
Remarque : dans certains cas, la qualité de l'estimateur peut empirer.
Dans l'exemple suivant, les prédictions sont correctes dans 99% des cas.
library(ipred)
do.it <- function (formula, data, test) {
r <- bagging(formula, data=data, coob=T, control=rpart.control(xval=10))
p2 <- test$Class
p1 <- predict(r,test)
p1 <- factor(p1, levels=levels(p2))
res1 <- sum(p1==p2) / length(p1)
# Avec les arbres seuls
r <- bagging(formula, data=data, nbagg=1, control=rpart.control(xval=10))
p2 <- test$Class
p1 <- predict(r,test)
p1 <- factor(p1, levels=levels(p2))
res2 <- sum(p1==p2) / length(p1)
c(res1, res2, res1/res2)
}
# Je prends un exemple dans "mlbench" (qui contient justement ce genre d'exemple).
library(mlbench)
data(Shuttle)
n <- dim(Shuttle)[1]
k <- sample(1:n,200)
do.it(Class~., data=Shuttle[k,], test=Shuttle[-k,]) # Pareil, 99.5%
rm(Shuttle)
data(Vowel)
n <- dim(Vowel)[1]
k <- sample(1:n,200)
do.it(Class~., data=Vowel[k,], test=Vowel[-k,]) # Amélioration : 47% au lieu de 36%
rm(Vowel)On peut interpréter le bagging comme une alternative à la méthode du maximum de vraissemblance : pour estimer un paramètre, la méthode du maximum de vraissemblance regarde la distribution de ce paramètre et choisit le mode ; le bagging consiste (en gros) à choisir la moyenne.
Voir aussi :
/usr/lib/R/library/ipred/doc/ipred-examples.pdf
A peu près comme le bagging (on prend un estimateur et on l'utilise sur plusieurs échantillons de bootstrap), mais les échantillons de bootstrap ne sont pas pris au hasard : ils sont choisis en fonction de la performance des estimateurs précédents. (Généralement, on se contente d'attribuer un poids aux observations en fonction des résultats précéndents.
Généralement, ça marche très bien, mieux que le bagging, mais dans certains cas, la qualité des prédictions empire.
A FAIRE : sous R ???
Les méthodes précédentes, bagging et boosting, remplacent un estimateur par un ensemble d'estimateurs. Dans ces situations, on utilise une famille d'estimateurs, tous construits sur le même principe.
Mais rien n'empèche de réunir des estimateurs complètement différents
A FAIRE : exemples (arbre + régression linéaire ?)
On peut aussi utiliser ces méthodes avec des de la classification non supervisée.
A FAIRE : exemples
A FAIRE : réorganiser cette partie.
C'est comme le bagging : on construit des arbres de régression sur des échantillons de bootstrap, mais à chaque noeud de chaque arbre, on ne regarde pas toutes les variables mais juste un petit nombre d'entre elles, choisies au hasard. Il s'agit donc d'une version "bruitée" du bagging.
Voici un exemple (compter trois ou quatre minutes de calcul -- il y a 500 arbres...)
library(randomForest)
do.it <- function (formula, data, test) {
r <- randomForest(formula, data=data)
p2 <- test$Class
p1 <- predict(r,test)
p1 <- factor(p1, levels=levels(p2))
res1 <- sum(p1==p2) / length(p1)
# Avec les arbres seuls
r <- bagging(formula, data=data, nbagg=1, control=rpart.control(xval=10))
p2 <- test$Class
p1 <- predict(r,test)
p1 <- factor(p1, levels=levels(p2))
res2 <- sum(p1==p2) / length(p1)
c(res1, res2, res1/res2)
}
library(mlbench)
data(Vowel)
n <- dim(Vowel)[1]
k <- sample(1:n,200)
do.it(Class~., data=Vowel[k,], test=Vowel[-k,]) # On passe de 42% à 67%
rm(Vowel)C'est mieux que le bagging (avec le même échantillon, il passe de 42% à 45% de bonnes réponses...).
En fait, la commande randomForest nous donne un peu plus d'informations.
> r <- randomForest(Class~., data=Vowel)
> r
Call:
randomForest.formula(x = Class ~ ., data = Vowel[k, ])
Type of random forest: classification
Number of trees: 500
No. of variables tried at each split: 3
OOB estimate of error rate: 26%
Confusion matrix:
hid hId hEd hAd hYd had hOd hod hUd hud hed class.error
hid 11 3 0 0 0 0 0 0 0 3 0 0.3529412
hId 2 11 1 0 0 0 0 0 1 0 0 0.2666667
hEd 0 2 6 2 0 0 0 0 0 0 2 0.5000000
hAd 0 0 0 20 0 1 0 0 0 0 1 0.0909091
hYd 0 0 0 0 23 2 0 0 0 0 1 0.1153846
had 0 0 0 2 5 7 0 0 0 0 1 0.5333333
hOd 0 0 0 0 2 0 13 1 1 0 0 0.2352941
hod 0 0 0 0 0 0 2 11 1 0 0 0.2142857
hUd 0 0 0 0 0 0 2 2 16 2 0 0.2727273
hud 1 0 0 0 0 0 0 1 2 15 0 0.2105263
hed 0 0 0 0 2 2 0 0 2 0 15 0.2857143Tout d'abord, on constate que l'estimation du taux d'erreurs est optimiste (26% au lieu de 33% -- et encore, le bootstrap oob est sensé être pessimiste...).
On a aussi une matrice de confusion, qui donne des "distances" entre les différentes classes : on peut les utiliser pour tenter de les représenter par des points dans le plan (à l'aide d'un algorithme de type MDS, comme nous l'avons déjà vu).
library(randomForest) library(mlbench) library(mva) data(Vowel) r <- randomForest(Class~., data=Vowel, importance=T) # Trois minutes... m <- r$confusion # On a une matrice de confusion alors qu'on veut une matrice de # distances. On essaye donc de tripatouiller un peu la matrice pour # se ramener à quelque chose qui ressemble à des distances -- il y a # peut-être de meilleures manière de procéder... m <- m[,-dim(m)[2]] m <- m+t(m)-diag(diag(m)) n <- dim(m)[1] m <- m/( matrix(diag(m),nr=n,nc=n) + matrix(diag(m),nr=n,nc=n, byrow=T) ) m <- 1-m diag(m) <- 0 # On peut le dessiner (il faudrait aussi regarder en dimensions supérieures) mds <- cmdscale(m,2) plot(mds, type='n') text(mds, colnames(m)) rm(Vowel)

On nous donne aussi l'importance de chacune des variables prédictives.
> r$importance
Measure 1 Measure 2 Measure 3 Measure 4
V1 178.94737 16.674731 0.9383838 0.4960153
V2 563.15789 38.323021 0.9222222 1.0000000
V3 100.00000 13.625267 0.8343434 0.4212575
V4 200.00000 23.420278 0.8909091 0.5169644
V5 321.05263 26.491365 0.8959596 0.5819186
V6 189.47368 20.299312 0.8828283 0.5022913
V7 84.21053 10.596949 0.7777778 0.3544800
V8 110.52632 16.071039 0.8454545 0.4107499
V9 47.36842 10.219346 0.8424242 0.3301638
V10 63.15789 8.857154 0.8292929 0.3274473A FAIRE : comprendre les valeurs préc
Graphiquement, cela nous suggère de nous limiter à V2, ou V2 et V5, ou encore V2, V5 et V1 :
op <- par(mfrow = c(2,2))
m <- r$importance
n <- dim(m)[1]
for (i in 1:4) {
plot(m[,i],
type = "h", lwd=3, col='blue', axes=F,
ylab='', xlab='Variables',
main = colnames(r$importance)[i] )
axis(2)
axis(1, at=1:n, labels=rownames(m))
# Je mets les deux valeurs les plus élevées en rouge
a <- order(m[,i], decreasing=T)
m2 <- m[,i]
m2[ -a[1:2] ] <- NA
lines(m2, type='h', lwd=5, col='red')
}
par(op)
Les exemples précédents se limitaient aux arbres de classification, mais ça marche aussi avec des arbres de régression.
On peut aussi utiliser les forêts aléatoires pour détecter les points atypiques (outliers).
A FAIRE : terminer de lire l'article de Rnews_2002-3.pdf (à la fin, ils parlent de ROC).
Voir :
Rnews_2002-3.pdf A FAIRE : URL A FAIRE : il y a d'autres références à Rnews : mettre un URL à chaque fois. A FAIRE : Je parle souvent d'"arbres de régression" alors que j'ai juste défini les "arbres de classification". Qu'est-ce qu'un "arbre de régression" ? (MARS ?)
A FAIRE : mettre cette partie au bon endroit
A FAIRE : trouver un exemple de données (si possible réelles) avec un (ou deux) groupes d'observations atypiques.
Il s'agit de demander à l'ordinateur d'essayer de trouver des classes dans les données : s'il met la majorité des données dans une classe et le reste dans des classes isolées, il faut s'inquiéter. L'arbre devrait être bien équilibré. (On fera ça après avoir regardé les variables une à la fois et en les transformant si nécessaire.)
A FAIRE : un exemple
De manière surprenante, on peut aussi utiliser les algorithmes d'apprentissage supervisé. Pour cela, on met toutes les observations dans la même classe et on construit une autre classe avec des données aléatoires (des données prises au hasard uniformément dans l'hypercube contenant les observations, ou des données obtenues par bootstrap indépendants sur chacune des variables).
A FAIRE : un exemple
A FAIRE : rappeler ce qu'est un réseau de neurones.
On peut les utiliser pour de la régression (prédiction d'une variable quantitative) ou la classification supervisée (prédiction d'une variable qualitative).
Si on reprend l'exemple de la reconnaissance des voyelles, on obtient 60% de bons résultats (entre 55% et 65%).
library(nnet)
do.it <- function (formula, data, test, size=20) {
r <- nnet(formula, data=data, size=size)
p2 <- test$Class
p1 <- predict(r,test)
nam <- colnames(p)
i <- apply(p1,1,function(x){order(x)[11]})
p1 <- nam[i]
p1 <- factor(p1, levels=levels(p2))
res1 <- sum(p1==p2) / length(p1)
res1
}
library(mlbench)
data(Vowel)
n <- dim(Vowel)[1]
k <- sample(1:n,200)
do.it(Class~., data=Vowel[k,], test=Vowel[-k,])
A FAIRE library(deal) demo(rats) A FAIRE : regarder les fichiers de /usr/lib/R/library/deal/demo/ hiscorelist <- heuristic(newrat, rats.df, rats.prior, restart = 10, degree = 7, trace = TRUE)
On cherche à prédire une variable quantitative Y à partir de variables quantitatives X. Pour cela, on cherche à écrire Y sous la forme d'une combinaison linéaire de fonctions de la forme (Xj-t)_+ ou (t-Xj)_+, où Xj est l'une des variables et t=xij est l'une des observations. C'est très semblable aux arbres de régression, mais les prédictions sont linéaires par morceau et non plus constantes par morceau.
L'algorithme est le suivant.
1. Commence avec une seule fonction, la fonction constante. 2. Calculer les coefficients du modèle 3. Ajouter la paire de fonctions (Xj-t)_+, (t-Xj)_+ qui diminue le plus l'erreur. 4. Reprendre en 2. 5. Ne pas oublier d'élaguer (comme pour les arbres de régression).
Cela se généralise à la régression logistique, éventuellement multiple (on utilise alors le maximum de vraissemblance pour trouver les coefficients).
Sous R, on peut utiliser la fonction mars de la bibliothèque mda.
Considérons l'exemple suivant.
library(mda) library(mlbench) data(BostonHousing) x <- BostonHousing x[,4] <- as.numeric(x[,4]) pairs(x)

Les variables donnent l'impression de bien se préter à la méthode : certaines présentent "deux bosses" -- or l'algorithme MARS consiste justement à séparer ces bosses : on risque de se retrouver avec des variables dont la distribution est plus normale.
op <- par(mfrow=c(4,4))
for (i in 1:14) {
hist(x[,i],probability=T,col='light blue', main=paste(i,names(x)[i]))
lines(density(x[,i]),col='red',lwd=3)
rug(jitter(x[,i]))
}
hist(log(x[,1]),probability=T,col='light blue', main="log(x1)")
lines(density(log(x[,1])),col='red',lwd=3)
rug(jitter(log(x[,1])))
par(op)
op <- par(mfrow=c(4,4))
for (i in 1:14) {
qqnorm(x[,i], main=paste(i,names(x)[i]))
qqline(x[,i], col='red')
}
qqnorm(log(x[,1]), main="log(x1)")
qqline(log(x[,1]), col='red')
par(op)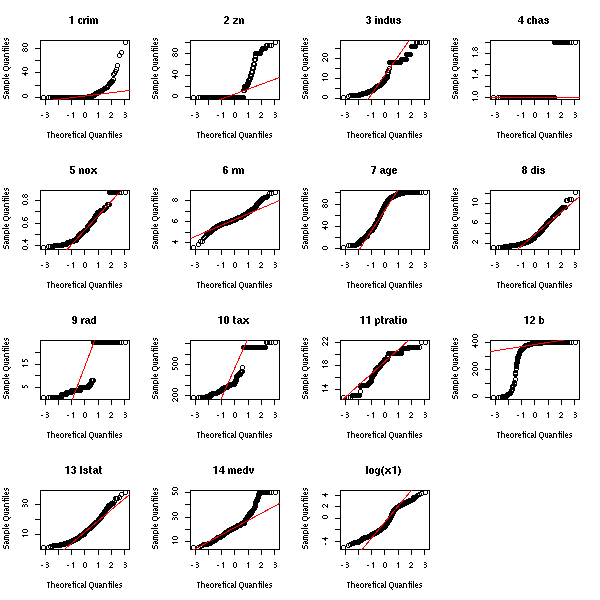
On va quand-même prendre le logarithme de la variable à prédire, car elle n'est vraiment pas normale (pour les autres, le défaut de normalité est dû à la présence de deux pics : MARS est fait pour ça). (Au début, je n'avais pas transformé la variable, pensant que ça n'avait pas trop d'importance : ça donnait vraiment n'importe quoi (moyenne de l'erreur de prédiction du même ordre de grandeur que l'écart-type de la variable...)).
x[,1] <- log(x[,1])
n <- dim(x)[1]
k <- sample(1:n, 100)
d1 <- x[k,]
d2 <- x[-k,]
r <- mars(d1[,-1],d1[,1])
p <- predict(r, d2[,-1])
res <- d2[,1] - p
op <- par(mfrow=c(4,4))
plot(res)
plot(res~p)
for (i in 2:14) {
plot(res~d2[,i])
}
par(op)
op <- par(mfrow=c(2,2)) qqnorm(r$fitted.values, main="fitted values") qqline(r$fitted.values) hist(r$fitted.values,probability=T,col='light blue', main='fitted values') lines(density(r$fitted.values),col='red',lwd=3) rug(jitter(r$fitted.values)) qqnorm(res, main="residues") qqline(res) hist(res,probability=T,col='light blue', main='residues') lines(density(res),col='red',lwd=3) rug(jitter(res)) par(op)

Si on compare avec une régression naïve, on constate que c'est légèrement mieux.
> mean(res^2) [1] 0.6970905 > r2 <- lm(crim~., data=d1) > res2 <- d2[,1] - predict(r2,d2) > mean(res2^2) [1] 0.7982593
Et avec une régression naïve qui ne fait intervenir que les variables pour lesquelles on a un point de coupure (mauvaise idée : il y a d'autres variables importantes, qui agissent linéairement, et pour lesquelles une coupure n'apporte rien) :
> kk <- apply(r$cuts!=0, 2, any) > kk <- (1:length(kk))[kk] > kk <- c(1, 1+kk) > r3 <- lm(crim~., data=d1[,kk]) > res3 <- d2[,1] - predict(r3,d2) > mean(res3^2) [1] 0.7930023
Essayons de sélectionner des variables comme nous l'avons vu plus haut.
> library(MASS) > r4 <- stepAIC(lm(crim~., data=d1)) > res4 <- d2[,1]-predict(r4,d2) > mean(res4^2) [1] 0.8195915
(On pourrait continuer d'essayer d'autres méthodes...)
C'est une méthode comparable à CART, avec les différences suivantes. Les branchements de l'arbre sont probabilistes. Les branchements de l'arbre dépendent de la valeur d'une combinaison linéaire des variables prédictives, et pas simplement d'une seule d'entre elles. On effectue une régression linéaire en chacune des feuilles de l'arbre (avec CART, on met une constante dans les feuilles). Il n'y a pas d'algorithme pour trouver la structure de l'arbre : il faut la choisir soi-même avant.
A FAIRE : Avec R ?
A FAIRE
heuristic(deal) Heuristic greedy search with random restart Title: Learning Bayesian Networks with Mixed Variables tune.rpart(e1071) Convenience tuning functions
??? A FAIRE pages 250-253
??? A FAIRE page 253
Vincent Zoonekynd
<zoonek@math.jussieu.fr>
latest modification on Wed Oct 13 22:33:03 BST 2004