The French version of this document is no longer maintained: be sure to check the more up-to-date English version.
Transformations
Valeurs manquantes
Valeurs aberrantes
A CLASSER
Avant de faire une régression, c'est probablement une bonne idée de se ramener à des variables à peu près normales. Cela permet, par exemple, de se ramener à des distributions symétriques, ou de se débarasser des valeurs extrèmes, qui peuvent avoir une très grande importantce sur le résultat de la régression. Dans beaucoup de cas, ça permet aussi de se débarasser des problèmes concernant les résidus, comme l'hétéroscédasticité.
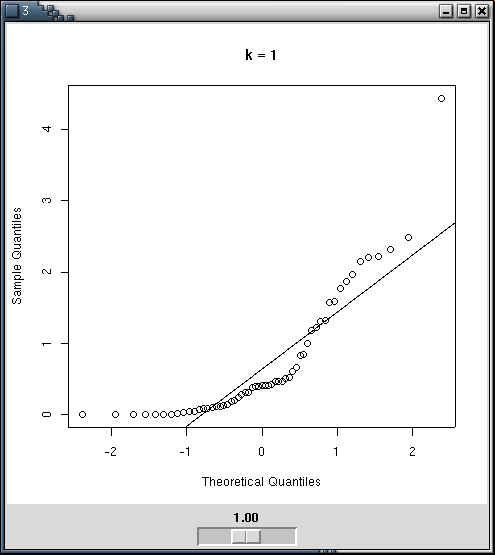
On peut faire ces transformations à la main, en utilisant des qqplots pour estimer la qualité de la transformation -- par exemple à l'aide d'un Widget Tk.
n <- 100
x <- abs(rnorm(n)) ^ runif(1,min=0,max=2)
library(tkrplot)
bb <- 1
my.qqnorm <- function () {
qqnorm(x^bb, main=paste('k =',bb, ", p-valeur (Shapiro) =", shapiro.test(x^bb)$p.value))
qqline(x^bb)
}
tt <- tktoplevel()
img <-tkrplot(tt, my.qqnorm)
f<-function(...) {
b <- as.numeric(tclvalue("bb"))
if (b != bb) {
bb <<- b
tkrreplot(img)
}
}
s <- tkscale(tt, command=f, from=0.05, to=2.00, variable="bb",
showvalue=TRUE, resolution=0.05, orient="horiz")
tkpack(img,s)

On peut aussi utiliser directement le test de Shapiro :
n <- 100
x <- abs(rnorm(n)) ^ runif(1,min=0,max=2)
kk <- seq(.01,5,by=.01)
N <- length(kk)
pv <- rep(NA, N)
for (i in 1:N) {
pv[i] <- shapiro.test( x^kk[i] )$p.value
}
plot( pv ~ kk, type='l', xlab='exposant', ylab='p-valeur' )
seuil <- .05
abline( v = kk[ range( (1:N)[pv>seuil] ) ], lty=3 )
abline( v = kk[pv==max(pv)], lty=3 )
abline( h = seuil, lty=3 )
title(main="Test de Shapiro")
Mais on peut aussi faire cela à l'aide de la fonction boxcox.
x <- exp( rnorm(100) ) y <- 1 + 2*x + .3*rnorm(100) y <- y^1.3 library(MASS) boxcox(y~x, plotit=T)

Il y en a une autre dans la bibliothèque car.
> summary( box.cox.powers(cbind(x,y)) ) Box-Cox Transformations to Multinormality Est.Power Std.Err. Wald(Power=0) Wald(Power=1) x 0.3994 0.0682 5.8519 -8.8011 y 0.2039 0.0683 2.9868 -11.6596 L.R. test, all powers = 0: 50.8764 df = 2 p = 0 L.R. test, all powers = 1: 263.585 df = 2 p = 0
Pour faciliter l'interprétation de la transformation, on s'efforcera toujours de choisir un exposant qui est une fraction simple (il est plus facile d'expliquer pourquoi on prend la racine cubique d'une certaine quantité, alors qu'expliquer aux commanditaires d'une étude statistiques pourquoi on éleve à la puissance 0.3994 une quantité qu'ils comprennent bien posera quelques petits problèmes...)
my.box.cox <- function (x, lambda=seq(-2,2,.01)) {
b <- boxcox(x, lambda=lambda)
# Calcul de l'intervalle de confiance (copié depuis le code de boxcox)
lim <- max(b$y) - qchisq(19/20,1)/2
l1 <- min(b$x[ b$y>lim ])
l2 <- max(b$x[ b$y>lim ])
# On cherche une fraction simple entre l1 et l2
done <- F
den <- 0
while (!done) {
den <- den+1
num <- floor(den*min(lambda))-1
nummax <- ceiling(den*max(lambda))
#cat(paste("DEN", den, "NUMMAX", nummax, "\n"))
while ((!done) & (num<=nummax)) {
num <- num+1
#cat(paste("den",den,"num",num,"\n"))
if( l1<=num/den & num/den<=l2 ){
done <- T
}
}
}
list(value=num/den, numérateur=num, dénominateur=den,
exact=b$x[ b$y==max(b$y) ],
int=c(l1,l2) )
}
my.box.cox(y~x) # 3/4Voici une comparaison des données initiales et des données transformées.
bc <- boxcox(y ~ x, plotit=F) a <- bc$x[ order(bc$y, decreasing=T)[1] ] op <- par( mfcol=c(1,2) ) plot( y~x ) plot( y^a ~ x ) par(op)

Voici des exemples plus concrets.
data(trees) plot(trees)

boxcox(Volume ~ Girth, data = trees)

boxcox(Volume ~ log(Height) + log(Girth), data = trees )

A FAIRE : je n'ai pas terminé de rédiger cette partie...
Il arrive que des valeurs manquent, car on n'a pas pu les observer, parce qu'on les a perdues ou parce qu'on s'est apperçu après coup qu'elles étaient incohérentes. Simplement oublier les individus correspondants n'est pas toujours une bonne idée : car cela revient à oublier toutes les observations de ces individus, même si elles ne manquaient pas. Si les données sont présentées sous forme de tableau, cela voudrait dire oublier une ligne dès qu'il manque une valeur dans cette ligne : on oublie donc aussi les autres valeurs de cette ligne, qui sont effectivement présentes.
Si les valeurs manquantes sont peu nombreuses, on peut les oublier sans aucun scrupule.
Si les valeurs manquantes sont absentes pour des raisons vraiment aléatoires (indépendemment des autres valeurs), on peut sans gros problème les remplacer par la moyenne ou la médiane des variables correspondantes.
Mais souvent, le fait qu'une valeur manque dépend de sa valeur : par exemple, si on demande le salaire dans un sondage, les gros revenus hésiteront à répondre : il faut en tenir compte.
n <- 100 v <- .1 x1 <- rlnorm(n) x2 <- rlnorm(n) x3 <- rlnorm(n) x4 <- x1 + x2 + x3 + v*rlnorm(n) m1 <- cbind(x1,x2,x3,x4) pairs(m1, main="Aucune valeur manquante")
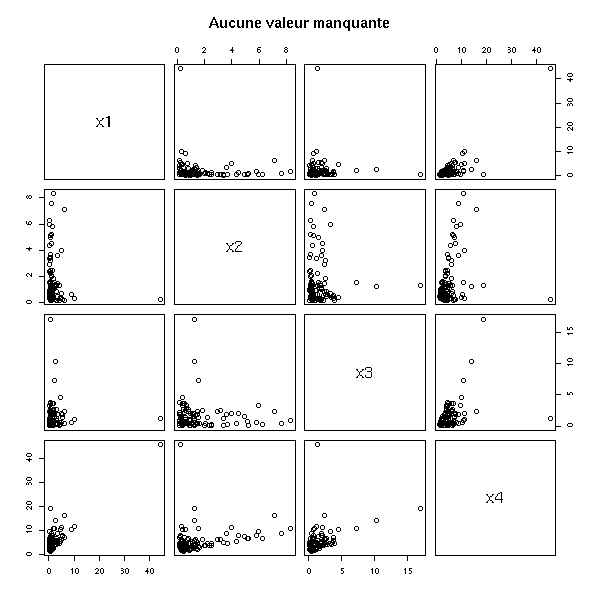
remove.higher.values <- function (x) {
n <- length(x)
ifelse( rbinom(n,1,(x-min(x))/(max(x)+1))==1 , NA, x)
}
x1 <- remove.higher.values(x1)
x2 <- remove.higher.values(x2)
x3 <- remove.higher.values(x3)
x4 <- remove.higher.values(x4)
m2 <- cbind(x1,x2,x3,x4)
pairs(m2, main="Quelques valeurs manquantes")
On constate, naturellement, que la moyenne des variables est plus basse qu'elle ne le devrait.
> apply(m2, 2, mean, na.rm=T)
x1 x2 x3 x4
1.158186 1.160651 1.298134 3.966040
> apply(m1, 2, mean, na.rm=T)
x1 x2 x3 x4
1.438024 1.652619 1.472807 4.710466A FAIRE : cet exemple est-il bon ??? Les valeurs manquantes ont-elles un effet réel sur le résultat d'une régression ou de prédictions ?
> lm(m2[,4]~m2[,-4]-1)
Coefficients:
m2[, -4]x1 m2[, -4]x2 m2[, -4]x3
1.026 1.030 1.021
> lm(m1[,4]~m1[,-4]-1)
Coefficients:
m1[, -4]x1 m1[, -4]x2 m1[, -4]x3
1.014 1.029 1.013
Pour tenter de voir si les données manquantes suivent un certain motif, on peut utiliser un arbre de décision.
for (i in 1:4) {
r <- rpart(factor(is.na(m2[,i]))~m2[,-i])
cat(paste("Coordonnée numéro", i, "\n"))
print(r)
}Il vient :
Coordonnée numéro 1
n= 100
node), split, n, loss, yval, (yprob)
* denotes terminal node
1) root 100 9 FALSE (9.1e-01 9.0e-02) *
Coordonnée numéro 2
n= 100
node), split, n, loss, yval, (yprob)
* denotes terminal node
1) root 100 9 FALSE (9.1e-01 9.0e-02) *
Coordonnée numéro 3
n=99 (1 observations deleted due to missing)
node), split, n, loss, yval, (yprob)
* denotes terminal node
1) root 99 13 FALSE (0.8686869 0.1313131) *
Coordonnée numéro 4
n= 100
node), split, n, loss, yval, (yprob)
* denotes terminal node
1) root 100 12 FALSE (0.88000000 0.12000000)
2) m2[, -i].x2< 3.397467 93 9 FALSE (0.90322581 0.09677419)
4) m2[, -i].x1< 1.066317 55 3 FALSE (0.94545455 0.05454545) *
5) m2[, -i].x1>=1.066317 38 6 FALSE (0.84210526 0.15789474)
10) m2[, -i].x1>=1.469563 31 2 FALSE (0.93548387 0.06451613) *
11) m2[, -i].x1< 1.469563 7 3 TRUE (0.42857143 0.57142857) *
3) m2[, -i].x2>=3.397467 7 3 FALSE (0.57142857 0.42857143) *On constate donc que le fait que l'une des trois premières variable manque ne dépend pas de la valeur des autres variables, par contre, le fait que la dernière variable manque dépend des valeurs des autres variables.
C'est généralement l'arbre de décision qui donne les résultats les plus intéressants (car c'est une méthode adaptée aux données manquantes), mais on peut en essayer d'autres.
A FAIRE : effacer ce paragraphe ?
On devrait arriver au même résultat avec une régression logistique,
mais ça n'est pas le cas (je ne comprends pas pourquoi).
for (i in 1:4) {
cat(paste("Coordonnée numéro", i, "\n"))
print(summary(glm( is.na(m2[,i]) ~ m2[,-i], family=binomial )))
}On peut commencer par regarder si le fait qu'une variable manque dépend du fait que les autres manquent, à l'aide d'une régression logistique
m3 <- data.frame(m2) summary(glm(is.na(x4) ~ is.na(x1) + is.na(x2) + is.na(x3), data=m3, family=binomial))
Il vient :
Coefficients:
Estimate Std. Error z value Pr(>|z|)
(Intercept) -1.8926 0.3613 -5.239 1.62e-07 ***
is.na(x1)TRUE 0.8266 0.7473 1.106 0.269
is.na(x2)TRUE -0.2042 0.7146 -0.286 0.775
is.na(x3)TRUE 0.7278 0.8865 0.821 0.412Donc le fait que x4 manque ne dépend pas du fait qu'une des autres variables manque. On pourrait aussi vérifier l'existence de relations plus complexes, avec des interactions :
summary(glm(is.na(x4) ~ is.na(x1) * is.na(x2) * is.na(x3), data=m3, family=binomial))
On arrive à la même conclusion.
Essayons maintenant de prédire le fait qu'une variable lanque en fonction de la valeur des autres variables. Si on essaye directement
r1 <- glm(is.na(x4) ~ x1+x2+x3, data=m3, family=binomial) r2 <- glm(is.na(x4) ~ 1, data=m3, family=binomial) anova(r1,r2)
Ca plante, car pour calculer la première régression, il commence par enlever les individus pour lesquels il manque au moins une observation.
m4 <- m3[!is.na(apply(m3,1,sum)),] r1 <- glm(is.na(x4) ~ x1+x2+x3, data=m4, family=binomial) r2 <- glm(is.na(x4) ~ 1, data=m4, family=binomial) anova(r1,r2) A FAIRE : revoir la régression logistique et interpréter ces résultats. A FAIRE : comprendre
Les fonctions naclus et naplot permettent de voir << où >> les données manquent.
op <- par(mfrow=c(2,2)) r <- naclus(data.frame(m2)) naplot(r) par(op)

op <- par(mfrow=c(2,2))
for(m in c("ward","complete","median")) {
plot(naclus(data.frame(m2), method=m))
title(m)
}
plot(naclus(data.frame(m2)))
title("Default")
par(op)
Essayons maintenant de montrer, sur cet exemple, qu'il est utile de tenir compte de ces valeurs manquantes.
Effectuons une régression, sans tenter de trouver les valeurs manquantes,
> lm(x4~x1+x2+x3)
Call:
lm(formula = x4 ~ x1 + x2 + x3)
Coefficients:
(Intercept) x1 x2 x3
0.1332 0.9874 1.0112 1.0133en les complétant avec la moyenne (ou la médiane) (ce qui donne des valeurs biaisées vers zéro),
median.impute <- function (x) {
x[ is.na(x) ] <- median(x)
x
}
y1 <- median.impute(x1)
y2 <- median.impute(x2)
y3 <- median.impute(x3)
y4 <- median.impute(x4)
> lm(y4 ~ x1+x2+x3)
Call:
lm(formula = y4 ~ x1 + x2 + x3)
Coefficients:
(Intercept) x1 x2 x3
0.2205 0.9890 0.9876 0.9732puis en tentant de les compléter, à l'aide de la fonction transcan.
library(Hmisc)
op <- par(mfrow=c(2,2))
w <- transcan(~x1+x2+x3+x4, imputed=T, transformed=T, trantab=T, impcat='tree',
data=data.frame(x1,x2,x3,x4), pl=TRUE)
par(op)
y1 <- impute(w,x1) y2 <- impute(w,x2) y3 <- impute(w,x3) y4 <- impute(w,x4)
Il vient :
> lm(y4~y1+y2+y3)
Call:
lm(formula = y4 ~ y1 + y2 + y3)
Coefficients:
(Intercept) y1 y2 y3
-0.4539 1.1403 1.2540 1.1498Sur cet exemple, les valeurs sont trop élevées, mais ça n'est pas général :
A FAIRE : comparer ces trois méthodes (oubli, médiane, transcan)
# La fonction transcan a changé depuis que j'ai écris ce code.
remove.higher.values <- function (x) {
n <- length(x)
ifelse( rbinom(n,1, ((x-min(x))/(max(x)+1))^.3 )==1 , NA, x)
}
N <- 100
# Oubli
c1 <- matrix(NA, nr=N, nc=4)
# Transcan
c2 <- matrix(NA, nr=N, nc=4)
# Médiane
c3 <- matrix(NA, nr=N, nc=4)
n <- 100
v <- .1
for (i in 1:N) {
x1 <- rlnorm(n)
x2 <- rlnorm(n)
x3 <- rlnorm(n)
x4 <- x1 + x2 + x3 + v*rlnorm(n)
m1 <- cbind(x1,x2,x3,x4)
x1 <- remove.higher.values(x1)
x2 <- ifelse(sample(c(T,F),n,replace=T), NA, x2)
x3 <- remove.higher.values(x3)
x4 <- remove.higher.values(x4)
m2 <- cbind(x1,x2,x3,x4)
d <- data.frame(x1,x2,x3,x4)
try( c1[i,] <- lm(x4~x1+x2+x3)$coefficients )
w <- NULL
try( w <- transcan(~x1+x2+x3+x4, imputed=T, transformed=T, impcat='tree', data=d) )
if(!is.null(w)){
y1 <- impute(w,x1,data=d)
y2 <- impute(w,x2,data=d)
y3 <- impute(w,x3,data=d)
y4 <- impute(w,x4,data=d)
try( c2[i,] <- lm(y4~y1+y2+y3)$coefficients )
}
median.impute <- function (x) {
x[ is.na(x) ] <- median(x)
x
}
y1 <- median.impute(x1)
y2 <- median.impute(x2)
y3 <- median.impute(x3)
y4 <- median.impute(x4)
try( c3[i,] <- lm(y4~x1+x2+x3)$coefficients )
}
boxplot(c2 ~ col(c2), col='light blue')
abline(h=c(0,1),lty=3)
%--Si on compare les valeurs avec ce que l'on obtiendrait en oubliant les valeurs manquantes, on se demande si c'était réellement une bonne idée...
#%G
boxplot( cbind(c1,c3,c2) ~
cbind( 3*col(c1)-2, 3*col(c3)-1, 3*col(c2)),
border=c(par('fg'), 'red', 'blue')[rep(c(1,2,3),4)],
ylim=c(-2,3)
)
abline(h=c(0,1),lty=3)
legend( par("usr")[1], par("usr")[3], yjust=0,
c("oubli", "médiane", "transcan"),
lwd=1, lty=1,
col=c(par('fg'),'red', 'blue') )
title(main="Traitement des données manquantes")
%--A FAIRE : donner un exemple un peu plus convainquant...
A FAIRE : expliquer pourquoi on a de si piètres résultats : transcan suppose que les données ne sont pas normales et les transforme avant de les traiter -- ici, elles sont réellement normales... (Mais ça ne devrait pas changer grand-chose...)
Il y a d'autres fonction pour inférer les valeurs manquantes :
A FAIRE ?transace
A FAIRE :
# Variables les plus liées plot(varclus(~x1+x2+x3))
A FAIRE : validation des imputations des valeurs manquantes (par exemple, avec du bootstrap : une fois qu'on a choisi un modèle, le calculer sur un échantillon de bootstrap et le valider sur l'échantillon initial) (plus simple : le calculer sur 90% des données et le valider sur les 10 % restants)
A FAIRE On peut les traiter comme les valeurs manquantes. A FAIRE : expliquer comment les repérer (graphiquement, en regardant les variables une par une (boxplot, histogramme, densité, qqnorm), deux par deux (pairs, ACP), en regardant les résidus, etc. A FAIRE : mentionner d'autres méthodes
Voir aussi les modèles linéaires généralisés (GAM), un peu plus loin.
A FAIRE : qu'est-ce que c'est ???
Find g, f1, ..., fn to maximize R^2 of the model g(Y) = f1(X1) + ... + fn(Xn) Quelle différence avec GAM ??? On transforme aussi la variable à prédire library(acepack) ?ace Exemple du manuel : library(acepack) TWOPI <- 8*atan(1) x <- runif(200,0,TWOPI) y <- exp(sin(x)+rnorm(200)/2) a <- ace(x,y) op <- par(mfrow=c(3,1)) plot(a$y,a$ty) # view the response transformation plot(a$x,a$tx) # view the carrier transformation plot(a$tx,a$ty) # examine the linearity of the fitted model par(op)

A FAIRE
Similar to ACE. library(acepack) ?avas library(acepack) TWOPI <- 8*atan(1) x <- runif(200,0,TWOPI) y <- exp(sin(x)+rnorm(200)/2) a <- avas(x,y) op <- par(mfrow=c(3,1)) plot(a$y,a$ty) # view the response transformation plot(a$x,a$tx) # view the carrier transformation plot(a$tx,a$ty) # examine the linearity of the fitted model par(op)

Vincent Zoonekynd
<zoonek@math.jussieu.fr>
latest modification on Wed Oct 13 22:32:58 BST 2004