The French version of this document is no longer maintained: be sure to check the more up-to-date English version.
Tests et intervalles de confiance
Comparaisons de modèles (Anova)
Quelques graphiques pour explorer une régression
Problèmes de la régression
A FAIRE
A FAIRE : regrouper ce chapitre avec le suivant ???
Après ce tour d'horizon des différentes régressions, revenons à la régression linéaire.
La commande summary permettait de faire un test T de Student sur les coefficients -- qui répond à la question << ce coefficient est-il significativement non nul ? >>.
> x <- rnorm(100)
> y <- 1 + 2*x + .3*rnorm(100)
> summary(lm(y~x))
...
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 1.08440 0.03224 33.64 <2e-16 ***
x 2.04051 0.03027 67.42 <2e-16 ***Dans le même exemple, on peut regarder si le coefficient constant est 1. (Quand on écrit une formule pour décrire un modèle, certaines opérations sont interprétées différemment (en particulier * et ^) : pour être sûr qu'elles seront interprétées comme des opérations arithmétiques sur les variables, on peut les entourer de I(...). Ici, ça n'est pas nécessaire.)
> x <- rnorm(100)
> y <- 1 + 2*x + .3*rnorm(100)
> summary(lm(I(y-1)~x))
Call:
lm(formula = I(y - 1) ~ x)
Residuals:
Min 1Q Median 3Q Max
-0.84692 -0.24891 0.02781 0.20486 0.60522
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) -0.01294 0.02856 -0.453 0.651
x 1.96405 0.02851 68.898 <2e-16 ***
---
Signif. codes: 0 `***' 0.001 `**' 0.01 `*' 0.05 `.' 0.1 ` ' 1
Residual standard error: 0.2855 on 98 degrees of freedom
Multiple R-Squared: 0.9798, Adjusted R-squared: 0.9796
F-statistic: 4747 on 1 and 98 DF, p-value: < 2.2e-16Sous l'hypothèse que ce coefficient est 1, regardons si le coefficient directer est nul.
> summary(lm(I(y-1)~0+x))
Call:
lm(formula = I(y - 1) ~ 0 + x)
Residuals:
Min 1Q Median 3Q Max
-0.85962 -0.26189 0.01480 0.19184 0.59227
Coefficients:
Estimate Std. Error t value Pr(>|t|)
x 1.96378 0.02839 69.18 <2e-16 ***
---
Signif. codes: 0 `***' 0.001 `**' 0.01 `*' 0.05 `.' 0.1 ` ' 1
Residual standard error: 0.2844 on 99 degrees of freedom
Multiple R-Squared: 0.9797, Adjusted R-squared: 0.9795
F-statistic: 4786 on 1 and 99 DF, p-value: < 2.2e-16Autre méthode :
> x <- rnorm(100)
> y <- 1 + 2*x + .3*rnorm(100)
> a <- rep(1,length(x))
> summary(lm(y~offset(a)-1+x))
Call:
lm(formula = y ~ offset(a) - 1 + x)
Residuals:
Min 1Q Median 3Q Max
-0.92812 -0.09901 0.09515 0.28893 0.99363
Coefficients:
Estimate Std. Error t value Pr(>|t|)
x 2.04219 0.03114 65.58 <2e-16 ***
---
Signif. codes: 0 `***' 0.001 `**' 0.01 `*' 0.05 `.' 0.1 ` ' 1
Residual standard error: 0.3317 on 99 degrees of freedom
Multiple R-Squared: 0.9816, Adjusted R-squared: 0.9815
F-statistic: 5293 on 1 and 99 DF, p-value: < 2.2e-16Regardons s'il est égal à deux.
> summary(lm(I(y-1-2*x)~0+x))
Call:
lm(formula = I(y - 1 - 2 * x) ~ 0 + x)
Residuals:
Min 1Q Median 3Q Max
-0.85962 -0.26189 0.01480 0.19184 0.59227
Coefficients:
Estimate Std. Error t value Pr(>|t|)
x -0.03622 0.02839 -1.276 0.205
Residual standard error: 0.2844 on 99 degrees of freedom
Multiple R-Squared: 0.01618, Adjusted R-squared: 0.006244
F-statistic: 1.628 on 1 and 99 DF, p-value: 0.2049Autre méthode :
> summary(lm(y~offset(1+2*x)+0+x))
Call:
lm(formula = y ~ offset(1 + 2 * x) + 0 + x)
Residuals:
Min 1Q Median 3Q Max
-0.92812 -0.09901 0.09515 0.28893 0.99363
Coefficients:
Estimate Std. Error t value Pr(>|t|)
x 0.04219 0.03114 1.355 0.179
Residual standard error: 0.3317 on 99 degrees of freedom
Multiple R-Squared: 0.9816, Adjusted R-squared: 0.9815
F-statistic: 5293 on 1 and 99 DF, p-value: < 2.2e-16De manière plus générale, on peut utiliser la commande offset lors d'une régression multilinéaire, lorsqu'on connait l'un des coefficients de manière exacte.
Autre méthode
x <- rnorm(100) y <- 1 + 2*x + .3*rnorm(100) library(car) linear.hypothesis( lm(y~x), matrix(c(1,0,0,1), 2, 2), c(1,2) )
Cela regarde si
[ 1 0 ] [ premier coefficient ] [ 1 ] [ ] * [ ] = [ ] [ 0 1 ] [ deuxième coefficient ] [ 2 ].
On obtient :
F-Test SS = 0.04165324 SSE = 9.724817 F = 0.2098763 Df = 2 and 98 p = 0.8110479
On peut calculer des intervalles de confiance des paramètres.
> library(MASS)
> n <- 100
> x <- rnorm(n)
> y <- 1 - 2*x + rnorm(n)
> r <- lm(y~x)
> r$coefficients
(Intercept) x
0.9569173 -2.1296830
> confint(r)
2.5 % 97.5 %
(Intercept) 0.7622321 1.151603
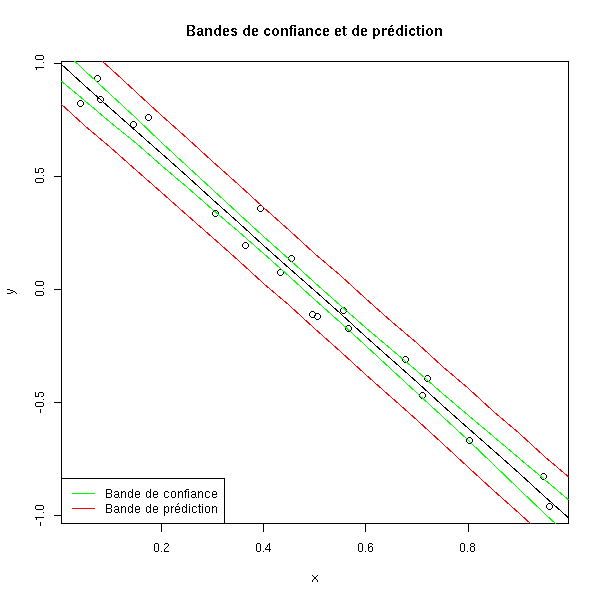
x -2.3023449 -1.957021On peut aussi chercher des intervalles de confiance des valeurs prédites. Il peut s'agir d'un intervale de confiance de aX+b (bande de confiance) ou, ce n'est pas pareil, de E[Y|X=x] (bande de prédiction).
x <- runif(20)
y <- 1-2*x+.1*rnorm(20)
res <- lm(y~x)
plot(y~x)
new <- data.frame( x=seq(0,1,length=21) )
p <- predict(res, new)
points( p ~ new$x, type='l' )
p <- predict(res, new, interval='confidence')
points( p[,2] ~ new$x, type='l', col="green" )
points( p[,3] ~ new$x, type='l', col="green" )
p <- predict(res, new, interval='prediction')
points( p[,2] ~ new$x, type='l', col="red" )
points( p[,3] ~ new$x, type='l', col="red" )
title(main="Bandes de confiance et de prédiction")
legend( par("usr")[1], par("usr")[3], yjust=0,
c("Bande de confiance", "Bande de prédiction"),
lwd=1, lty=1, col=c("green", "red") )
Si on s'éloigne, les intervalles grandissent démesurément.
plot(y~x, xlim=c(-1,2), ylim=c(-3,3))
new <- data.frame( x=seq(-2,3,length=200) )
p <- predict(res, new)
points( p ~ new$x, type='l' )
p <- predict(res, new, interval='confidence')
points( p[,2] ~ new$x, type='l', col="green" )
points( p[,3] ~ new$x, type='l', col="green" )
p <- predict(res, new, interval='prediction')
points( p[,2] ~ new$x, type='l', col="red" )
points( p[,3] ~ new$x, type='l', col="red" )
title(main="Bandes de confiance et de prédiction")
legend( par("usr")[1], par("usr")[3], yjust=0,
c("Bande de confiance", "Bande de prédiction"),
lwd=1, lty=1, col=c("green", "red") )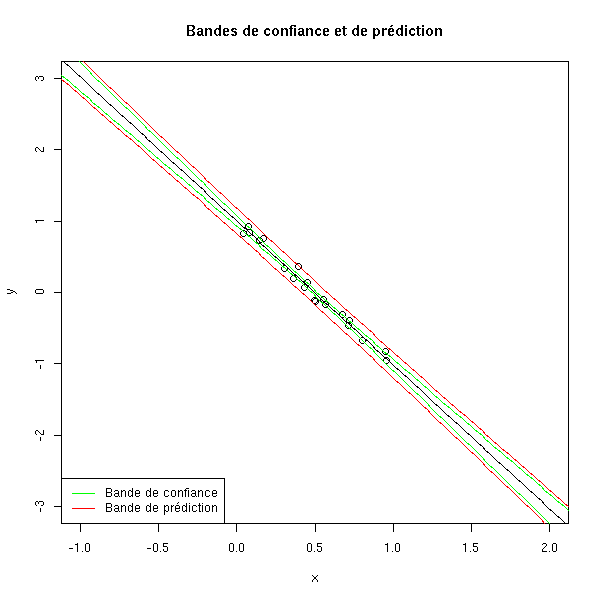
plot(y~x, xlim=c(-5,6), ylim=c(-11,11))
new <- data.frame( x=seq(-5,6,length=200) )
p <- predict(res, new)
points( p ~ new$x, type='l' )
p <- predict(res, new, interval='confidence')
points( p[,2] ~ new$x, type='l', col="green" )
points( p[,3] ~ new$x, type='l', col="green" )
p <- predict(res, new, interval='prediction')
points( p[,2] ~ new$x, type='l', col="red" )
points( p[,3] ~ new$x, type='l', col="red" )
title(main="Bandes de confiance et de prédiction")
legend( par("usr")[1], par("usr")[3], yjust=0,
c("Bande de confiance", "Bande de prédiction"),
lwd=1, lty=1, col=c("green", "red") )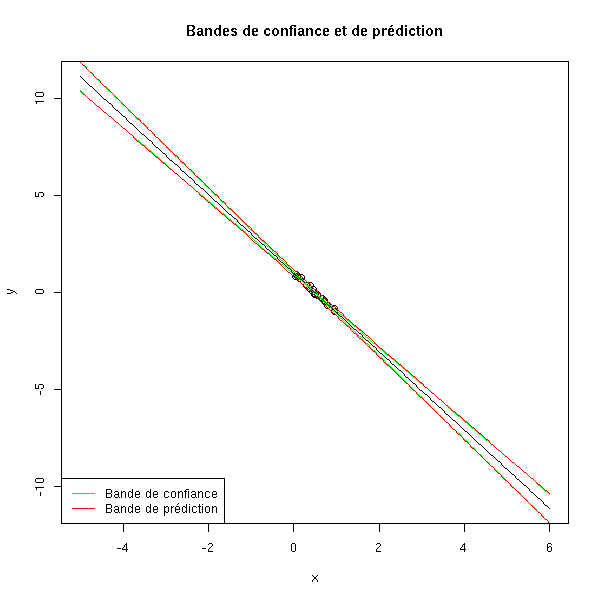
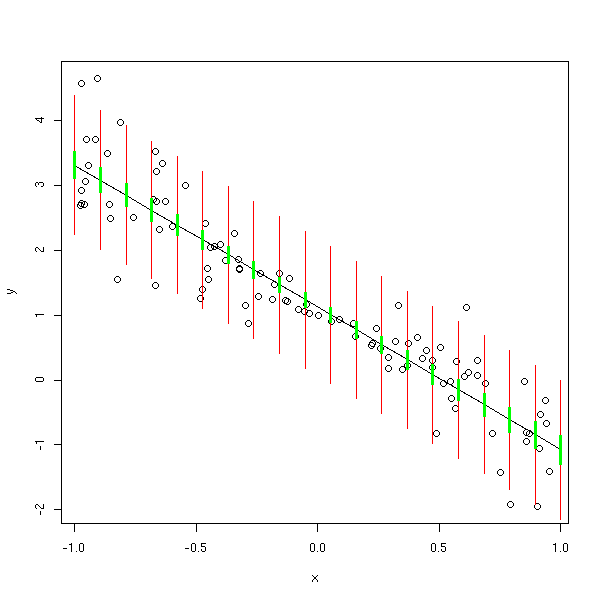
Voici d'autres manières de représenter les intervalles de confiance et de prédiction.
N <- 100 n <- 20 x <- runif(N, min=-1, max=1) y <- 1 - 2*x + rnorm(N, sd=abs(x)) res <- lm(y~x) plot(y~x) x0 <- seq(-1,1,length=n) new <- data.frame( x=x0 ) p <- predict(res, new) points( p ~ x0, type='l' ) p <- predict(res, new, interval='prediction') segments( x0, p[,2], x0, p[,3], col='red') p <- predict(res, new, interval='confidence') segments( x0, p[,2], x0, p[,3], col='green', lwd=3 )
mySegments <- function(a,b,c,d,...) {
u <- par('usr')
e <- (u[2]-u[1])/100
segments(a,b,c,d,...)
segments(a+e,b,a-e,b,...)
segments(c+e,d,c-e,d,...)
}
plot(y~x)
p <- predict(res, new)
points( p ~ x0, type='l' )
p <- predict(res, new, interval='prediction')
mySegments( x0, p[,2], x0, p[,3], col='red')
p <- predict(res, new, interval='confidence')
mySegments( x0, p[,2], x0, p[,3], col='green', lwd=3 )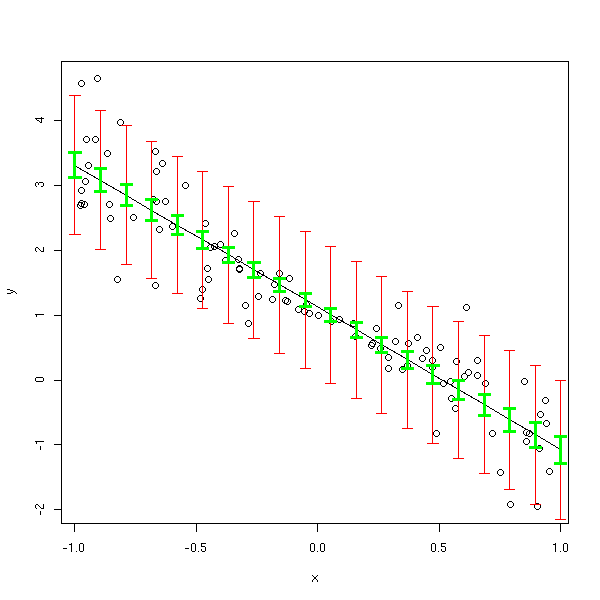
On peut chercher des intervalles de confiance pour un paramètre isolé -- on obtient un segment -- ou pour plusieurs paramètres en même temps -- on obtient un ellipsoïde plein : si on peut le tracer, il apporte plus d'information. On parle alors de région de confiance.
(L'ellipse qu'on obtient est penchée, car elle s'obtient à l'aide de la matrice de corrélation des deux variables : on diagonalise cette matrice dans une base othonormale et les vecteurs propres nous donnent les axes.)
library(ellipse)
my.confidence.region <- function (g, a=2, b=3) {
e <- ellipse(g,c(a,b))
plot(e,
type="l",
xlim=c( min(c(0,e[,1])), max(c(0,e[,1])) ),
ylim=c( min(c(0,e[,2])), max(c(0,e[,2])) ),
)
x <- g$coef[a]
y <- g$coef[b]
points(x,y,pch=18)
cf <- summary(g)$coefficients
ia <- cf[a,2]*qt(.975,g$df.residual)
ib <- cf[b,2]*qt(.975,g$df.residual)
abline(v=c(x+ia,x-ia),lty=2)
abline(h=c(y+ib,y-ib),lty=2)
points(0,0)
abline(v=0,lty="F848")
abline(h=0,lty="F848")
}
n <- 20
x1 <- rnorm(n)
x2 <- rnorm(n)
x3 <- rnorm(n)
y <- x1+x2+x3+rnorm(n)
g <- lm(y~x1+x2+x3)
my.confidence.region(g)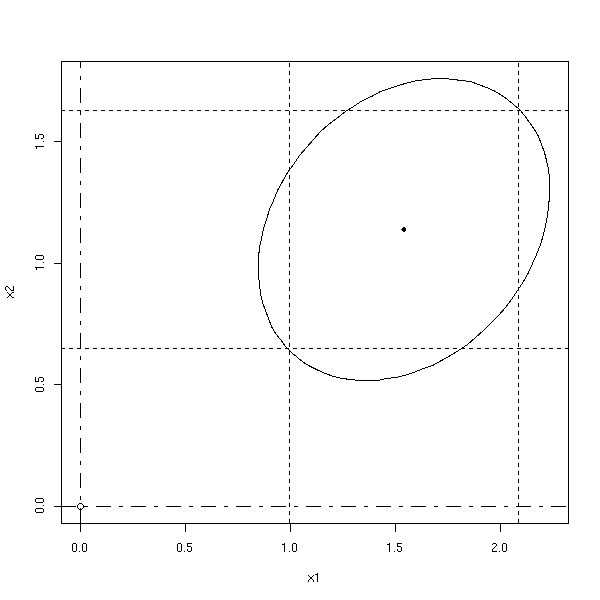
n <- 20 x <- rnorm(n) x1 <- x+.2*rnorm(n) x2 <- x+.2*rnorm(n) y <- x1+x2+rnorm(n) g <- lm(y~x1+x2) my.confidence.region(g)
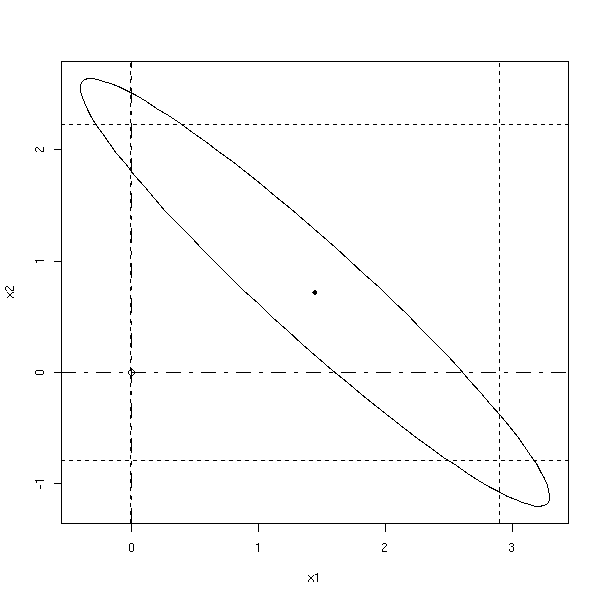
La probabilité que le point se trouve dans la zône coloriée est la même dans les trois cas :
my.confidence.region <- function (g, a=2, b=3, which=0, col='pink') {
e <- ellipse(g,c(a,b))
x <- g$coef[a]
y <- g$coef[b]
cf <- summary(g)$coefficients
ia <- cf[a,2]*qt(.975,g$df.residual)
ib <- cf[b,2]*qt(.975,g$df.residual)
xmin <- min(c(0,e[,1]))
xmax <- max(c(0,e[,1]))
ymin <- min(c(0,e[,2]))
ymax <- max(c(0,e[,2]))
plot(e,
type="l",
xlim=c(xmin,xmax),
ylim=c(ymin,ymax),
)
if(which==1){ polygon(e,col=col) }
else if(which==2){ rect(x-ia,par('usr')[3],x+ia,par('usr')[4],col=col,border=col) }
else if(which==3){ rect(par('usr')[1],y-ib,par('usr')[2],y+ib,col=col,border=col) }
lines(e)
points(x,y,pch=18)
abline(v=c(x+ia,x-ia),lty=2)
abline(h=c(y+ib,y-ib),lty=2)
points(0,0)
abline(v=0,lty="F848")
abline(h=0,lty="F848")
}
my.confidence.region(g, which=1)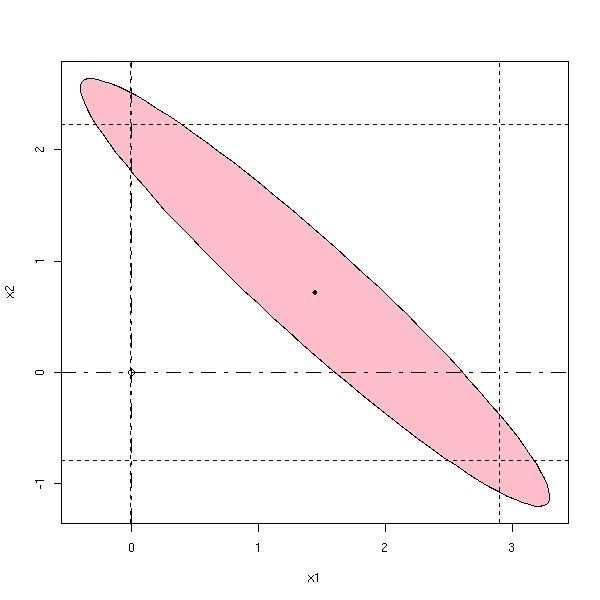
my.confidence.region(g, which=2)
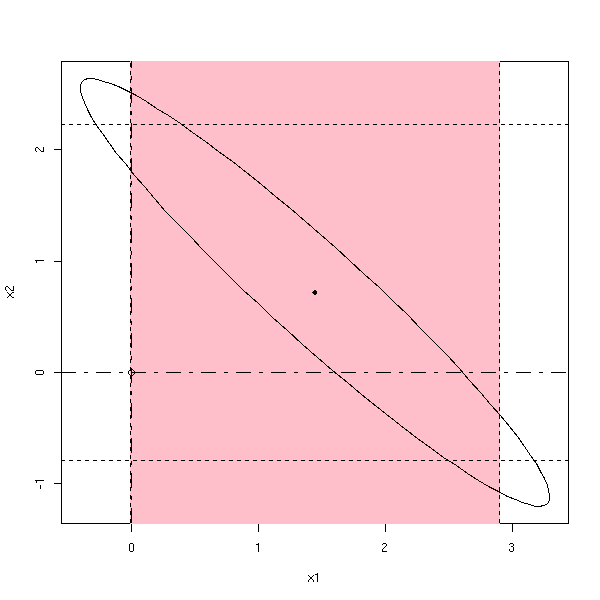
my.confidence.region(g, which=3)
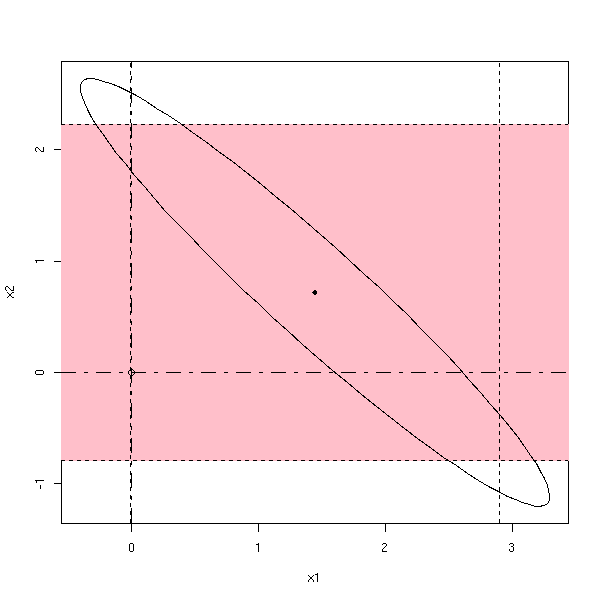
Lors d'une régression multiple, on s'efforce de prendre le moins de variables prédictives possibles, tout en ayant une prédiction correcte. Pour choisir ou éliminer des variables, on peut être tenté de faire plein de tests statistiques.
C'est une mauvaise idée.
En effet, à chaque test, on a un certain risque de commettre une erreur -- et ces risques d'erreur s'accumulent.
Néanmoins, on le fait souvent -- on a rarement le choix. On peut soit partir d'un modèle sans aucune variable, ajouter la variable Xi qui a la plus forte corrélation avec Y, puis ajouter successivement les variables qui procurent la plus grande augmentation de R^2, en s'arrétant lorsqu'on atteint une F-valeur préalablement fixée ; soit partir d'un modèle avec toutes les variables, et retirer successivement celles qui réduisent le moins R^2, en s'arrétant lorsqu'on atteint une F-valeur préalablement fixée.
A FAIRE : tukey, etc. (c'est dans le chapitre sur l'ANOVA).
Quand on écrit les résultats d'une régression ou d'une analyse de la variance, on se retrouve souvent avec un tableau rempli de << sommes de carrés >>.
RSS (Residual Sum of Squares) : c'est la quantité que l'on cherche à minimiser lors de la régression. On dispose d'une variable prédictive, X, et on cherche à prédire les valeurs d'une autre variable, Y. On écrit
hat Yi = b0 + b1 Xi
et on cherche les valeurs de b0 et b1 qui minimisent
RSS = Somme( (Yi - hat Yi)^2 ).
TSS (Total sum of squares) : c'est la quantité qu'on cherche à minimiser lorsqu'on définit la moyenne de Y.
TSS = Somme( (Yi - bar Y)^2 )
ESS (Explained Sum of Squares) : c'est la différence entre les valeurs précédentes. On peut aussi l'écrire comme une somme de carrés.
ESS = Somme( ( hat Yi - bar Y )^2 )
R-square : c'est le coefficient de détermination (ou pourcentage de variance de Y expliquée par X). Plus il est proche de 1, plus la régression explique les variations de Y.
R^2 = ESS/TSS.
On peut interpréter graphiquement le coefficient de détermination. Les données sont réparties autour d'une bande de hauteur RSS autour de la droite de régression, alors que la hauteur du dessin est TSS. On a alors R^2=1-RSS/TSS.
n <- 20000 x <- runif(n) y <- 4 - 8*x + rnorm(n) plot(y~x, pch='.') abline(lm(y~x), col='red') arrows( .1, -6, .1, 6, code=3, lwd=3, col='blue' ) arrows( .9, -3.2-2, .9, -3.2+2, code=3, lwd=3, col='blue' ) text( .1, 6, "TSS", adj=c(0,0), cex=2, col='blue' ) text( .9, -3.2+2, "RSS", adj=c(1,0), cex=2, col='blue' )
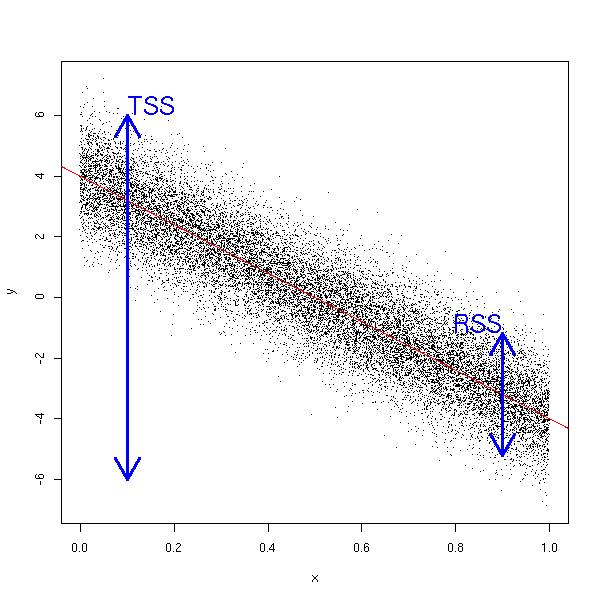
Nous avons vu trois manières d'afficher les résultats d'une régression : avec les commandes print, summary et anova. La dernière ligne du résultat de la commande summary fait une comparaison entre le modèle et un modèle nul.
> x <- rnorm(100)
> y <- 1 + 2*x + .3*rnorm(100)
> summary(lm(y~x))
Call:
lm(formula = y ~ x)
Residuals:
Min 1Q Median 3Q Max
-0.84692 -0.24891 0.02781 0.20486 0.60522
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 0.98706 0.02856 34.56 <2e-16 ***
x 1.96405 0.02851 68.90 <2e-16 ***
---
Signif. codes: 0 `***' 0.001 `**' 0.01 `*' 0.05 `.' 0.1 ` ' 1
Residual standard error: 0.2855 on 98 degrees of freedom
Multiple R-Squared: 0.9798, Adjusted R-squared: 0.9796
F-statistic: 4747 on 1 and 98 DF, p-value: < 2.2e-16Le résultat de la commande anova explique d'où viennent ces chiffres : on nous donne les sommes de carrés, leur moyenne (on les divise par le nombre de degrés de liberté), leur quotient (F value), et la probabilité que leur quotient soit aussi élevé si le coefficient directeur de la droite est nul (c'est donc la p-valeur d'un test dont l'hypothèse nulle est l'annulation de ce coefficient directeur).
> anova(lm(y~x))
Analysis of Variance Table
Response: y
Df Sum Sq Mean Sq F value Pr(>F)
x 1 386.97 386.97 4747 < 2.2e-16 ***
Residuals 98 7.99 0.08
---
Signif. codes: 0 `***' 0.001 `**' 0.01 `*' 0.05 `.' 0.1 ` ' 1De manière plus générale, la commande anova permet de comparer des modèles.
Lors d'une régression multiple, on s'efforce de prendre le moins de variables possibles. On est ainsi amené à comparer des modèles : par exemple, comparer un modèle avec plein de variables et un autre avec moins de variables.
La commande anova permet d'effectuer ce genre de comparaison.
data(trees) r1 <- lm(Volume ~ Girth, data=trees) r2 <- lm(Volume ~ Girth + Height, data=trees) anova(r1,r2)
Le résultat,
Analysis of Variance Table Model 1: Volume ~ Girth Model 2: Volume ~ Girth + Height Res.Df RSS Df Sum of Sq F Pr(>F) 1 29 524.30 2 28 421.92 1 102.38 6.7943 0.01449 * --- Signif. codes: 0 `***' 0.001 `**' 0.01 `*' 0.05 `.' 0.1 ` ' 1
nous dit que les deux modèles sont sensiblement différents avec un risque d'erreur inférieur à 2%.
Voici d'autres exemples.
x1 <- rnorm(100) x2 <- rnorm(100) x3 <- rnorm(100) b <- .1* rnorm(100) y <- 1 + x1 + x2 + x3 + b r1 <- lm( y ~ x1 ) r2 <- lm( y ~ x1 + x2 + x3 ) anova(r1,r2) # p-valeur = 2e-16 y <- 1 + x1 r1 <- lm( y ~ x1 ) r2 <- lm( y ~ x1 + x2 + x3 ) anova(r1,r2) # p-valeur = 0.25 y <- 1 + x1 + .02*x2 - .02*x3 + b r1 <- lm( y ~ x1 ) r2 <- lm( y ~ x1 + x2 + x3 ) anova(r1,r2) # p-valeur = 0.10
On peut comparer plus de 2 modèles (chaque modèle est inclus dans le suivant).
y <- 1 + x1 + x2 + x3 + b r1 <- lm( y ~ x1 ) r2 <- lm( y ~ x1 + x2 ) r3 <- lm( y ~ x1 + x2 + x3 ) anova(r1,r2,r3) # p-valeurs = 2e-16 (toutes les deux)
Si, lors de la comparaison de deux modèles, on trouve une p-valeur importante, i.e., si les deux modèles ne sont pas significativement différents, on peut abandonnera le plus complexe pour retenir le plus simple.
On peut présenter les calculs que l'on fait dans une régression linéaire dans un tableau d'analyse de variance. Et le principe des calculs est en fait le même : on cherche à exprimer la variance de Y comme somme de la variance d'une expression linéaire en X et d'une variance résiduelle, en minimisant cette variance résiduelle.
x <- runif(10) y <- 1 + x + .2*rnorm(10) anova(lm(y~x))
La table d'analyse de variance nous dit qu'effectivement, Y dépend de X (avec un risque d'erreur inférieur à 1%).
Analysis of Variance Table
Response: y
Df Sum Sq Mean Sq F value Pr(>F)
x 1 0.85633 0.85633 20.258 0.002000 **
Residuals 8 0.33817 0.04227Ca marche toujours avec plusieurs variables.
x <- runif(10) y <- runif(10) z <- 1 + x - y + .2*rnorm(10) anova(lm(z~x+y))
La table d'analyse de variance nous dit que z dépend de x et de y, avec un risque d'erreur inférieur à 1%.
Analysis of Variance Table
Response: z
Df Sum Sq Mean Sq F value Pr(>F)
x 1 2.33719 2.33719 45.294 0.0002699 ***
y 1 0.73721 0.73721 14.287 0.0068940 **
Residuals 7 0.36120 0.05160On peut remarquer que le résultat dépend de l'ordre des paramètres.
> anova(lm(z~y+x))
Analysis of Variance Table
Response: z
Df Sum Sq Mean Sq F value Pr(>F)
y 1 2.42444 2.42444 46.985 0.000241 ***
x 1 0.64996 0.64996 12.596 0.009355 **
Residuals 7 0.36120 0.05160Dans certains cas on peut même avoir des résultats contradictoires : selon l'ordre des variables indépendantes, on peut tantôt trouver que z dépend de x, tantôt qu'il n'en dépend pas.
> x <- runif(10)
> y <- runif(10)
> z <- 1 + x + 5*y + .2*rnorm(10)
> anova(lm(z~x+y))
Analysis of Variance Table
Response: z
Df Sum Sq Mean Sq F value Pr(>F)
x 1 0.0104 0.0104 0.1402 0.7192
y 1 7.5763 7.5763 102.1495 1.994e-05 ***
Residuals 7 0.5192 0.0742
> anova(lm(z~y+x))
Analysis of Variance Table
Response: z
Df Sum Sq Mean Sq F value Pr(>F)
y 1 7.1666 7.1666 96.626 2.395e-05 ***
x 1 0.4201 0.4201 5.664 0.04889 *
Residuals 7 0.5192 0.0742
Les résidus sont les différences entre les valeurs prédites et les valeurs observées.
Ca n'est pas exactement le bruit qui apparait dans le modèle (Y = a + b X + bruit). La simulation suivante permet d'estimer la variance des résidus : on trouve 0.008893307 alors que la variance du bruit était 0.01. En effet, le bruit est la différence entre les valeurs observées et le modèle réel, alors que les résidus sont la différence entre le modèle estimé d'après l'échantillon et les valeurs observées.
a <- 1
b <- -2
s <- .1
n <- 10
N <- 1e6
v <- NULL
for (i in 1:N) {
x <- rnorm(n)
y <- 1-2*x+s*rnorm(n)
v <- append(v, var(lm(y~x)$res))
}
mean(v)On peut montrer que la variance du résidu de l'observation i est :
sigma^2 * ( 1 - h_i )
où sigma^2 est la variance du bruit et h_i l'"effet de levier" ("leverage", en anglais) de l'observation i (le i-ième terme diagonal de t(X)%*%X).
Il s'agit des résidus normalisés. Pour estimer la variance, on prend tout l'échantillon.
?rstandard
Il s'agit encore des résidus normalisés, mais cette fois-ci, pour estimer la variance, on prend l'échantillon sans l'observation courrante.
?rstudent
Considérons l'exemple suivant.
n <- 100 x1 <- rnorm(n) x2 <- rnorm(n) x3 <- x1^2+rnorm(n) x4 <- 1/(1+x2^2)+.2*rnorm(n) y <- 1+x1-x2+x3-x4+.1*rnorm(n) pairs(cbind(x1,x2,x3,x4,y))
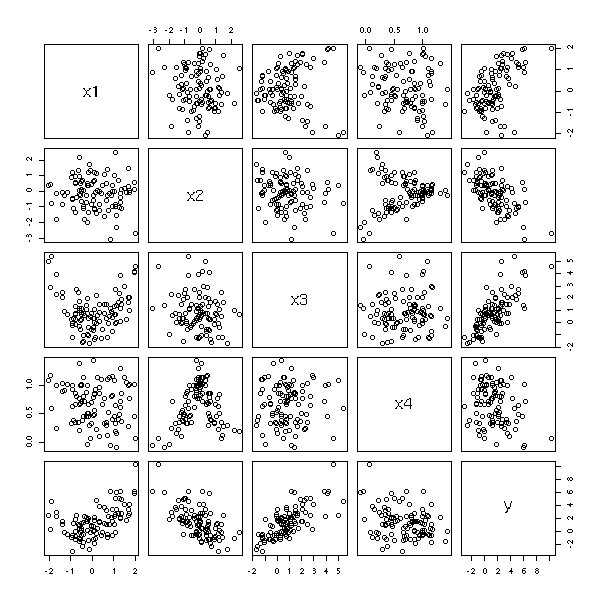
Les résidus constituent une variable statistique comme une autre : on peut les observer à l'aide de boite à moustaches, histogramme, qqplot, etc. On peut aussi les représenter en fonction des valeurs prédites, en fonction de chacune des cariables prédictives, ou en fonction du numéro de l'observation.
r <- lm(y~x1+x2+x3+x4) boxplot(r$res, horizontal=T)
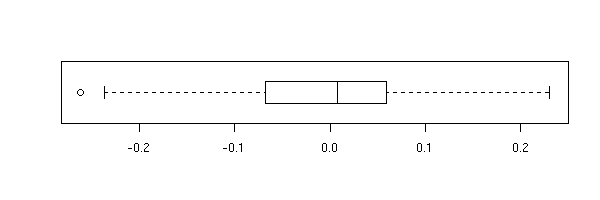
hist(r$res)
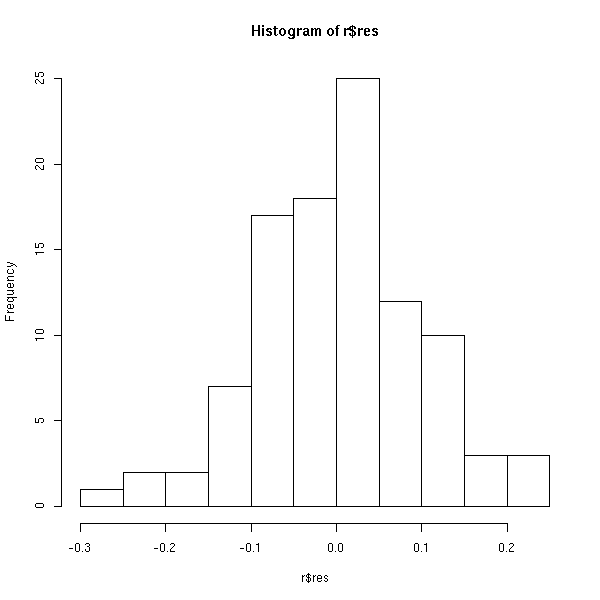
plot(r$res, main='Résidus')
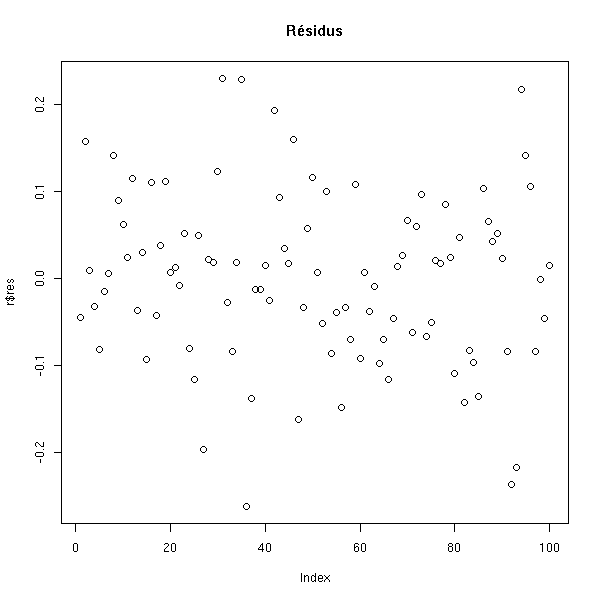
plot(rstandard(r), main='Résidus standardisés')
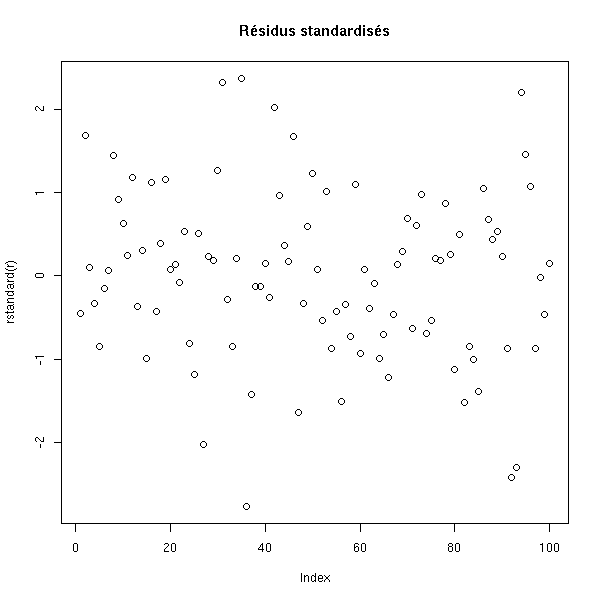
plot(rstudent(r), main="Résidus studentisés")
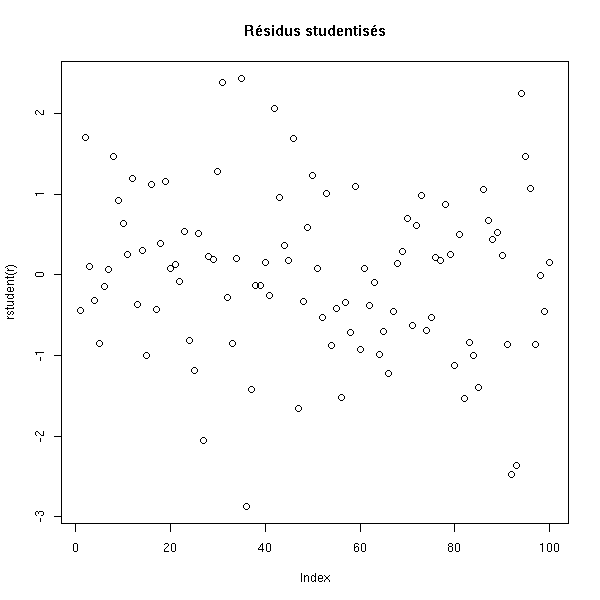
plot(r$res ~ r$fitted.values, main="Résidus et valeurs prédites") abline(h=0, lty=3)
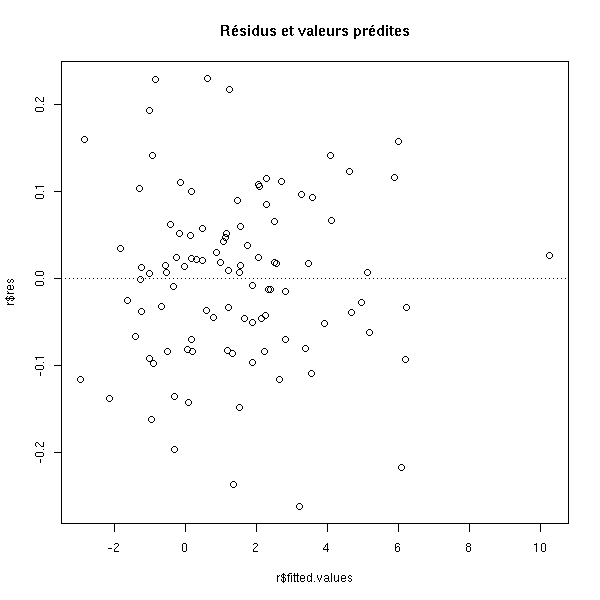
op <- par(mfrow=c(2,2)) plot(r$res ~ x1) abline(h=0, lty=3) plot(r$res ~ x2) abline(h=0, lty=3) plot(r$res ~ x3) abline(h=0, lty=3) plot(r$res ~ x4) abline(h=0, lty=3) par(op)
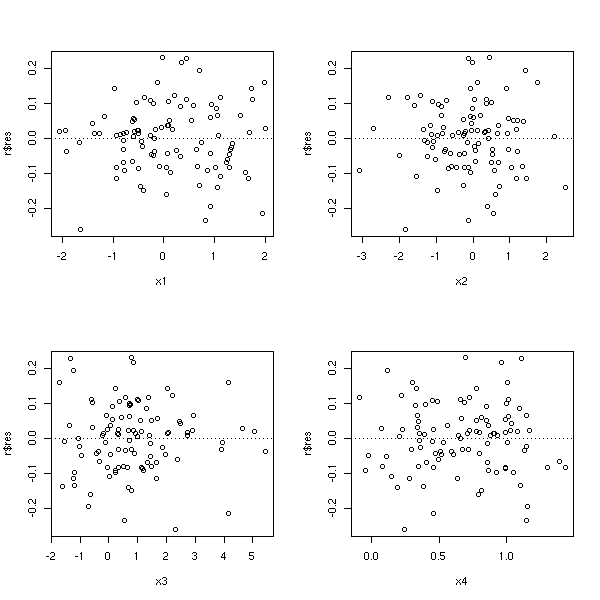
n <- 100
x1 <- rnorm(n)
x2 <- 1:n
y <- rnorm(1)
for (i in 2:n) {
y <- c(y, y[i-1] + rnorm(1))
}
y <- x1 + y
r <- lm(y~x1+x2) # Ou simplement : lm(y~x1)
op <- par(mfrow=c(2,1))
plot( r$res ~ x1 )
plot( r$res ~ x2 )
par(op)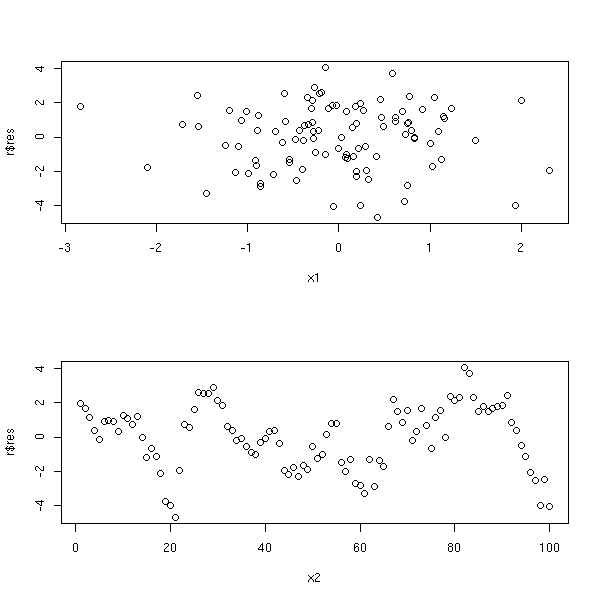
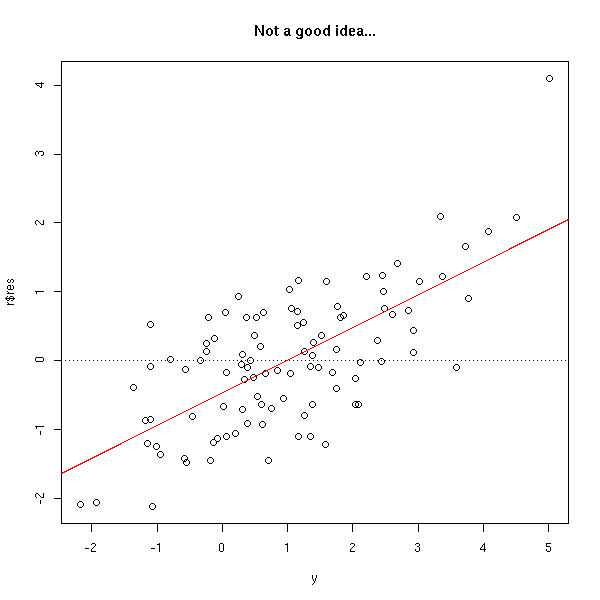
C'est généralement une mauvaise idée de représenter les résidus en fonction des valeurs effectivement observées, car le terme de bruit est présent sur les deux axes, et on représente presque le bruit en fonction de lui-même...
n <- 100 x <- rnorm(n) y <- 1-x+rnorm(n) r <- lm(y~x) plot(r$res ~ y) abline(h=0, lty=3) abline(lm(r$res~y),col='red') title(main='Not a good idea...')
On a une variable dépendante Y et deux variables indépendantes X1 et X2. On peut étudier l'effet de X1 sur Y après s'être débarassé de l'effet (linéaire) de X2. Pour cela, on fait une régression de Y sur X2, une régression de X1 sur X2, et on trace les résidus de la première en fonction de ceux de la seconde.
Ces graphiques permettent, par exemple, de repérer les points influents.
partial.regression.plot <- function (y, x, n, ...) {
m <- as.matrix(x[,-n])
y1 <- lm(y ~ m)$res
x1 <- lm(x[,n] ~ m)$res
plot( y1 ~ x1, ... )
abline(lm(y1~x1), col='red')
}
n <- 100
x1 <- rnorm(n)
x2 <- rnorm(n)
x3 <- x1+x2+rnorm(n)
x <- cbind(x1,x2,x3)
y <- x1+x2+x3+rnorm(n)
op <- par(mfrow=c(2,2))
partial.regression.plot(y, x, 1)
partial.regression.plot(y, x, 2)
partial.regression.plot(y, x, 3)
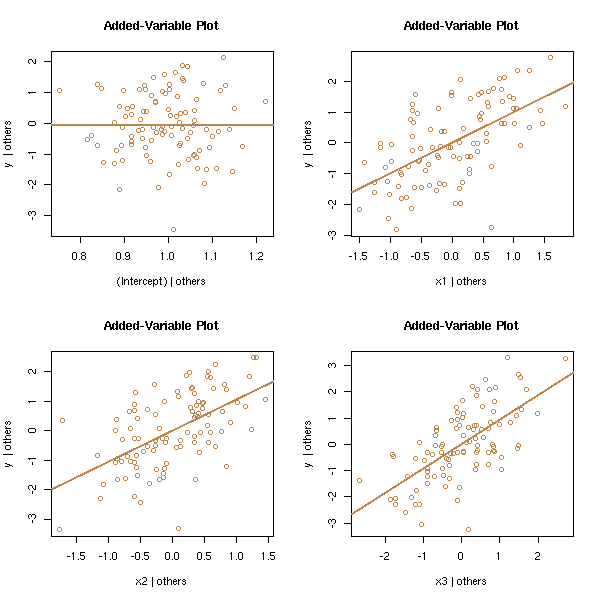
par(op)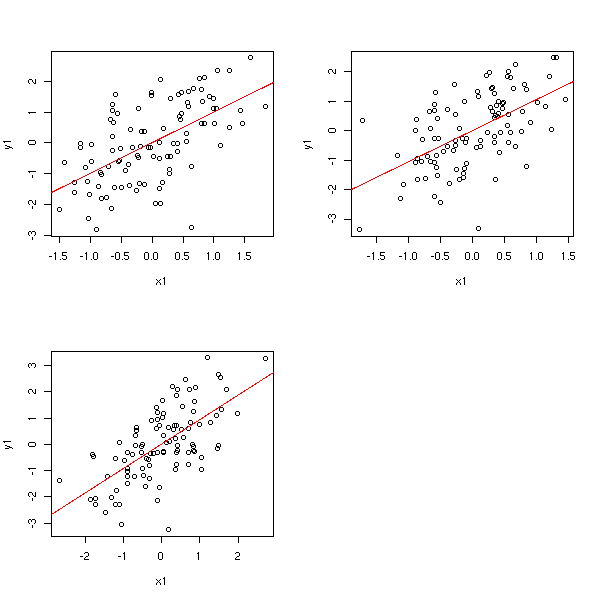
Il y a déjà une commande av.plot dans la bibliothèque car qui fait ce genre de chose.
library(car) av.plots(lm(y~x1+x2+x3),ask=F)
La commande leverage.plots, toujours dans la bibliothèque car, en est une généralisation.
?leverage.plots
Ca ressemble beaucoup à la régression partielle. On représente Y, auquel on a retiré l'effet des X_j (j différent de i), en fonction de X_i. C'est plus efficace que la régression partielle pour repérer la non-linéarité (mais la régression partielle permet mieux de repérer les points atypiques ou influents).
my.partial.residual.plot <- function (y, x, i, ...) {
r <- lm(y~x)
xi <- x[,i]
# Y, auquel on a retiré l'effet des X_j
yi <- r$residuals + r$coefficients[i] * x[,i]
plot( yi ~ xi, ... )
}
n <- 100
x1 <- rnorm(n)
x2 <- rnorm(n)
x3 <- x1+x2+rnorm(n)
x <- cbind(x1,x2,x3)
y <- x1+x2+x3+rnorm(n)
op <- par(mfrow=c(2,2))
my.partial.residual.plot(y, x, 1)
my.partial.residual.plot(y, x, 2)
my.partial.residual.plot(y, x, 3)
par(op)
Les bibliothèques car ou Design permettent de faire ces graphiques diretement.
library(car) ?cr.plots ?ceres.plots library(Design) ?plot.lrm.partial ?lrm
Dans cette partie, nous énumérons certains différents problèmes que l'on peut rencontrer lors d'une régression et expliquons comment les repérer à l'aide de graphiques. Souvent, on peut résoudre ces problèmes en transformant les variables, en changeant le modèle ou en utilisant un autre type de régression.
La commande plot produit quatre graphiques permettant d'évaluer la qualité et la pertinence d'une régression.
data(crabs) n <- length(crabs$RW) r <- lm(FL~RW, data=crabs) op <- par(mfrow=c(2,2)) plot(r) par(op)
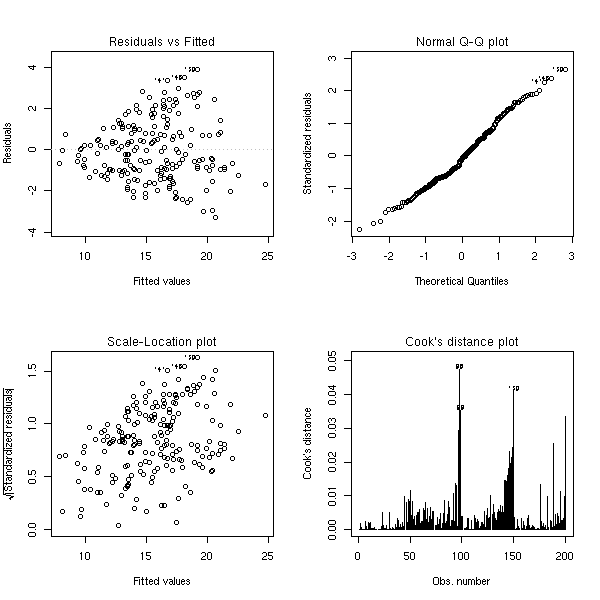
Ces graphiques restent valables en dimensions supérieures. Voici l'exemple du manuel (on prédit une variable à partir de quatre autres).
data(LifeCycleSavings) plot(LifeCycleSavings)
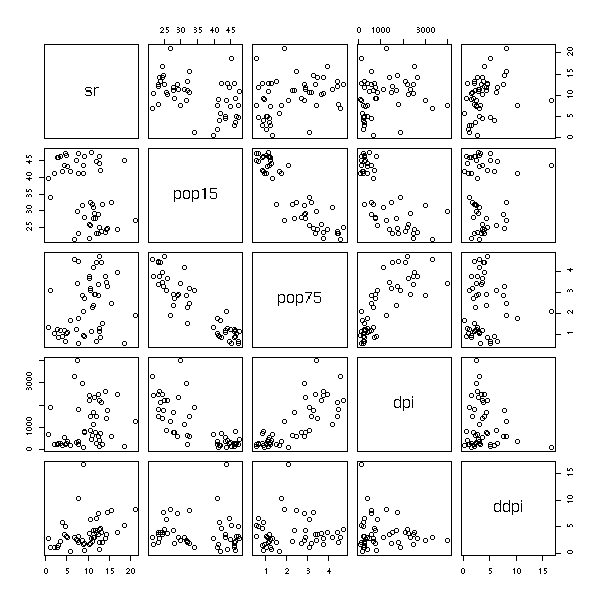
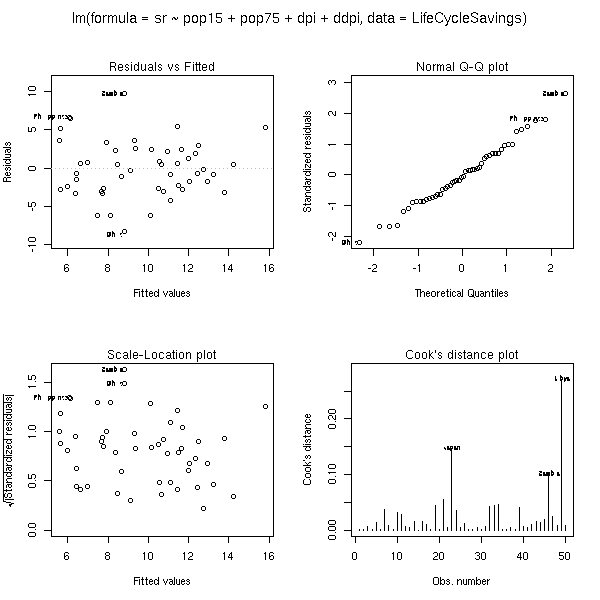
op <- par(mfrow = c(2, 2), oma = c(0, 0, 2, 0)) plot(lm.SR <- lm(sr ~ pop15 + pop75 + dpi + ddpi, data = LifeCycleSavings)) par(op)
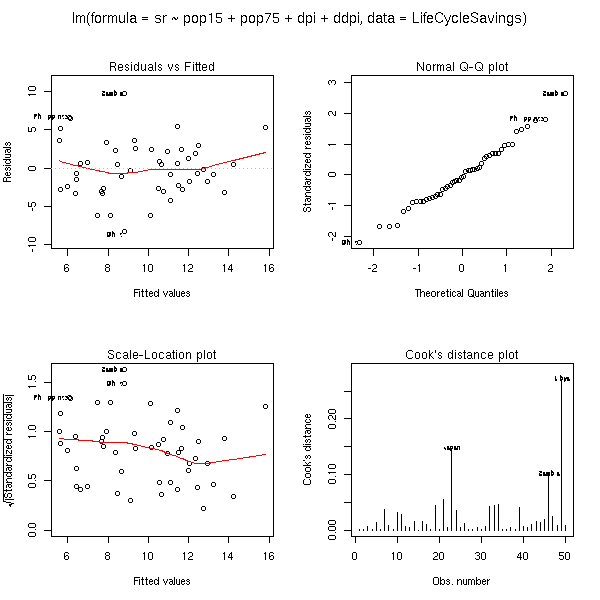
## 4 plots on 1 page; allow room for printing model formula in outer margin: op <- par(mfrow = c(2, 2), oma = c(0, 0, 2, 0)) #plot(lm.SR) #plot(lm.SR, id.n = NULL) # no id's #plot(lm.SR, id.n = 5, labels.id = NULL)# 5 id numbers plot(lm.SR, panel = panel.smooth) ## Gives a smoother curve #plot(lm.SR, panel = function(x,y) panel.smooth(x, y, span = 1)) par(op)
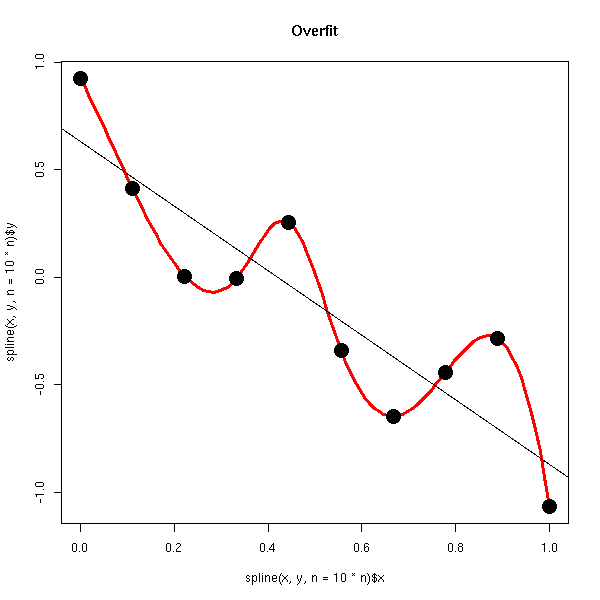
Il est possible que la régression colle trop près aux données, au point que le modèle en devienne irréaliste. La situation n'est pas toujours aussi flagrante que dans cet exemple. Néanmoins, si on est amené à choisir un modèle non linéaire, il faut pouvoir le justifier. En particulier, il faut comparer le nombre de paramètres à estimer avec le nombre d'observations...
n <- 10 x <- seq(0,1,length=n) y <- 1-2*x+.3*rnorm(n) plot(spline(x, y, n = 10*n), col = 'red', type='l', lwd=3) points(y~x, pch=16, lwd=3, cex=2) abline(lm(y~x)) title(main='Overfit')
C'est essentiellement du bon sens. On peut aussi comparer (dans le cas d'une régression linéaire) le coefficient de détermination (qui est proche de 1 dans ce cas) et le coefficient de détermination ajusté (qui tient compte de ce problème).
> summary(lm(y~poly(x,n-1)))
Call:
lm(formula = y ~ poly(x, n - 1))
Residuals:
ALL 10 residuals are 0: no residual degrees of freedom!
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 0.01196
poly(x, n - 1)1 -1.94091
poly(x, n - 1)2 -0.02303
poly(x, n - 1)3 -0.08663
poly(x, n - 1)4 -0.06938
poly(x, n - 1)5 -0.34501
poly(x, n - 1)6 -0.51048
poly(x, n - 1)7 -0.28479
poly(x, n - 1)8 -0.22273
poly(x, n - 1)9 0.39983
Residual standard error: NaN on 0 degrees of freedom
Multiple R-Squared: 1, Adjusted R-squared: NaN
F-statistic: NaN on 9 and 0 DF, p-value: NA
> summary(lm(y~poly(x,n-2)))
Call:
lm(formula = y ~ poly(x, n - 2))
Residuals:
1 2 3 4 5 6 7 8 9 10
-0.001813 0.016320 -0.065278 0.152316 -0.228473 0.228473 -0.152316 0.065278 -0.016320 0.001813
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 0.01196 0.12644 0.095 0.940
poly(x, n - 2)1 -1.94091 0.39983 -4.854 0.129
poly(x, n - 2)2 -0.02303 0.39983 -0.058 0.963
poly(x, n - 2)3 -0.08663 0.39983 -0.217 0.864
poly(x, n - 2)4 -0.06938 0.39983 -0.174 0.891
poly(x, n - 2)5 -0.34501 0.39983 -0.863 0.547
poly(x, n - 2)6 -0.51048 0.39983 -1.277 0.423
poly(x, n - 2)7 -0.28479 0.39983 -0.712 0.606
poly(x, n - 2)8 -0.22273 0.39983 -0.557 0.676
Residual standard error: 0.3998 on 1 degrees of freedom
Multiple R-Squared: 0.9641, Adjusted R-squared: 0.6767
F-statistic: 3.355 on 8 and 1 DF, p-value: 0.4Si on est plus raisonnable, le coefficient de détermination et le coefficient de détermination ajusté sont très proches.
> x <- seq(0,1,length=n)
> y <- 1-2*x+.3*rnorm(n)
> summary(lm(y~poly(x,10)))
Call:
lm(formula = y ~ poly(x, 10))
Residuals:
Min 1Q Median 3Q Max
-0.727537 -0.206951 -0.002332 0.177562 0.902353
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) -0.01312 0.02994 -0.438 0.662
poly(x, 10)1 -6.11784 0.29943 -20.431 <2e-16 ***
poly(x, 10)2 -0.11099 0.29943 -0.371 0.712
poly(x, 10)3 -0.04936 0.29943 -0.165 0.869
poly(x, 10)4 -0.28863 0.29943 -0.964 0.338
poly(x, 10)5 -0.15348 0.29943 -0.513 0.610
poly(x, 10)6 0.12146 0.29943 0.406 0.686
poly(x, 10)7 0.05066 0.29943 0.169 0.866
poly(x, 10)8 0.09707 0.29943 0.324 0.747
poly(x, 10)9 0.07554 0.29943 0.252 0.801
poly(x, 10)10 0.42494 0.29943 1.419 0.159
---
Signif. codes: 0 `***' 0.001 `**' 0.01 `*' 0.05 `.' 0.1 ` ' 1
Residual standard error: 0.2994 on 89 degrees of freedom
Multiple R-Squared: 0.8256, Adjusted R-squared: 0.8059
F-statistic: 42.12 on 10 and 89 DF, p-value: < 2.2e-16
> summary(lm(y~poly(x,1)))
...
Multiple R-Squared: 0.8182, Adjusted R-squared: 0.8164
...
Si l'échantillon est trop petit, on risque de ne pas pouvoir estimer grand-chose. On est alors contraint de se limiter à des modèles simples (linéaires), voire simplistes, car le risque de surmodélisation (overfitting) est trop grand.
Parfois, le modèle est trop simpliste.
x <- runif(100, -1, 1) y <- 1-x+x^2+.3*rnorm(100) plot(y~x) abline(lm(y~x), col='red')
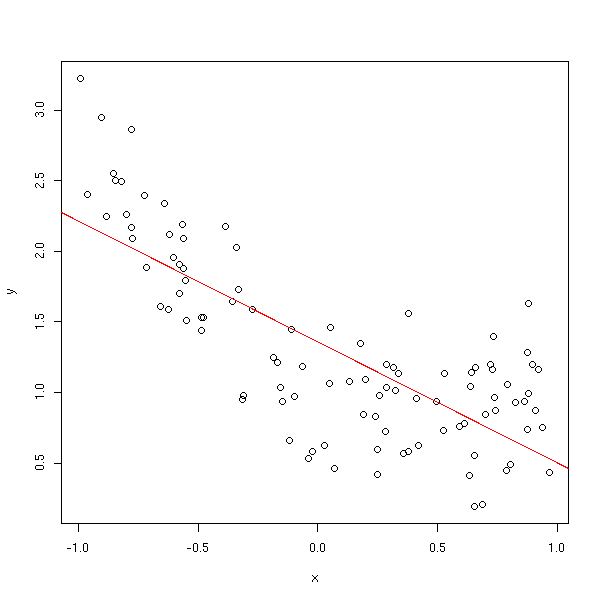
Sur le graphique précédent, ce n'est pas évident, mais on peut s'appercevoir du problème en regardant si un modèle polynomial ne serait pas préférable,
> summary(lm(y~poly(x,10)))
...
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 1.29896 0.02841 45.725 < 2e-16 ***
poly(x, 10)1 -4.98079 0.28408 -17.533 < 2e-16 ***
poly(x, 10)2 2.53642 0.28408 8.928 5.28e-14 ***
poly(x, 10)3 -0.06738 0.28408 -0.237 0.813
poly(x, 10)4 -0.15583 0.28408 -0.549 0.585
poly(x, 10)5 0.15112 0.28408 0.532 0.596
poly(x, 10)6 0.04512 0.28408 0.159 0.874
poly(x, 10)7 -0.29056 0.28408 -1.023 0.309
poly(x, 10)8 -0.39384 0.28408 -1.386 0.169
poly(x, 10)9 -0.25763 0.28408 -0.907 0.367
poly(x, 10)10 -0.09940 0.28408 -0.350 0.727en utilisant des splines (ou une autre méthode de régularisation), et en regardant graphiquement le résultat,
plot(y~x) lines(smooth.spline(x,y), col='red', lwd=2) title(main="Relation non linéaire mise en évidence par des splines")
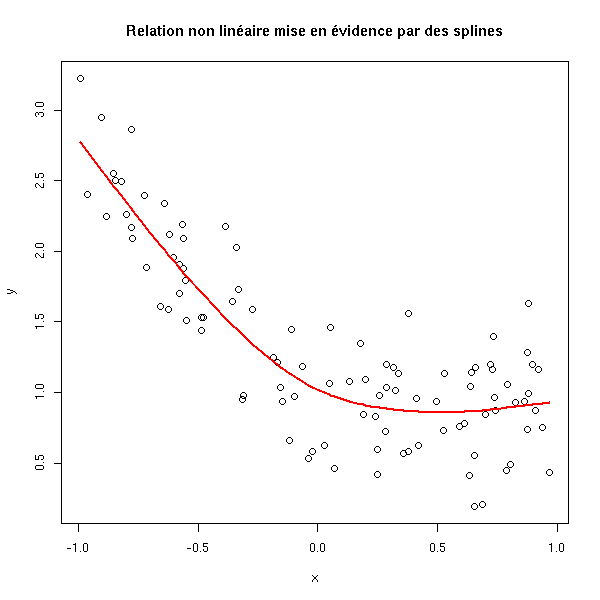
plot(y~x) lines(lowess(x,y), col='red', lwd=2) title(main='Relation non linéaire mise en évidence par "lowess"')
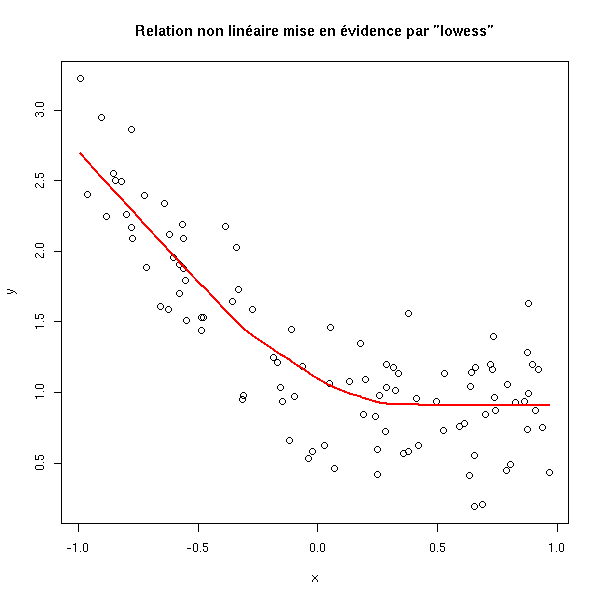
plot(y~x) xx <- seq(min(x),max(x),length=100) yy <- predict( loess(y~x), data.frame(x=xx) ) lines(xx,yy, col='red', lwd=3) title(main='Relation non linéaire mise en évidence par "loess"')
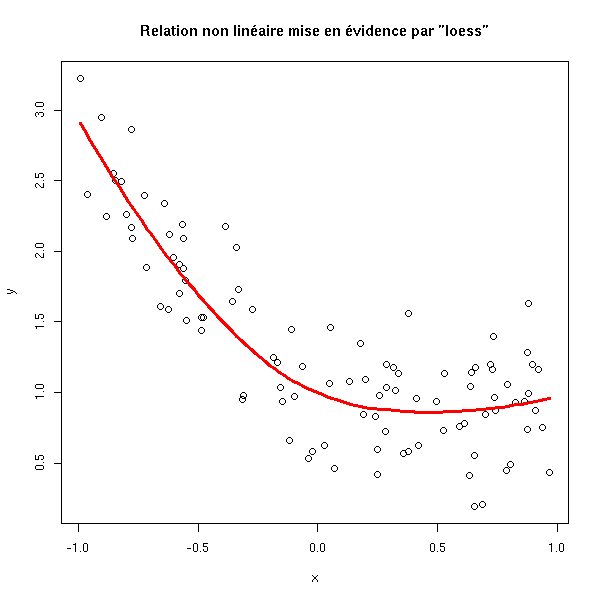
en regardant les résidus, et en leur appliquant une quelconque méthode de régularisation (on peut représenter les résidus en fonction des valeurs prédites ou en fonction des variables indépendantes).
r <- lm(y~x)
plot(r$residuals ~ r$fitted.values,
xlab='valeurs prédites', ylab='résidus',
main='résidus en fonction des valeurs prédites')
lines(lowess(r$fitted.values, r$residuals), col='red', lwd=2)
abline(h=0, lty=3)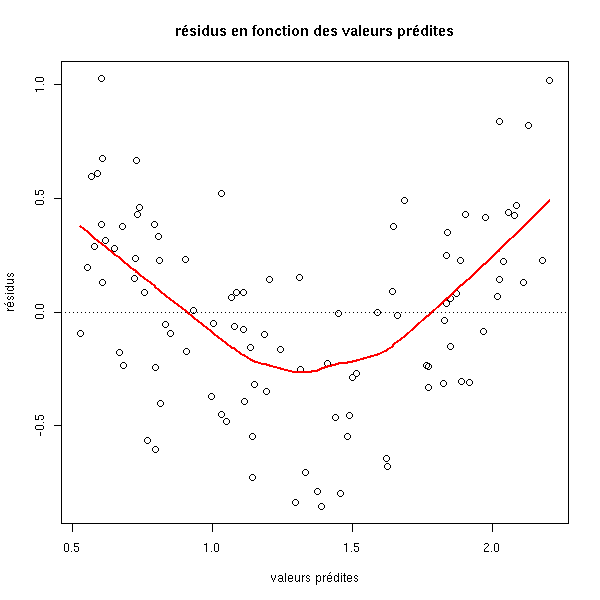
plot(r$residuals ~ x,
xlab='x', ylab='résidus',
main='résidus en fonction de la variable prédictive')
lines(lowess(x, r$residuals), col='red', lwd=2)
abline(h=0, lty=3)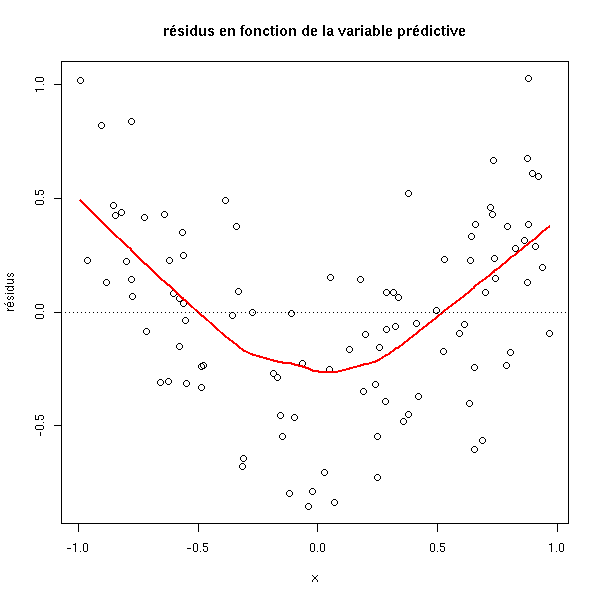
Dans certains cas, on dispose de plusieurs observations pour une même valeur des variables prédictives : on peut alors procéder au test suivant.
x <- rep(runif(10, -1, 1), 10) y <- 1-x+x^2+.3*rnorm(100) r1 <- lm(y ~ x) r2 <- lm(y ~ factor(x)) anova(r1,r2)
Les deux modèles devraient donner les mêmes prédictions : ici ce n'est pas le cas.
Analysis of Variance Table Model 1: y ~ x Model 2: y ~ factor(x) Res.Df RSS Df Sum of Sq F Pr(>F) 1 98 19.5259 2 90 6.9845 8 12.5414 20.201 < 2.2e-16 *** --- Signif. codes: 0 `***' 0.001 `**' 0.01 `*' 0.05 `.' 0.1 ` ' 1
Essayons avec une relation linéaire.
x <- rep(runif(10, -1, 1), 10) y <- 1-x+.3*rnorm(100) r1 <- lm(y ~ x) r2 <- lm(y ~ factor(x)) anova(r1,r2)
Les deux modèles ne sont pas sensiblement différents.
Analysis of Variance Table Model 1: y ~ x Model 2: y ~ factor(x) Res.Df RSS Df Sum of Sq F Pr(>F) 1 98 9.6533 2 90 8.9801 8 0.6733 0.8435 0.5671
Certains points peuvent beaucoup influencer la régression. Parfois, ils proviennent d'erreurs (qu'il faudra identifier et corriger), parfois ce sont des points tout à fait normaux, mais qui ont des valeurs extrèmes. De tels points peuvent exercer un effet de levier et fausser la régression.
n <- 20
done.outer <- F
while (!done.outer) {
done <- F
while(!done) {
x <- rnorm(n)
done <- max(x)>4.5
}
y <- 1 - 2*x + x*rnorm(n)
r <- lm(y~x)
done.outer <- max(cooks.distance(r))>5
}
plot(y~x)
abline(1,-2,lty=2)
abline(lm(y~x),col='red',lwd=3)
lm(y~x)$coef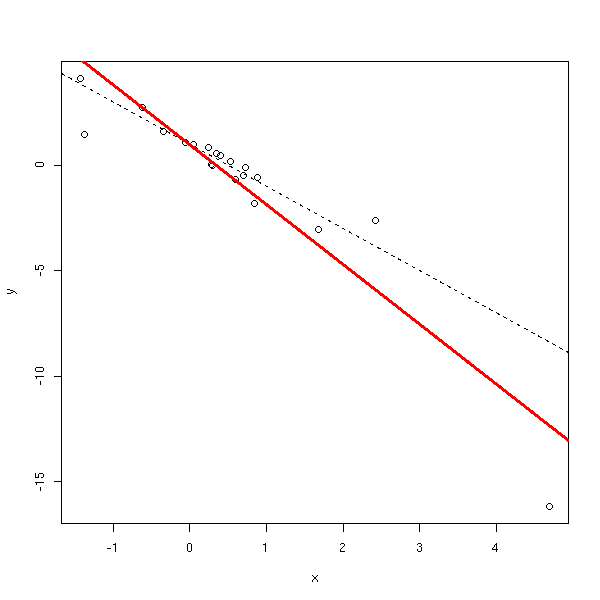
La première chose à faire consiste à observer les différentes variables (avant même de faire une régression).
boxplot(x, horizontal=T)

stripchart(x, method='jitter')
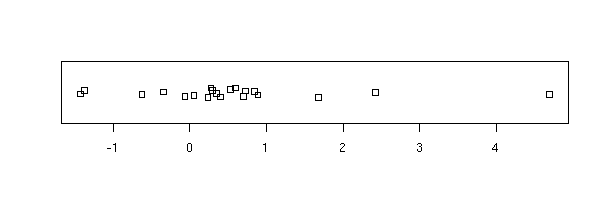
hist(x, col='light blue', probability=T) lines(density(x), col='red', lwd=3)
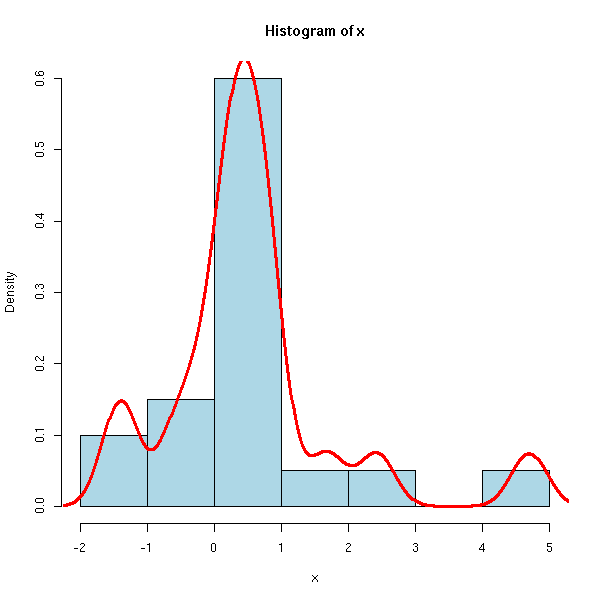
Idem pour y.
boxplot(y, horizontal=T)
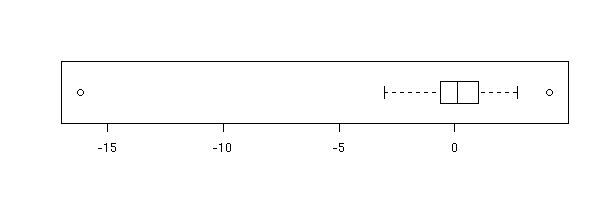
stripchart(y, method='jitter')
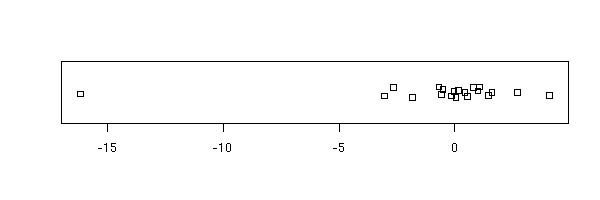
hist(y, col='light blue', probability=T) lines(density(y), col='red', lwd=3)
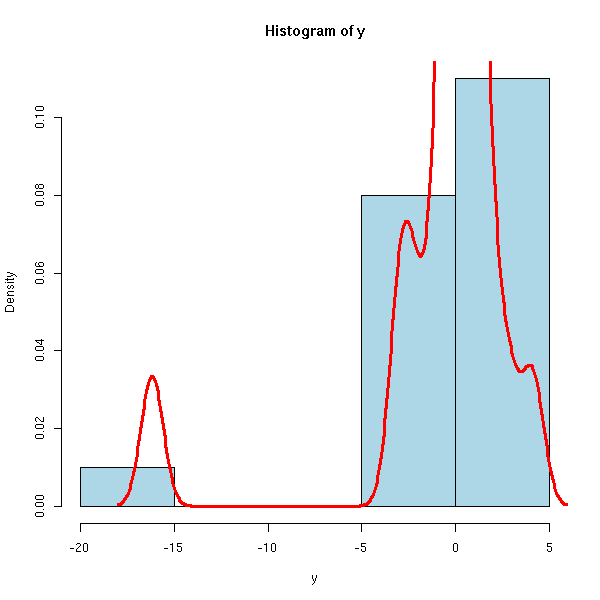
On voit ici qu'il y a un point extrème. Comme il n'y en a qu'un seul, on aurait bien envie de l'enlever -- s'il y en avait plusieurs, ce serait plus problématique : on essaierait de transformer les données.
Il y a une mesure du caractère extrème d'un point (leverage, en anglais) : ce sont le éléments diagonaux de la matrice chapeau
H = X (X' X)^-1 X'
appelée ainsi car
\hat Y = H Y.
Ces valeurs nous renseignent donc sur la manière dont une erreur sur une variable prédictive propage à la prédiction.
Ces valeurs sont entre 1/n et 1. Tant qu'on reste en dessous de 0.2, c'est bon. On remarquera qu'on n'utilise que les variables prédictives (X), pas du tout la variable à prédire (Y).
plot(hat(x), type='h', lwd=5)
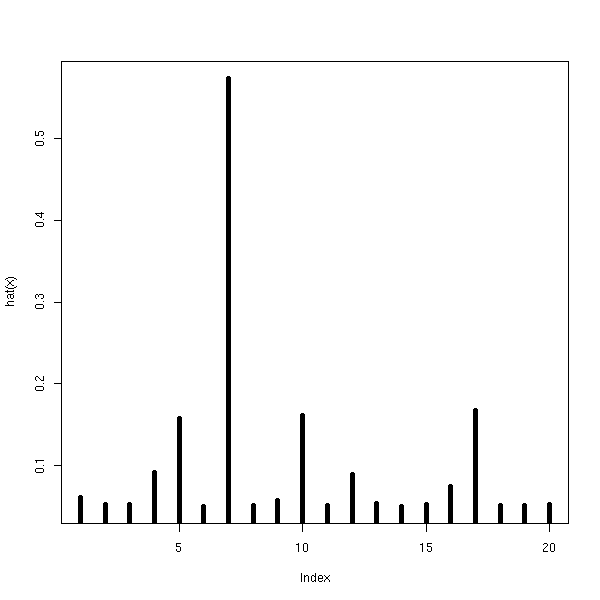
On peut ensuite mesurer l'effet de chacun des points sur chacun des coefficients de la régression : pour chacun des points, on refait la régression sans le point, et on compare les valeurs prédites :
plot(dffits(r),type='h',lwd=3)
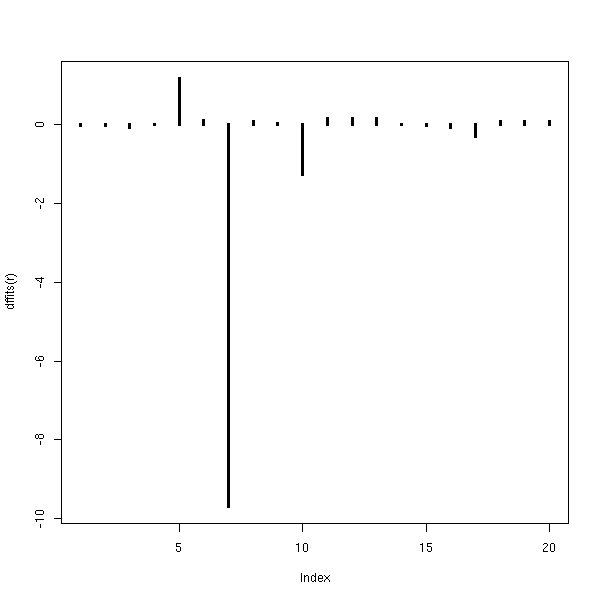
ou les coefficients :
plot(dfbetas(r)[,1],type='h',lwd=3)
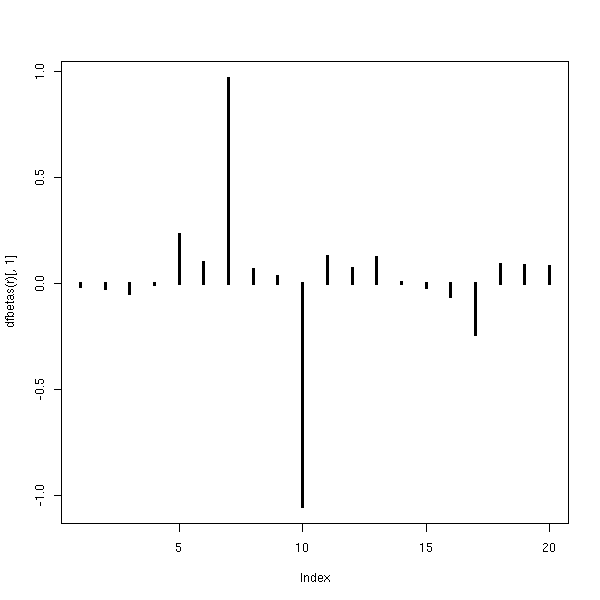
plot(dfbetas(r)[,2],type='h',lwd=3)
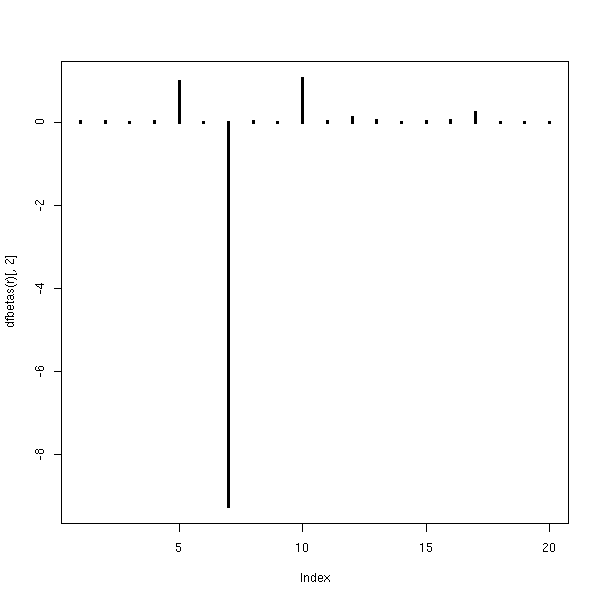
En dimensions supérieures, on peut représenter la variation d'un coefficient en fonction de la variation en les autres.
n <- 200 x1 <- rnorm(n) x2 <- rnorm(n) yy <- x1 - x2 + rnorm(n) yy[1] <- 10 r <- lm(yy~x1+x2) pairs(dfbetas(r))
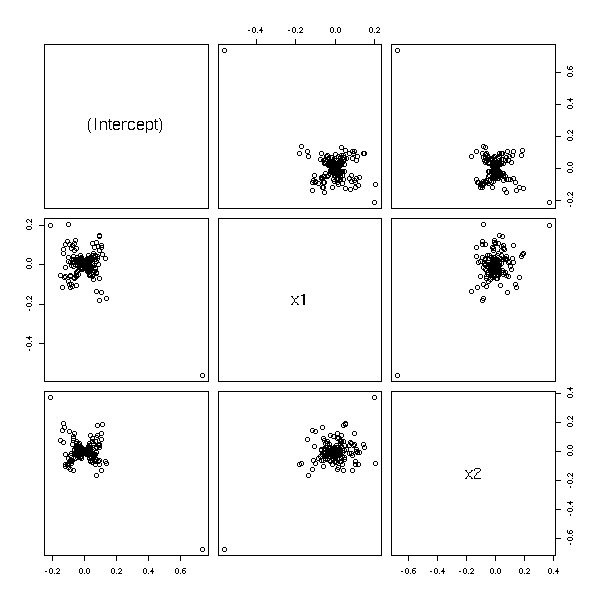
La distance de cook mesure l'effet du point sur la régression en général. En particulier, on fera attention si D>4/n.
cd <- cooks.distance(r) plot(cd,type='h',lwd=3)
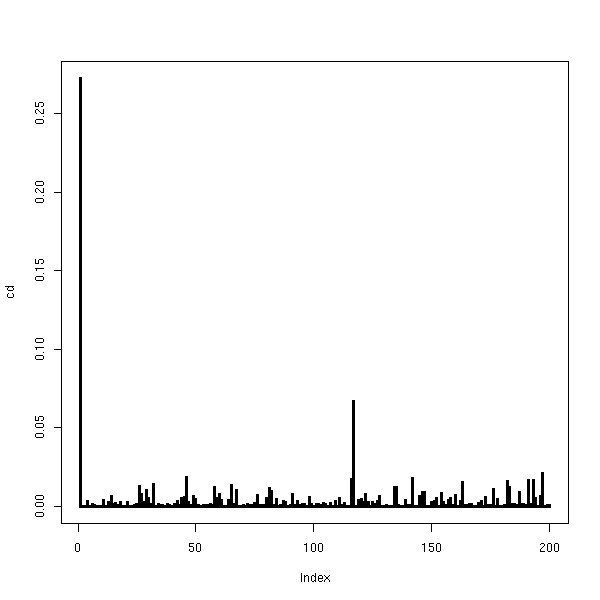
On peut aussi regarder la boite à moustache, le diagramme de dispersion, l'histogramme et la densité des distances de Cook (nous mettons momentanément de côté notre exemple pathologique).
n <- 100 xx <- rnorm(n) yy <- 1 - 2 * x + rnorm(n) rr <- lm(yy~xx) cd <- cooks.distance(rr) plot(cd,type='h',lwd=3)
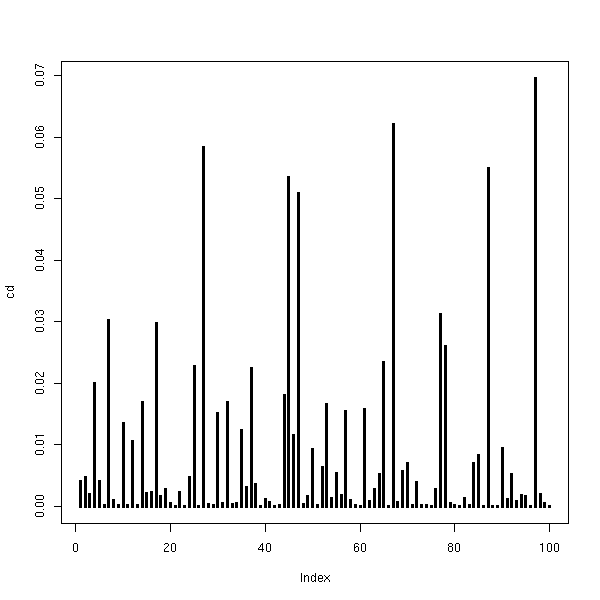
boxplot(cd, horizontal=T)
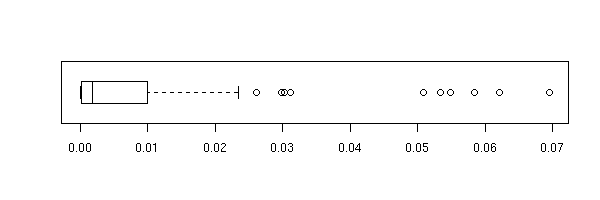
stripchart(cd, method='jitter')
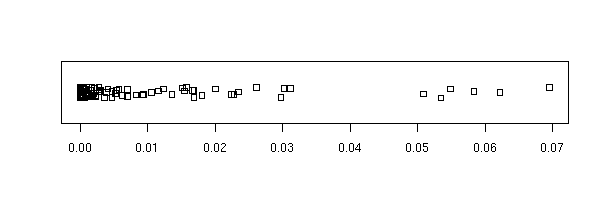
hist(cd, probability=T, breaks=20, col='light blue')
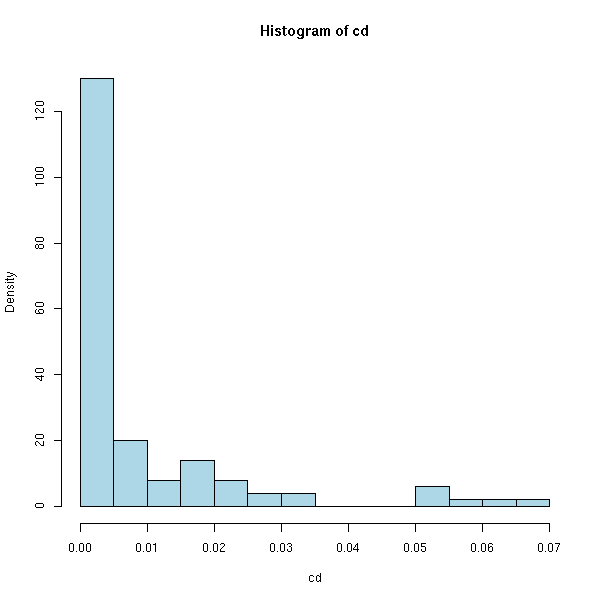
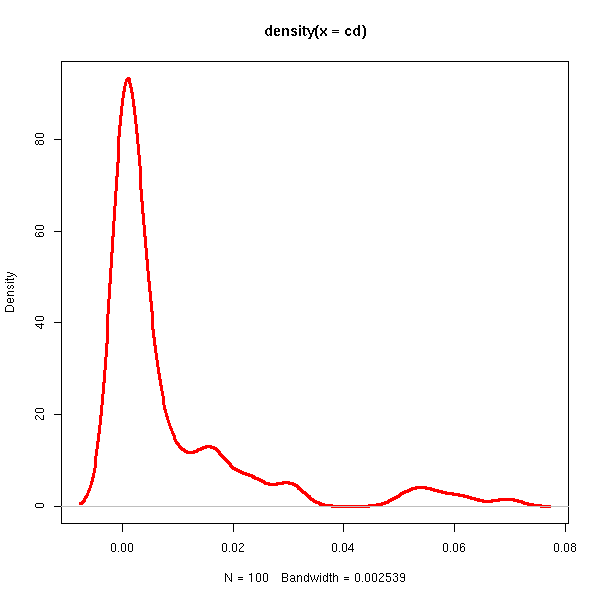
plot(density(cd), type='l', col='red', lwd=3)
qqnorm(cd) qqline(cd, col='red')
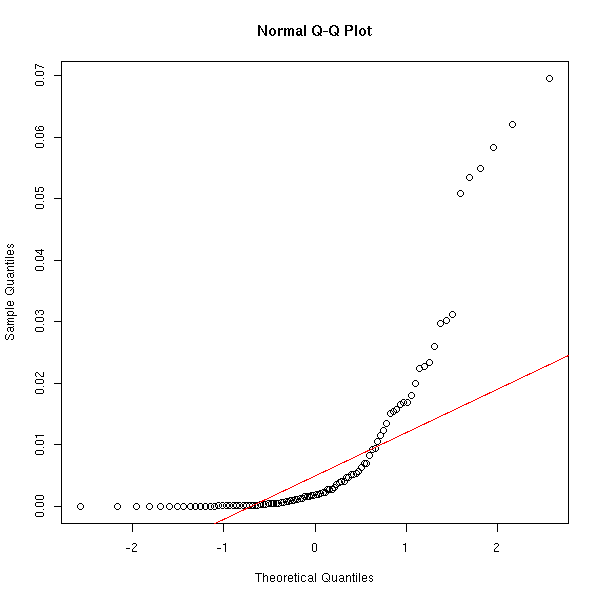
Certains suggèrent de comparer la distribution des distances de Cook avec une demi-gaussienne. On fait souvent ça pour les variables dont toutes les valeurs sont positives -- pourtant, ça ne ressemble pas vraiment à une demi-gaussienne.
half.qqnorm <- function (x) {
n <- length(x)
qqplot(qnorm((1+ppoints(n))/2), x)
}
half.qqnorm(cd)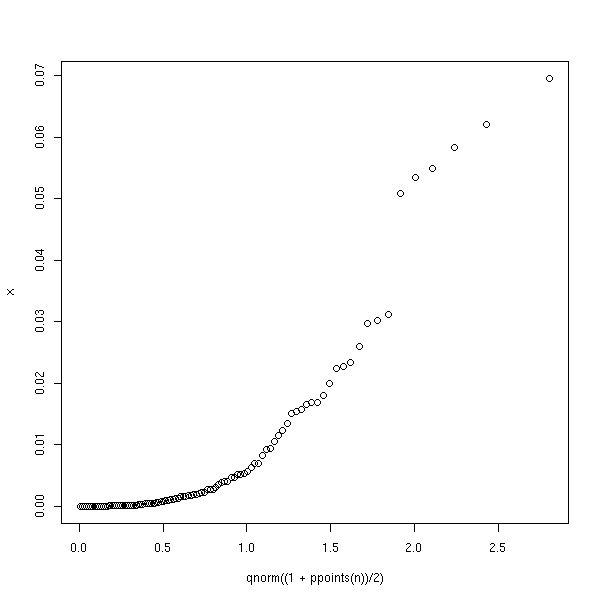
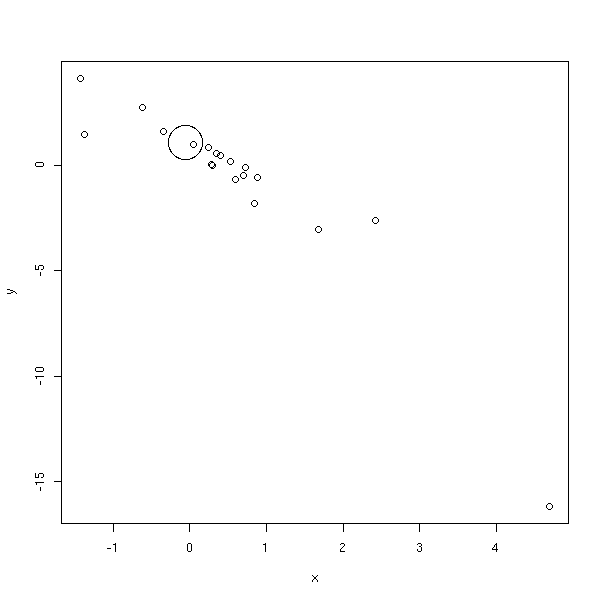
On peut utiliser ces valeurs pour représenter les points les plus importants en plus gros, sur le graphique de dispersion, ou sur les graphiques des résidus.
m <- max(cooks.distance(r)) plot(y~x, cex=1+5*cooks.distance(r)/m)
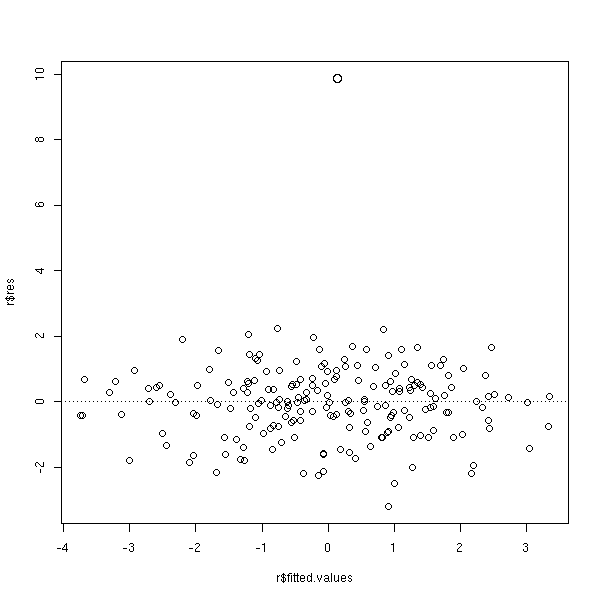
cd <- cooks.distance(r) # rescaled Cook's distance rcd <- (99/4) * cd*(cd+1)^2 rcd[rcd>100] <- 100 plot(r$res~r$fitted.values, cex=1+.05*rcd) abline(h=0,lty=3)
On peut aussi utiliser des couleurs.
m <- max(cd)
plot(r$res,
cex=1+5*cd/m,
col=heat.colors(100)[ceiling(70*cd/m)],
pch=16,
)
points(r$res, cex=1+5*cd/m)
abline(h=0,lty=3)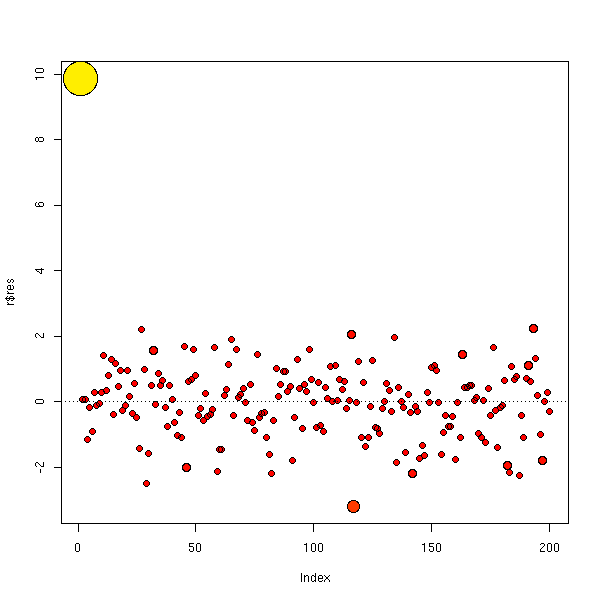
plot(r$res,
cex=1+.05*rcd,
col=heat.colors(100)[ceiling(rcd)],
pch=16,
)
points(r$res, cex=1+.05*rcd)
abline(h=0,lty=3)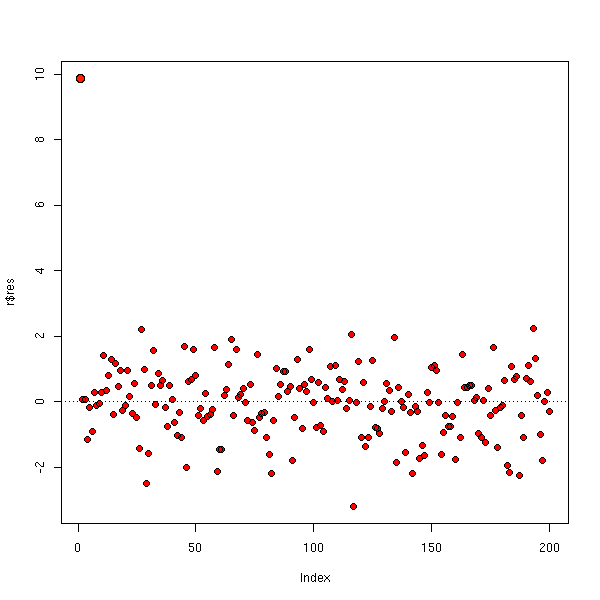
L'exemple suivant devrait être plus coloré.
n <- 100
x <- rnorm(n)
y <- 1 - 2*x + rnorm(n)
r <- lm(y~x)
cd <- cooks.distance(r)
m <- max(cd)
plot(r$res ~ r$fitted.values,
cex=1+5*cd/m,
col=heat.colors(100)[ceiling(70*cd/m)],
pch=16,
)
points(r$res ~ r$fitted.values, cex=1+5*cd/m)
abline(h=0,lty=3)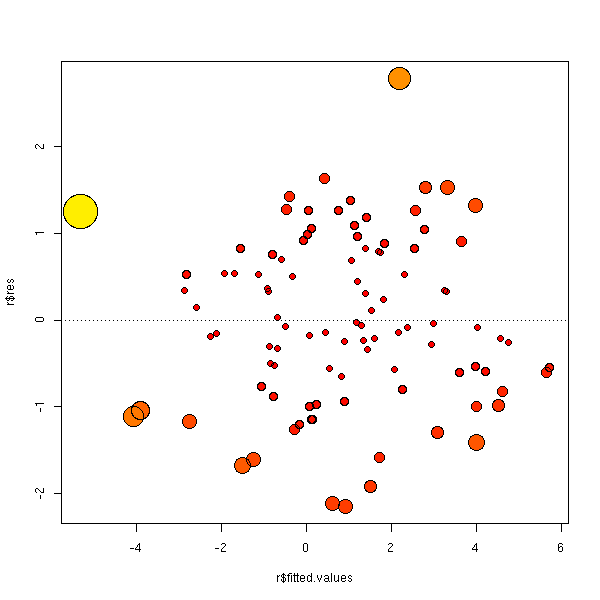
Sur un fond noir, c'est peut-être plus beau...
op <- par(fg='white', bg='black',
col='white', col.axis='white',
col.lab='white', col.main='white',
col.sub='white')
plot(r$res ~ r$fitted.values,
cex=1+5*cd/m,
col=heat.colors(100)[ceiling(100*cd/m)],
pch=16,
)
abline(h=0,lty=3)
par(op)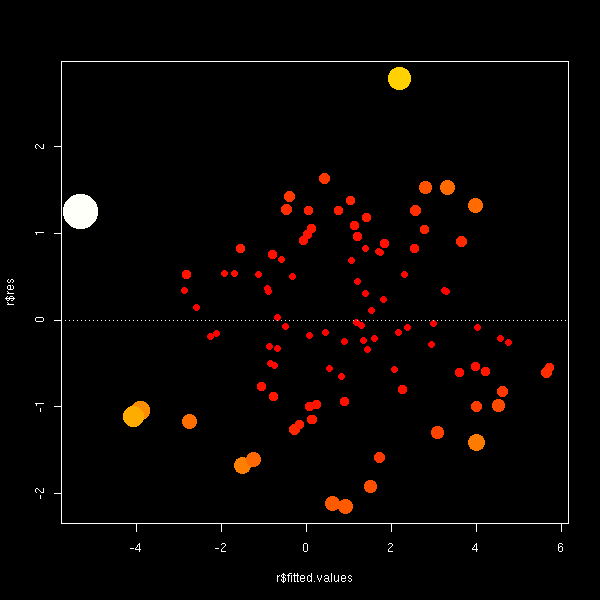
Voir aussi les commandes lm.influence, influence.measures et ls.diag.
A FAIRE : effacer le graphique suivant ?
# Avec la distance de Cook x <- rnorm(20) y <- 1 + x + rnorm(20) x <- c(x,10) y <- c(y,1) r <- lm(y~x) d <- cooks.distance(r) d <- (99/4)*d*(d+1)^2 + 1 d[d>100] <- 100 d[d<20] <- 20 d <- d/20 plot( y~x, cex=d ) abline(r) abline(coef(line(x,y)), col='red') abline(lm(y[1:20]~x[1:20]),col='blue')
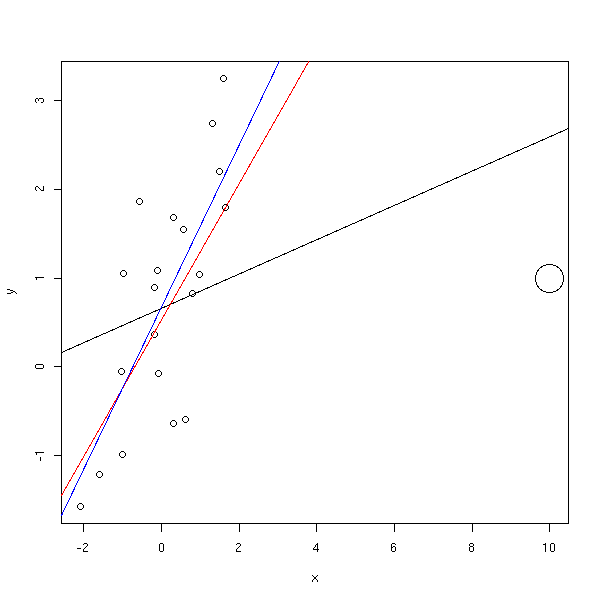
Quand il n'y a pas une seule observation extrème mais plusieurs, c'est beaucoup plus diffile à repérer. On peut utiliser une régression résistante, comme la régression élaguée (lts).
Généralement, ces valeurs extrèmes multiples ne proviennent pas du hasard (comme une valeur extrème isolée), mais ont une réelle signification. On peut tenter de les repérer avec des méthodes de classification non supervisée.
?hclust ?kmeans A FAIRE : donner un exemple
Un amas de valeurs extrèmes peut aussi signaler un modèle inadéquat.
A FAIRE : rédiger (et modéliser) l'exemple suivant (mixture) n <- 200 s <- .2 x <- runif(n) y1 <- 1 - 2 * x + s*rnorm(n) y2 <- 2 * x - 1 + s*rnorm(n) y <- ifelse( sample(c(T,F),n,replace=T,prob=c(.25,.75)), y1, y2 ) plot(y~x) abline(1,-2,lty=3) abline(-1,2,lty=3)
Si les résidus ne sont pas normaux, les estimateurs obtenus par la méthode des moindre carrés ne sont plus optimaux (certains estimateurs robustes sont alors préférables, même s'ils sont biaisés) et, pire encore, tous les tests et calculs de variance ou d'intervalles de confiance ou de prédiction sont faux.
Néanmoins, si les résidus sont moins dispersés qu'avec une loi normale ou, dans une moindre mesure, si l'échantillon est gros, on peut ignorer ces problèmes.
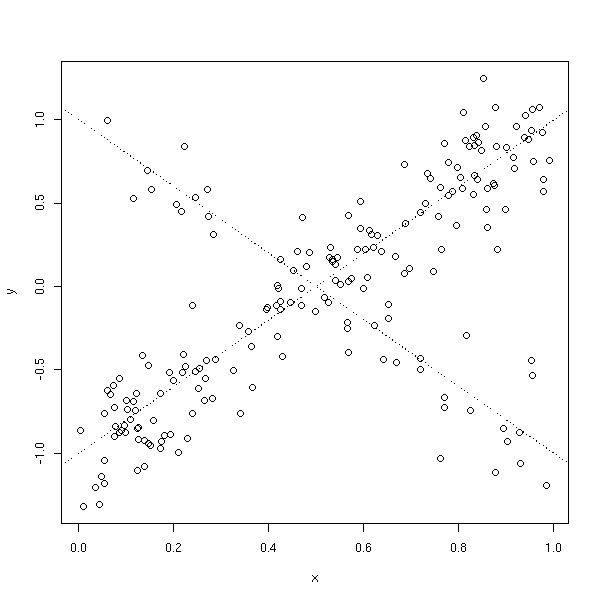
On peut repérer la non normalité des résidus à l'aide d'histogrammes, de boites à moustaches ou de graphiques quantiles-quantiles.
x <- runif(100) y <- 1 - 2*x + .3*exp(rnorm(100)-1) r <- lm(y~x) boxplot(r$residuals, horizontal=T)
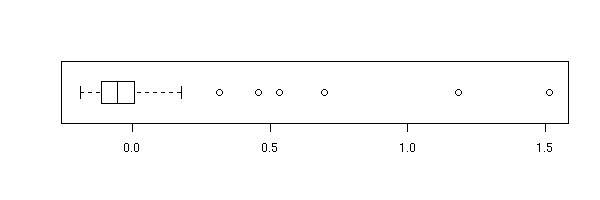
hist(r$residuals, breaks=20, probability=T, col='light blue')
lines(density(r$residuals), col='red', lwd=3)
f <- function(x) {
dnorm(x,
mean=mean(r$residuals),
sd=sd(r$residuals),
)
}
curve(f, add=T, col="red", lwd=3, lty=2)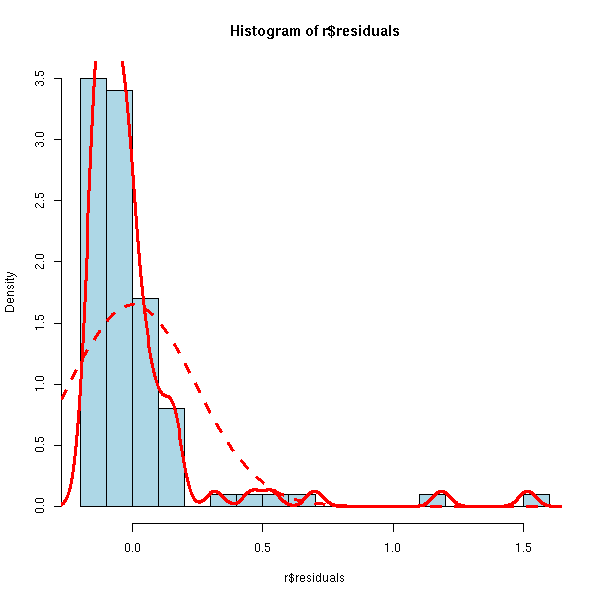
Ne pas oublier les graphiques quantiles/quantiles...
qqnorm(r$residuals) qqline(r$residuals, col='red')
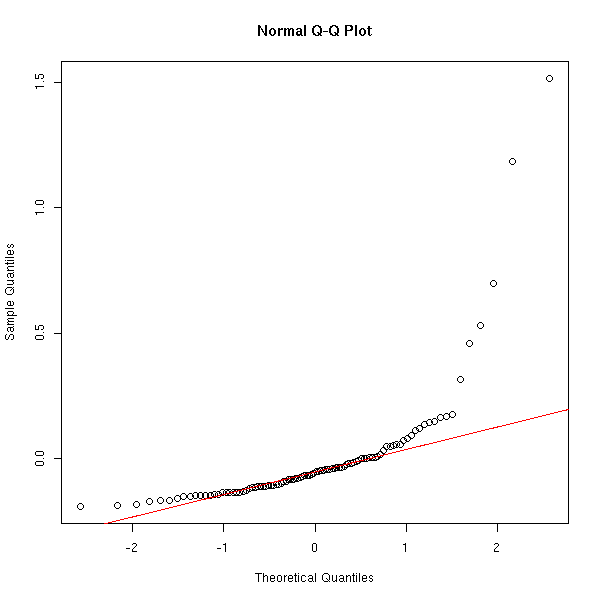
Regardons quels sont les effets réels de résidus non normaux. Nous allons prendre une situation extrème : une variable de Cauchy avec un trou au milieu, et un échantillon pas très grand.
rcauchy.with.hole <- function (n) {
x <- rcauchy(n)
x[x>0] <- 10+x[x>0]
x[x<0] <- -10+x[x<0]
x
}
n <- 20
x <- rcauchy(n)
y <- 1 - 2*x + .5*rcauchy.with.hole(n)
plot(y~x)
abline(1,-2)
r <- lm(y~x)
abline(r, col='red')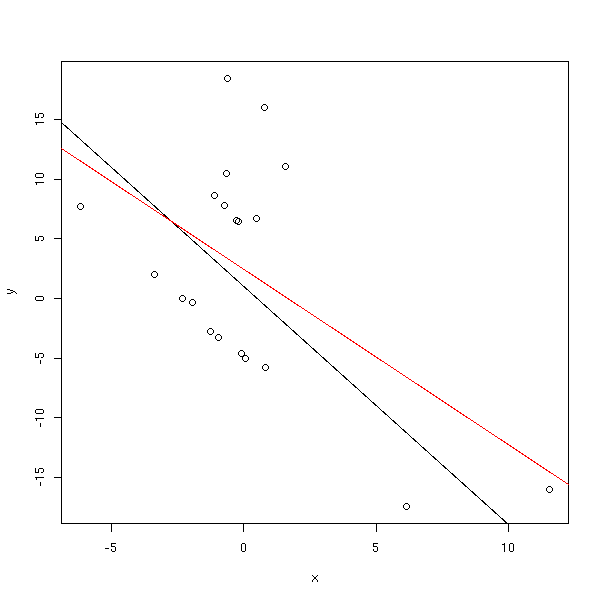
op <- par(mfrow=c(2,2))
hist(r$residuals, breaks=20, probability=T, col='light blue')
lines(density(r$residuals), col='red', lwd=3)
f <- function(x) {
dnorm(x,
mean=mean(r$residuals),
sd=sd(r$residuals),
)
}
curve(f, add=T, col="red", lwd=3, lty=2)
qqnorm(r$residuals)
qqline(r$residuals, col='red')
plot(r$residuals ~ r$fitted.values)
plot(r$residuals ~ x)
par(op)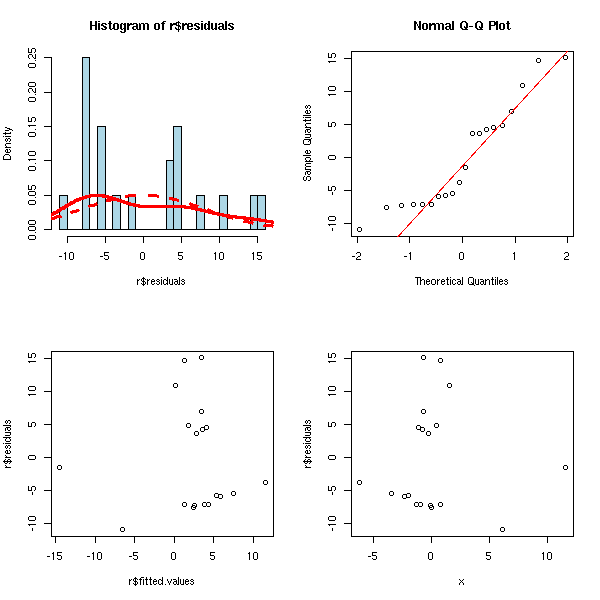
Faisons quelques prédictions.
n <- 10000 xp <- runif(n,-50,50) yp <- predict(r, data.frame(x=xp), interval="prediction") yr <- 1 - 2*xp + .5*rcauchy.with.hole(n) sum( yr < yp[,3] & yr > yp[,2] )/n
On obtient 0.9546, i.e., on est bien dans l'intervalle de prédiction dans (plus de) 5% des cas...
Réessayons avec un échantillon plus petit.
n <- 5 x <- rcauchy(n) y <- 1 - 2*x + .5*rcauchy.with.hole(n) r <- lm(y~x) n <- 10000 xp <- sort(runif(n,-50,50)) yp <- predict(r, data.frame(x=xp), interval="prediction") yr <- 1 - 2*xp + .5*rcauchy.with.hole(n) sum( yr < yp[,3] & yr > yp[,2] )/n
C'est encore pire, on obtient 0.9975.
Pour vérifier que je ne me plante pas complètement en faisant ces calculs, traçons certains de ces points.
done <- F
while(!done) {
# On choisit une situation où l'intervalle de prédiction n'est pas trop grand,
# de sorte qu'il soit sur le dessin
n <- 5
x <- rcauchy(n)
y <- 1 - 2*x + .5*rcauchy.with.hole(n)
r <- lm(y~x)
n <- 100000
xp <- sort(runif(n,-50,50))
yp <- predict(r, data.frame(x=xp), interval="prediction")
done <- ( yp[round(n/2),2] > -75 & yp[round(n/2),3] < 75 )
}
yr <- 1 - 2*xp + .5*rcauchy.with.hole(n)
plot(yp[,1]~xp, type='l',
xlim=c(-50,50), ylim=c(-100,100))
points(yr~xp, pch='.')
lines(xp, yp[,2], col='blue')
lines(xp, yp[,3], col='blue')
abline(r, col='red')
points(y~x, col='orange', pch=16, cex=1.5)
points(y~x, cex=1.5)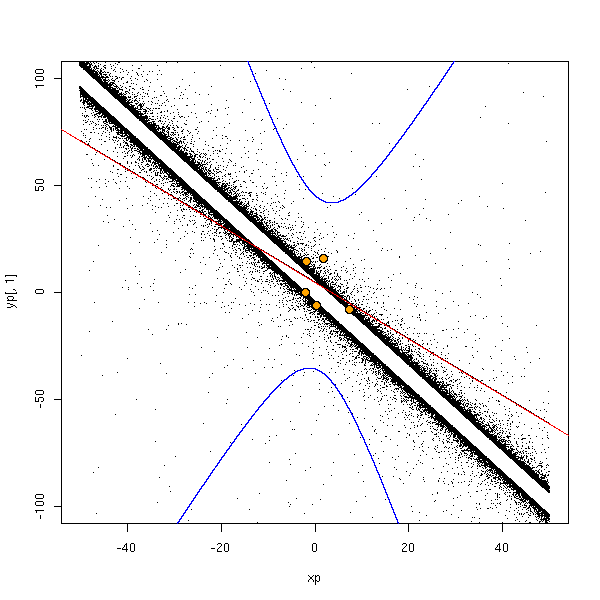
done <- F
while(!done) {
# On choisit une situation encore pire, dans laquelle le signe du
# coefficient directeur de la droite de régression n'est pas le bon
n <- 5
x <- rcauchy(n)
y <- 1 - 2*x + .5*rcauchy.with.hole(n)
r <- lm(y~x)
n <- 100000
xp <- sort(runif(n,-50,50))
yp <- predict(r, data.frame(x=xp), interval="prediction")
print(r$coef[2])
done <- ( yp[round(n/2),2] > -75 & yp[round(n/2),3] < 75 & r$coef[2]>0)
}
yr <- 1 - 2*xp + .5*rcauchy.with.hole(n)
plot(yp[,1]~xp, type='l',
xlim=c(-50,50), ylim=c(-100,100))
points(yr~xp, pch='.')
lines(xp, yp[,2], col='blue')
lines(xp, yp[,3], col='blue')
abline(r, col='red')
points(y~x, col='orange', pch=16, cex=1.5)
points(y~x, cex=1.5)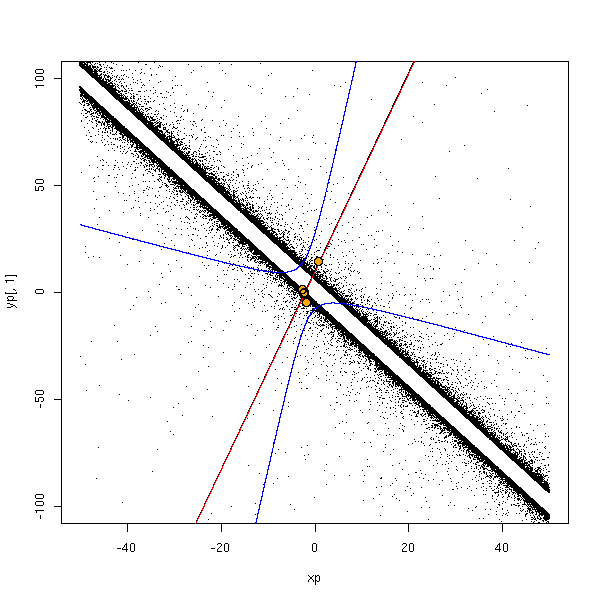
On constate que l'intervalle de prédiction est très grand si on prend des valeurs extrèmes. Essayons donc avec des valeurs plus modestes.
n <- 10000 xp <- sort(runif(n,-.1,.1)) yp <- predict(r, data.frame(x=xp), interval="prediction") yr <- 1 - 2*xp + .5*rcauchy.with.hole(n) sum( yr < yp[,3] & yr > yp[,2] )/n
On obtient 0.9932...
done <- F
while (!done) {
n <- 5
x <- rcauchy(n)
y <- 1 - 2*x + .5*rcauchy.with.hole(n)
r <- lm(y~x)
done <- T
}
n <- 10000
xp <- sort(runif(n,-2,2))
yp <- predict(r, data.frame(x=xp), interval="prediction")
yr <- 1 - 2*xp + .5*rcauchy.with.hole(n)
plot(c(xp,x), c(yp[,1],y), pch='.',
xlim=c(-2,2), ylim=c(-50,50) )
lines(yp[,1]~xp)
abline(r, col='red')
lines(xp, yp[,2], col='blue')
lines(xp, yp[,3], col='blue')
points(yr~xp, pch='.')
points(y~x, col='orange', pch=16)
points(y~x)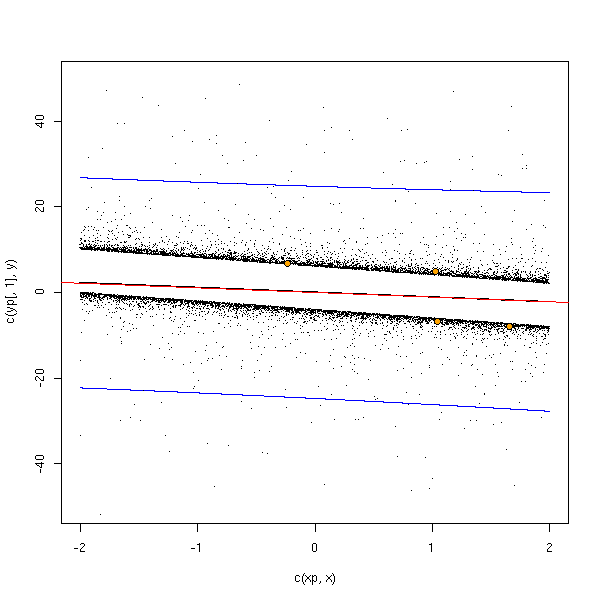
On constate quand-même que parfois (plus d'une fois sur 100), les données ne sont pas dans l'intervalle de prédiction à 95%.
done <- F
essais <- 0
while (!done) {
n <- 5
x <- rcauchy(n)
y <- 1 - 2*x + .5*rcauchy.with.hole(n)
r <- lm(y~x)
yp <- predict(r, data.frame(x=2), interval='prediction')
done <- yp[3]<0
essais <- essais+1
}
print(essais) # Autour de 20 ou 30
n <- 10000
xp <- sort(runif(n,-2,2))
yp <- predict(r, data.frame(x=xp), interval="prediction")
yr <- 1 - 2*xp + .5*rcauchy.with.hole(n)
plot(c(xp,x), c(yp[,1],y), pch='.',
xlim=c(-2,2), ylim=c(-50,50) )
lines(yp[,1]~xp)
points(yr~xp, pch='.')
abline(r, col='red')
lines(xp, yp[,2], col='blue')
lines(xp, yp[,3], col='blue')
points(y~x, col='orange', pch=16)
points(y~x)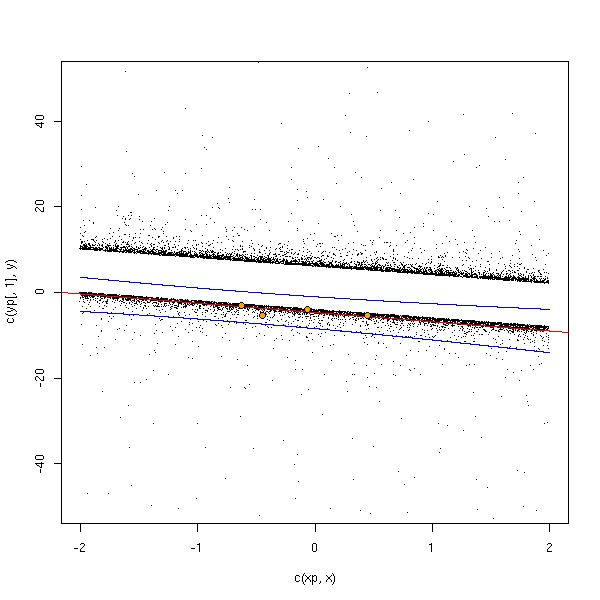
done <- F
e <- NULL
for (i in 1:100) {
essais <- 0
done <- F
while (!done) {
n <- 5
x <- rcauchy(n)
y <- 1 - 2*x + .5*rcauchy.with.hole(n)
r <- lm(y~x)
yp <- predict(r, data.frame(x=2), interval='prediction')
done <- yp[3]<0
essais <- essais+1
}
e <- append(e,essais)
}
hist(e, probability=T, col='light blue')
lines(density(e), col='red', lwd=3)
abline(v=median(e), lty=2, col='red', lwd=3)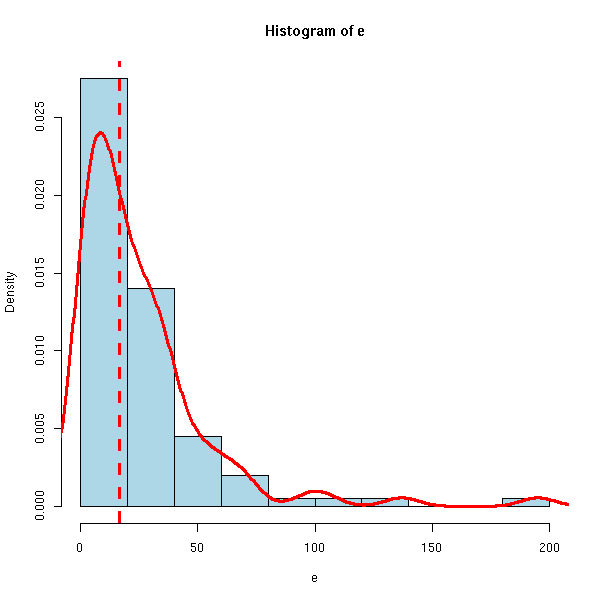
> mean(e) [1] 25.8 > median(e) [1] 19
En résumé, pour avoir l'intervalle de prédiction le plus incorrect possible, il faut prendre des valeurs de x pas trop petites (car au voisinage de zéro, les prédictions sont à peu près correctes) mais pas trop grandes non plus (car loin de zéro, les intervalles de prédiction sont démesurément grands).
Je voulais mettre en évidence, sur un exemple, que des résidus non normaux donnaient des intervalles de confiance trop petits, et donc des résultats faux : il n'en est rien. Si les résidus ne sont pas normaux, les intervalles de confiance calculés sont bien trop grands. Les prédictions sont donc annoncées comme peu précises, mais pas fausses.
Exercice : essayer avec d'autres distributions (uniforme, Cauchy, Cauchy trouée), que ce soit pour le bruit ou pour les variables.
Pour que les estimateurs soient optimaux et que les tests donnent des résultats corrects, on a du supposer (entre autres) que les résidus étaient de variance constante. S'ils ne sont pas de variance constante, on parle d'hétéroscédasticité.
x <- runif(100) y <- 1 - 2*x + .3*x*rnorm(100) plot(y~x) r <- lm(y~x) abline(r, col='red') title(main="Hétéroscédasticité")
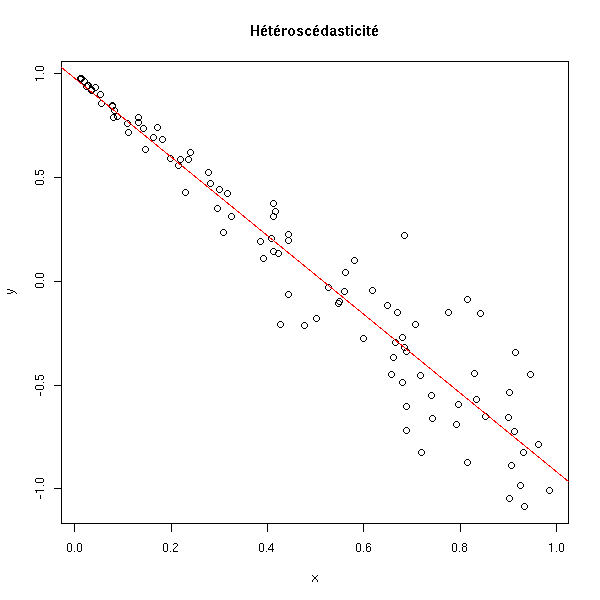
On peut voir ce problème sur les résidus
plot(r$residuals ~ r$fitted.values)
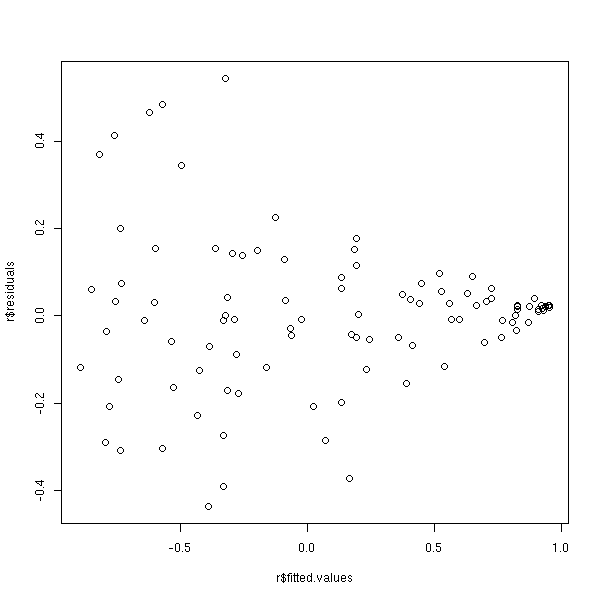
ou plus précisément sur leur valeur absolue, sur laquelle on peut faire une régression (non linéaire).
plot(abs(r$residuals) ~ r$fitted.values) lines(lowess(r$fitted.values, abs(r$residuals)), col='red')
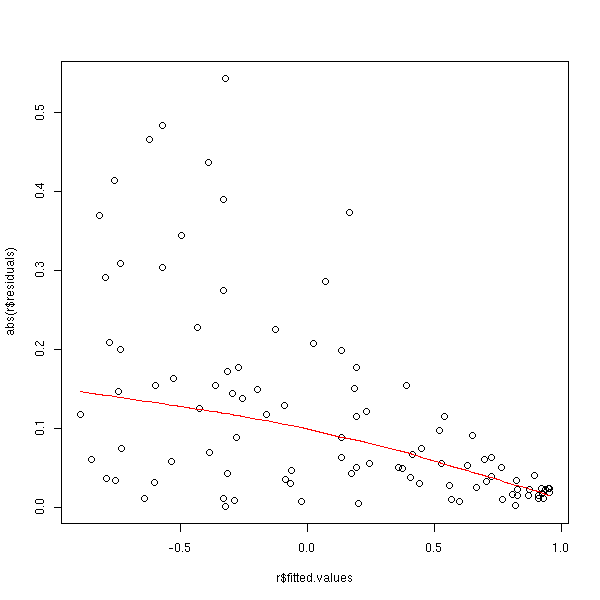
plot(abs(r$residuals) ~ x) lines(lowess(x, abs(r$residuals)), col='red')
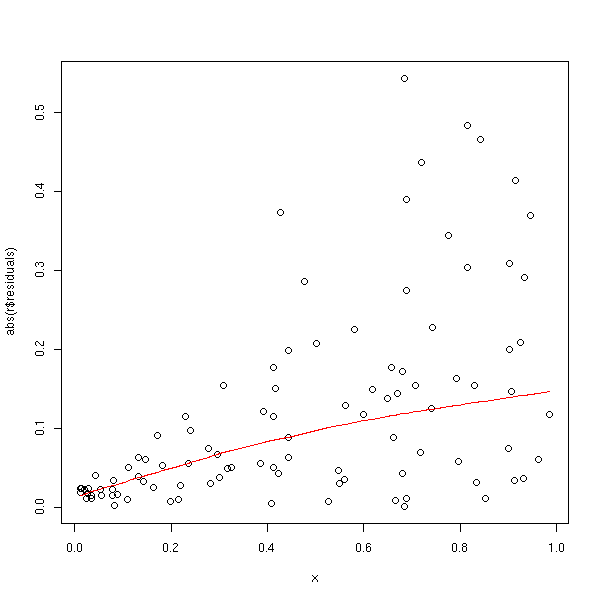
Voici un exemple concret.
data(crabs) plot(FL~RW, data=crabs)
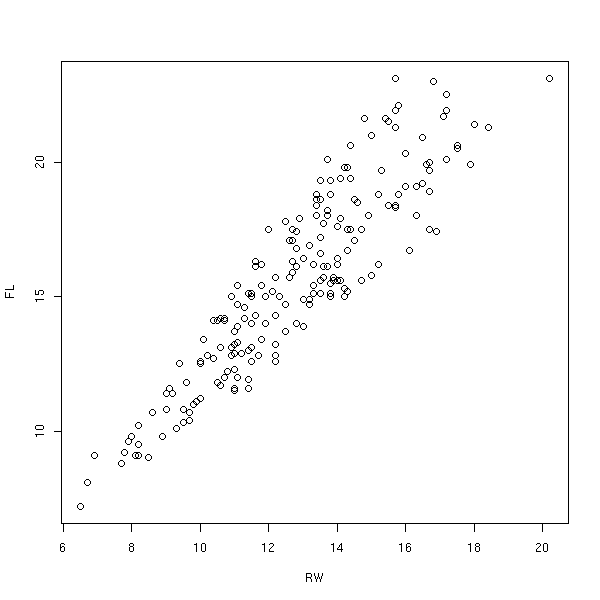
r <- lm(FL~RW, data=crabs) plot(r, which=1)
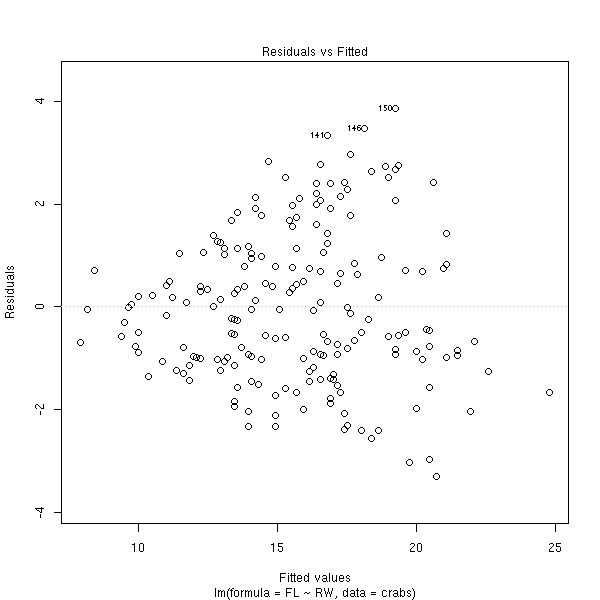
plot(r, which=3, panel = panel.smooth)
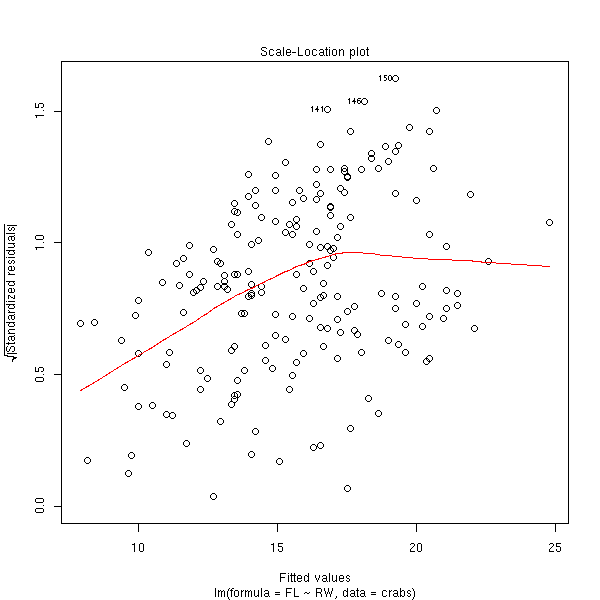
La commande spread.level.plot (dans la bibliothèque car) fait à peu près la même chose : elle représente la valeur absolue des résidus en fonction des valeurs prédites, sur des échelles logarithmiques, et suggère une transformation pour se débarasser de l'hétéroscédasticité.
library(car) spread.level.plot(r)
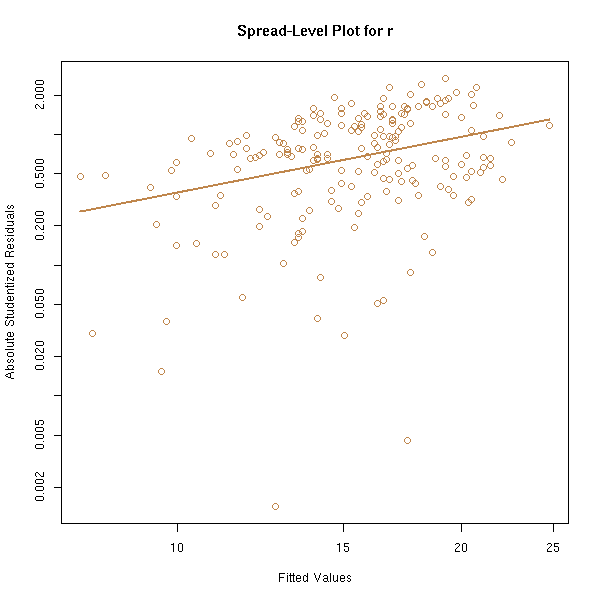
On peut aussi le vérifier par le calcul, en découpant l'échantillon en deux et en faisant un test pour voir si les deux morceaux ont la même variance.
n <- length(crabs$RW) m <- ceiling(n/2) o <- order(crabs$RW) r <- lm(FL~RW, data=crabs) x <- r$residuals[o[1:m]] y <- r$residuals[o[(m+1):n]] var.test(y,x) # p-value = 1e-4
Nous allons tenter de montrer l'effet de l'hétéroscédasticité sur un exemple.
x <- runif(100) y <- 1 - 2*x + .3*x*rnorm(100) r <- lm(y~x) xp <- runif(10000,0,.1) yp <- predict(r, data.frame(x=xp), interval="prediction") yr <- 1 - 2*xp + .3*xp*rnorm(100) sum( yr < yp[,3] & yr > yp[,2] )/n
On obtient 1 : pour les valeurs de x correspondant à une petite variance, les intervalles de confiance sont trop grands.
x <- runif(100) y <- 1 - 2*x + .3*x*rnorm(100) r <- lm(y~x) xp <- runif(10000,.9,1) yp <- predict(r, data.frame(x=xp), interval="prediction") yr <- 1 - 2*xp + .3*xp*rnorm(100) sum( yr < yp[,3] & yr > yp[,2] )/n
On obtient 0.67 : pour les valeurs de x correspondant à une grande variance, les intervalles de confiance sont trop petits.
On peut voir cela graphiquement.
x <- runif(100) y <- 1 - 2*x + .3*x*rnorm(100) r <- lm(y~x) n <- 10000 xp <- sort(runif(n,)) yp <- predict(r, data.frame(x=xp), interval="prediction") yr <- 1 - 2*xp + .3*xp*rnorm(n) plot(c(xp,x), c(yp[,1],y), pch='.') lines(yp[,1]~xp) abline(r, col='red') lines(xp, yp[,2], col='blue') lines(xp, yp[,3], col='blue') points(yr~xp, pch='.') points(y~x, col='orange', pch=16) points(y~x) title(main="Effet de l'hétéroscédasticité sur les intervalles de prédiction")
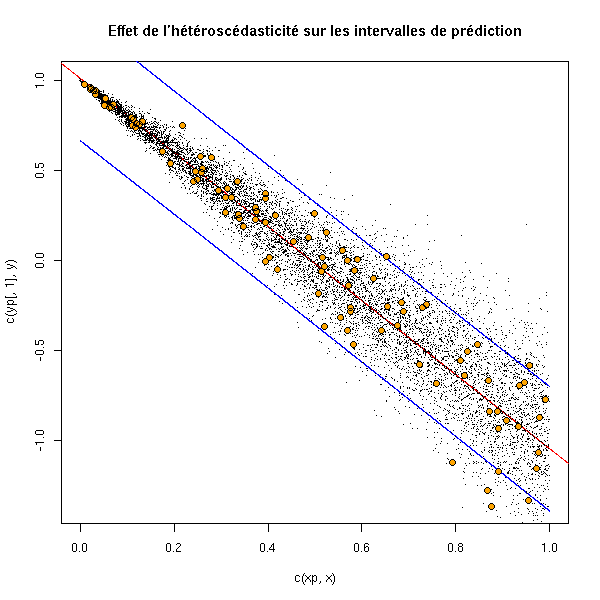
La manière la plus simple de se débarasser de l'hétéroscédasticité, c'est (quand ça marche) de transformer les données. Si c'est possible, on s'efforce en même temps de normaliser les données et de se débarasser de l'hétéroscédasticité.
Les moindres carrés généralisés permettent d'effectuer une régression même en présence d'hétéroscédasticité, mais il faut préalablement estimer la variance et la manière dont elle évolue.
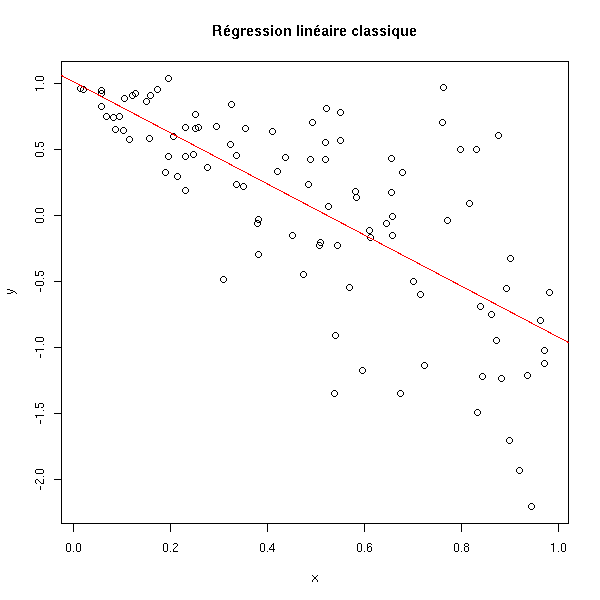
A FAIRE : mettre cet exemple plus loin ? n <- 100 x <- runif(n) y <- 1 - 2*x + x*rnorm(n) plot(y~x) r <- lm(y~x) abline(r, col='red') title(main="Régression linéaire classique")
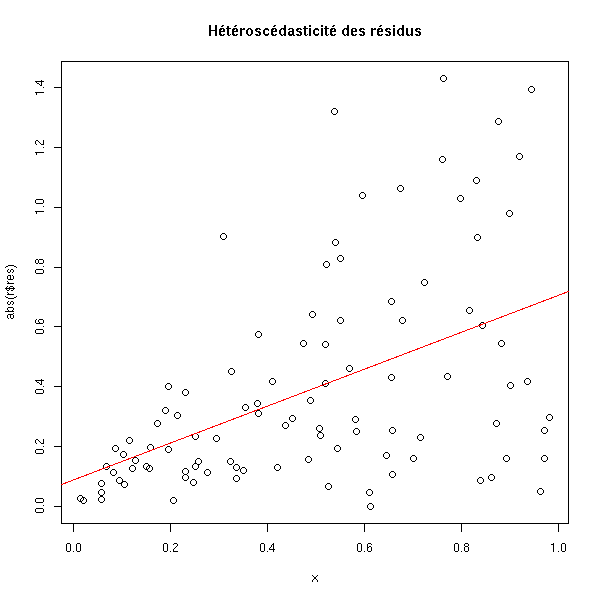
plot(abs(r$res) ~ x) r2 <- lm( abs(r$res) ~ x ) abline(r2, col="red") title(main="Hétéroscédasticité des résidus")
Les moindres carrés pondérés consistent à donner un poids (i.e., une importance) moindre aux observations dont la variance est élevée.
# On fait l'hypothèse que l'écart-type des résidus
# est de la forme a*x
a <- lm( I(r$res^2) ~ I(x^2) - 1 )$coefficients
w <- (a*x)^-2
r3 <- lm( y ~ x, weights=w )
plot(y~x)
abline(1,-2, lty=3)
abline(lm(y~x), lty=3, lwd=3)
abline(lm(y~x, weights=w), col='red')
legend( par("usr")[1], par("usr")[3], yjust=0,
c("modèle réel", "moindres carrés", "moindres carrés pondérés"),
lwd=c(1,3,1),
lty=c(3,3,1),
col=c(par("fg"), par("fg"), 'red') )
title("Moindres carrés pondérés et hétéroscédasticité")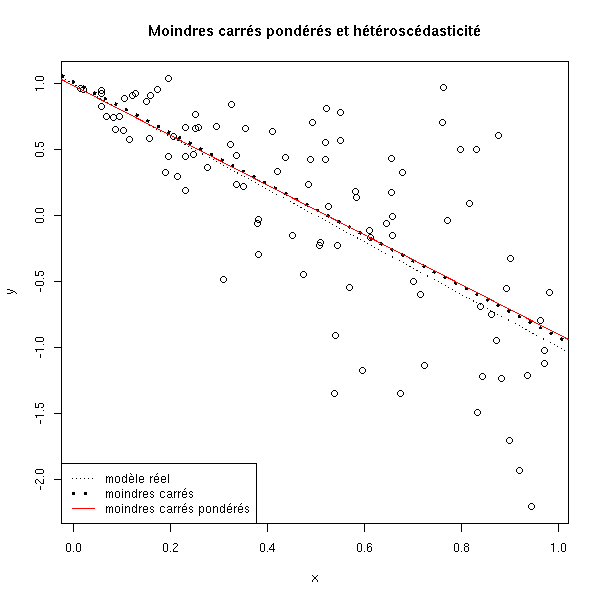
Par contre, les intervalles de prédiction ne sont pas vraiment convainquants...
A FAIRE : vérifier ce qui suit.
# Les intervalles de prédiction
N <- 10000
xx <- runif(N,min=0,max=2)
yy <- 1 - 2*xx + xx*rnorm(N)
plot(y~x, xlim=c(0,2), ylim=c(-3,2))
points(yy~xx, pch='.')
abline(1,-2, col='red')
xp <- seq(0,3,length=100)
yp1 <- predict(r, new=data.frame(x=xp), interval='prediction')
lines( xp, yp1[,2], col='red', lwd=3 )
lines( xp, yp1[,3], col='red', lwd=3 )
yp3 <- predict(r3, new=data.frame(x=xp), interval='prediction')
lines( xp, yp3[,2], col='blue', lwd=3 )
lines( xp, yp3[,3], col='blue', lwd=3 )
legend( par("usr")[1], par("usr")[3], yjust=0,
c("moindres carrés", "moindres carrés pondérés"),
lwd=3, lty=1,
col=c('red', 'blue') )
title(main="Bande de prédiction")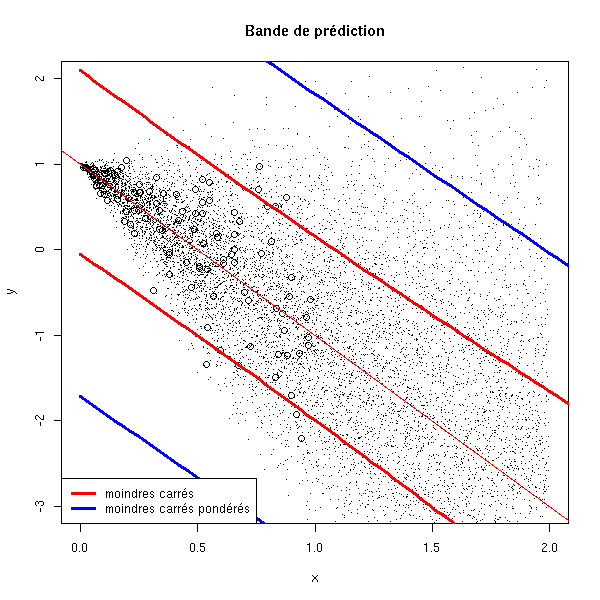
On peut aussi faire ça à l'aide de la commande gls :
A FAIRE ?gls ?varConstPower ?varPower r4 <- gls(y~x, weights=varPower(1, form= ~x)) ???
Dans le cas d'une série temporelle, de données géographiques (ou de manière générale de données pour les observations desquelles on a une notion de proximité) les erreurs entre deux observations successives peuvent être liées.
Dans le cas des séries temporelles, on peut voir le problème avec un autocorrélogramme.
my.acf.plot <- function (x, n=10, ...) {
y <- rep(NA,n)
l <- length(x)
for (i in 1:n) {
y[i] <- cor( x[1:(l-i)], x[(i+1):l] )
}
plot(y, type='h', ylim=c(-1,1),...)
}
n <- 100
x <- runif(n)
b <- .1*rnorm(n+1)
y <- 1-2*x+b[1:n]
my.acf.plot(lm(y~x)$res, lwd=10)
abline(h=0, lty=2)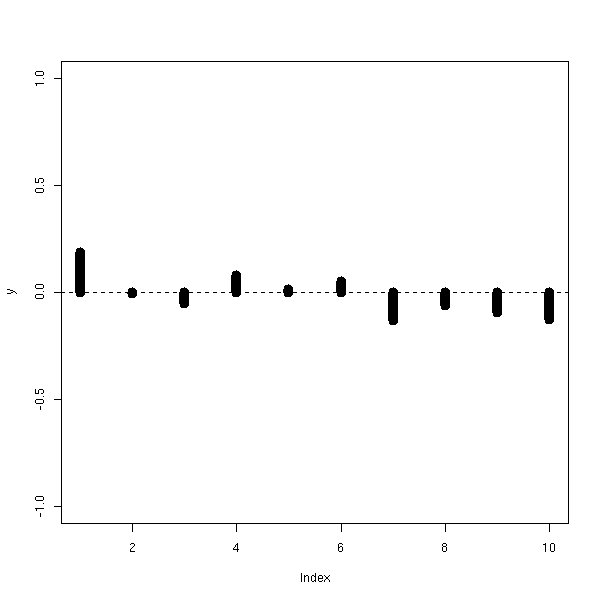
z <- 1-2*x+.5*(b[1:n]+b[1+1:n]) my.acf.plot(lm(z~x)$res, lwd=10) abline(h=0, lty=2)
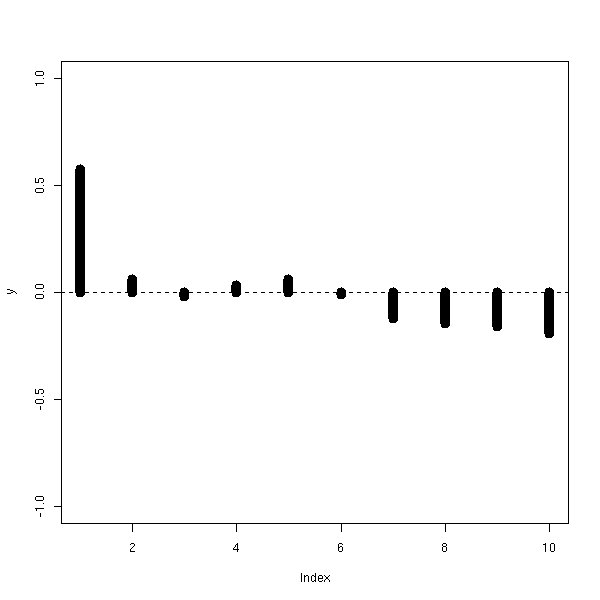
Voici un exemple hautement auto-corrélé.
n <- 500
x <- runif(n)
b <- rep(NA,n)
b[1] <- 0
for (i in 2:n) {
b[i] <- b[i-1] + .1*rnorm(1)
}
y <- 1-2*x+b[1:n]
my.acf.plot(lm(y~x)$res, n=100)
abline(h=0, lty=2)
title(main='Exemple hautement autocorrélé')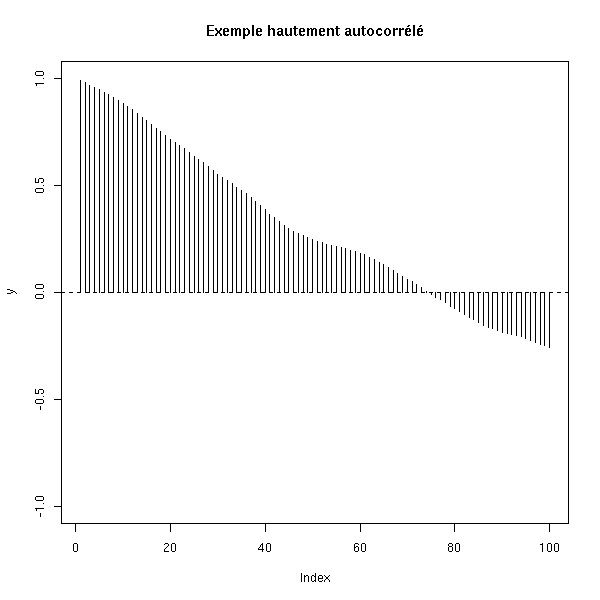
On ne voit rien sur le graphe des résidus en fonction des valeurs prédites.
r <- lm(y~x) plot(r$res ~ r$fitted.values) title(main="Résidus de l'exemple hautement autocorrélé")
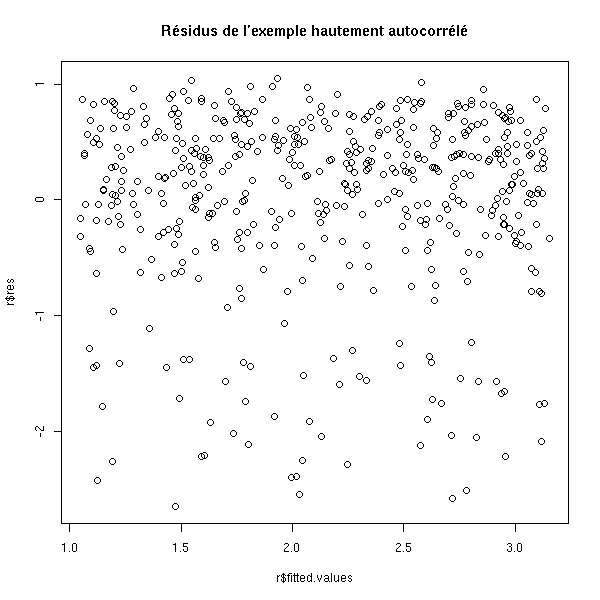
Par contre, si on représente les résidus en fonction du temps, c'est plus clair.
r <- lm(y~x) plot(r$res) title(main="Résidus de l'exemple hautement autocorrélé")
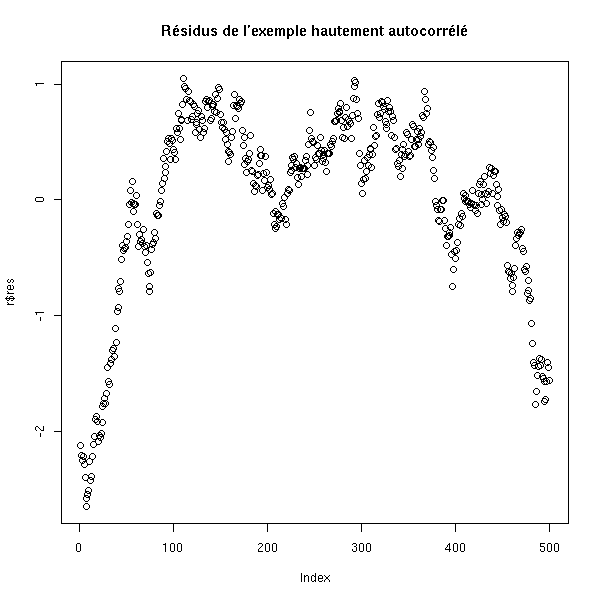
Une autre manière de repérer le problème, c'est de regarder si la corrélation entre x[i] et x[i-1] est significativement non nulle.
n <- 100
x <- runif(n)
b <- rep(NA,n)
b[1] <- 0
for (i in 2:n) {
b[i] <- b[i-1] + .1*rnorm(1)
}
y <- 1-2*x+b[1:n]
r <- lm(y~x)$res
cor.test(r[1:(n-1)], r[2:n]) # p-valeur inférieure à 1e-15
n <- 100
x <- runif(n)
b <- .1*rnorm(n+1)
y <- 1-2*x+b[1:n]
r <- lm(y~x)$res
cor.test(r[1:(n-1)], r[2:n]) # p-valeur = 0.3
y <- 1-2*x+.5*(b[1:n]+b[1+1:n])
cor.test(r[1:(n-1)], r[2:n]) # p-valeur = 0.3 (encore)Voir aussi le test de Durbin--Watson :
library(car) ?durbin.watson library(lmtest) ?dwtest
ainsi que le chapitre sur les séries temporelles.
Une troisième manière de voir le problème, c'est de tracer les résidus successifs, en 2 ou 3 dimensions.
n <- 500
x <- runif(n)
b <- rep(NA,n)
b[1] <- 0
for (i in 2:n) {
b[i] <- b[i-1] + .1*rnorm(1)
}
y <- 1-2*x+b[1:n]
r <- lm(y~x)$res
plot( r[1:(n-1)], r[2:n],
xlab='i-ième résidu',
ylab='(i+1)-ième résidu' )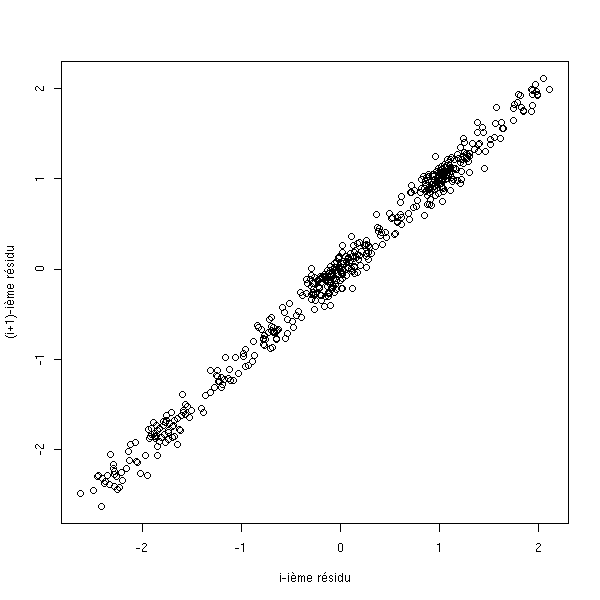
Dans l'exemple suivant, on ne voit rien en regardant deux termes successifs (enfin si, ça ressemble à un test de Rorschach, donc c'est suspect) : il en faut trois.
n <- 500
x <- runif(n)
b <- rep(NA,n)
b[1] <- 0
b[2] <- 0
for (i in 3:n) {
b[i] <- b[i-2] + .1*rnorm(1)
}
y <- 1-2*x+b[1:n]
r <- lm(y~x)$res
plot(data.frame(x=r[3:n-2], y=r[3:n-1], z=r[3:n]))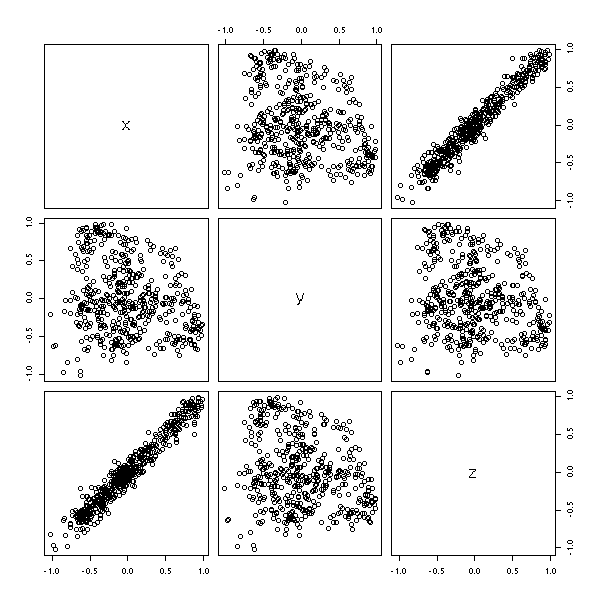
plot(r)
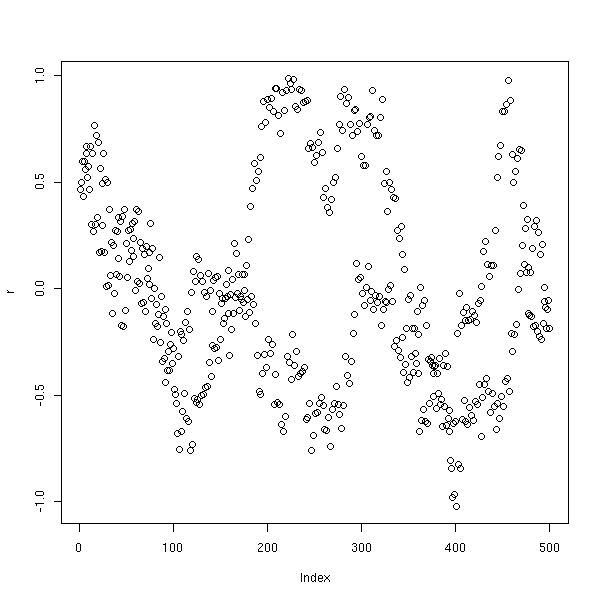
C'est d'ailleurs ainsi qu'on s'apperçoit des problèmes de certains vieux générateurs de nombres aléatoires. En 3D, de face, on ne voit rien,
data(randu) plot(randu) # On ne voit rien...
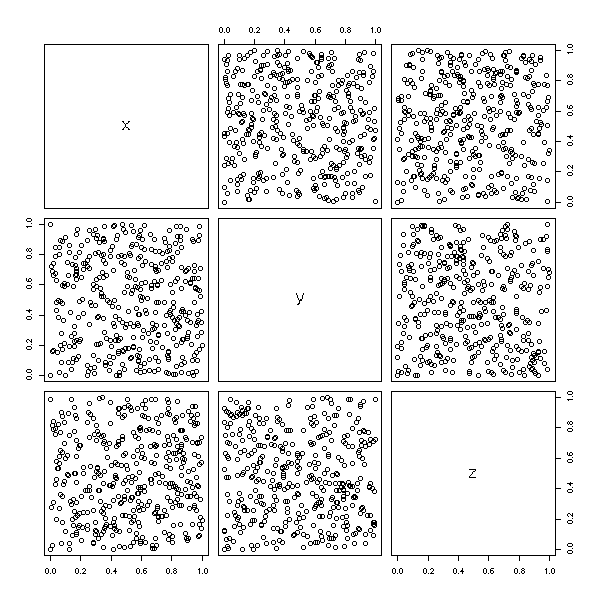
il faut tourner la figure...
library(xgobi) xgobi(randu)
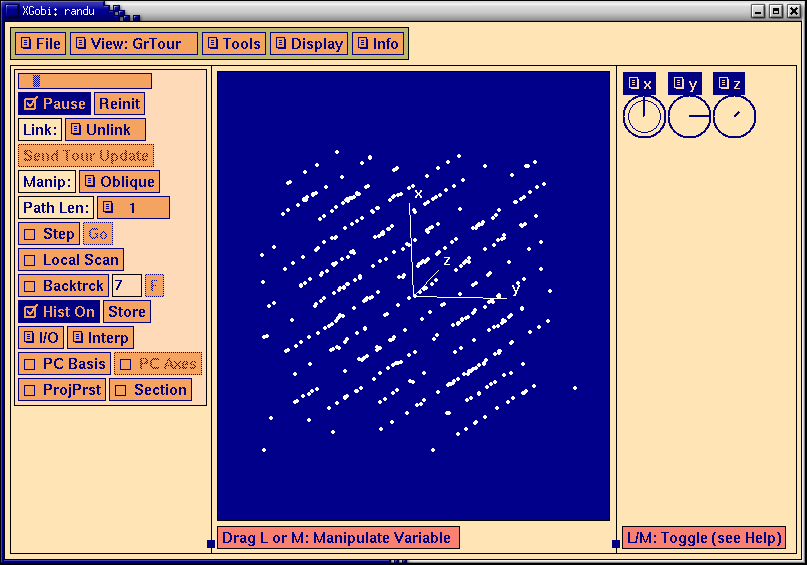
On peut aussi la faire tourner directement sous R, en prenant une matrice de rotation au hasard (Exercice : écrire une telle fonction (il y en a une quelque part dans ce document))
m <- matrix( c(0.0491788982891203, -0.998585856299176, 0.0201921658647648,
0.983046639705112, 0.0448184901961194, -0.177793720645666,
-0.176637312387723, -0.028593540105802, -0.983860594462783),
nr=3, nc=3)
plot( t( m %*% t(randu) )[,1:2] )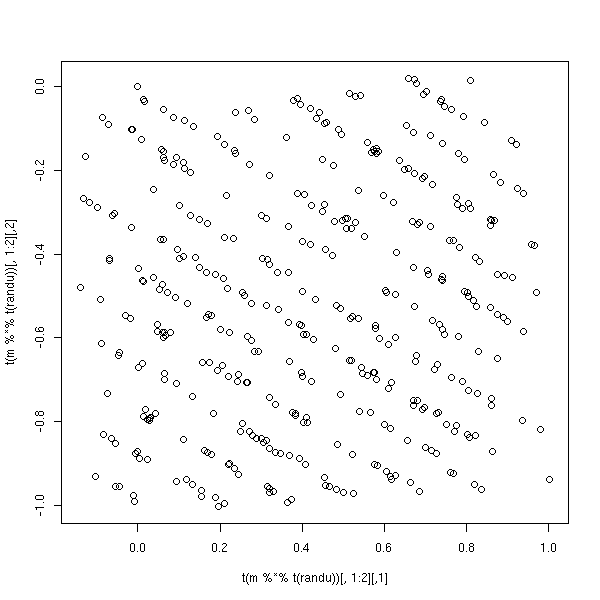
Voici un exemple réel.
data(EuStockMarkets) plot(EuStockMarkets)
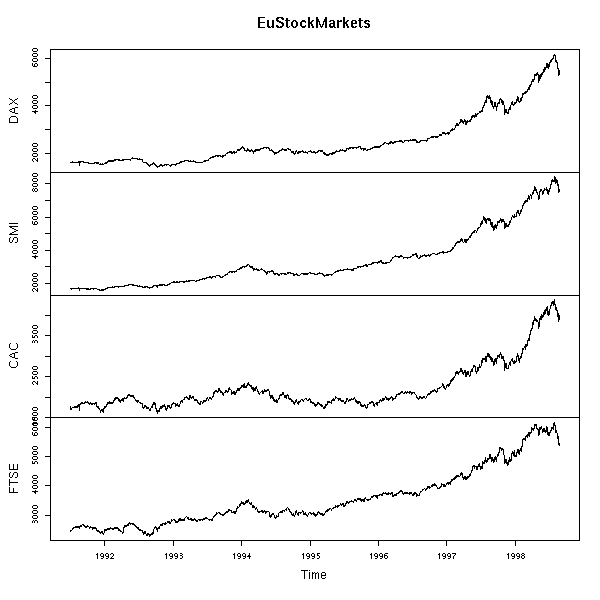
x <- EuStockMarkets[,1] y <- EuStockMarkets[,2] r <- lm(y~x) plot(y~x) abline(r, col='red', lwd=3)
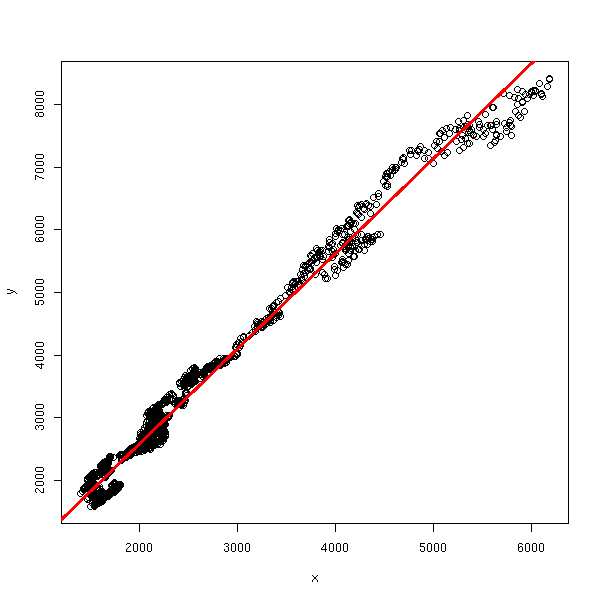
plot(r, which=1)
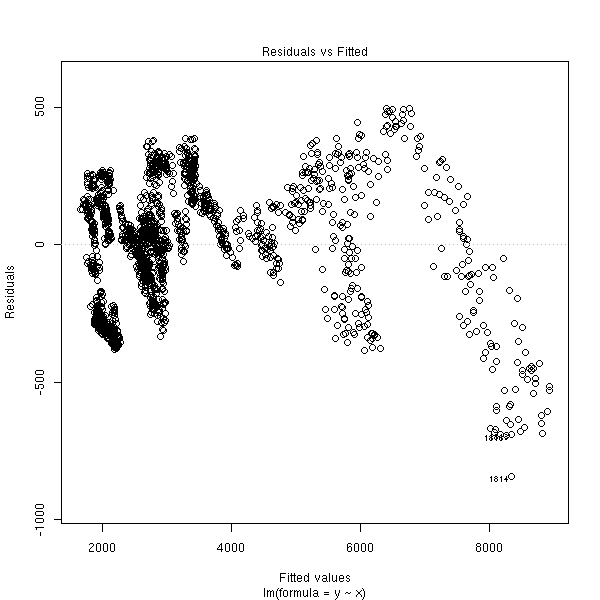
plot(r, which=3)
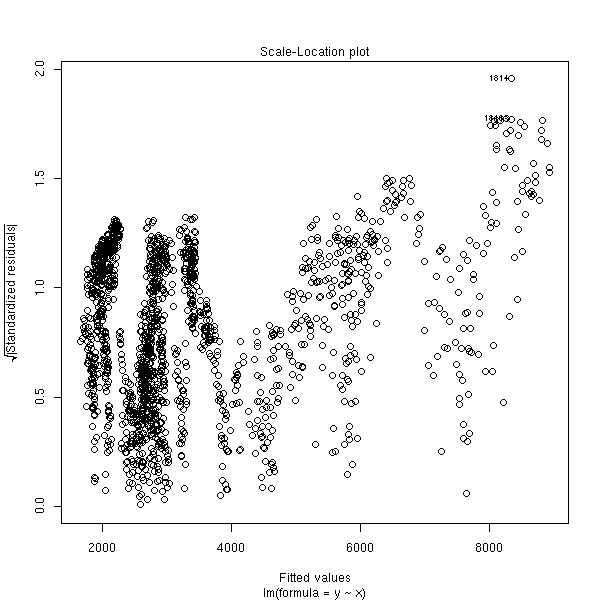
plot(r, which=4)
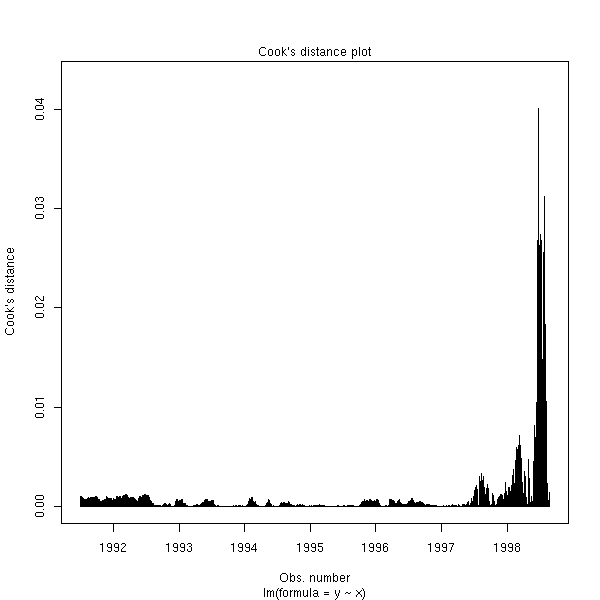
r <- r$res hist(r, probability=T, col='light blue') lines(density(r), col='red', lwd=3)
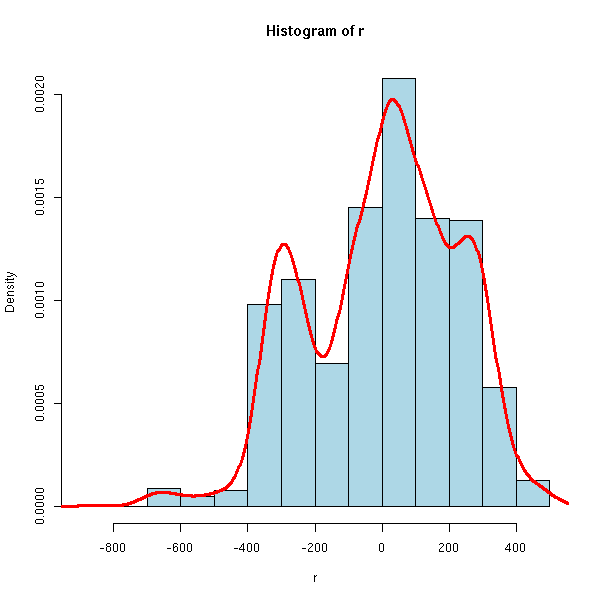
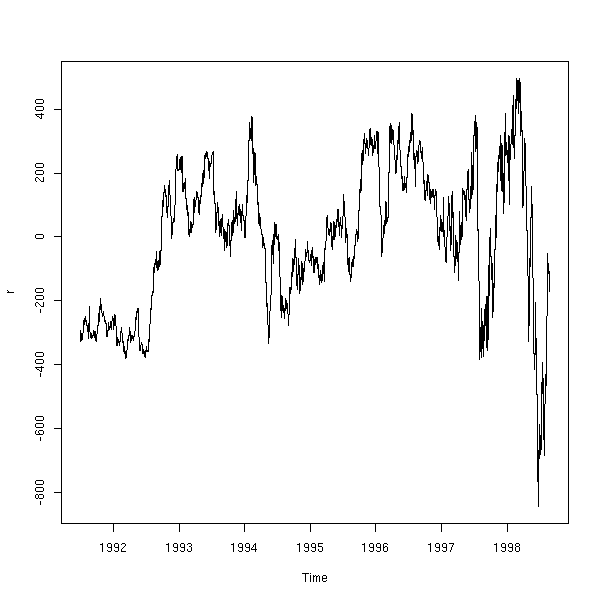
plot(r)
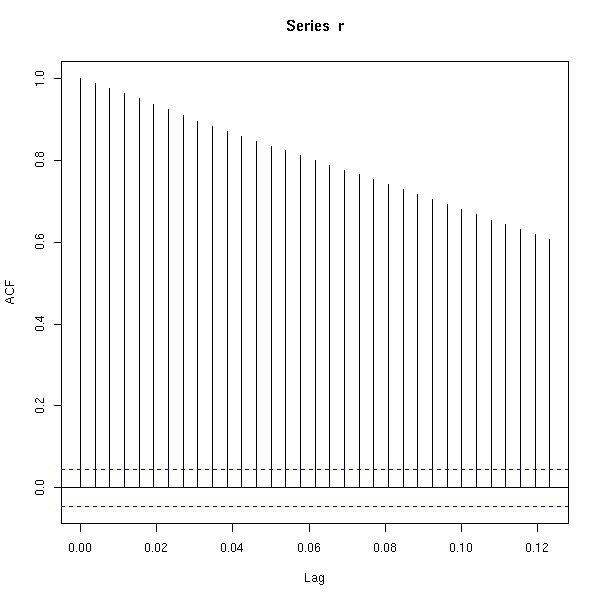
acf(r)
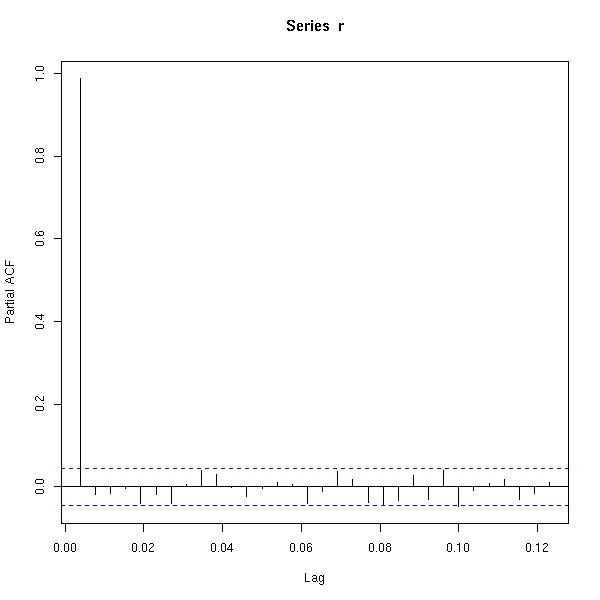
pacf(r)
r <- as.vector(r) x <- r[1:(length(r)-1)] y <- r[2:length(r)] plot(x,y, xlab='x[i]', ylab='x[i+1]')
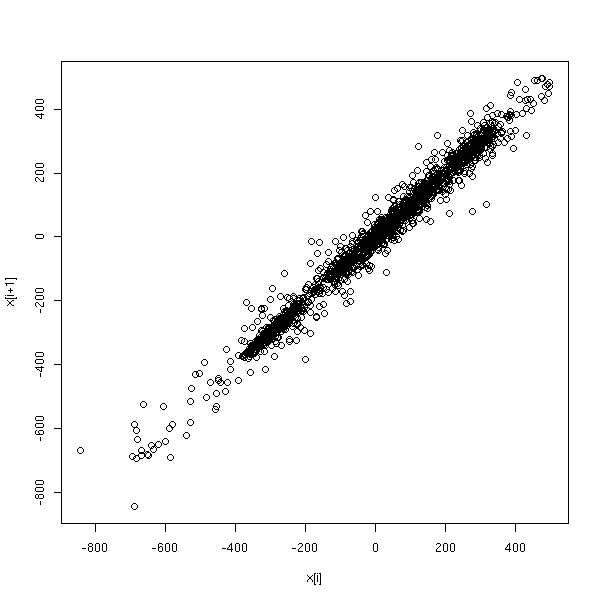
Dans ce genre de situation, on peut utiliser les moindres carrés généralisés. Le modèle AR1 suppose que les erreurs successives sont corrélées :
e_{i+1} = r * e_i + f_ioù r est le coefficient de corrélation et les f_i sont indépendantes.
n <- 100
x <- rnorm(n)
e <- vector()
e <- append(e, rnorm(1))
for (i in 2:n) {
e <- append(e, .6 * e[i-1] + rnorm(1) )
}
y <- 1 - 2*x + e
i <- 1:n
plot(y~x)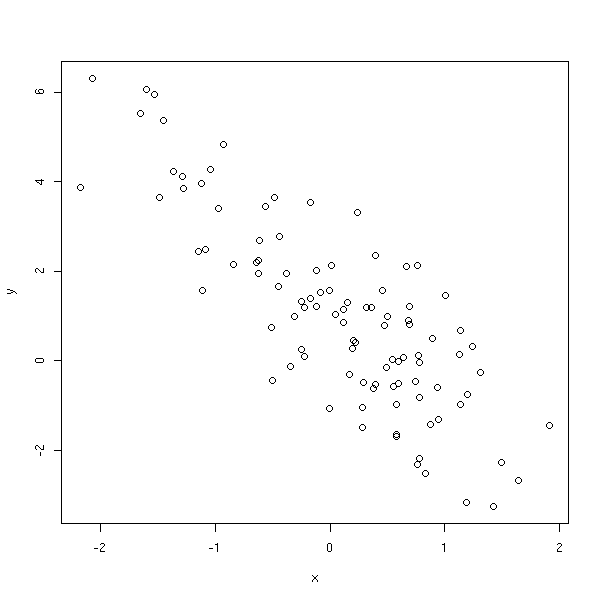
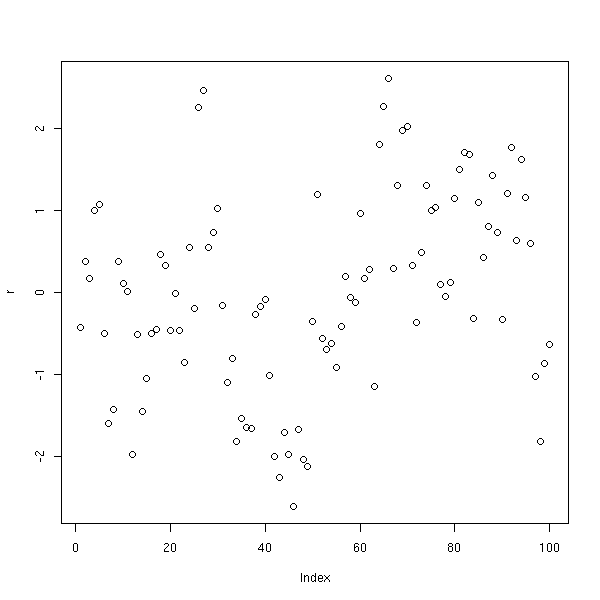
r <- lm(y~x)$residuals plot(r)
Les moindres carrés généralisés se trouvent dans la bibliothèque nlme.
library(nlme) g <- gls(y~x, correlation = corAR1(form= ~i))
Voici le résultat.
> summary(g)
Generalized least squares fit by REML
Model: y ~ x
Data: NULL
AIC BIC logLik
298.4369 308.7767 -145.2184
Correlation Structure: AR(1)
Formula: ~i
Parameter estimate(s):
Phi
0.3459834
Coefficients:
Value Std.Error t-value p-value
(Intercept) 1.234593 0.15510022 7.959971 <.0001
x -1.892171 0.09440561 -20.042992 <.0001
Correlation:
(Intr)
x 0.04
Standardized residuals:
Min Q1 Med Q3 Max
-2.14818684 -0.75053384 0.02200128 0.57222518 2.45362824
Residual standard error: 1.085987
Degrees of freedom: 100 total; 98 residualOn peut regarder l'intervalle de confiance sur le coefficient d'autocorrélation.
> intervals(g)
Approximate 95% confidence intervals
Coefficients:
lower est. upper
(Intercept) 0.926802 1.234593 1.542385
x -2.079516 -1.892171 -1.704826
Correlation structure:
lower est. upper
Phi 0.1477999 0.3459834 0.5174543
Residual standard error:
lower est. upper
0.926446 1.085987 1.273003Comparons avec la régression naïve.
library(nlme) plot(y~x) abline(lm(y~x)) abline(gls(y~x, correlation = corAR1(form= ~i)), col='red')
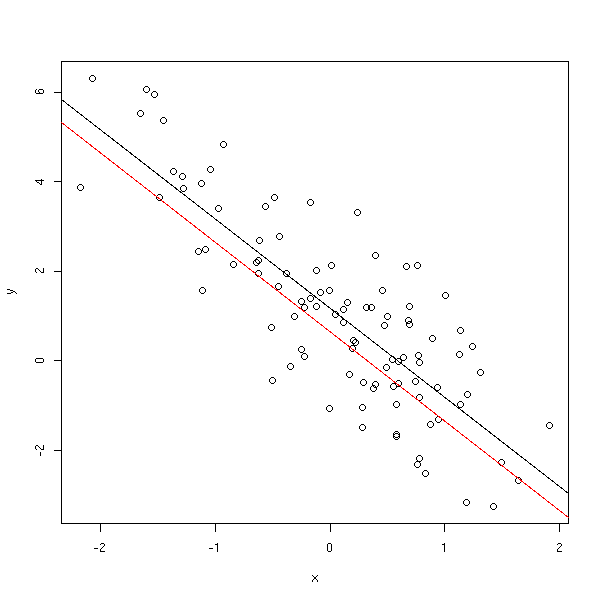
Dans cet exemple, il n'y a aucun effet notable. Dans le suivant, la situation est plus dramatique.
n <- 1000
x <- rnorm(n)
e <- vector()
e <- append(e, rnorm(1))
for (i in 2:n) {
e <- append(e, 1 * e[i-1] + rnorm(1) )
}
y <- 1 - 2*x + e
i <- 1:n
plot(lm(y~x)$residuals)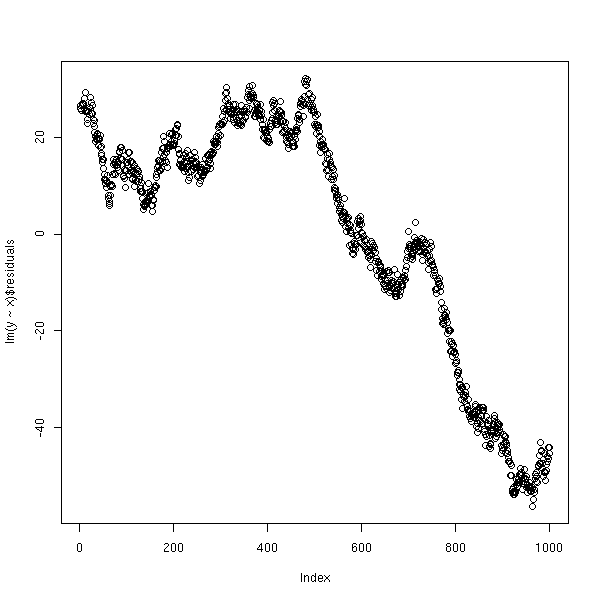
plot(y~x) abline(lm(y~x)) abline(gls(y~x, correlation = corAR1(form= ~i)), col='red') abline(1,-2, lty=2)
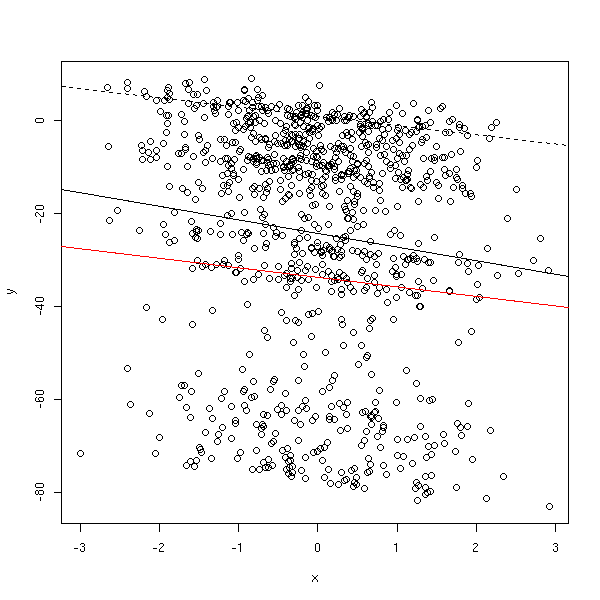
Nous reverrons cela quand nous parlerons de séries temporelles.
Dans le cas de données géographiques, c'est beaucoup plus compliqué.
A FAIRE : une référence ?
On constate que si on donne les mêmes données à différentes personnes (par exemple, des étudiants, lors d'un examen), chacun aura un modèle différent et des prévisions différentes. Ces prévisions et leurs intervalles de confiance sont généralement incompatibles -- et les intervalles de prédiction sont toujours trop petits...
Le coefficient de corrélation entre deux variables permet de voir si elles sont colinéaires. Mais on peut aussi avoir des relations entre plus de deux variables, du genre X3 = X1 + X2. Pour les détecter, on peut faire une régression de Xk par rapport aux autres Xi et regarder R^2 (le coefficient de corrélation ou pourcentage de la variance expliquée) : s'il est élevé (>1e-1), Xk se déduit des autres Xi.
n <- 100 x <- rnorm(n) x1 <- x+rnorm(n) x2 <- x+rnorm(n) x3 <- rnorm(n) y <- x+x3 summary(lm(x1~x2+x3))$r.squared # 1e-1 summary(lm(x2~x1+x3))$r.squared # 1e-1 summary(lm(x3~x1+x2))$r.squared # 1e-3
Autre exemple, avec 3 variables liées.
n <- 100 x1 <- rnorm(n) x2 <- rnorm(n) x3 <- x1+x2+rnorm(n) x4 <- rnorm(n) y <- x1+x2+x3+x4+rnorm(n) summary(lm(x1~x2+x3+x4))$r.squared # 0.5 summary(lm(x2~x1+x3+x4))$r.squared # 0.4 summary(lm(x3~x1+x2+x4))$r.squared # 0.7 summary(lm(x4~x1+x2+x3))$r.squared # 3e-3
Exemple réel (ici, je prends le coefficient de détermination ajusté) :
check.multicolinearity <- function (M) {
a <- NULL
n <- dim(M)[2]
for (i in 1:n) {
m <- as.matrix(M[, 1:n!=i])
y <- M[,i]
a <- append(a, summary(lm(y~m))$adj.r.squared)
}
names(a) <- names(M)
print(round(a,digits=2))
invisible(a)
}
data(freeny)
names(freeny) <- paste(
names(freeny),
" (",
round(check.multicolinearity(freeny), digits=2),
")",
sep='')
pairs(freeny,
upper.panel=panel.smooth,
lower.panel=panel.smooth)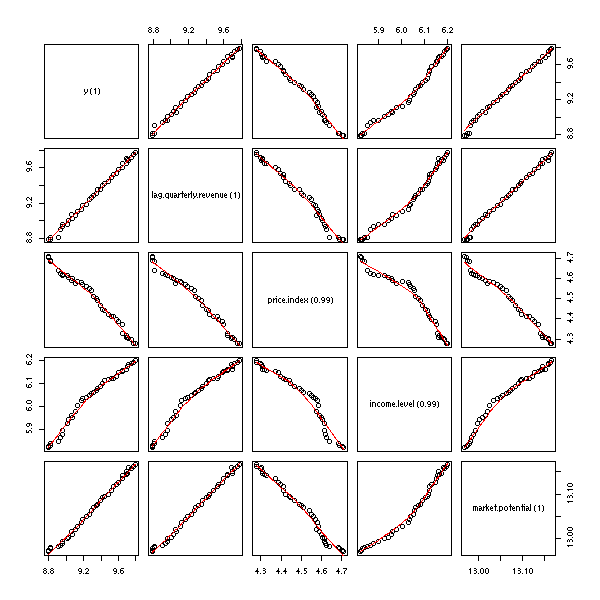
Dans une telle situation, le fait qu'un certain coefficient soit statistiquement non nul dépend de la présence des autres variables. Avec toutes les variables, la première variable explicative ne joue pas un rôle significatif, mais la seconde, si.
> summary(lm(freeny.y ~ freeny.x))
...
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) -10.4726 6.0217 -1.739 0.0911 .
freeny.xlag quarterly revenue 0.1239 0.1424 0.870 0.3904
freeny.xprice index -0.7542 0.1607 -4.693 4.28e-05 ***
freeny.xincome level 0.7675 0.1339 5.730 1.93e-06 ***
freeny.xmarket potential 1.3306 0.5093 2.613 0.0133 *
...
Multiple R-Squared: 0.9981, Adjusted R-squared: 0.9978Par contre, si on ne retient que les deux premières variables, c'est le contraire.
> summary(lm(freeny.y ~ freeny.x[,1:2]))
...
Estimate Std. Error t value Pr(>|t|)
(Intercept) 2.18577 1.47236 1.485 0.146
freeny.x[, 1:2]lag quarterly revenue 0.89122 0.07412 12.024 3.63e-14 ***
freeny.x[, 1:2]price index -0.25592 0.17534 -1.460 0.153
...
Multiple R-Squared: 0.9958, Adjusted R-squared: 0.9956De plus, l'estimation des coefficients et leur erreur standard sont assez inquiétants... A ce niveau, un autre problème peut apparaitre : en cas de multicolinéarité, le signe d'un coefficient n'est pas toujours bien déterminé.
n <- 100 v <- .1 x <- rnorm(n) x1 <- x + v*rnorm(n) x2 <- x + v*rnorm(n) x3 <- x + v*rnorm(n) y <- x1+x2-x3 + rnorm(n)
On vérifie que les variables sont bien liées.
> summary(lm(x1~x2+x3))$r.squared [1] 0.986512 > summary(lm(x2~x1+x3))$r.squared [1] 0.98811 > summary(lm(x3~x1+x2))$r.squared [1] 0.9862133
On regarde quelles sont les variables les plus pertinentes.
> summary(lm(y~x1+x2+x3))
Call:
lm(formula = y ~ x1 + x2 + x3)
Residuals:
Min 1Q Median 3Q Max
-3.0902 -0.7658 0.0793 0.6995 2.6456
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 0.06361 0.11368 0.560 0.5771
x1 1.47317 0.94653 1.556 0.1229
x2 1.18874 0.98481 1.207 0.2304
x3 -1.70372 0.94366 -1.805 0.0741 .
---
Signif. codes: 0 `***' 0.001 `**' 0.01 `*' 0.05 `.' 0.1 ` ' 1
Residual standard error: 1.135 on 96 degrees of freedom
Multiple R-Squared: 0.4757, Adjusted R-squared: 0.4593
F-statistic: 29.03 on 3 and 96 DF, p-value: 1.912e-13C'est la troisième.
> lm(y~x3)$coef (Intercept) x3 0.06970513 0.98313878
Son coefficient était négatif, mais si on enlève les autres variables, il devient positif.
Au lieu de regarder les R^2, on peut regarder les Facteurs d'Inflation de la Variance (VIF),
1
V_j = -----------
1 - R_j^2Au lieu de regarder les R^2, on peut regarder la matrice des corrélations entre les coefficients estimés.
n <- 100 v <- .1 x <- rnorm(n) x1 <- x + v*rnorm(n) x2 <- rnorm(n) x3 <- x + v*rnorm(n) y <- x1+x2-x3 + rnorm(n) summary(lm(y~x1+x2+x3), correlation=T)$correlation
On obtient
(Intercept) x1 x2 x3 (Intercept) 1.0000000000 -0.02036269 0.0001812560 0.02264558 x1 -0.0203626936 1.00000000 -0.1582002900 -0.98992751 x2 0.0001812560 -0.15820029 1.0000000000 0.14729488 x3 0.0226455841 -0.98992751 0.1472948846 1.00000000
On constate que les variables X1 et X3 sont relativement liées. On peut aussi le voir graphiquement.
n <- 100
v <- .1
x <- rnorm(n)
x1 <- x + v*rnorm(n)
x2 <- rnorm(n)
x3 <- x + v*rnorm(n)
y <- x1+x2-x3 + rnorm(n)
m <- summary(lm(y~x1+x2+x3), correlation=T)$correlation
plot(col(m), row(m), cex=10*abs(m),
xlim=c(0, dim(m)[2]+1),
ylim=c(0, dim(m)[1]+1),
main="Matrice de corrélation des coefficients d'une régression")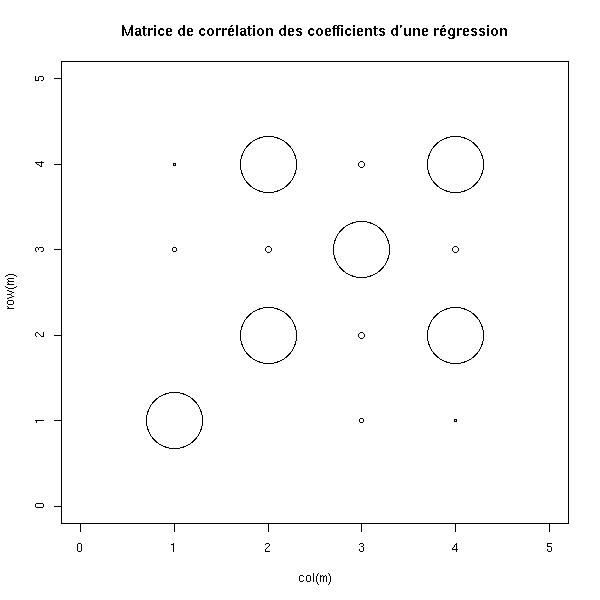
Une autre manière de voir le problème consiste à faire le rapport entre la plus grande valeur propre de la matrice et la plus petite : si c'est en dessous de 100, c'est bon, au dessus de 1000, c'est grave. C'est l'indice de conditionnement.
m <- model.matrix(y~x1+x2+x3) d <- eigen( t(m) %*% m, symmetric=T )$values d[1]/d[4] # 230
Pour résoudre ce problème, on peut enlever les variables superflues (mais se posent alors des problèmes d'interprétation). On peut aussi demander plus de données (les problèmes de multicolinéarité sont fréquents quand on a beaucoup de variables et peu d'individus).
Nous avons en fait déjà rencontré cette problématique avec la régression polynômiale : pour se débarasser de la multicolinéarité, nous avions orthonormalisé la famille de vecteurs.
> y <- cars$dist
> x <- cars$speed
> m <- cbind(x, x^2, x^3, x^4, x^5)
> cor(m)
x
x 1.0000000 0.9794765 0.9389237 0.8943823 0.8515996
0.9794765 1.0000000 0.9884061 0.9635754 0.9341101
0.9389237 0.9884061 1.0000000 0.9927622 0.9764132
0.8943823 0.9635754 0.9927622 1.0000000 0.9951765
0.8515996 0.9341101 0.9764132 0.9951765 1.0000000
> m <- poly(x,5)
> cor(m)
1 2 3 4 5
1 1.000000e+00 6.409668e-17 -1.242089e-17 -3.333244e-17 7.935005e-18
2 6.409668e-17 1.000000e+00 -4.468268e-17 -2.024748e-17 2.172470e-17
3 -1.242089e-17 -4.468268e-17 1.000000e+00 -6.583818e-17 -1.897354e-18
4 -3.333244e-17 -2.024748e-17 -6.583818e-17 1.000000e+00 -4.903304e-17
5 7.935005e-18 2.172470e-17 -1.897354e-18 -4.903304e-17 1.000000e+00La "ridge regression" (voir un peu plus haut dans ce document) est peu sensible à la multicolinéarité.
Il peut manquer des variables importantes, dont l'absence peut complètement changer les résultats de la régression et leur interprétation.
Dans l'exemple suivant, on a trois variables.
n <- 100
x <- runif(n)
z <- ifelse(x>.5,1,0)
y <- 2*z -x + .1*rnorm(n)
plot( y~x, col=c('red','blue')[1+z] )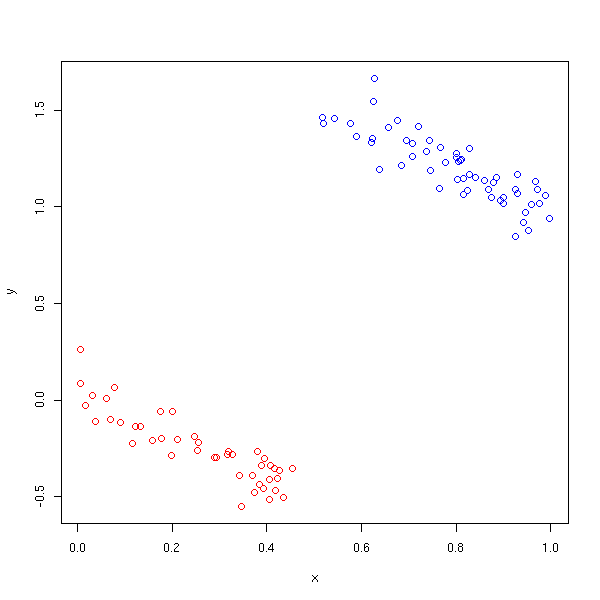
Si on tient compte des trois variables, il y a une corrélation négative entre y et x.
> summary(lm( y~x+z ))
Call:
lm(formula = y ~ x + z)
Residuals:
Min 1Q Median 3Q Max
-0.271243 -0.065745 0.002929 0.068085 0.215251
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 0.01876 0.02404 0.78 0.437
x -1.05823 0.07126 -14.85 <2e-16 ***
z 2.05321 0.03853 53.28 <2e-16 ***
---
Signif. codes: 0 `***' 0.001 `**' 0.01 `*' 0.05 `.' 0.1 ` ' 1
Residual standard error: 0.1008 on 97 degrees of freedom
Multiple R-Squared: 0.9847, Adjusted R-squared: 0.9844
F-statistic: 3125 on 2 and 97 DF, p-value: < 2.2e-16Par contre, si on n'a pas la variable z, la corrélation est positive...
> summary(lm( y~x ))
Call:
lm(formula = y ~ x)
Residuals:
Min 1Q Median 3Q Max
-1.05952 -0.38289 -0.01774 0.50598 1.05198
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) -0.5689 0.1169 -4.865 4.37e-06 ***
x 2.1774 0.2041 10.669 < 2e-16 ***
---
Signif. codes: 0 `***' 0.001 `**' 0.01 `*' 0.05 `.' 0.1 ` ' 1
Residual standard error: 0.5517 on 98 degrees of freedom
Multiple R-Squared: 0.5374, Adjusted R-squared: 0.5327
F-statistic: 113.8 on 1 and 98 DF, p-value: < 2.2e-16Pour contourner le problème, il faut inclure toutes les variables suceptibles d'être importantes (on sélectionne ces variables à l'aide de la connaissance préalable de domaine d'étude, i.e., par des moyens non statistiques). Pour confirmer un certain effet, on peut aussi essayer d'autre modèles (s'ils donnent tous un effet dans le même sens, c'est bon signe) ou faire d'autres études, dans des conditions différentes.
On veut parfois extrapoler à partir des données, i.e., voir ce qui se passe sur une échelle plus grande. C'est problématique pour plusieurs raisons. Tout d'abord, les intervalles de confiances augmentent quand on s'éloigne des valeurs de l'échantillon.
n <- 20 x <- rnorm(n) y <- 1 - 2*x - .1*x^2 + rnorm(n) #summary(lm(y~poly(x,10))) plot(y~x, xlim=c(-20,20), ylim=c(-30,30)) r <- lm(y~x) abline(r, col='red') xx <- seq(-20,20,length=100) p <- predict(r, data.frame(x=xx), interval='prediction') lines(xx,p[,2],col='blue') lines(xx,p[,3],col='blue') title(main="Augmentation de l'intervalle de prédiction")
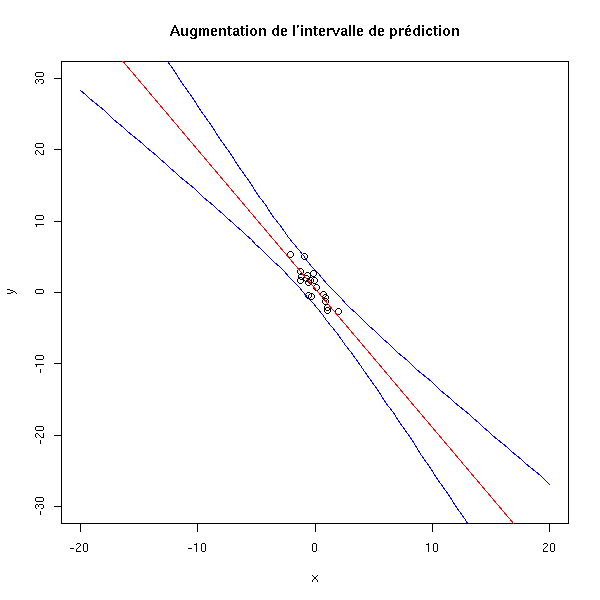
D'autre part, si la relation entre les données a l'air linéaire à petite échelle, il n'en va peut-être pas de même sur une échelle plus grande.
plot(y~x, xlim=c(-20,20), ylim=c(-30,30)) r <- lm(y~x) abline(r, col='red') xx <- seq(-20,20,length=100) yy <- 1 - 2*xx - .1*xx^2 + rnorm(n) p <- predict(r, data.frame(x=xx), interval='prediction') points(yy~xx) lines(xx,p[,2],col='blue') lines(xx,p[,3],col='blue') title(main="Problème d'extropolation : ça n'était pas linéaire...")
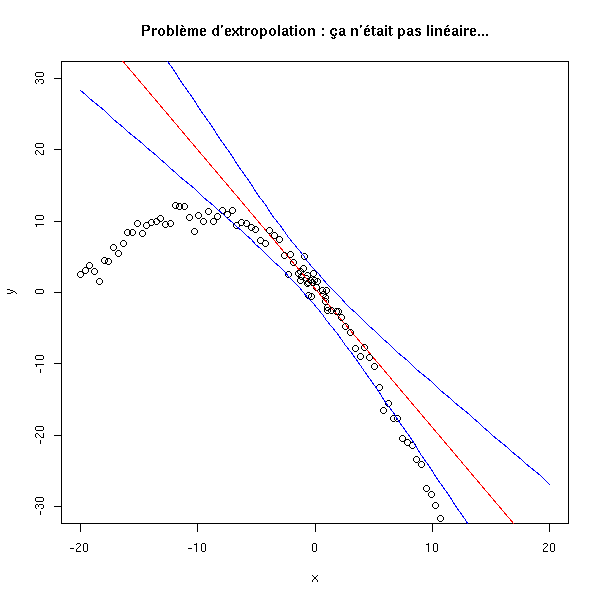
data(cars) y <- cars$dist x <- cars$speed o <- x<quantile(x,.25) x1 <- x[o] y1 <- y[o] r <- lm(y1~x1) xx <- seq(min(x),max(x),length=100) p <- predict(r, data.frame(x1=xx), interval='prediction') plot(y~x) abline(r, col='red') lines(xx,p[,2],col='blue') lines(xx,p[,3],col='blue')
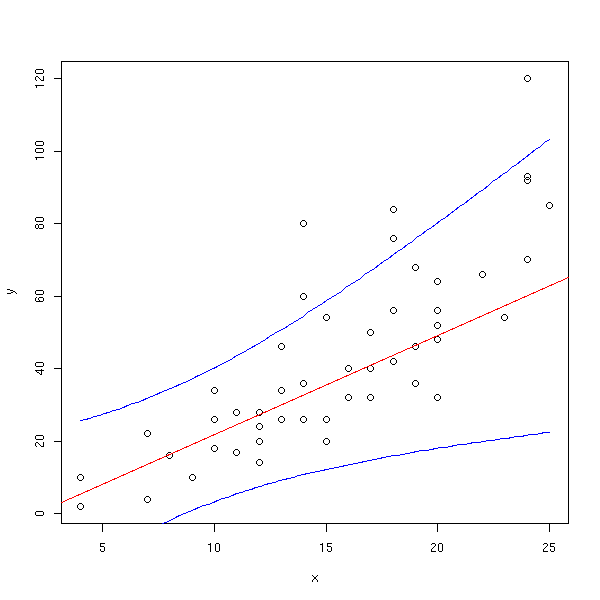
Il peut y avoir des erreurs de mesure sur la variable indépendante : cela conduit à une estimation biaisée (vers 0) des paramètres.
n <- 100 e <- .5 x0 <- rnorm(n) x <- x0 + e*rnorm(n) y <- 1 - 2*x0 + e*rnorm(n) plot(y~x) points(y~x0, col='red') abline(lm(y~x)) abline(lm(y~x0),col='red')
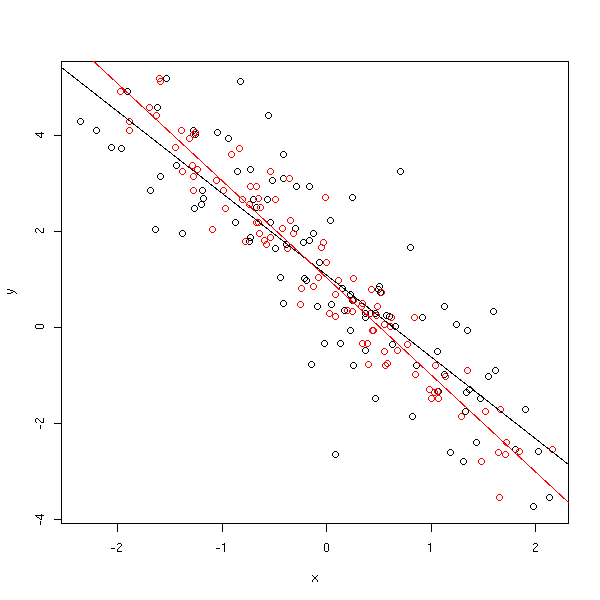
Par contre, ça n'est pas un problème sur les prédictions, car les erreurs de mesure sur les variables indépendantes seront toujours présentes.
library(help=lmtest) library(help=strucchange) # Hétéroscédasticité library(lmtest) ?dwtest ?bgtest ?bptest ?gqtest ?hmctest # Non-linearity library(lmtest) ?harvtest ?raintest ?reset
La bibliothèque "strucchange" permet de repérer les changements structurels (très souvent avec des séries temporelles, par exemple en économétrie). On parle de changement structurel quand la régression linéaire est un modèle correct, mais que les coefficients de la régression changent brutalement. Si on sait où le changement a lieu, on peut simplement couper les données en deux, faire deux régressions et procéder à un test pour voir si les coefficients des deux régressions sont les mêmes. Si on ne sait pas, on peut déplacer une fenêtre le long des données et faire une régression à chaque fois, en regardant si les coefficients changent (la fenêtre peut avoir une largeur constante ou contenir un nombre d'observations constant).
A FAIRE : un exemple # Structural change library(strucchange) efp(..., type="Rec-CUSUM") efp(..., type="OLS-MOSUM") plot(efp(...)) sctest(efp(...)) A FAIRE : on peut aussi regarder si une variable est constante (x~1).
On peut aussi déplacer le point en lequel on pense qu'il peut y avoir un changement et faire un test à chaque fois.
A FAIRE : un exemple Fstat(...) plot(Fstat(...)) sctest(Fstat(...))
Expliquer ce qu'on peut faire si on a plus de variables que d'observations. Une approche naïve ne marche pas : n <- 100 k <- 500 x <- matrix(rnorm(n*k), nr=n, nc=k) y <- apply(x, 1, sum) lm(y~x)
Vincent Zoonekynd
<zoonek@math.jussieu.fr>
latest modification on Wed Oct 13 22:32:57 BST 2004