
The French version of this document is no longer maintained: be sure to check the more up-to-date English version.
Définition générale de la régression
Quelques droites de régression
Asymétrie de la régression et ACP (Analyse en Composantes Principales)
Variantes des moindres carrés
Polynômes : régression curvilinéaire
Régressions locales
Régressions pénalisées
Régression non linéaire
A CLASSER
A FAIRE
A FAIRE : revoir l'ordre de ce chapitre
Définition générale de la régression Quelques droites de régression (droites des médianes, etc.) Régression et ACP Variantes des moindres carrés (L1, Huber, etc.) Moindres carrés généralisés (pondérés, IRLS, etc.) Régressions polynomiale, splines Régressions locales (on commence avec les lignes brisées) PCR, PLS, ridge, lasso, PMLE, etc. Régression non linéaire
Les moindres carrés ne sont pas la seule méthode pour approcher des données par une fonction : en voici quelques autres.
On s'intéresse à la prédiction d'une variable statistique Y à l'aide d'une autre variable X, toutes deux quantitatives.
La courbe de régression de Y sur X est la fonction f qui minimise
E( Y - f(X) )^2.
On peut l'obtenir ainsi :
f(x) = E[ Y | X=x ].
Le problème, c'est que pour calculer cette régression, on aurait besoin de connaître la distribution de Y|X, or on ne dispose que d'un échantillon. On peut tenter d'approcher la régression par des moyennes mobiles, ou des moyennes mobiles pondérées par un noyau.
Néanmoins, on se limite généralement à une fonction qui a une forme relativement simple, comme une fonction affine ou un polynôme (plus le modèle est simple, plus les estimateurs sont stables). On cherche alors à minimiser
E( Y - (aX+b) )^2.
C'est la régression linéaire.
On divise les données en deux groupes ; on prend le centre (le point médiant) de chaque, et on les relie.
data(cars) x <- cars$speed y <- cars$dist plot(y~x) o <- order(x) n <- length(x) m <- floor(n/2) p1 <- c( median(x[o[1:m]]), median(y[o[1:m]]) ) m <- ceiling(n/2) p2 <- c( median(x[o[m:n]]), median(y[o[m:n]]) ) p <- rbind(p1,p2) points(p, pch='+', lwd=3, cex=5, col='red' ) lines(p, col='red', lwd=3) title(main="Droite de Brown-Mood")

On sépare les données en trois groupes, on prend leurs centre, et on considère la droite passant par le centre de gravité du triangle ainsi obtenu et parallèle à sa base.
three.group.resistant.line <- function (y, x) {
o <- order(x)
n <- length(x)
o1 <- o[1:floor(n/3)]
o2 <- o[ceiling(n/3):floor(2*n/3)]
o3 <- o[ceiling(2*n/3):n]
p1 <- c( median(x[o1]), median(y[o1]) )
p2 <- c( median(x[o2]), median(y[o2]) )
p3 <- c( median(x[o3]), median(y[o3]) )
p <- rbind(p1,p2,p3)
g <- apply(p,2,mean)
plot(y~x)
points(p, pch='+', lwd=3, cex=3, col='red')
polygon(p, border='red')
a <- (p3[2] - p1[2])/(p3[1] - p1[1])
b <- g[2]-a*g[1]
abline(b,a,col='red')
}
three.group.resistant.line(cars$dist, cars$speed)
Si le triangle n'est pas complètement applati, c'est signe que la relation n'est probablement pas linéaire...
n <- 100 x <- runif(n,min=0,max=2) y <- x*(1-x) + rnorm(n) three.group.resistant.line(y,x)

On note b_ij la pente de la droite passant par les points i et j et on prend
b = median b_ij
a = median (yi - b xi)
i
droite.des.medianes <- function (y,x) {
n <- length(x)
b <- matrix(NA, nr=n, nc=n)
# Exercice : écrire ça sans aucune boucle
for (i in 1:n) {
for (j in 1:n) {
if(i!=j)
b[i,j] <- ( y[i] - y[j] )/( x[i] - x[j] )
}
}
b <- median(b, na.rm=T)
a <- median(y-b*x)
plot(y~x)
abline(a,b, col='red')
title(main="La droite des médianes")
}
droite.des.medianes(cars$dist, cars$speed)
On procède à peu près comme précédemment, mais avec :
b = median median b_ij
i j!=i
a = median (yi - b xi)
iCela donne :
autre.droite.des.medianes <- function (y,x) {
n <- length(x)
b <- matrix(NA, nr=n, nc=n)
# Exercice : écrire ça sans aucune boucle
for (i in 1:n) {
for (j in 1:n) {
if(i!=j)
b[i,j] <- ( y[i] - y[j] )/( x[i] - x[j] )
}
}
b <- median( apply(b, 1, median, na.rm=T), na.rm=T ) # Seule chose qui change
a <- median(y-b*x)
plot(y~x)
abline(a,b, col='red')
title(main="La droite des médianes")
}
autre.droite.des.medianes(cars$dist, cars$speed)
La régression linéaire cherche à minimiser la somme des carrés des distances, mesurées verticalement, entre la droite et le nuage de points.
data(cars) plot(cars) abline(lm(cars$dist ~ cars$speed), col='red') title(main="Régression dist ~ speed")

Ça n'est pas symétrique : si on intervertit les variables, on obtient quelque chose de différent (toutefois, les deux droites passent par le centre de gravité du nuage).
plot(cars) r <- lm(cars$dist ~ cars$speed) abline(r, col='red') r <- lm(cars$speed ~ cars$dist) a <- r$coefficients[1] # Intercept b <- r$coefficients[2] # slope abline(-a/b , 1/b, col="blue") title(main="Régression dist ~ speed et speed ~ dist")

Dans un cas, on cherche à minimiser la somme des carrés des distances entre la droite et les points, mesurées verticalement, dans l'autre, on mesure ces distances horizontalement. Il s'agit de de manières « raisonnables » mais différentes de mesurer la distance entre un nuage de points et une droite. C'est pourqhoi on obtient des résultats différents.
plot(cars) r <- lm(cars$dist ~ cars$speed) abline(r, col='red') segments(cars$speed, cars$dist, cars$speed, r$fitted.values,col="red") title(main="Régression dist ~ speed : on mesure les distances verticalement")

plot(cars) r <- lm(cars$speed ~ cars$dist) a <- r$coefficients[1] # Intercept b <- r$coefficients[2] # slope abline(-a/b , 1/b, col="blue") segments(cars$speed, cars$dist, r$fitted.values, cars$dist, col="blue") title(main="Régression speed ~ dist : on mesure les distances horizontalement")

Il y a une autre manière raisonnable de mesurer la distance entre un nuage de points et une droite : la somme des carrés des distances entre les points et la droite, mesurées orthogonalement à la droite. C'est ce qu'on appelle l'ACP (Analyse en Composantes Principales), et cette fois-ci, c'est symétrique.
plot(cars) r <- lm(cars$dist ~ cars$speed) abline(r, col='red') r <- lm(cars$speed ~ cars$dist) a <- r$coefficients[1] # Intercept b <- r$coefficients[2] # slope abline(-a/b , 1/b, col="blue") r <- princomp(cars) b <- r$loadings[2,1] / r$loadings[1,1] a <- r$center[2] - b * r$center[1] abline(a,b) title(main="Comparaison de trois régressions")

Dans cet exemple, les droites bleue et noire sont presque confondues. Voici une situation dans laquelle les trois droites devraient être distinctes.
x <- rnorm(100) y <- x + rnorm(100) plot(y~x) r <- lm(y~x) abline(r, col='red') r <- lm(x ~ y) a <- r$coefficients[1] # Intercept b <- r$coefficients[2] # slope abline(-a/b , 1/b, col="blue") r <- princomp(cbind(x,y)) b <- r$loadings[2,1] / r$loadings[1,1] a <- r$center[2] - b * r$center[1] abline(a,b) title(main="Comparaison de trois régressions")

plot(y~x, xlim=c(-4,4), ylim=c(-4,4) ) abline(a,b) # Matrice de changement de base u <- r$loadings # Projection sur le premier axe p <- matrix( c(1,0,0,0), nrow=2 ) X <- rbind(x,y) X <- r$center + solve(u, p %*% u %*% (X - r$center)) segments( x, y, X[1,], X[2,] ) title(main="ACP : on mesure les distances perpendiculairement à la droite")

On peut minimiser
Somme abs( y_i - a - b x_i ) i
au lieu de
Somme ( y_i - a - b x_i ) ^ 2
i
x <- cars$speed
y <- cars$dist
my.lar <- function (y,x) {
f <- function (arg) {
a <- arg[1]
b <- arg[2]
sum(abs(y-a-b*x))
}
r <- optim( c(0,0), f )$par
plot( y~x )
abline(lm(y~x), col='red', lty=2)
abline(r[1], r[2])
legend( par("usr")[1], par("usr")[4], yjust=1,
c("Moindres carrés", "Moindres valeurs absolues"),
lwd=1, lty=c(2,1),
col=c(par('fg'),'red'))
}
my.lar(y,x)
A FAIRE :
library(quantreg) ?rq
La régression au sens des moindres carrés consiste à minimiser
Somme( rho( (yi - \hat yi) / sigma ) ) i
où rho(x) = x^2. Nous avons aussi vu la régression L1, ou régression au sens des moindres valeurs absolues, qui consiste à minimiser la même quantité avec rho(x) = abs(x). La régression de Huber est entre les deux : elle consiste toujours à minimiser cette somme, mais avec
rho(x) = x^2/2 si abs(x) <= c
c * abs(x) - c^2/2 sinon(où c est choisi arbitrairement, proportionnel à un estimateur robuste de la médiane du bruit).
On peut aussi l'interpréter comme une régression pondérée, dans laquelle les poinds sont donnés par
w(u) = 1 si abs(u) < c
c/abs(u) sinonC'est une régression utile si l'erreur a une distribution très dispersée.
Sous R, c'est ce que fait la fonction rlm, dans la bibliothèque MASS.
Dans l'exemple suivant, on constate que la régression de Huber n'est pas résistante : en présence de valeurs atypiques, elles donne le même résultat que la régression classique.
library(MASS) n <- 20 x <- rnorm(n) y <- 1 - 2*x + rnorm(n) y[ sample(1:n, floor(n/4)) ] <- 10 plot(y~x) abline(1,-2,lty=3) abline(lm(rlm(y~x)), col='red') abline(lm(y~x), lty=3, lwd=3)

Par contre elle est sensée être robuste :
(A FAIRE : signaler que dans une situation comme la suivante, on commencerait par transformer les données pour les rendre un peu plus normales...) n <- 100 x <- rnorm(n) y <- 1 - 2*x + rcauchy(n,1) plot(y~x) abline(1,-2,lty=3) abline(lm(rlm(y~x)), col='red') abline(lm(y~x), lty=3, lwd=3)

A FAIRE : comprendre pourquoi le graphique précédent ne montre pas ce que je veux... en particulier, comparer avec le graphique suivant... #library(lqs) # merged into MASS x <- rnorm(20) y <- 1 - x + rnorm(20) x <- c(x,10) y <- c(y,1) plot(y~x) abline(1,-1, lty=3) abline(lm(y~x)) abline(rlm(y~x, psi = psi.bisquare, init = "lts"), col='orange',lwd=3) abline(rlm(y~x), col='red') abline(rlm(y~x, psi = psi.hampel, init = "lts"), col='green') abline(rlm(y~x, psi = psi.bisquare), col='blue') title(main='Régression de Huber (rlm)')

Il ne s'agit plus de minimiser la somme des carrés de toutes les erreurs, mais uniquement la somme des carrés des erreurs "les plus petites". Si on désire faire les calculs de manière exacte, ça peut être très long (si on a n observations et si on désire en enlever k, il faut regarder tous les ensembles de n-k observations et retenir celui dont la somme des carrés est la plus petite) -- on préfèrera souvent une méthode approchée.
?ltsreg
n <- 100
x <- rnorm(n)
y <- 1 - 2*x + rnorm(n)
y[ sample(1:n, floor(n/4)) ] <- 7
plot(y~x)
r1 <- lm(y~x)
r2 <- lqs(y~x, method='lts')
abline(r1, col='red')
abline(r2, col='green')
abline(1,-2,lty=3)
legend( par("usr")[1], par("usr")[3], yjust=0,
c("Régression linéaire", "Régression élaguée"),
lty=1, lwd=1,
col=c("red", "green") )
title("Moindres carrés élagués")
Si on se contente de regarder les graphiques de diagnostic de la régression classique, on ne voit rien...
op <- par(mfrow=c(2,2)) plot(r1) par(op)

A FAIRE : estimation de l'erreur par une méthode de bootstrap.
C'est une régression résistante.
La régression élaguée a quelques variantes :
lqs : c'est presque une régression normale, mais au lieu de minimiser la somme des carrés des résidus, on met les résidus dans l'ordre et on essaye de minimiser celui du milieu. lqs(..., method='lms') : idem, mais c'est le résidu numéro << floor(n/2) + floor((p+1)/2) >> où n est le nombre d'observations et p le nombre de variables prédictives. lqs(..., method='S') : je n'ai pas compris A FAIRE
La méthode des moindres carrés suppose que le terme d'erreur (le bruit) est formé de variables normales centrées, indépendantes et de même variance. Les moindres carrés généralisés traitent le cas de variables de variances différentes (mais il faut connaître ces variances) ou non indépendantes (par exemple, avec des séries temporelles : il faut alors choisir un modèle pour décrire cette dépendance).
Nous détaillons ces deux situations un peu plus loin dans ce document.
library(MASS) ?lm.gls library(nlme) ?gls A FAIRE : relire
La méthode des moindres carrés pondérés consiste à calculer la régression et les résidus, à assigner à chaque individu un poids, d'autant plus faible que le résidu est grand, et à faire une nouvelle régression.
# Des données pas trop gentilles...
n <- 10
x <- rnorm(n)
y <- 1 - 2*x + rnorm(n)
x[1] <- 5
y[1] <- 0
my.wls <- function (y,x) {
# On effectue une première régression
r <- lm(y~x)$residuals
# On calcule les poids
w <- compute.weights(r)
# on fait une nouvelle régression
lm(y~x, weights=w)
}
compute.weights <- function (r) {
# On calcule les poids comme on veut, du moment que la comme des
# poids est 1 et que les points de résidus élevés ont des poids faibles.
# Ce choix que je fais n'est probablement ni standard ni judicieux
w <- r*r
w <- w/mean(w)
w <- 1/(1+w)
w <- w/mean(w)
}
plot(y~x)
abline(1,-2, lty=3)
abline(lm(y~x))
abline(my.wls(y,x), col='red')
title(main="Régression pondérée")
Avec la méthode des moindres carrés itérativement repondérés, on fait pareil, mais on itère jusqu'à ce que ça se stabilise.
my.irls.plot <- function (y,x, n=10) {
plot(y~x)
abline(lm(y~x))
r <- lm(y~x)$residuals
for (i in 1:n) {
w <- compute.weights(r)
print(w)
r <- lm(y~x, weights=w)
abline(r, col=topo.colors(n)[i], lwd=ifelse(i==n,3,1))
r <- r$residuals
}
lm(y~x, weights=w)
}
my.irls.plot(y,x)
abline(1,-2, lty=3)
abline(my.wls(y,x), col='blue', lty=3, lwd=3)
title(main="Régression itérativement repondérée")
A FAIRE : IRLS On trace le graphe des poids en fonction des résidus : c'est sur une courbe en forme de cloche, sur laquelle on voit bien les points influents (leur poids est faible). On essayer alors de faire une nouvelle régression (à la fois classique et robuste) sans ces points. Si le résultat diffère, c'est mauvais signe.
A FAIRE : mettre cette partie avant les régressions précédentes ? (c'est plus élémentaire)
Reprenons l'exemple de la distance d'arret d'une voiture : on s'attend plutôt à ce que la distance dépende linéairement du carré de la vitesse (ou que ce soit un polynôme de degré 2).
y <- cars$dist
x <- cars$speed
o = order(x)
plot( y~x )
do.it <- function (model, col) {
r <- lm( model )
yp <- predict(r)
lines( yp[o] ~ x[o], col=col, lwd=3 )
}
do.it(y~x, col="red")
do.it(y~x+I(x^2), col="blue")
do.it(y~-1+I(x^2), col="green")
legend(par("usr")[1], par("usr")[4],
c("fonction affine", "polynôme de degré 2", "monôme de degré 2"),
lwd=3,
col=c("red", "blue", "green"),
)
Quand on définit un modèle à l'aide d'une telle formule, le caractère ^ a un sens précis (ainsi, (a+b+c)^2 signifie a+b+c+a:b+a:c+b:c). Si on rajoute I(...), il est bien interprété comme un carré. On a le même problème avec les caractères + et *.
Si on veut se débarasser du terme constant (c'est généralement une mauvaise idée : il permet d'absorber l'effet d'éventuelles variables manquantes), on peut ajouter -1 dans le modèle.
Nous avons donné un exemple avec des monômes, mais en fait, on peut prendre n'importe quoi comme fonctions.
n <- 100 x <- runif(n,min=-4,max=4) + sign(x)*.2 y <- 1/x + rnorm(n) plot(y~x) lm( 1/y ~ x ) n <- 100 x <- rlnorm(n)^3.14 y <- x^-.1 * rlnorm(n) plot(y~x) lm(log(y) ~ log(x))
Cela revient en fait à transformer les variables : nous reverrons cela un peu plus loin.
Pour faire une régression polynômiale, on peut procéder comme précédemment en ajoutant progressivement des termes.
y <- cars$dist x <- cars$speed summary( lm(y~x) ) summary( lm(y~x+I(x^2)) ) summary( lm(y~x+I(x^2)+I(x^3)) ) summary( lm(y~x+I(x^2)+I(x^3)+I(x^4)) ) summary( lm(y~x+I(x^2)+I(x^3)+I(x^4)+I(x^5)) )
Voici quelques morceaux du résultat.
lm(formula = y ~ x)
Estimate Std. Error t value Pr(>|t|)
(Intercept) -17.5791 6.7584 -2.601 0.0123 *
x 3.9324 0.4155 9.464 1.49e-12 ***
lm(formula = y ~ x + I(x^2))
Estimate Std. Error t value Pr(>|t|)
(Intercept) 2.47014 14.81716 0.167 0.868
x 0.91329 2.03422 0.449 0.656
I(x^2) 0.09996 0.06597 1.515 0.136
lm(formula = y ~ x + I(x^2) + I(x^3))
Estimate Std. Error t value Pr(>|t|)
(Intercept) -19.50505 28.40530 -0.687 0.496
x 6.80111 6.80113 1.000 0.323
I(x^2) -0.34966 0.49988 -0.699 0.488
I(x^3) 0.01025 0.01130 0.907 0.369
lm(formula = y ~ x + I(x^2) + I(x^3) + I(x^4))
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 45.845412 60.849115 0.753 0.455
x -18.962244 22.296088 -0.850 0.400
I(x^2) 2.892190 2.719103 1.064 0.293
I(x^3) -0.151951 0.134225 -1.132 0.264
I(x^4) 0.002799 0.002308 1.213 0.232
lm(formula = y ~ x + I(x^2) + I(x^3) + I(x^4) + I(x^5))
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) -2.650e+00 1.401e+02 -0.019 0.985
x 5.484e+00 6.736e+01 0.081 0.935
I(x^2) -1.426e+00 1.155e+01 -0.124 0.902
I(x^3) 1.940e-01 9.087e-01 0.214 0.832
I(x^4) -1.004e-02 3.342e-02 -0.300 0.765
I(x^5) 1.790e-04 4.648e-04 0.385 0.702On peut utiliser ces résultats dans les deux sens : soit on part d'un modèle simple et on rajoute des termes jusqu' ce que l'effet de ces termes devienne non significatif, soit on part d'un modèle compliqué et on retire des termes jusqu'à ce que le terme de plus haut degré ait un effet significatif.
Dans les deux cas, on se retrouve avec un modèle affine.
Néanmoins, on constate que des coefficients qui sont significativement non nuls au début ne le sont plus à la fin. Pire encore, à la fin il n'y a plus aucun terme significatif et la p-valeur des termes qu'on a retenus est plus élevée que celle des autres ! Heureusement, on peut faire en sorte que les coefficients ne s'influencent pas les uns les autres en choisissant une base de polynômes autre que 1, x, x^2, x^3, etc.
y <- cars$dist x <- cars$speed summary( lm(y~poly(x,1)) ) summary( lm(y~poly(x,2)) ) summary( lm(y~poly(x,3)) ) summary( lm(y~poly(x,4)) ) summary( lm(y~poly(x,5)) )
Les résultats sont beaucoup plus clairs : les p-valeurs changent, mais très peu.
lm(formula = y ~ poly(x, 1))
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 42.980 2.175 19.761 < 2e-16 ***
poly(x, 1) 145.552 15.380 9.464 1.49e-12 ***
lm(formula = y ~ poly(x, 2))
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 42.980 2.146 20.026 < 2e-16 ***
poly(x, 2)1 145.552 15.176 9.591 1.21e-12 ***
poly(x, 2)2 22.996 15.176 1.515 0.136
lm(formula = y ~ poly(x, 3))
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 42.98 2.15 19.988 < 2e-16 ***
poly(x, 3)1 145.55 15.21 9.573 1.6e-12 ***
poly(x, 3)2 23.00 15.21 1.512 0.137
poly(x, 3)3 13.80 15.21 0.907 0.369
lm(formula = y ~ poly(x, 4))
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 42.980 2.139 20.090 < 2e-16 ***
poly(x, 4)1 145.552 15.127 9.622 1.72e-12 ***
poly(x, 4)2 22.996 15.127 1.520 0.135
poly(x, 4)3 13.797 15.127 0.912 0.367
poly(x, 4)4 18.345 15.127 1.213 0.232
lm(formula = y ~ poly(x, 5))
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 42.980 2.160 19.899 < 2e-16 ***
poly(x, 5)1 145.552 15.273 9.530 2.88e-12 ***
poly(x, 5)2 22.996 15.273 1.506 0.139
poly(x, 5)3 13.797 15.273 0.903 0.371
poly(x, 5)4 18.345 15.273 1.201 0.236
poly(x, 5)5 5.881 15.273 0.385 0.702On peut visualiser l'évolution de ces p-valeurs sur un graphique.
n <- 5
p <- matrix( nrow=n, ncol=n+1 )
for (i in 1:n) {
p[i,1:(i+1)] <- summary(lm( y ~ poly(x,i) ))$coefficients[,4]
}
matplot(p, type='l', lty=1, lwd=3)
legend( par("usr")[1], par("usr")[4],
as.character(1:n),
lwd=3, lty=1, col=1:n
)
title(main="Evolution des p-valeurs (famille orthonormale)")
p <- matrix( nrow=n, ncol=n+1 )
p[1,1:2] <- summary(lm(y ~ x) )$coefficients[,4]
p[2,1:3] <- summary(lm(y ~ x+I(x^2)) )$coefficients[,4]
p[3,1:4] <- summary(lm(y ~ x+I(x^2)+I(x^3)) )$coefficients[,4]
p[4,1:5] <- summary(lm(y ~ x+I(x^2)+I(x^3)+I(x^4)) )$coefficients[,4]
p[5,1:6] <- summary(lm(y ~ x+I(x^2)+I(x^3)+I(x^4)+I(x^5)) )$coefficients[,4]
matplot(p, type='l', lty=1, lwd=3)
legend( par("usr")[1], par("usr")[4],
as.character(1:n),
lwd=3, lty=1, col=1:n
)
title(main="Evolution des p-valeurs (famille non orthonormale)")
On peut construire ces polynômes orthogonaux soi-même, à la main, en partant des vecteurs 1, x, x^2, ..., qui forment une famille libre, et en l'orthonormalisant.
# Construction de la matrice
n <- 5
m <- matrix( ncol=n+1, nrow=length(x) )
for (i in 2:(n+1)) {
m[,i] <- x^(i-1)
}
m[,1] <- 1
# Orthonormalisation (Gram--Schmidt)
for (i in 1:(n+1)) {
if(i==1) m[,1] <- m[,1] / sqrt( t(m[,1]) %*% m[,1] )
else {
for (j in 1:(i-1)) {
m[,i] <- m[,i] - (t(m[,i]) %*% m[,j])*m[,j]
}
m[,i] <- m[,i] / sqrt( t(m[,i]) %*% m[,i] )
}
}
p <- matrix( nrow=n, ncol=n+1 )
p[1,1:2] <- summary(lm(y~ -1 +m[,1:2] ))$coefficients[,4]
p[2,1:3] <- summary(lm(y~ -1 +m[,1:3] ))$coefficients[,4]
p[3,1:4] <- summary(lm(y~ -1 +m[,1:4] ))$coefficients[,4]
p[4,1:5] <- summary(lm(y~ -1 +m[,1:5] ))$coefficients[,4]
p[5,1:6] <- summary(lm(y~ -1 +m[,1:6] ))$coefficients[,4]
matplot(p, type='l', lty=1, lwd=3)
legend( par("usr")[1], par("usr")[4],
as.character(1:n),
lwd=3, lty=1, col=1:n
)
title(main="Idem, orthonormalisation à la main")
C'est en fait le même problème que la multicolinéarité (voir plus loin) : en orthogonalisant les polynômes, on se débarasse des redondances.
Autre exemple.
library(ts)
data(beavers)
y <- beaver1$temp
x <- 1:length(y)
plot(y~x)
for (i in 1:10) {
r <- lm( y ~ poly(x,i) )
lines( predict(r), type="l", col=i )
}
summary(r)
On obtient :
> summary(r)
Estimate Std. Error t value Pr(>|t|)
(Intercept) 36.86219 0.01175 3136.242 < 2e-16 ***
poly(x, i)1 0.86281 0.12549 6.875 4.89e-10 ***
poly(x, i)2 -0.73767 0.12549 -5.878 5.16e-08 ***
poly(x, i)3 -0.09652 0.12549 -0.769 0.44360
poly(x, i)4 -0.20405 0.12549 -1.626 0.10700
poly(x, i)5 1.00687 0.12549 8.023 1.73e-12 ***
poly(x, i)6 0.07253 0.12549 0.578 0.56457
poly(x, i)7 0.19180 0.12549 1.528 0.12950
poly(x, i)8 0.06011 0.12549 0.479 0.63294
poly(x, i)9 -0.22394 0.12549 -1.784 0.07730 .
poly(x, i)10 -0.39531 0.12549 -3.150 0.00214 **
---
Signif. codes: 0 `***' 0.001 `**' 0.01 `*' 0.05 `.' 0.1 ` ' 1
Residual standard error: 0.1255 on 103 degrees of freedom
Multiple R-Squared: 0.6163, Adjusted R-squared: 0.579
F-statistic: 16.54 on 10 and 103 DF, p-value: < 2.2e-16On notera toutefois que certaines relations ne sont pas polynômiales non plus (mais dans l'exemple suivant, il faudrait commencer par transformer la variable y pour que la distribution soit à peu près normale).
> n <- 100; x <- rnorm(n); y <- exp(x); summary(lm(y~poly(x,20)))
Call:
lm(formula = y ~ poly(x, 20))
Residuals:
Min 1Q Median 3Q Max
-4.803e-16 -9.921e-17 -3.675e-19 4.924e-17 1.395e-15
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 1.562e+00 2.250e-17 6.943e+16 < 2e-16 ***
poly(x, 20)1 1.681e+01 2.250e-16 7.474e+16 < 2e-16 ***
poly(x, 20)2 1.174e+01 2.250e-16 5.219e+16 < 2e-16 ***
poly(x, 20)3 5.491e+00 2.250e-16 2.441e+16 < 2e-16 ***
poly(x, 20)4 1.692e+00 2.250e-16 7.522e+15 < 2e-16 ***
poly(x, 20)5 4.128e-01 2.250e-16 1.835e+15 < 2e-16 ***
poly(x, 20)6 8.163e-02 2.250e-16 3.628e+14 < 2e-16 ***
poly(x, 20)7 1.495e-02 2.250e-16 6.645e+13 < 2e-16 ***
poly(x, 20)8 2.499e-03 2.250e-16 1.111e+13 < 2e-16 ***
poly(x, 20)9 3.358e-04 2.250e-16 1.493e+12 < 2e-16 ***
poly(x, 20)10 3.825e-05 2.250e-16 1.700e+11 < 2e-16 ***
poly(x, 20)11 3.934e-06 2.250e-16 1.749e+10 < 2e-16 ***
poly(x, 20)12 3.454e-07 2.250e-16 1.536e+09 < 2e-16 ***
poly(x, 20)13 2.893e-08 2.250e-16 1.286e+08 < 2e-16 ***
poly(x, 20)14 2.235e-09 2.250e-16 9.933e+06 < 2e-16 ***
poly(x, 20)15 1.524e-10 2.250e-16 6.773e+05 < 2e-16 ***
poly(x, 20)16 1.098e-11 2.250e-16 4.883e+04 < 2e-16 ***
poly(x, 20)17 6.431e-13 2.250e-16 2.858e+03 < 2e-16 ***
poly(x, 20)18 3.628e-14 2.250e-16 1.613e+02 < 2e-16 ***
poly(x, 20)19 1.700e-15 2.250e-16 7.558e+00 6.3e-11 ***
poly(x, 20)20 5.790e-16 2.250e-16 2.574e+00 0.0119 *
---
Signif. codes: 0 `***' 0.001 `**' 0.01 `*' 0.05 `.' 0.1 ` ' 1
Residual standard error: 2.25e-16 on 79 degrees of freedom
Multiple R-Squared: 1, Adjusted R-squared: 1
F-statistic: 4.483e+32 on 20 and 79 DF, p-value: < 2.2e-16
n <- 100
x <- rnorm(n)
y <- exp(x)
plot(y~x)
title(main="Relation non polynômiale")
Si on ajoute un peu de bruit :
> n <- 100; x <- rnorm(n); y <- exp(x) + .1*rnorm(n); summary(lm(y~poly(x,20)))
Call:
lm(formula = y ~ poly(x, 20))
Residuals:
Min 1Q Median 3Q Max
-2.059e-01 -5.577e-02 -4.859e-05 5.322e-02 3.271e-01
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 1.617035 0.010222 158.185 <2e-16 ***
poly(x, 20)1 15.802708 0.102224 154.588 <2e-16 ***
poly(x, 20)2 11.282604 0.102224 110.371 <2e-16 ***
poly(x, 20)3 4.688413 0.102224 45.864 <2e-16 ***
poly(x, 20)4 1.433877 0.102224 14.027 <2e-16 ***
poly(x, 20)5 0.241665 0.102224 2.364 0.0205 *
poly(x, 20)6 -0.009086 0.102224 -0.089 0.9294
poly(x, 20)7 -0.097021 0.102224 -0.949 0.3455
poly(x, 20)8 0.133978 0.102224 1.311 0.1938
poly(x, 20)9 0.077034 0.102224 0.754 0.4533
poly(x, 20)10 0.200996 0.102224 1.966 0.0528 .
poly(x, 20)11 -0.168632 0.102224 -1.650 0.1030
poly(x, 20)12 0.161890 0.102224 1.584 0.1173
poly(x, 20)13 -0.049974 0.102224 -0.489 0.6263
poly(x, 20)14 0.090020 0.102224 0.881 0.3812
poly(x, 20)15 -0.228817 0.102224 -2.238 0.0280 *
poly(x, 20)16 -0.005180 0.102224 -0.051 0.9597
poly(x, 20)17 -0.015934 0.102224 -0.156 0.8765
poly(x, 20)18 0.053635 0.102224 0.525 0.6013
poly(x, 20)19 0.059976 0.102224 0.587 0.5591
poly(x, 20)20 0.226613 0.102224 2.217 0.0295 *
---
Signif. codes: 0 `***' 0.001 `**' 0.01 `*' 0.05 `.' 0.1 ` ' 1
Residual standard error: 0.1022 on 79 degrees of freedom
Multiple R-Squared: 0.9979, Adjusted R-squared: 0.9974
F-statistic: 1920 on 20 and 79 DF, p-value: < 2.2e-16
n <- 100
x <- rnorm(n)
y <- exp(x) + .1*rnorm(n)
plot(y~x)
title(main="Relation non polynômiale")
La régression par lignes brisées est locale (ce qui se passe pour une valeur de X donnée ne dépend pas de ce qui se passe pour des valeurs de X très différentes), mais pas lisse. Au contraire, la régression polynomiale est lisse mais pas locale. Les splines permettent d'effectuer une régression à la fois locale et lisse.
Les splines sont en particulier utilisées lors de la recherche d'un modèle : elles permettent de voir (graphiquement) si un modèle non-linéaire est souhaitable et sinon, d'avoir une idée de la forme du modèle non-linéaire à choisir.
library(modreg) plot(cars$speed, cars$dist) lines( smooth.spline(cars$speed, cars$dist), col='red') abline(lm(dist~speed,data=cars), col='blue', lty=2)

plot(quakes$long, quakes$lat) lines( smooth.spline(quakes$long, quakes$lat), col='red', lwd=3)

Il y a différents types de splines : les splines cubiques (de classe C^2, obtenue en recollant des polynômes de degré 3), que nous venons d'utiliser, ou les splines cubiques restreintes (idem, mais c'est affine aux extrémités), obtenues à l'aide de la fonction rcs dans la bibliothèque Design.
library(Design)
# Spline à 4 noeuds
r3 <- lm( quakes$lat ~ rcs(quakes$long) )
plot( quakes$lat ~ quakes$long )
o <- order(quakes$long)
lines( quakes$long[o], predict(r)[o], col='red', lwd=3 )
r <- lm( quakes$lat ~ rcs(quakes$long,10) )
lines( quakes$long[o], predict(r)[o], col='blue', lwd=6, lty=3 )
title(main="Régression avec rcs")
legend( par("usr")[1], par("usr")[3], yjust=0,
c("4 noeuds", "10 noeuds"),
lwd=c(3,3), lty=c(1,3), col=c("red", "blue") )
En fait, il y a déjà une fonction bs (splines) et ns (splines restreintes) dans la bibliothèque splines.
library(splines) data(quakes) x <- quakes[,2] y <- quakes[,1] o <- order(x) x <- x[o] y <- y[o] r1 <- lm( y ~ bs(x,df=10) ) r2 <- lm( y ~ ns(x,df=6) ) plot(y~x) lines(predict(r1)~x, col='red', lwd=3) lines(predict(r2)~x, col='green', lwd=3)

?SafePrediction # Le manuel dit de faire attention aux prédictions # avec d'autres valeurs de x : je ne vois pas de problème. plot(y~x) xp <- seq(min(x), max(x), length=200) lines(predict(r2) ~ x, col='green', lwd=3) lines(xp, predict(r2,data.frame(x=xp)), col='blue', lwd=7, lty=3)

A FAIRE : ondelettes
Les données peuvent suggérer une régression dans une certaine base. Ainsi, en dimensions supérieures, on peut essayer d'écrire Y comme une somme de gaussiennes : on utilise des heuristiques pour estimer le nombre, le centre et la variance des noyaux (ça n'est pas du tout linéaire) et on passe aux moindres carrés pour trouver les coefficients.
A FAIRE : exemple
Une manière très simple de voir si une régression linéaire est une bonne idée (ou si un modèle plus complexe est souhaitable) consiste à découper les données en deux, selon les valeurs de l'une des variables prédictives, et de faire une régression pour chacun de ces deux sous-échantillons.
broken.line <- function (x, y) {
n <- length(x)
n2 = floor(n/2)
o <- order(x)
m <- mean(c(x[o[n2+0:1]]))
x1 <- x[o[1:n2]]
y1 <- y[o[1:n2]]
n2 <- n2+1
x2 <- x[o[n2:n]]
y2 <- y[o[n2:n]]
r1 <- lm(y1~x1)
r2 <- lm(y2~x2)
plot(y~x)
segments(x[o[1]], r1$coef[1] + x[o[1]]*r1$coef[2],
m, r1$coef[1] + m *r1$coef[2],
col='red')
segments(m, r2$coef[1] + m*r2$coef[2],
x[o[n]], r2$coef[1] + x[o[n]] *r2$coef[2],
col='blue')
abline(v=m, lty=3)
}
n <- 10
x <- runif(n)
y <- 1-x+.2*rnorm(n)
broken.line(x,y)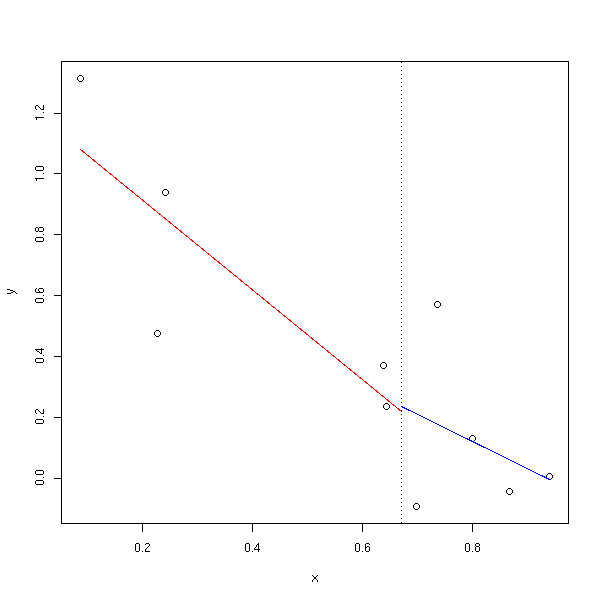
z <- x*(1-x) broken.line(x,z)

Mais ça n'est pas très continu : on peut exiger que les deux segments se rejoignent.
broken.line <- function (x,y) {
n <- length(x)
o <- order(x)
n1 <- floor((n+1)/2)
n2 <- ceiling((n+1)/2)
m <- mean(c( x[o[n1]], x[o[n2]] ))
plot(y~x)
B1 <- function (xx) {
x <- xx
x[xx<m] <- m - x[xx<m]
x[xx>=m] <- 0
x
}
B2 <- function (xx) {
x <- xx
x[xx>m] <- x[x>m] -m
x[xx<=m] <- 0
x
}
x1 <- B1(x)
x2 <- B2(x)
r <- lm(y~x1+x2)
xx <- seq(x[o[1]],x[o[n]],length=100)
yy <- predict(r, data.frame(x1=B1(xx), x2=B2(xx)))
lines( xx, yy, col='red' )
abline(v=m, lty=3)
}
broken.line(x,y)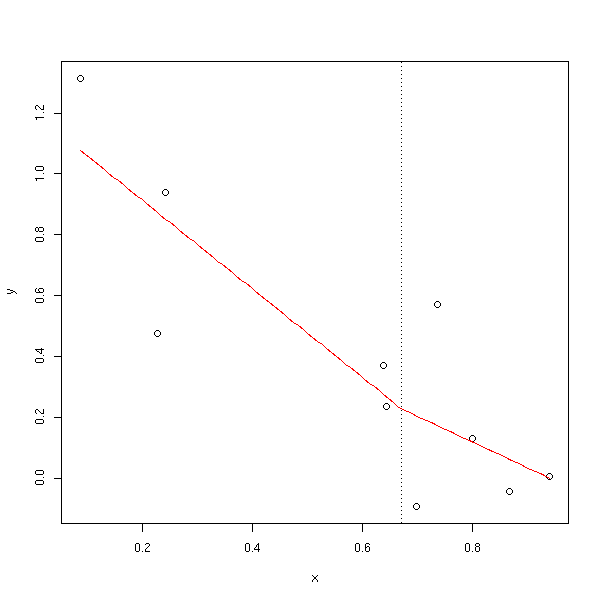
broken.line(x,z)

Exercice laissé au lecteur : réécrire la fonction précédente afin qu'elle accepte un argument supplémentaire, le nombre de segments constituant la droite brisée.
La fonction lowess permet d'obtenir une courbe (ligne brisée) "proche" du nuage de points.
plot(y~x) lines(lowess(x,y), col="red")

plot(z~x) lines(lowess(x,z), col="red")

data(quakes) plot(lat~long, data=quakes) lines(lowess(quakes$long, quakes$lat), col='red', lwd=3)

La fonction scatter.smooth fait la même chose.
Pour chaque point à prédire, on fait la moyenne des prédictions des points voisins.
En d'autres termes, on essaye localement d'approcher le nuage de points par une droite horizontale.
n <- 1000
x <- runif(n, min=-1,max=1)
y <- (x-1)*x*(x+1) + .5*rnorm(n)
# Ne pas utiliser ce code sur des données trop grosses
moyenne.mobile <- function (y,x, r=.1) {
o <- order(x)
n <- length(x)
m <- floor((1-r)*n)
p <- n-m
x1 <- vector(mode='numeric',length=m)
y1 <- vector(mode='numeric',length=m)
y2 <- vector(mode='numeric',length=m)
y3 <- vector(mode='numeric',length=m)
for (i in 1:m) {
xx <- x[ o[i:(i+p)] ]
yy <- y[ o[i:(i+p)] ]
x1[i] <- mean(xx)
y1[i] <- quantile(yy,.25)
y2[i] <- quantile(yy,.5)
y3[i] <- quantile(yy,.75)
}
plot(y~x)
lines(x1,y2,col='red', lwd=3)
lines(x1,y1,col='blue', lwd=2)
lines(x1,y3,col='blue', lwd=2)
}
moyenne.mobile(y,x)
Il y a aussi une telle fonction dans la bibliothèque gregmisc.
library(gregmisc) bandplot(x,y)

A FAIRE : le reprendre l'exemple précédent avec la commande filter (sans boucle).
La fonction ksmooth fait à peu près la même chose (les observations sont pondérées par un noyau).
library(modreg) plot(cars$speed, cars$dist) lines(ksmooth(cars$speed, cars$dist, "normal", bandwidth=2), col='red') lines(ksmooth(cars$speed, cars$dist, "normal", bandwidth=5), col='green') lines(ksmooth(cars$speed, cars$dist, "normal", bandwidth=10), col='blue')

La méthode que nous venons de présenter, la moyenne mobile, présente d'innombrables variantes. On peut tout d'abord changer le noyau.
curve(dnorm(x), xlim=c(-3,3), ylim=c(0,1.1))
x <- seq(-3,3,length=200)
D.Epanechikov <- function (t) {
ifelse(abs(t)<1, 3/4*(1-t^2), 0)
}
lines(D.Epanechikov(x) ~ x, col='red')
D.tricube <- function (t) { # aka "triweight kernel"
ifelse(abs(t)<1, (1-abs(t)^3)^3, 0)
}
lines(D.tricube(x) ~ x, col='blue')
legend( par("usr")[1], par("usr")[4], yjust=1,
c("noyau gaussien", "noyau d'Epanechikov", "noyau tricube"),
lwd=1, lty=1,
col=c(par('fg'),'red', 'blue'))
title(main="Différents noyaux")
De manière plus formelle, si D est l'une des fonctions définies ci-dessus, le lissage revient à minimiser
RSS(f,x0) = Somme K(x0,xi)(yi-f(xi))^2
où
K_lambda(x0,x) = D( abs(x-x0) / lambda )
pour un paramètre lambda choisi par l'utilisateur.
(On peut aussi imaginer des noyaux qui s'adaptent un peu mieux aux données, dont la fenêtre n'est pas de largeur constante mais dépend de la densité des observations -- fenêtre plus étroite s'il y en a beaucoup, plus large s'il y en a peu.)
Cela revient en fait à essayer d'approcher, localement, les données par une fonctions constante. On peut généraliser cette méthode, en prenant une fonction affine (on parle de régression linéaire locale) ou un polynôme de degré 2.
# Sur des données réelles...
library(KernSmooth)
data(quakes)
x <- quakes$long
y <- quakes$lat
plot(y~x)
bw <- dpill(x,y) # .2
lines( locpoly(x,y,degree=0, bandwidth=bw), col='red' )
lines( locpoly(x,y,degree=1, bandwidth=bw), col='green' )
lines( locpoly(x,y,degree=2, bandwidth=bw), col='blue' )
legend( par("usr")[1], par("usr")[3], yjust=0,
c("degré = 0", "degré = 1", "degré = 2"),
lwd=1, lty=1,
col=c('red', 'green', 'blue'))
title(main="Régression polynomiale locale")
plot(y~x)
bw <- .5
lines( locpoly(x,y,degree=0, bandwidth=bw), col='red' )
lines( locpoly(x,y,degree=1, bandwidth=bw), col='green' )
lines( locpoly(x,y,degree=2, bandwidth=bw), col='blue' )
legend( par("usr")[1], par("usr")[3], yjust=0,
c("degré = 0", "degré = 1", "degré = 2"),
lwd=1, lty=1,
col=c('red', 'green', 'blue'))
title(main="Régression polynomiale locale (fenêtre plus large)")
La moyenne mobile (régression de Nadaraya-Watson) est biaisée aux extrémités du domaine, la régression linéaire locale est biaisée dans les régions de courbure élevée.
On peut le vérifier sur les données artificielles : sur cet exemple, on constate qu'aux bornes de l'intervalle la régression polynomiale locale de degré 0 s'éloigne beaucoup des valeurs de l'échantillon.
n <- 50
x <- runif(n)
f <- function (x) { cos(3*x) + cos(5*x) }
y <- f(x) + .2*rnorm(n)
plot(y~x)
curve(f(x), add=T, lty=2)
bw <- dpill(x,y)
lines( locpoly(x,y,degree=0, bandwidth=bw), col='red' )
lines( locpoly(x,y,degree=1, bandwidth=bw), col='green' )
lines( locpoly(x,y,degree=2, bandwidth=bw), col='blue' )
legend( par("usr")[1], par("usr")[3], yjust=0,
c("degré = 0", "degré = 1", "degré = 2"),
lwd=1, lty=1,
col=c('red', 'green', 'blue'))
a <- locpoly(x,y,degree=0, bandwidth=bw)
b <- locpoly(x,y,degree=1, bandwidth=bw)
c <- locpoly(x,y,degree=2, bandwidth=bw)
matplot( cbind(a$x,b$x,c$x), abs(cbind(a$y-f(a$x), b$y-f(b$x), c$y-f(c$x)))^2,
xlab='', ylab='',
type='l', lty=1, col=c('red', 'green', 'blue') )
legend( .8*par("usr")[1]+.2*par("usr")[2], par("usr")[4], yjust=1,
c("degré = 0", "degré = 1", "degré = 2"),
lwd=1, lty=1,
col=c('red', 'green', 'blue'))
title(main="Erreur quadratique")
Si la courbe présente une courbure plus élevée, les polynômes de degré plus élevé l'approchent un peu mieux.
f <- function (x) { sqrt(abs(x-.5)) }
y <- f(x) + .1*rnorm(n)
plot(y~x)
curve(f(x), add=T, lty=2)
bw <- dpill(x,y)
lines( locpoly(x,y,degree=0, bandwidth=bw), col='red' )
lines( locpoly(x,y,degree=1, bandwidth=bw), col='green' )
lines( locpoly(x,y,degree=2, bandwidth=bw), col='blue' )
legend( par("usr")[1], par("usr")[3], yjust=0,
c("degré = 0", "degré = 1", "degré = 2"),
lwd=1, lty=1,
col=c('red', 'green', 'blue'))
a <- locpoly(x,y,degree=0, bandwidth=bw)
b <- locpoly(x,y,degree=1, bandwidth=bw)
c <- locpoly(x,y,degree=2, bandwidth=bw)
matplot( cbind(a$x,b$x,c$x), abs(cbind(a$y-f(a$x), b$y-f(b$x), c$y-f(c$x)))^2,
xlab='', ylab='',
type='l', lty=1, col=c('red', 'green', 'blue') )
legend( .8*par("usr")[1]+.2*par("usr")[2], par("usr")[4], yjust=1,
c("degré = 0", "degré = 1", "degré = 2"),
lwd=1, lty=1,
col=c('red', 'green', 'blue'))
title(main="Erreur quadratique")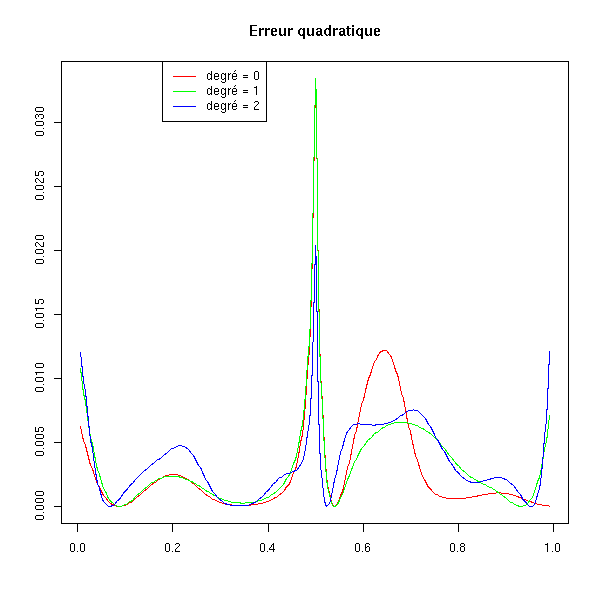
Remarque: Au lieu de faire des régression locales avec les moindres carrés, on peut aussi utiliser le maximum de vraissemblance.
On dispose de plein d'autres fonctions du même genre :
loess (modreg) régression polynomiale locale, avec un noyau tricubique
(si on ne sait pas quoi utiliser, c'est ce qu'on choisira)
lowess (base)
locpoly (KernSmooth) : régression polynômiale locale, dont on peut fixer le degré,
avec un noyau normal.
smooth (eda) : avec des médianes
supsmu (modreg)
density (base)En particulier, nous utiliserons ce genre de régression pour voir si un modèle linéaire suffit ou pas.
# C'est linéaire
library(modreg)
n <- 10
op <- par(mfrow=c(2,2))
for (i in 1:4) {
x <- rnorm(n)
y <- 1-2*x+.3*rnorm(n)
plot(y~x)
lo <- loess(y~x)
xx <- seq(min(x),max(x),length=100)
yy <- predict(lo, data.frame(x=xx))
lines(xx,yy, col='red')
lo <- loess(y~x, family='sym')
xx <- seq(min(x),max(x),length=100)
yy <- predict(lo, data.frame(x=xx))
lines(xx,yy, col='red', lty=2)
lines(lowess(x,y),col='blue',lty=2)
# abline(lm(y~x), col='green')
# abline(1,-2, col='green', lty=2)
}
par(op)
# Ça n'est pas linéaire
n <- 10
op <- par(mfrow=c(2,2))
for (i in 1:4) {
x <- rnorm(n)
y <- x*(1-x)+.3*rnorm(n)
plot(y~x)
lo <- loess(y~x)
xx <- seq(min(x),max(x),length=100)
yy <- predict(lo, data.frame(x=xx))
lines(xx,yy, col='red')
lo <- loess(y~x, family='sym')
xx <- seq(min(x),max(x),length=100)
yy <- predict(lo, data.frame(x=xx))
lines(xx,yy, col='red', lty=2)
lines(lowess(x,y),col='blue',lty=2)
# curve(x*(1-x), add = TRUE, col = "green", lty=2)
}
par(op)
A FAIRE : introduction (en particulier, il faudra expliquer pourquoi on met PCR et PLS ici, en les comparant à la ridge regression).
C'est une régression sur les premières composantes principales.
On peut la calculer à la main
# La matrice de changement de base e <- eigen(cor(x))) # On normalise x et on effectue le changement de base enx <- scale(x) %*% e$vec # On fait la régression sur ces nouveaux vecteurs lm(y ~ enx)
ou directement :
lm(y ~ princomp(x)$scores)
Si on veut juste les trois premières variables :
lm(y ~ princomp(x)$scores[,1:3])
L'interprétation des nouvelles coordonnées demande un peu plus de travail (on s'aidera de la commande biplot(princomp(x))).
Il y a toutefois un problème : lors du choix de la nouvelle base, on n'a tenu compte que de x et pas de y, or certaines variables prédictives peuvent être peu significatives si on les compare aux autres et bien plus significatives si on tient compte de y (ou le contraire).
Les poindres carrés partiels pallient à ce problème : c'est comme une régression sur les composantes principales, mais on tient compte de la variable à prédire lors du choix de la nouvelle base.
library(help=pls) library(help=pls.pcr) library(pls.pcr) ?simpls
A FAIRE : Comprendre les moindres carrés partiels...
Sur internet, on trouve l'algorithme suivant pour calculer la
décomposition en composantes principales à l'aide des moindres
carrés partiels itérés non linéairement (NIPALS) (t=scores,
p=loadings)
begin loop
select a proxy t-vector (any large column of X)
small = 10^(-6) (e.g.)
begin loop
p = X'*t
p is normalised to length one: abs(p)=1
t = X*p
end loop if convergence: (t_new - t_old) << small
remove the modelled information from X: X_new = X_old - t*p'
end loop (if all PCs are calculated)
http://www.bitjungle.com/~mvartools/muvanl/
PLS = entre la régression multiple et la régression sur les
composantes principales. On peut d'ailleurs imaginer d'autres
méthodes entr deux (on fait varier un paramétre entre 0 (MLR) et 1
(PCR), 0.5 correspondant aux PLS).
PCR: Factors from X'X
PLS: Factors from Y'XX'Y
The difference between PCR and PLS is the way factor scores are extracted.
Remarque : multi-way data analysis
On ne fait plus de l'algèbre linéaire sur des matrices, vues comme
des tableaux à deux dimensions, mais sur des tableaux à trois
dimensions (ou plus).A FAIRE : EFFACER CE QUI SUIT (c'est faux...)
C'est effacé.
Il existe une bibliothèque "pls" qui fait ce genre de chose :
http://cran.r-project.org/src/contrib/Devel/ http://www.gsm.uci.edu/~joelwest/SEM/PLS.html
La régression au sens des moindres carrés consiste à minimiser
RSS(f) = Somme (y_i - f(x_i))^2
iMais cela peut donner des fonctions assez "méchantes". Pour se limiter à des fonctions gentilles, on peut ajouter un terme
PRSS(f) = Somme (y_i - f(x_i))^2 + lambda J(f)
ioù J est d'autant plus grand que la fonction est "méchante" et lambda un réel. Par exemple, si on veut des fonctions dont la courbure n'est pas trop élevée, on pourra prendre
J(f) = \int f''^2
(en fait, on peut définir les splines comme ça).
La régression normale consiste à faire le calcul
b = (X'X)^-1 X' y.
Le problème, c'est que parfois, en cas de multicolinéarité (i.e., si on a des variables prédictives très liées, par exemple, si X1 = X2 + X3), la matrice X'X est presque singulière : l'estimateur obtenu a alors une variance très élevée. On peut contourner ce problème en décalant toutes les valeurs propres de la matrice, et en calculant
b = (X'X + kI)^-1 X' y.
Cela permet de réduire la variance -- mais en revanche, l'estimateur obtenu est biaisé.
On peut aussi présenter la ridge regression comme une régression pénalisée : au lieu de cherche b qui minimise
Somme( y_i - b0 - Somme( xij bj ) )^2 i j
On cherche b qui minimise
Somme( y_i - b0 - Somme( xij bj ) )^2 + k Somme bj^2 i j j>0
Cela permet d'éviter que les coefficients soient trop grands (c'est ce qui arrive en cas de multicolinéarité : on peut avoir un gros coefficient positid et un gros coefficient négatif qui se compensent).
Il revient au même de chercher b qui minimise
Somme( y_i - b0 - Somme( xij bj ) )^2 i j
soumis à la condition
Somme bj^2 <= s j>0
Le problème est alors de choisir la valeur de k (ou s) pour que la variance soit faible et le biais pas trop élevé : à l'aide d'heuristiques, de graphiques, ou par validation croisée.
Dans la pratique, on commence par centrer et renormaliser les colonnes de X -- il n'y aura donc pas de terme constant. On pourrait le programmer soi-même, à la main :
my.lm.ridge <- function (y, x, k=.1) {
my <- mean(y)
y <- y - my
mx <- apply(x,2,mean)
x <- x - matrix(mx, nr=dim(x)[1], nc=dim(x)[2], byrow=T)
sx <- apply(x,2,sd)
x <- x/matrix(sx, nr=dim(x)[1], nc=dim(x)[2], byrow=T)
b <- solve( t(x) %*% x + diag(k, dim(x)[2]), t(x) %*% y)
c(my - sum(b*mx/sx) , b/sx)
}ou directement en utilisant la définition en termes de moindres carrés pénalisés :
my.ridge <- function (y,x,k=0) {
xm <- apply(x,2,mean)
ym <- mean(y)
y <- y - ym
x <- t( t(x) - xm )
ss <- function (b) {
t( y - x %*% b ) %*% ( y - x %*% b ) + k * t(b) %*% b
}
b <- nlm(ss, rep(0,dim(x)[2]))$estimate
c(ym-t(b)%*%xm, b)
}
my.ridge.test <- function (n=20, s=.1) {
x <- rnorm(n)
x1 <- x + s*rnorm(n)
x2 <- x + s*rnorm(n)
x <- cbind(x1,x2)
y <- x1 + x2 + 1 + rnorm(n)
lambda <- c(0, .001, .01, .1, .2, .5, 1, 2, 5, 10)
b <- matrix(nr=length(lambda), nc=1+dim(x)[2])
for (i in 1:length(lambda)) {
b[i,] <- my.ridge(y,x,lambda[i])
}
plot(b[,2], b[,3], type="b", xlim=range(c(b[,2],1)), ylim=range(c(b[,3],1)))
text(b[,2], b[,3], lambda, adj=c(-.2,-.2), col="blue")
points(1,1,pch="+", cex=3, lwd=3)
points(b[8,2],b[8,3],pch=15)
}
my.ridge.test()
A FAIRE : donner un titre au graphique
(ridge regression et forte multicolinéarité)
op <- par(mfrow=c(3,3))
for (i in 1:9) {
my.ridge.test()
}
par(op)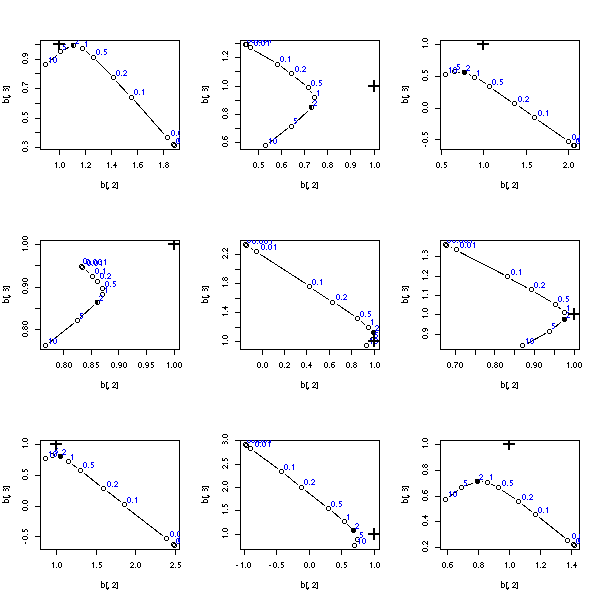
A FAIRE : donner un titre au graphique
(ridge regression et multicolinéarité plus légère)
op <- par(mfrow=c(3,3))
for (i in 1:9) {
my.ridge.test(20,10)
}
par(op)
mais il y a déjà une commande lm.ridge dans la bibliothèque MASS -- nous l'utiliserons.
Commençons par remarquer sur un exemple que dans certains cas (ici, de la multicolinéarité), la variance des estimateurs de la régression usuelle est très élevée. Par contre, la variance des estimateurs de la ridge regression est bien moindre -- mais ils sont biaisés.
my.sample <- function (n=20) {
x <- rnorm(n)
x1 <- x + .1*rnorm(n)
x2 <- x + .1*rnorm(n)
y <- 0 + x1 - x2 + rnorm(n)
cbind(y, x1, x2)
}
n <- 500
r <- matrix(NA, nr=n, nc=3)
s <- matrix(NA, nr=n, nc=3)
for (i in 1:n) {
m <- my.sample()
r[i,] <- lm(m[,1]~m[,-1])$coef
s[i,2:3] <- lm.ridge(m[,1]~m[,-1], lambda=.1)$coef
s[i,1] <- mean(m[,1])
}
plot( density(r[,1]), xlim=c(-3,3),
main="Variance élevée en cas de multicolinéarité")
abline(v=0, lty=3)
lines( density(r[,2]), col='red' )
lines( density(s[,2]), col='red', lty=2 )
abline(v=1, col='red', lty=3)
lines( density(r[,3]), col='blue' )
lines( density(s[,3]), col='blue', lty=2 )
abline(v=-1, col='blue', lty=3)
# On indique la moyenne, pour bien montrer que c'est biaisé
evaluate.density <- function (d,x, eps=1e-6) {
density(d, from=x-eps, to=x+2*eps, n=4)$y[2]
}
x<-mean(r[,2]); points( x, evaluate.density(r[,2],x) )
x<-mean(s[,2]); points( x, evaluate.density(s[,2],x) )
x<-mean(r[,3]); points( x, evaluate.density(r[,3],x) )
x<-mean(s[,3]); points( x, evaluate.density(s[,3],x) )
legend( par("usr")[1], par("usr")[4], yjust=1,
c("terme constant", "x1", "x2"),
lwd=1, lty=1,
col=c(par('fg'), 'red', 'blue') )
legend( par("usr")[2], par("usr")[4], yjust=1, xjust=1,
c("régression classique", "ridge regression"),
lwd=1, lty=c(1,2),
col=par('fg') )
On peut calculer la moyenne et la variance de nos estimateurs :
# LS regression > apply(r,2,mean) [1] -0.02883416 1.04348779 -1.05150408 > apply(r,2,var) [1] 0.0597358 2.9969272 2.9746692 # Ridge regression > apply(s,2,mean) [1] -0.02836816 0.62807824 -0.63910220 > apply(s,2,var) [1] 0.05269393 0.99976908 0.99629095
Mais ça ne permet pas de bien les comparer ; pour ce faire, on préfère utiliser la MSE (Mean Square Error) : c'est la moyenne des carrés des différences avec la valeur réelle du paramètre recherché (alors que pour la variance, on fait la différence avec la moyenne des estimations).
> v <- matrix(c(0,1,-1), nr=n, nc=3, byrow=T) > apply( (r-v)^2, 2, mean ) [1] 0.06044774 2.99282451 2.97137250 > apply( (s-v)^2, 2, mean ) [1] 0.05339329 1.13609534 1.12454560
On peut représenter l'évolution de cette MSE avec k.
n <- 500
v <- matrix(c(0,1,-1), nr=n, nc=3, byrow=T)
mse <- NULL
kl <- c(1e-4, 2e-4, 5e-4, 1e-3, 2e-3, 5e-3, 1e-2, 2e-2, 5e-2,
.1, .2, .3, .4, .5, .6, .7, .8, .9, 1, 1.2, 1.4, 1.6, 1.8, 2)
for (k in kl) {
r <- matrix(NA, nr=n, nc=3)
for (i in 1:n) {
m <- my.sample()
r[i,2:3] <- lm.ridge(m[,1]~m[,-1], lambda=k)$coef
r[i,1] <- mean(m[,1])
}
mse <- append(mse, apply( (r-v)^2, 2, mean )[2])
}
plot( mse ~ kl, type='l' )
title(main="Évolution de la MSE")
Avec une échelle logarithmique :
plot( mse-min(mse)+.01 ~ kl, type='l', log='y' ) title(main="Évolution de la MSE")

Avec les rangs :
plot( rank(mse) ~ kl, type='l' ) title(main="Évolution de la MSE")

Sur cet exemple, on constate que k=0.5 est une valeur convenable (mais d'après les livres, c'est vraiment une valeur très élevée : ils affirment qu'on ne dépasse pas 0.1...)
Le problème, c'est qu'en général on ne peut pas calculer la MSE : il faut connaître les valeurs exactes des paramètres, or c'est justement ce que l'on cherche.
On peut aussi choisir k en s'aidant de graphiques, en représentant la valeur des paramètres (ou autre chose que les paramètres, par exemple le coefficient de détermination, R^2) en fonction de k.
m <- my.sample()
b <- matrix(NA, nr=length(kl), nc=2)
for (i in 1:length(kl)) {
b[i,] <- lm.ridge(m[,1]~m[,-1], lambda=kl[i])$coef
}
matplot(kl, b, type="l")
abline(h=c(0,-1,1), lty=3)
# Estimation empirique de la valeur de k
k <- min( lm.ridge(m[,1]~m[,-1], lambda=kl)$GCV )
abline(v=k, lty=3)
title(main="Le biais vers 0 dans la ridge regression")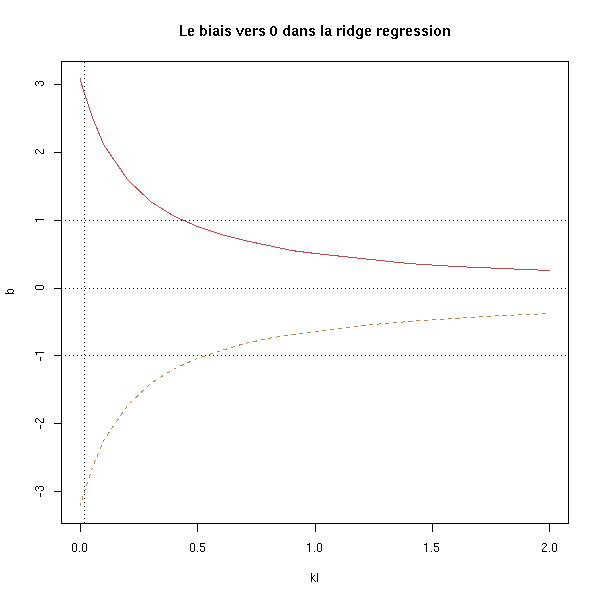
On voit peut-être mieux avec une échelle logarithmique :
m <- my.sample()
b <- matrix(NA, nr=length(kl), nc=2)
for (i in 1:length(kl)) {
b[i,] <- lm.ridge(m[,1]~m[,-1], lambda=kl[i])$coef
}
matplot(kl, b, type="l", log='x')
abline(h=c(0,-1,1), lty=3)
k <- min( lm.ridge(m[,1]~m[,-1], lambda=kl)$GCV )
abline(v=k, lty=3)
title(main="Le biais vers 0 dans la ridge regression")
On s'apperçoit que les estimateurs sont d'autant plus biaisés vers 0 que k est grand : sur cet exemple, une valeur entre 0.01 et 0.1 convient.
my.lm.ridge.diag <- function (y, x, k=.1) {
my <- mean(y)
y <- y - my
mx <- apply(x,2,mean)
x <- x - matrix(mx, nr=dim(x)[1], nc=dim(x)[2], byrow=T)
sx <- apply(x,2,sd)
x <- x/matrix(sx, nr=dim(x)[1], nc=dim(x)[2], byrow=T)
b <- solve( t(x) %*% x + diag(k, dim(x)[2]), t(x) %*% y)
v <- solve( t(x) %*% x + diag(k, dim(x)[2]),
t(x) %*% x %*% solve( t(x) %*% x + diag(k, dim(x)[2]),
diag( var(y), dim(x)[2] ) ))
ss <- t(b) %*% t(x) %*% y
list( b = b, varb = v, ss = ss )
}
m <- my.sample()
b <- matrix(NA, nr=length(kl), nc=2)
v <- matrix(NA, nr=length(kl), nc=1)
ss <- matrix(NA, nr=length(kl), nc=1)
for (i in 1:length(kl)) {
r <- my.lm.ridge.diag(m[,1], m[,-1], k=kl[i])
b[i,] <- r$b
v[i,] <- sum(diag(r$v))
ss[i,] <- r$ss
}
matplot(kl, b, type="l", lty=1, col=par('fg'), axes=F, ylab='')
axis(1)
abline(h=c(0,-1,1), lty=3)
par(new=T)
matplot(kl, v, type="l", col='red', axes=F, ylab='')
par(new=T)
matplot(kl, ss, type="l", col='blue', axes=F, ylab='')
legend( par("usr")[2], par("usr")[4], yjust=1, xjust=1,
c("paramètres", "variance", "sommes de carrés"),
lwd=1, lty=1, col=c(par('fg'), "red", "blue") )
matplot(log(kl), b, type="l", lty=1, col=par('fg'), axes=F, ylab='')
axis(1)
abline(h=c(0,-1,1), lty=3)
par(new=T)
matplot(log(kl), v, type="l", col='red', axes=F, ylab='')
par(new=T)
matplot(log(kl), ss, type="l", col='blue', axes=F, ylab='')
# Je n'arrive pas à placer la légende si l'échelle est logarithmique...
legend( par("usr")[1],
.9*par("usr")[3] + .1*par("usr")[4],
yjust=0, xjust=0,
c("paramètres", "variance", "sommes de carrés"),
lwd=1, lty=1, col=c(par('fg'), "red", "blue") )
Exercice : ajouter R^2 au graphique précédent.
En fait, si on regarde plusieurs simulations de ce genre, on s'apperçoit que le graphique n'aide pas du tout à choisir la valeur de k : les courbes ont toujours la même forme, mais les valeurs exactes des paramètres peuvent être n'importe où...
op <- par(mfrow=c(3,3))
for (j in 1:9) {
m <- my.sample()
b <- matrix(NA, nr=length(kl), nc=2)
for (i in 1:length(kl)) {
b[i,] <- lm.ridge(m[,1]~m[,-1], lambda=kl[i])$coef
}
matplot(kl, b, type="l", log='x')
abline(h=c(0,-1,1), lty=3)
k <- min( lm.ridge(m[,1]~m[,-1], lambda=kl)$GCV )
abline(v=k, lty=3)
}
par(op)
Pour choisir la valeur de k, on peut aussi recourrir à la validation croisée.
m <- my.sample()
N <- 20
err <- matrix(nr=length(kl), nc=N)
for (j in 1:N) {
s <- sample(dim(m)[1], floor(3*dim(m)[1]/4))
mm <- m[s,]
mv <- m[-s,]
for (i in 1:length(kl)) {
r <- lm.ridge(mm[,1]~mm[,-1], lambda=kl[i])
# BUG...
b <- r$coef / r$scales
a <- r$ym - t(b) %*% r$xm
p <- rep(a, dim(mv)[1]) + mv[,-1] %*% b
e <- p-mv[,1]
err[i,j] <- sum(e*e)
}
}
err <- apply(err, 1, mean)
plot(err ~ kl, type='l', log='x')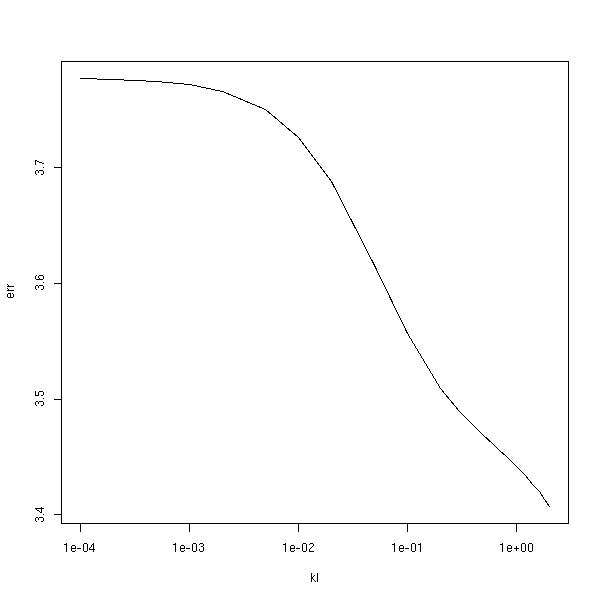
A FAIRE : il y a une erreur dans le code ci-dessus (on cherche à minimiser l'erreur, qui doit être d'autant plus grande que k est grand...)
En définitive, pour choisir les valeurs de k, on se contentera d'utiliser les différentes heuristiques proposées par la commande lm.ridge.
m <- my.sample() x <- m[,1] y <- m[,-1] r <- lm.ridge(y~x, lambda=kl); r$kHKB; r$kLW; min(r$GCV)
Pour cet exemple, il vient :
[1] 0 [1] 0 [1] 0.04624034
On nous suggère donc d'utiliser la régression usuelle -- alors que nous avons vu plus haut que, pour cet exemple, k=0.5 était une valeur convenable...
Autres exemple :
data(longley) y <- longley[,1] x <- as.matrix(longley[,-1]) r <- lm.ridge(y~x, lambda=kl); r$kHKB; r$kLW; min(r$GCV)
Il vient :
[1] 0.006836982 [1] 0.05267247 [1] 0.1196090
Voir aussi :
library(help=lpridge) # Local polynomial (ridge) regression.
On pourra aussi lire :
J.O. Rawlings, Applied Regression Analysis : A Research Tool (1988), chapter 12.
C'est une variante de la ridge regression, avec une contrainte L1 au lieu de L2 : on minimise
Somme( y_i - b0 - Somme( xij bj ) )^2 + k Somme abs(bj). i j j>0
On pourrait l'implémenter à la main :
my.lasso <- function (y,x,k=0) {
xm <- apply(x,2,mean)
ym <- mean(y)
y <- y - ym
x <- t( t(x) - xm )
ss <- function (b) {
t( y - x %*% b ) %*% ( y - x %*% b ) + k * sum(abs(b))
}
b <- nlm(ss, rep(0,dim(x)[2]))$estimate
c(ym-t(b)%*%xm, b)
}
my.lasso.test <- function (n=20) {
s <- .1
x <- rnorm(n)
x1 <- x + s*rnorm(n)
x2 <- x + s*rnorm(n)
x <- cbind(x1,x2)
y <- x1 + x2 + 1 + rnorm(n)
lambda <- c(0, .001, .01, .1, .2, .5, 1, 2, 5, 10)
b <- matrix(nr=length(lambda), nc=1+dim(x)[2])
for (i in 1:length(lambda)) {
b[i,] <- my.lasso(y,x,lambda[i])
}
plot(b[,2], b[,3], type="b", xlim=range(c(b[,2],1)), ylim=range(c(b[,3],1)))
text(b[,2], b[,3], lambda, adj=c(-.2,-.2), col="blue")
points(1,1,pch="+", cex=3, lwd=3)
points(b[8,2],b[8,3],pch=15)
}
my.lasso.test()
op <- par(mfrow=c(3,3))
for (i in 1:9) {
my.lasso.test()
}
par(op)
op <- par(mfrow=c(3,3))
for (i in 1:9) {
my.lasso.test(1000)
}
par(op)
Mais il existe déjà une fonction qui fait ça :
library(help=lasso2) library(lasso2) ?l1ce ?gl1ce
Reprenons le même exemple.
# Je ne mets pas de dessin à cause d'un bug dans la fonction l1ce :
# d'une part, elle exige qu'on lui donne un data.frame ; d'autre part,
# elle exige que ce data.frame soit une variable globale...
library(lasso2)
set.seed(73823)
#other.lasso.test <- function (n=20) {
s <- .1
x <- rnorm(n)
x1 <- x + s*rnorm(n)
x2 <- x + s*rnorm(n)
y <- x1 + x2 + 1 + rnorm(n)
d <- data.frame(y,x1,x2)
lambda <- c(0, .001, .01, .1, .2, .5, 1, 2, 5, 10)
b <- matrix(nr=length(lambda), nc=dim(d)[2])
for (i in 1:length(lambda)) {
try( b[i,] <- l1ce(y~x1+x2, data=d, bound=lambda[i], absolute.t=T)$coefficients )
# J'ai eu le message d'erreur très informatif :
# Oops, something went wrong in .C("lasso",..): -1
}
plot(b[,2], b[,3], type="b", xlim=range(c(b[,2],1)), ylim=range(c(b[,3],1)))
text(b[,2], b[,3], lambda, adj=c(-.2,-.2), col="blue")
points(1,1,pch="+", cex=3, lwd=3)
points(b[8,2],b[8,3],pch=15)
#}
#other.lasso.test()
op <- par(mfrow=c(3,3))
for (i in 1:9) {
other.lasso.test()
}
par(op)
A FAIRE : y ~ x1 + x2 LS, ridge, lasso, PLS, PCR, best subset (leap): plot(b2~b1) (some of these methods are discrete, others are continuous) In particular, remark that ridge regression is very similar to PLS ou PCR.
Commençons par comparer la ridge regression (en rouge) avec la méthode du lasso (en noir) : la première semble préférable...
get.sample <- function (n=20,s=.1) {
x <- rnorm(n)
x1 <- x + s*rnorm(n)
x2 <- x + s*rnorm(n)
y <- x1 + x2 + 1 + rnorm(n)
data.frame(y,x1,x2)
}
lambda <- c(0, .001, .01, .1, .2, .5, 1, 2, 5, 10)
do.it <- function (n=20,s=.1) {
d <- get.sample(n,s)
y <- d$y
x <- cbind(d$x1,d$x2)
ridge <- matrix(nr=length(lambda), nc=1+dim(x)[2])
for (i in 1:length(lambda)) {
ridge[i,] <- my.ridge(y,x,lambda[i])
}
lasso <- matrix(nr=length(lambda), nc=1+dim(x)[2])
for (i in 1:length(lambda)) {
lasso[i,] <- my.lasso(y,x,lambda[i])
}
xlim <- range(c( 1, ridge[,2], lasso[,2] ))
ylim <- range(c( 1, ridge[,3], lasso[,3] ))
plot(ridge[,2], ridge[,3], type="b", col='red', xlim=xlim, ylim=ylim)
points(ridge[8,2],ridge[8,3],pch=15,col='red')
lines(lasso[,2], lasso[,3], type="b")
points(lasso[8,2],lasso[8,3],pch=15)
points(1,1,pch="+", cex=3, lwd=3)
}
op <- par(mfrow=c(3,3))
for (i in 1:9) {
do.it()
}
par(op)
Avec des échantillons plus gros, le lasso ne s'en va pas dans la bonne direction...
op <- par(mfrow=c(3,3))
for (i in 1:9) {
do.it(100)
}
par(op)
Par contre, quand la multicolinéarité est faible, les deux méthodes sont comparables (et mauvaises).
op <- par(mfrow=c(3,3))
for (i in 1:9) {
do.it(20,10)
}
par(op)
En fait, la régression sur les composantes principales et les moindres carrés partiels sont des analogues discrets de la ridge regression. On préfèrera donc la ridge régression, car on peut faire varier le paramètre de manière continue.
my.pcr <- function (y,x,k) {
n <- dim(x)[1]
p <- dim(x)[2]
ym <- mean(y)
xm <- apply(x,2,mean)
# Idéalement, il faudrait aussi normaliser x et y... (Exercice laissé au lecteur)
y <- y - ym
x <- t( t(x) - xm )
pc <- princomp(x)
b <- lm(y~pc$scores[,1:k]-1)$coef
b <- c(b, rep(0,p-k))
b <- pc$loadings %*% b
names(b) <- colnames(x)
b <- c(ym-t(b)%*%xm, b)
b
}
get.sample <- function (n=20, s=.1) {
x <- rnorm(n)
x1 <- x + s*rnorm(n)
x2 <- x + s*rnorm(n)
x3 <- x + s*rnorm(n)
x4 <- x + s*rnorm(n)
x <- cbind(x1,x2,x3,x4)
y <- x1 + x2 - x3 - x4 + 1 + rnorm(n)
list(x=x,y=y)
}
pcr.test <- function (n=20, s=.1) {
s <- get.sample(n,s)
x <- s$x
y <- s$y
pcr <- matrix(nr=4,nc=5)
for (k in 1:4) {
pcr[k,] <- my.pcr(y,x,k)
}
plot(pcr[,2], pcr[,3], type="b", xlim=range(c(pcr[,2],1)), ylim=range(c(pcr[,3],1)))
points(pcr[4,2],pcr[4,3], lwd=2)
points(1,1,pch="+", cex=3, lwd=3)
}
pcr.test()
A FAIRE : ajouter les PLS
A FAIRE : mettre un titre au graphique suivant
(comparaison PCR/ridge regression)
pcr.test <- function (n=20, s=.1) {
s <- get.sample(n,s)
x <- s$x
y <- s$y
lambda <- c(0, .001, .01, .1, .2, .5, 1, 2, 5, 10)
ridge <- matrix(nr=length(lambda), nc=1+dim(x)[2])
for (i in 1:length(lambda)) {
ridge[i,] <- my.ridge(y,x,lambda[i])
}
pcr <- matrix(nr=4,nc=5)
for (k in 1:4) {
pcr[k,] <- my.pcr(y,x,k)
}
xlim <- range(c( 1, ridge[,2], pcr[,2] ))
ylim <- range(c( 1, ridge[,3], pcr[,3] ))
plot(ridge[,2], ridge[,3], type="b", col='red', xlim=xlim, ylim=ylim)
points(ridge[4,2],ridge[4,3],pch=15,col='red')
lines(pcr[,2], pcr[,3], type="b")
points(pcr[4,2],pcr[4,3], lwd=2)
points(1,1,pch="+", cex=3, lwd=3)
}
op <- par(mfrow=c(3,3))
for (i in 1:9) {
pcr.test()
}
par(op)
Nous avons vu que la ridge regression, la méthode du lasso ou les splines minimisaient des sommes de carrés pénalisées. On peut aussi modifier la méthode du maximum de vraissemblance en la penalisant.
A FAIRE : trouver des exemples (non, je n'en ai pas...)
On peut aussi avoir des modèles vraiment non linéaires (pour les modèles polynômiaux précédents, on rajoutait des termes correspondant à d'autres monômes, mais à la fin, on faisait toujours une régression linéaire). On conseille d'avoir une raison valable pour les utiliser. En voici quelques exemples.
Croissance ou décroissance exponentielle, Y = a e^(bX) + bruit
n <- 100 x <- seq(-2,2,length=n) y <- exp(x) plot(y~x, type='l', lwd=3) title(main='Croissance exponentielle')

x <- seq(-2,2,length=n) y <- exp(-x) plot(y~x, type='l', lwd=3) title(main='Décroissance exponentielle')
Exponentielle négative, Y = a(1-e^(bX)) + bruit
x <- seq(-2,4,length=n) y <- 1-exp(-x) plot(y~x, type='l', lwd=3) title(main='Exponentielle négative')

Exponentielle double, Y = u/(u-v) * (e^(-vX) - e^(-uX)) + bruit
x <- seq(0,5,length=n) u <- 1 v <- 2 y <- u/(u-v) * (exp(-v*x) - exp(-u*x)) plot(y~x, type='l', lwd=3) title(main='Exponentielle double')
Croissance sigmoïde, Y = a/( 1+ce^(-bX) ) + bruit
x <- seq(-5,5,length=n) y <- 1/(1+exp(-x)) plot(y~x, type='l', lwd=3) title(main='Croissance sigmoïde')

Sigmoïde moins symétrique, Y = a exp( -ce^(-bX) ) + bruit
x <- seq(-2,5,length=n) y <- exp(-exp(-x)) plot(y~x, type='l', lwd=3) title(main='Sigmoïde moins symétrique')

Pour effectuer ces régressions, on utilise toujours les moindres carrés, mais on se retrouve avec un système non linéaire, qui l'on résout de manière approchée (par exemple, par la méthode de Newton--Raphson).
library(help=nls) library(nls) ?nls
On définit une fonction f(x,p), où x est la variable et p un vecteur contenant les paramètres. On l'utilisera ainsi : f(x,c(a,b,c)).
library(nls)
f <- function (x,p) {
u <- p[1]
v <- p[2]
u/(u-v) * (exp(-v*x) - exp(-u*x))
}
n <- 100
x <- runif(n,0,2)
y <- f(x, c(3.14,2.71)) + .1*rnorm(n)
r <- nls( y ~ f(x,c(a,b)), start=c(a=3, b=2.5) )
plot(y~x)
xx <- seq(0,2,length=200)
lines(xx, f(xx,r$m$getAllPars()), col='red', lwd=3)
lines(xx, f(xx,c(3.14,2.71)), lty=2)
Voici le résultat.
> summary(r)
Formula: y ~ f(x, c(a, b))
Parameters:
Estimate Std. Error t value Pr(>|t|)
a 3.0477 0.3358 9.075 1.23e-14 ***
b 2.6177 0.1459 17.944 < 2e-16 ***
---
Signif. codes: 0 `***' 0.001 `**' 0.01 `*' 0.05 `.' 0.1 ` ' 1
Residual standard error: 0.1059 on 98 degrees of freedom
Correlation of Parameter Estimates:
a
b -0.06946On peut représenter des intervalles de confiance :
op <- par(mfrow=c(2,2)) p <- profile(r) plot(p, conf = c(95, 90, 80, 50)/100) plot(p, conf = c(95, 90, 80, 50)/100, absVal = FALSE) par(op)

Il y a quelques modèles non-linéaires prédéfinis. Pour certains d'entre eux, R est capable de trouver des valeurs approchées initiales des paramètres.
rm(r)
while(!exists("r")) {
x <- runif(n,0,2)
y <- SSbiexp(x,1,1,-1,2) + .01*rnorm(n)
try( r <- nls(y ~ SSbiexp(x,a,u,b,v)) )
}
plot(y~x)
xx <- seq(0,2,length=200)
lines(xx, SSbiexp(xx,
r$m$getAllPars()[1],
r$m$getAllPars()[2],
r$m$getAllPars()[3],
r$m$getAllPars()[4],
), col='red', lwd=3)
title(main='biexponential')
op <- par(mfrow=c(2,2)) try(plot(profile(r))) par(op)

rm(r)
while(!exists("r")) {
x <- runif(n,-5,5)
y <- SSlogis(x,1,0,1) + .1*rnorm(n)
try( r <- nls(y ~ SSlogis(x,a,m,s)) )
}
plot(y~x)
xx <- seq(-5,5,length=200)
lines(xx, SSlogis(xx,
r$m$getAllPars()[1],
r$m$getAllPars()[2],
r$m$getAllPars()[3],
), col='red', lwd=3)
title(main='logistic')
rm(r)
while(!exists("r")) {
x <- runif(n,-5,5)
y <- SSfpl(x,-1,1,0,1) + .1*rnorm(n)
try( r <- nls(y ~ SSfpl(x,a,b,m,s)) )
}
plot(y~x)
xx <- seq(-5,5,length=200)
lines(xx, SSfpl(xx,
r$m$getAllPars()[1],
r$m$getAllPars()[2],
r$m$getAllPars()[3],
r$m$getAllPars()[4],
), col='red', lwd=3)
title(main='4-parameter logistic model')
rm(r)
while(!exists("r")) {
x <- runif(n,-5,5)
y <- SSmicmen(x,1,1) + .01*rnorm(n)
try( r <- nls(y ~ SSmicmen(x,m,h)) )
}
plot(y~x, ylim=c(-5,5))
xx <- seq(-5,5,length=200)
lines(xx, SSmicmen(xx,
r$m$getAllPars()[1],
r$m$getAllPars()[2],
), col='red', lwd=3)
title(main='Michaelis-Menten')
rm(r)
while(!exists("r")) {
x <- runif(n,0,5)
y <- SSmicmen(x,1,1) + .1*rnorm(n)
try( r <- nls(y ~ SSmicmen(x,m,h)) )
}
plot(y~x)
xx <- seq(0,5,length=200)
lines(xx, SSmicmen(xx,
r$m$getAllPars()[1],
r$m$getAllPars()[2],
), col='red', lwd=3)
title(main='Michaelis-Menten')
rm(r)
while(!exists("r")) {
x <- runif(n,0,1)
y <- SSfol(1,x,1,2,1) + .1*rnorm(n)
try( r <- nls(y ~ SSfol(1,x,a,b,c)) )
}
plot(y~x)
xx <- seq(0,1,length=200)
lines(xx, SSfol(1,
xx,
r$m$getAllPars()[1],
r$m$getAllPars()[2],
r$m$getAllPars()[3],
), col='red', lwd=3)
title(main='SSfol')
rm(r)
while(!exists("r")) {
x <- runif(n,0,2)
y <- SSasymp(x,1,.5,1) + .1*rnorm(n)
try( r <- nls(y ~ SSasymp(x,a,b,c)) )
}
plot(y~x, xlim=c(-.5,2),ylim=c(0,1.3))
xx <- seq(-1,2,length=200)
lines(xx, SSasymp(xx,
r$m$getAllPars()[1],
r$m$getAllPars()[2],
r$m$getAllPars()[3],
), col='red', lwd=3)
title(main='SSasymp')
# Voir aussi SSasympOff et SSasympOrig
Le manuel explique comment interpréter ces paramètres.
# Copié sur le manuel
xx <- seq(0, 5, len = 101)
yy <- 5 - 4 * exp(-xx/(2*log(2)))
par(mar = c(0, 0, 4.1, 0))
plot(xx, yy, type = "l", axes = FALSE, ylim = c(0,6), xlim = c(-1, 5),
xlab = "", ylab = "", lwd = 2,
main = "Parameters in the SSasymp model")
usr <- par("usr")
arrows(usr[1], 0, usr[2], 0, length = 0.1, angle = 25)
arrows(0, usr[3], 0, usr[4], length = 0.1, angle = 25)
text(usr[2] - 0.2, 0.1, "x", adj = c(1, 0))
text(-0.1, usr[4], "y", adj = c(1, 1))
abline(h = 5, lty = 2, lwd = 0)
arrows(-0.8, 2.1, -0.8, 0, length = 0.1, angle = 25)
arrows(-0.8, 2.9, -0.8, 5, length = 0.1, angle = 25)
text(-0.8, 2.5, expression(phi[1]), adj = c(0.5, 0.5))
segments(-0.4, 1, 0, 1, lty = 2, lwd = 0.75)
arrows(-0.3, 0.25, -0.3, 0, length = 0.07, angle = 25)
arrows(-0.3, 0.75, -0.3, 1, length = 0.07, angle = 25)
text(-0.3, 0.5, expression(phi[2]), adj = c(0.5, 0.5))
segments(1, 3.025, 1, 4, lty = 2, lwd = 0.75)
arrows(0.2, 3.5, 0, 3.5, length = 0.08, angle = 25)
arrows(0.8, 3.5, 1, 3.5, length = 0.08, angle = 25)
text(0.5, 3.5, expression(t[0.5]), adj = c(0.5, 0.5))
# Copié sur le manuel
xx <- seq(0.5, 5, len = 101)
yy <- 5 * (1 - exp(-(xx - 0.5)/(2*log(2))))
par(mar = c(0, 0, 4.0, 0))
plot(xx, yy, type = "l", axes = FALSE, ylim = c(0,6), xlim = c(-1, 5),
xlab = "", ylab = "", lwd = 2,
main = "Parameters in the SSasympOff model")
usr <- par("usr")
arrows(usr[1], 0, usr[2], 0, length = 0.1, angle = 25)
arrows(0, usr[3], 0, usr[4], length = 0.1, angle = 25)
text(usr[2] - 0.2, 0.1, "x", adj = c(1, 0))
text(-0.1, usr[4], "y", adj = c(1, 1))
abline(h = 5, lty = 2, lwd = 0)
arrows(-0.8, 2.1, -0.8, 0, length = 0.1, angle = 25)
arrows(-0.8, 2.9, -0.8, 5, length = 0.1, angle = 25)
text(-0.8, 2.5, expression(phi[1]), adj = c(0.5, 0.5))
segments(0.5, 0, 0.5, 3, lty = 2, lwd = 0.75)
text(0.5, 3.1, expression(phi[3]), adj = c(0.5, 0))
segments(1.5, 2.525, 1.5, 3, lty = 2, lwd = 0.75)
arrows(0.7, 2.65, 0.5, 2.65, length = 0.08, angle = 25)
arrows(1.3, 2.65, 1.5, 2.65, length = 0.08, angle = 25)
text(1.0, 2.65, expression(t[0.5]), adj = c(0.5, 0.5))
# Copié sur le manuel
xx <- seq(0, 5, len = 101)
yy <- 5 * (1- exp(-xx/(2*log(2))))
par(mar = c(0, 0, 3.5, 0))
plot(xx, yy, type = "l", axes = FALSE, ylim = c(0,6), xlim = c(-1, 5),
xlab = "", ylab = "", lwd = 2,
main = "Parameters in the SSasympOrig model")
usr <- par("usr")
arrows(usr[1], 0, usr[2], 0, length = 0.1, angle = 25)
arrows(0, usr[3], 0, usr[4], length = 0.1, angle = 25)
text(usr[2] - 0.2, 0.1, "x", adj = c(1, 0))
text(-0.1, usr[4], "y", adj = c(1, 1))
abline(h = 5, lty = 2, lwd = 0)
arrows(-0.8, 2.1, -0.8, 0, length = 0.1, angle = 25)
arrows(-0.8, 2.9, -0.8, 5, length = 0.1, angle = 25)
text(-0.8, 2.5, expression(phi[1]), adj = c(0.5, 0.5))
segments(1, 2.525, 1, 3.5, lty = 2, lwd = 0.75)
arrows(0.2, 3.0, 0, 3.0, length = 0.08, angle = 25)
arrows(0.8, 3.0, 1, 3.0, length = 0.08, angle = 25)
text(0.5, 3.0, expression(t[0.5]), adj = c(0.5, 0.5))
# Copié sur le manuel
xx <- seq(-0.5, 5, len = 101)
yy <- 1 + 4 / ( 1 + exp((2-xx)))
par(mar = c(0, 0, 3.5, 0))
plot(xx, yy, type = "l", axes = FALSE, ylim = c(0,6), xlim = c(-1, 5),
xlab = "", ylab = "", lwd = 2,
main = "Parameters in the SSfpl model")
usr <- par("usr")
arrows(usr[1], 0, usr[2], 0, length = 0.1, angle = 25)
arrows(0, usr[3], 0, usr[4], length = 0.1, angle = 25)
text(usr[2] - 0.2, 0.1, "x", adj = c(1, 0))
text(-0.1, usr[4], "y", adj = c(1, 1))
abline(h = 5, lty = 2, lwd = 0)
arrows(-0.8, 2.1, -0.8, 0, length = 0.1, angle = 25)
arrows(-0.8, 2.9, -0.8, 5, length = 0.1, angle = 25)
text(-0.8, 2.5, expression(phi[1]), adj = c(0.5, 0.5))
abline(h = 1, lty = 2, lwd = 0)
arrows(-0.3, 0.25, -0.3, 0, length = 0.07, angle = 25)
arrows(-0.3, 0.75, -0.3, 1, length = 0.07, angle = 25)
text(-0.3, 0.5, expression(phi[2]), adj = c(0.5, 0.5))
segments(2, 0, 2, 3.3, lty = 2, lwd = 0.75)
text(2, 3.3, expression(phi[3]), adj = c(0.5, 0))
segments(3, 1+4/(1+exp(-1)) - 0.025, 3, 2.5, lty = 2, lwd = 0.75)
arrows(2.3, 2.7, 2.0, 2.7, length = 0.08, angle = 25)
arrows(2.7, 2.7, 3.0, 2.7, length = 0.08, angle = 25)
text(2.5, 2.7, expression(phi[4]), adj = c(0.5, 0.5))
# Copié sur le manuel
xx <- seq(-0.5, 5, len = 101)
yy <- 5 / ( 1 + exp((2-xx)))
par(mar = c(0, 0, 3.5, 0))
plot(xx, yy, type = "l", axes = FALSE, ylim = c(0,6), xlim = c(-1, 5),
xlab = "", ylab = "", lwd = 2,
main = "Parameters in the SSlogis model")
usr <- par("usr")
arrows(usr[1], 0, usr[2], 0, length = 0.1, angle = 25)
arrows(0, usr[3], 0, usr[4], length = 0.1, angle = 25)
text(usr[2] - 0.2, 0.1, "x", adj = c(1, 0))
text(-0.1, usr[4], "y", adj = c(1, 1))
abline(h = 5, lty = 2, lwd = 0)
arrows(-0.8, 2.1, -0.8, 0, length = 0.1, angle = 25)
arrows(-0.8, 2.9, -0.8, 5, length = 0.1, angle = 25)
text(-0.8, 2.5, expression(phi[1]), adj = c(0.5, 0.5))
segments(2, 0, 2, 4.0, lty = 2, lwd = 0.75)
text(2, 4.0, expression(phi[2]), adj = c(0.5, 0))
segments(3, 5/(1+exp(-1)) + 0.025, 3, 4.0, lty = 2, lwd = 0.75)
arrows(2.3, 3.8, 2.0, 3.8, length = 0.08, angle = 25)
arrows(2.7, 3.8, 3.0, 3.8, length = 0.08, angle = 25)
text(2.5, 3.8, expression(phi[3]), adj = c(0.5, 0.5))
# Copié sur le manuel
xx <- seq(0, 5, len = 101)
yy <- 5 * xx/(1+xx)
par(mar = c(0, 0, 3.5, 0))
plot(xx, yy, type = "l", axes = FALSE, ylim = c(0,6), xlim = c(-1, 5),
xlab = "", ylab = "", lwd = 2,
main = "Parameters in the SSmicmen model")
usr <- par("usr")
arrows(usr[1], 0, usr[2], 0, length = 0.1, angle = 25)
arrows(0, usr[3], 0, usr[4], length = 0.1, angle = 25)
text(usr[2] - 0.2, 0.1, "x", adj = c(1, 0))
text(-0.1, usr[4], "y", adj = c(1, 1))
abline(h = 5, lty = 2, lwd = 0)
arrows(-0.8, 2.1, -0.8, 0, length = 0.1, angle = 25)
arrows(-0.8, 2.9, -0.8, 5, length = 0.1, angle = 25)
text(-0.8, 2.5, expression(phi[1]), adj = c(0.5, 0.5))
segments(1, 0, 1, 2.7, lty = 2, lwd = 0.75)
text(1, 2.7, expression(phi[2]), adj = c(0.5, 0))
Pour des modèles autres que ceux-ci, le gros problème est de trouver des valeurs initiales des paramètres, pas trop éloignées.
x <- runif(100)
w <- runif(100)
y <- x^2.4*w^3.2+rnorm(100,0,0.01)
# On utilise une régression linéaire pour avoir des valeurs approchées.
r1 <- lm(log(y) ~ log(x)+log(w)-1)
r2 <- nls(y~x^a*w^b,start=list(a=coef(r1)[1],b=coef(r1)[2]))
> coef(r1)
log(x) log(w)
1.500035 2.432708
> coef(r2)
a b
2.377525 3.185556En faisant tous ces calculs, je constate que ces méthodes ne marchent pas toujours. Voici quelques exemples de messages d'erreur que j'ai obtenus. (Je ne pense pas que cela soit problématique avec des données réelles.) C'est pourquoi j'utilise une boucle avec la commande try dans les exemples précédents.
> r <- nls(y ~ SSfol(1,x,a,b,c)) Error in numericDeriv(form[[3]], names(ind), env) : Missing value or an Infinity produced when evaluating the model In addition: Warning messages: 1: NaNs produced in: log(x) 2: NaNs produced in: log(x) > r <- nls(y ~ SSfol(1,x,a,b,c)) Error in nls(resp ~ (Dose * (exp(-input * exp(lKe)) - exp(-input * exp(lKa))))/(exp(lKa) - : singular gradient Error in nls(y ~ cbind(exp(-exp(lrc1) * x), exp(-exp(lrc2) * x)), data = xy, : step factor 0.000488281 reduced below `minFactor' of 0.000976562
La comparaison des modèles non linéaires est un peu plus délicate. Il y a toutefois une fonction anova.nls.
library(nls) ?anova.nls
A FAIRE : Cette partie n'est pas encore écrite...
library(help=nlme) (C'est par exemple là qu'il y a la fonction gls, pour les moindres carrés généralisés.) Je me contente de reprendre quelques exemples du manuel. library(help=nlme) library(nlme) library(nlme) data(Orthodont) fm1 <- lme(distance ~ age, Orthodont, random = ~ age | Subject) # standardized residuals versus fitted values by gender plot(fm1, resid(., type = "p") ~ fitted(.) | Sex, abline = 0)

# box-plots of residuals by Subject plot(fm1, Subject ~ resid(.))

# observed versus fitted values by Subject plot(fm1, distance ~ fitted(.) | Subject, abline = c(0,1))

La bibliothèque nlme contient une fonction plot pour les modèles non linéaires -- nous y reviendrons plus loin. A FAIRE
# library(lqs) # now part of MASS
n <- 100
x <- rnorm(n)
y <- 1 - 2*x + rnorm(n)
y[ sample(1:n, floor(n/4)) ] <- 7
plot(y~x)
abline(1,-2,lty=3)
r1 <- lm(y~x)
r2 <- lqs(y~x, method='lts')
r3 <- lqs(y~x, method='lqs')
r4 <- lqs(y~x, method='lms')
r5 <- lqs(y~x, method='S')
abline(r1, col='red')
abline(r2, col='green')
abline(r3, col='blue')
abline(r4, col='orange')
abline(r5, col='purple')
legend( par("usr")[1], par("usr")[3], yjust=0,
c("Régression linéaire", "lts (régression élaguée)",
"lqs", "lms", "S"),
lty=1, lwd=1,
col=c("red", "green", "blue", "orange", "purple") )
title("Moindres carrés élagués et variantes")
On dit qu'une régression est résistante si elle est peu sensible à des observations atypiques ou aberrantes. On dit qu'elle est robuste si elle reste toujours valable quand ses hypothèses (données normales) ne sont plus vérifiées.
Nous en avons déjà vu quelques exemples, comme la régression élaguée (lqs) ou la régression de Huber (rlm). En voici quelques autres -- que je ne détaille pas.
A FAIRE : modifier les exemples suivants pour avoir une comparaison des différentes régressions, dans différentes situations (une observation atypique, plusieurs observations atypiques, prédicteur non normal, erreurs non normales). A FAIRE : idem avec les régressions non linéaires # Exemple x <- rnorm(20) y <- 1 - x + rnorm(20) x <- c(x,10) y <- c(y,1) plot(y~x) abline(lm(y~x), col='blue') title(main="Régression classique")

# How bad usual regression is
plot(lm(y~x), which=4,
main="Distances de Cook pour la régression classique")
plot(y~x) for (i in 1:length(x)) abline(lm(y~x, subset= (1:length(x))!=i ), col='red') title(main="Régression classique après avoir enlevé un point")

# line (in the eda library) library(eda) plot(y~x) abline(1,-1, lty=3) abline(lm(y~x)) abline(coef(line(x,y)), col='red') title(main='Regression avec "line", dans la bibliothèque "eda"')

# Régression élaguée #library(lqs) plot(y~x) abline(1,-1, lty=3) abline(lm(y~x)) abline(lqs(y~x), col='red') title(main='Moindres carrés élagués (lqs)')

# glm (d'après le manuel, il s'agit bien des IWLS, # mais on obtient exactement le même résultat...) plot(y~x) abline(1,-1, lty=3) abline(lm(y~x)) abline(glm(y~x), col='red') title(main='Régression avec "glm"')

plot(y~x) abline(1,-1, lty=3) abline(lm(y~x)) abline(rlm(y~x, psi = psi.bisquare, init = "lts"), col='orange',lwd=3) abline(rlm(y~x), col='red') abline(rlm(y~x, psi = psi.hampel, init = "lts"), col='green') abline(rlm(y~x, psi = psi.bisquare), col='blue') title(main='Régression de Huber (rlm)') %--
Voici comment on utilise généralement la régression robuste. On commence par faire une régression classique et une régression robuste. Si les deux diffèrent, c'est mauvais signe...
Quantile regression library(quantreg) ?rq rq(y~x, tau=.5) # Median regression ?table.rq http://www.econ.uiuc.edu/~econ472/tutorial15.html
Vincent Zoonekynd
<zoonek@math.jussieu.fr>
latest modification on Wed Oct 13 22:32:53 BST 2004