The French version of this document is no longer maintained: be sure to check the more up-to-date English version.
Régression linéaire
On dispose de deux variables X et Y, et on essaye de prédire les valeurs de Y à partir de celles de X. Pour cela, on suppose que Y s'obtient à partir de X de la manière suivante :
Y = a + b * X + bruit
où a et b sont des réels (à déterminer) et le bruit suit une distribution gaussienne de moyenne nulle.
Plus précisément, si on note X_i et Y_i les valeurs correspondant à la i-ième observation, on a Y_i = a + b X_i + e_i où les e_i sont des variables indépendantes, gaussiennes, de moyenne nulle et de même variance.
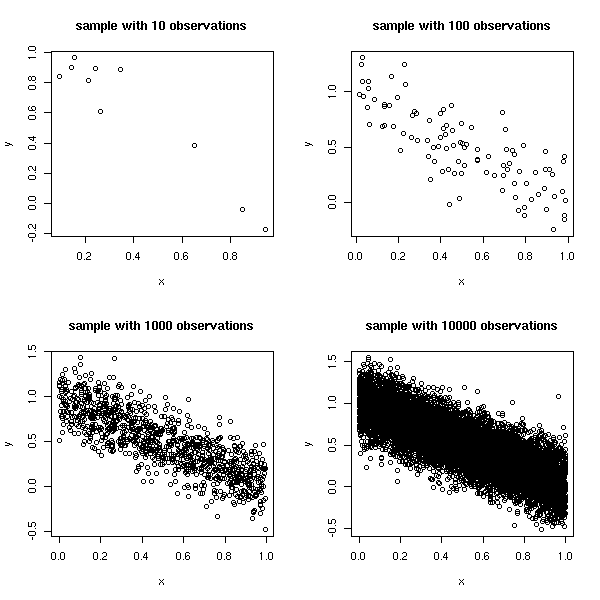
Voici des exemples de telles variables.
op <- par(mfrow=c(2,2))
for (n in c(10,1e2,1e3,1e4)) {
x <- runif(n)
y <- 1 - x + .2*rnorm(n)
plot(y~x, main=paste("sample with", n, "observations"))
}
par(op)
Il y a deux interprétations possibles de ce modèle : soit ce sont les couples (X,Y) qui sont tirés au hasard, soit on choisit les valeurs de X et seules les valeurs de Y sont aléatoires. Cela ne change pas les calculs et l'interprétation des résultats.
L'idée est de chercher des valeurs de a et b qui minimisent la somme des carrés des distances entre les valeurs de Y prédites et les valeurs de Y réelles (sur le graphique précédent, ça veut dire qu'on mesure la distance verticale entre chaque point et la droite).
Si on fait les calculs à la main (on écrit la somme des carrés et on demande que les dérivées partielles par rapport à a et b s'annullent), on trouve :
my.lss <- function (x, y, ...) {
n <- length(x)
sx <- sum(x)
sy <- sum(y)
sxx <- sum(x*x)
sxy <- sum(x*y)
d <- n*sxx-sx*sx
a <- (sxx*sy - sx*sxy)/d
b <- (-sx*sy + n*sxy)/d
plot(x,y, ...)
abline(a, b, col='red', ...)
c(a,b)
}
n <- 10
x <- runif(n)
y <- 1 - 2*x + .3*rnorm(n)
my.lss(x,y)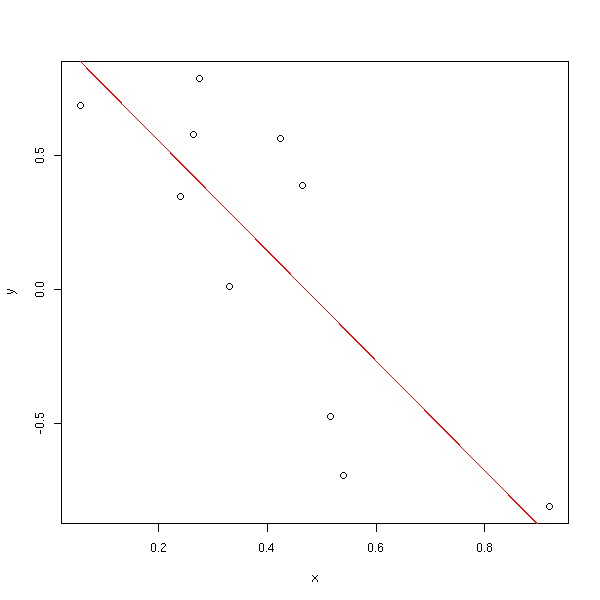
Pour faire la même chose en dimensions supérieures, on peut écrire cela sous forme matricielle.
my.lss <- function (x,y, ...) {
x <- as.matrix(x)
x <- cbind(rep(1,dim(x)[1]), x)
t(solve( t(x) %*% x, t(x) %*% y ))
}
n <- 50
x1 <- runif(n)
x2 <- runif(n)
x <- cbind(x1,x2)
y <- 1+x1-x2 + .3*rnorm(n)
my.lss(x, y)On peut aboutir à cette formule assez facilement. On a :
Y = X B + Bruitdonc
X' Y = X' X B + X' Bruit
puis
(X' X)^-1 X' Y = B + (X' X) X' Bruit
puis
E[ (X' X)^-1 X' Y ] = E [ B + (X' X) X' Bruit ]
ie,
E[ (X' X)^-1 X' Y ] = E [ B ] + A [ (X' X) X' Bruit ]
ie,
E[ (X' X)^-1 X' Y ] = B + 0
ie, (X' X)^-1 X' Y est un estimateur non biaisé de B.
Bien sûr, il y a déjà une fonction qui fait ce genre de calcul. La ligne suivante cherche à écrire Y comme fonction affine de X (on ne précise pas qu'il y a un coefficient constant, mais il y en a toujours un : c'est une mauvaise idée de l'enlever, mais si on y tient, on peut, en écrivant y~-1+X).
res <- lm( y ~ x )
(Si on voulait écrire soi-même des fonctions acceptant des formules en argument, on utiliserait la fonction model.matrix pour transformer la formule en matrice.)
L'objet res contient alors le résultat de la régression. On peut le dessiner (nous verrons plus loin le résultat de la commande plot(res) : elle donne des graphiques permettant d'apprécier la qualité de la régression).
n <- 10 x <- runif(n) y <- 1 - x + .2*rnorm(n) res <- lm( y ~ x ) plot(y~x, pch=16) abline(res, col='red')
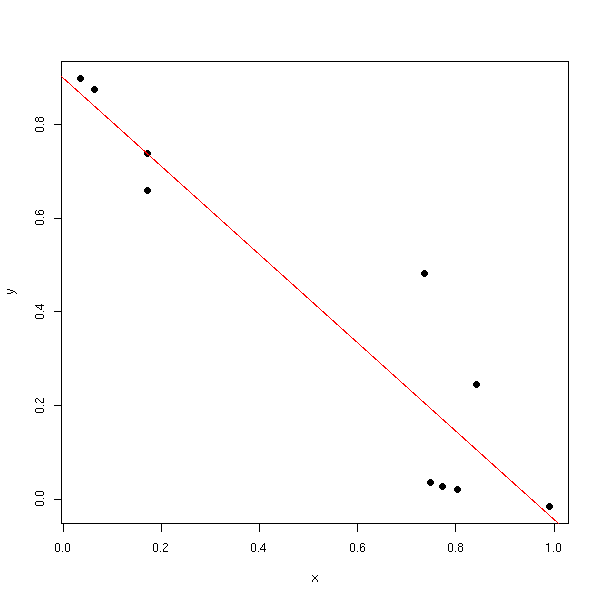
On peut regarder son contenu.
> str(res) List of 12 $ coefficients : Named num [1:2] 0.946 -0.925 ..- attr(*, "names")= chr [1:2] "(Intercept)" "x" $ residuals : Named num [1:10] -0.218 0.201 0.109 0.148 0.127 ... ..- attr(*, "names")= chr [1:10] "1" "2" "3" "4" ... $ effects : Named num [1:10] -1.053 -0.725 0.196 0.208 0.219 ... ..- attr(*, "names")= chr [1:10] "(Intercept)" "x" "" "" ... $ rank : int 2 $ fitted.values: Named num [1:10] 0.212 0.637 0.160 0.270 0.140 ... ..- attr(*, "names")= chr [1:10] "1" "2" "3" "4" ... $ assign : int [1:2] 0 1 $ qr :List of 5 ..$ qr : num [1:10, 1:2] -3.162 0.316 0.316 0.316 0.316 ... .. ..- attr(*, "dimnames")=List of 2 .. .. ..$ : chr [1:10] "1" "2" "3" "4" ... .. .. ..$ : chr [1:2] "(Intercept)" "x" .. ..- attr(*, "assign")= int [1:2] 0 1 ..$ qraux: num [1:2] 1.32 1.46 ..$ pivot: int [1:2] 1 2 ..$ tol : num 1e-07 ..$ rank : int 2 $ df.residual : int 8 $ xlevels : list() $ call : language lm(formula = y ~ x) $ terms :Classes 'terms', 'formula' length 3 y ~ x .. ..- attr(*, "variables")= language list(y, x) .. ..- attr(*, "factors")= int [1:2, 1] 0 1 .. .. ..- attr(*, "dimnames")=List of 2 .. .. .. ..$ : chr [1:2] "y" "x" .. .. .. ..$ : chr "x" .. ..- attr(*, "term.labels")= chr "x" .. ..- attr(*, "order")= int 1 .. ..- attr(*, "intercept")= int 1 .. ..- attr(*, "response")= int 1 .. ..- attr(*, ".Environment")=length 6 <environment> .. ..- attr(*, "predvars")= language list(y, x) $ model :`data.frame': 10 obs. of 2 variables: ..$ y: num [1:10] -0.00579 0.83807 0.26913 0.41728 0.26766 ... ..$ x: num [1:10] 0.792 0.334 0.849 0.731 0.870 ... ..- attr(*, "terms")=Classes 'terms', 'formula' length 3 y ~ x .. .. ..- attr(*, "variables")= language list(y, x) .. .. ..- attr(*, "factors")= int [1:2, 1] 0 1 .. .. .. ..- attr(*, "dimnames")=List of 2 .. .. .. .. ..$ : chr [1:2] "y" "x" .. .. .. .. ..$ : chr "x" .. .. ..- attr(*, "term.labels")= chr "x" .. .. ..- attr(*, "order")= int 1 .. .. ..- attr(*, "intercept")= int 1 .. .. ..- attr(*, "response")= int 1 .. .. ..- attr(*, ".Environment")=length 6 <environment> .. .. ..- attr(*, "predvars")= language list(y, x) - attr(*, "class")= chr "lm"
On peut afficher sont contenu de manière laconique, à l'aide de la commande print. On a simplement les coefficients que l'on cherchait.
> res
Call:
lm(formula = y ~ x)
Coefficients:
(Intercept) x
0.9457 -0.9254On peut afficher son contenu sous forme moins laconique. On a beaucoup plus d'information. Tout d'abord, les résidus (i.e., la différence entre la valeur prédite et la valeur réelle). Ensuite les coefficients avec, pour chacun d'entre eux, sa valeur, un estimation de l'erreur standard, et un test permettant de savoir si le coefficient en question est significativement différent de zéro. Ici, les deux étoiles permettent d'affirmer que le coefficient directeur est différent de zéro avec un risque d'erreur de l'ordre d'un pour mille (.001926). Idem pour l'ordonnée à l'origine. Le coefficient de détermination (R-squared), entre 0 et 1, indique si le modèle colle aux données (nous reverrons son interprétation un peu plus loin, avec l'analyse de la variance) ; le coefficient de détermination ajusté corrige cette valeur en tenant compte d'une éventuelle surmodélisation (overfit) (par exemple, s'il y a autant de paramètres que d'observations, on aura R^2=1, mais ça ne sera pas significatif). Le test de F et la p-valeur correspondante sont les résultats d'une comparaison entre ce modèle et le modèle nul (c'est le modèle Y = constante + bruit).
> summary(res)
Call:
lm(formula = y ~ x)
Residuals:
Min 1Q Median 3Q Max
-0.21828 -0.12899 0.01060 0.12269 0.20110
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 0.9457 0.1444 6.548 0.000179 ***
x -0.9254 0.2043 -4.529 0.001926 **
---
Signif. codes: 0 `***' 0.001 `**' 0.01 `*' 0.05 `.' 0.1 ` ' 1
Residual standard error: 0.16 on 8 degrees of freedom
Multiple R-Squared: 0.7194, Adjusted R-squared: 0.6844
F-statistic: 20.51 on 1 and 8 DF, p-value: 0.001926Il y a encore une autre manière d'afficher le résultat, qui donnent des informations comparables aux trois dernières lignes précédentes : nous y reviendrons un peu plus loin.
> anova(res)
Analysis of Variance Table
Response: y
Df Sum Sq Mean Sq F value Pr(>F)
x 1 0.52503 0.52503 20.514 0.001926 **
Residuals 8 0.20475 0.02559
---
Signif. codes: 0 `***' 0.001 `**' 0.01 `*' 0.05 `.' 0.1 ` ' 1Dans la suite, nous utiliserons essentiellement la commande summary.
Tirés du manuel, voici quatre exemples de données, très différentes, qui donnent la même droite de régression. Moralité : il faut toujours regarder les données, à l'aide de graphiques.
data(anscombe)
ff <- y ~ x
op <- par(mfrow=c(2,2), mar=.1+c(4,4,1,1), oma= c(0,0,2,0))
for(i in 1:4) {
ff[2:3] <- lapply(paste(c("y","x"), i, sep=""), as.name)
## or ff[[2]] <- as.name(paste("y", i, sep=""))
## ff[[3]] <- as.name(paste("x", i, sep=""))
assign(paste("lm.",i,sep=""), lmi <- lm(ff, data= anscombe))
#print(anova(lmi))
}
for(i in 1:4) {
ff[2:3] <- lapply(paste(c("y","x"), i, sep=""), as.name)
plot(ff, data =anscombe, col="red", pch=21, bg = "orange", cex = 1.2,
xlim=c(3,19), ylim=c(3,13))
abline(get(paste("lm.",i,sep="")), col="blue")
}
mtext("Anscombe's 4 Regression data sets", outer = TRUE, cex=1.5)
par(op)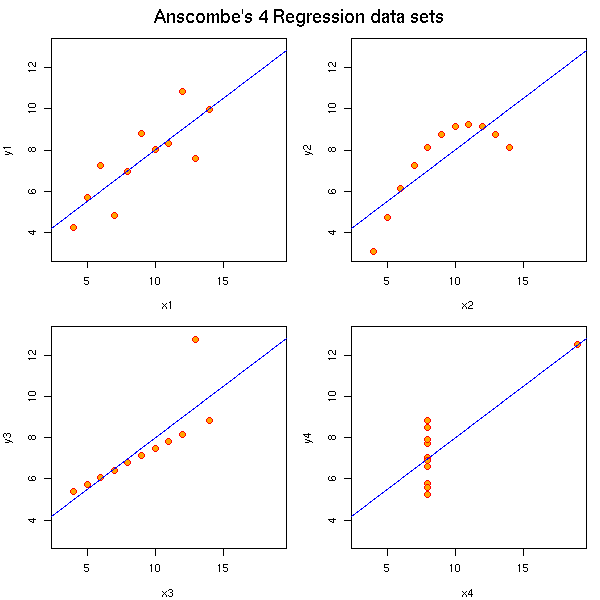
On peut voir la régression linéaire comme une projection orthogonale de Y sur le sous-espace engendré par 1, X1, X2, etc. (ici, 1 désigne le vecteur de même dimension que X dont toutes les composantes sont des 1).
Les estimateurs obtenus à l'aide des moindres carrés sont les meilleurs (leur variance est la plus faible) estimateurs linéaires non biaisés (BLUE: Best Linear Unbiaised Estimators).
Néanmoins, certains estimateurs biaisés ont une variance moindre et sont donc très intéressants.
De plus, certains estimateurs non linéaires robustes sont plus efficaces pour des distributions non normales.
Dans la pratique, on comparera le résultat obtenu avec les moindres carrés et ceux obtenus par d'autres méthodes.
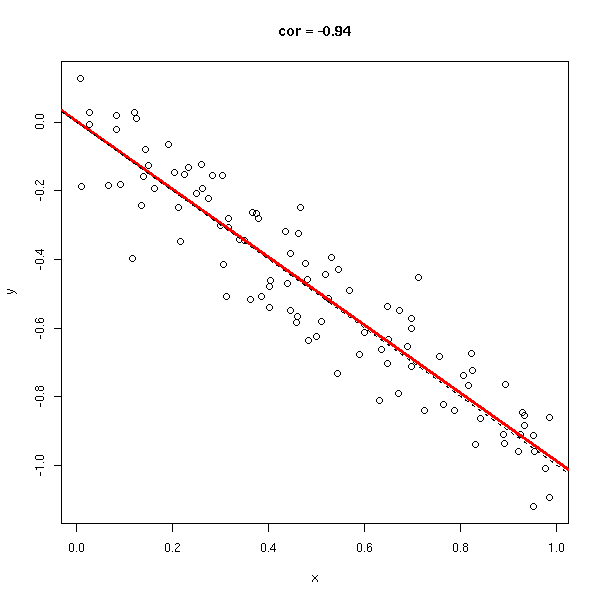
Le coefficient de corrélation (sans unité, entre -1 et 1), permet de voir s'il est facile d'approcher les données par une droite. Dans les exemples suivants, le coefficient de corrélation passe progressivement de 1 à -1.
do.it <- function (x, y) {
plot(x,y, main=paste("cor =", round(cor(x,y), digits=2)))
abline(lm(y~x), col='red', lwd=3)
}
n <- 100
x <- runif(n)
x <- x[order(x)]
y <- x
do.it(x,y)
abline(0,1,lty=2)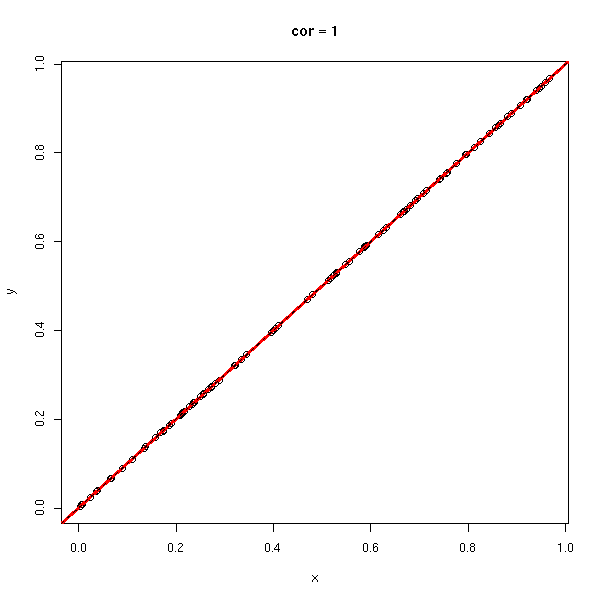
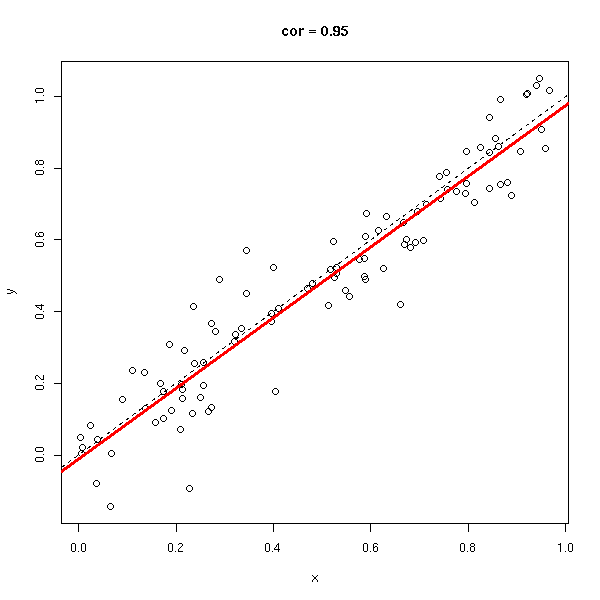
y <- rnorm(n,x,.1) do.it(x,y) abline(0,1,lty=2)
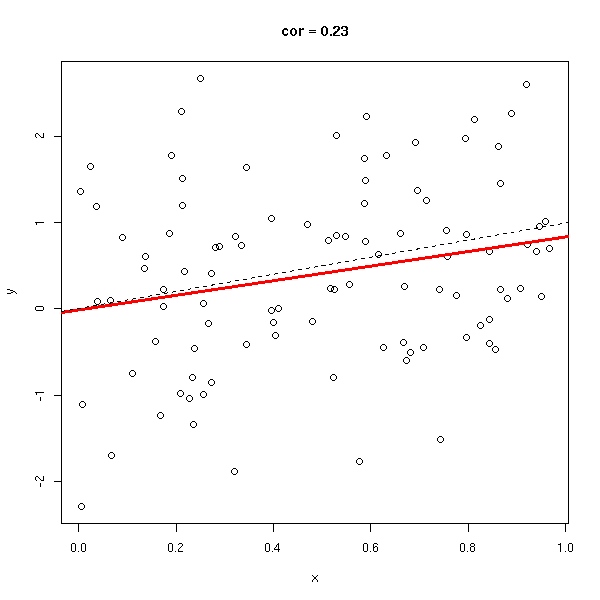
y <- rnorm(n,x,1) do.it(x,y) abline(0,1,lty=2)
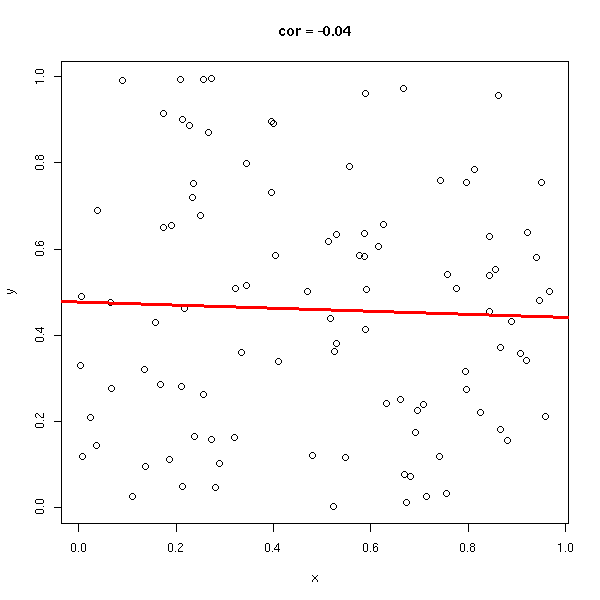
y <- runif(n) do.it(x,y)
x <- runif(n,-1,1) y <- x*x do.it(x,y)
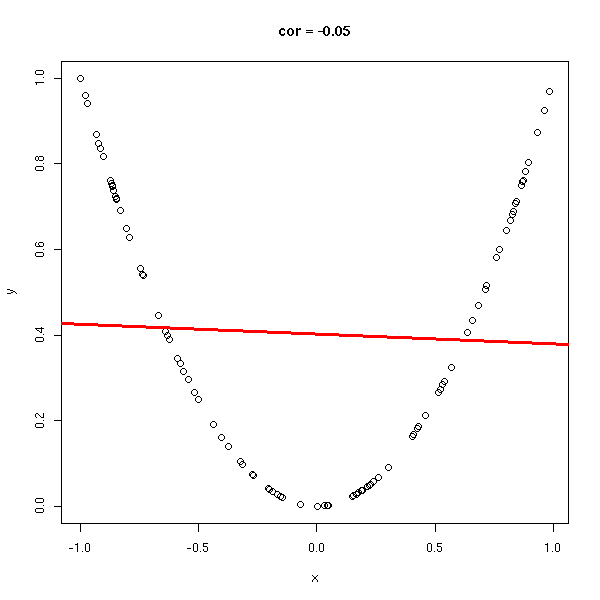
y <- rnorm(n, x*x, .1) do.it(x,y) x <- sort(x) lines(x,x*x,lty=2)
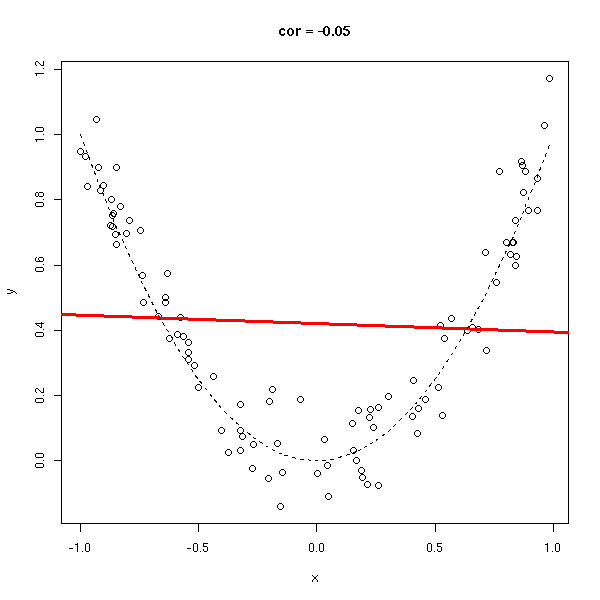
y <- rnorm(n, x*x, 1) do.it(x,y) x <- sort(x) lines(x,x*x,lty=2)
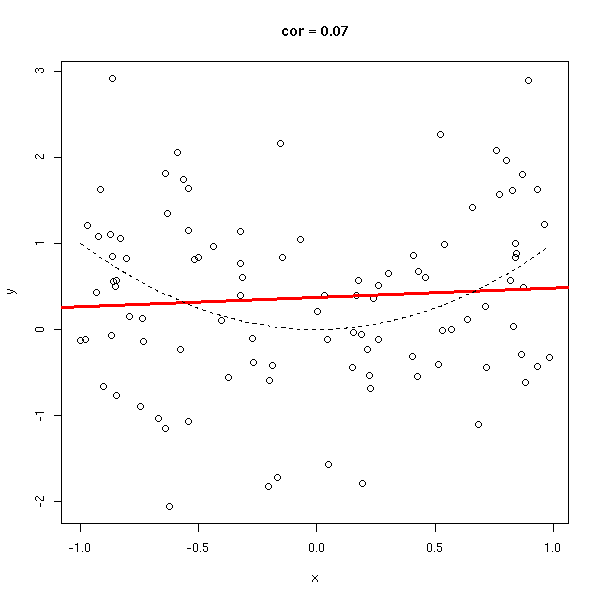
x <- runif(n) y <- rnorm(n,-x,1) do.it(x,y) abline(0,-1,lty=2)
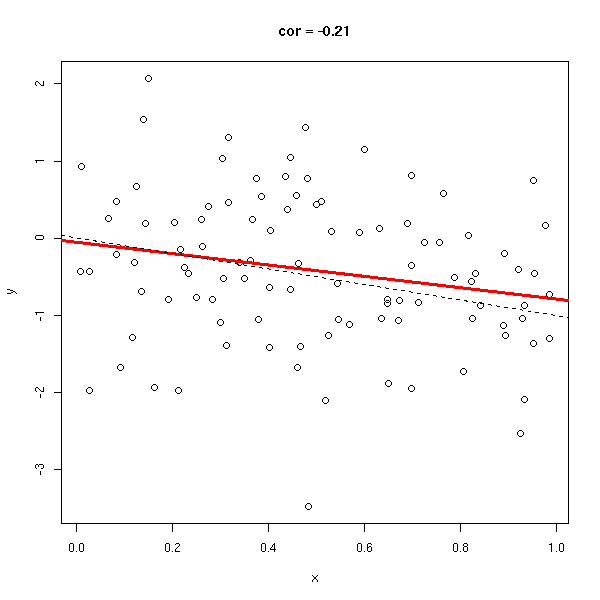
y <- rnorm(n,-x,.1) do.it(x,y) abline(0,-1,lty=2)
y <- -x do.it(x,y) abline(0,-1,lty=2)
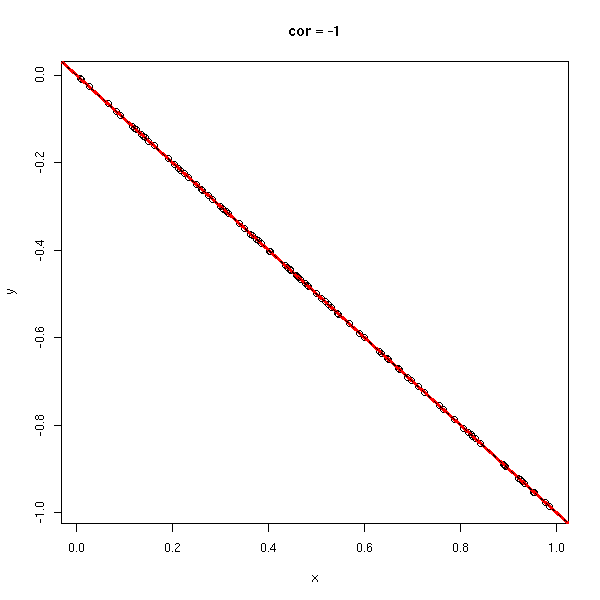
Dans certaines situations, il y a clairement un lien entre les deux variables, mais il n'est pas affine : on peut alors regarder s'il n'y a pas un lien linéaire, non pas entre les données, mais entre leur rangs (c'est la corrélation de Spearman). Cela permet de repérer les liens monotones entre les données.
> b <- (0:100)/100 > c <- b^2 > cor(b,c) [1] 0.9676503 > cor(rank(b),rank(c)) [1] 1
Vincent Zoonekynd
<zoonek@math.jussieu.fr>
latest modification on Wed Oct 13 22:32:49 BST 2004