
The French version of this document is no longer maintained: be sure to check the more up-to-date English version.
Echantillons et tests statistiques
Présentation des tests statistiques sous R
Le Zoo des tests paramétriques
Le zoo des tests statistiques : variables discrètes et test du Chi2
Le zoo des test statistiques : tests non paramétriques
Très souvent, la série statistique que l'on étudie n'est pas la population entière mais juste un échantillon. On peut facilement calculer les paramètres (moyenne, écart-type) de l'échantillon, mais ce sont des approximations des paramètres de la population : comment mesurer l'exactitude de cette approximation ?
Voici quelques exemples concrets de cette situation.
Un industriel doit choisir une variété de Maïs. Il sera destiné à la consommation animale et on cherche la variété qui contient le plus de protéines possible : il faut connaître précisément la teneur moyenne en protéines (non pas de l'échantillon, mais bien de la population).
Un industriel doit choisir une variété de Maïs. Il sera destiné à la consommation humaine et, pour des raisons de conditionnement, on veut que tous les épis aient la même taille ; on cherche donc à avoir l'écart-type le plus petit possible.
En termes simples : on tire au hasard des individus dans une population et on mesure sur cet échantillon les variables statistiques qui nous intéressent (taille de l'épi de maïs, teneur en protéines, etc.)
En termes algorithmiques :
Répéter un grand nombre de fois : Prendre un échantillon de la population Evaluer, sur cet échantillon, la quantité qui nous intéresse (cette quantité s'appelle une statistique) Comparer ces différentes évaluations (on peut les représenter par un histogramme) avec la valeur sur toute la population.
En termes plus mathématiques : on considère X1, X2, ... Xn des variables aléatoires indépendantes identiquement distribuées (vaiid). À l'aide des valeurs que ces variables prennent en un point de l'univers, on tente d'obtenir des informations sur la loi qu'elles suivent (par exemple, on s'attend à ce que (X1+...+Xn)/n soit une approximation de l'espérance de cette loi : est-ce bien le cas ? en quel sens ? Quelle loi sui cette nouvelle variable ? Comment apprécier la qualité de cette approximation ?).
On considère une expérience statistique, i.e., on considère des vaiid X1,...Xn ; on suppose qu'on connait la forme de la loi, mais pas tous ses « paramètres » (par exemple, on sait que c'est une loi normale, mais on ne connait pas l'espérance, ou pas l'écart-type). Un estimateur est une fonction de X1,...,Xn qui donne une approximation de ces paramètres (si on voit les variables aléatoires X1,...Xn comme des applications d'un univers Oméga vers la droite réelle R, un estimateur est une variable aléatoire obtenue en composant (X1,...,Xn) avec une application R^n ----> R). Par exemple, (X1+...+Xn)/n est un estimateur de l'espérance.
C'est un estimateur dont l'espérance est effectivement la valeur du paramètre. Par exemple la moyenne empirique (X1+...+Xn)/n est un estimateur sans biais de l'espérance. Par contre, le calcul montre que l'écart-type empirique est un estimateur avec biais de l'écart-type (mais si on prend la même formule avec « n-1 » au dénominateur à la place de « n », ou avec l'espérance vrai à la place de la moyenne empirique, on obtient un estimateur sans biais.
On peut vérifier cela par une simulation, comme suit.
On considère 5 tirages aléatoires indépendants suivant une loi normale de moyenne 1 et d'écart-type 1.
En répétant cette expérience 10000 fois, on obtient (une approximation de) l'espérance de la moyenne empirique : elle est à peu près égale à la moyenne vraie (ici, 0).
x <- vector()
for(i in 1:10000){
x <- append(x, mean(rnorm(5)))
}
mean(x)
[1] 9.98948e-05Si on fait pareil avec la variance empirique, on constate que son espérance est sensiblement différente de la variance réelle (on obtient 0.8 au lieu de 1) : on dit que la variance empirique est un estimateur biaisé de la variance.
n <- 5
x <- vector()
for(i in 1:10000){
t <- rnorm(n)
t <- t - mean(t)
t <- t*t
x <- append(x, sum(t)/n)
}
mean(x)
[1] 0.806307Pour avoir un estimateur non biaisé de la variance, il suffit de remplacer le « n » dans la définition de la variance par n-1 (c'est ce que l'on appelle la variance de l'échantillon, par opposition à la variance de la population).
n <- 5
y <- vector()
for(i in 1:10000){
t <- rnorm(n)
t <- t - mean(t)
t <- t*t
y <- append(y, sum(t)/(n-1))
}
mean(y)
[1] 1.000129Une autre manière d'obtenir un estimateur non biaisé de la variance consiste à utiliser la moyenne vraie au lieu de la moyenne empirique (c'est peu réaliste, car dans les situations concrètes, on connait rarement la moyenne vraie).
n <- 5
z <- vector()
for(i in 1:10000){
t <- rnorm(n)
t <- t - 0
t <- t*t
z <- append(z, sum(t)/n)
}
mean(x)
[1] 1.001210On peut comparer graphiquement ces trois estimateurs de la variance.
n <- 5
x <- y <- z <- vector()
for(i in 1:10000){
t <- rnorm(n)
z <- append(z, sum(t*t)/n)
t <- t - mean(t)
t <- t*t
x <- append(x, sum(t)/n)
y <- append(y, sum(t)/(n-1))
}
boxplot(x,y,z)
plot(density(x)) points(density(y), type="l", col="red") points(density(z), type="l", col="blue")

op <- par( mfrow = c(3,1) ) hist(x, xlim=c(0,5), breaks=20) hist(y, xlim=c(0,5), breaks=20) hist(z, xlim=c(0,5), breaks=20) par(op)

Ou plutôt leur racine carrée (c'est plus symétrique).
x <- sqrt(x) y <- sqrt(x) z <- sqrt(z) boxplot(x,y,z)

plot(density(x)) points(density(y), type="l", col="red") points(density(z), type="l", col="blue")

op <- par( mfrow = c(3,1) ) hist(x, xlim=c(0,5), breaks=20) hist(y, xlim=c(0,5), breaks=20) hist(z, xlim=c(0,5), breaks=20) par(op)

Il y a plein de notions autres que le biais qui mesurent la qualité d'un estimateur ou d'une suite d'estimateurs. Par exemple, on dit qu'un estimateur est consistant si, quand on augmente la taille de l'échantillon, il tend, en probabilité, vers la valeur réelle du paramètre. Ainsi, la loi faible des grands nombres affirme que la moyenne empirique est un estimateur cohérent de la moyenne.
C'est une méthode pour trouver un estimateur (on ne sait pas s'il vérifira de « bonnes » propriétés, en particulier il sera souvent biaisé, mais c'est déjà un bon départ). Elle consiste à regarder pour quelle valeur du paramètre on a le plus de chance d'obtenir le résultat qu'on a observé, i.e., à maximiser la vraissemblance.
Par exemple, cherchons, avec cette méthode, un estimateur de la moyenne d'une variable suivant une loi normale de variance 1 à l'aide d'un échantillon de 5 individus (dans cet exemple, on obtient en fait la moyenne empirique).
# Choix de la moyenne
m <- runif(1, min=-1, max=1)
# Les n individus
n <- 5
v <- rnorm(n, mean=m)
# Calcul de la densité
N <- 1000
l <- seq(-2,2, length=N)
y <- vector()
for (i in l) {
y <- append(y, prod(dnorm(v,mean=i)))
}
plot(y~l, type='l')
# Moyenne réelle
points(m, prod(dnorm(v,mean=m)), lwd=3)
# Moyenne empirique
points(mean(v), prod(dnorm(v,mean=mean(v))), col='red', lwd=3)
La commande optimize permet de trouver un tel maximum, en dimension 1.
> optimize(dnorm, c(-1,2), maximum=T) $maximum [1] 1.307243e-05 $objective [1] 0.3989423
En dimensions supérieures, on peut utiliser la commande optim (pour trouver un minimum).
f <- function (arg) {
x <- arg[1]
y <- arg[2]
(x-1)^2 + (y-3.14)^2
}
optim(c(0,0), f)ou la commande nlm
A FAIRE
On obtient :
$par
[1] 0.9990887 3.1408265
$value
[1] 1.513471e-06
$counts
function gradient
59 NA
$convergence
[1] 0
$message
NULLOn peut exiger une méthode d'optimisation particulière, par exemple le recuit simulé (Simulated Annealing, en anglais) -- qui donne en fait un résultat très imprécis.
optim(c(0,0), f, method="SANN")
Prenons la durée des éruptions du geyser Faithful et essayons d'approcher ces données par une somme de variables gaussiennes.
f <- function (x, p, m1, s1, m2, s2) {
p*dnorm(x,mean=m1,sd=s1) + (1-p)*dnorm(x,mean=m2,sd=s2)
}
data(faithful)
fn <- function(arg) {
prod(f(faithful$eruptions, arg[1], arg[2], arg[3], arg[4], arg[5]))
}
start <- c(.5,
min(faithful$eruptions), var(faithful$eruptions),
max(faithful$eruptions), var(faithful$eruptions),
)
p <- optim(start, function(a){-fn(a)/fn(start)}, control=list(trace=1))$par
hist(faithful$eruptions, breaks=20, probability=T, col='light blue')
lines(density(faithful$eruptions,bw=.15), col='blue', lwd=3)
curve(f(x, p[1], p[2], p[3], p[4], p[5]), add=T, col='red', lwd=3)
#curve(dnorm(x, mean=p[2], sd=p[3]), add=T, col='red', lwd=3, lty=2)
#curve(dnorm(x, mean=p[4], sd=p[5]), add=T, col='red', lwd=3, lty=2)
legend(par('usr')[2], par('usr')[4], xjust=1,
c('sample density', 'theoretical density'),
lwd=3, lty=1,
col=c('blue', 'red'))
On vient de voir, dans les exemple précédents, que la vraissemblance se définissait comme un produit, avec autant de facteurs que d'observations. Comme des produits aussi gros sont difficiles à manipuler, on préfère minimiser leur logarithme.
A FAIRE : la fonction fitdistr, dans la bibliothèque MASS, permet de calculer des estimateurs u minimum de vraissemblance pour des variables univariées.
La log-vraissemblance est
-2 log (vraissemblance).
C'est la quantité qu'on essaye de minimiser quand on cherche un estimateur à l'aide de la méthode du maximum de vraissemblance.
A FAIRE : qu'appelle-t-on log-vraissemblance ? le logarithme de la vraissemblance ? ???
(Le coefficient 2 est là pour que ça coïncide avec le logarithme des sommes de carrés dans le cas gaussien.)
Si L est la log-vraissemblance et p le paramètre à estimer, le score est défini par
d log L
U = ---------
d pet l'information de Fisher par
d^2 L
I(p) = -------
d p^2L'information de Fisher est d'autant plus grande que L est pointue.
On remarque que
V si H0 est vraie
LR = - 2 log ---------------------------------------
V avec les paramètres obtenus par MLE
V(b0)
= - 2 log ------- (si b est le paramètre à estimer)
V(b)où V est la vraissemblance, suit à peu près une loi du Chi^2 à m degrés de liberté, où m est le nombre de paramètres à estimer.
A FAIRE : expliquer pourquoi (dans le cas gaussien (dire ce que ça signifie), c'est exactement une loi du Chi^2) A FAIRE : expliquer comment on évalue la variance de l'estimateur. A FAIRE : un exemple (prendre une gaussienne et la modéliser comme un mélange de deux gaussiennes, prendre ensuite un mélange de deux gaussiennes et le modéliser comme tel, dans les deux cas, faire un test pour savoir si les deux gaussiennes ont la même moyenne)
Les test de Wald et du score sont des approximations de ce test. Plus précisément, si on note b le paramètre à estimer, on définit le score (c'est un vecteur)
U(b) = Nabla log V(b)
( d log V(b) )
= ( ------------ )
( d bi ) il'information (c'est une matrice)
( d^2 )
I(b) = ( - ----------- log V(b) )
( d bi d bj ) i,jla statistique de Wald (c'est un développement limité à l'ordre 2 de LR)
W = (b-b0)' * I(b) * (b-b0)
et la statistique du score (qui ne dépend pas de b : c'est très imprécis, mais ça se calcule très vite)
S = U(b0)' * I(b0)^-1 * U(b0).
On peut voir la vraissemblance comme la densité de probabilité du paramètre, conditionnellement aux observations de l'échantillon.
A FAIRE : graphique
La méthode du maximum de vraissemblance consiste à prendre le mode de cette distribution. Cela pose plusieurs problèmes.
D'une part, on oublie complètement la distribution de cet estimateur : on regarde souvent sa variance, mais s'il n'est pas normal, c'est loin d'être suffisant. (On peut utiliser cette densité pour juger de la qualité de l'estimateur ou pour faire des simulations (bootstrap paramétrique)).
D'autre part, le mode n'est pas toujours un choix judicieux. Pourquoi ne pas prendre la moyenne [ça s'appelle le bagging : voir un peu plus loin], ou la médiane ? Que fait-on si le mode n'est pas unique ? Ou, plus raisonablement, si la vraissemblance présente plusieurs maxima locaux ? Ou encore si la distribution présente plusieurs pics, l'un élevé mais très étroit (de sorte qu'une observation aura une probabilité faible de s'y trouver) l'autre moins haut mais plus large (de sorte qu'une observation aura une probabilité élevée de s'y trouver) ?
op <- par(mfrow=c(2,2)) curve(dnorm(x-5)+dnorm(x+5), xlim=c(-10,10)) curve(dnorm(x-5)+.4*dnorm(x+5), xlim=c(-10,10)) curve(dnorm(5*(x-5)) + .5*dnorm(x+5), xlim=c(-10,10)) par(op)

Cela dit, je n'ai réussi à construire de situation dans laquelle on observe réellement ce genre de situation (si vous en avez, n'hésitez pas à m'en faire part). Et si on y parvient, ce sera probablement une indication que le modèle est faux ou que l'estimateur n'est pas pertinent...
Ah, si ! J'ai réussi. J'ai simplement pris un estimateur qui s'extrapole mal d'un échantillon à une population : le maximum.
get.sample <- function (n=10, p=1/100) {
ifelse( runif(n)>p, runif(n), 2 )
}
N <- 1000
d <- rep(NA,N)
for (i in 1:N) {
d[i] <- max(get.sample())
}
hist(d, probability=T, ylim=c(0, max(density(d)$y)), col='light blue')
lines(density(d), type='l', col='red', lwd=3)
get.sample <- function (n=100, p=1/100) {
ifelse( runif(n)>p, runif(n), 2 )
}
N <- 1000
d <- rep(NA,N)
for (i in 1:N) {
d[i] <- max(get.sample())
}
#hist(d, breaks=seq(0,3,by=.02),
# probability=T, ylim=c(0, max(density(d)$y)), col='light blue')
#lines(density(d), type='l', col='red', lwd=3)
plot(density(d), type='l', col='red', lwd=3)
get.sample <- function (n=100, p=1/100) {
ifelse( runif(n)>p, runif(n), 2+2*runif(n) )
}
N <- 1000
d <- rep(NA,N)
for (i in 1:N) {
d[i] <- max(get.sample())
}
#hist(d, breaks=seq(0,4,by=.05),
# probability=T, ylim=c(0, max(density(d)$y)), col='light blue')
#lines(density(d), type='l', col='red', lwd=3)
plot(density(d), type='l', col='red', lwd=3)
Néamoins, certaines méthodes permettent d'obtenir des distributions de probabilités au lieu des paramètres : c'est en particulier le cas des méthodes utilisant le bootstrap, comme le bagging.
Nous venons de voir qu'il pouvait être intéressant d'avoir non pas un estimateur (avec éventuellement sa variance) mais toute une distribution de probabilité. Les méthodes bayesiennes poussent cette remarque un cran plus loin.
On suppose que les paramètres du modèle sont choisis au hasard selon une certaine distribution -- la distribution a priori. Les méthodes baysiennes cherchent la distribution a posteriori, i.e., la distribution de ces paramètres conditionnellement à l'échantillon observé.
A FAIRE : rédiger Z : données t : paramètres Le modèle nous donne P(Z|t) On suppose qu'on connait P(t) (prior distribution). On calcule alors P(t|Z) (posterior distribution) en fonction de P(Z|t) et P(t), à l'aide de la formule de Bayes. A FAIRE : rappeler cette formule. A FAIRE : MCMC (Markov Chain Monte Carlo) to sample from the posterior distribution parametric bootstrap = computational implementation of the maximum likelihood method MLE = mode bagged estimator = mean A FAIRE : EM algorithm (to find MLE in a 2-component misture model) 1. find first estimates (m1, m2 : random; s1, s2 : sd(whole sample)) 2. Compute the responsabilities gamma(i) = probability that observation i comes from the second component 1-gamma(i)=probability that observation i comes from the first component 3. new estimators = weighted means and variances (use gamma(i), resp 1-gamma(i), as weights) 4. Iterate A FAIRE : Cet algorithme se généralise à d'autres modèles. A FAIRE : c'est un cas particulier de REML A FAIRE : mettre ces exemples un peu plus compliqués dans la partie sur le bootstrap ??? A FAIRE : dire que les méthodes bayesiennes se prêtent bien à des raisonnements itératifs : Initial data --> prior New data --> posterior Update prior New data --> posterior Update prior ... A FAIRE : The theory behind the Kalman Filter (State Space Models) is bayesian.
A FAIRE (A peu près comme les réseaux de neurones, mais on peut interpréter le modèle obtenu, on peut y ajouter des informations.)
On dispose d'un estimateur U d'un paramètre u d'une loi F(u). Le problème, c'est qu'on ne connait pas exactement la loi F. Pour juger de la robustesse de l'estimateur, on regarde comment il varie si on modifie F en un point. Plus précisément, on calcule
U( (1-h) F + h 1x ) - U(F)
w(x) = lim ----------------------------
h -> 0 hoù 1x est la mesure de Dirac en x.
A FAIRE : exemple de la moyenne A FAIRE : exemple de la variance A FAIRE : exemple de la corrélation (en dimension 2) ?contour ?persp
A FAIRE : estimation empirique de la fonction d'influence à l'aide du bootstrap.
library(boot) ?empinf
A FAIRE : A CLASSER ?
C'est une autre méthode pour obtenir un estimateur. S'il n'y a qu'un seul paramètre, on le choisit de sorte que le premier moment (i.e., le moyenne) de la variable coïncide avec sa valeur empirique. S'il y a k paramètres, on les choisit de sorte que les k premiers moments coïncident avec leur valeur empirique. (Comme pour la méthode du maximum de vraissemblance, on ne connait rien, a priori, de la qualité de l'estimateur obtenu -- il est même souvent biaisé.)
Utilisons cette méthode pour étudier la durée des éruptions du geyser Faithful. Soit X0 une v.a. de Bernoulli, de paramètre p, et X1, X2, des variables gaussiennes de moyenne m1, m2 et d'écart-type s1 et s2. On cherche à mettre nos données sous la forme
Y = X0 X1 + (1-X0) X2.
En remarquant que X0^2=X0, (1-X0)^2=1-X0 et X0*(1-X0), on montre que
Y^2 = X0 X1^2 + (1-X0) X2^2 Y^3 = X0 X1^3 + (1-X0) X2^3 Y^4 = X0 X1^4 + (1-X0) X2^4.
Comme X0, X1, X2 sont indépendantes, on a
E(Y) = X(X0) E(X1) + E(1-X0) E(X2) E(Y^2) = X(X0) E(X1^2) + E(1-X0) E(X2^2) E(Y^3) = X(X0) E(X1^3) + E(1-X0) E(X2^3) E(Y^4) = X(X0) E(X1^4) + E(1-X0) E(X2^4)
Mais comme
E(X0)=p E(X1) = m E(X1^2) = m^2 + s^2 E(X1^3) = 3 m s^2 + m^3 E(X1^4) = 10 s^4 + 6 s^2 m^2 + m^4 E(X1^5) = 50 s^4 m + 5 s^2 m^3 + m^5
(et de même pour X2), il vient
E(Y) = p m1 + (1-p) m2 E(Y^2) = p (m1^2 + s1^2) + (1-p) (m2^2 + s2^2) E(Y^3) = p (3 m1 s1^2 + m1^3) + (1-p) (3 m2 s2^2 + m2^3) E(Y^4) = p (10 s1^4 + 6 s1^2 m1^2 + m1^4) + (1-p) (10 s2^4 + 6 s2^2 m2^2 + m2^4) E(Y^4) = p (50 s1^4 m1 + 5 s1^2 m1^3 + m1^5) + (1-p) (50 s2^4 m2 + 5 s2^2 m2^3 + m2^5)
On demande alors à R de trouver (numériquement) les valeurs des 5 paramètres.
(exercice laissé au lecteur)
Il y a une commande pour trouver le minimum d'une fonction de plusieurs variables (optimize, optim, nlm, nls), il y a des commandes pour trouver les zéros d'une fonction d'une variable (uniroot, polyroot), mais pour trouver les zéros d'une fonction de plusieurs variables, i.e., pour résoudre un système non linéaire ??? (On peut faire ça très simplement à l'aide de l'algorithme de Newton, comme en dimension 1 -- mais la dérivée est alors une matrice.)
L'inégalité de Cramer-Rao nous dit qu'on ne peut pas trouver des estimateurs arbitrairement bons : plus précisément, il donne une borne inférieure pour la variance d'un estimateur non borné.
La première étape pour construire un estimateur le meilleur possible consiste à remplacer les données X1,X2,...,Xn par un (ou plusieurs) nombre(s) qui contienne autant d'information : on dit que ce nombre est une statistique suffisante. Plus précisément, si
P( (X1,X2,...,Xn) \in U | t(X1,...,Xn) = c )
ne dépend que de U et c mais pas du paramètre que l'on cherche, on dit que t est une statistique suffisante. On dispose d'un critère simple (le théorème de factorisation de Neyman) pour reconnaitre une statistique suffisante. Plus précisément, on cherche une statistique suffisante minimale, i.e., dont les "lignes" de niveau soient les plus grandes possibles.
Estimateurs non biaisés dont la variance est la plus faible possible (de sorte que l'inégalité de Cramer-Rao devienne une égalité).
On cherche à répondre à une question du genre « le tabac augmente-t-il le risque de cancer ? », « la proximité d'une usine de retraitement de déchets radioactifs augmente-t-elle le risque de leucémie ? », « la moyenne de la population dont est extraite cet échantillon de moyenne empirique 0.02 est-elle nulle ? ».
Détaillons l'exemple du problème « ces deux échantillons proviennent-ils de la même population (plus précisément : ce deux populations de même moyenne) ? ».
On considère une première population, pour laquelle on observe une variable statistique (de distribution normale), à partir d'un échantillon. On fait pareil avec une deuxième population, pour laquelle on observe une variable (normale, de même moyenne) et un deuxième échantillon.
On peut alors calculer la loi de la variable :
estimation de la moyenne dans le premier échantillon - estimation dans le second
Si on mesure une certaine valeur de cette différence, on peut calculer la probabilité qu'il y avait d'obtenir une différence aussi importante. Si
P( différence > différence observée ) < alpha,
on rejette l'hypothèse « les deux moyennes sont égales », avec un risque d'erreur égal à alpha.
On prendra garde que ce résultat n'est pas certain : il peut y avoir deux types d'erreurs, on peut dire à tors que les moyennes sont différentes ou dire à tors que les moyennes sont égales.
On prendra aussi garde que ces tests ne sont valables que sous certaines conditions (normalité, équivariance, etc.).
En toute rigueur, on ne considère pas une seule hypothèse, mais deux : par exemple « les moyennes sont égales » et « les moyennes sont différentes » ; ou alors « les moyennes sont égales » et « la première moyenne est plus grande », ou encore « les moyennes sont égales » et « la première est plus petite ». On utilisera l'un des deux derniers couples d'hypothèses si l'une des moyenne est plus grande que l'autre et si on a un embryon d'explication plausible pour cela.
Les tests statistiques ne vont jamais dire << l'hypothèse est vraie >>. Ils vont se limiter à rejeter ou à ne pas rejeter l'hypothèse. (C'est très semblable au développement de la science tel qu'expliqué par K. Popper : on ne démontre jamais que quelque chose est vrai, on se contente d'essayer sans cesse de démontrer que c'est faux, et d'échouer.)
On considère alors deux hypothèses : l'hypothèse nulle H0, « il n'y a aucun effet » (par exemple, « le tabac n'augmente pas le risque de cancer », « la proximité d'une usine n'augmente pas le risque de leucémie ») ; l'hypothèse alternative H1, « il y a un effet » (par exemple, « le tabac augmente les risques de cancer »). L'hypothèse alternative peut être symétrique (« le tabac a un effet sur le risque de cancer » : il l'augmente ou il le diminue) ou non (« le tabac augmente le risque de cancer »). Choisir une hypothèse alternative non symétrique signifie donc que l'on rejette a priori la moitié de l'hypothèse : il peut s'agir d'un préjugé, il convient donc de bien réfléchir avant de choisir une hypothèse alternative non symétrique.
On appelle parfois H0 l'hypothèse conservative, car c'est l'hypothèse qu'on conserve si le résultat du test n'est pas clair.
Rejeter à tors l'hypothèse nulle (i.e., dire « il n'y a un effet » ou « il n'y a une différence » et se tromper).
Par exemple, si la variable suit une loi normale, on s'attend à obtenir des valeurs << au milieu >> de la courbe en cloche. Si on obtient des valeurs trop éloignées, on rejettera (parfois à tors) l'hypothèse nulle. Le risque d'erreur de type I correspond donc à l'aire de la partie en rouge sur la figure suivante.
colorie <- function (x, y1, y2, N=1000, ...) {
for (t in (0:N)/N) {
lines(x, t*y1+(1-t)*y2, ...)
}
}
# Non, il y a déjà une fonction qui fait ça...
colorie <- function (x, y1, y2, ...) {
polygon( c(x, x[length(x):1]), c(y1, y2[length(y2):1]), ... )
}
x <- seq(-6,6, length=100)
y <- dnorm(x)
plot(y~x, type='l')
i = x<qnorm(.025)
colorie(x[i],y[i],rep(0,sum(i)) ,col='red')
i = x>qnorm(.975)
colorie(x[i],y[i],rep(0,sum(i)) ,col='red')
lines(y~x)
title(main="Risque d'erreur de type I")
Probabilité, (si l'hypothèse nulle est vraie), d'obtenir un résultat au moins aussi extrème. C'est la probabilité de commettre une erreur de type I en rejettant l'hypothèse nulle.
Accepter à tors l'hypothèse nulle (i.e., dire « il n'y a pas d'effet statistiquement significatif » ou « il n'y a aucune différence » et se tromper).
En toute rigueur, ce n'est pas une erreur, car on ne doit jamais dire << H0 est vraie >>, mais juste << on ne rejette pas H0 >>. Ce n'est pas une erreur, mais une occasion ratée.
Le risque d'erreur de type II, c'est l'aire de la partie rouge dans le dessin suivant. La coube en cloche du milieu, c'est la distribution prévue par l'hypothèse nulle, l'autre courbe, c'est la distribution effectivement suivie par l'échantillon.
x <- seq(-6,6, length=1000) y <- dnorm(x) plot(y~x, type='l') y2 <- dnorm(x-.5) lines(y2~x) i <- x>qnorm(.025) & x<qnorm(.975) colorie(x[i],y2[i],rep(0,sum(i)), col='red') segments( qnorm(.025),0,qnorm(.025),dnorm(qnorm(.025)), col='red' ) segments( qnorm(.975),0,qnorm(.975),dnorm(qnorm(.975)), col='red' ) lines(y~x) lines(y2~x) title(main="Risque d'erreur de type II élevé")

Si les deux courbes sont suffisemment éloignées, le risque d'erreur de type II est beaucoup plus faible.
x <- seq(-6,6, length=1000) y <- dnorm(x) plot(y~x, type='l') y2 <- dnorm(x-3.5) lines(y2~x) i <- x>qnorm(.025) & x<qnorm(.975) colorie(x[i],y2[i],rep(0,sum(i)), col='red') segments( qnorm(.025),0,qnorm(.025),dnorm(qnorm(.025)), col='red' ) segments( qnorm(.975),0,qnorm(.975),dnorm(qnorm(.975)), col='red' ) lines(y~x) lines(y2~x) title(main="Risque d'erreur de type II plus faible")

On peut représentere l'erreur de type II en fonction de la différence entre les moyennes (contrairement au risque d'erreur de type I, le risque d'erreur de type II n'est pas une constante mais dépend de la valeur réelle du paramètre : c'est pour ça que ce risque est difficile à calculer et qu'on a tendance à le passer sous silence dans les cours élémentaires).
delta <- seq(-1.5, 1.5, length=500)
p <- NULL
for (d in delta) {
p <- append(p,
power.t.test(delta=abs(d), sd=1, sig.level=0.05, n=20,
type='one.sample')$power)
}
plot(1-p~delta, type='l',
xlab='différence entre les moyennes', ylab="probabilité d'une erreur de type II",
main="Variation des risques d'erreurs de type II dans un test T de Student")
abline(h=0,lty=3)
abline(h=0.05,lty=3)
abline(v=0,lty=3)
Par définition, la puissance d'un test, c'est
1 - P( erreur de type II ).
Généralement, la puissance n'est pas un nombre mais une fonction. l'hypothèse nulle est souvent de la forme H0 : << mu = mu0 >> et l'hypothèse alternative de la forme H1: << mu différent de mu0 >>. La puissance va dépendre de la valeur réelle de mu : si mu est proche de mu0, le risque d'erreur est grand et la puissance faible, par contre, si mu et mu0 sont très différents, le risque d'erreur est plus faible et la puissance plus élevée.
delta <- seq(0, 1.5, length=100)
p <- NULL
for (d in delta) {
p <- append(p,
power.t.test(delta=d, sd=1, sig.level=0.05, n=20,
type='one.sample')$power)
}
plot(p~delta, type='l',
ylab='power', main='Power of a one-sample t-test')
La puissance intervient dans la conception d'une expérience. Imaginons que l'on veuille savoir si la moyenne mu d'une certaine variable d'une population est bien égale à mu0. On veut pouvoir détecter une différence égale à epsilon dans au moins 80% des cas, avec un risque d'erreur inférieur à 0.05 : quelle doit être la taille de l'échantillon ? En d'autre termes, on veut que la puissance du test de H0 : << mu = mu0 >> contre H1: << abs(mu - mu0) > epsilon >> soit au moins 0.80 (la tradition veut que l'on prenne 0.80 pour la puissance des tests et 0.05 pour le risque)
La commande power.t.test fait exactement ça.
> power.t.test(delta=.1, sd=1, sig.level=.05, power=.80, type='one.sample')
One-sample t test power calculation
n = 786.8109
delta = 0.1
sd = 1
sig.level = 0.05
power = 0.8
alternative = two.sidedOn peut poser la question dans plein d'autres sens. Par exemple, l'expérience a déja été faite, avec un échantillon de taille n : quelle est la différence minimale sur la moyenne que l'on peut repérer si on veut que la puissance du test soit 0.80 ?)
> power.t.test(n=100, sd=1, sig.level=.05, power=.80, type='one.sample')
One-sample t test power calculation
n = 100
delta = 0.2829125
sd = 1
sig.level = 0.05
power = 0.8
alternative = two.sidedOn peut aussi voir l'évolution de la différence que l'on peut repérer en fonction de la taille de l'échantillon.
N <- seq(10,200, by=5)
delta <- NULL
for (n in N) {
delta <- append(delta,
power.t.test(n=n, sd=1, sig.level=.05,
power=.80, type='one.sample')$delta
)
}
plot(delta~N, type='l', xlab='sample size')
delta <- NULL
for (n in N) {
delta <- append(delta,
power.t.test(n=n, sd=1, sig.level=.01,
power=.80, type='one.sample')$delta
)
}
lines(delta~N, col='red')
delta <- NULL
for (n in N) {
delta <- append(delta,
power.t.test(n=n, sd=1, sig.level=.001,
power=.80, type='one.sample')$delta
)
}
lines(delta~N, col='blue')
legend(par('usr')[2], par('usr')[4], xjust=1,
c('significance level=.05', 'significance level=.01', 'significance level=.001'),
col=c(par('fg'), 'red', 'blue'),
lwd=1, lty=1)
title(main='Sample size and difference detected for tests of pover 0.80')
Lire :
http://www.stat.uiowa.edu/~rlenth/Power/2badHabits.pdf http://www.stat.uiowa.edu/techrep/tr303.pdf
On dit qu'une hypothèse est simple si elle implique une connaissance complète de la loi suivie par les v.a.. Par exemple, si on cherche la moyenne d'une v.a. dont on sait qu'elle est normale de variance 1, l'hypothèse H0 : « la moyenne est nulle » est simple. Par contre, si on ne connait pas la variance, cette hypothèse H0 n'est pas simple. Autre exemple : on observe un échantillon statistique et on sait qu'il provient soit d'une population 1 (décrite par une v.a. normale de moyenne 3 et de variance 2), soit d'une population 2 (décrite par une v.a. normale de moyenne 1 et de variance 1) ; les hypothèses H0 : « l'échantillon provient de la population 1 » et H1 : « l'échantillon provient de la population 2 » sont toutes deux simples.
Une hypothèse qui n'est pas simple. Très souvent, les hypothèses alternatives (H1) sont composites (si H1 est vrai, on sait que la loi est d'une certaine forme, avec un paramètre qui n'a pas une certaine valeur -- mais on ne sait pas quelle valeur il a).
On sait qu'une variable aléatoire suit une loi d'une certaine forme, que l'on ne connait pas entièrement, par exemple, une loi normale de variance 1 dont on ne connait pas la moyenne.
On a deux manières d'interpréter un (article indéfini : il y en a plein) intervalle de confiance à 95% pour la moyenne.
(1) C'est un intervalle dans lequel on a 95% de chances de trouver la moyenne empirique. C'est la définition.
(2) Plus naïvement, c'est un intervalle dans lequel on a 95% de chances de trouver la moyenne réelle.
En fait, ces deux interprétations sont équivalentes. Vérifons-le sur une simulation (ici, je tire la moyenne réelle au hasard, suivant une loi quelconque).
# Taille des échantillons
n <- 100
# Nombre de points de la courbe
N <- 1000
v <- vector()
for (i in 1:N) {
m <- runif(1)
x <- m+rnorm(n)
int <- t.test(x)$conf.int
v <- append(v, int[1]<m & m<int[2])
}
sum(v)/NOn trouve 0.95.
On en déduit donc deux interprétations de la p-valeur : d'une part, comme la probabilité d'obtenir des résultats au moins aussi extrèmes si H0 est vraie (c'est la définition) ; d'autre part, c'est la probabilité d'être dans l'intervalle de confiance.
La p-valeur n'est PAS la probabilité pour que H0 soit vraie. Pour s'en convaincre, donnons-nous une variable X, normale, de variance 1 et de moyenne inconnue. A l'aide d'un échantillon, on effectue un test de H0: << la moyenne est nulle >> contre H1: << la moyenne n'est pas nulle >>. On trouvera une certaine p-valeur.
> n <- 10 > m <- rnorm(1) > x <- m + rnorm(n) > t.test(x)$p.value [1] 0.2574325
Mais quelle est la probabilité pour que la moyenne soit effectivement nulle ? Dans notre simulation, cette probabilité égale zéro : la moyenne est presque sûrement non nulle.
> m [1] 0.7263967
On aimerait bien fixer la puissance d'un test, de la même manière qu'on fixe son niveau. Mais il y a un problème : si H1 n'est pas une hypothèse simple (mais un ensembe d'hypothèses simples), la puissance n'est pas un nombre, mais une fonction, qui dépend de l'hypothèse simple dans H1.
On dit qu'un test est UMP si, pour toute hypothèse simple dans H1, il possède la plus grande puissance parmi tous les tests de niveau alpha.
La plupart du temps, les tests statistiques supposent que les variables sont normales (et même, quand il y en a plusieurs, qu'elles ont la même variance). Les tests non paramétriques ne font pas ce genre d'hypothèse.
Voici quelques exemples de tests paramétriques et non paramétriques.
Objet Tests paramétriques Tests non paramétriques ---------------------------------------------------------------------------- comparaison de test T de Student test U de Wilcoxon 2 moyennes comparaison de analyse de la variance test de Kruskal--Wallis plus de 2 moyennes comparaison de 2 test F de Fisher tests d'Ansari-Bradley variances ou Mood comparaison de plus test de Bartlett test de Fligner de 2 variances
On dit qu'un test (paramétrique) est robuste s'il donne toujours des résultats corrects quand ses hypothèses ne sont plus vérifiées (en particulier quand les données ne sont plus normales).
On dit qu'un paramètre statistique est résistant s'il est peu dépendant des valeurs extrèmes. Par exemple, la moyenne n'est pas résistante, contrairement à la médiane.
> x <- rnorm(10) > mean(x) [1] -0.08964153 > mean(c(x,10^10)) [1] 909090909 > median(x) [1] -0.2234618 > median(c(x,10^10)) [1] -0.1949206
Le point de rupture est le nombre d'observations qu'il est possible de modifier sans que la valeur de l'estimateur change.
A FAIRE : vérifier que c'est bien ça (je suis tout à coup saisi d'un doute).
A FAIRE : un exemple.
1. On peut chercher un paramètre de la loi décrivant la population : on utilise alors un estimateur. Si possible, on en prendra un qui soit non biaisé et dont la variance soit la plus faible possible. (Si on n'y arrive pas, en particulier si la variable étudiée n'est pas normale, on pourra utiliser respectivement les méthodes du Jackknife et du Bootstrap, que nous présenterons plus tard.) (Nous verrons plus loin que certains estimateurs biaisés sont intéressants, car ils donnent une erreur quadratique moyenne inférieure aux meilleurs estimateurs non biaisés ; c'est par exemple le cas de la ridge regression.)
2. On peut chercher un intervalle dans lequel se trouve ce paramètre : on construit alors un intervalle de confiance.
3. On peut chercher à savoir si ce paramètre a une valeur prédéfinie : on effectue alors un test.
Une p-valeur proche de zéro peut signifier deux choses : soit l'hypothèse nulle est très fausse, soit elle ne l'est qu'un peu mais l'échantillon est suffisemment grand pour qu'on s'en apperçoive. Dans le second cas, on a une différence statistiquement notable entre l'hypothèse nulle et la réalité, mais, pratiquement, cette différence est négligeable.
Parmi tous les tests possibles, on en cherche un pour lequel les risques d'erreur de type I et II soient les plus bas possibles. Parmi les tests qui ne sont pas perfectibles (que l'on ne peut pas modifier pour en obtenir un pour lequel le risque d'erreur de type I soit le même et le risque d'erreur de type II plus bas (ou le contraire)), il n'existe pas de moyen de choisir LE meilleur (mais la théorie de la décision permet à chacun de choisir parmi ces tests celui qui convient le mieux à son propre gout du risque). Généralement, on fixe une borne supérieure pour la probabilité d'une erreur de type I (alpha) et on minimise le risque d'erreur de type II.
Pour plus de détails, lire le livre de Simon French, Decision theory : an introduction to the mathematics of rationality, Ellis Horwood series in mathematics and its applications, Halsted Press, 1988.
La plupart des fonctions R qui effectuent des tests statistiques sont dans « ctest » (classical tests). Cette bibliothèque est déjà chargée.
library(help="ctest")
On s'attendrait à ce que les fonctions de R qui effectuent ces tests nous disent « hypothèse rejetée » ou « hypothèse non rejetée » -- mais non. L'utilisateur doit savoir interpréter lui-même les résultats, avec éventuellement un certain esprit critique.
Le résultat des tests est essentiellement un nombre, la « p-valeur ». C'est la probabilité d'obtenir un résultat au moins aussi extrème. S'il est proche de 1, on ne rejette pas l'hypothèse, i.e., il n'y a rien de statistiquement significatif, s'il est proche de 0, on peut la rejeter. Plus précisément, si on veut un risque d'erreur de alpha % (par exemple, 5%), on ne rejette pas l'hypothèse si p>alpha/100 (par exemple, p>.05) et on la rejette sinon.
Il convient de choisir le risque d'erreur de type I AVANT d'effectuer le test.
Par exemple,
> x <- rnorm(200)
> t.test(x)
One Sample t-test
data: x
t = 3.1091, df = 199, p-value = 0.002152
alternative hypothesis: true mean is not equal to 0
95 percent confidence interval:
0.07855896 0.35102887
sample estimates:
mean of x
0.2147939Si on rejette l'hypothèse (ici : « la moyenne est nulle »), on aura tors avec une probabilité de 0.002152, soit 2 fois sur mille.
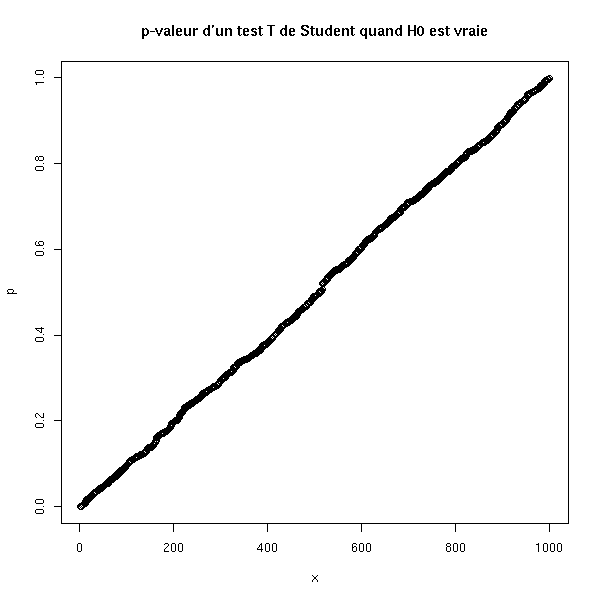
On retrouve cela à l'aide de simulations : dans 95% des cas, on a p>.05. Plus précisément, la distribution de p est uniforme dans [0,1].
p <- c()
for (i in 1:1000) {
x <- rnorm(200)
p <- append(p, t.test(x)$p.value)
}
hist(p, col='light blue')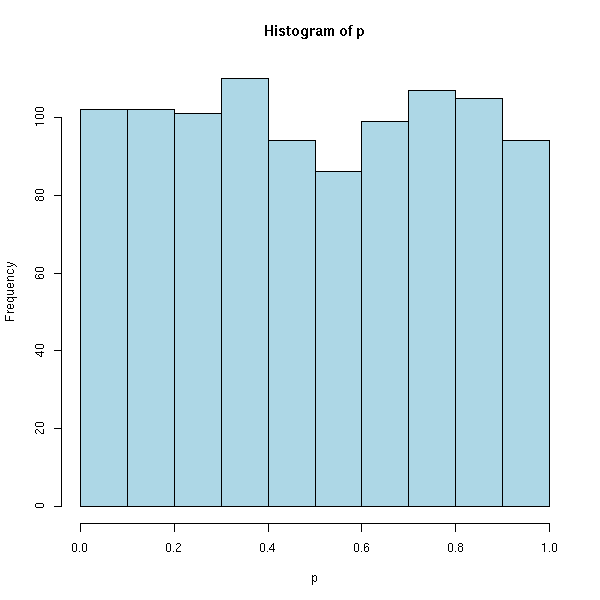
p <- sort(p) p[950] p[50] x <- 1:1000 plot(p ~ x, main="p-valeur d'un test T de Student quand H0 est vraie")
Il s'agissait ici du risque d'erreur de type I (rejeter à tors l'hypothèse nulle). Examinons maintenant le risque d'erreur de type II (accepter à tors l'hypothèse nulle). Ce risque dépend de la moyenne (que l'on ne connait pas) : si la moyenne est proche de zéro, ce risque est grand, si est est éloignée, il est plus faible.
# Taille de chaque échantillon
n <- 10
# Nombre de simulations à effectuer pour avoir une bonne
# approximation de la probabilité
m <- 1000
# Nombre de points pour tracer la courbe
k <- 50
# Valeur maximale de la moyenne
M <- 2
r <- vector()
for (j in M*(0:k)/k) {
res <- 0
for (i in 1:m) {
x <- rnorm(10, mean=j)
if( t.test(x)$p.value > .05 ){
res <- res + 1
}
}
r <- append(r, res/m)
}
rr <- M*(0:k)/k
plot(r~rr, type="l",
xlab='différence entre les moyennes',
ylab="probabilité d'une erreur de type II")
# Comparaison avec la courbe obtenue par power.t.test
x <- seq(0,2,length=200)
y <- NULL
for (m in x) {
y <- append(y, 1-power.t.test(delta=m, sd=1, n=10, sig.level=.05,
type='one.sample')$power)
}
lines(x,y,col='red')
# Courbe théorique
# (c'est un test de Z, ce n'est pas trop différent...)
r2 <- function (p,q,conf,x) {
p(q(1-conf/2)-x) - p(q(conf/2)-x)
}
f <- function(x) {
p <- function (t) { pnorm(t, sd=1/sqrt(10)) }
q <- function (t) { qnorm(t, sd=1/sqrt(10)) }
r2(p,q,.05,x)
}
curve( f(x) , add=T, col="blue" )
# Courbe théorique (pour un test T)
f <- function(x) {
p <- function (t) { pt(sqrt(10)*t, 10) } # Est-ce correct ?
q <- function (t) { qt(t, 10)/sqrt(10) }
r2(p,q,.05,x)
}
curve( f(x) , add=T, col="green" )
legend(par('usr')[2], par('usr')[4], xjust=1,
c('simulation', 'power.t.test', 'valeur exacte pour un test de Z',
'valeur exacte'),
col=c(par('fg'),'red','blue','green'),
lwd=1,lty=1)
title(main="Risque d'erreur de type II dans un test T de Student, en fonction de la différence des moyennes")
Nous avons vu un peu plus haut que, si l'hypothèse nulle est vraie, les p-valeurs sont réparties uniformément. Voici leur répartition si H0 est fausse, pour différentes valeurs de la moyenne.
N <- 10000
x <- 100*(1:N)/N
plot( x~I(x/100), type='n', ylab="pourcentages cumulés", xlab="p-value" )
do.it <- function (m, col) {
p <- c()
for (i in 1:N) {
x <- m+rnorm(200)
p <- append(p, t.test(x)$p.value)
}
p <- sort(p)
x <- 100*(1:N)/N
lines(x ~ p, type='l', col=col)
}
do.it(0, par('fg'))
do.it(.05, 'red')
do.it(.1, 'green')
do.it(.15, 'blue')
do.it(.2, 'orange')
abline(v=.05)
title(main='répartition des p-valeurs')
legend(par('usr')[2],par('usr')[3],xjust=1,yjust=1,
c('m=0', 'm=0.05', 'm=.01', 'm=.015', 'm=.02'),
col=c(par('fg'), 'red', 'green', 'blue', 'orange'),
lty=1,lwd=1)
Le manuel donne cet exemple, assez troublant, qui explique pourquoi R ne donne pas un résultat tranché « hypothèse rejetée » ou « hypothèse non rejetée ». Si on regarde les données à l'oeil nu, on peut affirmer sans grand risque que les moyennes sont très distinctes. Pourtant, la p-valeur est très élevée et conduit à ne pas rejeter l'hypothèse nulle (les moyennes sont égales). Le problème, c'est la taille de l'intervalle de confiance, qui est énorme. Il faut donc bien regarder les données et bien lire le résultat. (Cet exemple présente d'autres problèmes : pour appliquer un test T de Student sur les moyennes, il faut que les échantillons soient normaux, équivariants et indépendants -- ça n'a pas l'air d'être le cas).
x <- 1:10 y <- c(7:20, 200) boxplot(x,y, horizontal=T)

boxplot(x,y, log="x", horizontal=T)
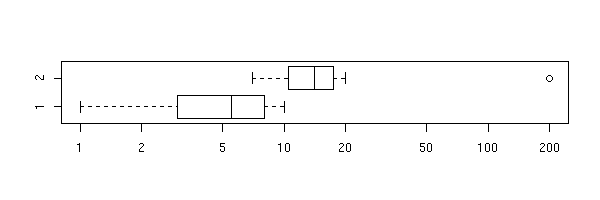
> t.test(x, y)
Welch Two Sample t-test
data: x and y
t = -1.6329, df = 14.165, p-value = 0.1245
alternative hypothesis: true difference in means is not equal to 0
95 percent confidence interval:
-47.242900 6.376233
sample estimates:
mean of x mean of y
5.50000 25.93333Bien sûr, si on enlève la valeur 200, on obtient un résultat plus conforme à l'intuition.
> t.test(1:10,y=c(7:20))
Welch Two Sample t-test
data: 1:10 and c(7:20)
t = -5.4349, df = 21.982, p-value = 1.855e-05
alternative hypothesis: true difference in means is not equal to 0
95 percent confidence interval:
-11.052802 -4.947198
sample estimates:
mean of x mean of y
5.5 13.5De même si on utilise un test non paramétrique (ce qu'il fallait faire depuis le début).
> wilcox.test(x,y)
Wilcoxon rank sum test with continuity correction
data: x and y
W = 8, p-value = 0.0002229
alternative hypothesis: true mu is not equal to 0
Warning message:
Cannot compute exact p-value with ties in: wilcox.test.default(x, y)
La plupart de ces tests ne sont valables que pour des distributions normales. S'il y a plusieurs échantillons, on demande aussi souvent qu'ils aient la même variance et qu'ils soient indépendants.
Il s'agit de trouver la moyenne d'un échantillon, ou plus précisément de comparer cette moyenne à une valeur prédéfinie.
?t.test
Conditions d'application : la variable est normale (sinon, on peut utiliser le test U de Wilcoxon).
Nous avons déjà donné un exemple quelques lignes plus haut, dans la présentation générale des tests statistiques sous R.
Voici la théorie.
L'hypothèse nulle est H0 : « la moyenne réelle est m », l'hypothèse alternative est H1 : « la moyenne réelle n'est pas m ». On calcule la quantité
T = ( moyenne empirique - m ) / ( écart-type empirique de l'échantillon / sqrt(n) )
(attention, on prend l'écart-type de l'échantillon (celui avec n-1), pas de la population (celui avec n) -- R utilise uniquement le premier) et on rejette H0 si
abs( T ) > t_{n-1} ^{-1} ( 1 - alpha/2 )où T_{n-1} est la loi T de Student à n-1 degrés de liberté. (Si on observe des vaiid normales, T suit effectivement cette loi de Student : on peut d'ailleur définir la loi de Student ainsi.)
Voici le graphe des densités des lois de Student. On constate que pour n grand, on se rapproche d'une loi normale.
curve(dnorm(x), from=-5, to=5, add=F, col="orange", lwd=3, lty=2)
curve(dt(x,100), from=-5, to=5, add=T, col=par('fg'))
curve(dt(x,5), from=-5, to=5, add=T, col="red")
curve(dt(x,2), from=-5, to=5, add=T, col="green")
curve(dt(x,1), from=-5, to=5, add=T, col="blue")
legend(par('usr')[2], par('usr')[4], xjust=1,
c('loi normale', 'df=100', 'df=5', 'df=2', 'df=1'),
col=c('orange', par('fg'), 'red', 'green', 'blue'),
lwd=c(3,1,1,1,1),
lty=c(2,1,1,1,1))
title(main="Densité de la loi T de Student")
Voyons maintenant comment mettre cela en pratique, à la main.
On part d'un échantillon de population normale, dont on calcule la moyenne.
> x <- rnorm(200) > m <- mean(x) > m [1] 0.05875323
On cherche maintenant un intervalle, centré autour de cette moyenne empirique, dans lequel on ait 95% de chances de trouver la moyenne réelle (qui est 0).
x <- rnorm(100) n <- length(x) m <- mean(x) m alpha <- .05 m + sd(x)/sqrt(n)*qt(alpha/2, df=n-1, lower.tail=T) m + sd(x)/sqrt(n)*qt(alpha/2, df=n-1, lower.tail=F)
On obtient [m - 0.19, m + 0.19].
La fonction t.test nous donne un résultat comparable.
> t.test(x, mu=0, conf.level=0.95)
One Sample t-test
data: x
t = 0.214, df = 99, p-value = 0.831
alternative hypothesis: true mean is not equal to 0
95 percent confidence interval:
-0.1987368 0.2467923
sample estimates:
mean of x
0.02402775On peut aussi vérifier cela expérimentalement, à l'aide de simulations.
> m = c()
> for (i in 1:10000) {
+ m <- append(m, mean(rnorm(100)) )
+ }
> m <- sort(m)
> m[250]
[1] -0.1982188
> m[9750]
[1] 0.1999646L'intervalle est donc [-0.20, +0.20] : on retrouve approximativement le résultat théorique (l'approximation est grossière, comme toujours pour les méthodes de type Monté-Carlo).
On peut aussi représenter graphiquement une telle simulation. On voit que la moyenne réelle est parfois en dehors de l'intervalle de confiance.
N <- 50
n <- 5
v <- matrix(c(0,0),nrow=2)
for (i in 1:N) {
x <- rnorm(n)
v <- cbind(v, t.test(x)$conf.int)
}
v <- v[,2:(N+1)]
plot(apply(v,2,mean), ylim=c(min(v),max(v)),
ylab='Intervalle de confiance', xlab='')
abline(0,0)
c <- apply(v,2,min)>0 | apply(v,2,max)<0
segments(1:N,v[1,],1:N,v[2,], col=c(par('fg'),'red')[c+1], lwd=3)
title(main="la moyenne réelle est parfois en dehors de l'intervalle de confiance")
Faisons une simulation pour voir ce qui se passe si on tente de faire un test de Student avec des données non normales (dans une telle situation, on devrait utiliser un test U de Wilcoxon).
Dans un premier temps, regardons ce qui se passe avec une loi moins dispersée que la normale : la loi uniforme.
> N <- 1000
> n <- 3
> v <- vector()
> for (i in 1:N) {
x <- runif(n, min=-1, max=1)
v <- append(v, t.test(x)$p.value)
}
> sum(v>.05)/N
[1] 0.932Maintenant avec des données normales.
> N <- 1000
> n <- 3
> v <- vector()
> for (i in 1:N) {
x <- rnorm(n, sd=1/sqrt(3))
v <- append(v, t.test(x)$p.value)
}
> sum(v>.05)/N
[1] 0.952Par conséquent, la p-valeur est fausse si la variable n'est plus normale : quand on croit rejeter l'hypothèse en avec un risque d'erreur de type I de 5%, le risque est en fait (pour une distribution uniforme) de 7%.
Regardons maintenant ce qui se passe avec l'intervalle de confiance : on devrait être dedans dans 95% des cas.
Distribution uniforme :
> N <- 1000
> n <- 3
> v <- vector()
> for (i in 1:N) {
x <- runif(n, min=-1, max=1)
r <- t.test(x)$conf.int
v <- append(v, r[1]<0 & r[2]>0)
}
> sum(v)/N
[1] 0.919Distribution normale :
> N <- 1000
> n <- 100
> v <- vector()
> for (i in 1:N) {
x <- rnorm(n, sd=1/sqrt(3))
r <- t.test(x)$conf.int
v <- append(v, r[1]<0 & r[2]>0)
}
> sum(v)/N
[1] 0.947Pour la loi uniforme, on est dans l'intervalle de confiance dans 92% des cas, au lieu des 95% prévus. Pour la loi de Cauchy, c'est le contraire (mais on a une chute de la puissance du test : il ne teste pour insi dire plus rien du tout...).
Par contre, avec des échantillons assez grands, l'erreur devient négligeable.
> N <- 1000
> n <- 100
> v <- vector()
> for (i in 1:N) {
x <- runif(n, min=-1, max=1)
v <- append(v, t.test(x)$p.value)
}
> sum(v>.05)/N
[1] 0.947
> N <- 1000
> n <- 100
> v <- vector()
> for (i in 1:N) {
x <- runif(n, min=-1, max=1)
r <- t.test(x)$conf.int
v <- append(v, r[1]<0 & r[2]>0)
}
> sum(v)/N
[1] 0.945Regardons maintenant la puissance du test.
N <- 1000
n <- 10
delta <- .8
v <- vector()
w <- vector()
for (i in 1:N) {
x <- delta+runif(n, min=-1, max=1)
v <- append(v, t.test(x)$p.value)
w <- append(w, wilcox.test(x)$p.value)
}
plot(sort(v), type='l', lwd=3, lty=2, ylab="p-valeur")
lines(sort(w), col='red')
legend(par('usr')[1], par('usr')[4], xjust=0,
c('test de Student', 'test de Wilcoxon'),
lwd=c(2,1),
lty=c(2,1),
col=c(par("fg"), 'red'))
N <- 1000
n <- 100
delta <- .1
v <- vector()
w <- vector()
for (i in 1:N) {
x <- delta+runif(n, min=-1, max=1)
v <- append(v, t.test(x)$p.value)
w <- append(w, wilcox.test(x)$p.value)
}
plot(sort(v), type='l', lwd=3, lty=2)
lines(sort(w), col='red')
legend(par('usr')[1], par('usr')[4], xjust=0,
c('test de Student', 'test de Wilcoxon'),
lwd=c(2,1),
lty=c(2,1),
col=c(par("fg"), 'red'))
N <- 1000
n <- 100
delta <- .8
v <- vector()
w <- vector()
for (i in 1:N) {
x <- delta+runif(n, min=-1, max=1)
v <- append(v, t.test(x)$p.value)
w <- append(w, wilcox.test(x)$p.value)
}
plot(sort(v), type='l', lwd=3, lty=2)
lines(sort(w), col='red')
legend(par('usr')[1], par('usr')[4], xjust=0,
c('test de Student', 'test de Wilcoxon'),
lwd=c(2,1),
lty=c(2,1),
col=c(par("fg"), 'red'))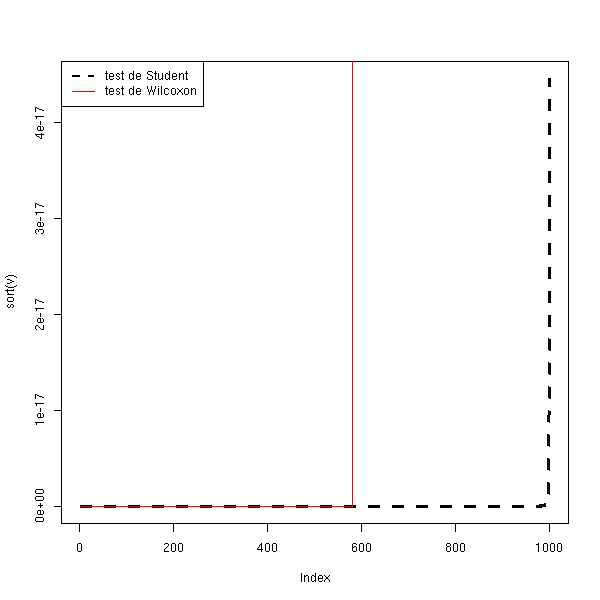
On pourra retenir que le test de Student est robuste : si les données sont moins dispersées qu'avec une loi normale, la p-valeur et le diamètre de l'intervalle de confiance sont sous-estimés, mais pas trop. Cet effet disparait si l'échantillon est grand.
Examinons maintenant la robustesse du test T de Student face à une distribution plus dispersée qu'avec une loi normale : la distribution de Cauchy.
> N <- 1000
> n <- 3
> v <- vector()
> for (i in 1:N) {
+ x <- rcauchy(n)
+ v <- append(v, t.test(x)$p.value)
+ }
> sum(v>.05)/N
[1] 0.974
> N <- 1000
> n <- 3
> v <- vector()
> for (i in 1:N) {
+ x <- rcauchy(n)
+ r <- t.test(x)$conf.int
+ v <- append(v, r[1]<0 & r[2]>0)
+ }
> sum(v)/N
[1] 0.988Et avec un échantillon plus gros.
> N <- 1000
> n <- 100
> v <- vector()
> for (i in 1:N) {
+ x <- rcauchy(n)
+ v <- append(v, t.test(x)$p.value)
+ }
> sum(v>.05)/N
[1] 0.982
> N <- 1000
> n <- 100
> v <- vector()
> for (i in 1:N) {
+ x <- rcauchy(n)
+ r <- t.test(x)$conf.int
+ v <- append(v, r[1]<0 & r[2]>0)
+ }
> sum(v)/N
[1] 0.986Regardons maintenant la puissance du test : c'est désastreux.
N <- 1000
n <- 10
delta <- 1
v <- vector()
w <- vector()
for (i in 1:N) {
x <- delta+rcauchy(n)
v <- append(v, t.test(x)$p.value)
w <- append(w, wilcox.test(x)$p.value)
}
plot(sort(v), type='l', lwd=3, lty=2)
lines(sort(w), col='red')
N <- 1000
n <- 100
delta <- 1
v <- vector()
w <- vector()
for (i in 1:N) {
x <- delta+rcauchy(n)
v <- append(v, t.test(x)$p.value)
w <- append(w, wilcox.test(x)$p.value)
}
plot(sort(v), type='l', lwd=3, lty=2)
lines(sort(w), col='red')
On retiendra que si les données sont plus dispersées qu'avec une loi normale, la puissance du test décroit, et il ne teste plus rien du tout. Cet effet ne décroit que légèrement avec la taille de l'échantillon. Dans ce cas, il faut se tourner vers des test non paramétriques.
> N <- 1000
> n <- 100
> v <- vector()
> w <- vector()
> for (i in 1:N) {
+ x <- rcauchy(n)
+ v <- append(v, t.test(x)$p.value)
+ w <- append(w, wilcox.test(x)$p.value)
+ }
> sum(v>.05)/N
[1] 0.976
> sum(w>.05)/N
[1] 0.948
> N <- 1000
> n <- 100
> v <- vector()
> w <- vector()
> for (i in 1:N) {
+ x <- 1+rcauchy(n)
+ v <- append(v, t.test(x)$p.value)
+ w <- append(w, wilcox.test(x)$p.value)
+ }
> sum(v<.05)/N
[1] 0.22
> sum(w<.05)/N
[1] 0.992
C'est comme le test de Student, mais cette fois-ci, on connait la valeur exacte de la variance : on n'utilise donc plus la distribution T de Student, mais simplement la distribution normale (souvent notée Z).
Dans la pratique, quand on ne connait pas la valeur exacte de la moyenne, on ne connait généralement pas non plus la valeur exacte de la variance -- ce test a donc une utilité pratique assez limitée.
Pour les gros échantillons, la loi du T de Student est bien approchée par la loi normale, on peut donc faire un test de Z au lieu d'un test de T (mais comme c'est de toute manière l'ordinateur qui fait les calculs à notre place...)
On a maintenant deux échantillons dont on aimerait savoir s'ils viennent de la même population ; et plus particulièrement s'ils ont la même moyenne.
On suppose ici que les lois sont normales (faire un qqplot ou un test de Shapiro pour s'en assurer), de même variance (utiliser un test F pour s'en assurer). Si ces conditions ne sont pas vérifiées, on peut utiliser un test U de Wilcoxon. On suppose aussi que les variables sont indépendantes (ce n'est pas toujours le cas : par exemple, on peut vouloir comparer la longueur de l'humérus droit et de l'humérus gauche chez des individus ; pour se ramener à des choses indépendantes, on peut considérer la différence de longueur entre les deux os).
Si les deux échantillons sont de taille n (ça marche aussi si les échantillons sont de tailles différentes, mais la formule est beaucoup plus compliquée), on montre que la quantité
t = différence des moyennes / sqrt( (somme des variances)/n )
suit une loi de Student à 2n-2 degrés de liberté.
On rejette l'hypothèse « les moyennes sont égales » si
abs(t) > abs( t(alpha, 2n-2) )
On pourrait le faire à la main, comme plus haut, mais il y a déjà une fonction.
?t.test
> x <- rnorm(100)
> y <- rnorm(100)
> t.test(x,y)
Welch Two Sample t-test
data: x and y
t = -1.3393, df = 197.725, p-value = 0.182
alternative hypothesis: true difference in means is not equal to 0
95 percent confidence interval:
-0.46324980 0.08851724
sample estimates:
mean of x mean of y
-0.03608115 0.15128514
> t.test(x, y, alternative="greater")
Welch Two Sample t-test
data: x and y
t = -1.3393, df = 197.725, p-value = 0.909
alternative hypothesis: true difference in means is greater than 0
95 percent confidence interval:
-0.4185611 Inf
sample estimates:
mean of x mean of y
-0.03608115 0.15128514Voici l'exemple du manuel : l'étude de l'efficacité d'un somnifère.
> data(sleep)
> plot(extra ~ group, data = sleep)
> t.test(extra ~ group, data = sleep)
Welch Two Sample t-test
data: extra by group
t = -1.8608, df = 17.776, p-value = 0.0794
alternative hypothesis: true difference in means is not equal to 0
95 percent confidence interval:
-3.3654832 0.2054832
sample estimates:
mean in group 1 mean in group 2
0.75 2.33Ici, comme la p-valeur est supérieure à 5%, on concluerait que le somnifère a des effets non significatifs. Néanmoins, si on travaille pour le laboratoire qui le fabrique, on voudra une conclusion différente. On peut l'obtenir en changenant l'hypothèse alternative, qui devient « le somnifère augmente le temps de sommeil ». (Normalement, on doit choisir l'hypothèse alternative avant de faire l'expérience, et ce choix doit être appuyé par des faits extérieurs à l'expérience : constater que dans cette expérience la moyenne empirique d'un échantillon est plus grande ne suffit pas.)
> t.test(extra ~ group, data = sleep, alternative="less")
Welch Two Sample t-test
data: extra by group
t = -1.8608, df = 17.776, p-value = 0.0397
alternative hypothesis: true difference in means is less than 0
95 percent confidence interval:
-Inf -0.1066185
sample estimates:
mean in group 1 mean in group 2
0.75 2.33Si on a plus de deux échantillons, on peut faire une analyse de la variance. Si on a deux échantillons non normaux, on peut faire un test U de Wilcoxon. Si on a plus de deux échantillon, non normaux, on peut faire une analyse de la variance non paramétrique, i.e., un test de Kruskal--Wallis.
Pour comparer des moyennes avec un test T de Student, il faut que les échantillons proviennent de populations indépendantes, normales de même variance. Regardons ce qui se passe avec des échantillons normaux non équivariants.
N <- 1000
n <- 10
v <- 100
a <- NULL
b <- NULL
for (i in 1:N) {
x <- rnorm(n)
y <- rnorm(n, 0, v)
a <- append(a, t.test(x,y)$p.value)
b <- append(b, t.test(x/var(x), y/var(y))$p.value)
}
plot(sort(a), type='l', col="green")
points(sort(b), type="l", col="red")
abline(0,1/N)
Et pour la puissance :
N <- 1000
n <- 10
v <- 100
a <- NULL
b <- NULL
c <- NULL
d <- NULL
for (i in 1:N) {
x <- rnorm(n)
y <- rnorm(n, 100, v)
a <- append(a, t.test(x,y)$p.value)
b <- append(b, t.test(x/var(x), y/var(y))$p.value)
c <- append(c, t.test(x, y/10000)$p.value)
d <- append(d, wilcox.test(x, y)$p.value)
}
plot(sort(a), type='l', col="green")
points(sort(b), type="l", col="red")
points(sort(c), type="l", col="blue")
points(sort(d), type="l", col="orange")
abline(0,1/N)
legend(par('usr')[1], par('usr')[4],
c('Test de Student', 'Test de Student renormalisé',
'Test de Student renormalisé avec les variances expérimentales',
'Test U de Wilcoxon (non paramétrique)'),
col=c('green', 'blue', 'red', 'orange'),
lwd=1,lty=1)
title(main='Test de Student sur des échantillons non équivariants')
Face à des échantillons non équivariants, la p-valeur donnée par le test de Student reste correcte, par contre sa puissance décroit lamentablement. Si les données semblement normales, mais de variances différentes, il vaut mieux les normaliser pour faire un test de Student plutôt que faire un test non paramétrique.
Il existe plusieurs manières de comparer deux moyennes.
data(sleep)
boxplot(extra ~ group, data=sleep,
horizontal=T,
xlab='extra', ylab='group')
A l'aide d'un test de Student, si on suppose que les données sont normales.
> t.test(extra ~ group, data=sleep)
Welch Two Sample t-test
data: extra by group
t = -1.8608, df = 17.776, p-value = 0.0794
alternative hypothesis: true difference in means is not equal to 0
95 percent confidence interval:
-3.3654832 0.2054832
sample estimates:
mean in group 1 mean in group 2
0.75 2.33A l'aide d'un test de Wilcoxon, si on ne sait pas que les données sont normales, on si on soupçonne (test de Shapiro--Wilk) qu'elles ne le sont pas.
> wilcox.test(extra ~ group, data=sleep)
Wilcoxon rank sum test with continuity correction
data: extra by group
W = 25.5, p-value = 0.06933
alternative hypothesis: true mu is not equal to 0
Warning message:
Cannot compute exact p-value with ties in: wilcox.test.default(x = c(0.7, -1.6,A l'aide d'une analyse de la variance (nous expliquerons plus loin ce que c'est).
> anova(lm(extra ~ group, data=sleep))
Analysis of Variance Table
Response: extra
Df Sum Sq Mean Sq F value Pr(>F)
group 1 12.482 12.482 3.4626 0.07919 .
Residuals 18 64.886 3.605
---
Signif. codes: 0 `***' 0.001 `**' 0.01 `*' 0.05 `.' 0.1 ` ' 1A l'aide d'une analyse de la variance non paramétrique, i.e., un test de Kruskal--Wallis.
> kruskal.test(extra ~ group, data=sleep)
Kruskal-Wallis rank sum test
data: extra by group
Kruskal-Wallis chi-squared = 3.4378, df = 1, p-value = 0.06372Voici les résultats.
Méthode p-valeur Test T de Student 0.0794 Test de Wilcoxon 0.06933 Analyse de la variance 0.07919 Test de Kruskal--Wallis 0.06372
On cherche la variance la variance d'un échantillon (on ne connait pas la moyenne de la population).
Voici la théorie.
L'hypothèse nulle est H0 : « la variance réelle est v », l'hypothèse alternative est « la variance réelle n'est pas v ». On calcule la quantité
Chi2 = (n-1) * (variance empirique) / v
et on rejette l'hypothèse H0 si
Chi2 > Chi2_{n-1} ^{-1} ( 1 - alpha/2 )
ou
Chi2 < Chi2_{n-1} ^{-1} ( alpha/2 )où Chi2_{n-1} est la loi du Chi2 à n-1 degrés de liberté.
Voici le graphe de la densité du Chi2, selon le nombre de degrés de liberté.
curve(dchisq(x,2), from=0, to=5, add=F, col="red",
ylab="dchisq(x,i)")
n <- 10
col <- rainbow(n)
for (i in 1:n) {
curve(dchisq(x,i), from=0, to=5, add=T, col=col[i])
}
legend(par('usr')[2], par('usr')[4], xjust=1,
paste('df =',1:n),
lwd=1,
lty=1,
col=col)
title(main="Densité de la loi du Chi^2")
Voici comment on peut obtenir à la main un intervalle de confiance pour l'écart-type.
alpha <- .05 x <- rnorm(200) n <- length(x) v = var(x) sd(x) sqrt( (n-1)*v / qchisq(alpha/2, df=n-1, lower.tail=F) ) sqrt( (n-1)*v / qchisq(alpha/2, df=n-1, lower.tail=T) )
On obtient [0.91, 1.11].
On peut vérifier cela par la simulation :
v <- c(0)
for (i in 1:10000) {
v <- append(v, var(rnorm(200)) )
}
v <- sort(v)
sqrt(v[250])
sqrt(v[9750])On obtient l'intervalle [0.90, 1.10].
Avec des échantillons plus petits, on obtient une estimation moins fiable : l'intervalle est [0.68, 1.32].
v <- c(0)
for (i in 1:10000) {
v <- append(v, var(rnorm(20)) )
}
v <- sort(v)
sqrt(v[250])
sqrt(v[9750])Je n'ai pas trouvé de fonction R qui fasse ça : on peut en écrire une.
chisq.var.test <- function (x, var=1, conf.level=.95,
alternative='two.sided') {
result <- list()
alpha <- 1-conf.level
n <- length(x)
v <- var(x)
result$var <- v
result$sd <- sd(x)
chi2 <- (n-1)*v/var
result$chi2 <- chi2
p <- pchisq(chi2,n-1)
if( alternative == 'less' ) {
stop("Not implemented yet")
} else if (alternative == 'greater') {
stop("Not implemented yet")
} else if (alternative == 'two.sided') {
if(p>.5)
p <- 1-p
p <- 2*p
result$p.value <- p
result$conf.int.var <- c(
(n-1)*v / qchisq(alpha/2, df=n-1, lower.tail=F),
(n-1)*v / qchisq(alpha/2, df=n-1, lower.tail=T),
)
}
result$conf.int.sd <- sqrt( result$conf.int.var )
result
}
x <- rnorm(100)
chisq.var.test(x)
# On peut vérifier que les résultats sont corrects en regardant si
# la distribution des p-valeurs est bien uniforme dans [0,1].
v <- NULL
for (i in 1:1000) {
v <- append(v, chisq.var.test(rnorm(100))$p.value)
}
plot(sort(v))
On peut aussi comparer avec les résultats de la fonction var.test, qui prend deux échantillons. Soit graphiquement,
p1 <- NULL
p2 <- NULL
for (i in 1:100) {
x <- rnorm(10)
p1 <- append(p1, chisq.var.test(x)$p.value)
p2 <- append(p2, var.test(x, rnorm(10000))$p.value)
}
plot( p1 ~ p2 )
abline(0,1,col='red')
Soit par le calcul (nous verrons plus loin à quoi cela correspond : c'est un test sur une régression, qui nous dit que p1=p2 avec une p-valeur de 0.325).
> summary(lm(p1-p2~0+p2))
Call:
lm(formula = p1 - p2 ~ 0 + p2)
Residuals:
Min 1Q Median 3Q Max
-0.043113 -0.007930 0.001312 0.009386 0.048491
Coefficients:
Estimate Std. Error t value Pr(>|t|)
p2 -0.002609 0.002638 -0.989 0.325
Residual standard error: 0.01552 on 99 degrees of freedom
Multiple R-Squared: 0.009787, Adjusted R-squared: -0.0002151
F-statistic: 0.9785 on 1 and 99 DF, p-value: 0.325
Il s'agit de savoir si deux échantillon proviennent de deux populations ayant ou non la même variance (on ne tient pas compte de la moyenne).
C'est comme pour la comparaison des moyennes, mais ici, on prend le quotient des variances.
On utilise par exemple ce test avant un test t de Student (comparaison des moyennes), car l'équivariance en est une condition d'application.
Voici l'exemple avec lequel nous avons illustré le test de Student : il est effectivement vraissemblable que les variances sont égales.
?var.test
> var.test( sleep[,1] [sleep[,2]==1], sleep[,1] [sleep[,2]==2] )
F test to compare two variances
data: sleep[, 1][sleep[, 2] == 1] and sleep[, 1][sleep[, 2] == 2]
F = 0.7983, num df = 9, denom df = 9, p-value = 0.7427
alternative hypothesis: true ratio of variances is not equal to 1
95 percent confidence interval:
0.198297 3.214123
sample estimates:
ratio of variances
0.7983426Voici la théorie.
L'hypothèse nulle est H0 : « les deux populations ont la même variance », l'hypothèse alternative est H1 : « les deux populations n'ont pas la même variance ». On calcule la quantité (pour simplifier, je suppose que les échantillons ont le même effectif).
F = (variance empirique du premier échantillon) / (variance empirique du deuxième)
et on rejette H0 si
F < F _{n1-1, n2-2} ^{-1} ( alpha/2 )
ou
F > F _{n1-1, n2-2} ^{-1} ( 1 - alpha/2 )où F est la loi de Fisher.
Dans la pratique, on calcule le quotient F des deux variances (en mettant la plus grande au numérateur), et on rejette l'hypothèse d'égalité des variances si
F > F(alpha/2, n1-1, n2-1)
où n1 et n2 sont les effectifs des échantillons.
Voici un exemple, à la main :
> x <- rnorm(100, 0, 1) > y <- rnorm(100, 0, 2) > f <- var(y)/var(x) > f [1] 5.232247 > qf(alpha/2, 99, 99) [1] 0.6728417 > f > qf(alpha/2, 99, 99) [1] TRUE
Si on a plus de deux échantillons, on peut utiliser le test de Bartlett. Si on a deux échantillons non normaux, on peut utiliser les tests non paramétriques d'Ansari ou de Mood. Si on a plus de deux échantillons non normaux, on peut utiliser le test de Fligner
?bartlett.test ?ansari.test ?mood.test ?fligner.test
Dans un échantillon de 100 papillons, on a observé 45 mâles et 55 femelles. Cela permet-t-il d'affirmer qu'il y a plus de femelles que de mâles dans la population ?
Le nombre de papillons femelles dans un échantillon de 100 individus suit une loi binomiale B(100,p), et on test H0: << p = 0.5 >> contre H1: << p différent de 0.5 >>.
> binom.test(55, 100, .5)
Exact binomial test
data: 55 and 100
number of successes = 55, number of trials = 100, p-value = 0.3682
alternative hypothesis: true probability of success is not equal to 0.5
95 percent confidence interval:
0.4472802 0.6496798
sample estimates:
probability of success
0.55Eh bien non, la différence n'est pas statistiquement significative.
Si on faisait les calculs à la main, on n'utiliserait pas le test binômial, mais une approximation, à l'aide de la commande prop.test. Comme c'est l'ordinateur qui fait les calculs, on n'a pas à utiliser ce test.
p <- .3
col.values <- c(par('fg'),'red', 'blue', 'green', 'orange')
n.values <- c(5,10,20,50,100)
plot(0, type='n', xlim=c(0,1), ylim=c(0,1), xlab='exact', ylab='approximate')
for (i in 1:length(n.values)) {
n <- n.values[i]
x <- NULL
y <- NULL
for (a in 0:n) {
x <- append(x, binom.test(a,n,p)$p.value)
y <- append(y, prop.test(a,n,p)$p.value)
}
o <- order(x)
lines(x[o],y[o], col=col.values[i])
}
legend(par('usr')[1],par('usr')[4],
as.character(n.values),
col=col.values,
lwd=1,lty=1)
title(main="Comparaison du test binômial et de son approximation")
On peut aussi comparer la répartition des p-valeurs pour les deux tests.
p <- .3
n <- 5
N <- 1000
e <- rbinom(N, n, p)
x <- y <- NULL
for (a in e) {
x <- append(x, binom.test(a,n,p)$p.value)
y <- append(y, prop.test(a,n,p)$p.value)
}
x <- sort(x)
y <- sort(y)
plot(x, type='l', lwd=3, ylab='p-valeur')
lines(y, col='red')
legend(par('usr')[2], par('usr')[3], xjust=1, yjust=0,
c('exact', 'approché'),
lwd=c(3,1),
lty=1,
col=c(par("fg"),'red'))
title(main="Test binomial (H0 vraie)")
p1 <- .3
p2 <- .5
n <- 5
N <- 1000
e <- rbinom(N, n, p1)
x <- y <- NULL
for (a in e) {
x <- append(x, binom.test(a,n,p2)$p.value)
y <- append(y, prop.test(a,n,p2)$p.value)
}
x <- sort(x)
y <- sort(y)
plot(x, type='l', lwd=3, ylab='p-valeur')
lines(y, col='red')
legend(par('usr')[2], par('usr')[3], xjust=1, yjust=0,
c('exact', 'approché'),
lwd=c(3,1),
lty=1,
col=c(par("fg"),'red'))
title(main="Test binomial (H0 fausse)")
On constate que si H0 est vraie, la p-valeur est surestimée (le test nous dit que la différence n'est pas du tout significative alors qu'elle n'est pas vraiment significative), par contre, plus H0 est fausse, plus la p-valeur est correcte. On retiendra que le test approché est légèrement moins puissant que le test exact, mais que la différence est faible.
Le test binomial, introduit plus haut, est très bien, mais il ne se généralise pas : il permet d'étudier une unique variable binaire, rien d'autre. Or, on aurait parfois besoin d'un test comparable, soit pour étudier des variables discrètes à plus de deux modalités ou pour étudier plusieurs variables. Il n'y a pas de tel test multinomial exact (on peut toujours en imaginer un, bien sûr, mais il faudrait ensuite l'implémenter...) : le test (approché) du Chi2 le remplacera.
Le test du Chi2 est un test non paramétrique et non rigoureux (c'est une approximation) pour comparer des distributions. C'est néanmoins le test discret le plus important.
On constate que, si (X1, X2, ..., Xr) est une variable multinomiale, alors
( X_1 - n p_1 )^2 ( X_r - n p_r )^2
Chi^2 = ------------------- + ... + --------------------
n p_1 n p_rsuit asymptotiquement une loi du Chi^2 à (r-1) degrés de liberté. Mais c'est juste un résultat asymptotique, qui est suffisemment valable si
n >= 100 (l'échantillon est suffisemment gros) n p_i >= 10 (les effectifs théoriques ne sont pas trop petits)
En particulier, cela nous donne un autre faux test binomial.
p <- .3
col.values <- c(par('fg'),'red', 'blue', 'green', 'orange')
n.values <- c(5,10,20,50,100)
plot(0, type='n', xlim=c(0,1), ylim=c(0,1), xlab='exact', ylab='approximate')
for (i in 1:length(n.values)) {
n <- n.values[i]
x <- NULL
y <- NULL
z <- NULL
for (a in 0:n) {
x <- append(x, binom.test(a,n,p)$p.value)
y <- append(y, chisq.test(c(a,n-a),p=c(p,1-p))$p.value)
z <- append(z, prop.test(a,n,p)$p.value)
}
o <- order(x)
lines(x[o],y[o], col=col.values[i])
lines(x[o],z[o], col=col.values[i], lty=3)
}
legend(par('usr')[1],par('usr')[4],
as.character(c(n.values, "prop.test", "chisq.test")),
col=c(col.values, par('fg'), par('fg')),
lwd=1,
lty=c(rep(1,length(n.values)), 1,3)
)
title(main="Comparaison du test binômial et de ses approximations")
Ou un faux test multinomial : vérifions, par une simultation de Monté-Carlo, que les p-valeurs sont proches.
multinom.test <- function (x, p, N=1000) {
n <- sum(x)
m <- length(x)
chi2 <- sum( (x-n*p)^2/(n*p) )
v <- NULL
for (i in 1:N) {
x <- table(factor(sample(1:m, n, replace=T, prob=p), levels=1:m))
v <- append(v, sum( (x-n*p)^2/(n*p) ))
}
sum(v>=chi2)/N
}
multinom.test( c(25,40,25,25), p=c(.25,.25,.25,.25) ) # 0.13
chisq.test( c(25,40,25,25), p=c(.25,.25,.25,.25) ) # 0.12
N <- 100
m <- 4
n <- 10
p <- c(.25,.25,.1,.4)
x <- NULL
y <- NULL
for (i in 1:N) {
a <- table( factor(sample(1:m, n, replace=T, prob=p), levels=1:m) )
x <- append(x, multinom.test(a,p))
y <- append(y, chisq.test(a,p=p)$p.value)
}
plot(y~x)
abline(0,1,col='red')
title("Comparaison d'un test multinomial de Monte-Carlo et du test du Chi^2")
On peut regarder la répartition des p-valeurs lors d'un test du Chi^2.
# On tire 10 individus au hasard, dans une population répartie
# en 4 classes. On répète l'expérience 100 fois.
N <- 1000
m <- 4
n <- 10
p <- c(.24,.26,.1,.4)
p.valeur.chi2 <- rep(NA,N)
for (i in 1:N) {
echantillon <- table(factor(sample(1:m, replace=T, prob=p), levels=1:m))
p.valeur.chi2[i] <- chisq.test(echantillon,p=p)$p.value
}
plot( sort(p.valeur.chi2), type='l', lwd=3 )
abline(0, 1/N, lty=3, col='red', lwd=3)
title(main="Répartition des p-valeurs lors d'un test du Chi2")
Considérons la situation suivante : on mesure deux variables qualitatives, chacune à deux valeurs, sur un échantillon. Dans la population complète, on observe les quatre classes dans les proportions 10%, 20%, 60%, 10%.
A B total
C 10 20 30
D 60 10 70
total 70 30 100On peut obtenir un échantillon ainsi.
foo <- function (N) {
population1 <- c(rep('A',10), rep('B',20), rep('A',60), rep('B',10))
population1 <- factor(population1, levels=c('A','B'))
population2 <- c(rep('C',10), rep('C',20), rep('D',60), rep('D',10))
population2 <- factor(population2, levels=c('C','D'))
o <- sample(1:100, N, replace=T)
table( population2[o], population1[o] )
}
a <- foo(1000)
op <- par(mfcol=c(1,2))
plot( a, shade=T )
plot( t(a), shade=T )
par(op)
On aimerait maintenant savoir si ces deux variables sont indépendantes ou pas. Pour ce faire, on prend un échantillon, on calcule les proportions marginales (i.e., la ligne et la colonne "total"), on fait le produit de cette colonne et de cette ligne pour obtenir les proportions en cas d'indépendance, et on compare ces proportions avec celles effectivement observées.
> n <- 100
> a <- foo(n)
> a/n
A B
C 0.09 0.15
D 0.65 0.11
> a1 <- apply(a/n,2,sum) # La ligne "total"
> a1
A B
0.74 0.26
> a2 <- apply(a/n,1,sum) # La colonne "total"
> a2
C D
0.24 0.76
> b <- a1 %*% t(a2)
> b
C D
[1,] 0.1776 0.5624
[2,] 0.0624 0.1976
> chisq.test(as.vector(a),p=as.vector(b))
Chi-squared test for given probabilities
data: as.vector(a)
X-squared = 591.7683, df = 3, p-value = < 2.2e-16
A FAIRE
Je crois que la syntaxe est différente
chisq.test(rbind(as.vector(a), as.vector(b)))
Le résultat est-il le même ?
A FAIRE
Remarque : on peut aussi utiliser le Chi^2 pour faire un test d'homogénéité,
pour vérifier que a et b proviennent de la même distribution.
C'est en fait exactement le chi^2 d'indépendance (indépendance entre la variable
et le numéro de l'échantillon) : la syntaxe est la même.
chisq.test(rbind(as.vector(a), as.vector(b)))
Il s'agit de vérifier que deux variables qualitatives, données par une table de contingence, sont indépendantes. Contrairement au Chi2, il s'agit d'un test exact.
Reprenons l'exemple donné plus haut, que nous avions examiné avec le test du Chi2 :
> a
A B
C 9 15
D 65 11
> fisher.test(a)
Fisher's Exact Test for Count Data
data: a
p-value = 1.178e-05
alternative hypothesis: true odds ratio is not equal to 1
95 percent confidence interval:
0.03127954 0.32486526
sample estimates:
odds ratio
0.1048422Par contre, sur un échantillon de taille plus petite, c'est beaucoup moins clair.
> fisher.test( foo(10) )
Fisher's Exact Test for Count Data
data: foo(10)
p-value = 1
alternative hypothesis: true odds ratio is not equal to 1
95 percent confidence interval:
0.003660373 39.142615141
sample estimates:
odds ratio
0.3779644
n1 <- 10
n2 <- 100
N <- 1000
x1 <- rep(NA,N)
x2 <- rep(NA,N)
for (i in 1:N) {
x1[i] <- fisher.test(foo(n1))$p.value
x2[i] <- fisher.test(foo(n2))$p.value
}
plot( sort(x1), type='l', lwd=3, ylab='p-valeur')
lines( sort(x2), col='blue', lwd=3 )
abline(0,1/N,col='red',lwd=3,lty=3)
abline(h=c(0,.05),lty=3)
abline(v=c(0,N*.05),lty=3)
title(main="p-valeurs d'un test de Fisher, H0 faux")
legend(par('usr')[1],par('usr')[4],
c("n=10", "n=100"),
col=c(par('fg'), 'blue'),
lwd=3,
lty=1)
foo <- function (N) {
population1 <- c(rep('A',2), rep('B',8), rep('A',18), rep('B',72))
population1 <- factor(population1, levels=c('A','B'))
population2 <- c(rep('C',2), rep('C',8), rep('D',18), rep('D',72))
population2 <- factor(population2, levels=c('C','D'))
o <- sample(1:100, N, replace=T)
table( population2[o], population1[o] )
}
n1 <- 10
n2 <- 100
N <- 1000
x1 <- rep(NA,N)
x2 <- rep(NA,N)
for (i in 1:N) {
x1[i] <- fisher.test(foo(n1))$p.value
x2[i] <- fisher.test(foo(n2))$p.value
}
plot( sort(x1), type='l', lwd=3, ylab='p-valeur', ylim=c(0,1))
lines( sort(x2), col='blue', lwd=3 )
abline(0,1/N,col='red',lwd=3,lty=3)
abline(h=c(0,.05),lty=3)
abline(v=c(0,N*.05),lty=3)
title(main="p-valeurs d'un test de Fisher, H0 vrai")
legend(par('usr')[2], .2, xjust=1, yjust=0,
c("n=10", "n=100"),
col=c(par('fg'), 'blue'),
lwd=3,
lty=1)
C'est un test non paramétrique sur la médiane d'une variable aléatoire dont on ne connait absolument rien.
Le principe est simple : on regarde le nombre de valeurs qui sont en dessous de la moyenne supposée -- or on sait que, si la médiane est bien celle-là, ce nombre suit une loi binomiale, car une valeur a exactement une chance sur deux d'être en dessous de la médiane.
Je n'ai pas trouvé de fonction déjà écrite qui effectue ce test, donc je vais écrire la mienne.
sign.test <- function (x, mu=0) { # does not handle NA
n <- length(x)
y <- sum(x<mu) # should warn about ties!
p.value <- min(c( pbinom(y,n,.5), pbinom(y,n,.5,lower.tail=F) ))*2
p.value
}Pour vérifier que ça marche, remarquons que la distribution des p-valeurs est à peu près uniforme si la médiane est bonne.
sign.test <- function (x, mu=0) {
n <- length(x)
y <- sum(x<mu) # should warn about ties!
p.value <- min(c( pbinom(y,n,.5), pbinom(y,n,.5,lower.tail=F) ))*2
p.value
}
N <- 500
n <- 200
res <- rep(NA,N)
for (i in 1:N) {
res[i] <- sign.test(rlnorm(n),mu=1)
}
plot(sort(res))
abline(0,1/N,lty=2)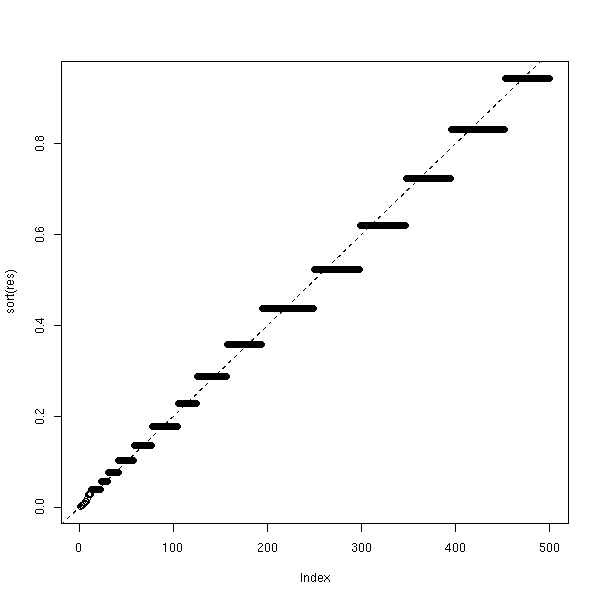
Si la médiane proposée est fausse, les p-valeurs sont beaucoup plus basses.
N <- 500
n <- 10
res <- rep(NA,N)
for (i in 1:N) {
res[i] <- sign.test(rlnorm(n),mu=2)
}
plot(sort(res), ylim=c(0,1))
abline(0,1/N,lty=2)
On peut maintenant compléter notre fonction pour avoir des intervalles de confiance.
sign.test <- function (x, mu=0, alpha=0.05) {
n <- length(x)
y <- sum(x<mu) # should warn about ties!
p.value <- min(c( pbinom(y,n,.5), pbinom(y,n,.5,lower.tail=F) ))*2
x <- sort(x)
q1 <- qbinom(alpha/2,n,.5,lower.tail=T)
q2 <- qbinom(alpha/2,n,.5,lower.tail=F)
ci <- c(x[q1], x[q2])
new.alpha = pbinom(q1,n,.5) + (1-pbinom(q2,n,.5))
list(p.value=p.value, ci=ci, alpha=new.alpha)
}On peut vérifier que les intervalles de confiance ont bien le risque annoncé (ce risque ne sera pas exactement 0.05, c'est pourquoi la fonction de test renvoie sa valeur théorique).
test.sign.test <- function (n=100, N=500) {
N <- 500
res <- matrix(NA, nr=N, nc=3)
n <- 100
for (i in 1:N) {
r <- sign.test(rlnorm(n))
ci <- r$ci
res[i,] <- c( ci[1]<1 & 1<ci[2], n, r$alpha )
}
c(
1-sum(res[,1], na.rm=T)/sum(!is.na(res[,1])),
res[1,3]
)
}
N <- 10
res <- matrix(NA, nc=3, nr=N, dimnames=list(NULL,
c("Valeur empirique", "Valeur théorique", "n")) )
for (i in 1:N) {
n <- sample(1:200, 1)
res[i,] <- round(c( test.sign.test(n), n ), digits=2)
}
resIl vient :
> res
Valeur empirique Valeur théorique n
[1,] 0.06 0.05 96
[2,] 0.04 0.05 138
[3,] 0.05 0.05 6
[4,] 0.06 0.05 135
[5,] 0.03 0.05 138
[6,] 0.04 0.05 83
[7,] 0.03 0.05 150
[8,] 0.05 0.05 91
[9,] 0.05 0.05 144
[10,] 0.04 0.05 177
A FAIRE : relire et éventuellement corriger cette partie...
Il s'agit d'un test non paramétrique : on ne connait presque rien sur la loi suivie par les données, en particulier, on pense qu'elle n'est pas normale (pour s'en appercevoir, on a fait un graphique quantiles-quantiles, ou un test de Shapiro--Wilk) -- sinon, on prendrait le test du T de Student, qui est plus puissant).
Il y a quand-même une hypothèse : la variable est symétrique (sinon, on utiliserait un test du signe). C'est d'ailleurs pour cette raison qu'on parle de moyenne et pas de médiane.
A FAIRE : la description qui suit ne correspond pas au test de Wilcoxon que je connais, qui suppose la variable symétrique, et qui consiste à construire les variables Xij=(Xi+Xj)/2 et à regarder le nombre de ces nouvelles variables qui sont supérieures à la moyenne supposée. (d'ailleurs, c'est à cause de cette symétrie qu'on parle de moyenne)
On prend les deux échantillons, on les met ensemble et on met le tout dans l'ordre. On regarde ensuite si les éléments des deux échantillons sont « bien mélangés » ou au contraire si les éléments d'un échantillon sont plutôt au début alors que ceux de l'autre sont plutôt à la fin.
L'hypothèse que l'on teste est ici « P(X1_i > X2_i) = 0.5 ».
En supposant les échantillons déjà triés, on calcule
U1 = nombre de couples (i,j) tels que X1_i>X2_j
+ (1/2) * nombre de couples (i,j) tels que X1_i=X2_j
U2 = nombre de couples (i,j) tels que X1_j>X2_i
+ (1/2) * nombre de couples (i,j) tels que X1_i=X2_j
U = min(U1,U2)Autre méthode de calcul :
Mettre tous les éléments dans l'ordre et leur assigner un rang R1 = somme des rangs du premier échantillon R2 = somme des rangs du deuxième échantillon U2 = n1*n2 + n1(n1+1)/2 - R1 U1 = n1*n2 + n2(n2+1)/2 - R2 U = min(U1, U2)
Voici l'exemple de la page de manuel (ici, on a des raisons de penser que x>y).
help.search("wilcoxon")
?wilcox.test
> x <- c(1.83, 0.50, 1.62, 2.48, 1.68, 1.88, 1.55, 3.06, 1.30)
> y <- c(0.878, 0.647, 0.598, 2.05, 1.06, 1.29, 1.06, 3.14, 1.29)
> wilcox.test(x, y, paired = TRUE, alternative = "greater", conf.level=.95, conf.int=T)
Wilcoxon signed rank test
data: x and y
V = 40, p-value = 0.01953
alternative hypothesis: true mu is greater than 0
95 percent confidence interval:
0.175 Inf
sample estimates:
(pseudo)median
0.46Vérifions sur un exemple que le test reste valable pour des distributions non normales.
N <- 1000
n <- 4
v <- vector()
w <- vector()
for (i in 1:N) {
x <- runif(n, min=-10, max=-9) + runif(n, min=9, max=10)
v <- append(v, wilcox.test(x)$p.value)
w <- append(w, t.test(x)$p.value)
}
sum(v>.05)/N
sum(w>.05)/NOn obtient 1 et 0.93 : on commet moins d'erreurs avec le test U de Wilcoxon, mais sa puissance est moindre, i.e., on laisse passer plein d'occasions de rejeter l'hypothèse nulle :
# Probabilité de rejet d'une hypothèse fausse (=puissance)
N <- 1000
n <- 5
v <- vector()
w <- vector()
for (i in 1:N) {
x <- runif(n, min=0, max=1)
v <- append(v, wilcox.test(x)$p.value)
w <- append(w, t.test(x)$p.value)
}
sum(v<.05)/N
sum(w<.05)/NOn obtient 0 (la puissance du test est alors nulle : il ne rejette jamais l'hypothèse nulle -- si on a un échantillon très petit et si on ne sait rien sur la loi, on ne peut pas dire grand-chose) contre 0.84
Prenons une loi plus éloignée de la normale.
# Probabilité de rejet d'une hypothèse fausse (=puissance)
N <- 1000
n <- 5
v <- vector()
w <- vector()
for (i in 1:N) {
x <- runif(n, min=-10, max=-9) + runif(n, min=9, max=10)
v <- append(v, wilcox.test(x)$p.value)
w <- append(w, t.test(x)$p.value)
}
sum(v<.05)/N
sum(w<.05)/NOn obtient 0 et 0.05. Pour n=10, on obtiendrait 0.05 dans les deux cas.
Regardons maintenant l'intervalle de confiance.
N <- 1000
n <- 3
v <- vector()
w <- vector()
for (i in 1:N) {
x <- runif(n, min=-10, max=-9) + runif(n, min=9, max=10)
r <- wilcox.test(x, conf.int=T)$conf.int
v <- append(v, r[1]<0 & r[2]>0)
r <- t.test(x)$conf.int
w <- append(w, r[1]<0 & r[2]>0)
}
sum(v)/N
sum(w)/NOn obtient 0.75 contre 0.93.
A FAIRE Je ne comprends pas : comme le test U est non-paramétrique, il devrait donner des intervalles de confiance plus grands, et donc se tromper moins souvent. L'intervalle de confiance du test de Wilcoxon est trois fois plus petit que celui du test T de Student. ??? On retiendra de cette comparaison des tests de Wilcoxon et de Student que le test de Student est robuste (i.e., quand ses conditions d'application ne sont pas vérifiées, il marche quand même assez bien). A FAIRE : relire ce qui précède et regarder la puissance (la puissance du test de Student est presque nulle si ses hypothèses ne sont pas vérifiées).
L'exemple suivant regarde si la variable est symétrique autour de sa moyenne.
> x <- rnorm(100)^2
> x <- x - mean(x)
> wilcox.test(x)
Wilcoxon signed rank test with continuity correction
data: x
V = 1723, p-value = 0.005855
alternative hypothesis: true mu is not equal to 0L'exemple suivant regarde si la variable est symétrique autour de sa médiane.
> x <- x - median(x)
> wilcox.test(x)
Wilcoxon signed rank test with continuity correction
data: x
V = 3360.5, p-value = 0.004092
alternative hypothesis: true mu is not equal to 0Si on a plus de deux échantillons, on peut utiliser le test de Kruskal-Wallis.
?kruskal.test
Il s'agit de voir si deux variables (quantitatives) suivent la même loi.
> ks.test( rnorm(100), 1+rnorm(100) )
Two-sample Kolmogorov-Smirnov test
data: rnorm(100) and 1 + rnorm(100)
D = 0.43, p-value = 1.866e-08
alternative hypothesis: two.sided
> ks.test( rnorm(100), rnorm(100) )
Two-sample Kolmogorov-Smirnov test
data: rnorm(100) and rnorm(100)
D = 0.11, p-value = 0.5806
alternative hypothesis: two.sided
> ks.test( rnorm(100), 2*rnorm(100) )
Two-sample Kolmogorov-Smirnov test
data: rnorm(100) and 2 * rnorm(100)
D = 0.19, p-value = 0.0541
alternative hypothesis: two.sided
Il permet de savoir si une variable est normale.
> shapiro.test(rnorm(10))$p.value [1] 0.09510165 > shapiro.test(rnorm(100))$p.value [1] 0.8575329 > shapiro.test(rnorm(1000))$p.value [1] 0.1853919 > shapiro.test(runif(10))$p.value [1] 0.5911485 > shapiro.test(runif(100))$p.value [1] 0.0002096377 > shapiro.test(runif(1000))$p.value [1] 2.385633e-17
C'est une bonne idée de faire un graphique quantiles-quantiles pour voir ce qui se passe, car il est possible que les données ne soient pas du tout normales, mais que ce ne soit pas grave (soit, comme ici, parce que les données sont moins dispersées que des données normales, soit parce que l'écart à la normalité est statistiquement significatif mais pratiquement négligeable (c'est courrant si l'échantillon est gros)).
Il en existe plein d'autres, que nous ne détaillons pas, et pour lesquels nous renvoyons au manuel.
?kruskal.test
?ansari.test
?mood.test
?fligner.test
library(help=ctest)
help.search('test')
A FAIRE : cette partie n'est pas encore écrite...
Likelihood-Ratio test LR = -2 ln ( L at H0 / L at MLE ) LR ~ Chi2 df = number of parameters (eg, 1). Other tests for MLE: Wald test, Score test. To compare two models fitted with MLE, compare AIC = LRChi^2 - 2 p where p is the number of parameters. This is an approximative criterion. There are other questionable such criteria, eg, BIC (Bayesian Information Criterion). r <- lm(...) AIC(r) library(nlme) BIC(r) r <- gls(...) summary(r) The AIC says that adding a useless parameter generally increases the log likelihood by about 1 unit. So if adding a parameter increases the log like- lihood by more than 1, it is not useless.
Vincent Zoonekynd
<zoonek@math.jussieu.fr>
latest modification on Wed Oct 13 22:32:48 BST 2004