
The French version of this document is no longer maintained: be sure to check the more up-to-date English version.
Le zoo des distributions de probabilité discrètes
Le zoo des lois de probabilités continues
Les lois discrètes les plus importantes sont la loi de Bernoulli, la loi binomiale et la loi de Poisson.
Tirer une pièce à pile ou face revient à examiner une variable aléatoire suivant une loi de Bernoulli de paramètre 0.5. Si la pièce est truquée et que « pile » apparait avec une probabilité p, c'est une loi de Bernoulli de paramètre p.
P( X=1 ) = p P( X=0 ) = 1-p
En cas d'équiprobabilité, on peut simuler une telle expérience à l'aide de la commande sample, qui permet de faire des tirages, avec ou sans remise, dans un ensemble.
n <- 100 x <- sample(c(-1,1), n, replace=T) plot(x, type='h', main="Tirages de Bernoulli")

n <- 1000
x <- sample(c(-1,1), n, replace=T)
plot(cumsum(x), type='l',
main="Sommes cumulées de tirages de Bernoulli")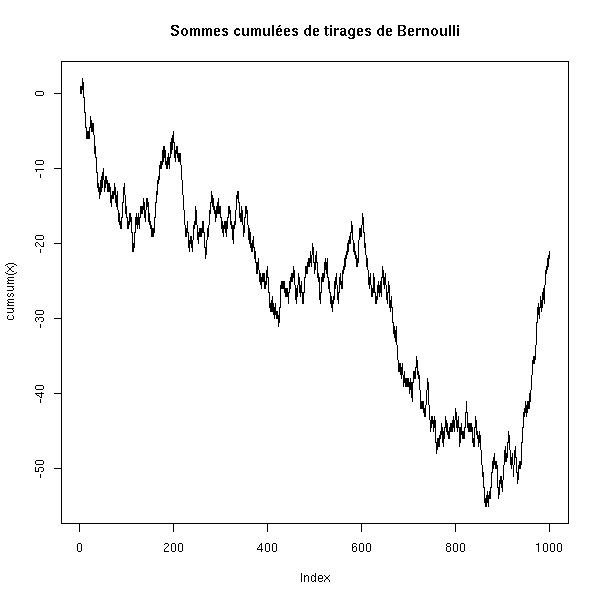
Si les probabilités sont distinctes, on peut toujours utiliser la commande sample.
n <- 100
x <- sample(c(-1,1), n, replace=T, prob=c(.2,.8))
plot(x, type='h',
main="Tirages de Bernoulli sans équiprobabilité")
n <- 200
x <- sample(c(-1,1), n, replace=T, prob=c(.2,.8))
plot(cumsum(x), type='l',
main="Sommes cumulées de tirages de Bernoulli")
Mais on peut aussi faire les tirages << à la main >>.
n <- 200 x <- runif(n) x <- x>.3 plot(x, type='h', main="Tirages de Bernoulli")

C'est une généralisation des épreuves de Bernouilli : on tire au hasard un nombre parmi 1, 2, 3, ..., n.
On peut simuler cette loi à l'aide de la commande sample.
> sample(1:10, 20, replace=T) [1] 1 5 6 4 7 5 3 6 2 9 10 10 8 3 10 7 4 1 1 3
On tire une pièce à pile ou face n fois et on regarde le nombre de « pile ». Il s'agit en fait d'une somme de vaiid de Bernoulli.
On peut la simuler ainsi.
N <- 10000
n <- 20
p <- .5
x <- rep(0,N)
for (i in 1:N) {
x[i] <- sum(runif(n)<p)
}
hist(x,
col='light blue',
main="Simulation d'une loi binomiale")
On peut aussi utiliser la commande rbinom.
N <- 1000
n <- 10
p <- .5
x <- rbinom(N,n,p)
hist(x,
xlim=c(min(x),max(x)), probability=T, nclass=max(x)-min(x)+1,
col='lightblue',
main='Loi binomiale, n=10, p=.5')
lines(density(x,bw=1), col='red', lwd=3)
N <- 100000
n <- 100
p <- .5
x <- rbinom(N,n,p)
hist(x,
xlim=c(min(x),max(x)), probability=T, nclass=max(x)-min(x)+1,
col='lightblue',
main='Loi binomiale, n=100, p=p')
lines(density(x,bw=1), col='red', lwd=3)
p <- .9
x <- rbinom(N,n,p)
hist(x,
xlim=c(min(x),max(x)), probability=T, nclass=max(x)-min(x)+1,
col='lightblue',
main='Loi binomiale, n=100, p=p')
lines(density(x,bw=1), col='red', lwd=3)
C'est aussi la loi qu'on rencontre lors d'un échantillonage avec remise (quand on tire des boules dans une urne, et qu'on remet la boule dans l'urne avant de tirer la suivante) : on peut donc la simuler avec la commande sample.
N <- 10000
n <- 100
p <- .5
x <- NULL
for (i in 1:N) {
x <- append(x, sum(sample( c(1,0), n, replace=T, prob=c(p, 1-p) )))
}
hist(x,
xlim=c(min(x),max(x)), probability=T, nclass=max(x)-min(x)+1,
col='lightblue',
main='Loi binomiale, n=100, p=.5')
lines(density(x,bw=1), col='red', lwd=3)
On la rencontre par exemple en écologie, quand on cherche à dénombrer les individus d'une espèce. On capture des animaux, régulièrement, et on les marque (par exemple avec des bagues). Au bout d'un moment, une partie de la population est baguée (on connait son effectif, car on a numéroté les bagues), l'autre pas. Lors de nouvelles captures, on a un certain nombre d'animaux marqués et un certain nombre d'animaux non marqués : ces nombres vont nous aider à déterminer la taille de la population.
C'est la loi qu'on rencontre lors d'un échantillonage sans remise.
Voyons ce que cela donne sur un exemple, à l'aide d'une simulation. On tire 5 boules d'une urne qui en contient 15 blanches et 5 rouges, et on compte le nombre de boules blanches.
N <- 10000
n <- 5
urne <- c(rep(1,15),rep(0,5))
x <- NULL
for (i in 1:N) {
x <- append(x, sum(sample( urne, n, replace=F )))
}
hist(x,
xlim=c(min(x),max(x)), probability=T, nclass=max(x)-min(x)+1,
col='lightblue',
main='Loi hypergéométrique, n=20, p=.75; k=5')
lines(density(x,bw=1), col='red', lwd=3)
On peut aussi utiliser directement la commande rhyper (c'est plus rapide).
N <- 10000
n <- 5
x <- rhyper(N, 15, 5, 5)
hist(x,
xlim=c(min(x),max(x)), probability=T, nclass=max(x)-min(x)+1,
col='lightblue',
main='Loi hypergéométrique, n=20, p=.75, k=5')
lines(density(x,bw=1), col='red', lwd=3)
N <- 10000
n <- 5
x <- rhyper(N, 300, 100, 100)
hist(x,
xlim=c(min(x),max(x)), probability=T, nclass=max(x)-min(x)+1,
col='lightblue',
main='Loi hypergéométrique, n=400, p=.75, k=100')
lines(density(x,bw=1), col='red', lwd=3)
C'est la loi qui décrit le nombre de clients qui arrivent dans une file d'attente pendant une unité de temps. Ou le nombre de fautes dans un texte. Ou le nombre de désintégrations radioactives par unité de temps.
De manière plus formelle, c'est une loi de probabilité telle que : (1) la probabilité d'observer un évènement dans un "petit" intervalle est proportionnelle à la taille de cet intervalle (en particulier, ça ne dépend que de la taille, pas la position de l'intervalle) ; (2) la probabilité que l'évènement se produise dans un intervalle est indépendante de la probabilité d'apparition dans n'importe quel intervalle disjoint ; (3) il n'y a pas d'évènements simultanés.
On montre que :
P( X=k ) = e^(-mu) * mu^k / k!
On peut simuler cette loi à l'aide de la commande rpoiss.
N <- 10000
x <- rpois(N, 1)
hist(x,
xlim=c(min(x),max(x)), probability=T, nclass=max(x)-min(x)+1,
col='lightblue',
main='Loi de Poisson, lambda=1')
lines(density(x,bw=1), col='red', lwd=3)
N <- 10000
x <- rpois(N, 3)
hist(x,
xlim=c(min(x),max(x)), probability=T, nclass=max(x)-min(x)+1,
col='lightblue',
main='Loi de Poisson, lambda=3')
lines(density(x,bw=1), col='red', lwd=3)
N <- 10000
x <- rpois(N, 5)
hist(x,
xlim=c(min(x),max(x)), probability=T, nclass=max(x)-min(x)+1,
col='lightblue',
main='Loi de Poisson, lambda=5')
lines(density(x,bw=1), col='red', lwd=3)
N <- 10000
x <- rpois(N, 20)
hist(x,
xlim=c(min(x),max(x)), probability=T, nclass=max(x)-min(x)+1,
col='lightblue',
main='Loi de Poisson, lambda=20')
lines(density(x,bw=1), col='red', lwd=3)
C'est la loi du nombre d'essais avant une réussite lors d'une suite d'épreuves de Bernoulli.
On pourrait la simuler à la main, mais le plus simple est d'utiliser directement la commande rgeom.
N <- 10000
x <- rgeom(N, .5)
hist(x,
xlim=c(min(x),max(x)), probability=T, nclass=max(x)-min(x)+1,
col='lightblue',
main='Loi géométrique, p=.5')
lines(density(x,bw=1), col='red', lwd=3)
N <- 10000
x <- rgeom(N, .1)
hist(x,
xlim=c(min(x),max(x)), probability=T, nclass=max(x)-min(x)+1,
col='lightblue',
main='Loi géométrique, p=.1')
lines(density(x,bw=1), col='red', lwd=3)
N <- 10000
x <- rgeom(N, .01)
hist(x,
xlim=c(min(x),max(x)), probability=T, nclass=20,
col='lightblue',
main='Loi géométrique, p=.01')
lines(density(x), col='red', lwd=3)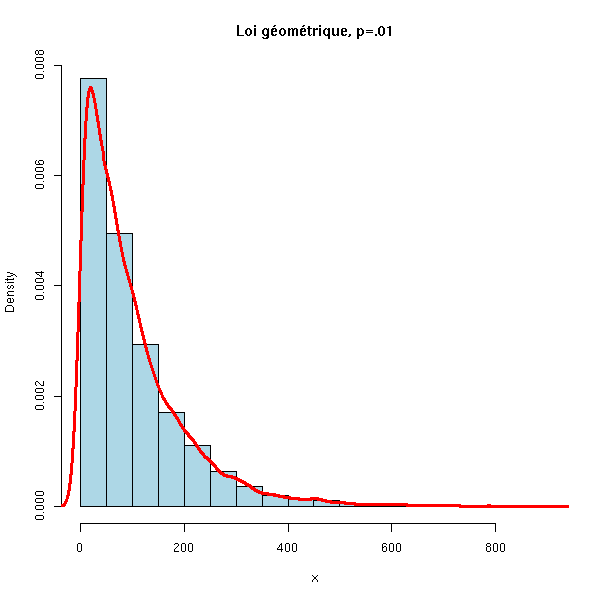
C'est la loi du nombre d'échecs avant k réussites lors d'une suite d'épreuves de Bernoulli.
On peut la simuler à la main, mais le plus simple est d'utiliser la commande rnbinom.
N <- 100000
x <- rnbinom(N, 10, .25)
hist(x,
xlim=c(min(x),max(x)), probability=T, nclass=max(x)-min(x)+1,
col='lightblue',
main='Loi binomiale négative, n=10, p=.25')
lines(density(x,bw=1), col='red', lwd=3)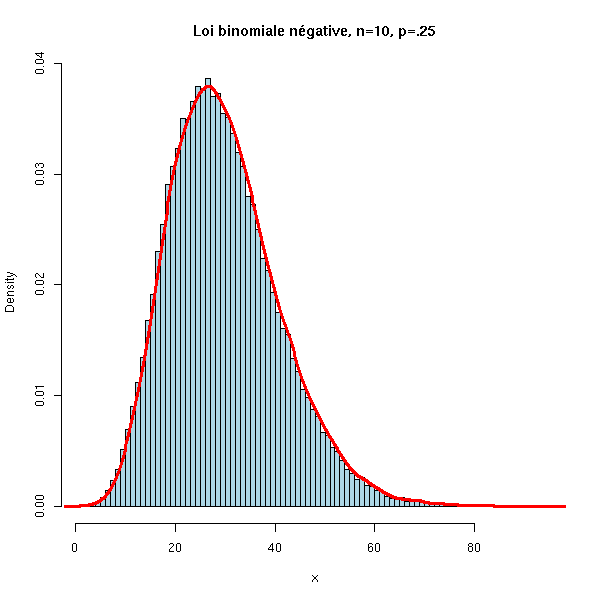
N <- 10000
x <- rnbinom(N, 10, .5)
hist(x,
xlim=c(min(x),max(x)), probability=T, nclass=max(x)-min(x)+1,
col='lightblue',
main='Loi binomiale négative, n=10, p=.5')
lines(density(x,bw=1), col='red', lwd=3)
N <- 10000
x <- rnbinom(N, 10, .75)
hist(x,
xlim=c(min(x),max(x)), probability=T, nclass=max(x)-min(x)+1,
col='lightblue',
main='Loi binomiale négative, n=10, p=.75')
lines(density(x,bw=1), col='red', lwd=3)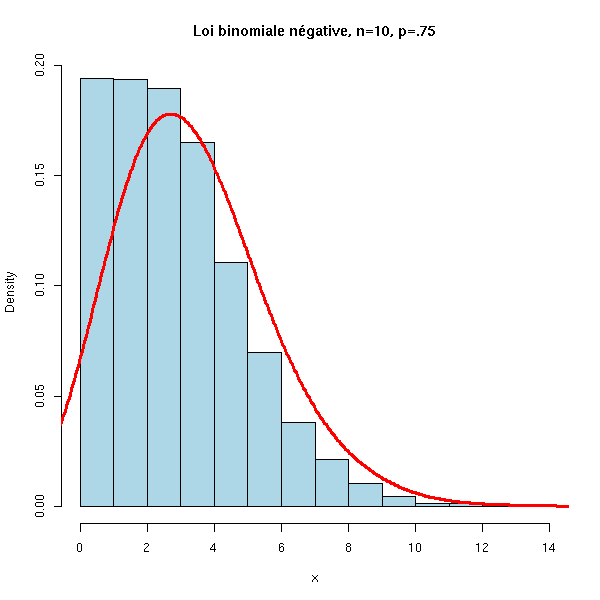
C'est l'équivalent de la loi binomiale, mais cette fois-ci, les expériences ont plusieurs résultats possibles.
P( (X1,X2,...,Xn)=(k1,k2,...,kn) ) = m! p1^k1 ... pn^kn / (k1! ... kn!)
On peut la simuler ainsi.
n <- 5 N <- 100 p <- c(.2,.5,.1,.1,.1) x <- factor(sample(1:n, N, replace=T, prob=p), levels=1:n) table(x)
Il vient :
x 1 2 3 4 5 19 47 13 7 14
Les lois continues les plus importantes sont les lois gaussienne, exponentielle et uniforme.
On peut la simuler à l'aide de la commande runif.
> round(runif(20), digits=4) [1] 0.6187 0.4653 0.0806 0.5425 0.4418 0.4485 0.4685 0.4461 0.9195 0.6127 [11] 0.9132 0.8607 0.1341 0.3795 0.8608 0.9100 0.1545 0.7401 0.2990 0.8714
On peut la voir comme un analogue continu de la loi de Poisson. C'est en fait le temps entre deux évènements d'un processus de Poisson (intuitivement : le temps entre deux évènements rares). Par exemple, le temps entre deux désintégrations radioactives.
curve(dexp(x), xlim=c(0,10), col='red', lwd=3,
main='Densité de la loi exponentielle')
n <- 1000
x <- rexp(n)
hist(x, probability=T,
col='light blue', main='Loi exponentielle')
lines(density(x), col='red', lwd=3)
curve(dexp(x), xlim=c(0,10), col='red', lwd=3, lty=2,
add=T)
Il s'agit de la fameuse << courbe en cloche >>.
Plus précisément, le théorème de la limite centrale affirme que si X1, X2, X3, etc. sont des vaiid d'espérance m et de variance s^2, alors
(X1+X2+...+Xn) - nm
---------------------
sqrt(n) sconverge en loi vers la loi normale standard quand n end vers l'infini.
Il revient au même de dire que la moyenne empirique
X1+...Xn
--------
nconverge en loi vers une loi normale de moyenne m et d'écart-type s/sqrt(n). Cela explique son omniprésence : quand on fait une expérience et qu'on la répète un nombre de fois suffisant, la moyenne des résultats suit à peu près une loi normale.
limite.centrale <- function (r=runif, m=.5, s=1/sqrt(12), n=c(1,3,10,30), N=1000) {
for (i in n) {
x <- matrix(r(i*N),nc=i)
x <- ( apply(x, 1, sum) - i*m )/(sqrt(i)*s)
hist(x, col='light blue', probability=T, main=paste("n =",i),
ylim=c(0,max(.4, density(x)$y)))
lines(density(x), col='red', lwd=3)
curve(dnorm(x), col='blue', lwd=3, lty=3, add=T)
if( N>100 ) {
rug(sample(x,100))
} else {
rug(x)
}
}
}
op <- par(mfrow=c(2,2))
limite.centrale()
par(op)
op <- par(mfrow=c(2,2)) limite.centrale(rexp, m=1, s=1) par(op)

op <- par(mfrow=c(2,2)) limite.centrale(rexp, m=1, s=1) par(op)

op <- par(mfrow=c(2,2))
limite.centrale(function (n) { rnorm(n, sample(c(-3,3),n,replace=T)) },
m=0, s=sqrt(10), n=c(1,2,3,10))
par(op)
Exercice : Tracer un graphique semblable au précédent mais avec les densités théoriques.
La loi normale standard (de moyenne 0 et de variance 1) a pour densité
f(x) = exp( -x^2/2 ) / sqrt( 2 pi )
Comme pour toutes les lois (continues) connues de R, on dispose de la densité,
curve(dnorm(x), xlim=c(-3,3), col='red', lwd=3) title(main='Densité de la loi normale')

de la primitive de la densité,
curve(pnorm(x), xlim=c(-3,3), col='red', lwd=3) title(main='Primitive de la densité de la loi normale')

de l'inverse de cette primitive (la fonction quantiles)
curve(qnorm(x), xlim=c(0,1), col='red', lwd=3) title(main='Fonction quantile de la loi normale')

et on peut faire des simulations.
n <- 1000
x <- rnorm(n)
hist(x, probability=T, col='light blue', main='Loi normale')
lines(density(x), col='red', lwd=3)
curve(dnorm(x), add=T, col='red', lty=2, lwd=3)
legend(par('usr')[2], par('usr')[4], xjust=1,
c('sample density', 'theoretical density'),
lwd=2, lty=c(1,2),
col='red')
On en déduit la loi normale de moyenne mu et de variance sigma^2 par une transformation affine :
f(x) = exp( -( (x-mu) / sigma )^2 /2 ) / sqrt( 2 pi sigma )
C'est la loi de X^2, si X est une va suivant une loi normale standard.
curve(dchisq(x,1), xlim=c(0,5), col='red', lwd=3) abline(h=0,lty=3) abline(v=0,lty=3) title(main="Loi du Chi2 à un degré de liberté")

C'est la loi de X1^2+...+Xn^2, où les Xi sont des vaiid normales standard.
On la rencontre en statisitique, quand on ne dispose pas de la variance de la population et qu'on utilise à la place la variance de l'échantillon.
curve(dchisq(x,1), xlim=c(0,10), ylim=c(0,.6), col='red', lwd=3)
curve(dchisq(x,2), add=T, col='green', lwd=3)
curve(dchisq(x,3), add=T, col='blue', lwd=3)
curve(dchisq(x,5), add=T, col='orange', lwd=3)
abline(h=0,lty=3)
abline(v=0,lty=3)
legend(par('usr')[2], par('usr')[4], xjust=1,
c('df=1', 'df=2', 'df=3', 'df=5'),
lwd=3,
lty=1,
col=c('red', 'green', 'blue', 'orange')
)
title(main='Lois du Chi^2')
Si X1, X2, X3,... sont des v.a.i.i.d. normales de moyenne mu et d'écart-type sigma, alors
X1 + X2 + ... + Xn
-------------------- - mu
n
-----------------------------
sigma
---------
sqrt(n)suit une loi normale. Mais si on rempace l'écart-type réel sigma par l'écart-type empirique, on obtient une quantité qui suit une loi T de Student à (n-1) degrés de liberté.
curve( dt(x,1), xlim=c(-3,3), ylim=c(0,.4), col='red', lwd=2 )
curve( dt(x,2), add=T, col='blue', lwd=2 )
curve( dt(x,5), add=T, col='green', lwd=2 )
curve( dt(x,10), add=T, col='orange', lwd=2 )
curve( dnorm(x), add=T, lwd=3, lty=3 )
title(main="Lois T de Student")
legend(par('usr')[2], par('usr')[4], xjust=1,
c('df=1', 'df=2', 'df=5', 'df=10', 'loi normale'),
lwd=c(2,2,2,2,2),
lty=c(1,1,1,1,3),
col=c('red', 'blue', 'green', 'orange', par("fg")))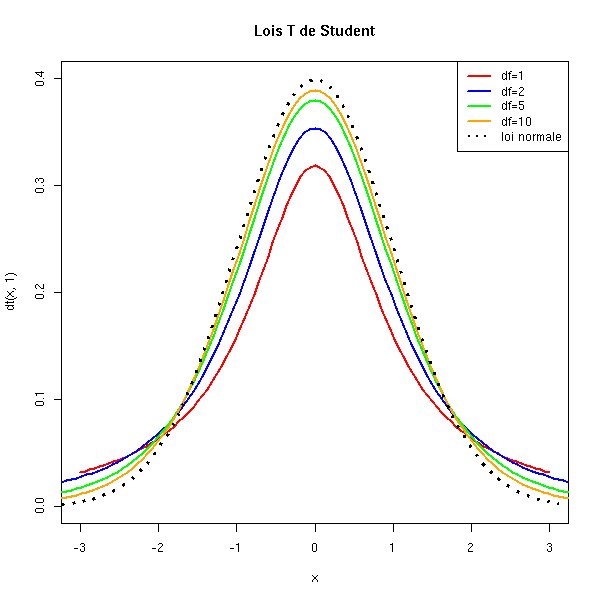
Si X1, X2, ... Xn et Y1, Y2,... Ym sont des vaiid normales standard, alors la variable
X1^2 + X2^2 + ... + Xn^2
--------------------------
n
----------------------------
Y1^2 + Y2^2 + ... + Ym^2
--------------------------
msuit une loi de F à n et m degrés de liberté. C'est donc la loi d'un quotient de variales du Chi^2, chacune divisée par son degré de liberté.
On la rencontre quand on compare des variances (en particulier dans l'anova).
curve(df(x,1,1), xlim=c(0,2), ylim=c(0,.8), lty=2)
curve(df(x,3,1), add=T)
curve(df(x,6,1), add=T, lwd=3)
curve(df(x,3,3), add=T, col='red')
curve(df(x,6,3), add=T, lwd=3, col='red')
curve(df(x,3,6), add=T, col='blue')
curve(df(x,6,6), add=T, lwd=3, col='blue')
title(main="Densité de la loi de Fisher")
legend(par('usr')[2], par('usr')[4], xjust=1,
c('df=(1,1)', 'df=(3,1)', 'df=(6,1)',
'df=(3,3)', 'df=(6,3)',
'df=(3,6)', 'df=(6,6)'),
lwd=c(1,1,3,1,3,1,3),
lty=c(2,1,1,1,1,1,1),
col=c(par("fg"), par("fg"), par("fg"), 'red', 'red', 'blue', 'blue'))
Souvent, les variables que l'on rencontre ont des valeurs positives, ce qui contredit l'hypothèse d'une loi normale. On regarde alors si le logarithme de la variable ne suit pas une loi normale, i.e., si la variable n'est pas l'exponentielle d'une variable normale.
curve(dlnorm(x), xlim=c(-.2,5), lwd=3,
main="Densité de la loi log-normale")
C'est un exemple de loi pathologique, très dispersée : sa variance est infinie.
curve(dcauchy(x),xlim=c(-5,5), ylim=c(0,.5), lwd=3)
curve(dnorm(x), add=T, col='red', lty=2)
legend(par('usr')[2], par('usr')[4], xjust=1,
c('Loi de Cauchy', 'Loi normale'),
lwd=c(3,1),
lty=c(1,2),
col=c(par("fg"), 'red'))
La loi de Cauchy fait partie de la famille des lois stables (comme la loi normale) : une somme de variables de Cauchy en est encore une.
La loi de Weibull est une généralisation de la loi exponentielle, dans laquelle le taux de décroissance n'est pas constant. Elle sert en particulier à modèliser le temps de fonctionnement sans panne d'un appareil (le "taux de décroissance", i.e., la probabilité d'apparition d'une panne, est d'autant plus grand que l'appareil est vieux).
Nous la rencontrerons dans l'analyse de la survie. Sa densité est de la forme exp(-a t^b).
curve(dexp(x), xlim=c(0,3), ylim=c(0,2))
curve(dweibull(x,1), lty=3, lwd=3, add=T)
curve(dweibull(x,2), col='red', add=T)
curve(dweibull(x,.8), col='blue', add=T)
title(main="Densité de la loi de Weibull")
legend(par('usr')[2], par('usr')[4], xjust=1,
c('Loi exponentielle', 'Loi de Weibull, shape=1',
'Loi de Weibull, shape=2', 'Loi de Weibull, shape=.8'),
lwd=c(1,3,1,1),
lty=c(1,3,1,1),
col=c(par("fg"), par("fg"), 'red', 'blue'))
C'est la distribution du logarithme d'une variable aléatoire de Weibull.
A FAIRE evd/doc/guide.pdf densité = exp(-x-exp(-x))
C'est la loi d'une somme de vaiid exponentielles. C'est donc une généralisation de la loi exponentielle, que l'on utilise aussi pour modéliser des durées de vie (exemple : une machine fiable qui devrait subir trois pannes consécutives pour ne plus fonctionner, le temps d'attente d'une panne suivant une loi exponentielle).
Les temps d'arrivée dans un processus de Poisson suivent des lois Gamma.
curve( dgamma(x,1,1), xlim=c(0,5) )
curve( dgamma(x,2,1), add=T, col='red' )
curve( dgamma(x,3,1), add=T, col='green' )
curve( dgamma(x,4,1), add=T, col='blue' )
curve( dgamma(x,5,1), add=T, col='orange' )
title(main="Densité de la loi gamma")
legend(par('usr')[2], par('usr')[4], xjust=1,
c('k=1 (loi exponentielle)', 'k=2', 'k=3', 'k=4', 'k=5'),
lwd=1, lty=1,
col=c(par('fg'), 'red', 'green', 'blue', 'orange') )
n <- 500
x1 <- rexp(n,17)
x2 <- rexp(n,17)
x3 <- rexp(n,17)
x <- x1 + x2 + x3
# Plus simple, mais moins lisible :
# k <- 3
# x <- drop(apply( matrix( rexp(n*k,17), nr=n, nc=k ), 1, sum))
y <- qgamma(ppoints(n),3,17)
plot( sort(x) ~ sort(y), log='xy' )
abline(0,1, col='red')
title("Comparaison d'une loi Gamma et d'une somme de vaiid exponentielles")
Voir aussi :
http://www.math.uah.edu/statold/special/special3.html
Voici la définition qu'on trouve généralement dans les livres (je la trouve peu éclairante, j'en donne des formes plus intuitives, plus compréhensibles, plus bas) : Si X et Y sont des variables aléatoires de loi Gamma de paramètres (a,r) et (b,r), alors X/(X+Y) suit une loi Béta de paramètres (a,b).
curve( dbeta(x,1,1), xlim=c(0,1), ylim=c(0,4) )
curve( dbeta(x,2,1), add=T, col='red' )
curve( dbeta(x,3,1), add=T, col='green' )
curve( dbeta(x,4,1), add=T, col='blue' )
curve( dbeta(x,2,2), add=T, lty=2, lwd=2, col='red' )
curve( dbeta(x,3,2), add=T, lty=2, lwd=2, col='green' )
curve( dbeta(x,4,2), add=T, lty=2, lwd=2, col='blue' )
curve( dbeta(x,2,3), add=T, lty=3, lwd=3, col='red' )
curve( dbeta(x,3,3), add=T, lty=3, lwd=3, col='green' )
curve( dbeta(x,4,3), add=T, lty=3, lwd=3, col='blue' )
title(main="Densité de la loi béta")
legend(par('usr')[1], par('usr')[4], xjust=0,
c('(1,1)', '(2,1)', '(3,1)', '(4,1)',
'(2,2)', '(3,2)', '(4,2)',
'(2,3)', '(3,3)', '(4,3)' ),
lwd=1, #c(1,1,1,1, 2,2,2, 3,3,3),
lty=c(1,1,1,1, 2,2,2, 3,3,3),
col=c(par('fg'), 'red', 'green', 'blue',
'red', 'green', 'blue',
'red', 'green', 'blue' ))
Si X1, X2, ..., Xn sont des vaiid uniformes dans [0,1], alors max(X1,X2,...,Xn) suit une loi Béta de paramètres (n,1).
N <- 500
n <- 5
y <- drop(apply( matrix( runif(n*N), nr=N, nc=n), 1, max ))
x <- qbeta(ppoints(N), n, 1)
plot( sort(y) ~ x )
abline(0,1, col='red')
title("Statistique d'ordre et loi béta")
Les autres statistiques d'ordre (le k-ième élément le plus grand de X1,...,Xn) suivent d'autres lois Béta.
N <- 500
n <- 5
k <- 3
y <- drop(apply( matrix( runif(n*N), nr=n, nc=N), 2, sort )[n-k,])
x <- qbeta(ppoints(N), n-k, k+1) # Exercice : d'où viennent ces coefficients ?
plot( sort(y) ~ x )
abline(0,1, col='red')
title("Statistique d'ordre et loi béta")
# Je reconnais avoir tout d'abord trouvé les coefficients en tatonnant :
op <- par(mfrow=c(5,5), mar=c(0,0,0,0) )
for (i in 1:5) {
for (j in 1:5) {
plot( sort(y) ~ qbeta(ppoints(N), j, i), xlab='', ylab='', axes=F )
abline(0,1, col='red')
box()
text( (par('usr')[1]+par('usr')[2])/2,
(par('usr')[3]+par('usr')[4])/2,
paste(j,i),
cex=3, col='blue' )
}
}
par(op)
Voir aussi :
http://www.math.uah.edu/statold/special/special9.html
Voici encore une autre motivation, bayesienne, de la loi béta.
A FAIRE : détailler un peu plus : le lecteur ne sait pas encore ce que sont les statistiques bayesiennes.
On tire à pile ou face et on cherche la probabilité d'observer "pile" (pour que ce soit non trivial, on peut utiliser une punaise au lieu d'une pièce). On ne sait rien a priori sur cette probabilité : sa distribution a priori est uniforme. On lance la punaise 10 fois et on constate 7 piles et 3 faces. La densité de la probabilité a posteriori est proportionnelle à
p^7 * (1-p)^3.
C'est une loi Béta(8,4).
curve(dbeta(x,8,4),xlim=c(0,1)) title(main="Distribution a posteriori")

Si on fait l'expérience en deux temps, on a au départ une distribution a priori uniforme, qui donne une distribution a posteriori béta, qui est utilisée comme distribution a priori de la deuxième partie de l'expérience. C'est pourquoi on utilise souvent la distribution béta comme distribution a priori dans un contexte bayesien.
De manière plus simple, plus intuitive, on utilise la famille des lois béta quand on veut une loi continue, dans l'intervalle [0,1], plus ou moins applatie, plus ou moins décalée.
A FAIRE : dessin
curve(dbeta(x,10,10), xlim=c(0,1), lwd=3)
curve(dbeta(x,1,1), add=T, col='red', lwd=3)
curve(dbeta(x,2,2), add=T, col='green', lwd=3)
curve(dbeta(x,5,2), add=T, col='blue',lwd=3)
curve(dbeta(x,.1,.5), add=T, col='orange')
legend(par('usr')[2], par('usr')[4], xjust=1,
c('B(10,10)', 'B(1,1)', 'B(2,2)', 'B(5,2)', 'B(.1,.5)'),
lwd=c(3,3,3,3,1), lty=1,
col=c(par('fg'),'red','green','blue','orange'))
title("Densité de quelques lois Béta")
Voici une autre présentation de cette motivation de la loi béta, qui n'utilise plus d'idées bayesiennes, mais simplement de la vraissemblance. La situation est la même : on lance une punaise et on regarde de quelle côté elle tombe. On note p la probabilité d'observer "pile". On a obtenu 7 piles et 3 faces. On peut voir 7 comme la valeur d'une variable binomiale de paramètres (10,p). La probabilité d'observer 7 fois pile et 3 fois face sachant p, est
L(p) = p^7 * (1-p)^3.
C'est ce qu'on appelle la vraissemblance. Comme précédemment, c'est proportionnel à la densité de la distribution béta.
On dit que la distribution binomiale et la distribution béta sont conjuguées : leur densité est donnée par la même formule en intervertissant le rôle des paramètres et de la variable.
La plupart des lois que l'on rencontre font partie de la famille des lois exponentielles, qui interviennent dans certains résultats théoriques -- je ne donne pas leur définition.
y theta - v(theta)
f(y, theta,phi) = exp ( -------------------- + w(y,phi) )
u(phi)
A FAIRE : expliquer ???
non.
Pour faire des tests, on peut regarder les densités de Marron--Wand, dans la bibliothèque nor1mix.
# Exemple du manuel
library(nor1mix)
ppos <- which("package:nor1mix" == search())
nms <- ls(pat="^MW.nm", pos = ppos)
nms <- nms[order(as.numeric(substring(nms,6)))]
op <- par(mfrow=c(4,4), mgp = c(1.2, 0.5, 0), tcl = -0.2,
mar = .1 + c(2,2,2,1), oma = c(0,0,3,0))
for(n in nms) { plot(get(n, pos = ppos)) }
mtext("The Marron-Wand Densities", outer = TRUE,
font = 2, cex = 1.6)
par(op)
Il n'y a pas de fonction prédéfinie pour avoir un échantillon normal multivarié avec une matrice de covariance. On peut en construire un de la manière suivante : on part de variables aléatoires normales standard indépendantes X1, X2, X3, etc. et on construit
Y1 = a*X1 Y2 = b*X1 + c*X2 Y3 = d*X1 + e*X2 + f*X3 etc.
Un calcul assez rapide montre
cov(Y) = t(A) %*% A
où
a 0 0 ...
A = b c 0
d e f
...Il suffit donc de décomposer la matrice de covariance souhaitée en un produit d'une matrice triangulaire par sa transposée : c'est la décomposition de Cholesky.
rmnorm <- function (R, C, mu=rep(0,dim(C)[1])) {
A <- t(chol(C))
n <- dim(C)[1]
t(mu + A %*% matrix(rnorm(R*n),nr=n))
}
C <- matrix(c(2,.5,.5,1),nr=2)
mu <- c(2,1)
y <- rmnorm(1000,C, mu)
cov(y)
plot(y)
abline(h=mu[2], lty=3, lwd=3, col='blue')
abline(v=mu[1], lty=3, lwd=3, col='blue')
e <- eigen(C)
r <- sqrt(e$values)
v <- e$vectors
N <- 100
theta <- seq(0,2*pi, length=N)
x <- mu[1] + r[1]*v[1,1]*cos(theta) +
r[2]*v[1,2]*sin(theta)
y <- mu[2] + r[1]*v[2,1]*cos(theta) +
r[2]*v[2,2]*sin(theta)
lines(x,y, lwd=3, col='blue')
Pour faire des calculs (et pas des simulations, comme nous venons de le faire), voir la bibliothèque mvtnorm.
library(help=mvtnorm)
"If things go wrong, how wrong can they go?"
Très souvent, pour étudier des données nombreuses, on commence par supposer qu'elles suivent une distribution normale. Pour vérifier que cette hypothèse est fondée, on regarde essentiellement la distribution des valeurs proches de la moyenne, en occultant les valeurs extrèmes.
L'approximation normale (avec éventuelle suppression des valeurs extrèmes) est suffisante si on s'intéresse au comportement "habituel" des données -- mais quand les valeurs extrèmes jouent un rôle central, cela devient problématique.
C'est par exemple le cas en gestion du risque : les catastrophes naturelles (pour les assureurs et les réassureurs) ou les crachs boursiers sont des évènements rares aux conséquences désastreuses -- on ne peut pas se permettre de mal évaluer leur probabilité.
Voici par exemple des données boursières (elles proviennent de Yahoo).
x <- read.table("SUNW.csv", header=T, sep=",")
x <- x$Close
x <- diff(log(x)) # Compute the returns
qqnorm(x, main="Normality of stock returns (15 years)")
qqline(x, col='red')
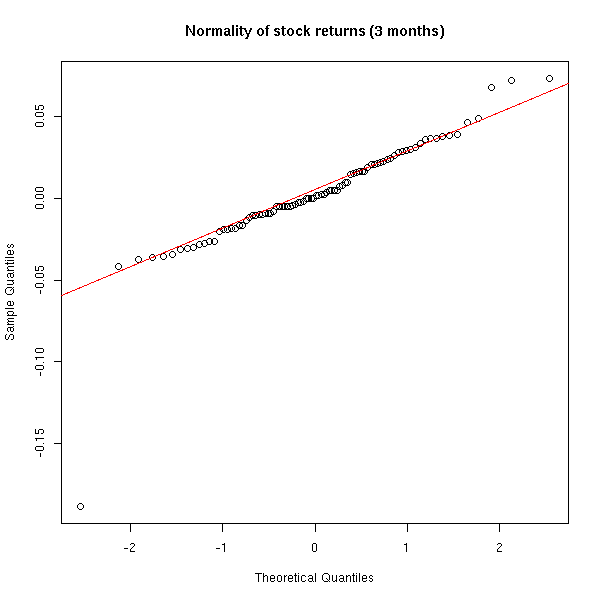
Pour s'appercevoir de la non normalité, il faut regarder ce qui se passe à long terme : à court terme l'approximation normale est justifiée.
qqnorm(x[1:90], main="Normality of stock returns (3 months)") qqline(x[1:90], col='red')
On peut comparer graphiquement la densité de la distribution observée et une densité normale.
plot(density(x), main="Stock returns density vs normal density") m <- mean(x) s <- sd(x) curve( dnorm(x, m, s), col='red', add=T)

Sur une échelle logarithmique, on voit mieux.
plot(density(x), log='y', main="Stock returns density vs normal density") curve( dnorm(x, m, s), col='red', add=T)

plot(density(x), log='y', ylim=c(1e-1,1.5e1), xlim=c(-.2,.2),
main="Stock returns density vs normal density (detail)")
curve( dnorm(x, m, s), col='red', add=T)
On constate que la distribution effectivement observée a une densité "plus pointue" que la distribution normale correspondante et qu'elle est beaucoup moins courbe (sur une échelle logarithmique) : on dirait presque deux segments de droites.
Moralité : dans les données réelles, les valeurs extrèmes sont souvent plus fréquentes que dans une distribution normale.
En gestion du risque on calcule trois quantités pour estimer le risque d'un évènement rare.
The Value at Risk (VaR) is the alpha-% quantile of the Profits & Losses (P&L) distribution, which is assumed normal.
For internal risk control purposes, most of the financial firms compute a 5% VaR over a one-day holding period. The Basle accord proposed that VaR for the next 10 days and p = 1%, based on a historical observation period of at least 1 year (220 days) of data, should be computed and then multiplied by the `safety factor' 3. The safety factor was introduced because the normal hypothesis for the profit and loss distribution is widely recognized as unrealistic.
The Expected Shortfall (ES), or tail conditionnal expectation, expectation of the P&L given that it exceeds the VaR.
ES(alpha) = E[ X | X > VaR(alpha) ]
One may consider a third quantity: the n-day k-th return level is the 1/k-quantile of Max(X1,...,Xn), i.e., in one case out of k, the maximum loss in an n-day period will exceed R(n,k).
Nous retrouverons ces quantités dans la thérie des valeurs extrèmes ; en effet, il ne s'agit pas d'une théorie mais de deux :
GEV: L'étude de la distribution de Max(X1,...,Xn) (pour n grand) GPD: L'étude de la distribution de X|X>a (pour a grand)
Nous avons vu que la loi béta donnait la distribution du maximum de X1, X2, ..., Xn quand les Xi sont des variables uniformes. Mais si les Xi sont des vaiid qui suivent une autre distribution, que peut-on dire ?
Et si les Xi suivent une distribution qu'on ne connait pas, peut-on dire quelque-chose ? Cette question ressemble à celle qui motive le théorème de la limite centrale, qui dit que la moyenne de X1,...,Xn, normalisée, suit une loi normale standard (sous quelques hypothèses peu restrictives sur la loi des Xi).
Eh bien justement, un tel théorème existe :
S'il existe une manière de "normaliser" Max(X1,...,Xn) de sorte que sa distribution converge vers une certaine loi, alors cette loi est l'une des suivantes.
Fréchet: exp( - x^-alpha ) Weibul: exp( - (-x)^-alpha ) Gumbel: exp( - e^-x )
La distribution GEV (Generalized Extreme Value) est une paramétrisation de ces trois lois, en une seule formule :
exp( -(1+ax)^(-1/a) ) if a != 0 exp( - e^-x )
Voici le graphe de ces distributions.
library(evd)
curve(dfrechet(x, shape=1), lwd=3, xlim=c(-1,2), ylim=c(0,1),
ylab="", main="density of the Frechet distribution")
for (s in seq(.1,2,by=.1)) {
curve(dfrechet(x, shape=s), add=T)
}
curve(dfrechet(x, shape=2), lwd=3, add=T, col='red')
curve(dfrechet(x, shape=.5), lwd=3, add=T, col='blue')
curve(drweibull(x, shape=1), lwd=3, xlim=c(-2,1), ylim=c(0,1),
ylab="", main="density of the (reverse) Weibull distribution")
for (s in seq(.1,2,by=.1)) {
curve(drweibull(x, shape=s), add=T)
}
curve(drweibull(x, shape=2), lwd=3, add=T, col='red')
curve(drweibull(x, shape=.5), lwd=3, add=T, col='blue')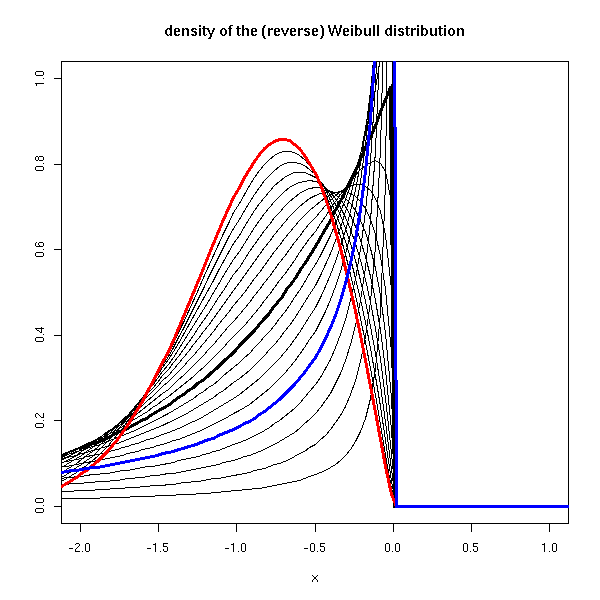
curve(dgumbel(x), lwd=3, xlim=c(-2,2), ylim=c(0,1),
ylab="", main="density of the Gumbel distribution")
curve(dgev(x, shape=0), lwd=3, xlim=c(-2,2), ylim=c(0,1),
ylab="", main="density of the GEV distribution")
for (s in seq(-2,2,by=.1)) {
curve(dgev(x, shape=s), add=T)
}
curve(dgev(x, shape=-1), lwd=3, add=T, col='red')
curve(dgev(x, shape=1), lwd=3, add=T, col='blue')
On s'intéresse maintenant à la distribution de X|X>a (i.e., "X sachant que X>a"), quand a devient grand.
A FAIRE : rédiger cdf de X, avec la partie X>a en couleurs
x <- read.table("SUNW.csv", header=T, sep=",")
x <- x$Close
x <- diff(log(x)) # Compute the returns
x <- sort(x)
n <- length(x)
m <- floor(.9*n)
y <- (1:n)/n
plot(x,y, type='l', main="empirical cdf of stock returns")
lines(x[m:n], y[m:n], col='red', lwd=3)
cdf de X-a|X>a, dans la même couleur
plot(x[m:n], y[m:n], col='red', lwd=3,
type='l', main="empirical conditionnal excess cdf of stock returns")
rescaled cdf of X-a|X>a
plot(x[m:n], (y[m:n] - y[m])/(1-y[m]) , col='red', lwd=3,
type='l', main="rescaled empirical conditionnal excess cdf of stock returns")
La distribution de Pareto généralisée (GPD) en est souvent une bonne approximation.
G(x) = 1 - (1 + a/b * x)^ -1/a si a !=0 G(x) = 1 - exp(-x/b) si a = 0
Voici sa densité
curve(dgpd(x, shape=0), lwd=3, xlim=c(-.1,2), ylim=c(0,2),
ylab="", main="density of the Generalized Pereto Distribution (GPD)")
for (s in seq(-2,2,by=.1)) {
curve(dgpd(x, shape=s), add=T)
}
curve(dgpd(x, shape=-1), lwd=3, add=T, col='red')
curve(dgpd(x, shape=1), lwd=3, add=T, col='blue')
(plus les valeurs extrèmes sont extrèmes, plus le paramètre "shape" est élevé -- pour notre exemple, nous nous attendrons à une valeur positive) et sa cdf
curve(pgpd(x, shape=0), lwd=3, xlim=c(-.1,2), ylim=c(0,1),
ylab="", main="cdf of the Generalized Pereto Distribution (GPD)")
for (s in seq(-2,2,by=.1)) {
curve(pgpd(x, shape=s), add=T)
}
curve(pgpd(x, shape=-1), lwd=3, add=T, col='red')
curve(pgpd(x, shape=1), lwd=3, add=T, col='blue')
Pour tenter de trouver la valeur de ce paramètre, on peut utiliser des graphiques quantiles-quantiles.
x <- read.table("SUNW.csv", header=T, sep=",")
x <- x$Close
x <- diff(log(x)) # Compute the returns
x <- sort(x)
n <- length(x)
m <- floor(.9*n)
y <- (1:n)/n
op <- par(mfrow=c(3,3), mar=c(2,2,2,2))
for (s in seq(0,2,length=9)) {
plot(qgpd(ppoints(n-m+1),shape=s), x[m:n],
xlab='', ylab='')
}
par(op)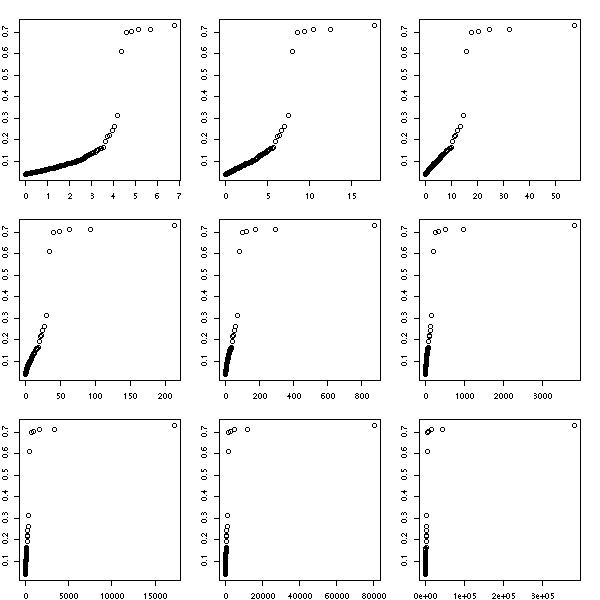
Ici, on ne voit pas grand-chose : on a l'impression qu'il y a une demi-douzaine de points qui ne suivent pas la même loi que les autres. On les voyait déjà dans le graphique quantiles-quantiles usuel.
qqnorm(x)

Il y a un léger problème : certes, c'est une bonne idée de chercher la distribution de X|X>a quand on s'intéresse aux valeurs extrèmes, mais comment choisir a ? En d'autres termes, où commence la queue d'une distribution ?
A FAIRE
Sample mean excess plot
(u, e(u))
où e(u) = moyenne des (x_i - u), pour les i tels que x_i > u
Ce qui pourrait s'écrire :
mean( (x-u)[x>u] )
x <- sort(x)
e <- rep(NA, length(x))
for (i in seq(along=x)) {
u <- x[i]
e[i] <- mean( (x-u)[x>u] )
}
plot(x, e, type='o', main="Sample mean excess plot")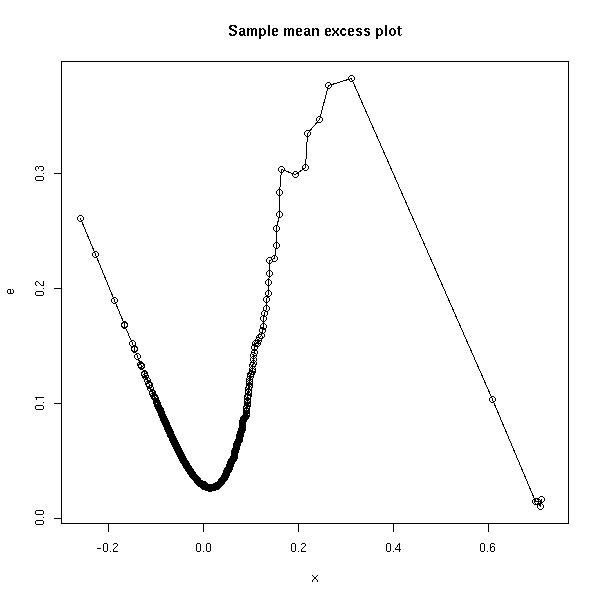
Ici, on retrouve notre pathologie de tout-à l'heure. On observe trois parties : la parie qui ne nous intéresse pas, la queue "régulière", qui nous intéresse, et les quelques observations atypiques. On choisit "a" au début de la queue régulière.
(En fait, je ne suis pas vraiment sûr de moi : il y a trop d'observations dans la "queue irrégulière" pour qu'on puisse simplement les oublier, mais trop peu (et elles sont trop regroupées) pour qu'on puisse réellement les utiliser.)
A FAIRE : comprendre...
Regardons d'autres exemples.
op <- par(mfrow=c(3,3))
for (f in c("SUNW", "ADBE", "ADPT",
"PCAR", "COST", "INTC",
"MSFT", "ADCT", "BMET")) {
x <- read.table(paste(f,".csv", sep=''), header=T, sep=",")
x <- x$Close
x <- diff(log(x)) # Compute the returns
x <- sort(x)
e <- rep(NA, length(x))
for (i in seq(along=x)) {
u <- x[i]
e[i] <- mean( (x-u)[x>u] )
}
plot(x, e, type='o', main="Sample mean excess plot")
}
par(op)
Regardons l'autre queue de ces exemples.
op <- par(mfrow=c(3,3))
for (f in c("SUNW", "ADBE", "ADPT",
"PCAR", "COST", "INTC",
"MSFT", "ADCT", "BMET")) {
x <- read.table(paste(f,".csv", sep=''), header=T, sep=",")
x <- x$Close
x <- -diff(log(x)) # Compute the returns
x <- sort(x)
e <- rep(NA, length(x))
for (i in seq(along=x)) {
u <- x[i]
e[i] <- mean( (x-u)[x>u] )
}
plot(x, e, type='o', main="Sample mean excess plot")
}
par(op)
A FAIRE : URL: evtrm.pdf An Application of Extreme Value Theory for Measuring Risk
A FAIRE
Les lois qu'on rencontre un peu plus rarement sont dans des paquetages séparés. Par exemple :
evd (extreme value distribution) gld (generalizes lambda distribution) SuppDists
Vincent Zoonekynd
<zoonek@math.jussieu.fr>
latest modification on Wed Oct 13 22:32:44 BST 2004