
The French version of this document is no longer maintained: be sure to check the more up-to-date English version.
Aggrégation autour des centres mobiles
Classification hiérarchique (dendogramme)
Comparaison de ces deux méthodes
Densité
A FAIRE : on réserve généralement le terme de classification à l'apprentissage supervisé (or je parle ici d'apprentissage non supervisé)...
Nous nous intéressons maintenant à la classification des observations en différents groupes. Par exemple, on a mesuré et pesé des animaux, et on aimerait savoir s'il y a une ou plusieurs espèces : les observations forment-elles un nuage de points bien homogène ? Ou bien y a-t-il des "grumeaux", le nuage est-il en fait la superposition de plusieurs nuages homogènes ?
On parle d'apprentissage non supervisé, quand on ne connait pas la répartition en classes (ni même, souvent, le nombre de classes). Quand on connait les classes et qu'on essaye de trouver des critères permettant de savoir à quelle classe rattacher une nouvelle observation, on parle d'apprentissage supervisé (c'est une forme de régression).
On choisit au hasard k points, les centres, et on répartit l'ensemble des données en k classes, en mettant un point dans la même classe que le centre dont il est le plus proche. On remplace chaque centre par le centre de gravité de sa classe. Et on itère.
Cette méthode présente plusieurs problèmes : le résultat dépend des premiers centre mobiles choisis (mais on peut recommencer avec d'autres centres et comparer -- ou carrément modifier l'algorithme avec des algorithmes génétiques) ; elle est mal adaptée aux données fortement bruitées ; elle préfère des classes de tailles comparables (en particulier, elle réagit mal aux observations atypiques) ; il faut choisir le nombre de classes a priori (contrairement à la classification hiérarchique).
La méthode des K-moyennes (k-means) est assez proche.
A FAIRE : expliquer la méthode des k-moyennes
the nonhierarchical k means or iterative relocation algorithm. Each
case is initially placed in one of k clusters, cases are then moved
between clusters if it minimises the differences between cases
within a cluster.
x <- rbind(matrix(rnorm(100, sd = 0.3), ncol = 2),
matrix(rnorm(100, mean = 1, sd = 0.3), ncol = 2))
cl <- kmeans(x, 2, 20)
plot(x, col = cl$cluster, pch=3, lwd=1)
points(cl$centers, col = 1:2, pch = 7, lwd=3)
segments( x[cl$cluster==1,][,1], x[cl$cluster==1,][,2],
cl$centers[1,1], cl$centers[1,2])
segments( x[cl$cluster==2,][,1], x[cl$cluster==2,][,2],
cl$centers[2,1], cl$centers[2,2],
col=2)
Voici ce que ça donne avec les notes de mes élèves.
# Ça n'est pas ça cl <- kmeans(notes, 6, 20) plot(notes, col = cl$cluster, pch=3, lwd=3) points(cl$centers, col = 1:6, pch=7, lwd=3)

Ce n'est pas du tout ce que l'on veut : il a fait le dessin dans le plan engendré par les deux premiers axes de coordonnées, au lieu de prendre le premier plan factoriel.
n <- 6
cl <- kmeans(notes, n, 20)
p <- princomp(notes)
u <- p$loadings
x <- (t(u) %*% t(notes))[1:2,]
x <- t(x)
plot(x, col=cl$cluster, pch=3, lwd=3)
c <- (t(u) %*% t(cl$center))[1:2,]
c <- t(c)
points(c, col = 1:n, pch=7, lwd=3)
for (i in 1:n) {
print(paste("Cluster", i))
for (j in (1:length(notes[,1]))[cl$cluster==i]) {
print(paste("Point", j))
segments( x[j,1], x[j,2], c[i,1], c[i,2], col=i )
}
}
text( x[,1], x[,2], attr(x, "dimnames")[[1]] )
En fait, la commande clusplot fait déjà des choses comparables. On lui donne le résultat d'une des commandes suivantes, qui sont des variantes de l'algorithme des k-moyennes.
pam partitionning around medoids (more robust) clara other partitionning, well-suited for large data sets daisy dissimilarity matrix: qualitative or quantative variables dist dissimilarity matrix: quantitative variables only fanny fuzzy clustering
Voici quelques exemples de résultats.
clusplot( notes, pam(notes, 6)$clustering )

clusplot( notes, pam(notes, 2)$clustering )

clusplot( daisy(notes), pam(notes,2)$clustering, diss=T )

clusplot( daisy(notes), pam(notes,6)$clustering, diss=T )

clusplot(fanny(notes,2))

clusplot(fanny(notes,10))

On répartit les points en n classes (un point par classe). On cherche les deux classes les plus proches (on prend par exemple la distance entre leurs centres de gravité -- mais on peut être un peu plus subtil) et on les aggrège. On se retrouve avec une classe de moins. On itère. On représente le résultat sous forme d'un dendogramme.
data(USArrests) hc <- hclust(dist(USArrests), "ave") plot(hc)

plot(hc, hang = -1)

Voici ce que ça donne avec les notes de mes élèves : j'essaye de représenter l'arbre sur le plan des deux premières composantes de l'ACP.
plot(hclust(dist(notes)))

p <- princomp(notes)
u <- p$loadings
x <- (t(u) %*% t(notes))[1:2,]
x <- t(x)
plot(x, col="red")
c <- hclust(dist(notes))$merge
y <- NULL
n <- NULL
for (i in (1:(length(notes[,1])-1))) {
print(paste("Step", i))
if( c[i,1]>0 ){
a <- y[ c[i,1], ]
a.n <- n[ c[i,1] ]
} else {
a <- x[ -c[i,1], ]
a.n <- 1
}
if( c[i,2]>0 ){
b <- y[ c[i,2], ]
b.n <- n[ c[i,2] ]
} else {
b <- x[ -c[i,2], ]
b.n <- 1
}
n <- append(n, a.n+b.n)
m <- ( a.n * a + b.n * b )/( a.n + b.n )
y <- rbind(y, m)
segments( m[1], m[2], a[1], a[2], col="red" )
segments( m[1], m[2], b[1], b[2], col="red" )
if( i> length(notes[,1])-1-6 ){
op=par(ps=30)
text( m[1], m[2], paste(length(notes[,1])-i), col="red" )
par(op)
}
}
text( x[,1], x[,2], attr(x, "dimnames")[[1]] )
Moralité : il vaut mieux utiliser soit la représentation en forme d'arbre, soit ne représenter qu'un nombre fixé de branches de l'arbre (juste des leux premières, ou les trois premières, etc. -- comme nous n'avons fait plus haut).
Voir aussi la bibliothèque mclust (model-based cluster analysis) qui, si j'ai bien compris, essaye de voir les données comme un mélange (mixture, en anglais) de données gaussiennes.
library(help=mclust)
Pour faire une classification hiérarchique, il faut choisir une notion de distance entre les points et une notion de distance entre les amas.
On a parfois plusieurs choix raisonnables de distance entre les points : par exemple, pour faire une analyse hiérarchique sur des séquences de protéines, on peut (après les avoir alignées) compter le nombre de différences. On peut aussi compter les différences en les pondérant : si les propriétés physico-chimiques des acides aminés sont proches, la différence sera peu importante, si elles sont radicalement différentes, la distance sera plus grande. (Pour faire d'autres analyses, on dispose aussi d'une autre notion de distances, qui n'est disponible qu'après la classification hiérarchique : il s'agit de mesurer la distance entre les séquences le long du dendogramme.)
A FAIRE : un exemple d'alignement...
A FAIRE : d'autres exemples de distances
Cosinus : produit scalaire de deux vecteurs (unitaires), i.e., coef de corrélation
C'est une mesire de similarité
Count data:
Chi2 : Chi2 correspondant au test d'égalité des effectifs
Phi2 : ??? This measure is equal to the chi-square measure
normalized by the square root of the combined frequency.
Données binaires : il y a plusieurs dizaines de notions de distance
ou de similarité...
La notion de distance entre les amas est plus délicate. Voici quelques exemples de telles distances.
d(A,B) = Max { d(a,b) ; a \in A et b \in B }
d(A,B) = Min { d(a,b) ; a \in A et b \in B }
d(A,B) = d(centre de gravité de A, centre de gravité de B) (non utilisé ?)
d(A,B) = moyenne des d(a,b) où a \in A et b \in B (UPGMA: Unweighted Pair-Groups Method Average)A FAIRE : dessins illustrant ces différentes notions.
A FAIRE : en fait, on utilise ces méthodes pour aggréger deux observations en une seule : le fait que ces observations proviennent de l'aggrégation d'autres observations est complètement occulté -- ce qui fait que les distances ne sont pas vraiment celles ci-dessus...
A FAIRE : Ward's method
Ward's method Cluster membership is assessed by calculating the total sum of squared deviations from the mean of a cluster. The criterion for fusion is that it should produce the smallest possible increase in the error sum of squares.
A FAIRE : dire que les les mêmes données peuvent produire des dendogrammes complètement différents.
A FAIRE Détection d'observations atypiques (elles feront un amas très isolé du reste) Classification quand on ne connait pas le nombre de classes
La méthode des centres mobiles est très rapide, et bien adaptée aux données volumineuses, mais non déterministe, tout le contraire de la classification hiérarchique. C'est pourquoi on utilise souvent un algorithme mixte (hybrid clustering) : on commence par utiliser la méthode des centres mobiles pour obtenir quelques dizaines ou centaines de classes, on utilise ensuite la classification hiérarchique pour regrouper ces classes et choisir le nombre de classes. Finalement, on rafine (on applique à nouveau la méthode des centres mobiles, avec les classes que l'on vient d'obtenir).
Exercice : faire ça, en s'inspirant de l'exemple suivant (tiré du manuel).
## Do the same with centroid clustering and squared Euclidean distance,
## cut the tree into ten clusters and reconstruct the upper part of the
## tree from the cluster centers.
hc <- hclust(dist(USArrests)^2, "cen")
memb <- cutree(hc, k = 10)
cent <- NULL
for(k in 1:10){
cent <- rbind(cent, colMeans(USArrests[memb == k, , drop = FALSE]))
}
hc1 <- hclust(dist(cent)^2, method = "cen", members = table(memb))
opar <- par(mfrow = c(1, 2))
plot(hc, labels = FALSE, hang = -1, main = "Original Tree")
plot(hc1, labels = FALSE, hang = -1, main = "Re-start from 10 clusters")

Les méthodes précédentes supposaient que les amas étaient sphériques, en particulier convexes. Mais ce n'est pas toujours le cas...
Dans l'exemple suivant, on aimerait que l'ordinateur nous dise que les points sont répartis en deux amas.
n <- 1000 x <- runif(n,-1,1) y <- ifelse(runif(n)>.5,-.1,.1) + .02*rnorm(n) d <- data.frame(x=x, y=y) plot(d,type='p', xlim=c(-1,1), ylim=c(-1,1))

Avec les K-moyennes :
test.kmeans <- function (d, ...) {
cl <- kmeans(d,2)
plot(d, col=cl$cluster, main="kmeans", ...)
points(cl$centers, col=1:2, pch=7, lwd=3)
}
test.kmeans(d, xlim=c(-1,1), ylim=c(-1,1))
Avec la classification hiérarchique :
test.hclust <- function (d, ...) {
hc <- hclust(dist(d))
remplir <- function (m, i, res=NULL) {
if(i<0) {
return( c(res, -i) )
} else {
return( c(res, remplir(m, m[i,1], NULL), remplir(m, m[i,2], NULL) ) )
}
}
a <- remplir(hc$merge, hc$merge[n-1,1])
b <- remplir(hc$merge, hc$merge[n-1,2])
co <- rep(1,n)
co[b] <- 2
plot(d, col=co, main="hclust", ...)
}
test.hclust(d, xlim=c(-1,1), ylim=c(-1,1))
On peut imaginer d'autres pathologies, avec des amas non connexes.
get.sample <- function (n=1000, p=.7) {
x1 <- rnorm(n)
y1 <- rnorm(n)
r2 <- 7+rnorm(n)
t2 <- runif(n,0,2*pi)
x2 <- r2*cos(t2)
y2 <- r2*sin(t2)
r <- runif(n)>p
x <- ifelse(r,x1,x2)
y <- ifelse(r,y1,y2)
d <- data.frame(x=x, y=y)
d
}
d <- get.sample()
plot(d,type='p', xlim=c(-10,10), ylim=c(-10,10))
test.kmeans(d, xlim=c(-10,10), ylim=c(-10,10))

test.hclust(d, xlim=c(-10,10), ylim=c(-10,10))

y <- abs(y) d <- data.frame(x=x, y=y) plot(d,type='p', xlim=c(-10,10), ylim=c(0,10))

test.kmeans(d)

test.hclust(d)

On peut penser à ajouter des variables (c'est la même idée que pour la régression polynomiale).
d <- get.sample() x <- d$x; y <- d$y d <- data.frame(x=x, y=y, xx=x*x, yy=y*y, xy=x*y) test.kmeans(d)
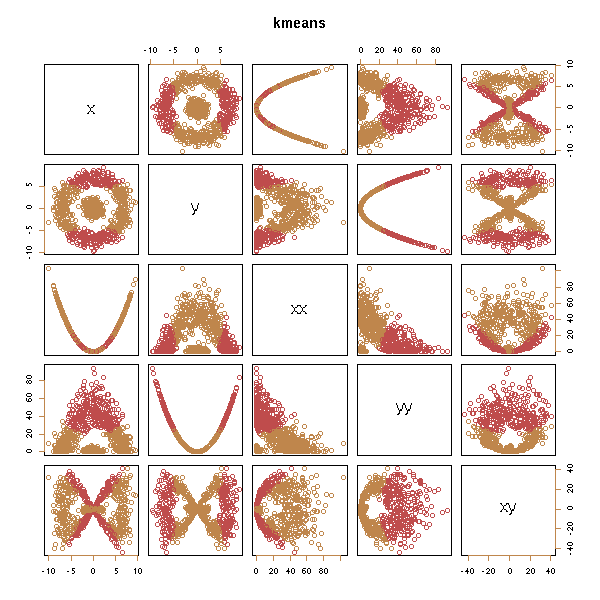
test.hclust(d)

Ca ne marche pas, sauf si on ajoute les "bonnes" variables...
d <- data.frame(x=x, y=y, xx=x*x, yy=y*y, xy=x*y, xpy=x*x+y*y) test.kmeans(d)

test.hclust(d)

Dans ce genre de situation, si on n'a que deux dimensions, on peut penser estimer la densité de probabilité correspondante et espérer y voir deux pics.
help.search("density")
# Suggests:
# KernSur(GenKern) Bivariate kernel density estimation
# bkde2D(KernSmooth) Compute a 2D Binned Kernel Density Estimate
# kde2d(MASS) Two-Dimensional Kernel Density Estimation
# density(mclust) Kernel Density Estimation
# sm.density(sm) Nonparametric density estimation in 1, 2 or 3 dimensions.
library(KernSmooth)
r <- bkde2D(d, bandwidth=c(.5,.5))
persp(r$fhat)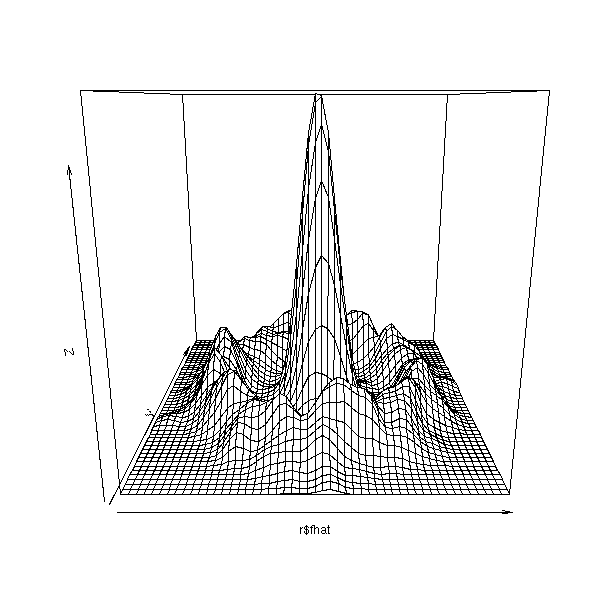
n <- length(r$x1)
plot( matrix(r$x1, nr=n, nc=n, byrow=F),
matrix(r$x2, nr=n, nc=n, byrow=T),
col=r$fhat>.001 )
(On laisse au lecteur le soin de compléter cet exemple, en expliquant à l'ordinateur comment trouver les composantes connexes du graphique précédent et comment les utiliser à des fins prédictives).
On peut utiliser la même idée de manière plus algorithmique ainsi : Pour chaque observation, on regarde combien il y a d'observations à une distance inférieure à 0.1 (on peut chager cette valeur) ; s'il y en a plus de 5 (on peut aussi changer cette valeur), on dit qu'elle est dense, i.e., à l'intérieur d'un amas. On définit une relation d'équivalence sur les observations denses en décrétant que deux observations sont dans le même amas dès que leur distance est inférieure à 0.1.
http://www.genopole-lille.fr/fr/formation/cib/doc/datamining/DM-Bio.pps (page 66)
On peut l'implémenter ainsi
density.classification.plot <- function (x,y,d.lim=.5,n.lim=5) {
n <- length(x)
# Calcul des distances
a <- matrix(x, nr=n, nc=n, byrow=F) - matrix(x, nr=n, nc=n, byrow=T)
b <- matrix(y, nr=n, nc=n, byrow=F) - matrix(y, nr=n, nc=n, byrow=T)
a <- a*a + b*b
# On regarde si chaque observation est dans un amas
b <- apply(a<d.lim, 1, sum)>=n.lim
plot(x, y, col=b)
points(x,y,pch='.')
}
density.classification.plot(d$x,d$y)
Il reste à reconnaitre les différents amas :
# Attention : le code qui suit est très récursif -- or, oar défaut,
# R limite la pile des appels de fonctions à 500 éléments. On
# commence donc par augmenter cette valeur.
options(expressions=10000)
density.classification.plot <- function (x,y,d.lim=.5,n.lim=5) {
n <- length(x)
# Calcul des distances
a <- matrix(x, nr=n, nc=n, byrow=F) - matrix(x, nr=n, nc=n, byrow=T)
b <- matrix(y, nr=n, nc=n, byrow=F) - matrix(y, nr=n, nc=n, byrow=T)
a <- a*a + b*b
# On regarde si chaque observation est dans un amas
b <- apply(a<d.lim, 1, sum)>=n.lim
# On classe les observations
cl <- rep(0,n)
m <- 1
numerote <- function (i,co,cl) {
print(paste(co, i))
for (j in (1:n)[ a[i,]<d.lim & b & cl==0 ]) {
#print(paste(" ",j))
cl[j] <- co
try( cl <- numerote(j,co,cl) ) # Trop récursif...
}
cl
}
for (i in 1:n) {
if (b[i]) { # Est-on dans un amas ?
# Numéro de l'amas
if (cl[i] == 0) {
co <- m
cl[i] <- co
m <- m+1
} else {
co <- cl[i]
}
# On numérote les points proches
#print(co)
cl <- numerote(i,co,cl)
}
}
plot(x, y, col=cl)
points(x,y,pch='.')
}
density.classification.plot(d$x,d$y)
Réessayons, de manière itérative :
density.classification.plot <- function (x,y,d.lim=.5,n.lim=5, ...) {
n <- length(x)
# Calcul des distances
a <- matrix(x, nr=n, nc=n, byrow=F) - matrix(x, nr=n, nc=n, byrow=T)
b <- matrix(y, nr=n, nc=n, byrow=F) - matrix(y, nr=n, nc=n, byrow=T)
a <- a*a + b*b
# On regarde si chaque observation est dans un amas
b <- apply(a<d.lim, 1, sum)>=n.lim
# On classe les observations
cl <- rep(0,n)
m <- 0
for (i in 1:n) {
if (b[i]) { # Est-on dans un amas ?
# Numéro de l'amas
if (cl[i] == 0) {
m <- m+1
co <- m
cl[i] <- co
print(paste("Processing cluster", co))
done <- F
while (!done) {
done <- T
for (j in (1:n)[cl==co]) {
l <- (1:n)[ a[j,]<d.lim & b & cl==0 ]
if( length(l)>0 ) {
done <- F
for (k in l) {
cl[k] <- co
#print(k)
}
}
}
}
} else {
# Amas déjà traité : on ne fait rien
}
}
}
plot(x, y, col=cl, ...)
points(x,y,pch='.')
}
density.classification.plot(d$x,d$y)
Jouons un peu sur les paramètres :
op <- par(mfrow=c(3,3))
for (d.lim in c(.2,1,2)) {
for (n.lim in c(3,5,10)) {
density.classification.plot(d$x,d$y,d.lim,n.lim,
main=paste("d.lim = ",d.lim, ", n.lim = ",n.lim, sep=''))
}
}
par(op)
Vincent Zoonekynd
<zoonek@math.jussieu.fr>
latest modification on Wed Oct 13 22:32:42 BST 2004