The French version of this document is no longer maintained: be sure to check the more up-to-date English version.
Analyse en composantes principales (ACP)
PCO (Principal COordinate Analysis), MDS (Multidimensionnal Scaling)
SOM (Self-Organizing Maps)
Analyse des correspondances simples
Analyse des correspondances multiples
A FAIRE : A CLASSER
Analyse discriminante
A FAIRE : classer
Il y a deux types de méthodes en statistique multidimensionnelle : les méthodes factorielles, qui consistent à projeter le nuage de points sur un sous-espace, en perdant le moins d'information possible ; les méthodes de classification, qui tentent de regrouper les points.
Les méthodes factorielles regroupent trois techniques fondamentales : l'analyse en composantes principales (plusieurs variables quantitatives), l'analyse des correspondances (deux variables qualitatives, représentées par un tableau de contingences) et l'analyse des correspondances multiples (plus de deux variables qualitatives).
Le tableau suivant regroupe ces différentes méthodes :
Méthode Variables quantitatives Variables qualitatives ---------------------------------------------------------- ACP plusieurs aucune MDS plusieurs aucune AC aucune deux ACM aucune plusieurs
Les méthodes suivantes ne sont pas symétriques : elles privilégient l'une des variables (généralement, celle qu'on essaye de prédire ou d'expliquer à partir des autres)
Méthode V. quantitatives V. qualitatives Variable à prédire ---------------------------------------------------------------------------------- régression plusieurs plusieurs quantitative anova aucune une quantitative régression logistique plusieurs plusieurs binaire régression de Poisson plusieurs plusieurs comptage régression logistique plusieurs plusieurs qualitative ordonnée Analyse Discriminante plusieurs une CART plusieurs plusieurs binaire ...
Voici une première manière de voir l'ACP. On dispose d'un nuage de points, dans un espace de dimension élevée, dans le quel on ne voit pas grand-chose. L'ACP va nous donner un sous-espace de dimension raisonnable, tel que la projection sur ce sous-espace retienne le plus d'information possible, i.e., tel que le nuage de points projecté soit le plus dispersé possible. Cela permet de réduire la dimension du nuage de points.
L'algorithme est le suivant. On commence par translater les données pour que le point moyen du nuage de points soit à l'origine (afin de pouvoir utiliser de l'algèbre linéaire). Ensuite, on essaye d'effectuer une rotation pour que l'écart-type de la première coordonnée soit le plus grand possible : cela revient à diagonaliser la matrice des covariances (c'est une matrice symétrique réelle (elle est même positive), elle est donc diagonalisable dans une base orthonormale), en commençant par les vecteurs propres les plus grands Le premier axe des nouvelles coordonnées correspond à une approximation du nuage de point par un sous-espace de dimension un ; si on veut une approximation par un sous-espace de dimension k, on prend les k premiers vecteurs propres.
Pour choisir la dimension de ce sous-espace, on regarde (graphiquement) les valeurs propres, et on s'arrête quand elles se mettent à décroitre rapidement (si elles décroissent très lentement, on est mal).
Une autre manière de voir l'ACP, c'est comme un analogue de la méthode des moindres carrés (voir ailleurs dans ce document) pour trouver une droite qui passe « au plus proche » d'un nuage de points. Mais alors que la méthode des moindres carrés est asymétrique (les deux dimensions jouent des rôles complètement différents, et elles ne sont donc pas interchangeables), l'ACP est symétrique.
Voici encore une autre manière de voir l'ACP. On modélise les données sous la forme X = Y + E, où X représente les données dont on dispose (dans un espace de dimension n), Y est une variable aléatoire à valeur dans sous-espace de dimension k, et E est un terme d'erreur ou de bruit, une variable aléatoire (d'espérance nulle) à valeurs dans l'espace de dimension n. Le but du jeu est de retrouver l'espace de dimension k dans lequel vit Y.
On peut aussi voir l'ACP comme un jeu sur un tableau de nombres (en fait, c'est très pertinent : on obtient presque aussitôt l'analyse des correspondances et des correspondances multiples). Ainsi, on peut faire jouer le même rôle aux lignes et aux colonnes : d'un côté, on cherche les similitudes ou les différences entre les individus, de l'autre, les similitudes ou les différences entre les variables. (On a donc deux matrices a diagonaliser, mais il suffit d'en diagonaliser une : elles ont les mêmes valeurs-propres non nulles et les vecteurs propres de l'une ce déduisent de ceux de l'autre.) On s'arrange pour que les variables soient centrées (et souvent aussi normées). On peut représenter les points correspondant aux variables dans l'espace des individus : ils sont sur la sphère de rayon unité. Leur projection forme le « cercle des corrélations ». On peut représenter les points-variables au milieu des points-individus : ces premiers sont alors les projections sur le plan des axes de coordonnées.
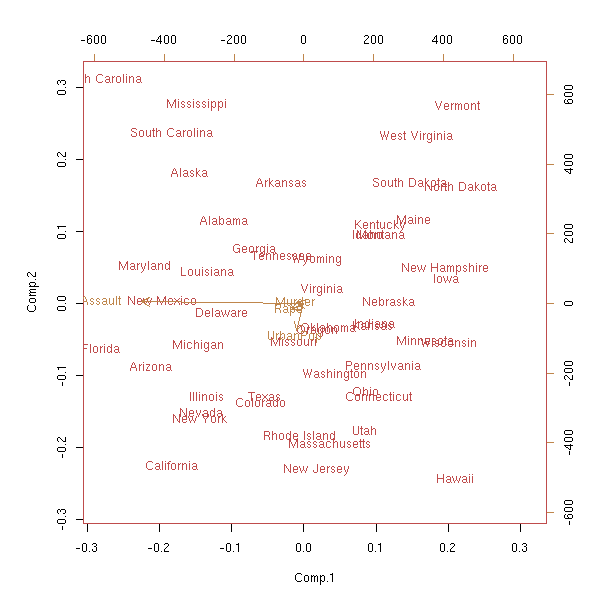
Après avoir effectué l'ACP, on peut ajouter des individus sur le dessin (groupe témoin, ou individus fictifs « représentatifs » de certaines classes d'individus). Dualement, on peut aussi ajouter des variables (généralement à des fins explicatives). Si ces variables sont qualitatives (on dit parfois « nominales »), on rajoute en fait un « individu moyen » pour chacune des valeur de cette variable. (Les anglophones appellent ça un « biplot » car on représente sur un même graphique les individus (en noir) et les variables (en rouge).)
#library(help=mva) library(mva) data(USArrests) p <- princomp(USArrests) biplot(p)

A FAIRE : trouver une situation dans laquelle on ait réellement envie d'ajouter des variables et/ou des individus. n <- 100 # Nombre d'individus nn <- 10 # Nombre d'individus supplémentaires k <- 5 # Nombre de variables initiales kk <- 3 # Nombre de variables supplémentaires x <- matrix(rnorm(n*k), nr=n, nc=k) x <- t(rnorm(k) + t(x)) # Données de départ y <- matrix(rnorm(n*kk), nr=n, nc=kk) # Variables supplémentaires z <- matrix(rnorm(nn*k), nr=nn, nc=k) # Individus supplémentaires r <- princomp(x) # Je vérifie que je ne me suis pas trompé dans mes # formules de changement de base all(abs( t(r$center + t(x %*% r$loadings)) - r$scores )<1e-8) # Coordonnées des individus de départ t(r$center + t(x %*% r$loadings)) # Coordonnées des nouveaux individus t(r$center + t(z %*% r$loadings)) # Pour chaque variable supplémentaire, on construit un individu "moyen" # (plus précisément : x %*% t(yy[1,]) = projection orthogonale de # y[,1] sur le sous-espace engendré par les colonnes de x). yy <- t(lm(y~x-1)$coef) t(r$center + t(yy %*% r$loadings))
Voici les valeurs propres. On constate qu'il y a une chute brutale : cela signifie que l'analyse en composantes principales est pertinente et qu'on peut se limiter aux vecteurs propres dont les valeurs propres sont élevées (ici : le premier, on aurait donc même pu faire un dessin en dimension 1).
plot(p)
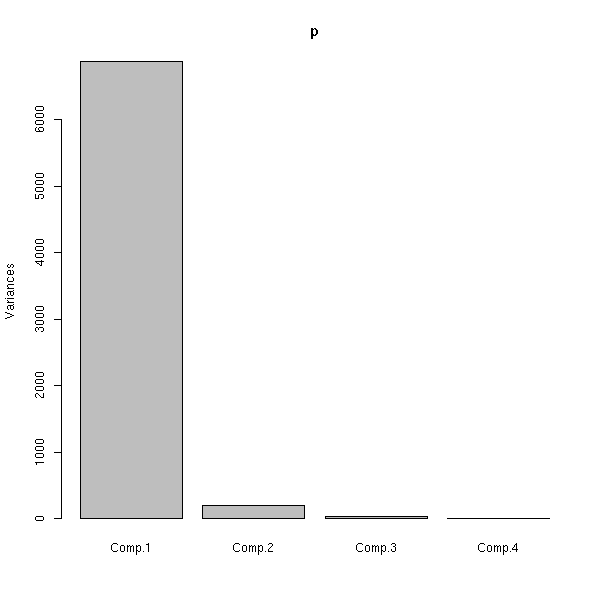
(Il existe aussi une commande prcomp, qui fait à peu près la même chose.)
Dans la figure précédente, les anciens vecteurs de base ont été représentés en rouge. On les représente parfois sur un dessin isolé, dans un cercle, le cercle des corrélations (comme on a préalablement normé les variables, ce sont ces vecteurs unitaires, ils sont donc sur la sphère de rayon 1 : le cercle des corrélations est la projection de cette sphère).
a <- seq(0,2*pi,length=100)
plot( cos(a), sin(a), type='l', lty=3,
xlab='comp 1', ylab='comp 2', main="Cercle des corrélations" )
v <- t(p$loadings)[1:2,]
arrows(0,0, v[1,], v[2,], col='red')
text(v[1,], v[2,],colnames(v))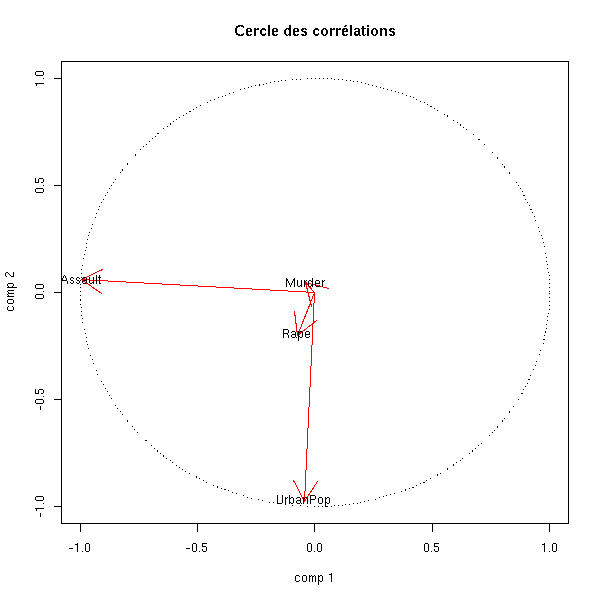
Voici maintenant un exemple où l'analyse en composantes principales n'est pas pertinente (les notes de mes élèves).
# Copy-pasted with the help of the "deparse" command:
# cat( deparse(x), file='foobar')
notes <- matrix( c(15, NA, 7, 15, 11, 7, 7, 8, 11, 11, 13, 6, 14, 19, 9,
8, 6, NA, 7, 14, 11, 13, 16, 10, 18, 7, 7, NA, 11, NA, NA, 6,
15, 5, 11, 7, 3, NA, 3, 1, 10, 1, 1, 18, 13, 2, 2, 0, 7, 9, 13,
NA, 19, 0, 17, 8, 2, 9, 2, 5, 12, 0, 8, 12, 8, 4, 8, 0, 5, 5.5,
1, 12, 4, 13, 5, 11, 6, 0, 7, 8, 11, 9, 9, 9, 14, 8, 5, 8, 5, 5,
12, 6, 16.5, 13.5, 15, 3, 10.5, 1.5, 10.5, 9, 15, 7.5, 12, 13.5,
4.5, 13.5, 13.5, 6, 12, 7.5, 9, 6, 13.5, 13.5, 15, 13.5, 6, NA,
13.5, 4.5, 14, NA, 14, 14, 14, 8, 16, NA, 6, 6, 12, NA, 7, 15,
13, 17, 18, 5, 14, 17, 17, 13, NA, NA, 16, 14, 18, 13, 17, 17,
8, 4, 16, 16, 16, 10, 15, 8, 10, 13, 12, 14, 8, 19, 7, 7, 9, 8,
15, 16, 8, 7, 12, 5, 11, 17, 13, 13, 7, 12, 15, 8, 17, 16, 16,
6, 7, 11, 15, 15, 19, 12, 15, 16, 13, 19, 14, 4, 13, 13, 19, 11,
15, 7, 20, 16, 10, 12, 16, 14, 0, 0, 11, 9, 4, 10, 0, 0, 5, 11,
12, 7, 12, 17, NA, 6, 6, 9, 7, 0, 7, NA, 15, 3, 20, 11, 10, 13,
0, 0, 6, 1, 5, 6, 5, 4, 2, 0, 8, 9, NA, 0, 11, 11, 0, 7, 0, NA,
NA, 7, 0, NA, NA, 6, 9, 6, 4, 5, 4, 3 ),
nrow=30)
notes <- data.frame(notes)
# Ce ne sont pas les vrais noms
row.names(notes) <- c("Anouilh", "Balzac", "Camus", "Dostoievski",
"Eschyle", "Fénelon", "Giraudoux", "Homère",
"Ionesco", "Jarry", "Kant", "La Fontaine",
"Marivaux", "Nerval", "Ossian", "Platon",
"Quevedo", "Racine", "Shakespeare", "Térence",
"Updike", "Voltaire", "Whitman", "X", "Yourcenar",
"Zola", "27", "28", "29", "30")
attr(notes, "names") <- c("C1", "DM1", "C2", "DS1", "DM2", "C3", "DM3",
"DM4", "DS2")
notes <- as.matrix(notes)
notes <- t(t(notes) - apply(notes, 2, mean, na.rm=T))
# Get rid of NAs
notes[ is.na(notes) ] <- 0
# plots
plot(princomp(notes))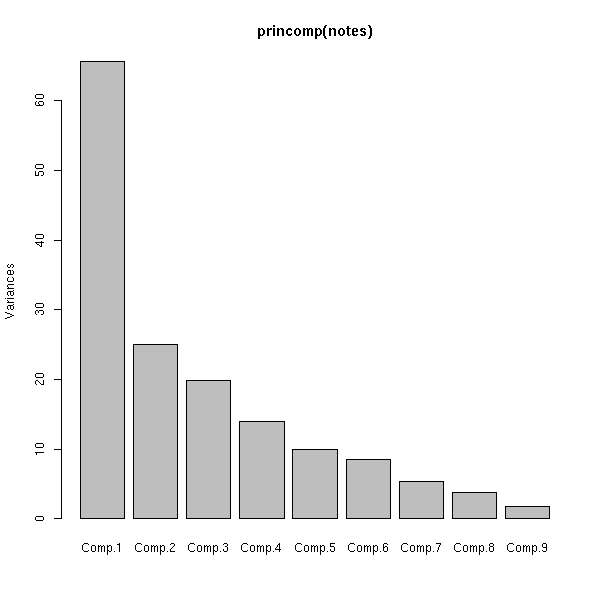
biplot(princomp(notes))
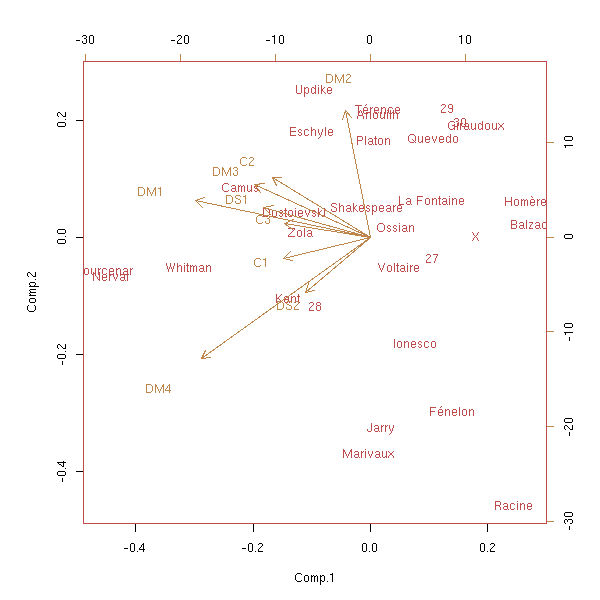
Nous avons ici donné la même importance à chaque note et à chaque individu. On aurait pu donner plus d'importance à certaines (les notes des devoirs en classe) (au lieu de prendre les notes de chaque devoir dans une matière donnée, on peut prendre les moyennes dans chaque matière, et les affecter des coefficients du bac) : c'est le même algorithme, il suffit de munir l'espace d'une métrique reflétant ces différences d'importance.
On a vu que la commande biplot ne donnait que les deux premières dimensions de l'ACP : on peut (parfois) en voir un peu plus à l'aide de la commande pairs.
pairs(princomp(notes)$scores)
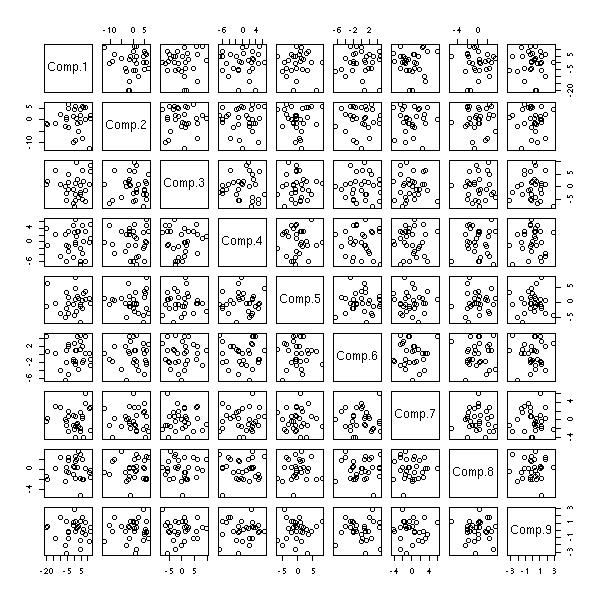
pairs(princomp(notes)$scores[,1:3])
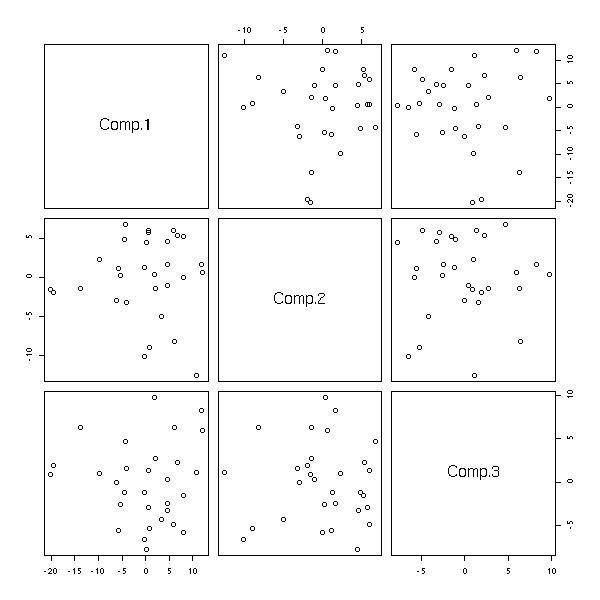
p <- princomp(notes)
pairs( rbind(p$scores, p$loadings)[,1:3],
col=c(rep(1,p$n.obs),rep(2, length(p$center))),
pch=c(rep(1,p$n.obs),rep(3, length(p$center))),
)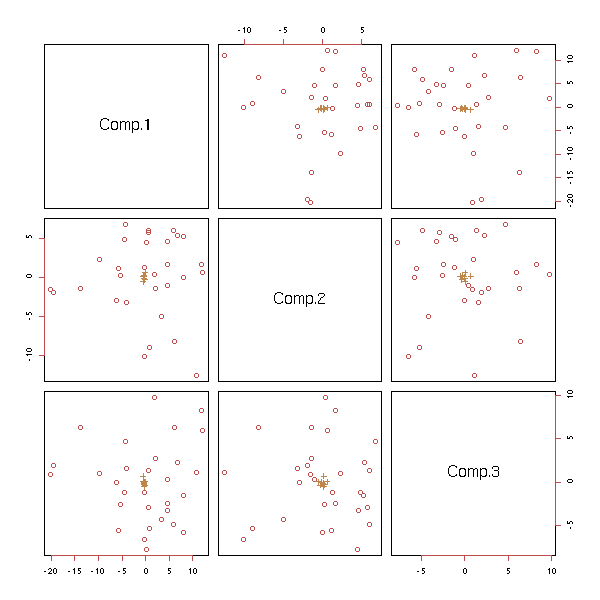
Nous laissons au lecteur le soin de mettre des flèches rouges (à la place des points rouges) pour les vecteurs de la base initiale -- je trouve que la fonction pairs est très peu configurable : les différents panneaux attendent comme arguments des coordonnées de points à tracer, alors que l'on pourrait vouloir tracer, dans une même case, des choses très différentes -- or on ne dispose même pas du numéro de la ligne et de la colonne. La fonction correspondante de la bibliothèque lattice ne me semble guère plus configurable.
library(lattice) splom(princomp(notes)$scores[,1:3])
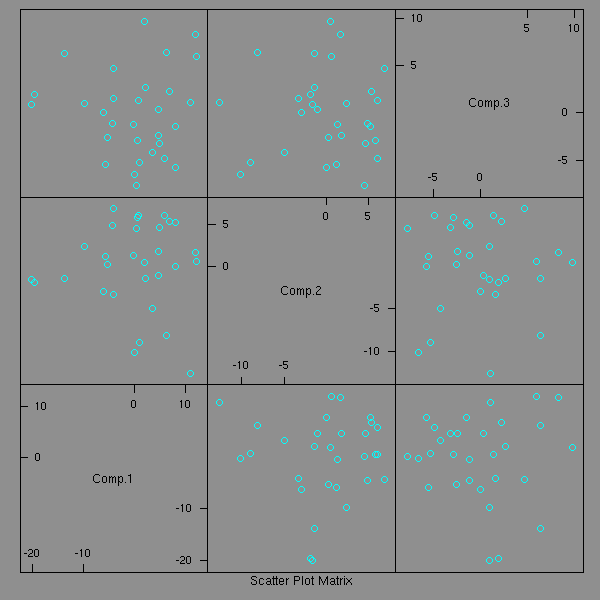
Voici un autre exemple d'application de l'ACP : le classement des textes d'un corpus : les lignes du tableau (les individus) sont les textes, les colonnes les mots de vocabulaire, les valeurs dans le tableau sont le nombre d'occurrence du mot dans le texte. Comme la dimension de l'espace (i.e., le nombre de colonnes) est très grande (quelques milliers), il n'est pas très commode de calculer la matrice des covariances et encore moins de la diagonaliser : on peut néanmoins réaliser l'ACP, de manière approchée, à l'aide de réseaux de neurones.
http://www.loria.fr/projets/TALN/actes/TALN/articles/TALN02.pdf
Ca n'a rien à voir avec l'ACP, mais ça répond au même problème, toujours avec de la géométrie dans des espaces de dimension élevée :
http://www.perl.com/lpt/a/2003/02/19/engine.html
Pour bien comprendre ce qui se passe, c'est un bon exercice que d'implémenter l'ACP. Voici une solution.
my.acp <- function (x) {
n <- dim(x)[1]
p <- dim(x)[2]
# Translation pour se ramener à de l'algèbre linéaire
centre <- apply(x, 2, mean)
x <- x - matrix(centre, nr=n, nc=p, byrow=T)
# diagonalisations, changements de bases
e1 <- eigen( t(x) %*% x, symmetric=T )
e2 <- eigen( x %*% t(x), symmetric=T )
variables <- t(e2$vectors) %*% x
individus <- t(e1$vectors) %*% t(x)
# Les vecteurs qui nous intéressent sont les colonnes
# des matrices précédentes. Pour les dessiner, en particulier
# avec la commande pairs, on les transpose.
variables <- t(variables)
individus <- t(individus)
valeurs.propres <- e1$values
# Dessin
plot( individus[,1:2],
xlim=c( min(c(individus[,1],-individus[,1])),
max(c(individus[,1],-individus[,1])) ),
ylim=c( min(c(individus[,2],-individus[,2])),
max(c(individus[,2],-individus[,2])) ),
xlab='', ylab='', frame.plot=F )
par(new=T)
plot( variables[,1:2], col='red',
xlim=c( min(c(variables[,1],-variables[,1])),
max(c(variables[,1],-variables[,1])) ),
ylim=c( min(c(variables[,2],-variables[,2])),
max(c(variables[,2],-variables[,2])) ),
axes=F, xlab='', ylab='', pch='.')
axis(3, col='red')
axis(4, col='red')
arrows(0,0,variables[,1],variables[,2],col='red')
# On renvoie les données
invisible(list(donnees=x, centre=centre, individus=individus,
variables=variables, valeurs.propres=valeurs.propres))
}
n <- 20
p <- 5
x <- matrix( rnorm(p*n), nr=n, nc=p )
my.acp(x)
title(main="ACP à la main")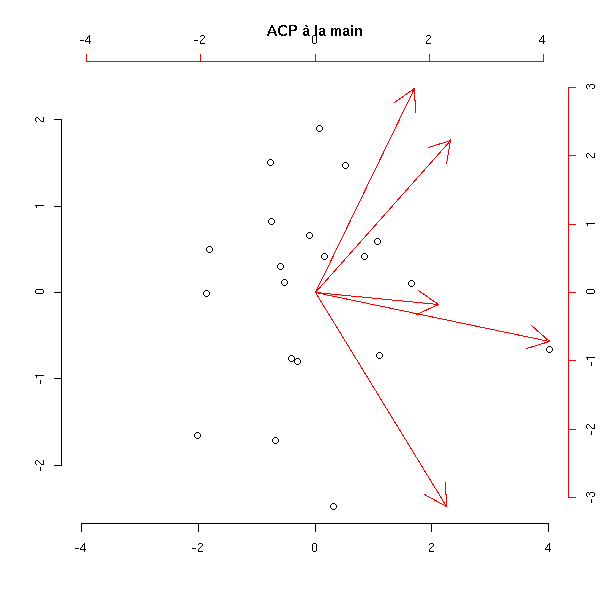
Pour vérifier qu'on n'a pas commis d'erreur en implémentant l'algorithme, on peut comparer avec le résultat de la commande princomp.
biplot(princomp(x))
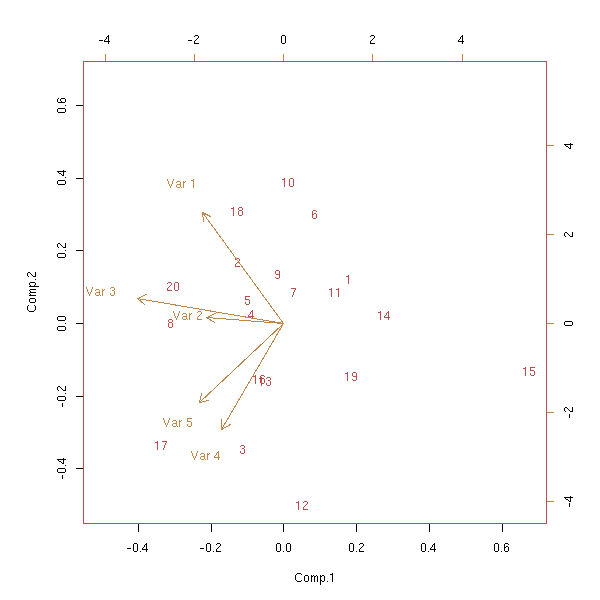
Exercice : Ajouter le nom des individus ; le nom des variables ; représenter les premières dimensions de l'ACP (et pas simplement les deux premières), comme avec la commande pairs ; ajouter des variables (s'il s'agit d'une variable quantitative, on fait le même changement de base que pour les autres, s'il s'agit d'une variable qualitative, on calcule un "individu moyen" pour chacune de ses classes, et on fait le changement de base).
Exercice : Modifier le code précédent en remplaçant la commande eigen par la commande svd (qui effectue une décomposition en valeurs singulières).
Il y a plusieurs types d'analyse en composantes principales : centrée ou non, normalisée (basée sur la matrice de corrélations) ou non (basée sur la matrice de variance-covariance).
Commençons par considérer l'analyse en composantes principales (centrée) non normalisée, i.e., celle basée sur la matrice des covariances.
d <- USArrests[,1:3] # Données dd <- t(t(d)-apply(d, 2, mean)) # Données centrées m <- cov(d) # Calcul de ma matrice des covariances e <- eigen(m) # Valeurs propres et vecteurs propres p <- princomp( ~ Murder + Assault + UrbanPop, data = USArrests)
La matrice de changement de base est la même dans les deux cas :
> e$vectors
[,1] [,2] [,3]
[1,] -0.04181042 -0.04791741 0.99797586
[2,] -0.99806069 -0.04410079 -0.04393145
[3,] -0.04611661 0.99787727 0.04598061
> unclass(p$loadings)
Comp.1 Comp.2 Comp.3
Murder -0.04181042 -0.04791741 0.99797586
Assault -0.99806069 -0.04410079 -0.04393145
UrbanPop -0.04611661 0.99787727 0.04598061et les coordonnées sont aussi les mêmes :
> p$scores[1:3,]
Comp.1 Comp.2 Comp.3
Alabama -64.99204 -10.660459 2.188264
Alaska -91.34472 -21.676617 -2.651214
Arizona -123.68089 8.979374 -4.437864
> (dd %*% p$loadings) [1:3,]
Comp.1 Comp.2 Comp.3
Alabama -64.99204 -10.660459 2.188264
Alaska -91.34472 -21.676617 -2.651214
Arizona -123.68089 8.979374 -4.437864Regardons maintenant l'analyse en composantes principales normalisée : on ne se contente pas de centrer chaque colonne du tableau, on les normalise.
d <- USArrests[,1:3]
dd <- apply(d, 2, function (x) { (x-mean(x))/sd(x) })La matrice de variance-covariance de cette nouvelle matrice coïncide avec la matrice de corrélations de la matrice de départ.
> cov(dd)
Murder Assault UrbanPop
Murder 1.00000000 0.8018733 0.06957262
Assault 0.80187331 1.0000000 0.25887170
UrbanPop 0.06957262 0.2588717 1.00000000
> cor(d)
Murder Assault UrbanPop
Murder 1.00000000 0.8018733 0.06957262
Assault 0.80187331 1.0000000 0.25887170
UrbanPop 0.06957262 0.2588717 1.00000000Poursuivons le calcul :
m <- cov(dd) e <- eigen(m) p <- princomp( ~ Murder + Assault + UrbanPop, data = USArrests, cor=T)
La matrice de changement de base est la même :
> e$vectors
[,1] [,2] [,3]
[1,] 0.6672955 0.30345520 0.6801703
[2,] 0.6970818 0.06713997 -0.7138411
[3,] 0.2622854 -0.95047734 0.1667309
> unclass(p$loadings)
Comp.1 Comp.2 Comp.3
Murder 0.6672955 -0.30345520 0.6801703
Assault 0.6970818 -0.06713997 -0.7138411
UrbanPop 0.2622854 0.95047734 0.1667309On constate avec effroi que les coordonnées ne sont pas les mêmes...
> p$scores[1:3,]
Comp.1 Comp.2 Comp.3
Alabama 1.2508055 -0.9341207 0.2015063
Alaska 0.8006592 -1.3941923 -0.6532667
Arizona 1.3542765 0.8368948 -0.8488785
> (dd %*% e$vectors) [1:3,]
[,1] [,2] [,3]
Alabama 1.2382343 0.9247323 0.1994810
Alaska 0.7926121 1.3801799 -0.6467010
Arizona 1.3406654 -0.8284836 -0.8403468On remarque néanmoins que l'erreur est toujours la même (au signe près, mais le signe n'a aucune importance) :
> p$scores[1:3,] / (dd %*% e$vectors) [1:3,]
Comp.1 Comp.2 Comp.3
Alabama 1.010153 -1.010153 1.010153
Alaska 1.010153 -1.010153 1.010153
Arizona 1.010153 -1.010153 1.010153La différence vient simplement des deux définitions de la covariance : on peut choisir de diviser par n ou par (n-1).
> dim(d) [1] 50 3 > sqrt(50/49) [1] 1.010153
A FAIRE : est-ce le bon endroit ?
Non. Quand on parlera de LDA.
for i in `ls *.txt | cat_rand | head -20`
do
perl -n -e 'BEGIN {
foreach ("a".."z") { $a{$_}=0 }
};
y/A-Z/a-z/;
s/[^a-z]//g;
foreach (split("")) { $a{$_}++ }
END {
foreach("a".."z"){print "$a{$_} "}
}' <$i
echo E
done > ling.txt
# Puis la même chose dans un répertoire contenant des textes en français.
b <- read.table('ling.txt')
names(b) <- c(letters[1:26], 'langue')
a <- b[,1:26]
a <- a/apply(a,1,sum)
biplot(princomp(a))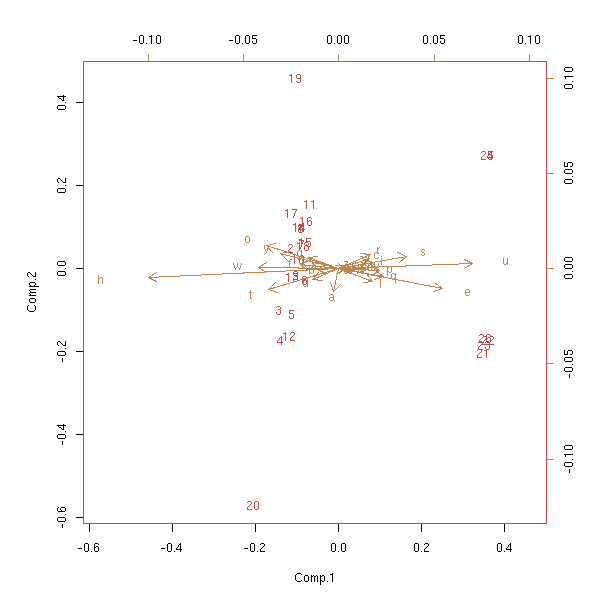
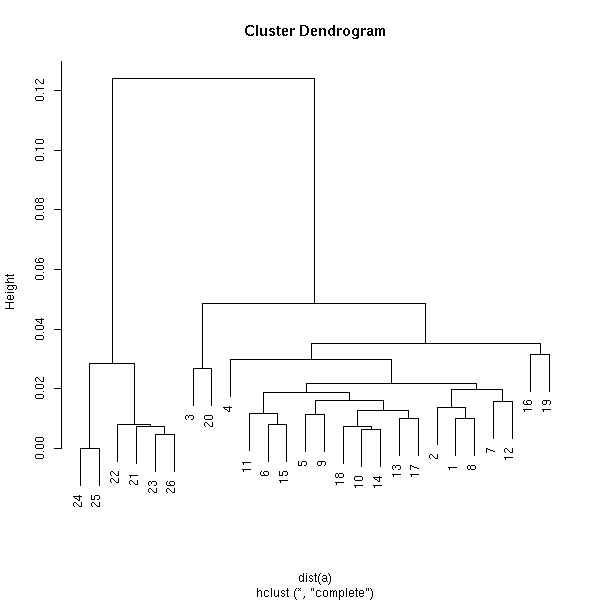
plot(hclust(dist(a)))
kmeans.plot <- function (data, n=2, iter.max=10) {
k <- kmeans(data,n,iter.max)
p <- princomp(data)
u <- p$loadings
# Les observations
x <- (t(u) %*% t(data))[1:2,]
x <- t(x)
# Les centres
plot(x, col=k$cluster, pch=3, lwd=3)
c <- (t(u) %*% t(k$center))[1:2,]
c <- t(c)
points(c, col = 1:n, pch=7, lwd=3)
# Un segment joignant chaque observation à son centre
for (i in 1:n) {
for (j in (1:length(data[,1]))[k$cluster==i]) {
segments( x[j,1], x[j,2], c[i,1], c[i,2], col=i )
}
}
text( x[,1], x[,2], attr(x, "dimnames")[[1]] )
}
kmeans.plot(a,2)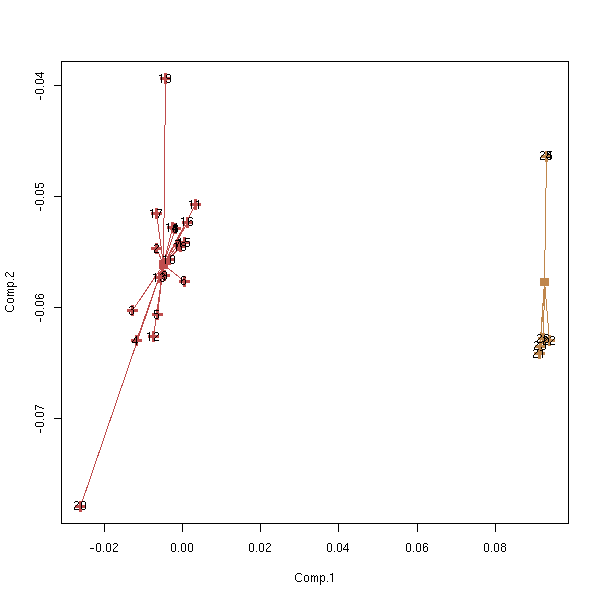
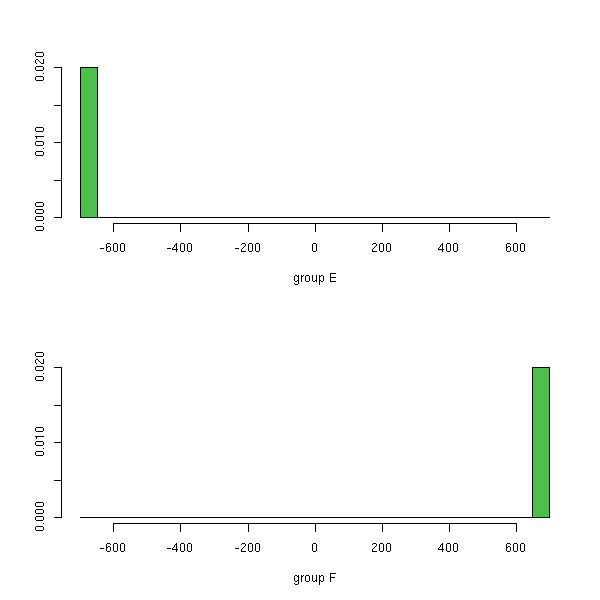
# plot(lda(a,b[,27])) # Bug ? plot(lda(as.matrix(a),b[,27]))
On peut remplacer les variables par leur rang. Mais alors, les variables suivent une distribution uniforme, et le traitement usuel (avec des carrés partout) donne trop d'importance aux valeurs extrèmes. On peut faire une transformation pour se ramener à une distribution normale.
n <- 100
v <- .1
a <- rcauchy(n)
b <- rcauchy(n)
c <- rcauchy(n)
d <- data.frame( x1 = a+b+c+v*rcauchy(n),
x2 = a+b-c+v*rcauchy(n),
x3 = a-b+c+v*rcauchy(n),
x4 = -a+b+c+v*rcauchy(n),
x5 = a-b-c+v*rcauchy(n),
x6 = -a+b-c+v*rcauchy(n) )
biplot(princomp(d))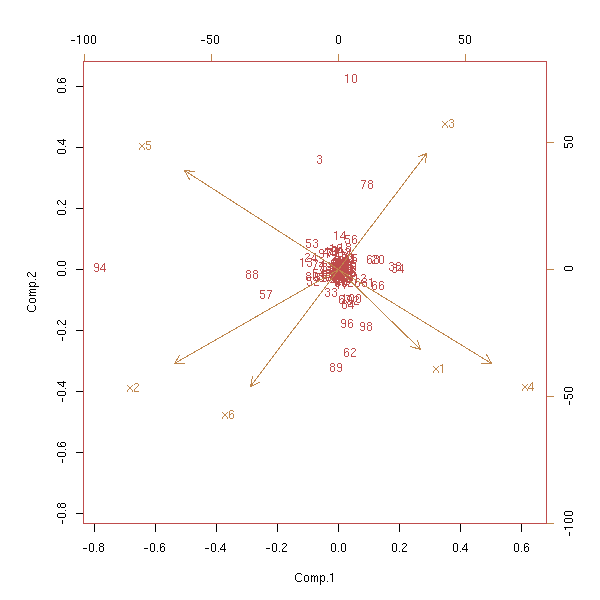
rank.and.normalize.vector <- function (x) {
x <- (rank(x)-.5)/length(x)
x <- qnorm(x)
}
rank.and.normalize <- function (x) {
if( is.vector(x) )
return( rank.and.normalize.vector(x) )
if( is.data.frame(x) ) {
d <- NULL
for (v in x) {
if( is.null(d) )
d <- data.frame( rank.and.normalize(v) )
else
d <- data.frame(d, rank.and.normalize(v))
}
names(d) <- names(x)
return(d)
}
stop("Data type not handled")
}
biplot(princomp(apply(d,2,rank.and.normalize)))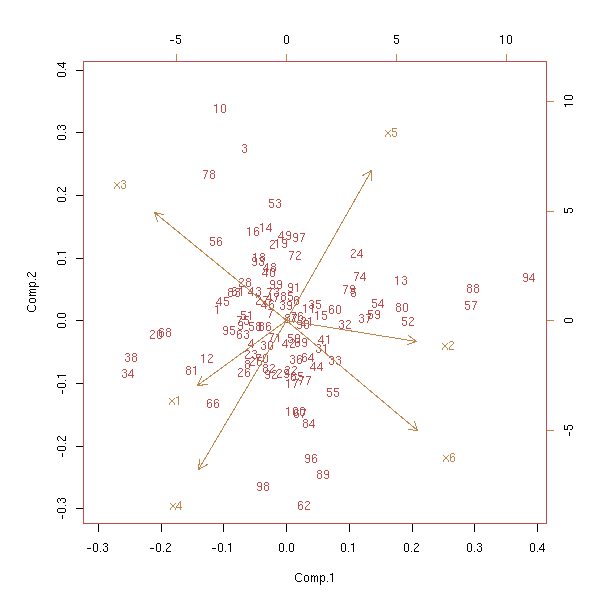
Regardons sur les autres composantes de l'ACP.
pairs( princomp(d)$scores )
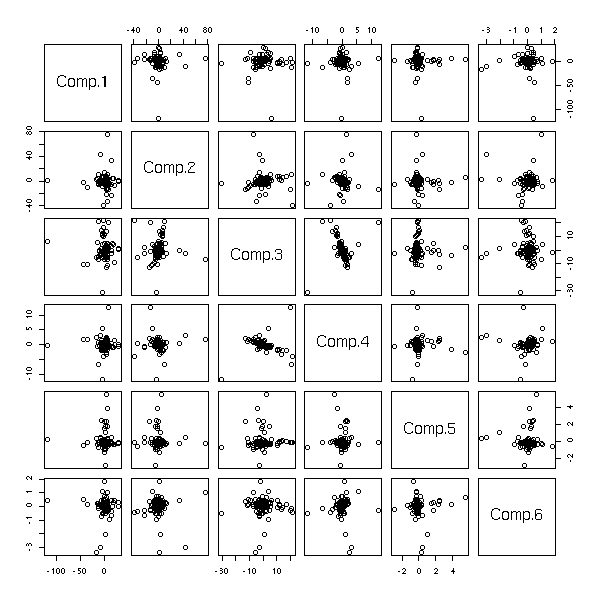
pairs( princomp(apply(d,2,rank.and.normalize))$scores )
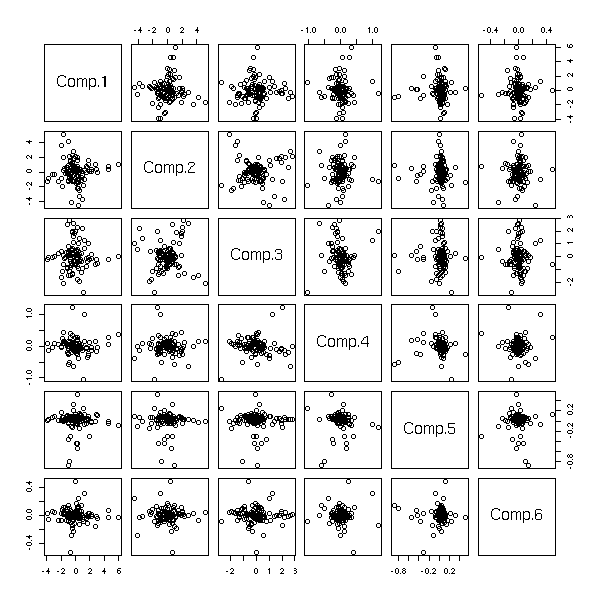
Pour des problèmes non linéaires, on peut commencer par plonger notre espace dans un espace plus gros, par une application du genre
(x,y) |--> (x^2, x*y, y^2).
En fait, comme l'ACP ne fait intervenir que des produits scalaires, on n'a pas réellement besoin de calculer ces nouvelles coordonnées : il suffit de remplacer toutes les occurrences du produit scalaire <x,y> par celui du nouvel espace (cette fonction s'appelle un noyau, et en fait, on peut prendre n'importe quel noyau).
A FAIRE : traiter un exemple.
Nous rencontrerons à nouveau cette idée (passer dans un espace de dimension plus grande pour linéariser un problème non linéaire, à l'aide d'un noyau) quand nous parlerons des SVM (Support Vector Machines).
http://www.kernel-machines.org/papers/talk-dagm99_4.ps.gz
On s'intéresse au problème suivant : étant donné un ensemble de points dans un espace de dimension n, retrouver leurs coordonnées à partir des distances entre ces points. Généralement, on ne connait pas non plus la dimension de l'espace.
C'est proche de l'analyse en composantes principales, avec toutefois quelques différences : l'ACP cherche des relations entre les variables alors que la PCO cherche des similarités entre les observations ; on peut interpréter les axes de l'ACP à l'aide des variables alors que la PCO ne le permet pas (tout simplement parce qu'il n'y a plus de variables).
Comme l'ACP, la PCO est linéaire, et les calculs sont les mêmes. En effet, dans l'ACP, on considère une matrice de variance-covariance, i.e., une matrice dont les entrées sont des sommes de carrés. Or, dans l'analyse des distances, on considère une matrice de distances, ou une matrice de distances au carré, i.e., d'après le théorème de Pythagore, une matrice dont les entrées sont des sommes de carrés.
A FAIRE : terminer de décrire l'algorithme. A FAIRE : sous R (il doit y avoir une fonction pour faire ça dans ade4).
MDS est un équivalent non-linéaire de l'analyse des distances. On tente de minimiser une "fonction de Stress", par exemple la somme des carrés des différences entre les distances que l'on cherche à obtenir et celles que l'on a avec les propositions de coordonnées dont on dispose.
Il existe quelques fonctions sous R pour faire ce genre de chose.
library(mva)
?cmdscale
library(MASS)
?isoMDS
?sammon
library(xgobi)
?xgvis
A FAIRE : parler un peu plus de xgvis
xgvis slides and tutorial:
http://industry.ebi.ac.uk/%257Ealan/VisWorkshop99/XGvis_Talk/sld001.htm
http://industry.ebi.ac.uk/%257Ealan/VisWorkshop99/XGvis_Tutorial/index.html
(restart the MDS optimization with a different starting point to
avoid local minima ("scramble" button))
(one may change the parameters (euclidian/L1/Linfty distance,
removal of outliers, weights, etc.)
(one may ask for a 3D or 4D layout and the rotate it in xgobi)
(restart the MDS optimization with only a subset of the data --
interactivity)
What is a Shepard diagram ??? (change the power transformation)
MDS to get a picture of protein similarity
MDS warning: The global shape of MDS configurations is determined by
the large dissimilarities; consequently, small distances should be
in terpreted with caution: they may not reflect small
dissimilarities.Les applications sont diverses, par exemple
1. La réduction de la dimension : on part d'un ensemble de points dans un espace de dimension élevée, on calcule leurs distances, et on utilise le MDS pour tenter de les mettre dans un espace de dimension plus petite.
On peut donc voir le MDS comme un analogue non linéaire de l'analyse en composantes principales.
n <- 100
v <- .1
# Des données à peu près planes
x <- rnorm(n)
y <- x*x + v*rnorm(n)
z <- v*rnorm(n)
d <- cbind(x,y,z)
# On effectue une rotation
random.rotation.matrix <- function (n) {
m <- NULL
for (i in 1:n) {
x <- rnorm(n)
x <- x / sqrt(sum(x*x))
y <- rep(0,n)
if (i>1) for (j in 1:(i-1)) {
y <- y + sum( x * m[,j] ) * m[,j]
}
x <- x - y
x <- x / sqrt(sum(x*x))
m <- cbind(m, x)
}
m
}
m <- random.rotation.matrix(3)
d <- t( m %*% t(d) )
pairs(d)
title(main="Les points sont dans un plan")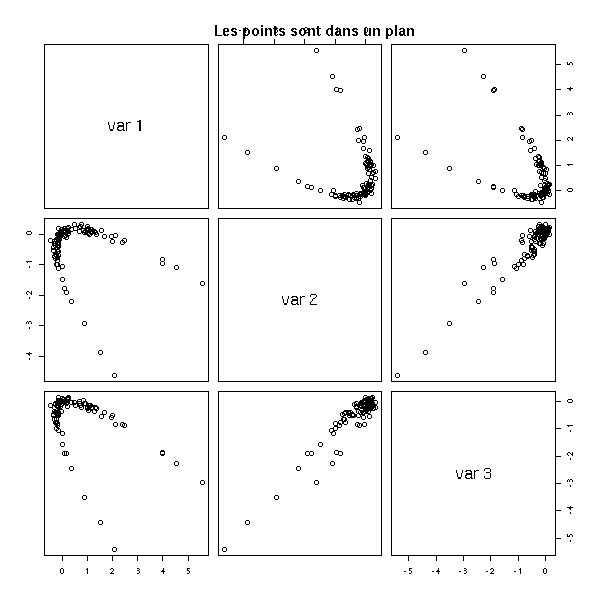
pairs(cmdscale(dist(d),3)) title(main="MDS")
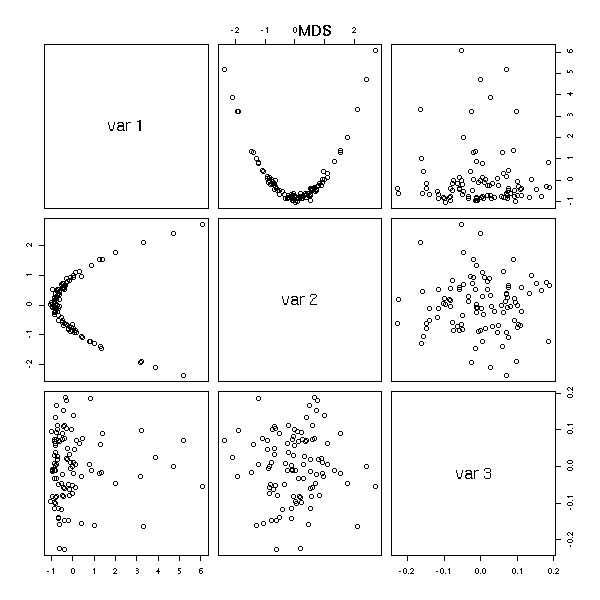
pairs(princomp(d)$scores) title(main="Analyse en composantes principales")
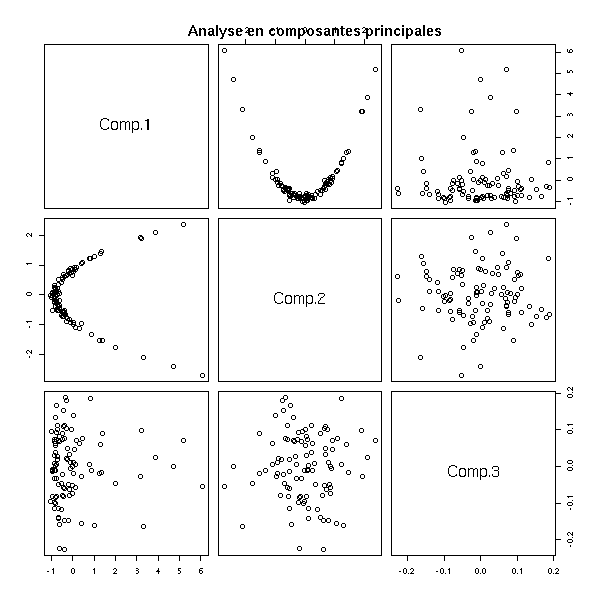
2. L'étude de données dans lesquelles on n'a pas de coordonnées. Par exemple, la similarité des protéines : on sait quand deux protéines sont proches, on peut quantifier cette proximité, mais on n'a pas de coordonnées, on n'a pas d'espace dans lequel on pourrait représenter les protéines.
On rencontre aussi cela en psychologie : on peut demander à des cobayes de reconnaitre des objets (des visages, des lettres en morse, etc.) et regarder le nombre de confusions entre deux objets : cela permet à nouveau de quantifier la proximité de ces objets et le MDS permet de leur attribuer des coordonnées.
On rencontre aussi ces erreurs de classifications en statistiques : on peut ainsi utiliser le MDS pour étudier les erreurs de prédiction d'une variable qualitative à l'aide de variables quantitatives.
A FAIRE : il faudra mentionner le MDS quand je parlerai de ces prédictions...
3. Représenter graphiquement des variables (et non plus des observations), après avoir estimé les distances à l'aide des corrélations.
A FAIRE : un tel dessin quand on parlera de sélection des variables.
4. Le tracé de graphes dans le plan, décrits par la relation d'incidence entre leurs sommets et leurs arrêtes. (Mais pour ça, on peut aussi utiliser GraphViz,
http://www.graphviz.org/
éventuellement depuis R à l'aide de certaines bibliothèques (par exemple, sem ou Rgraphviz).)
A FAIRE
5. La reconstruction d'une molécule, en particulier de sa forme, à l'aide des distances entre les atomes.
Pour plus de détails, voir
http://www.research.att.com/areas/stat/xgobi/papers/xgvis.ps.gz
Les réseaux de Kohonen (SOM, Self-Organizing Maps) sont un équivalent qualitatif et non-linéaire de l'analyse en composantes principales ou de l'analyse des coordonnées : on cherche à classer les observations dans différentes classes (inconnues, a priori), qui s'organisent dans l'espace. Par exemple, on peut vouloir que les classes soient alignées :
* * * * * * * * * *
ou qu'elles forment une grille :
* * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * *
On part d'un nuage de points dans un espace de dimension n, dont on notera les coordonnées (x1,x2,...,xi,...,xn) et on essaye de trouver, pour tout élément j de la grille des coordonnées (w(1,j),w(2,j),...,w(i,j),...,w(n,j)).
1. Choisir des valeurs aléatoires pour les w(i,j).
2. Prendre un point x = (x1,...,xn) du nuage.
2a. Prendre le point j de la grille sont les coordonnées sont les plus proches de x :
j = ArgMin Somme( (x_i - w(i,j))^2 )
i2b. Calculer le vecteur d'erreur
d_i = x_i - w(i,j)
2c. Pour tout point k de la grille dans le voisinage de j, remplacer la valeur de w(i,k) :
w(i,k) <- w(i,k) + h * d_i.
3. Reprendre en 2, en diminuant un peu la taille du voisinage et en diminuant un peu le coefficient d'apprentissage h.
On peut remplacer la notion de voisinage par une "fonction de voisinage" :
w(i,k) <- w(i,k) + h * v(i,k) * d_i
où v(i,i) = 1 et v(i,k) décroit quand k s'éloigne de i. Lors du déroulement de l'algorithme, la fonction v deviendra "de plus en plus pointue".
On peut choisir la géométrie de la grille : il s'agit souvent d'un tableau de dimension 1, 2 ou 3, mais on peut aussi utiliser un cercle, un tore, etc. C'est en ce sens qu'on peut dire que les réseaux de Kohonen sont non-linéaires.
On peut aussi interpréter les cartes de Kohonen comme un mélange d'analyse en composantes principales (représenter graphiquement, dans le plan, le nuage de points) et de classification non supervisée (faire apparaître des classes).
On peut estimer la qualité du résultat en regardant l'erreur, i.e., la moyenne des
Somme( (x_i - w(i,j))^2 ) i
quand x parcourt l'ensemble des points du nuage à classer et quand j est la classe qui minimise cette somme :
MSE = Moyenne Min Somme (x_i - w(i,j))^2
x j i
On présente souvent les cartes de Kohonen comme un cas particulier de réseaux de neurones : si les dessins que l'on fait pour en expliquer le fonctionnement sont effectivement proches, chercher à tout prix à y voir un réseau de neurone risque de ralentir la compréhension du sujet (les poids ne sont pas du tout les mêmes, il n'y a pas de fonction de transfert, etc.).
On peut représenter chaque classe j par un rond (ou un carré) à l'intérieur duquel on indique les coordonnées w(1,j),...,w(n,j), soit par un graphe en étoile, soit par un graphe parallèle.
Sous R, il y a deux fonctions pour calculer des cartes de Kohonen, dans les bibliothèques "class" et "som" (si vous hésitez, prenez "class").
Les exemples suivants utilisent une carte de Kohonen pour représenter la palette de couleurs d'une image.

library(pixmap)
x <- read.pnm("photo1.ppm")
d <- cbind( as.vector(x@red),
as.vector(x@green),
as.vector(x@blue) )
m <- apply(d,2,mean)
d <- t( t(d) - m )
s <- apply(d,2,sd)
d <- t( t(d) / s )
library(som)
r1 <- som(d,5,5)
plot(r1)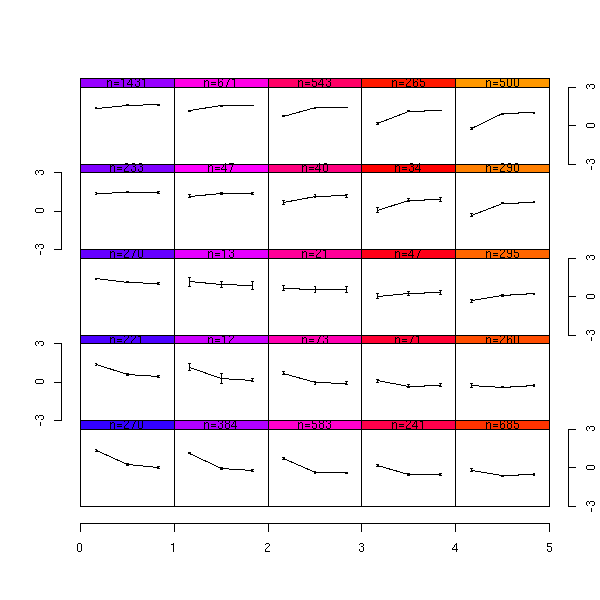
x <- r1$code.sum$x
y <- r1$code.sum$y
n <- r1$code.sum$nobs
co <- r1$code # Is it in the same order that x, y and n?
co <- t( t(co) * s + m )
plot(x, y,
pch=15,
cex=5,
col=rgb(co[,1], co[,2], co[,3])
)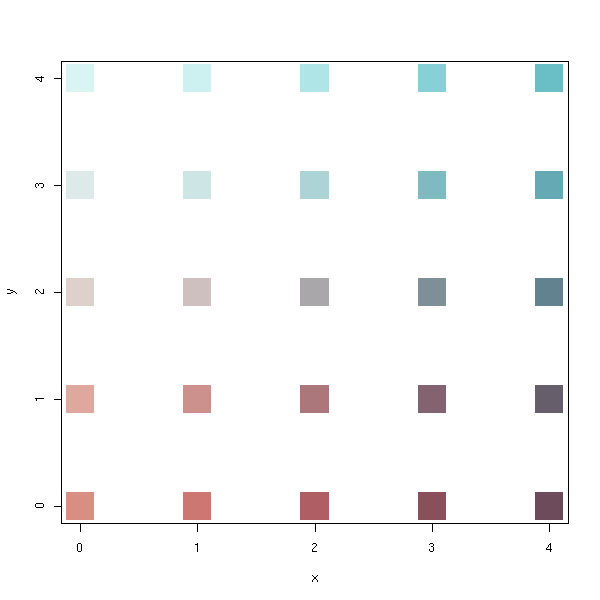
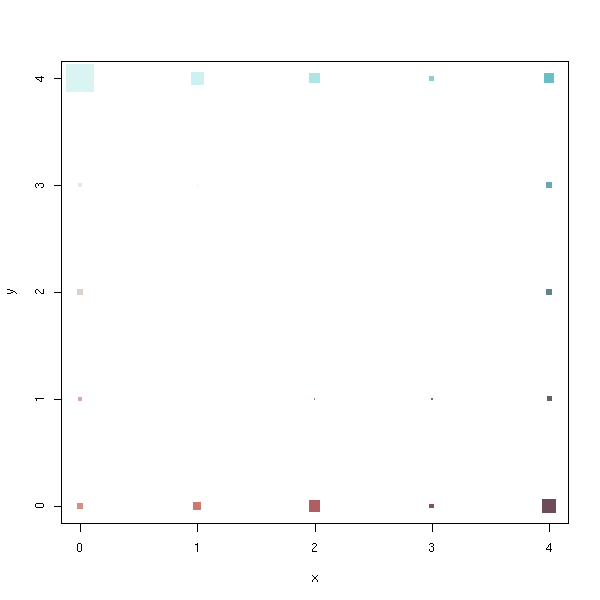
x <- r1$code.sum$x
y <- r1$code.sum$y
n <- r1$code.sum$nobs
co <- r1$code # Is it in the same order that x, y and n?
co <- t( t(co) * s + m )
plot(x, y,
pch=15,
cex=5*n/max(n),
col=rgb(co[,1], co[,2], co[,3])
)
library(class) r2 <- SOM(d) plot(r2)

x <- r2$grid$pts[,1]
y <- r2$grid$pts[,2]
n <- 1 # Where???
co <- r2$codes
co <- t( t(co) * s + m )
plot(x, y,
pch=15,
cex=5*n/max(n),
col=rgb(co[,1], co[,2], co[,3])
)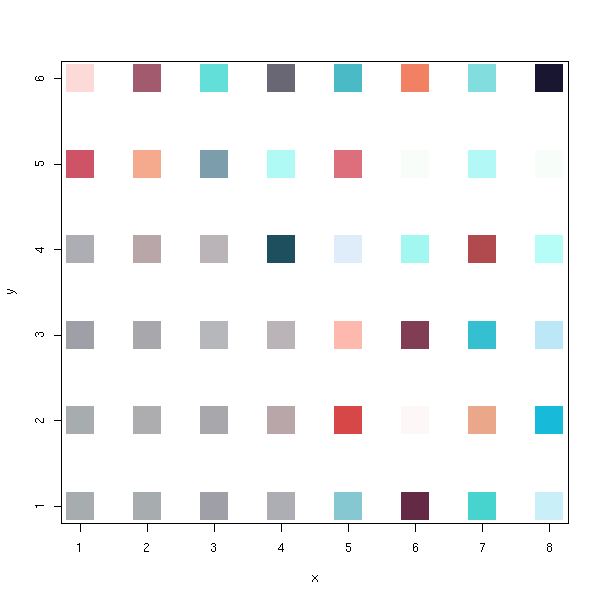
On remarquera que le résultat n'est pas toujours le même :
op <- par(mfrow=c(2,2))
for (i in 1:4) {
r2 <- SOM(d)
plot(r2)
}
par(op)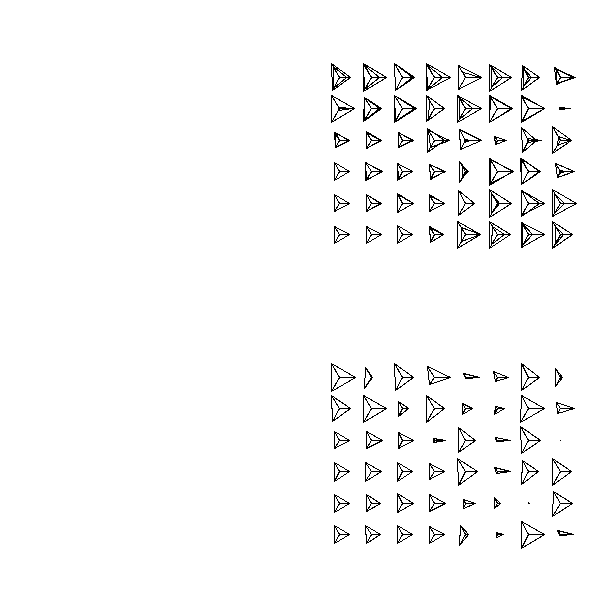
On peut aussi vouloir représenter les coordonnées des noeuds : on peut représenter une coordonnée en la codant par une couleur. Cela permet ensuite de choisir, graphiquement, les variables à utiliser : on peut éliminer celles qui participent peu à la classification et celles qui font double usage.
Dans le premier exemple, la première coordonnée est informative (elle coïncide avec l'une des coordonnées de la carte). Les deux autres coordonnées contiennent la même information (donc on peut en éliminer une sans scrupule) et correspondent à une direction diagonale sur la carte.
x <- r1$code.sum$x
y <- r1$code.sum$y
v <- r1$code
op <- par(mfrow=c(2,2), mar=c(1,1,1,1))
for (k in 1:dim(v)[2]) {
m <- matrix(NA, nr=max(x), nc=max(y))
for (i in 1:length(x)) {
m[ x[i], y[i] ] <- v[i,k]
}
image(m, col=rainbow(255), axes=F)
}
par(op)
x <- r2$grid$pts[,1]
y <- r2$grid$pts[,2]
v <- r2$codes
op <- par(mfrow=c(2,2), mar=c(1,1,1,1))
for (k in 1:dim(v)[2]) {
m <- matrix(NA, nr=max(x), nc=max(y))
for (i in 1:length(x)) {
m[ x[i], y[i] ] <- v[i,k]
}
image(m, col=rainbow(255), axes=F)
}
par(op)
Les coordonnées des noeuds de la carte de Kohonen permettent de définir une application du plan (l'espace dans lequel vit la carte de Kohonen) vers R^n (l'espace dans lequel vit le nuage de points) : on peut représenter l'image de cette application -- en particulier quand l'espace R^n est de petite dimension.
A FAIRE : dessin
Analyse d'images (médicales : échographie, etc. ; écriture manuscrite) : une image n*m peut être vue comme un point dans un espace de dimension n*m. On doit pouvoir imaginer des distances plus pertinentes que la distance euclidienne, mais ça marche déjà bien avec elle.
On peut aussi utiliser des cartes de Kohonen pour prédire des séries temporelles : on essaye généralement d'écrire
y[n+1] = f( y[n], y[n-1], ..., y[n-k] )
pour k "bien choisi" et f à déterminer (par exemple, avec une régression, une analyse en composantes principales (PCA) ou curvilignes (CCA)). Au lieu de cela, on peut construire une carte de Kohonen avec ( y[n], y[n-1], ..., y[n-k] ) et regarder les valeurs de y[n+1] en chaque noeud de la carte. On peut aussi utiliser ( y[n+1], y[n], y[n-1], ..., y[n-k] ) pour construire la carte.
On peut utiliser les cartes de Kohonen pour quantifier les couleurs d'une image (par exemple, pour la convertir de 16 bits en 8 bits, ou pour la convertir en un format indexé qui limite le nombre de couleurs) : les coordonnées des noeuds sont les couleurs quantifiées.
A FAIRE : URL Time Series Forecasting using CCA and Kohonen Maps - Application to Electricity Consumption esann00.pdf
On peut aussi utiliser les réseaux de Kohonen pour l'aprentissage supervisé : on part toujours d'un nuage de points, mais cette fois, à chaque point est associée une classe -- en d'autres termes, on a des variables prédictives (quantitatives) comme précédemment et une variable à prédire, qualitative.
On lance l'algorithme sur les variables prédictives puis on associe une (ou plusieurs) classe(s) à chaque noeud du réseau : les classes d'un noeud sont les classes des points qu'il contient. Les noeuds qui ont plusieurs classes sont dans un état indécis (clash state).
Cela permet, d'une part de classer de nouveaux points, d'autre part de représenter graphiquement, sur la carte de Kohonen, les classes de la variable à prédire.
On a constaté ci-dessus que les cartres de Kohonen n'étaient pas très stables : si on change certains points du nuage, ou même simplement si on change l'initialisation de la carte, on obtient des résultats complètement différents.
Néanmoins, les cartes de petites taille (3x3) sont relativement stables -- en fait, c'est général : on constate que les méthodes d'apprentissage non supervisé donnent des résultats reproductibles s'il y a moins de 10 classes.
On peut néanmoins simplifier une carte de Kohonen de grande taille, de la manière suivante : si on colorie les noeuds de la carte avec le nombre de points qu'ils contiennent, on obtient une image, à laquelle on peut appliquer des traitements de morphologie mathématique, comme l'ouverture (pour se débarasser du bruit de petite taille) ou la ligne de partage des eaux (qui sépare l'image en différentes zônes, en différents "bassins d'attraction).
On peut modéliser la situation décrite par un réseau de Kohonen comme suit. Pour obtenir un nouveau point du nuage :
1. Prendre un point au hasard dans le plan, suivant une distribution qu'on cherchera à déterminer.
2. Appliquer une transformation (qu'on cherchera à déterminer) pour se pour envoyer le point dans l'espace de dimension n dans lequel vivent les points du nuage. Notre point se trouve alors sur un sous-espace de dimension deux de R^n.
3. Ajouter du bruit.
La carte de Kohonen est une estimation de la distribution de la première étape : les lignes et les colonnes correspondent aux coordonnées dans le plan ; le nombre de points classés dans chaque noeud donne une estimation de la densité.
Les coordonnées w(i,j) des noeuds sont une estimation de la sous-variété de R^n obtenue.
Dans ces estimations, le plan R^2 de départ et la sous-variété de R^n ont été discrétisés.
Les GTM (Generative Topographic Mapping) sont un remplacement possible des SOM qui formalisent cette description géométrique des cartes de Kohonen.
A FAIRE : URL Bishop-GTM-Ncomp-98.pdf
A FAIRE : introduction A FAIRE : relire le paragraphe suivant
Les méthodes qui suivent sont toutes basées sur l'analyse en composantes principales : on part d'un tableau de nombres (les valeurs des variables ou une table de contingence), on regarde ses colonnes comme des points d'un espace de dimension n (idem pour les lignes), on cherche un sous-espace de dimension deux sur lequel on voit le plus de choses (on fait une projection orthogonale sur ce sous-espace, au sens du produit scalaire canonique de R^n ou d'un autre produit scalaire).
L'analyse des correspondances s'intéresse aux tableaux de contingence, i.e., aux variables qualitatives. Plaçons-nous dans la cas de deux variables. On commence par transformer le tableau en deux tableaux : celui des profils-lignes (la somme des éléments de chaque ligne égale 1 (ou 100%)) et celui des profils-colonnes.
Si les deux variables sont indépendantes, on a f(i,j)=f(i,*)f(*,j). On peut utiliser le test du Chi2 de Pearson pour comparer les distributions de f(i,j) et de f(i,*)f(*,j).
D'un point de vue technique, l'analyse des correspondances ressemble beaucoup à l'analse des composantes principales. Il s'agit de représenter graphiquement les points correspondant aux différentes lignes du tableau (resp, les colonnes), de manière à avoir un nuage de points les plus espacés possibles (i.e., en maximisant la variance). On procède donc exactement comme pour l'ACP, à ceci près qu'on ne mesure pas les distances avec la métrique canonique, mais à l'aide de la « distance du chi2 »,
library(MASS) data(HairEyeColor) x <- HairEyeColor[,,1]+HairEyeColor[,,2] biplot(corresp(x, nf = 2))
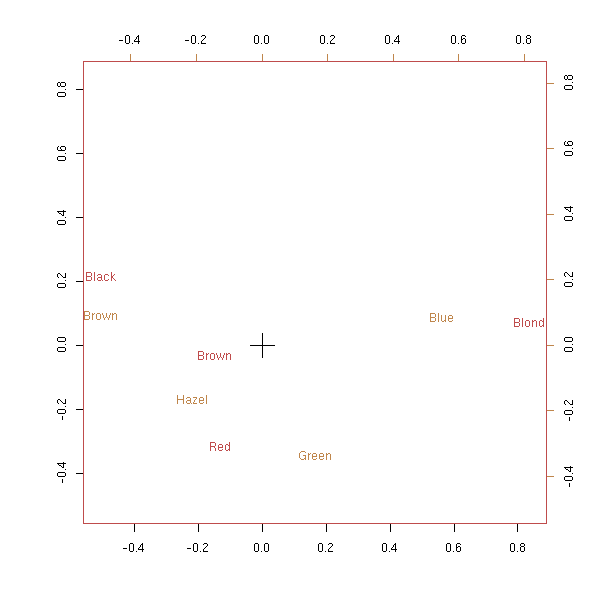
biplot(corresp(t(x), nf = 2))
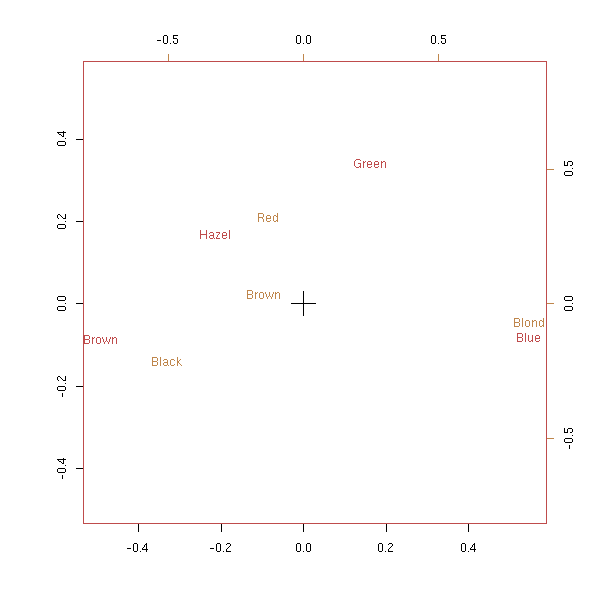
# ??? plot(corresp(x, nf=1))
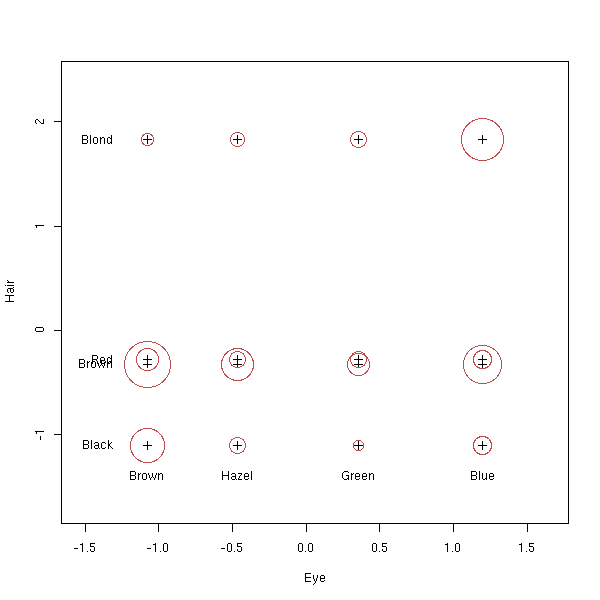
Si on a d'autres variables, on peut les rajouter, a posteriori, sur le dessin, à l'aide de la fonction predict.mca.
Autres exemples
n <- 100 m <- matrix(sample(c(T,F),n^2,replace=T), nr=n, nc=n) biplot(corresp(m, nf=2), main="Analyse des correspondances de données aléatoires")
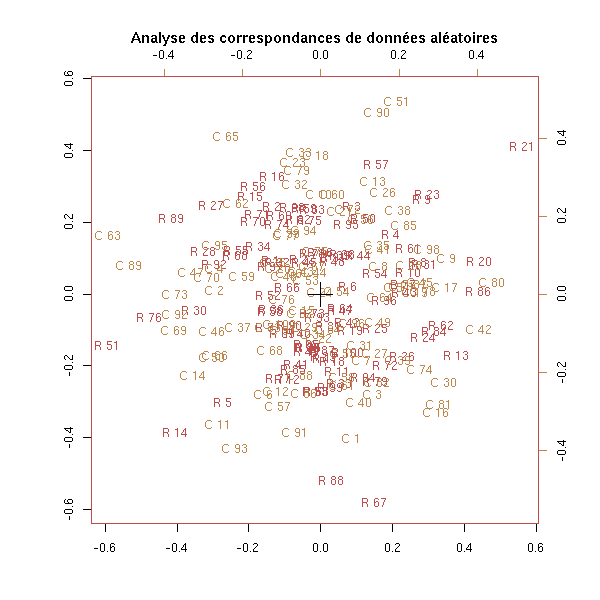
vp <- corresp(m, nf=100)$cor
plot(vp, ylim=c(0,max(vp)), type='l',
main="Analyse des correspondances de données aléatoires")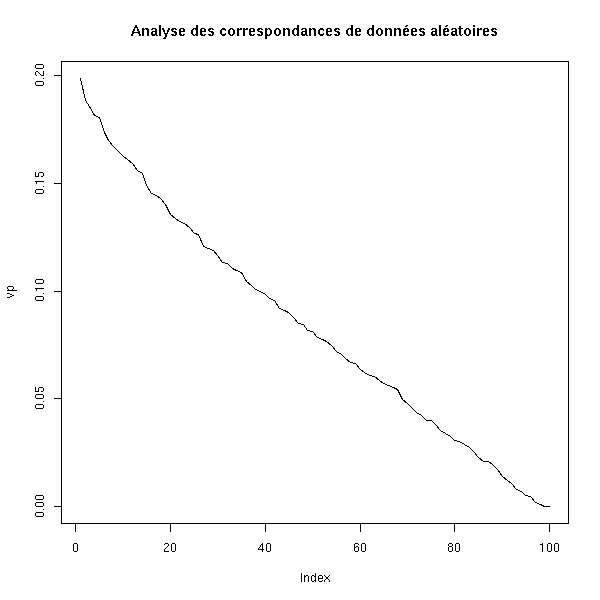
n <- 100
x <- matrix(1:n, nr=n, nc=n, byrow=F)
y <- matrix(1:n, nr=n, nc=n, byrow=T)
m <- abs(x-y) <= n/10
biplot(corresp(m, nf=2),
main='Analyse des correspondances de données "en bande"')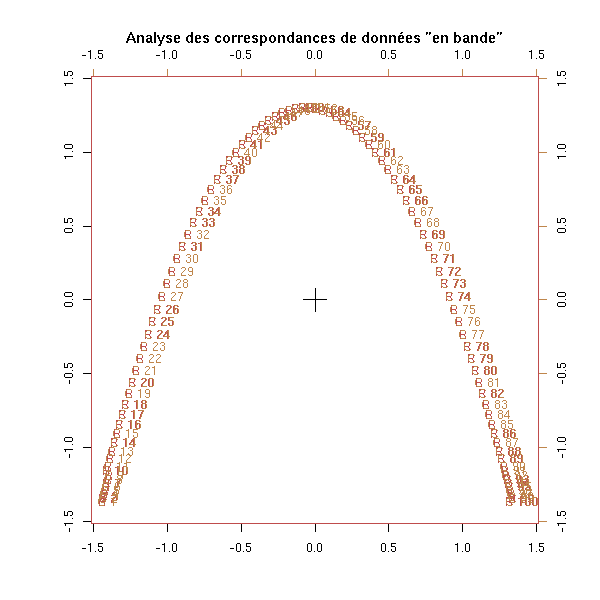
vp <- corresp(m, nf=100)$cor
plot(vp, ylim=c(0,max(vp)), type='l',
main='Analyse des correspondances de données "en bande"')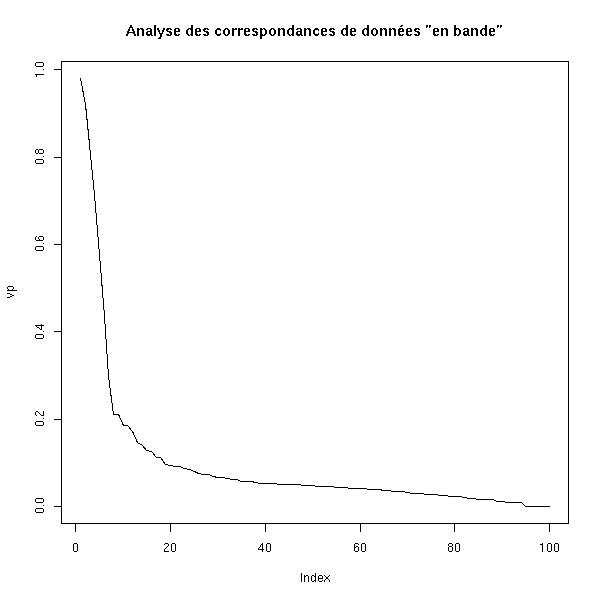
Voir aussi la fonction ca.
library(multiv) ?ca
On part d'un tableau qui a une forme très simple.
n <- 100
x <- matrix(1:n, nr=n, nc=n, byrow=F)
y <- matrix(1:n, nr=n, nc=n, byrow=T)
m <- abs(x-y) <= n/10
plot.boolean.matrix <- function (m) { # Voir aussi levelplot
nx <- dim(m)[1]
ny <- dim(m)[2]
x <- matrix(1:nx, nr=nx, nc=ny, byrow=F)
y <- matrix(1:ny, nr=nx, nc=ny, byrow=T)
plot( as.vector(x)[ as.vector(m) ], as.vector(y)[ as.vector(m) ], pch=16 )
}
plot.boolean.matrix(m)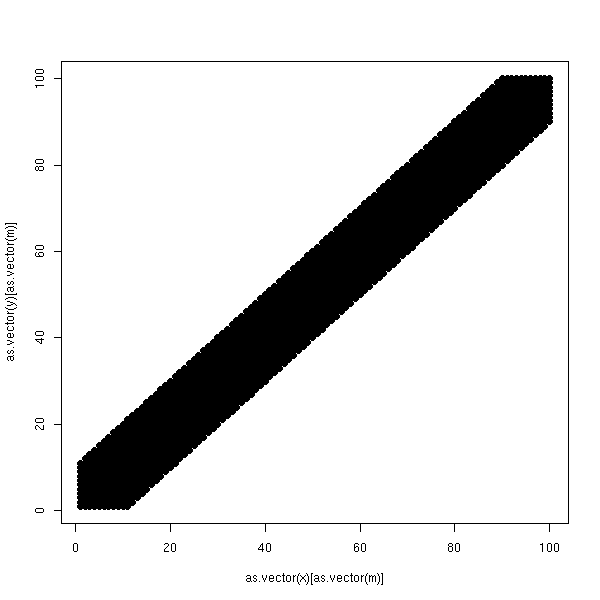
Mais quelqu'un a changé l'ordre des lignes et des colonnes. (De manière plus réaliste, il n'y a pas de saboteur, mais ce sont des données expérimentales, et comme on ne savait pas dans quel ordre placer les lignes et les colonnes, on les a mises n'importe comment...)
ox <- sample(1:n, n, replace=F)
oy <- sample(1:n, n, replace=F)
reorder.matrix <- function (m,ox,oy) {
m <- m[ox,]
m <- m[,oy]
m
}
m2 <- reorder.matrix(m,ox,oy)
plot.boolean.matrix(m2)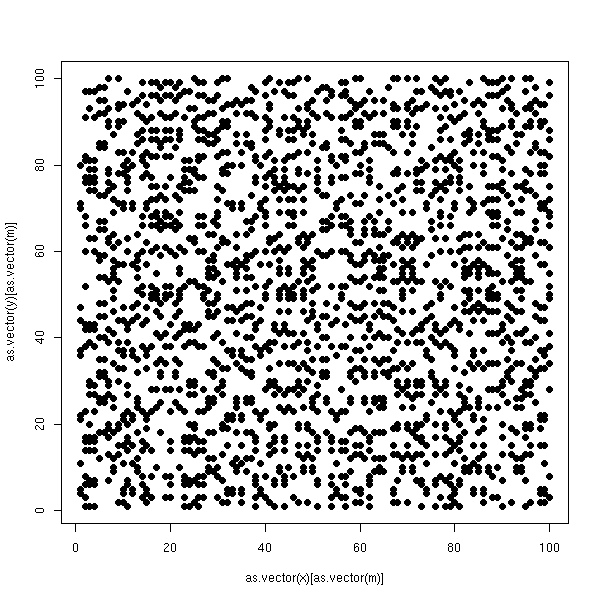
On peut les remettre dans l'ordre ainsi :
a <- corresp(m2) o1 <- order(a$rscore) o2 <- order(a$cscore) m3 <- reorder.matrix(m2,o1,o2) plot.boolean.matrix(m3)
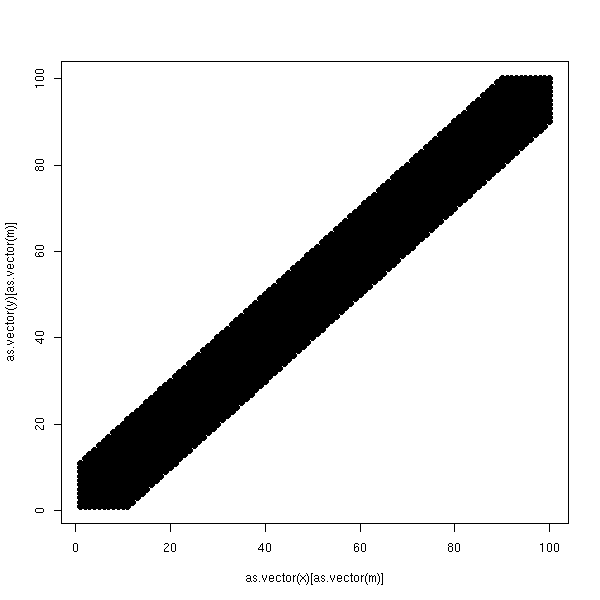
Si on était parti d'un tableau aléatoire, on aurait eu :
n <- 100
p <- .05
done <- F
while( !done ){
# On obtient souvent des matrices singulières
m2 <- matrix( sample(c(F,T), n*n, replace=T, prob=c(1-p, p)), nr=n, nc=n )
done <- det(m2) != 0
}
plot.boolean.matrix(m2)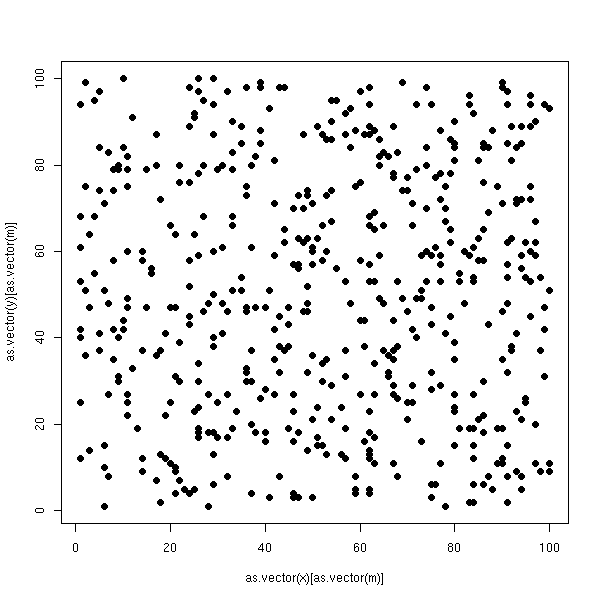
a <- corresp(m2) o1 <- order(a$rscore) o2 <- order(a$cscore) m3 <- reorder.matrix(m2,o1,o2) plot.boolean.matrix(m3)
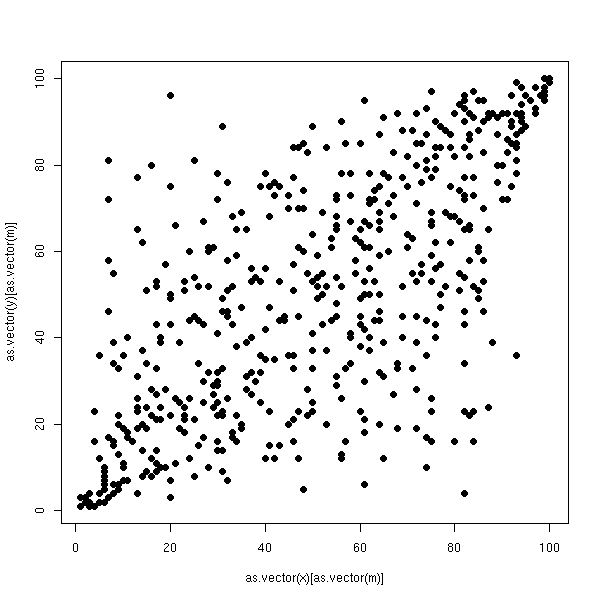
Le principe est très simple. On part d'une matrice de contingence, on la transforme en une matrice de fréquences, on calcule les fréquences marginales et la matrice de contingence que l'on aurait si les deux variables étaient indépendantes et on fait la différence : on se retrouve avec une matrice "centrée", i.e., une matrice qui décrit simplement la non-indépendance des deux variables. On fait ensuite une analyse en composantes principales, mais pas pour la métrique canonique : on prend la distance entre les profils-lignes (resp. -colonnes), pondérée de sorte que les colonnes (resp. lignes) aient toutes la même importance. C'est ce qu'on appelle la distance du Chi^2.
# Distance euclidienne
sum ( f_{i,j} - f_{i',j} )^2
# Distance euclidienne entre les profils-lignes
f_{i,j} f_{i',j}
sum ( --------- - ---------- )^2
j f_{i,.} f_{i',.}
# Distance du Chi^2
1 f_{i,j} f_{i',j}
sum --------- ( --------- - ---------- )^2
j j_{.,j} f_{i,.} f_{i',.}Cette métrique a la propriété suivante : on peut regrouper certaines des valeurs d'une variable sans rien changer au résultat.
# Analyse des correspondances
my.ac <- function (x) {
if(any(x<0))
stop("Expecting a contingency matrix -- with no negative entries")
x <- x/sum(x)
nr <- dim(x)[1]
nc <- dim(x)[2]
marges.lignes <- apply(x,2,sum)
marges.colonnes <- apply(x,1,sum)
profils.lignes <- x / matrix(marges.lignes, nr=nr, nc=nc, byrow=F)
profils.colonnes <- x / matrix(marges.colonnes, nr=nr, nc=nc, byrow=T)
# On n'oublie pas de centrer la matrice : on calcule la
# matrice des fréquences sous l'hypothèse d'indépendance des deux variables
# et on fait la différence.
x <- x - outer(marges.colonnes, marges.lignes)
e1 <- eigen( t(x) %*% diag(1/marges.colonnes) %*% x %*% diag(1/marges.lignes) )
e2 <- eigen( x %*% diag(1/marges.lignes) %*% t(x) %*% diag(1/marges.colonnes) )
v.col <- solve( e2$vectors, x )
v.row <- solve( e1$vectors, t(x) )
v.col <- t(v.col)
v.row <- t(v.row)
if(nr<nc)
valeurs.propres <- e1$values
else
valeurs.propres <- e2$values
# Dessin
plot( v.row[,1:2],
xlab='', ylab='', frame.plot=F )
par(new=T)
plot( v.col[,1:2], col='red',
axes=F, xlab='', ylab='', pch='+')
axis(3, col='red')
axis(4, col='red')
# On renvoie les données
invisible(list(donnees=x, colonnes=v.col, lignes=v.row,
valeurs.propres=valeurs.propres))
}
nr <- 3
nc <- 5
x <- matrix(rpois(nr*nc,10), nr=nr, nc=nc)
my.ac(x)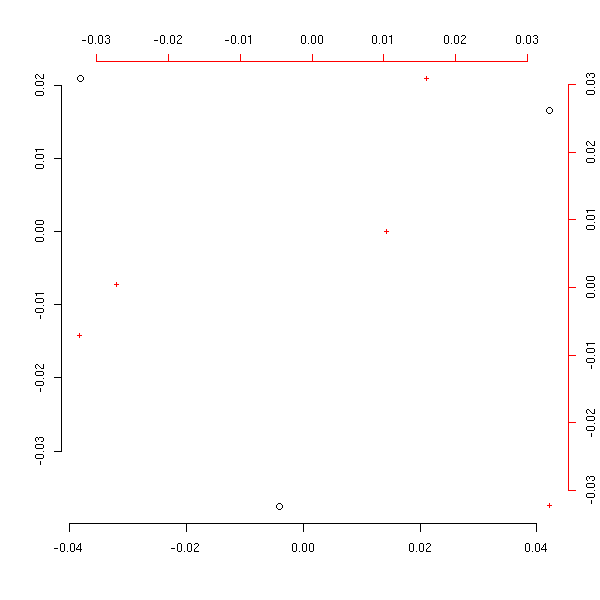
Comparons cela aux résultat de la commande corresp.
plot(corresp(x,nf=2))
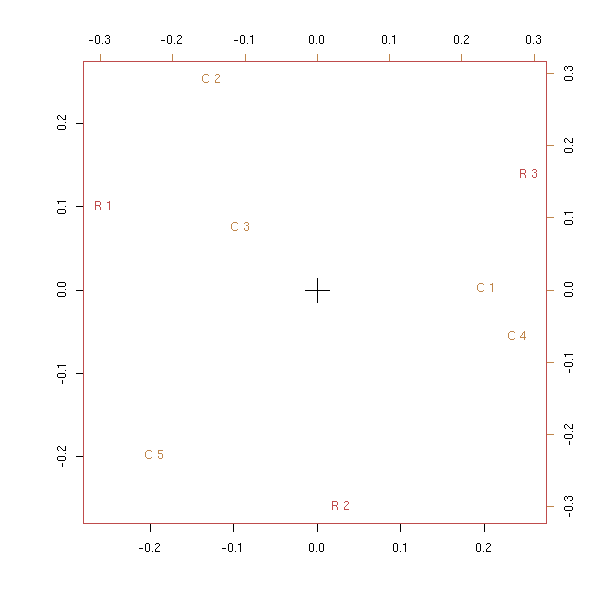
Exercice : modifier le code précédent pour qu'il utilise la commande svd au lieu de eigen (le problème est réel : comme la matrice n'est plus symétrique (bien qu'on puisse s'y ramener), on peut donc avoir des valeurs propres non réelles !).
Sur le graphique représentant la première variable, on peut placer des points correspondant aux valeurs de la seconde : on prend simplement des barycentres des premiers points, pondérés par le profil (ligne ou colonne) correspondant. On peut faire la même chose sur le graphique représentant la seconde variables : à l'échelle près, on obtient le même dessin. C'est cette propriété qui permet de justifier la superposition des deux graphiques.
A FAIRE : les deux dessins
Toujours en utilisant cette notion de barycentre, on peut ajouter de nouvelles variables.
A FAIRE
library(CoCoAn) library(multiv)
A FAIRE : introduction
L'analyse des correspondances simples s'intéressait à deux variables statistiques qualitatives ; l'analyse des correspondances multiples s'intéresse à plusieurs variables qualitatives. Les données ne sont généralement pas représentées par une matrice de contingence (on devrait plutôt dire une hypermatrice de contingence), car cette matrice aurait un nombre d'éléments vraiment énorme, et la plupart ce ces éléments seraient nuls, mais par un tableau du même genre que pour les variables quantitatives.
Hair Eye Sex
1 Blond Blue Male
2 Brown Brown Female
3 Brown Blue Female
4 Red Brown Male
5 Red Brown Female
6 Brown Brown Female
7 Brown Brown Female
8 Black Brown Male
9 Brown Blue Female
10 Blond Blue Male
...Voici tout d'abord l'exemple du manuel.
library(MASS) data(farms) farms.mca <- mca(farms, abbrev=TRUE) farms.mca plot(farms.mca)
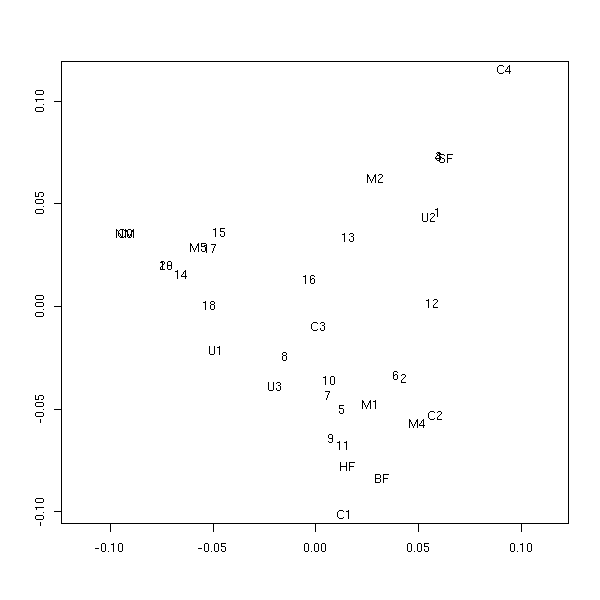
Reprenons l'exemple de la couleur des yeux et de cheveux des étudiants : comme les données sont sous forme d'une hypermatrice, il faut préalablement les transformer.
# Pas beau
my.table.to.data.frame <- function (a) {
r <- NULL
d <- as.data.frame.table(a)
n1 <- dim(d)[1]
n2 <- dim(d)[2]-1
for (i in 1:n1) {
for (j in 1:(d[i,n2+1])) {
r <- rbind(r, d[i,1:n2])
}
row.names(r) <- 1:dim(r)[1]
}
r
}
r <- my.table.to.data.frame(HairEyeColor)
plot(mca(r))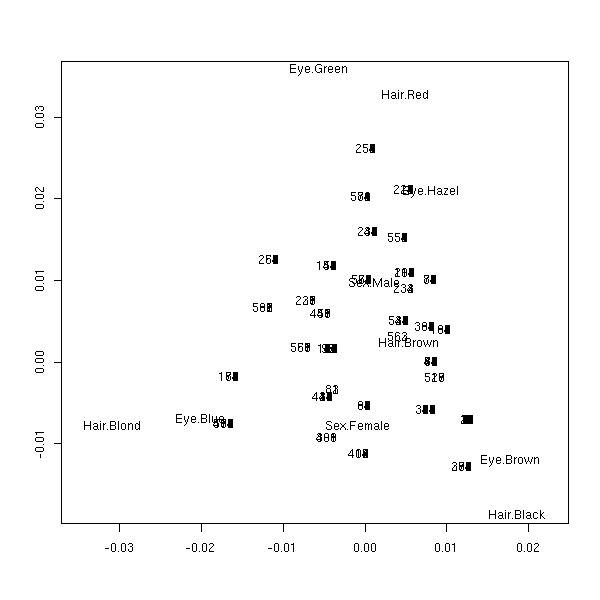
On peut aussi ajouter des individus ou des variables, a posteriori, à l'aide de la commande predict.mca.
?predict.mca
S'il n'y a que deux variables, on peut faire une analyse des correspondances simples ou multiples : ça n'est pas la même chose, mais on peut reconnaître certaines similitudes.
x <- HairEyeColor[,,1]+HairEyeColor[,,2]
op <- par(mfcol=c(1,2))
biplot(corresp(x, nf = 2),
main="Analyse des correspondances simples")
plot(mca(my.table.to.data.frame(x)), rows=F,
main="Analyse des correspondances multiples")
par(op)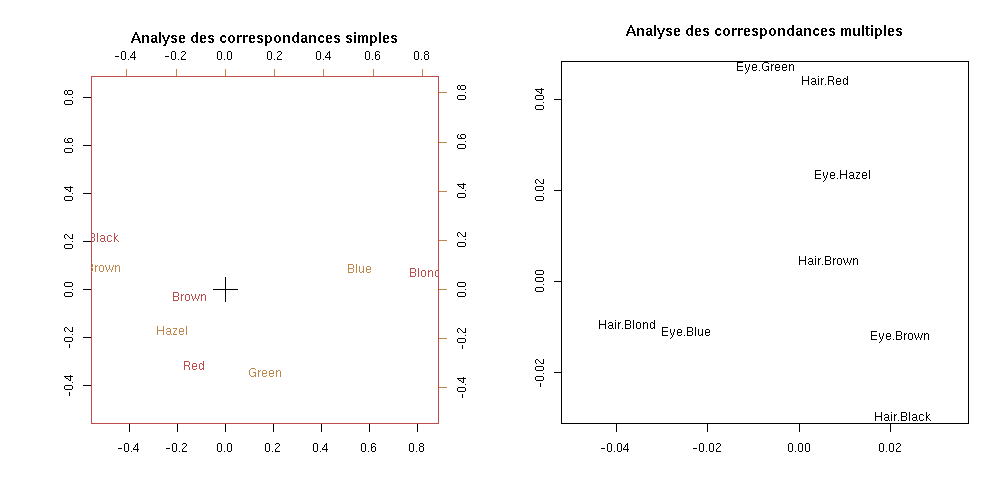
On commence par transformer les données, pour les mettre sous la forme d'un << tableau disjonctif >> :
HairBlack HairBrown HairRed HairBlond EyeBrown EyeBlue EyeHazel EyeGreen SexMale SexFemale
[1,] 0 0 0 1 0 1 0 0 1 0
[2,] 0 1 0 0 1 0 0 0 0 1
[3,] 0 1 0 0 0 1 0 0 0 1
[4,] 0 0 1 0 1 0 0 0 1 0
[5,] 0 0 1 0 1 0 0 0 0 1
[6,] 0 1 0 0 1 0 0 0 0 1
[7,] 0 1 0 0 1 0 0 0 0 1
[8,] 1 0 0 0 1 0 0 0 1 0
[9,] 0 1 0 0 0 1 0 0 0 1
[10,] 0 0 0 1 0 1 0 0 1 0Ensuite, on fait une analyse : les poids des observations sont tous les mêmes, et les poids des variables sont calculés exactement comme pour l'analyse des correspondances simples. On remarque que 1 est toujours une valeur propre : on enlève le vecteur correspondant.
A FAIRE : expliquer d'où vient ce 1 et justifier le fait qu'on l'enlève.
Voici un exemple de code réalisant ce genre de calcul.
# Analyse des correspondances multiples
tableau.disjonctif.vecteur <- function (x) {
y <- matrix(0, nr=length(x), nc=length(levels(x)))
for (i in 1:length(x)) {
y[i, as.numeric(x[i])] <- 1
}
y
}
tableau.disjonctif <- function (x) {
if( is.vector(x) )
y <- tableau.disjonctif.vecteur(x)
else {
y <- NULL
y.names <- NULL
for (i in 1:length(x)) {
y <- cbind(y, tableau.disjonctif.vecteur(x[,i]))
y.names <- c( y.names, paste(names(x)[i], levels(x[,i]), sep='') )
}
}
colnames(y) <- y.names
y
}
my.acm <- function (x, garder.un=F) {
# x est un data.frame qui contient uniquement des facteurs
# y est une matrice qui contient des 0 et des 1
y <- tableau.disjonctif(x)
# Nombre d'observations
n <- dim(y)[1]
# Nombre de variables
s <- length(x)
# Nombre de colonnes du tableau disjonctif
p <- dim(y)[2]
# La matrice et les poids
F <- y/(n*s)
Dp <- diag(t(y)%*%y) / (n*s)
Dn <- rep(1/n,n)
# On effectue l'analyse
# Ne pas oublier d'enlever la valeur propre 1 !!!
# (elle provient du fait qu'on n'a pas centré la matrice)
e1 <- eigen( t(F) %*% diag(1/Dn) %*% F %*% diag(1/Dp) )
e2 <- eigen( F %*% diag(1/Dp) %*% t(F) %*% diag(1/Dn) )
variables <- t(e2$vectors) %*% F
individus <- t(e1$vectors) %*% t(F)
variables <- t(variables)
individus <- t(individus)
valeurs.propres <- e1$values
if( !garder.un ) {
variables <- variables[,-1]
individus <- individus[,-1]
valeurs.propres <- valeurs.propres[-1]
}
plot( jitter(individus[,2], factor=5) ~ jitter(individus[,1], factor=5),
xlab='', ylab='', frame.plot=F )
par(new=T)
plot( variables[,1:2], col='red',
axes=FALSE, xlab='', ylab='', type='n' )
text( variables[,1:2], colnames(y), col='red')
axis(3, col='red')
axis(4, col='red')
j <- 1
col = rainbow(s)
for (i in 1:s) {
jj <- j + length(levels(x[,i])) - 1
print( paste(j,jj) )
lines( variables[j:jj,1], variables[j:jj,2], col=col[i] )
j <- jj+1
}
invisible(list( donnees=x, variables=variables, individus=individus,
valeurs.propres=valeurs.propres ))
}
random.data.1 <- function () {
n <- 100
m <- 3
l <- c(3,2,5)
x <- NULL
for (i in 1:m) {
v <- factor( sample(1:l[i], n, replace=T), levels=1:l[i] )
if( is.null(x) )
x <- data.frame(v)
else
x <- data.frame(x, v)
}
names(x) <- LETTERS[1:m]
x
}
r <- NULL
while(is.null(r)) {
x1 <- random.data.1()
try(r <- my.acm(x1))
}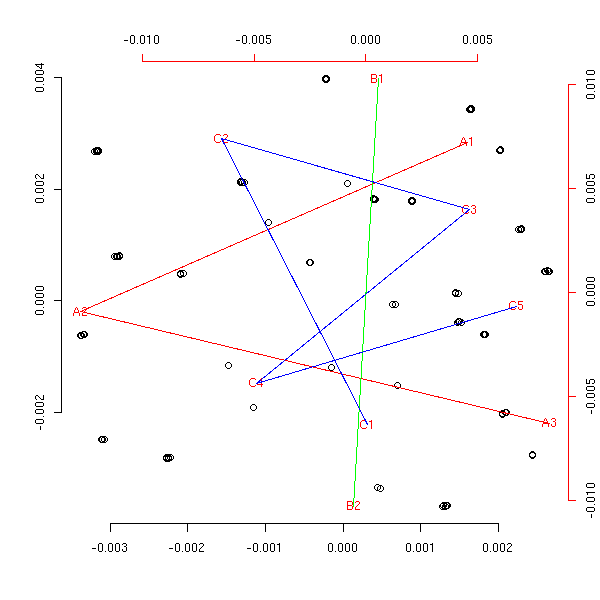
Sur le graphique précédent, les trois variables dont bien séparées, signe qu'elles sont indépendantes. Voici ce qui se passe en cas de dépendance.
my.random.data.2 <- function () {
n <- 100
m <- 3
l <- c(3,2,3)
x <- NULL
for (i in 1:m) {
v <- factor( sample(1:l[i], n, replace=T), levels=1:l[i] )
if( is.null(x) )
x <- data.frame(v)
else
x <- data.frame(x, v)
}
x[,3] <- factor( ifelse( runif(n)>.8, x[,1], x[,3] ), levels=1:l[1])
names(x) <- LETTERS[1:m]
x
}
r <- NULL
while(is.null(r)) {
x2 <- my.random.data.2()
try(r <- my.acm(x2))
}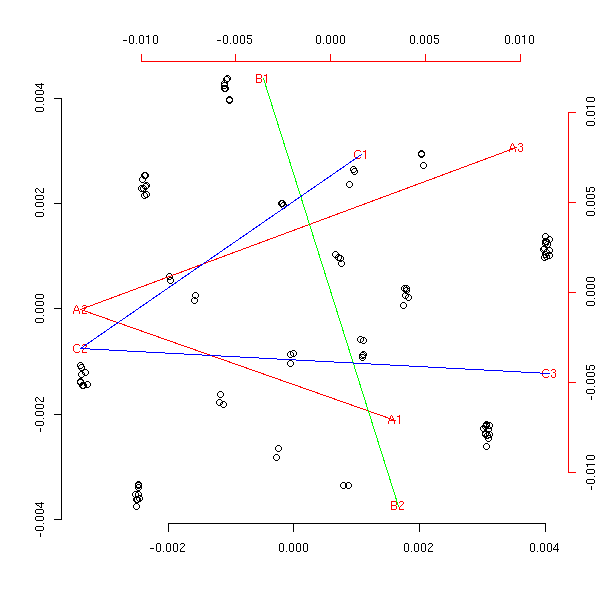
Comparons avec le résultat de la commande mca :
library(MASS) plot(mca(x1))
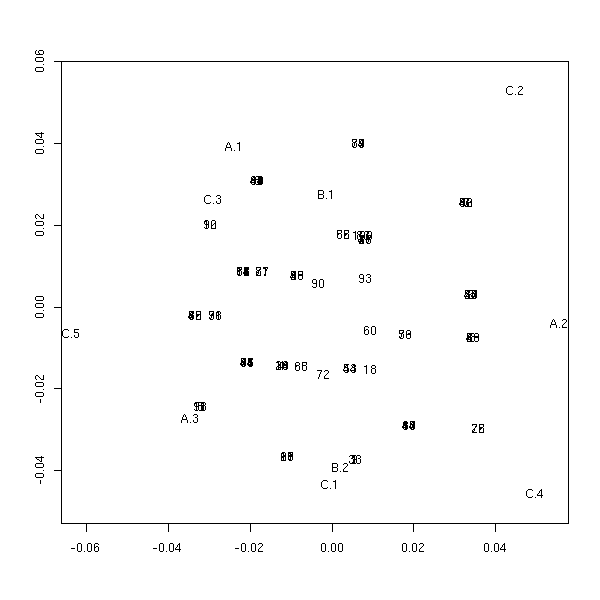
plot(mca(x2))
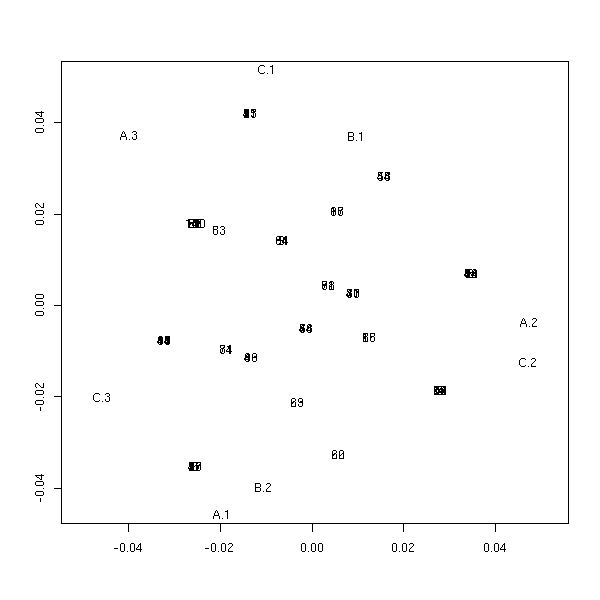
Initialement, j'avais oublié de retirer la valeur propre 1, ce qui donnait :
my.acm(x1, garder.un=T)
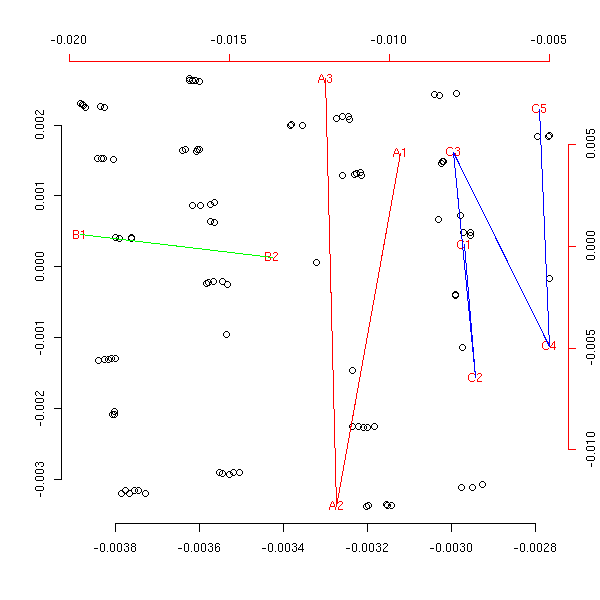
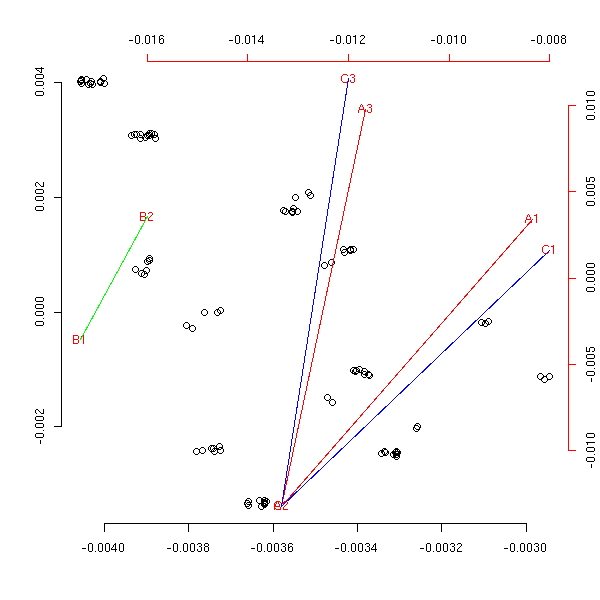
my.acm(x2, garder.un=T)
On peut penser analyser un ensemble de variables qualitatives et quantitatives en mélangeant l'analyse en composantes principale et l'analyse des correspondances multiples : il suffit de mettre les deux tableaux côte-à-côte et de concaténer les vecteur poids des colonnes des deux tableaux. Regardons ce que cela donne.
tableau.disjonctif.vecteur <- function (x) {
if( is.factor(x) ){
y <- matrix(0, nr=length(x), nc=length(levels(x)))
for (i in 1:length(x)) {
y[i, as.numeric(x[i])] <- 1
}
return(y)
} else
return(x)
}
tableau.disjonctif <- function (x) {
if( is.vector(x) )
y <- tableau.disjonctif.vecteur(x)
else {
y <- NULL
y.names <- NULL
for (i in 1:length(x)) {
y <- cbind(y, tableau.disjonctif.vecteur(x[,i]))
if( is.factor(x[,i]) )
y.names <- c( y.names, paste(names(x)[i], levels(x[,i]), sep='') )
else
y.names <- c(y.names, names(x)[i])
}
}
colnames(y) <- y.names
y
}
my.am <- function (x) {
y <- tableau.disjonctif(x)
# Nombre d'observations
n <- dim(y)[1]
# Nombre de variables
s <- length(x)
# Nombre de colonnes du tableau disjonctif
p <- dim(y)[2]
# La matrice et les poids
# Chaque variable a un poids égal à 1,
# mais pour les variables qualitatives, qui sont éclatées en
# plusieurs "sous-variables", c'est la somme des poids de ces
# "sous-variables" qui vaut 1.
Dp <- diag(t(y)%*%y) / n
j <- 1
for(i in 1:s){
if( is.factor(x[,i]) )
j <- j + length(levels(x[,i]))
else {
Dp[j] <- 1
j <- j+1
}
}
Dn <- rep(1,n)
# Ce n'est pas une bonne idée de centrer la variable...
f <- ne.pas.centrer(y)
# On effectue l'analyse
e1 <- eigen( t(f) %*% diag(1/Dn) %*% f %*% diag(1/Dp) )
e2 <- eigen( f %*% diag(1/Dp) %*% t(f) %*% diag(1/Dn) )
variables <- t(e2$vectors) %*% f
individus <- t(e1$vectors) %*% t(f)
variables <- t(variables)
individus <- t(individus)
valeurs.propres <- e1$values
# Il arrive que les erreurs d'arrondi rendent la matrice
# non diagonalisable sur R. On se retrouve alors avec des
# valeurs propres complexes et (pire) des vecteurs sur C.
# C'est pour cette raison qu'il est préférable d'utiliser
# la SVD, qui donne toujours des résultats réels...
if( any(Im(variables)!=0) | any(Im(individus)!=0) |
any(Im(valeurs.propres)!=0) ){
warning("Matrice non diagonalisable sur R !!!")
variables <- Re(variables)
individus <- Re(individus)
valeurs.propres <- Re(valeurs.propres)
}
plot( jitter(individus[,2], factor=5) ~ jitter(individus[,1], factor=5),
xlab='', ylab='', frame.plot=F )
par(new=T)
plot( variables[,1:2], col='red',
axes=FALSE, xlab='', ylab='', type='n' )
text( variables[,1:2], colnames(y), col='red')
axis(3, col='red')
axis(4, col='red')
col = rainbow(s)
j <- 1
for (i in 1:s) {
if( is.factor(x[,i]) ){
jj <- j + length(levels(x[,i])) - 1
print( paste(j,jj) )
lines( variables[j:jj,1], variables[j:jj,2], col=col[i] )
j <- jj+1
} else {
arrows(0,0,variables[j,1],variables[j,2],col=col[i])
j <- j+1
}
}
}
ne.pas.centrer <- function (y) { y }
n <- 500
m <- 3
p <- 2
l <- c(3,2,5)
x <- NULL
for (i in 1:m) {
v <- factor( sample(1:l[i], n, replace=T), levels=1:l[i] )
if( is.null(x) )
x <- data.frame(v)
else
x <- data.frame(x, v)
}
x <- cbind( x, matrix( rnorm(n*p), nr=n, nc=p ) )
names(x) <- LETTERS[1:(m+p)]
x1 <- x
my.am(x1)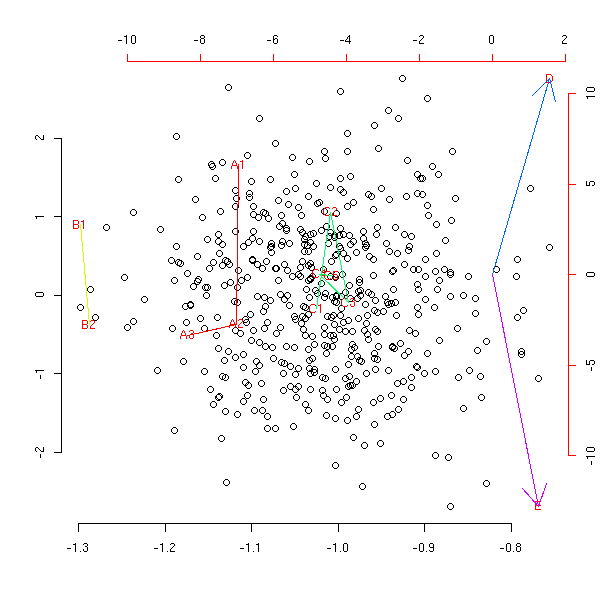
Avec des variables liées : comme pour l'analyse des correspondances multiples, on voit clairement que deux des variables qualitatives sont liées, mais pour ce qui est de la variable quantitative, on ne voit rien...
n <- 500
m <- 3
p <- 2
l <- c(3,2,5)
x <- NULL
for (i in 1:m) {
v <- factor( sample(1:l[i], n, replace=T), levels=1:l[i] )
if( is.null(x) )
x <- data.frame(v)
else
x <- data.frame(x, v)
}
x <- cbind( x, matrix( rnorm(n*p), nr=n, nc=p ) )
names(x) <- LETTERS[1:(m+p)]
x[,3] <- factor( ifelse( runif(n)>.8, x[,1], x[,3] ), levels=1:l[1])
x[,5] <- scale( ifelse( runif(n)>.9, as.numeric(x[,1]), as.numeric(x[,2]) )) + .1*rnorm(n)
x2 <- x
my.am(x2)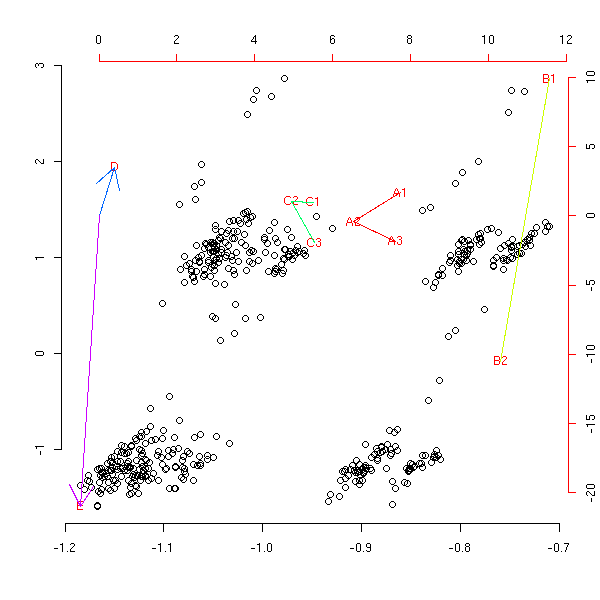
Si on s'amuse à centrer la matrice, ça donne n'importe quoi (par contre, on peut centrer les colonnes correspondant aux variables quantitatives).
ne.pas.centrer <- function (y) {
centre <- apply(y, 2, mean)
y - matrix(centre, nr=n, nc=dim(y)[2], byrow=T)
}
my.am(x1)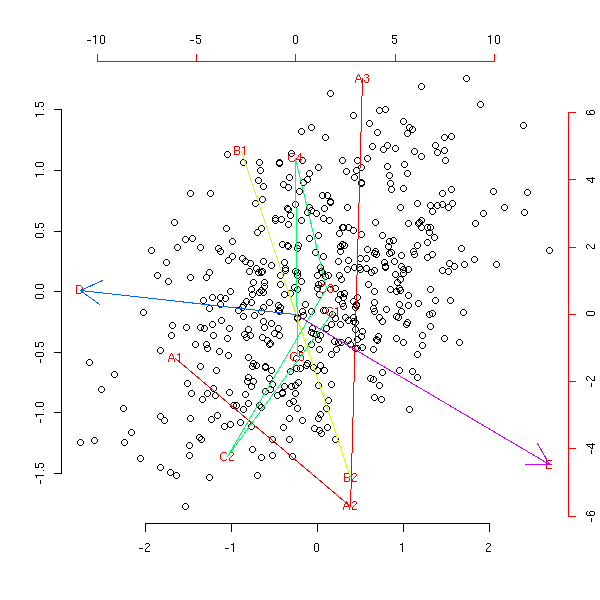
my.am(x2)
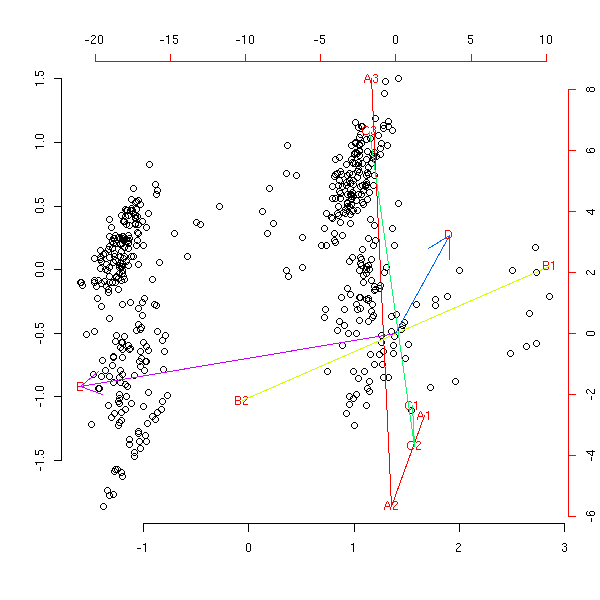
Moralité : si on veut représenter, sur un même dessin des variables qualitatives et quantitatives, on préfèrera transformer les variables quantitatives en variables qualitatives (heu... on ne voit pas grand chose non plus...) :
to.factor.numeric.vector <- function (x, number) {
resultat <- NULL
intervalles <- co.intervals(x,number,overlap=0)
for (i in 1:number) {
if( i==1 ) intervalles[i,1] = min(x)
else
intervalles[i,1] <- intervalles[i-1,2]
if( i==number )
intervalles[i,2] <- max(x)
}
for (valeur in x) {
r <- NA
for (i in 1:number) {
if( valeur >= intervalles[i,1] & valeur <= intervalles[i,2] )
r <- i
}
resultat <- append(resultat, r)
}
factor(resultat, levels=1:number)
}
to.factor.vector <- function (x, number) {
if( is.factor(x) )
return(x)
else
return(to.factor.numeric.vector(x,number))
}
to.factor <- function (x, number=4 ) {
y <- NULL
for (a in x) {
aa <- to.factor.vector(a, number)
if( is.null(y) )
y <- data.frame(aa)
else
y <- data.frame(y,aa)
}
names(y) <- names(x)
y
}
my.am(to.factor(x1))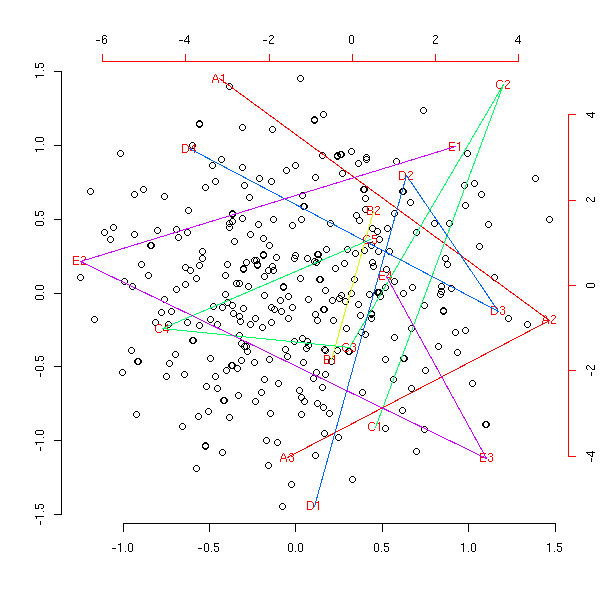
En découpant les variables quantitatives en trois morceaux au lieu de quatre.
my.am(to.factor(x1, number=3))
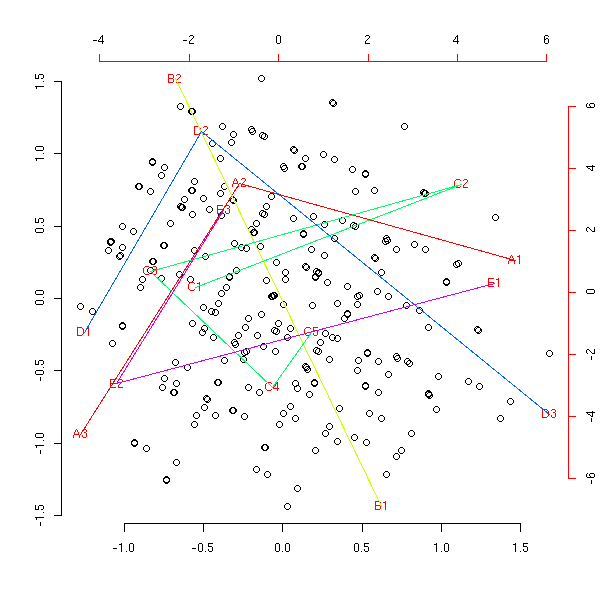
Avec des variables liées.
my.am(to.factor(x2))
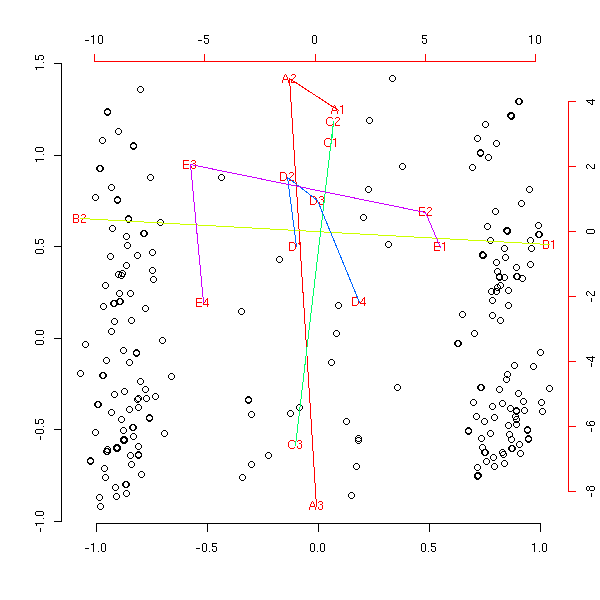
my.am(to.factor(x2, number=3))
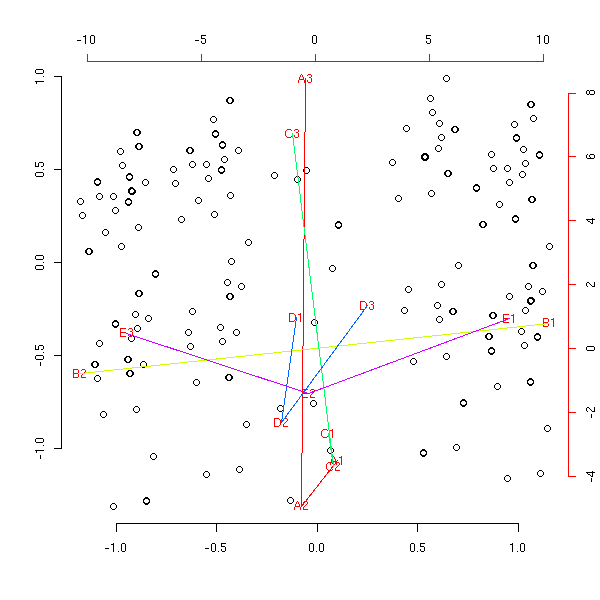
Le modèle log-linéaire remplit à peu près les mêmes rôles que l'analyse des correspondances multiples -- mais il a l'avantage, comme toute régression, de permettre de faire des test. On a un tableau de contingence t_{i,j} et on tente d'écrire
log t_{i,j} = a_0 + a_1(i) + a_2(j) + a_3(i,j).Cela se généralise immédiatement en dimensions supérieures (mais les notations deviennent assez lourdes), en se limitant aux interaction de deux (ou trois) variables (sinon, on risque d'avoir trop de paramètres par rapport au nombre d'observations).
Sous R, on utilise la commande glm avec l'argument << family=poisson >>.
m <- data.frame(table(random.data.1())) y <- m[,4] x1 <- m[,1] x2 <- m[,2] x3 <- m[,3] summary(glm( y ~ x1 + x2 + x3, family=poisson ))
Il vient :
> summary(glm( y ~ x1 + x2 + x3, family=poisson ))
Call:
glm(formula = y ~ x1 + x2 + x3, family = poisson)
Deviance Residuals:
Min 1Q Median 3Q Max
-2.6060 -0.8723 -0.2724 0.4264 3.2634
Coefficients:
Estimate Std. Error z value Pr(>|z|)
(Intercept) 9.981e-01 2.965e-01 3.366 0.000762 ***
x12 3.314e-01 2.476e-01 1.338 0.180799
x13 1.643e-01 2.568e-01 0.640 0.522302
x22 -4.000e-02 1.999e-01 -0.200 0.841418
x32 5.129e-02 3.203e-01 0.160 0.872784
x33 5.057e-09 3.244e-01 1.56e-08 1.000000
x34 1.001e-01 3.163e-01 0.316 0.751674
x35 1.001e-01 3.166e-01 0.316 0.751912
---
Signif. codes: 0 `***' 0.001 `**' 0.01 `*' 0.05 `.' 0.1 ` ' 1
(Dispersion parameter for poisson family taken to be 1)
Null deviance: 38.794 on 29 degrees of freedom
Residual deviance: 36.735 on 22 degrees of freedom
AIC: 139.11
Number of Fisher Scoring iterations: 4A FAIRE : comprendre ce résultat.
A FAIRE : expliquer comment ajouter/retirer certains des termes d'interaction. > r1 <- glm( y ~ x1 + x2 + x3 + x1*x2 + x2*x3 + x1*x3, family=poisson ) > r2 <- glm( y ~ x1 + x2 + x3, family=poisson ) > anova(r1,r2) Analysis of Deviance Table Model 1: y ~ x1 + x2 + x3 + x1 * x2 + x2 * x3 + x1 * x3 Model 2: y ~ x1 + x2 + x3 Resid. Df Resid. Dev Df Deviance 1 8 6.9906 2 22 13.1344 -14 -6.1438
A FAIRE : introduction A FAIRE : revoir le titre du paragraphe suivant
On cherche à prédire une variable qualitative, qui peut être « le patient a-t-il eu un infarctus ? », à l'aide de variables quantitatives représentant différents facteurs de risque potentiels (tension artérielle, nombre de calories ingérées par jour, exercice physique, poids, etc.). On essaye de déterminer quels sont les facteurs de risque les plus importants, i.e., quelles variables déterminent le mieux la variable qualitative.
On peut aussi utiliser l'AFD de manière prédictive , i.e., répondre à la question « la patient aura-t-il un infarctus ? ».
A FAIRE : expliquer comment on fait.
Plus précisément, la variable à prédire permet de séparer les
observations en différents groupes, et on cherche une combinaison
linéaire des variables prédictives sur laquelle on voit le mieux les
différences entre les groupes.
A FAIRE : vérifier ce qui suit.
J'imagine qu'on cherche à maximiser le quotient de la moyenne des
variances de cette combinaison linéaire dans chaque groupe et de sa
variance globale (comme pour l'anova).
???
Pour une variable binaire :
On normalise les variables prédictives
On calcule la matrice des covariances A
On calcule le vecteur des moyennes des différences des variables pour les deux groupes : d
On montre (?) que A w = d
w = A^-1 * d, ce sont les poids recherchés.
(C'est une bonne idée, aussi, de représenter graphiquement les observations --
si l'espace est de dimension supérieure à deux, on peut utiliser xgobi
pour faire tourner la figure.)
Diagnostics:
Matrice de confusion : lignes = valeurs réelles, colonnes = valeurs
prédites, cases = nombre de cas correspondants.
A partir de la matrice de confusion, on peut construire plus d'une
dizaines de mesures différentes de la pertinence de l'analyse
discriminante
http://149.170.199.144/multivar/da4.htm
On peut commencer par réduire la dimension, par exemple avec une
analyse en composantes principales.
On peut aussi faire une analyse discriminante pas à pas (stepwise discriminant analysis)
library(MASS)
n <- 100
k <- 5
x1 <- runif(k,-5,5) + rnorm(k*n)
x2 <- runif(k,-5,5) + rnorm(k*n)
x3 <- runif(k,-5,5) + rnorm(k*n)
x4 <- runif(k,-5,5) + rnorm(k*n)
x5 <- runif(k,-5,5) + rnorm(k*n)
y <- factor(rep(1:5,n))
plot(lda(y~x1+x2+x3+x4+x5))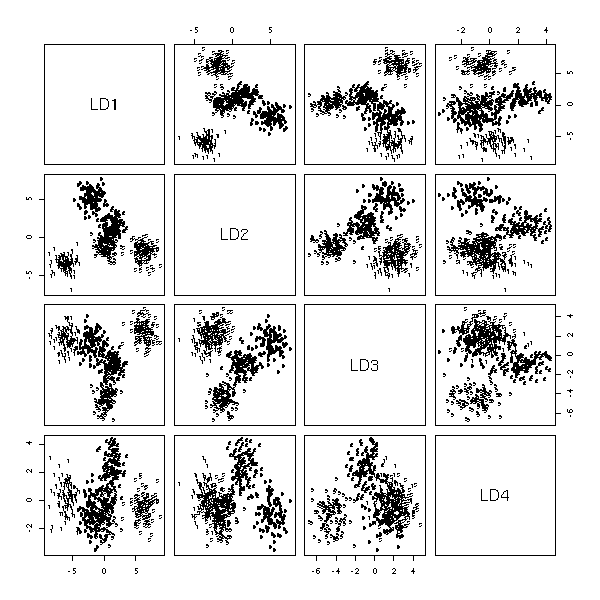
On peut choisir de ne retenir que les deux premières dimensions.
plot(lda(y~x1+x2+x3+x4+x5), dimen=2)
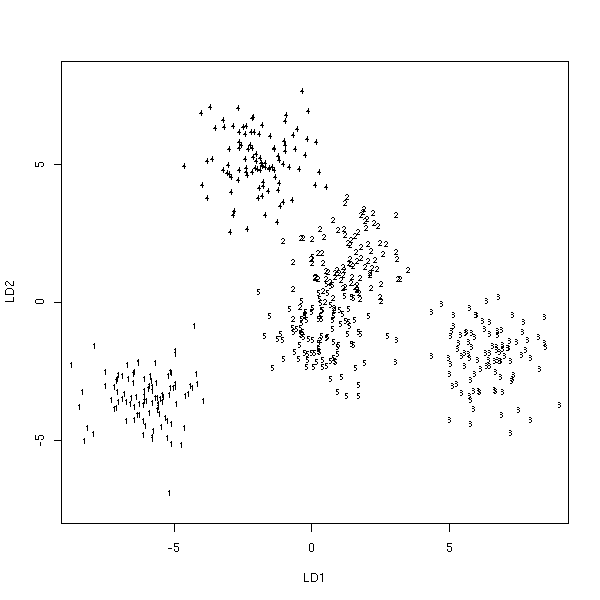
Ou même uniquement la première.
plot(lda(y~x1))
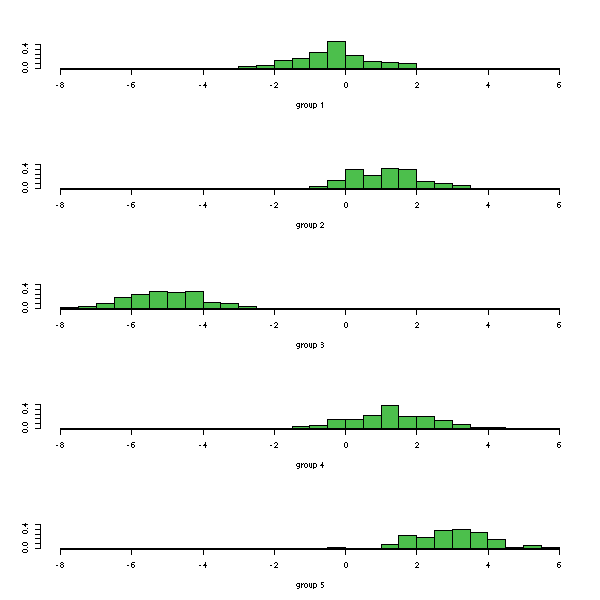
Comme pour l'analyse en composantes principales, on choisit le nombre de dimensions à garder en regardant les valeurs propres.
plot(lda(y~x1+x2+x3+x4+x5)$svd, type='h')
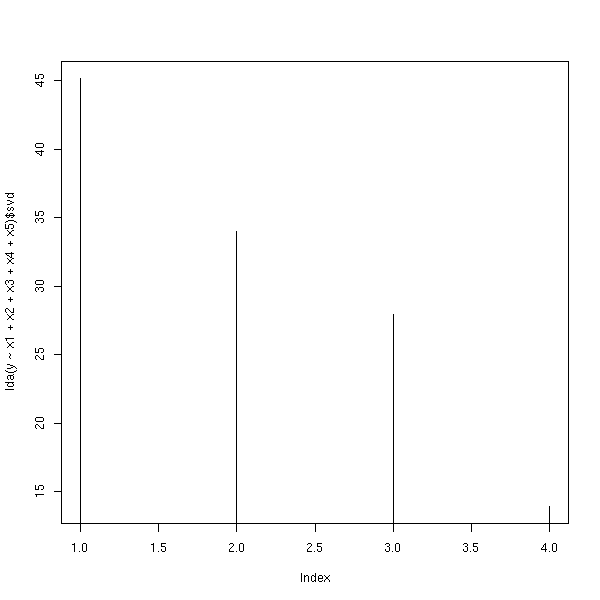
Les fonctions qda et predict.qda remplissent un rôle similaire, mais dans une situation non linéaire (quadratique).
?qda
Voir aussi la bibliothèque mda.
library(help=mda)
C'est pareil, mais on connait les probabilités
P ( Y == i ).
(On utilise toujours la commande lda, avec un argument de plus.)
On a des variables statistiques X1, X2, ..., Xp, Y1, Y2, ..., Yq et on cherche une combinaison linéaire Xa des Xi et une combinaison linéaire Yb des Yj de sorte que Xa et Yb soient les plus corrélées possible.
library(ade4) ?cca
Exemple : la partie 4 de
http://www.cg.ensmp.fr/%7Evert/talks/021205inria/inria.pdf
Je ne sais pas ce que c'est...
A FAIRE
La bibliothèque ade4 contient plein d'autres choses du même genre.
library(help=ade4)
Voir aussi
library(help=pcurve)
L'analyse en composantes principales et les méthodes qui s'en déduisent sont linéaires : si les données ne sont pas linéaires, leur résultat n'aura pas grand sens.
http://nitro.biosci.arizona.edu/courses/EEB581-2004/handouts/Eigenstructure.pdf
Vincent Zoonekynd
<zoonek@math.jussieu.fr>
latest modification on Wed Oct 13 22:32:41 BST 2004