
Problématique
Plan de ce document
Données
Idée 1 : Réduction de la dimension
Idée 2
Idée 2 bis
Idée 3 : Problème du voyageur de commerce
A FAIRE
Attention : ce document est encore à l'état de brouillon
A FAIRE : Remettre de l'rodre dans ce document 0. Problématique, données 1. Noyaux 2. Réseaux de neurones 3. k-means + MST 4. Isomap 5. Optimisation 6. pruned MST 7. TSP 8. SVM
On dispose d'un nuage de points (40), dans un espace de dimension raisonnable (10) ou moins raisonnable (7000). Ces points sont à peu près alignés sur une courbe que l'on cherche à décrire.
L'exemple motivant ce problème est le suivant. A l'aide de puces à ADN, on a examiné l'expression de 7000 gènes chez 40 patients souffrant d'une même maladie, mais à des stades différents. On s'en apperçoit en effectuant une analyse en composantes principales (ou en appliquant d'autres méthodes de réduction de la dimension) : les points correspondant aux patients semblent alignés le long d'une courbe (en dimension deux, cette courbe peut présenter des singularités, par exemple, elle peut se recouper -- mais si on tient compte des dimensions suivantes, ce problème disparait). A l'aide de l'expression de ces gènes (ou juste de certains de ces gènes) on aimerait pouvoir définir un "indice" qui indique la position sur la courbe et donc le degré d'avancement de la maladie.
Après avoir présenté les quelques jeux de données (réels ou simulés) sur lesquels nous travaillerons, nous commencerons par appliquer des méthodes de réduction de la dimension (analyse en composantes principales après des transformations non linéaires, réseaux de neurones), des méthodes d'optimisation et des méthodes de résolution du problème du voyageur de commerce, puis nous comparerons toutes ces méthodes.
Dans un dernier temps, nous considérerons un problème un peu différent : on dispose du nuage de points et, pour chaque point, son indice. On tentera de prédire l'indice d'un nouveau point.
Au lieu d'une courbe, commençons par prendre une ligne brisée.
n <- 200 # Nombre de sujets, nombre de colonnes
k <- 10 # Dimension de l'espace dans lequel la courbe recherchée vit
nb.points <- 5
p <- matrix( 5*rnorm(nb.points*k), nr=k )
barycentre <- function (x, n) {
# Ajouter des nombres entre les valeurs de x afin d'obtenir un
# vecteur de longueur n.
i <- seq(1,length(x)-.001,length=n)
j <- floor(i)
l <- i-j
(1-l)*x[j] + l*x[j+1]
}
m <- apply(p, 1, barycentre, n)
data.broken.line <- t(m)
pairs(t(data.broken.line))
plot(princomp(t(data.broken.line)))

pairs(princomp(t(data.broken.line))$scores[,1:5])

data.noisy.broken.line <- data.broken.line + rnorm(length(data.broken.line)) pairs(princomp(t(data.noisy.broken.line))$scores[,1:5])

Pour avoir une courbe au lieu des segments, il suffit de changer notre fonction "barycentre".
library(splines)
barycentre2 <- function (y,n) {
m <- length(y)
x <- 1:m
r <- interpSpline(x,y)
#r <- lm( y ~ bs(x, knots=m) )
predict(r, seq(1,m,length=n))$y
}
k <- 5
y <- sample(1:100,k)
x <- seq(1,k,length=100)
plot(barycentre2(y,100) ~ x)
lines(y, col='red', lwd=3, lty=2)
data.curve <- apply(p, 1, barycentre2, n) data.curve <- t(data.curve) pairs(t(data.curve))

plot(princomp(t(data.curve)))

pairs(princomp(t(data.curve))$scores[,1:5])

On va quand-même ajouter un peu de bruit :
data.noisy.curve <- data.curve + rnorm(length(data.curve)) pairs(t(data.noisy.curve))

plot(princomp(t(data.noisy.curve)))

pairs(princomp(t(data.noisy.curve))$scores[,1:5])

Réfléchissons un peu sur la forme possible de la courbe que l'on va obtenir. S'il s'agit d'une maladie mortelle (ou si, chez tous les patients de l'étude, la maladie évolue vers la mort), on peut s'attendre à observer un segment, éventuellement un peu déformé, une extrémité correspondant aux individus sains, l'autre à la mort.
S'il s'agit d'une maladie bénigne, on pourrait s'attendre à observer des points répartis le long d'un cercle, correspondant au cycle sain, malade, en rémission, sain.
S'il s'agit d'une maladie parfois mortelle, mais parfois curable, on peut imaginer un mélange des deux : une réunion d'un cercle et d'un segment.
random.rotation.matrix <- function (n=3) {
m <- NULL
for (i in 1:n) {
x <- rnorm(n)
x <- x / sqrt(sum(x*x))
y <- rep(0,n)
if (i>1) for (j in 1:(i-1)) {
y <- y + sum( x * m[,j] ) * m[,j]
}
x <- x - y
x <- x / sqrt(sum(x*x))
m <- cbind(m, x)
}
m
}
n <- 200
k <- 10
x <- seq(0,2*pi,length=n)
data.circle <- matrix(0, nr=n, nc=k)
data.circle[,1] <- cos(x)
data.circle[,2] <- sin(x)
data.circle <- data.circle %*% random.rotation.matrix(k)
data.circle <- t( t(data.circle) + rnorm(k) )
pairs(data.circle[,1:3])
data.circle <- data.circle + .1*rnorm(n*k) pairs(data.circle[,1:3])

pairs(princomp(data.circle)$scores[,1:3])

A FAIRE : l'autre exemple.
data.real <- read.table("Tla_z.txt", sep=",")
data.real.group <- factor(substr(names(data.real),0,1))
r <- prcomp(t(data.real))
plot(r$sdev, type='h')
data.real.3d <- r$x[,1:3] pairs(data.real.3d, pch=16, col=as.numeric(data.real.group))

Pour voir un peu mieux ce qui se passe, on peut tenter de mettre les points d'un même groupe dans une ellipse.
draw.ellipse <- function (
x, y=NULL, N=100,
method=lines, ...
) {
if (is.null(y)) {
y <- x[,2]
x <- x[,1]
}
centre <- c(mean(x), mean(y))
m <- matrix(c(var(x),cov(x,y),
cov(x,y),var(y)),
nr=2,nc=2)
e <- eigen(m)
r <- sqrt(e$values)
v <- e$vectors
theta <- seq(0,2*pi, length=N)
x <- centre[1] + r[1]*v[1,1]*cos(theta) +
r[2]*v[1,2]*sin(theta)
y <- centre[2] + r[1]*v[2,1]*cos(theta) +
r[2]*v[2,2]*sin(theta)
method(x,y,...)
}
draw.star <- function (x, y=NULL, ...) {
if (is.null(y)) {
y <- x[,2]
x <- x[,1]
}
d <- cbind(x,y)
m <- apply(d, 2, mean)
segments(m[1],m[2],x,y,...)
}
my.plot <- function (
d, f=rep(1,dim(d)[1]),
col=rainbow(length(levels(f))),
variables=NULL, legend=T, legend.position=1,
draw=draw.ellipse, ...) {
xlim <- range(d[,1])
ylim <- range(d[,2])
if(!is.null(variables)){
xlim <- range(xlim, variables[,1])
ylim <- range(ylim, variables[,2])
}
plot(d, col=col[as.numeric(f)], pch=16,
xlim=xlim, ylim=ylim, ...)
for (i in 1:length(levels(f))) {
try(
draw(d[ as.numeric(f)==i, ], col=col[i])
)
}
if(!is.null(variables)){
arrows(0,0,variables[,1],variables[,2])
text(1.05*variables,rownames(variables))
}
abline(h=0,lty=3)
abline(v=0,lty=3)
if(legend) {
if(legend.position==1) {
l=c( par('usr')[1],par('usr')[4], 0, 1 )
} else if (legend.position==2) {
l=c( par('usr')[2],par('usr')[4], 1, 1 )
} else if (legend.position==3) {
l=c( par('usr')[1],par('usr')[3], 0, 0 )
} else if (legend.position==4) {
l=c( par('usr')[2],par('usr')[3], 1, 0 )
} else {
l=c( mean(par('usr')[1:2]),
mean(par('usr')[1:2]), .5, .5 )
}
legend(l[1], l[2], xjust=l[3], yjust=l[4],
levels(f),
col=col,
lty=1,lwd=3)
}
}
my.plot(data.real.3d[,1:2], data.real.group)
op <- par(mfrow=c(3,3), mar=c(0,0,0,0))
plot.new();
my.plot(data.real.3d[,c(2,1)], data.real.group,
xlab='',ylab='',axes=F,legend=F)
box()
my.plot(data.real.3d[,c(3,1)], data.real.group,
xlab='',ylab='',axes=F,legend=F)
box()
my.plot(data.real.3d[,c(1,2)], data.real.group,
draw=draw.star,
xlab='',ylab='',axes=F,legend=F)
box()
plot.new()
my.plot(data.real.3d[,c(3,2)], data.real.group,
xlab='',ylab='',axes=F,legend=F)
box()
my.plot(data.real.3d[,c(1,2)], data.real.group,
draw=draw.star,
xlab='',ylab='',axes=F,legend=F)
box()
my.plot(data.real.3d[,c(2,3)], data.real.group,
draw=draw.star,
xlab='',ylab='',axes=F,legend=F)
box()
plot.new()
par(op)
On peut aussi faire tourner l'image dans tous les sens.
set.seed(66327)
random.rotation.matrix <- function (n=3) {
m <- NULL
for (i in 1:n) {
x <- rnorm(n)
x <- x / sqrt(sum(x*x))
y <- rep(0,n)
if (i>1) for (j in 1:(i-1)) {
y <- y + sum( x * m[,j] ) * m[,j]
}
x <- x - y
x <- x / sqrt(sum(x*x))
m <- cbind(m, x)
}
m
}
op <- par(mfrow=c(3,3), mar=c(0,0,0,0))
for (i in 1:9) {
#plot( (data.real.3d %*% random.rotation.matrix(3))[,1:2],
# pch=16, col=as.numeric(data.real.group),
# xlab='', ylab='', axes=F )
my.plot((data.real.3d %*% random.rotation.matrix(3))[,1:2],
data.real.group,
draw=draw.ellipse,
xlab='',ylab='',axes=F,legend=F)
box()
}
par(op)
Des méthodes comme l'analyse en composantes principales (PCA) permettent de réduire la dimension du nuage de points mais, étant linéaires, ne permettent pas de "déméler" la courbe observée : elle restera courbe et ne donnera pas un segment.
Une idée consiste à plonger notre espace (de dimension raisonnable (10) ou non (7000)) dans un espace de dimension plus grande, de manière non linéaire. En appliquant des méthodes linéaires dans cet espace plus grand, on peut espérer mettre en évidence des phénomènes non linéaires dans l'espace de départ.
Voici un exemple de tel plongement :
(x,y) ---> (x^2, x*y, y^2).
Il peut paraître déraisonnable de plonger un espace de dimension déjà élevée dans un espace de dimension encore plus grande. Ce serait le cas si on avait besoin de calculer les coordonnées des points dans ce nouvel espace, mais nous avons juste besoin de savoir calculer des produits scalaires dans ce nouvel espace.
Plus précisément, l'analyse en composantes principales (ou d'autres méthodes semblables) partent de la matrice de variance-covariance
t(m) %*% m
Avec la matrice de variance-covariance dans le nouvel espace, ça donne :
m <- data.curve
mm <- apply(m, 2, function (x) { x %o% x } )
r <- princomp(t(mm))
plot(r)
pairs(r$scores[,1:5])

Rien de très concluant...
Essayons en degré 3.
# Noyau de degré 1
noyau1 <- function (x,y) { sum(x*y) }
m <- data.curve
m <- t(t(m) - apply(m,2,mean))
k <- dim(m)[1]
wrapper <- function(x, y, my.fun, ...) {
sapply(seq(along=x), FUN = function(i) my.fun(x[i], y[i], ...))
}
mm <- outer(1:k, 1:k, wrapper, function (i,j) { noyau1(m[,i],m[,j]) })
# Noyau de degré 2
noyau2 <- function (x,y) {
a <- x*y
n <- length(a)
i <- gl(n,1,n^2)
j <- gl(n,n,n^2)
i <- as.numeric(i)
j <- as.numeric(j)
w <- which( i <= j & j <= k )
i <- i[w]
j <- j[w]
sum(a[i]*a[j])
}
stopifnot( noyau2(1:2,2:1) == 12 )
# Noyau de degré 3
noyau3 <- function (x,y) {
a <- x*y
n <- length(a)
i <- gl(n,1,n^3)
j <- gl(n,n,n^3)
k <- gl(n,n^2,n^3)
i <- as.numeric(i)
j <- as.numeric(j)
k <- as.numeric(k)
w <- which( i <= j & j <= k )
i <- i[w]
j <- j[w]
k <- k[w]
sum(a[i]*a[j]*a[k])
}
stopifnot( noyau3(1:2,2:1) == 32 )
wrapper <- function(x, y, my.fun, ...) {
sapply(seq(along=x), FUN = function(i) my.fun(x[i], y[i], ...))
}
k <- dim(m)[1]
mm <- outer(1:k, 1:k, FUN=wrapper, my.fun = function (i,j) { noyau3(m[,i],m[,j]) })
r <- princomp(covmat=mm)
plot(r)
#pairs(r$scores[,1:5]) plot((t(m) %*% r$loadings) [,1:2])

k <- dim(data.noisy.curve)[1]
mm <- outer(1:k, 1:k, FUN=wrapper, my.fun = function (i,j) {
noyau3(data.noisy.curve[,i],data.noisy.curve[,j])
})
r <- princomp(t(data.noisy.curve), covmat=mm)
plot(r)
pairs((t(m) %*% r$loadings) [,1:5])

plot((t(m) %*% r$loadings) [,1:2]) lines((t(m) %*% r$loadings) [,1:2], col='red')

x <- 1:dim(data.noisy.curve)[2] y1 <- (t(m) %*% r$loadings) [,1] y2 <- (t(m) %*% r$loadings) [,2] r1 <- loess(y1~x) r2 <- loess(y2~x) plot(y1,y2) lines(y1,y2, col='red') lines(predict(r1), predict(r2), col='blue', lwd=3)

Essayons en combinant ces différents noyaux.
noyau <- function (x,y) {
noyau1(x,y) + noyau2(x,y) + noyau3(x,y)
}
mm <- outer(1:k, 1:k, FUN=wrapper, my.fun = function (i,j) {
noyau(data.curve[,i],data.curve[,j])
})
r <- princomp(covmat=mm)
plot(r)
pairs((t(m) %*% r$loadings) [,1:5])

En définitive, ces méthodes sont peu concluantes.
On peut réduire la dimension d'un nuage de points à l'aide d'un réseau à 5 couches, une couche d'entrée (avec les données), une couche de compression (non linéaire), une couche représentant les données dans l'espace de dimension réduite recherché (linéaire), une couche de décompression (non linéaire), une couche de sortie (sur laquelle on essaye de retrouver les données de départ).
Je n'ai pas l'impression que R prévoie de tels réseaux, on va donc les implémenter nous-même. (Il faudra faire TRÈS attention à la convergence.)
Comme je ne connais pas vraiment les réseaux de neurones (je m'y suis intéressé très superficiellement il y a une dizaine d'années), je cherche un peu sur internet et je trouve une page qui les explique assez clairement et, en particulier, qui mentionne l'application à la réduction de la dimension :
http://www.willamette.edu/%7Egorr/classes/cs449/backprop.html
Voici le code que j'en déduis.
A FAIRE : commencer par regarder sur un exemple de petite taille,
pour lequel le calcul sera rapide, et pour lequel on saiit à quel
résultat s'attendre. Par exemple, prendre un nuage des points de
dimension 2 dans un espace de dimension 3, avec uniquement des
neurones linéaires et juste deux neurones dans la couche du
milieu.
Problème : dans ce cas, les couches intermédiaires ne servent pas
à grand-chose, et risquent même de nuire à la stabilité de
l'algorithme.
# x : matrice, les colonnes sont les différents vecteurs à apprendre
# n : nombre de neurones sur la couche du milieu
# m : nombre de neurones sur les deux autres couches cachées
# (on devrait avoir m>n)
drnn <- function (M, n, m, e=.1, N=100) {
# Les fonctions d'activation
id <- function (t) { t }
f1 <- tanh
f2 <- id
f3 <- tanh
f4 <- id
# Le nombre de neurones dans chaque couche
n0 <- dim(M)[1]
n1 <- m
n2 <- n
n3 <- m
n4 <- n0
# Les poids -- on les initialise à des valeurs aléatoires
w1 <- matrix( rnorm(n0*n1), nc=n0, nr=n1 )
w2 <- matrix( rnorm(n1*n2), nc=n1, nr=n2 )
w3 <- matrix( rnorm(n2*n3), nc=n2, nr=n3 )
w4 <- matrix( rnorm(n3*n4), nc=n3, nr=n4 )
# Les biais
b1 <- rnorm(n1)
b2 <- rnorm(n2)
b3 <- rnorm(n3)
b4 <- rnorm(n4)
# L'algorithme (backpropagation)
r <- list()
err <- rep(0, N)
for (i in 1:N) {
cat(paste("Itération", i, "\n"))
res <- matrix(NA, nr=n, nc=dim(M)[2])
for (j in 1:dim(M)[2]) {
x <- M[,j]
# Calcul des valeurs des noeuds
y0 <- x
y1 <- f1( w1 %*% y0 + b1 )
y2 <- f2( w2 %*% y1 + b2 )
y3 <- f3( w3 %*% y2 + b3 )
y4 <- f4( w4 %*% y3 + b4 )
# Calcul des erreurs
d4 <- x - y4
d3 <- (t(w4) %*% d4) * (1 - y3^2)
d2 <- (t(w3) %*% d3) * 1
d1 <- (t(w2) %*% d2) * (1 - y1^2)
# Mise à jour des poids et des biais
dw4 <- d4 %*% t(y3)
dw3 <- d3 %*% t(y2)
dw2 <- d2 %*% t(y1)
dw1 <- d1 %*% t(y0)
w4 <- w4 + e * dw4
w3 <- w3 + e * dw3
w2 <- w2 + e * dw2
w1 <- w1 + e * dw1
b4 <- b4 + e * d4
b3 <- b3 + e * d3
b2 <- b2 + e * d2
b1 <- b1 + e * d1
res[,j] <- y2
err[i] <- err[i] + sum(d4^2)
}
r[[i]] <- res
}
list(scores=res, errors=err, r=r)
}
r <- drnn(data.curve, 1, 4, N=30, e=.02)
plot(r$err, ylim=range(c(0,r$err)), type='l')
i <- order(drop(r$scores)) plot(t(data.curve)[,1:2]) lines(t(data.curve)[,1:2][i,], col='red')

Ça n'est pas exactement ce à quoi on s'attendait. Mais c'est quand même mieux que rien...
op <- par(mfrow=c(2,2))
for (k in c(1, 3, 7, 30)) {
i <- order(drop(r$r[[k]]))
plot(t(data.curve)[,1:2], main=paste("après",k,"itération(s)"))
lines(t(data.curve)[,1:2][i,], col='red')
}
par(op)
Changer l'ordre dans lequel on présente les points au réseau de neurone n'a pas de réel effet.
op <- par(mfrow=c(2,4))
for (i in 1:4) {
m <- data.curve[,sample(1:dim(data.curve)[2])]
r <- drnn(m, 1, 4, N=30, e=.02)
plot(r$err, ylim=range(c(0,r$err)), type='l')
i <- order(drop(r$scores))
plot(t(m)[,1:2])
lines(t(m)[,1:2][i,], col='red')
}
par(op)
(Le graphique des erreurs est assez inquiétant : l'erreur est sensée baisser, itération après itération -- or elle augmente parfois...)
Regardons maintenant ce qui se passe si on met deux neurones dans la couche du milieu.
i <- sample(1:dim(data.curve)[2]) m <- data.curve[,i] r <- drnn(m, 2, 8, N=30, e=.02) plot(r$err, ylim=range(c(0,r$err)), type='l') plot(t(r$scores)[i,], type='l')

(Oui, c'est sensé être une courbe...)
A FAIRE : regarder un peu mieux ce qui se passe quand on change l'un des paramètres. A chaque fois, faire 4 graphiques : la décroissance de l'erreur, le premier chemin, le dernier. A FAIRE : vérifier que mon implémentation est correcte, en l'utilisant dans une situation plus simple. (L'évolution de l'erreur suggère une erreur quelque part...)
- Répartir les points dans 4 ou 5 classes (classification hiérarchique) - Prendre le point médiant de ces classes. - Le MST de ces 4 ou 5 points est-il ramifié ?
Sur nos exemples :
library(cluster)
library(ape)
mst.of.classification <- function (x, k=6, ...) {
x <- t(x)
x <- t( t(x) - apply(x,2,mean) )
r <- prcomp(x)
y <- r$x
u <- r$rotation
r <- kmeans(y,k)
z <- r$centers
m <- mst(dist(z))
plot(y[,1:2], ...)
points(z[,1:2], col='red', pch=15)
w <- which(m!=0)
i <- as.vector(row(m))[w]
j <- as.vector(col(m))[w]
segments( z[i,1], z[i,2], z[j,1], z[j,2], col='red' )
}
set.seed(1)
mst.of.classification(data.curve, 6)
mst.of.classification(data.curve, 6)

op <- par(mfrow=c(2,2),mar=c(0,0,0,0))
for (k in c(4,6,10,15)) {
mst.of.classification(data.curve, k, axes=F)
box()
}
par(op)
op <- par(mfrow=c(2,2),mar=c(0,0,0,0))
for (k in c(4,6,10,15)) {
mst.of.classification(data.noisy.curve, k, axes=F)
box()
}
par(op)
op <- par(mfrow=c(2,2),mar=c(0,0,0,0))
for (k in c(4,6,10,15)) {
mst.of.classification(data.broken.line, k, axes=F)
box()
}
par(op)
op <- par(mfrow=c(2,2),mar=c(0,0,0,0))
for (k in c(4,6,10,15)) {
mst.of.classification(data.noisy.broken.line, k, axes=F)
box()
}
par(op)
Sur des données réelles, ça marche moins bien :
op <- par(mfrow=c(2,2),mar=c(0,0,0,0))
for (k in c(4,6,10,15)) {
mst.of.classification(data.real, k, axes=F)
box()
}
par(op)
Détails :
op <- par(mfrow=c(3,3),mar=c(0,0,0,0))
for (k in c(4:6)) {
for (i in 1:3) {
mst.of.classification(data.real, k, axes=F)
box()
}
}
par(op)
op <- par(mfrow=c(3,3),mar=c(0,0,0,0))
for (k in c(7:9)) {
for (i in 1:3) {
mst.of.classification(data.real, k, axes=F)
box()
}
}
par(op)
op <- par(mfrow=c(3,3),mar=c(0,0,0,0))
for (k in c(10:12)) {
for (i in 1:3) {
mst.of.classification(data.real, k, axes=F)
box()
}
}
par(op)
op <- par(mfrow=c(3,5),mar=c(0,0,0,0))
for (k in c(13:15)) {
for (i in 1:3) {
mst.of.classification(data.real, k, axes=F)
box()
}
}
par(op)
Il y a quelque temps, j'ai vu passer un article sur la réduction de la dimension (dans Rnews, ou une vignette dans la documentation de R). Le relire. Implémenter Isomap (assez facile, utiliser MST.) Regarder d'autres articles sur la réduction de la dimension. google: dimensionality reduction
A FAIRE : référence
A FAIRE : expliquer
Construction du graphe
# k: each point is linked to its k nearest neighbors
# eps: each point is linked to all its neighbors within a radius eps
isomap.incidence.matrix <- function (d, eps=NA, k=NA) {
stopifnot(xor( is.na(eps), is.na(k) ))
d <- as.matrix(d)
if(!is.na(eps)) {
im <- d <= eps
} else {
im <- apply(d,1,rank) <= k+1
diag(im) <- F
}
im | t(im)
}
plot.graph <- function (im,x,y=NULL, ...) {
if(is.null(y)) {
y <- x[,2]
x <- x[,1]
}
plot(x,y, ...)
k <- which( as.vector(im) )
i <- as.vector(col(im))[ k ]
j <- as.vector(row(im))[ k ]
segments( x[i], y[i], x[j], y[j], col='red' )
}
d <- dist(t(data.noisy.curve))
r <- princomp(t(data.noisy.curve))
x <- r$scores[,1]
y <- r$scores[,2]
plot.graph(isomap.incidence.matrix(d, k=5), x, y)
Pour l'instant, il y a un problème : le graphe obtenu n'est pas nécessairement connexe -- c'est très génant pour calculer des distances.
plot.graph(isomap.incidence.matrix(d, eps=quantile(as.vector(d), .05)),
x, y)
On voit aisément que le graphe obtenu est connexe si et seulement si il contient l'arbre couvrant minimal (MST) : on va donc simplement rajouter les arrêtes de let arbre couvrant minimal qui ne sont pas encore présentes.
isomap.incidence.matrix <- function (d, eps=NA, k=NA) {
stopifnot(xor( is.na(eps), is.na(k) ))
d <- as.matrix(d)
if(!is.na(eps)) {
im <- d <= eps
} else {
im <- apply(d,1,rank) <= k+1
diag(im) <- F
}
im | t(im) | mst(d)
}
plot.graph(isomap.incidence.matrix(d, eps=quantile(as.vector(d), .05)),
x, y)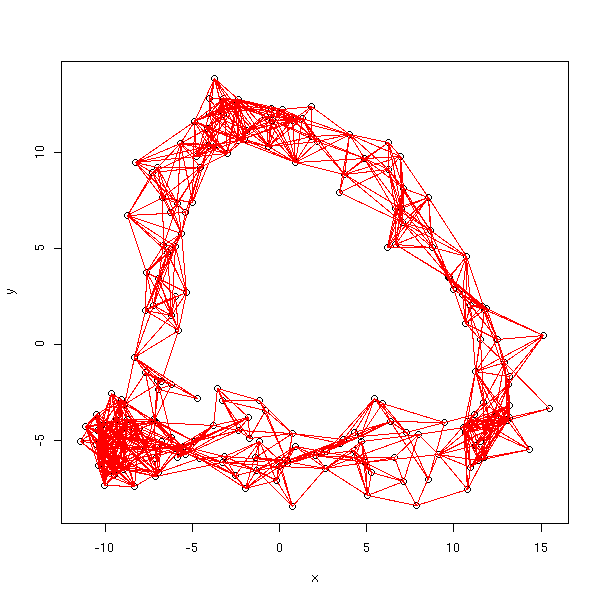
A FAIRE : mesure de la distance dans le graphe. C'est un problème de plus court chemin dans un graphe...
inf <- function (x,y) { ifelse(x<y,x,y) }
isomap.distance <- function (im, d) {
d <- as.matrix(d)
n <- dim(d)[1]
dd <- ifelse(im, d, Inf)
for (k in 1:n) {
dd <- inf(dd, matrix(dd[,k],nr=n,nc=n) + matrix(dd[k,],nr=n,nc=n,byrow=T))
}
dd
}
isomap <- function (x, d=dist(x), eps=NA, k=NA) {
im <- isomap.incidence.matrix(d, eps, k)
dd <- isomap.distance(im,d)
r <- list(x,d,incidence.matrix=im,distance=dd)
class(r) <- "isomap"
r
}
r <- isomap(t(data.noisy.curve), k=5)
xy <- cmdscale(r$distance,2) # long : compter une trentaine de secondes...
plot.graph(r$incidence.matrix, xy)
Dans un repère orthonormé :
plot.graph(r$incidence.matrix, xy, ylim=range(xy))

A FAIRE :
D'autres manières d'afficher les résultats : 1. Données initiales, graphe 2. MDS 3. Données initiales, graphe, couleurs correspondant à la première coordonnée de l'analyse des coordonnées 4. La courbe ?
A FAIRE : appliquer ça à nos données
A FAIRE : le choix des paramètres (eps ou k)
On peut présenter ce problème comme un problème d'optimisation : on cherche les coordonnées de 5 points A1, A2, A3, A4, A5 afin de minimiser la somme des (carrés des) distances des points du nuage à la ligne brisée A1-A2-A3-A4-A5.
A FAIRE : pour vérifier que cet algorithme fonctionne, commencer par
lui donner
- un seul segment à retrouver, en dimension 1.
- un seul segment à retrouver, en dimension 2.
- une courbe (parabole, assez applatie) à approcher par un seul
segment.
- une courbe (parabole) à approcher par deux segments.
- enfin, seulement, la situation qui nous intéresse.
distance.broken.line <- function (point, ligne) {
# point : vecteur contenant les coordonnées du point du nuage dont
# on calcule la distance à la ligne
# ligne : coordonnées, en colonnes, des points constituant la
# ligne brisée.
# Distance aux sommets de la ligne brisée
d.points <- apply( (ligne-point)^2, 2, sum )
# Position de la projection du point sur chacune des droites
# constituant la ligne brisée
v <- t(apply(ligne,1,diff)) # vecteurs A(i)A(i+1)
w <- -ligne + point # vecteurs A(i)M
w <- w[, -dim(w)[2]] # on enlève le dernier
lambda <- apply(v*w, 2, sum) / apply(v^2,2,sum)
lambda[ is.nan(lambda) ] <- 0
# Distance aux droites constituant la ligne brisée
d.segments <- apply( (w - t(lambda*t(v)))^2, 2, sum )
d.segments <- d.segments[ lambda>0 & lambda<1 ]
min(c( d.points, d.segments ))
}
# Vérifications : les distances suivantes sont (à peu près) nulles
stopifnot( distance.broken.line(p[,1], p) < 1e-6 )
stopifnot( distance.broken.line(.5*p[,1]+.5*p[,2], p) < 1e-6 )
# Il y a un gros problème de vitesse : il faut deux secondes pour
# calculer la distance sur cet exemple :
sum(apply(data.noisy.broken.line, 2, distance.broken.line, p))
broken.line <- function (
d, # données
np=4, # Nombre de sommets de la ligne brisée recherchée
deb = as.vector(d[,sample(1:dim(d)[2], np)])
# Valeurs de départ : ligne brisée passant par np points
# du nuage, pris au hasard.
) {
f <- function (x) {
sum(apply(d, 2, distance.broken.line, matrix(x, nc=np) ))
}
# Très, très long
r <- optim(deb, f, control=list(trace=1, maxit=50)) # Par défaut : 500 itérations
list(par=r$par, method="optim", value=r$value, deb=deb, np=np, r=r)
}
r <- broken.line(data.noisy.broken.line)
pc <- princomp(t(data.noisy.broken.line))
plot(pc$scores[,1:2])
lines( (t(matrix(r$deb,nc=r$np) - pc$center) %*% pc$loadings)[,1:2], col='red',lwd=3,lty=3)
lines((t(matrix(r$par,nc=r$np) - pc$center) %*% pc$loadings)[,1:2], col='blue',lwd=3,lty=2)
# Exemple : un segment, en dimension un
l <- c(-5, 3, 2, -1)
deb <- c(1,2,3,4)
d <- rbind( seq(l[1],l[2],length=10), seq(l[3],l[4],length=10) )
r <- broken.line(d, np=2, deb=deb)
plot(t(d), xlim=c(-10,10), ylim=c(-10,10))
# Je m'embrouille dans l'ordre des paramètres à estimer...
for (i in 1:100) { lines(matrix(sample(r$par), nr=2) ) }
# valeurs de départ : certains points du nuage, pris au hasard
op <- par(mfrow=c(3,3), mar=c(0,0,0,0))
for (i in 1:9) {
l <- runif(4, -8,8)
d <- rbind( seq(l[1],l[2],length=10), seq(l[3],l[4],length=10) )
r <- broken.line(d, np=2)
plot(t(d), xlim=c(-10,10), ylim=c(-10,10),
xlab='', ylab='', axes=F)
box()
lines( r$par[c(1,3)], r$par[c(2,4)], col='red' )
}
par(op)
# Valeurs de départ complètement aléatoires
op <- par(mfrow=c(3,3), mar=c(0,0,0,0))
for (i in 1:9) {
l <- runif(4, -8,8)
deb <- runif(4, -8,8)
d <- rbind( seq(l[1],l[2],length=10), seq(l[3],l[4],length=10) )
r <- broken.line(d, np=2, deb=deb)
plot(t(d), xlim=c(-10,10), ylim=c(-10,10),
xlab='', ylab='', axes=F)
box()
lines( r$par[c(1,3)], r$par[c(2,4)], col='red' )
lines( deb[c(1,3)], deb[c(2,4)], col='blue', lty=2 )
}
par(op)
Aaaaaaahhhhhhhhhhhh... Ca ne converge pas vraiment. Essayons d'insister, en lançant l'algorithme plusieurs fois,
op <- par(mfrow=c(3,3), mar=c(0,0,0,0))
for (i in 1:9) {
l <- runif(4, -8,8)
deb <- runif(4, -8,8)
d <- rbind( seq(l[1],l[2],length=10), seq(l[3],l[4],length=10) )
plot(t(d), xlim=c(-10,10), ylim=c(-10,10),
xlab='', ylab='', axes=F)
box()
lines( deb[c(1,3)], deb[c(2,4)], col='blue', lty=2 )
for (j in 1:10) {
r <- broken.line(d, np=2, deb=deb)
lines( r$par[c(1,3)], r$par[c(2,4)], col='red' )
deb <- r$par
}
}
par(op)
%--Non, ça ne converge décidément pas.
A FAIRE : regarder quelle est la valeur de la distance à la fin de l'algorithme... J'obtient des valeurs extrèmenent faibles, alors que le segment est assez loin des points : pourquoi ??? (Ce bug pourrait expliquer les problèmes de convergence...)
Il y a un autre problème : la solution qu'on cherche n'est pas unique. Si un segment est solution de notre problème d'optimisation, alors tout segment plus long le sera aussi.
Ca converge trop lentement pour qu'on ait un résultat. Essayons avec la fonction nlm (après réflexions, il semblerait qu'"optim" soit efficace sur des fonctions "méchantes" et "nlm" sur des fonctions gentilles -- or la fonction qu'on cherche à minimiser me semble quadratique par morceaux, avec un unique minimum local, qui est donc aussi global).
# Encore plus long... r <- nlm(f, deb, iterlim=20) # Par défaut, iterlim=100... pc <- princomp(t(data.noisy.broken.line)) plot(pc$scores[,1:2]) lines( (t(matrix(deb, nc=np) - pc$center) %*% pc$loadings)[,1:2], col='red', lwd=3, lty=3 ) lines((t(matrix(r$estimate,nc=np) - pc$center) %*% pc$loadings)[,1:2], col='blue', lwd=3, lty=2)
On peut tenter d'accélérer ces convergences en traitant séparément les dimensions.
NON, on ne peut pas... A FAIRE
Dans l'exemple précédent, la courbe était constituée de 4 segments mais on demandait une courbe constituée de 3 segments : si on en avait demandé plus, on aurait (probablement : les calculs sont longs je n'ai pas eu la patience d'attendre...) obtenu des segments de longueur nulle, sur lesquels la fonction de calcul des distance risque d'avoir des problèmes. Je suggère donc d'ajouter une pénalité à la fonction qu'on cherche à minimiser afin que les segments aient des longueurs comparables.
# J'ajoute la somme des inverses des carrés des longueurs des segments
f <- function (x) {
sum(apply(data.noisy.broken.line, 2, distance, matrix(x, nc=np) )) +
sum( 1/apply(t(apply(matrix(x,nc=np), 1,diff))^2, 2, sum) )
}
A FAIRE : un exemple de calcul avec 6 ou 7 points (alors que la
droite brisée en compte 5).
Idem, avec des courbes (par exemple, des splines).
A FAIRE
library(ape)
my.plot.mst <- function (d) {
r <- mst(dist(t(d)))
d <- prcomp(t(d))$x[,1:2]
plot(d)
n <- dim(r)[1]
w <- which(r!=0)
i <- as.vector(row(r))[w]
j <- as.vector(col(r))[w]
segments( d[i,1], d[i,2], d[j,1], d[j,2], col='red' )
}
my.plot.mst(data.broken.line)
my.plot.mst(data.noisy.broken.line)

my.plot.mst(data.curve)

my.plot.mst(data.noisy.curve)

my.plot.mst(data.real)

my.plot.mst(t(data.real.3d))

# Donne la liste des chemins des noeuds de branchement vers les
# feuilles
chemins.vers.les.feuilles <- function (G) {
nodes <- which(apply(G,2,sum)>2)
leaves <- which(apply(G,2,sum)==1)
res <- list()
for (a in nodes) {
for (b in which(G[a,]>0)) {
if (! b %in% nodes) {
res <- append(res,list(c(a,b)))
}
}
}
chemins.vers.les.feuilles.suite(G, nodes, leaves, res)
}
# Derniere coordonnée d'un vecteur
end1 <- function (x) {
n <- length(x)
x[n]
}
# Deux dernières coordonnées d'un vecteur
end2 <- function (x) {
n <- length(x)
x[c(n-1,n)]
}
chemins.vers.les.feuilles.suite <- function (G, nodes, leaves, res) {
new <- list()
done <- T
for (ch in res) {
if( end1(ch) %in% nodes ) {
# Pass
} else if ( end1(ch) %in% leaves ) {
new <- append(new, list(ch))
} else {
done <- F
a <- end2(ch)[1]
b <- end2(ch)[2]
for (x in which(G[b,]>0)) {
if( x != a ){
new <- append(new, list(c( ch, x )))
}
}
}
}
if(done) {
return(new)
} else {
return(chemins.vers.les.feuilles.suite(G,nodes,leaves,new))
}
}
G <- matrix(c(0,1,0,0, 1,0,1,1, 0,1,0,0, 0,1,0,0), nr=4)
chemins.vers.les.feuilles(G)
# Calcul de la longueur d'un chemin
longueur.chemin <- function (chemin, d) {
d <- as.matrix(d)
n <- length(chemin)
i <- chemin[ 1:(n-1) ]
j <- chemin[ 2:n ]
if (n==2) {
d[i,j]
} else {
sum(diag(d[i,][,j]))
}
}
G <- matrix(c(0,1,0,0, 1,0,1,1, 0,1,0,0, 0,1,0,0), nr=4)
d <- matrix(c(0,2,4,3, 2,0,2,1, 4,2,0,3, 3,1,3,0), nr=4)
chemins <- chemins.vers.les.feuilles(G)
chemins
l <- sapply(chemins, longueur.chemin, d)
l
stopifnot( l == c(2,2,1) )
élague <- function (G0, d0) {
d0 <- as.matrix(d0)
G <- G0
d <- d0
res <- 1:dim(d)[1]
chemins <- chemins.vers.les.feuilles(G)
while (length(chemins)>0) {
longueurs <- sapply(chemins, longueur.chemin, d)
# Numéro du chemin le plus court
i <- which( longueurs == min(longueurs) )[1]
cat(paste("Removing", paste(res[chemins[[i]]],collapse=' '), "length =", longueurs[i],"\n"))
# Noeuds à enlever
j <- chemins[[i]] [-1]
res <- res[-j]
G <- G[-j,][,-j]
d <- d[-j,][,-j]
cat(paste("Removing", paste(j), "\n" ))
cat(paste("", paste(res, collapse=' '), "\n"))
chemins <- chemins.vers.les.feuilles(G)
}
res
}
library(ape)
my.plot.mst <- function (x0) {
cat("Plotting the points\n")
x <- prcomp(t(x0))$x[,1:2]
plot(x)
cat("Computing the distance matrix\n")
d <- dist(t(x0))
cat("Computing the MST (Minimum Spanning Tree)\n")
G <- mst(d)
cat("Plotting the MST\n")
n <- dim(G)[1]
w <- which(G!=0)
i <- as.vector(row(G))[w]
j <- as.vector(col(G))[w]
segments( x[i,1], x[i,2], x[j,1], x[j,2], col='red' )
cat("Pruning the tree\n")
k <- élague(G,d)
cat("Plotting the pruned tree\n")
x <- x[k,]
G <- G[k,][,k]
n <- dim(G)[1]
w <- which(G!=0)
i <- as.vector(row(G))[w]
j <- as.vector(col(G))[w]
segments( x[i,1], x[i,2], x[j,1], x[j,2], col='red', lwd=3 )
}
my.plot.mst(data.noisy.broken.line)
my.plot.mst(data.noisy.curve)

my.plot.mst(data.real)

my.plot.mst(t(data.real.3d))

Remarque : en analyse d'image, on utilise parfois une simplification de cet algorithme (qui s'appelle encore "élagage") pour se débarasser des ramifications dans le squelette d'une image : on se contente de grignoter deux ou trois segments à partir de chaque feuille.
A FAIRE : une référence
Le problème du voyageur de commerce est le suivant : on dispose d'un nuage de points (dans un espace métrique) et on cherche un chemin, de longueur minimale, qui passe par chacun d'eux. Il s'agit donc de trouver un ordre sur un ensemble de points qui minimise une certaine fonction.
Présenté ainsi, ce problème a déjà beaucoup d'applications (par exemple, établir des circuits de livraison ; par exemple, définir le trajet d'un fer à souder, dans une chaine de montage d'appareils électroniques), mais beaucoup d'autres problèmes qui semblent ne rien à voir avec le TSP peuvent se reformuler en termes de TSP (par exemple, des problèmes de cartographie génétique : voir le livre de Setubal -- que je n'ai jamais ouvert).
On peut appliquer un algorithme de résolution du TSP à notre nuage de points, on obtient un ordre sur ces points, que l'on peut voir comme une ligne brisée. Ensuite, on "lisse" cette ligne brisée : on obtient une courbe, paramétrée par [0,1] : ce paramètre est l'indice recherché. Enfin, étant donné un nouveau point, il suffit de le projeter sur cette courbe pour obtenir la valeur du paramètre.
Je constate que des algorithmes de résolution du TSP ne sont pas implémentés sous R : il va nous falloir programmer...
Voici une implémentation de la descente simple.
longueur <- function (d,o) {
n <- length(o)
sum(diag( d [o[1:(n-1)],] [,o[2:n]] ))
}
tsp.descent <- function (d, N=1000) {
# d : matrice des distances.
d <- as.matrix(d)
n <- dim(d)[1]
o <- sample(1:n)
v <- longueur(d,o)
k <- 0
res <- list()
k.res <- c()
l.res <- c(v)
while (k<N) {
i <- sample(1:n, 2)
oo <- o
oo[ i[1] ] <- o[ i[2] ]
oo[ i[2] ] <- o[ i[1] ]
w <- longueur(d,oo)
if (w<v) {
v <- w
o <- oo
res <- append(res, list(o))
k.res <- append(k.res, k)
l.res <- append(l.res, v)
k <- 0
} else {
k <- k+1
}
}
list(o=o, détails=res, k=k.res, longueur=v, longueurs=l.res)
}
n <- 100
x <- matrix(runif(2*n), nr=n)
r <- tsp.descent(dist(x))
o <- r$o
plot(x)
lines(x[o,], col='red')
op <- par(mfrow=c(2,2))
n <- length(r$détails)
for (i in floor(c(1, n/4, n/2, n))) {
plot(x, main=paste("n =",i))
lines(x[r$détails[[i]],], col='red')
}
par(op)
La valeur de N que nous avons prise est insuffisante :
plot(r$k)

n <- 100
x <- seq(0,6, length=n)
x <- sample(x)
x <- cbind(cos(x), sin(x))
r <- tsp.descent(dist(x), N=10000)
op <- par(mfrow=c(2,2))
n <- length(r$détails)
for (i in floor(c(1, n/4, n/2, n))) {
plot(x, main=paste("n =",i))
lines(x[r$détails[[i]],], col='red')
}
par(op)
plot(r$k)

On peut tenter d'améliorer les résultats en lançant l'algorithme plusieurs fois.
# Très long...
op <- par(mfrow=c(3,3))
for (i in 1:9) {
r <- tsp.descent(dist(x), N=1000)
plot(x, main=signif(r$longueur))
lines( x[r$o,], col='red', type='l' )
}
par(op)
Ça n'est toujours pas concluant.
On peut modifier l'algorithme précédent en acceptant un nouveau chemin moins bon avec une probabilité initialement élevée (0.8) et qui décroit progressivement.
tsp.recuit <- function (d, N=1000, taux=.99) {
# d : matrice des distances.
d <- as.matrix(d)
n <- dim(d)[1]
o <- sample(1:n)
v <- longueur(d,o)
# Calcul de la température initiale
dE <- NULL
j <- 0
for (i in 1:100) {
i <- sample(1:n, 2)
oo <- o
oo[ i[1] ] <- o[ i[2] ]
oo[ i[2] ] <- o[ i[1] ]
w <- longueur(d,oo)
if (w<v) {
dE <- append(dE,abs(w-v))
j <- j+1
}
}
print(dE)
T <- - max(dE) / log(.8)
print(T)
# Initialisations
k <- 0
res <- list()
k.res <- c()
l.res <- c(v)
t.res <- c(T)
p.res <- c()
while (k<N) {
i <- sample(1:n, 2)
oo <- o
oo[ i[1] ] <- o[ i[2] ]
oo[ i[2] ] <- o[ i[1] ]
w <- longueur(d,oo)
p.res <- append(p.res, exp((v-w)/T))
if ( runif(1) < exp((v-w)/T) ) {
v <- w
o <- oo
res <- append(res, list(o))
k.res <- append(k.res, k)
l.res <- append(l.res, v)
k <- 0
T <- T*taux
t.res <- append(t.res, T)
} else {
k <- k+1
}
}
list(o=o, détails=res, k=k.res, longueur=v, longueurs=l.res, T=t.res, p=p.res)
}
n <- 100
x <- seq(0,5, length=n)
x <- sample(x)
x <- cbind(cos(x), sin(x))
r <- tsp.recuit(dist(x), N=1000, taux=.995)
op <- par(mfrow=c(2,2))
n <- length(r$détails)
for (i in floor(c(1, n/4, n/2, n))) {
plot(x, main=paste("n =",i))
lines(x[r$détails[[i]],], col='red')
}
par(op)
op <- par(mfrow=c(2,2)) plot(r$k) plot(r$longueurs, main="Longueurs") plot(r$T, main="Température") plot(r$p, ylim=0:1, main="Probabilités") par(op)

On sait actuellement résoudre, de manière exacte, des problèmes du voyageur de commerce avec plusieurs milliers de villes, en exprimant le problème sous forme d'un programme linéaire. (C'est un peu délicat à décrire, car les contraintes sont en nombre exponentiel : on commence par résoudre le problème sans aucune contrainte, on regarde quelles sont les contraintes violées (c'est facile : la solution comporte des cycles ; ces cycles correspondent aux contraintes), et on les ajoute ; on recommence ensuite, jusqu'à ce que la solution soit correcte.)
A FAIRE : expliquer plus en détails comment on fait...
Voici quelques logiciels qui permettent de le résoudre.
Concorde est un solveur de TSP (développé à Princeton, librement utilisable dans un cadre universitaire) qui repose sur un solveur de programmes linéaires, comme QSoft (même licence) ou CPlex (commercial).
A FAIRE : URL de Concorde et QSoft La documentation du format des fichiers : http://www.informatik.uni-heidelberg.de/groups/comopt/software/TSPLIB95/DOC.PS
Le site http://www.branchandcut.org/ liste des logiciels de Branch and Cut. Symphony est un logiciel (open source) de résolution de problèmes par Branch & Cut -- entres autres, le TSP. Il suppose aussi qu'on dispose d'un solveur de programmes linéaires, par exemple le CLP, Coin LP Solver (COIN, COmputational INfrasctructure for Operations Research, dépend d'IBM).
A FAIRE : URL de Symphony. http://www.coin-or.org/
Voici un exemple d'utilisation de "Linkern" (ce programme utilise une heuristique, mais il est un peu plus rapide) pour résoudre un TSP.
print.tsp <- function (x, d=dist(x), f="") {
## BEWARE: The documentation states "All explicit [weight] data is
## integral"
## If the best tour has length 0, the problem may come from there.
d <- round(as.dist(d))
n <- dim(x)[1]
cat("TYPE : TSP\n", file=f) # Création du fichier
cat("DIMENSION : ", file=f, append=T)
cat(n, file=f, append=T)
cat("\n", file=f, append=T)
cat("EDGE_WEIGHT_TYPE : EXPLICIT\n", file=f, append=T)
cat("EDGE_WEIGHT_FORMAT : UPPER_ROW\n", file=f, append=T)
cat("DISPLAY_DATA_TYPE : NO_DISPLAY\n", file=f, append=T)
cat("EDGE_WEIGHT_SECTION\n", file=f, append=T)
cat(paste(as.vector(d), collapse=" "), file=f, append=T)
cat("\n", file=f, append=T)
cat("EOF\n", file=f, append=T)
}
tsp.plot.linkern <- function (x, d=dist(x), ...) {
print.tsp(x, d, f="tmp.tsp")
system(paste("./linkern", "-o", "tmp.tsp_result", "tmp.tsp"))
ij <- 1+read.table("tmp.tsp_result", skip=1)[,1:2]
xy <- prcomp(x)$x[,1:2]
plot(xy, ...)
segments( xy[,1][ ij[,1] ],
xy[,2][ ij[,1] ],
xy[,1][ ij[,2] ],
xy[,2][ ij[,2] ],
col='red' )
ij
}
op <- par(mfrow=c(3,3), mar=c(0,0,0,0))
for (i in 1:9) {
n <- 50
k <- 3
x <- matrix(rnorm(n*k), nr=n, nc=k)
tsp.plot.linkern(x, d=round(100*dist(x)), axes=F)
box()
}
par(op)
Utilisons maintenant Concorde.
tsp.plot.concorde <- function (x, d=dist(x), plot=T, ...) {
print.tsp(x, d, f="tmp.tsp")
system(paste("./concorde", "tmp.tsp"))
i <- scan("tmp.sol")[-1]
ij <- 1+matrix(c(i, i[-1], i[1]), nc=2)
xy <- prcomp(x)$x[,1:2]
if (plot) {
plot(xy, ...)
n <- dim(ij)[1]
segments( xy[,1][ ij[,1] ],
xy[,2][ ij[,1] ],
xy[,1][ ij[,2] ],
xy[,2][ ij[,2] ],
col=rainbow(n) )
}
ij
}
op <- par(mfrow=c(3,3), mar=c(0,0,0,0))
for (i in 1:9) {
n <- 50
k <- 3
x <- matrix(rnorm(n*k), nr=n, nc=k)
tsp.plot.concorde(x, d=round(100*dist(x)), axes=F)
box()
}
par(op)
Si on applique cela à nos données simulées, il vient :
tsp.plot.concorde(t(data.broken.line))

Il y a un segment en trop, car l'algorithme recherche un chemin fermé -- nous, non.
Sur des données bruitées, c'est encore pire : le chemin est parcourru dans un sens, puis dans l'autre...
tsp.plot.concorde(t(data.noisy.broken.line))

On le voit mieux en lissant la courbe :
x <- t(data.noisy.broken.line) ij <- tsp.plot.concorde(x, plot=F) xy <- prcomp(x)$x[,1:2] y <- xy[ij[,1],] x <- 1:dim(ij)[1] plot(xy) x1 <- predict(loess(y[,1]~x, span=.2)) x2 <- predict(loess(y[,2]~x, span=.2)) n <- length(x1) segments(x1[-n], x2[-n], x1[-1], x2[-1], col=rainbow(n-1), lwd=3)

On peut transformer un problème du voyageur de commerce ouvert en un problème fermé en ajoutant un sommet dont la distance à tous les autres est nulle (ou dont la distance à tous les noeuds est la même).
print.open.tsp <- function (x, d=dist(x), f="") {
## BEWARE: The documentation states "All explicit [weight] data is
## integral"
## If the best tour has length 0, the problem may come from there.
d <- as.matrix(d)
d <- cbind(0,rbind(0,d))
d <- round(as.dist(d))
n <- dim(x)[1] + 1
cat("TYPE : TSP\n", file=f) # Création du fichier
cat("DIMENSION : ", file=f, append=T)
cat(n, file=f, append=T)
cat("\n", file=f, append=T)
cat("EDGE_WEIGHT_TYPE : EXPLICIT\n", file=f, append=T)
cat("EDGE_WEIGHT_FORMAT : UPPER_ROW\n", file=f, append=T)
cat("DISPLAY_DATA_TYPE : NO_DISPLAY\n", file=f, append=T)
cat("EDGE_WEIGHT_SECTION\n", file=f, append=T)
cat(paste(as.vector(d), collapse=" "), file=f, append=T)
cat("\n", file=f, append=T)
cat("EOF\n", file=f, append=T)
}
tsp.plot.concorde.open <- function (x, d=dist(x), plot=T, smooth=F, span=.2,...) {
print.open.tsp(x, d, f="tmp.tsp")
system(paste("./concorde", "tmp.tsp"))
i <- scan("tmp.sol")[-1] # On enlève le nombre de
i <- i[-1] # On enlève le premier noeud : 0
ij <- matrix(c(i[-length(i)], i[-1] ), nc=2)
xy <- prcomp(x)$x[,1:2]
if (plot) {
if (smooth) {
y <- xy[ij[,1],]
x <- 1:dim(ij)[1]
plot(xy, ...)
x1 <- predict(loess(y[,1]~x, span=span))
x2 <- predict(loess(y[,2]~x, span=span))
n <- length(x1)
segments(x1[-n], x2[-n], x1[-1], x2[-1], col=rainbow(n-1), lwd=3)
} else {
plot(xy, ...)
n <- dim(ij)[1]
segments( xy[,1][ ij[,1] ],
xy[,2][ ij[,1] ],
xy[,1][ ij[,2] ],
xy[,2][ ij[,2] ],
col=rainbow(n) )
}
}
ij
}
x <- t(data.noisy.broken.line)
tsp.plot.concorde.open(x)
tsp.plot.concorde.open(x, smooth=T)

tsp.plot.concorde.open(t(data.curve), smooth=T)

tsp.plot.concorde.open(t(data.noisy.curve), smooth=T)

tsp.plot.concorde.open(t(data.real), smooth=F)

tsp.plot.concorde.open(t(data.real), smooth=T)

op <- par(mfrow=c(2,2))
for (s in c(.2, .3, .4, .5)) {
tsp.plot.concorde.open(t(data.real), smooth=T, span=s)
}
par(op)
tsp.plot.concorde.open(data.real.3d, smooth=F)

tsp.plot.concorde.open(data.real.3d, smooth=T)

tsp.plot.concorde.open(data.real.3d, smooth=T, span=.5)

On prend notre nuage de points, on munit chacun d'une masse et ils s'attirent. On peut choisir le type de loi d'attraction : par exemple, une force inversement proportionnelle au carré de la distance qui les sépare, dans un espace de dimension 3. On simule ensuite l'évolution de ce système (mais pas jusqu'à l'équilibre : on s'arrête avant. Au bout d'un moment, les points forment bien une courbe. [C'est l'un des algorithmes qu'ion utilise pour dessiner des noeuds -- mais c'est très délicat à paramétrer : on risque de se trouver avec des points qui s'effondrent les uns sur les autres ou qui s'envoient à l'infini.] Il y a plusieurs choix délicats à faire : 1. Le choix de la loi d'attraction 1bis. La dimension de l'espace (dans lequel les points se trouvent et dans lequel on calcule les distances) a peut-être une influence. 2. La simulation de l'évolution (ni trop lent, ni trop rapide) 3. Quand s'arrêter ? Idée pour l'arrêt : regarder la "ramification" de l'arbre couvrant minimal (je défini la ramification d'un arbre comme le nombre de noeuds qui ne sont pas sur le chemin le plus long -- mais je ne sais pas si ça se calcule facilement). (Pour un arbre binaire, ça se calcule facilement) Enraciner l'arbre en un noeud quelconque, pour chacune des trois branches qui en partent, prendre les deux noeuds les plus profonds, le chemin reliant les deux noeuds les plus profonds parmi ces six est le plus long. (sous toutes réserves) Algorithme : Tant qu'il reste des noeuds d'arité au moins trois : parmi les branches partant de ces noeuds, retirer la plus petite
Assigner une valeur aléatoire de l'indice à chaque point du nuage En déduire un ordre sur les points En déduire la courbe sur laquelle ils sont Lisser cette courbe A l'aide de cette courbe, donner une nouvelle valeur à l'indice Itérer
Répartir les points en quelques groupes Trouver une droite (un segment) pour chacun de ces groupes Essayer de recoller (comment ???)
A FAIRE : svm si on connait l'indice de chaque patient.
Ajouter le temps de calcul
Tenter de reconstruire une ligne brisée à 5 sommet avec plus de 5 points
Légendes
Pour les réseaux de neurones, présenter les choses un peu
différemment :
Algorithme "en ligne", qui prend toujours de nouvelles données
(c'est facile, car on sait comment nos données ont été obtenues,
on peut dons en avoir un nombre infini).
Commencer par implémenter une ACP linéaire et comparer avec l'ACP.
Algorithmes d'optimisation :
Commencer par une situation simple : un seul segment, sans bruit,
en dimension deux (ou même en dimension un).
En particulier, cela permettra de vérifier que mon code fonctionne
correctement.
A FAIRE : pour les exemples simulés, diviser les points en quatre
groupes et les indiquer par des couleurs.
Ainsi, on pourra voir si on est sensé voir quelque-chose ou pas.
Idéalement, on pourrait aussi mettre tous ces graphiques dans une
même fonction, qu'on appellerait pour chacun des exemples.
Pour cela, il faudrait mettre les données réelles en premier.Vincent Zoonekynd
<zoonek@math.jussieu.fr>
latest modification on Mon Jul 26 09:33:43 CEST 2004