
Introduction
Simple time series models
ARIMA
Validating a model
Spectral Analysis
Wavelets
Digital Signal Processing (DSP)
Modeling volatility: GARCH models (Generalized AutoRegressive Conditionnal Heteroscedasticity)
Multivariate time series
State-Space Models and Kalman Filtering
Non-linear time series and chaos
Other times
Discrete-valued time series: Markov chains and beyond
Variants of Markov chains
Untackled subjects
TO SORT
This chapter contrasts with the topics we have seen up to now: we were interested in the study of several independant realizations of a simple statistical process (e.g., a gaussian random variable, or a mixture of gaussians, or a linear model); we shall now focus on a single realization of a more complex process.
Here is the structure of this chapter.
After an introduction, motivating the notion of a time series and giving several examples, simulated or real, we shall present the classical models of time series (AR, MA, ARMA, ARIMA, SARIMA), that provide recipes to build time series with desired properties. We shall then present spectral methods, that focus on the discovery of periodic elements in time series. The simplicity of those models makes them amenable, but they cannot describe the properties of some real-world time series: non-linear methods, built upon the classical models (GARCH) are called for. State-Space Models and the Kalman filter follow the same vein: they assume that the data is build from linear algebra, but that we do not observe everything -- there are "hidden" (unobserved, latent) variables.
Some of those methods readily generalize to higher dimensions, i.e., to the study of vector-valued time-series, i.e., to the study of several related time series at the same time -- but some new phenomena appear (e.g., cointegration). Furthermore, if the number of time series to study becomes too large, the vector models have too many parameters to be useful: we enter the realm of panel data.
We shall then present some less mainstream ideas: instead of linear algebra, time series can be produced by analytical (read: differential equations) or procedural (read: chaos, fractals) means.
We finally present generalizations of time series: stochastic processes, in which time is continuous; irregular time series, in which time is discrete but irregular; and discrete-valued time series (with Markov chains and Hidden Markov Models instead of AR and state-space models).
In probability theory, a time series (you will also hear mention of "stochastic process": in a time series, time is discrete, in a stochastic process, it is continuous) is a sequence of random variables. In statistics, it is a variable that depends on time: for instance, the price of a stock, that changes every day; the air temperature, measured every month; the heart rate of a patient, minute after minute, etc.
plot(LakeHuron,
ylab = "",
main = "Level of Lake Huron")
Sometimes, it is so noisy that you do not see much,
x <- window(sunspots, start=1750, end=1800)
plot(x,
ylab = "",
main = "Sunspot numbers")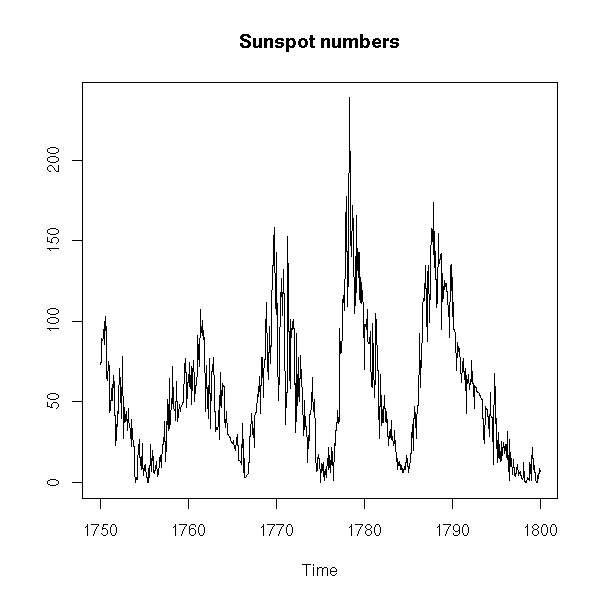
You can then smooth the curve.
plot(x,
type = 'p',
ylab = "",
main = "Sunspot numbers")
k <- 20
lines( filter(x, rep(1/k,k)),
col = 'red',
lwd = 3 )
You can underline the periodicity, graphically, with vertical bars.
data(UKgas)
plot.band <- function (x, ...) {
plot(x, ...)
a <- time(x)
i1 <- floor(min(a))
i2 <- ceiling(max(a))
y1 <- par('usr')[3]
y2 <- par('usr')[4]
if( par("ylog") ){
y1 <- 10^y1
y2 <- 10^y2
}
for (i in seq(from=i1, to=i2-1, by=2)) {
polygon( c(i,i+1,i+1,i),
c(y1,y1,y2,y2),
col = 'grey',
border = NA )
}
par(new=T)
plot(x, ...)
}
plot.band(UKgas,
log = 'y',
ylab = "",
main = "UK gas consumption")
As always, before analysing the series, we have a look at it (evolution with time, pattern changes, misordered values (sometimes, you have both the value and the time: you should then check that the order is the correct one), distribution (histogram or, better, density estimation), y[i+1] ~ y[i], outliers -- the more data you have, the dirtier: someone may have forgotten the decimal dot while entering the data, someone may have decided to replace missing values by 0 or -999, etc.)
x <- LakeHuron
op <- par(mfrow = c(1,2),
mar = c(5,4,1,2)+.1,
oma = c(0,0,2,0))
hist(x,
col = "light blue",
xlab = "",
main = "")
qqnorm(x,
main = "")
qqline(x,
col = 'red')
par(op)
mtext("Lake Huron levels",
line = 2.5,
font = 2,
cex = 1.2)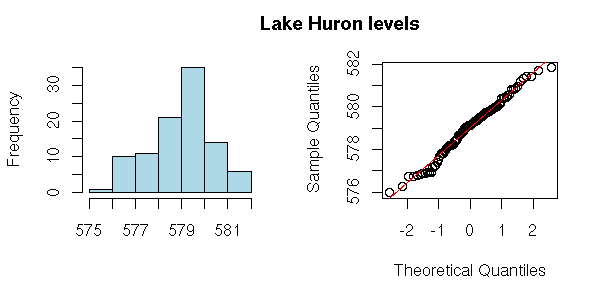
x <- diff(LakeHuron)
op <- par(mfrow = c(1,2),
mar = c(5,4,1,2)+.1,
oma = c(0,0,2,0))
hist(x,
col = "light blue",
xlab = "",
main = "")
qqnorm(x,
main = "")
qqline(x,
col = 'red')
par(op)
mtext("Lake Huron level increments",
line = 2.5,
font = 2,
cex = 1.2)
boxplot(x,
horizontal = TRUE,
col = "pink",
main = "Lake Huron levels")
plot(x,
ylab = "",
main = "Lake Huron levels")
n <- length(x)
k <- 5
m <- matrix(nr=n+k-1, nc=k)
colnames(m) <- c("x[i]", "x[i-1]", "x[i-2]",
"x[i-3]", "x[i-4]")
for (i in 1:k) {
m[,i] <- c(rep(NA,i-1), x, rep(NA, k-i))
}
pairs(m,
gap = 0,
lower.panel = panel.smooth,
upper.panel = function (x,y) {
panel.smooth(x,y)
par(usr = c(0, 1, 0, 1))
a <- cor(x,y, use='pairwise.complete.obs')
text(.1,.9,
adj=c(0,1),
round(a, digits=2),
col='blue',
cex=2*a)
})
title("Lake Huron levels: autocorrelations",
line = 3)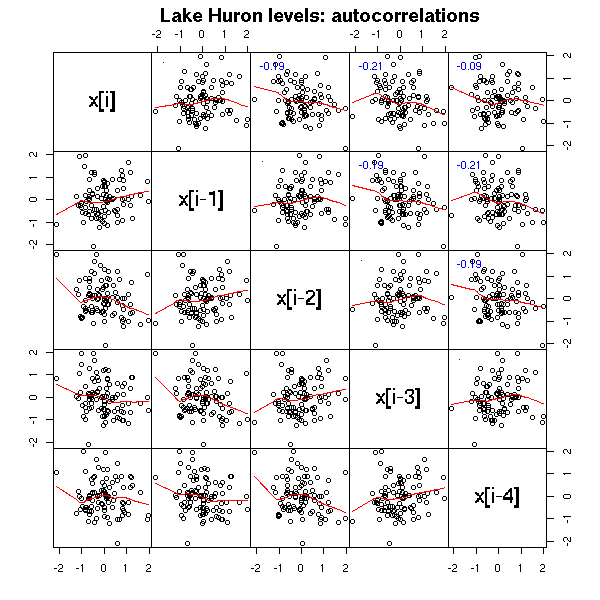
We shall also see other plots, more specific to time series. The first one, the AutoCorrelation Function (ACF) gives the correlation between x[i] and x[i-k], for increasing values of k (these are the numbers that already appeared in the previous pair plot). The second one, the PACF (Partial AutoCorrelation Function), contains the same information, but gives the correlation between x[i] and x[i-k] that is not explained by the correlations with a shorter lag (more about this later, when we speak of AR models). The last one, the spectrogram, tries to find periodic components, of various frequencies, in the signal and displays the importance of the various frequencies (more about this later).
op <- par(mfrow = c(3,1),
mar = c(2,4,1,2)+.1)
acf(x, xlab = "")
pacf(x, xlab = "")
spectrum(x, xlab = "", main = "")
par(op)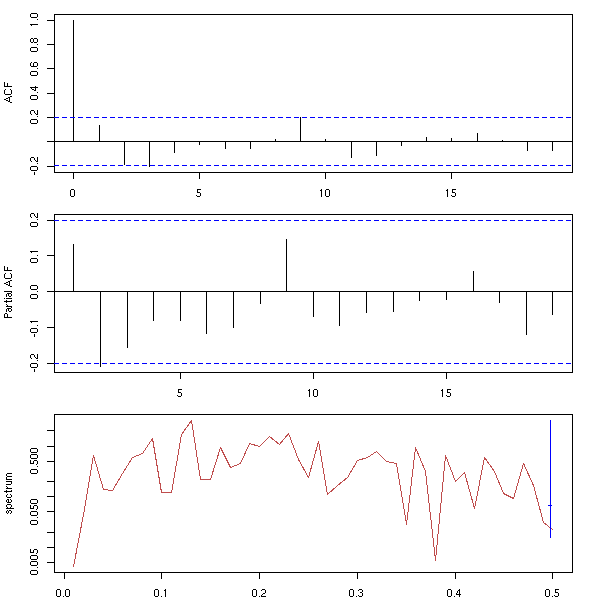
One aim (or one step) of time series analysis is to find the "structure" of a time series, i.e., to find how it was build, i.e., to find a simple algorithm that could produce similar-looking data. Here are, in no particular order, a few simulated time series.
The first is just gaussian noise; the second is an integrated noise (a "random walk"). We can then build on those, integrating several times, adding noise to the result, adding a linear or periodic trend, etc.
op <- par(mfrow = c(3,3),
mar = .1 + c(0,0,0,0))
n <- 100
k <- 5
N <- k*n
x <- (1:N)/n
y1 <- rnorm(N)
plot(ts(y1),
xlab="", ylab="", main="", axes=F)
box()
y2 <- cumsum(rnorm(N))
plot(ts(y2),
xlab="", ylab="", main="", axes=F)
box()
y3 <- cumsum(rnorm(N))+rnorm(N)
plot(ts(y3),
xlab="", ylab="", main="", axes=F)
box()
y4 <- cumsum(cumsum(rnorm(N)))
plot(ts(y4),
xlab="", ylab="", main="", axes=F)
box()
y5 <- cumsum(cumsum(rnorm(N))+rnorm(N))+rnorm(N)
plot(ts(y5),
xlab="", ylab="", main="", axes=F)
box()
# With a trend
y6 <- 1 - x + cumsum(rnorm(N)) + .2 * rnorm(N)
plot(ts(y6),
xlab="", ylab="", main="", axes=F)
box()
y7 <- 1 - x - .2*x^2 + cumsum(rnorm(N)) +
.2 * rnorm(N)
plot(ts(y7),
xlab="", ylab="", main="", axes=F)
box()
# With a seasonnal component
y8 <- .3 + .5*cos(2*pi*x) - 1.2*sin(2*pi*x) +
.6*cos(2*2*pi*x) + .2*sin(2*2*pi*x) +
-.5*cos(3*2*pi*x) + .8*sin(3*2*pi*x)
plot(ts(y8+ .2*rnorm(N)),
xlab="", ylab="", main="", axes=F)
box()
lines(y8, type='l', lty=3, lwd=3, col='red')
y9 <- y8 + cumsum(rnorm(N)) + .2*rnorm(N)
plot(ts(y9),
xlab="", ylab="", main="", axes=F)
box()
par(op)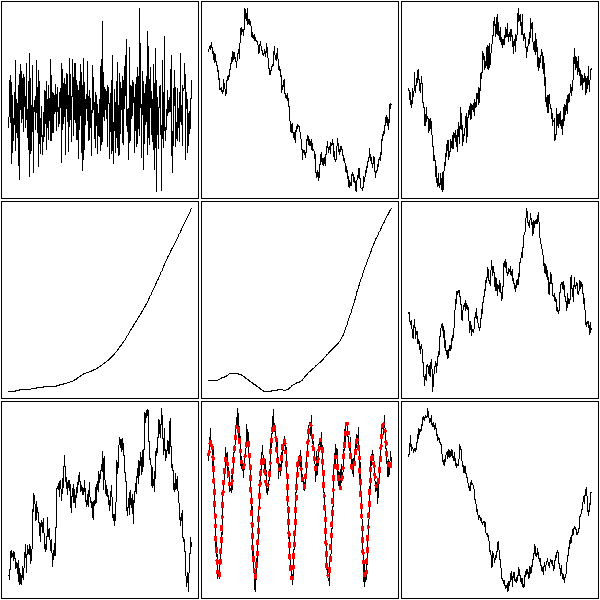
In statistics, we like independent data -- the problem is that time series contain dependent data. The aim of a time series analysis will thus be to extract this structure and transform the initial time series into a series of independant values often called "innovations", usually by going in the other direction: by providing a recipe (a "model") to build a series similar to the one we have with noise as only ingredient.
We can present this problem from another point of view: when you study a statistical phenomenon, you usually have several realizations of it. With time series, you have a single one. Therefore, we replace the study of several realizations at a given point in time by the study of a single realization at several points in time. Depending on the statistical phenomenon, these two points of view may be equivalent or not -- this problem is called ergodicity -- more about this later.
As the observations in a time series are generally not independant, we can first have a look at their correlation: the AutoCorrelation Function (ACF) (strictly speaking, one can consider the Sample ACF, if it is computed from a sample, or the theoretical autocorrelation function, if it is not computed from actual data but from a model) at lag k is the correlation between observation number n and observation number n - k. In order to compute it from a sample, you have to assume that it does not depend on n but only on the lag, k.
We could do it by hand
my.acf <- function (
x,
lag.max = ceiling(5*log(length(x)))
) {
m <- matrix(
c( NA,
rep( c(rep(NA, lag.max-1), x),
lag.max ),
rep(NA,, lag.max-1)
),
byrow=T,
nr=lag.max)
x0 <- m[1,]
apply(m,1,cor, x0, use="complete")
}
n <- 200
x <- rnorm(n)
plot(my.acf(x),
xlab = "Lag",
type = 'h')
abline(h=0)
but there is already such a function.
op <- par(mfrow=c(2,1)) acf(x, main="ACF of white noise") x <- LakeHuron acf(x, main="ACF of a time series (Lake Huron)") par(op)
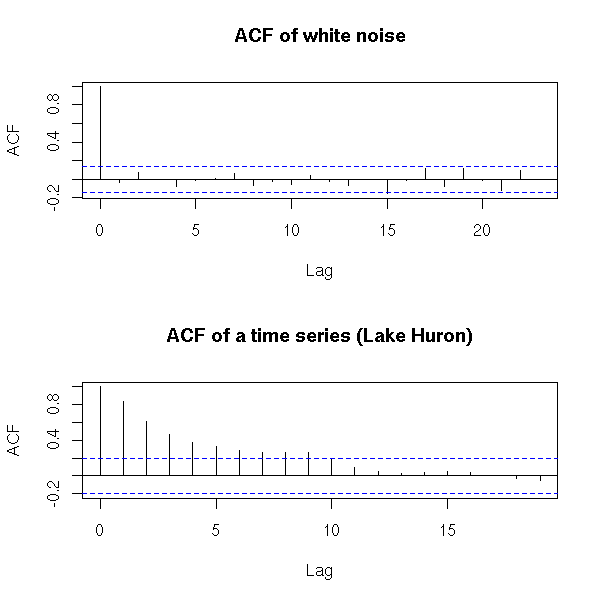
The y=0 line traditionnally added to those plots can be misleading: it can suggest that the sign of a coefficient is known, while this coefficient is not significantly different from zero. The boundaries of the confidence interval are sufficient
op <- par(mfrow=c(2,1))
set.seed(1)
x <- rnorm(100)
# Default plot
acf(x, main = "ACF with a distracting horizontal line")
# Without the axis, with larger bars
r <- acf(x, plot = FALSE)
plot(r$lag, r$acf,
type = "h", lwd = 20, col = "grey",
xlab = "lag", ylab = "autocorrelation",
main = "Autocorrelation without the y=0 line")
ci <- .95
clim <- qnorm( (1+ci) / 2 ) / sqrt(r$n.used)
abline(h = c(-1,1) * clim,
lty = 2, col = "blue", lwd = 2)
Here are the autocorrelation functions of the simulated examples from the introduction, but the plots have been shuffled: can you put them back in the correct order? Alternatively, can you see several groups among those time series?
op <- par(mfrow=c(3,3), mar=c(0,0,0,0))
for (y in sample(list(y1,y2,y3,y4,y5,y6,y7,y8,y9))) {
acf(y,
xlab="", ylab="", main="", axes=F)
box(lwd=2)
}
par(op)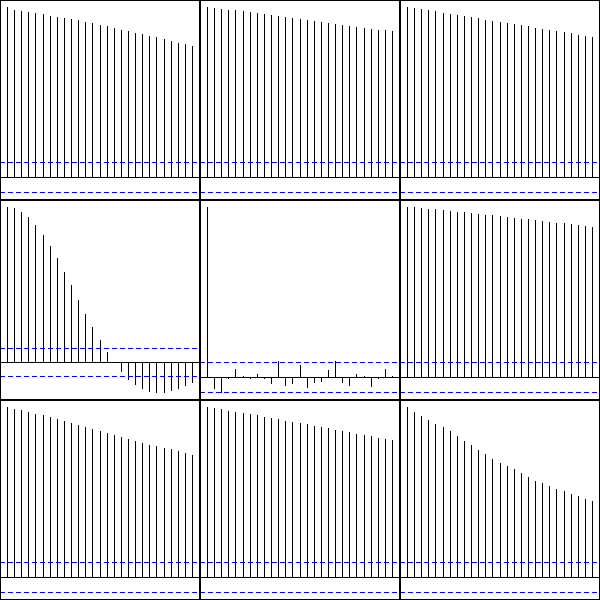
Personnally, I can see three groups: when the ACF is almost zero, the data are not correlated; when the ACF is sometimes positive sometimes negative, the data might be periodic; in the other cases, the data are correlated -- but the speed at which the autocorrelation decreases can vary.
A white noise is a series of uncorrelated random variables, whose expectation is zero, whose variance is constant.
In other words, these are iid (independant, identically distributed) random variables, to the second order. (They may be dependent, but in non-linear ways, that cannot be seen from the correlation; they may have different distributions, as long as the mean and variance remain the same; their distribution need not be symetric.)
Quite often, we shall try to decompose our time series into a "trend" (or anything interpretable) plus a noise term, that should be white noise.
For instance, a series of iid random variables is a white noise.
my.plot.ts <- function (x, main="") {
op <- par(mar=c(2,2,4,2)+.1)
layout( matrix(c(1,2),nr=1,nc=2), widths=c(3,1) )
plot(x, xlab="", ylab="")
abline(h=0, lty=3)
title(main=main)
hist(x, col="light blue", main='', ylab="", xlab="")
par(op)
}
n <- 100
x <- ts(rnorm(n))
my.plot.ts(x, "Gaussian iid noise")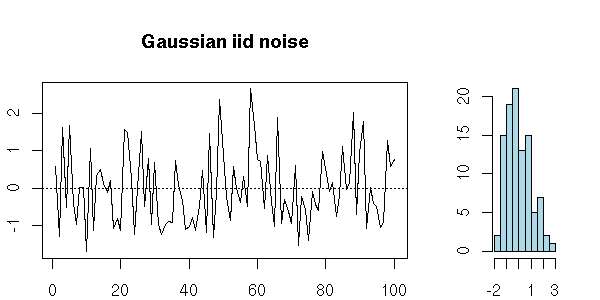
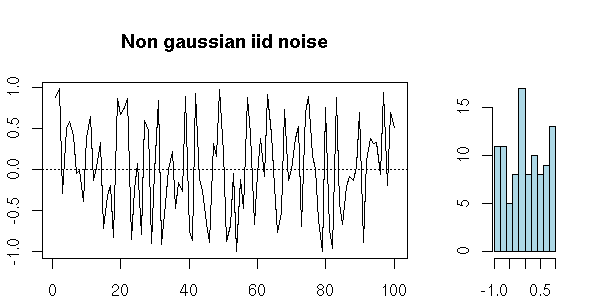
A series of iid random variables of mean zero is also a white noise.
n <- 100 x <- ts(runif(n,-1,1)) my.plot.ts(x, "Non gaussian iid noise")
x <- ts(rnorm(100)^3) my.plot.ts(x, "Non gaussian iid noise")
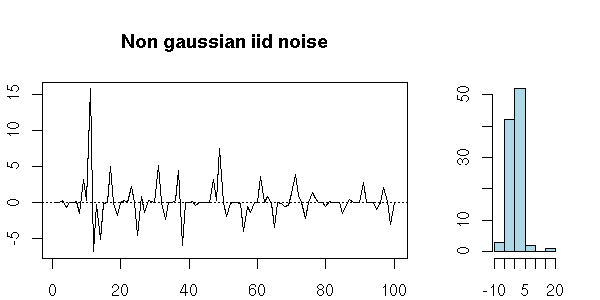
But you can also have a series of uncorrelated random variables that are not independant: the definition just asks that they be "independant to the second order".
n <- 100
x <- rep(0,n)
z <- rnorm(n)
for (i in 2:n) {
x[i] <- z[i] * sqrt( 1 + .5 * x[i-1]^2 )
}
my.plot.ts(x, "Non iid noise")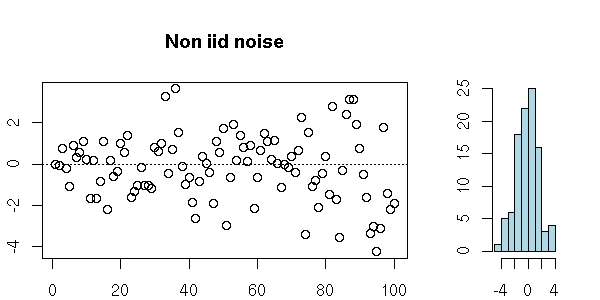
Some deterministic sequences look like white noise.
n <- 100
x <- rep(.7, n)
for (i in 2:n) {
x[i] <- 4 * x[i-1] * ( 1 - x[i-1] )
}
my.plot.ts(x, "A deterministic time series")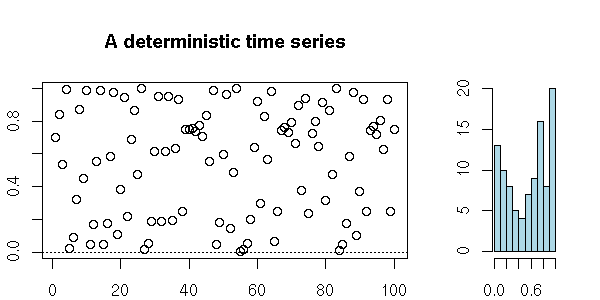
n <- 1000
tn <- cumsum(rexp(n))
# A C^infinity function defined as a sum
# of gaussian densities
f <- function (x) {
# If x is a single number: sum(dnorm(x-tn))
apply( dnorm( outer(x,rep(1,length(tn))) -
outer(rep(1,length(x)),tn) ),
1,
sum )
}
op <- par(mfrow=c(2,1))
curve(
f(x),
xlim = c(1,500),
n = 1000,
main = "From far away, it looks random..."
)
curve(
f(x),
xlim = c(1,10),
n = 1000,
main="...but it is not: it is a C^infinity function"
)
par(op)
We have a few tests to check if a given time series actually is white noise.
The analysis of a time series mainly consists in finding out a recipe to build it (or to build a similar-looking series) from white noise, as we said in the introduction. But to find this recipe, we proceed in the other direction: we start with our time series and we try to transform it into something that looks like white noise. To check if our analysis is correct, we have to check that the residuals are indeed white noise (exactly as we did with regression). To this end, we can start to have a look at the ACF (on average, 5% of the values should be beyond the dashed lines -- if there are much more, there might be a problem).
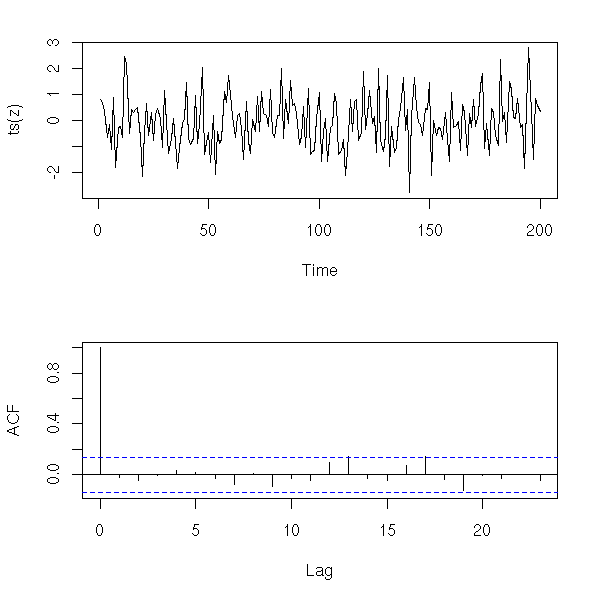
z <- rnorm(200) op <- par(mfrow=c(2,1), mar=c(5,4,2,2)+.1) plot(ts(z)) acf(z, main = "") par(op)
x <- diff(co2) y <- diff(x,lag=12) op <- par(mfrow=c(2,1), mar=c(5,4,2,2)+.1) plot(ts(y)) acf(y, main="") par(op)

To have a numerical result (a p-value), we can perform a Box--Pierce or Ljung--Box test (these are also called "portmanteau statistics"): the idea is to consider the (weighted) sum of the first autocorrelation coefficients -- those sums (asymptotically) follow a chi^2 distribution (the Ljung-Box is a variant of the Box-Pierce one that gives a better Chi^2 approximation for small samples).
> Box.test(z) # Box-Pierce
Box-Pierce test
X-squared = 0.014, df = 1, p-value = 0.9059
> Box.test(z, type="Ljung-Box")
Box-Ljung test
X-squared = 0.0142, df = 1, p-value = 0.9051
> Box.test(y)
Box-Pierce test
X-squared = 41.5007, df = 1, p-value = 1.178e-10
> Box.test(y, type='Ljung')
Box-Ljung test
X-squared = 41.7749, df = 1, p-value = 1.024e-10
op <- par(mfrow=c(2,1))
plot.box.ljung <- function (
z,
k = 15,
main = "p-value of the Ljung-Box test",
ylab = "p-value"
) {
p <- rep(NA, k)
for (i in 1:k) {
p[i] <- Box.test(z, i,
type = "Ljung-Box")$p.value
}
plot(p,
type = 'h',
ylim = c(0,1),
lwd = 3,
main = main,
ylab = ylab)
abline(h = c(0,.05),
lty = 3)
}
plot.box.ljung(z, main="Random data")
plot.box.ljung(y, main="diff(diff(co2),lag=12)")
par(op)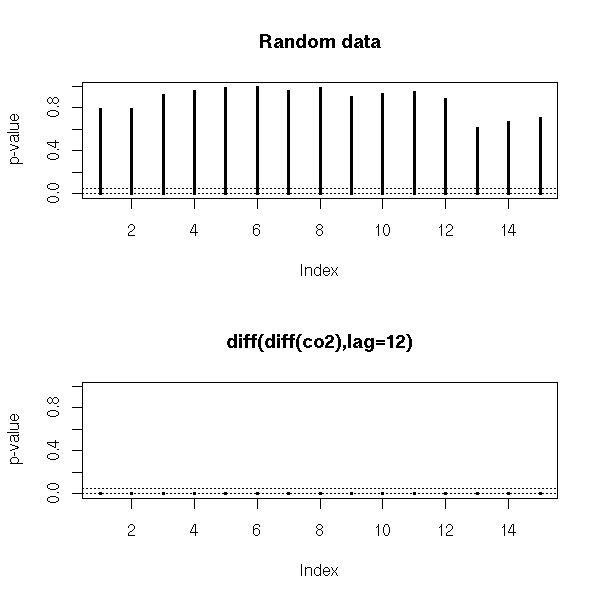
There are other such tests: McLeod-Li, Turning-point, difference-sign, rank test, etc.
We can also use the Durbin--Watson we have already mentionned when we tackled regression.
TODO: check that I actually mention it. library(car) ?durbin.watson library(lmtest) ?dwtest
Here (it is the same test, but it is not implemented in the same way: the results may differ):
> dwtest(LakeHuron ~ 1)
Durbin-Watson test
data: LakeHuron ~ 1
DW = 0.3195, p-value = < 2.2e-16
alternative hypothesis: true autocorrelation is greater than 0
> durbin.watson(lm(LakeHuron ~ 1))
lag Autocorrelation D-W Statistic p-value
1 0.8319112 0.3195269 0
Alternative hypothesis: rho != 0
op <- par(mfrow=c(2,1))
library(lmtest)
plot(LakeHuron,
main = "Lake Huron")
acf(
LakeHuron,
main = paste(
"Durbin-Watson: p =",
signif( dwtest( LakeHuron ~ 1 ) $ p.value, 3 )
)
)
par(op)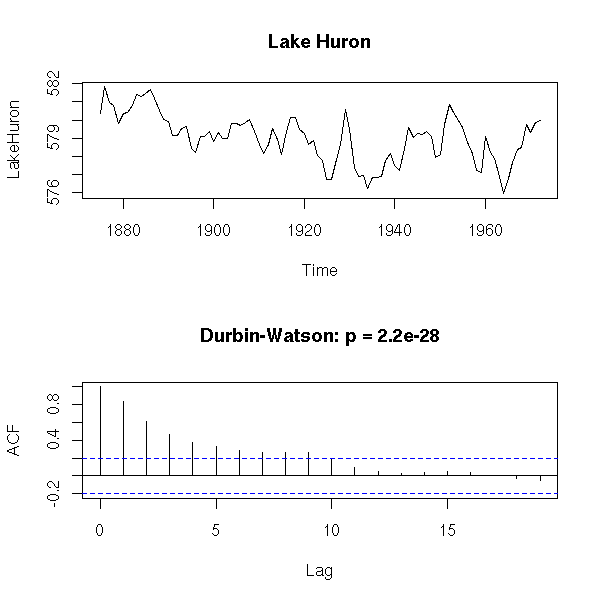
n <- 200
x <- rnorm(n)
op <- par(mfrow=c(2,1))
x <- ts(x)
plot(x, main="White noise", ylab="")
acf(
x,
main = paste(
"Durbin-Watson: p =",
signif( dwtest( x ~ 1 ) $ p.value, 3)
)
)
par(op)
n <- 200
x <- rnorm(n)
op <- par(mfrow=c(2,1))
y <- filter(x,.8,method="recursive")
plot(y, main="AR(1)", ylab="")
acf(
y,
main = paste(
"p =",
signif( dwtest( y ~ 1 ) $ p.value, 3 )
)
)
par(op)
But beware: the default options tests wether the autocorrelation is positive or zero -- if it is significantly negative, the result will be misleading...
set.seed(1)
n <- 200
x <- rnorm(n)
y <- filter(x, c(0,1), method="recursive")
op <- par(mfrow=c(3,1), mar=c(2,4,2,2)+.1)
plot(
y,
main = paste(
"one-sided DW test: p =",
signif( dwtest ( y ~ 1 ) $ p.value, 3 )
)
)
acf( y, main="")
pacf(y, main="")
par(op)
op <- par(mfrow=c(3,1), mar=c(2,4,2,2)+.1)
res <- dwtest( y ~ 1, alternative="two.sided")
plot(
y,
main = paste(
"two-sided p =",
signif( res$p.value, 3 )
)
)
acf(y, main="")
pacf(y, main="")
par(op)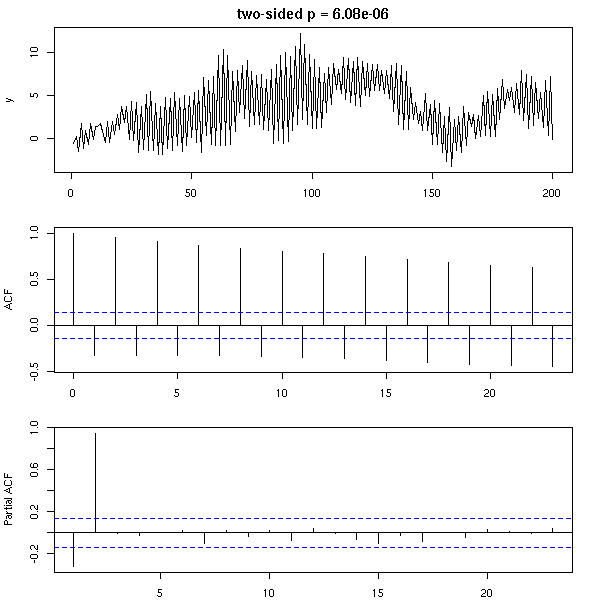
There are other tests, such as the runs test (that looks at the number of runs, a run being consecutive observations of the same sign; that kind of test is mainly used for qualitative time series or for time series that leave you completely clueless).
library(tseries) ?runs.test
or the Cowles-Jones test
TODO
A sequence is a pair of consecutive returns of the same sign; a
reversal is a pair of consecutive returns of opposite signs.
Their ratio, the Cowles-Jones ratio,
number of sequences
CJ = ---------------------
number of reversals
should be around one IF the drift is zero.
Actually, there is already a function, "tsdiag", that performs some tests on a time series (plot, ACF and Ljung-Box test).
data(co2) r <- arima( co2, order = c(0, 1, 1), seasonal = list(order = c(0, 1, 1), period = 12) ) tsdiag(r)

Classically, one tries to decompose a time series into a sum of three terms: a trend (often, an affine function), a seasonal component (a perdiodic function) and white noise.
In this section, we shall try to model time series from this idea, using classical statistical methods (mainly regression). Some of the procedures we shall present will be relevant, useful, but others will not work -- they are just ideas that one might think could work but turn out not to. Keep your eyes open!
TODO: give the structure of this section
We shall first start to model the time series to be studied with regression, as a polynomial plus a sine wave or, more generally, as a polynomial plus a periodic signal.
We shall then present modelling techniques based on the (exponential) moving average, that assume that the series locally looks like a constant plus noise or a linear function plus noise -- this is the Holt-Winters filter.
data(co2) plot(co2)

Here, we consider time as a predictive variable, as when we were playing with regressions. Let us first try to write the data as the sum of an affine function and a sine function.
y <- as.vector(co2) x <- as.vector(time(co2)) r <- lm( y ~ poly(x,1) + cos(2*pi*x) + sin(2*pi*x) ) plot(y~x, type='l', xlab="time", ylab="co2") lines(predict(r)~x, lty=3, col='red', lwd=3)
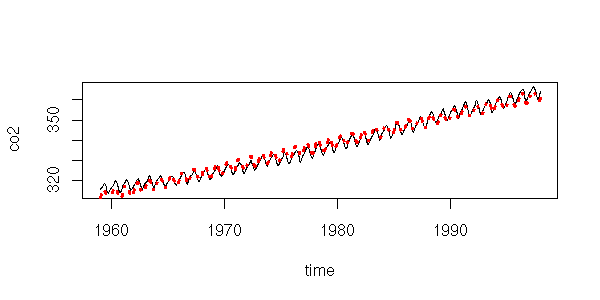
This is actually insufficient. It might not be that clear on this plot, but if you look at the residuals, it becomes obvious.
plot( y-predict(r),
main = "The residuals are not random yet",
xlab = "Time",
ylab = "Residuals" )
Let us complicate the model: a degree 2 polynomial plus a sine function (if it were not sufficient, we would replace the polynomial by splines) (we could also transform the time series, e.g., with a logarithm -- here, it does not work).
r <- lm( y ~ poly(x,2) + cos(2*pi*x) + sin(2*pi*x) ) plot(y~x, type='l', xlab="Time", ylab="co2") lines(predict(r)~x, lty=3, col='red', lwd=3)
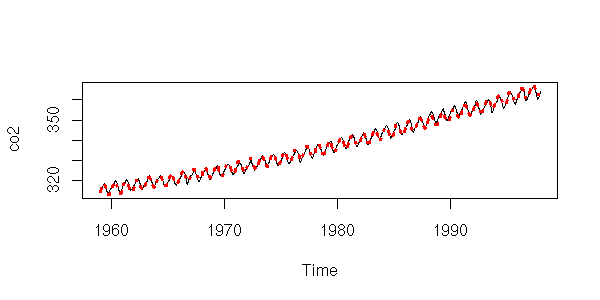
That is better.
plot( y-predict(r),
main = "Better residuals -- but still not random",
xlab = "Time",
ylab = "Residuals" )
We could try to refine the periodic component, but it would not really improve things.
r <- lm( y ~ poly(x,2) + cos(2*pi*x) + sin(2*pi*x)
+ cos(4*pi*x) + sin(4*pi*x) )
plot(y~x, type='l', xlab="Time", ylab="co2")
lines(predict(r)~x, lty=3, col='red', lwd=3)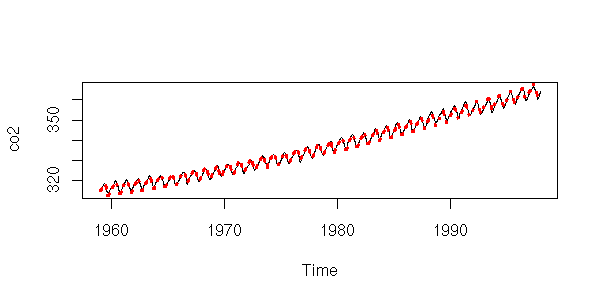
plot( y-predict(r),
type = 'l',
xlab = "Time",
ylab = "Residuals",
main = "Are those residuals any better?" )
However, the ACF suggests that those models are not as good as they seemed: if the residuals were really white noise, we would have very few values beyond the dashed lines...
r1 <- lm( y ~ poly(x,2) +
cos(2*pi*x) +
sin(2*pi*x) )
r2 <- lm( y ~ poly(x,2) +
cos(2*pi*x) +
sin(2*pi*x) +
cos(4*pi*x) +
sin(4*pi*x) )
op <- par(mfrow=c(2,1))
acf(y - predict(r1))
acf(y - predict(r2))
par(op)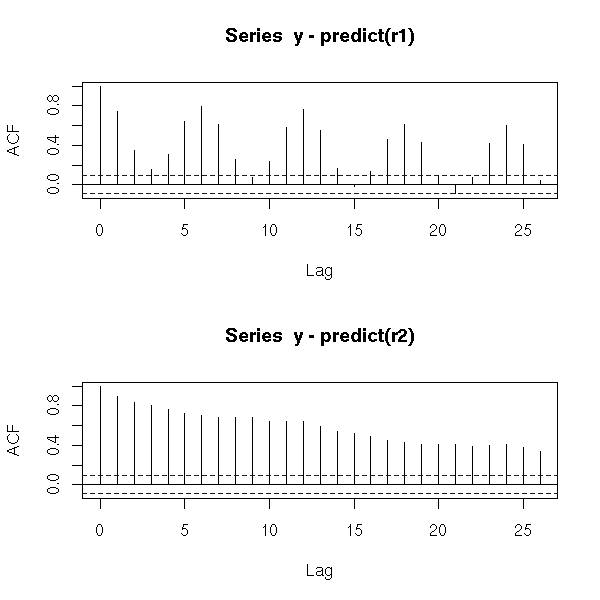
Those plots tell us two things: first, after all, it was useful to refine the periodic component; second, we still have autocorrelation problems.
To estimate the periodic component, we could average the january values, then the february values, etc.
m <- tapply(co2, gl(12,1,length(co2)), mean) m <- rep(m, ceiling(length(co2)/12)) [1:length(co2)] m <- ts(m, start=start(co2), frequency=frequency(co2)) op <- par(mfrow=c(3,1), mar=c(2,4,2,2)) plot(co2) plot(m, ylab = "Periodic component") plot(co2-m, ylab = "Withou the periodic component") r <- lm(co2-m ~ poly(as.vector(time(m)),2)) lines(predict(r) ~ as.vector(time(m)), col='red') par(op)
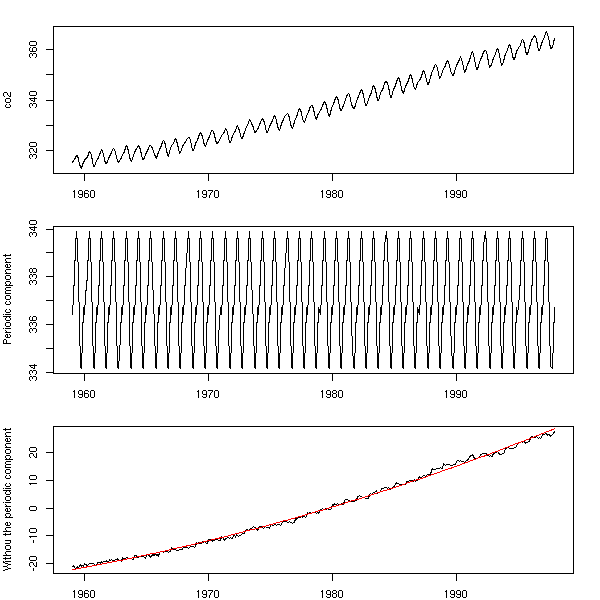
However, a look at the residuals tell us that the periodic component is still there...
op <- par(mfrow=c(4,1), mar=c(2,4,2,2)+.1)
plot(r$res, type = "l")
acf(r$res, main="")
pacf(r$res, main="")
spectrum(r$res, col=par('fg'), main="")
abline(v=1:6, lty=3)
par(op)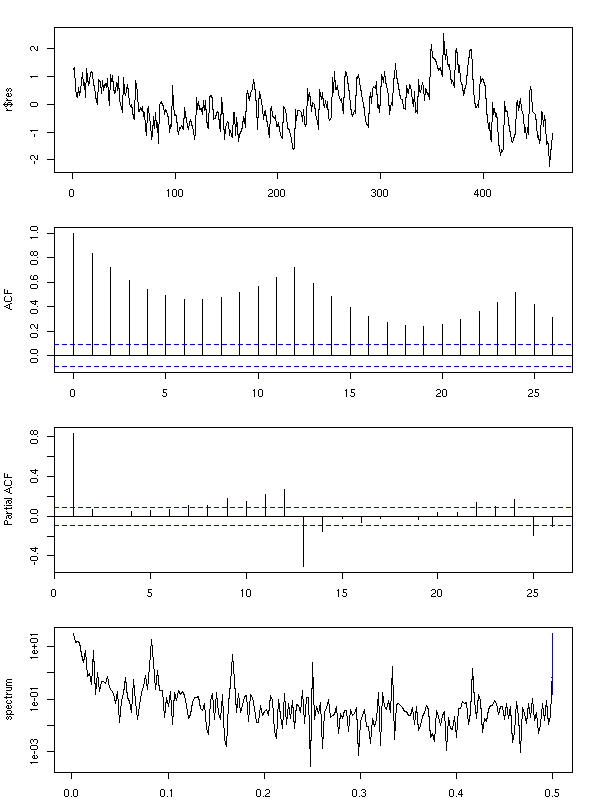
Using the mean as above to estimate the periodic component would only work if the model were of the form
y ~ a + b x + periodic component.
But here, we have a quadratic term: averaging for each month will nt work. However, we can reuse the same idea with a single regression, to find both the periodic component and the trend. Here, the periodic component can be anything: we have 12 coefficients to estimate on top of those of the trend.
k <- 12
m <- matrix( as.vector(diag(k)),
nr = length(co2),
nc = k,
byrow = TRUE )
m <- cbind(m, poly(as.vector(time(co2)),2))
r <- lm(co2~m-1)
summary(r)
b <- r$coef
y1 <- m[,1:k] %*% b[1:k]
y1 <- ts(y1,
start=start(co2),
frequency=frequency(co2))
y2 <- m[,k+1:2] %*% b[k+1:2]
y2 <- ts(y2,
start=start(co2),
frequency=frequency(co2))
res <- co2 - y1 - y2
op <- par(mfrow=c(3,1), mar=c(2,4,2,2)+.1)
plot(co2)
lines(y2+mean(b[1:k]) ~ as.vector(time(co2)),
col='red')
plot(y1)
plot(res)
par(op)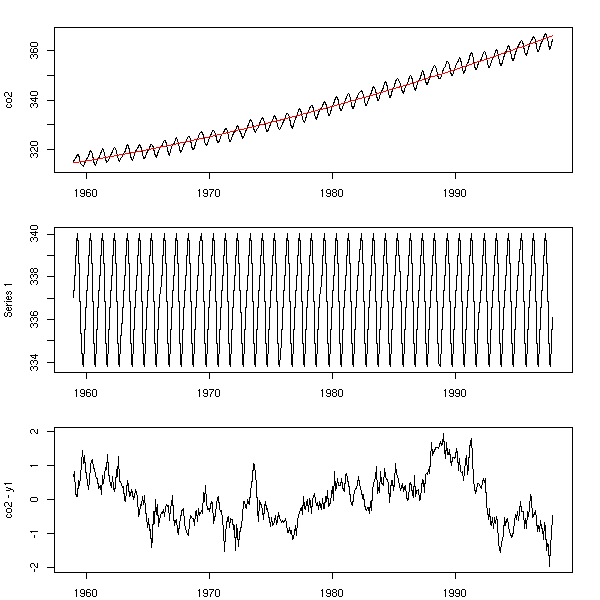
Here, the analysis is not finished: we still have to study the resulting noise -- but we did get rid of the periodic component.
op <- par(mfrow=c(3,1), mar=c(2,4,2,2)+.1)
acf(res, main="")
pacf(res, main="")
spectrum(res, col=par('fg'), main="")
abline(v=1:10, lty=3)
par(op)
To pursue the example to its end, one is tempted to fit an AR(2) (an ARMA(1,1) would do, as well) to the residuals.
innovations <- arima(res, c(2,0,0))$residuals op <- par(mfrow=c(4,1), mar=c(3,4,2,2)) plot(innovations) acf(innovations) pacf(innovations) spectrum(innovations) par(op)

In the last example, if the period was longer, we would use splines to find a smoother periodic component -- and also to have fewer parameters: 15 was really a lot.
Exercise left to the reader...
To find the trend of a time series, you can simply "smooth" it, e.g., with a Moving Average (MA).
x <- co2 n <- length(x) k <- 12 m <- matrix( c(x, rep(NA,k)), nr=n+k-1, nc=k ) y <- apply(m, 1, mean, na.rm=T) y <- y[1:n + round(k/2)] y <- ts(y, start=start(x), frequency=frequency(x)) y <- y[round(k/4):(n-round(k/4))] yt <- time(x)[ round(k/4):(n-round(k/4)) ] plot(x, ylab="co2") lines(y~yt, col='red')

The Moving average will leave invariant some functions (e.g., polynomials of degree up to three -- choose the coefficients accordingly).
The "filter" function already does this. Do not forget the "side" argument: otherwise, it will use values from the past and the future -- for time series this is rarely desirable: it would introduce a look-ahead bias.
x <- co2 plot(x, ylab="co2") k <- 12 lines( filter(x, rep(1/k,k), side=1), col='red')

Actually, one should distinguish between "smoothing" with a Moving Average (to find the value at a point, one uses the whole sample, including what happend after that point) and "filtering" with a Moving Average (to find the smoothed value at a point, one only uses the information up to that point).
When we perform a usual regression, we are interested in the shape of our data in the whole interval. On the contrary, quite often, when we study time series, we are interested in what happens at the end of the interval -- and try to forecast beyond.
In the first case, we use smoothing: to compute the Moving Average at time t, we average over an interval centered on t. The drawback is that we cannot do that at the two ends of the interval: there will be missing values at the begining and the end.
In the second case, as we do want values at the end of the interval, we do not average on an interval centered on t, but on the values up to time t. The drawback is that this introduces a lag: we have the same values as before, but t/2 units later.
The "side" argument of the filter() function lest you choose between smoothing and filtering.
x <- co2
plot(window(x, 1990, max(time(x))), ylab="co2")
k <- 12
lines( filter(x, rep(1/k,k)),
col='red', lwd=3)
lines( filter(x, rep(1/k,k), sides=1),
col='blue', lwd=3)
legend(par('usr')[1], par('usr')[4], xjust=0,
c('smoother', 'filter'),
lwd=3, lty=1,
col=c('red','blue'))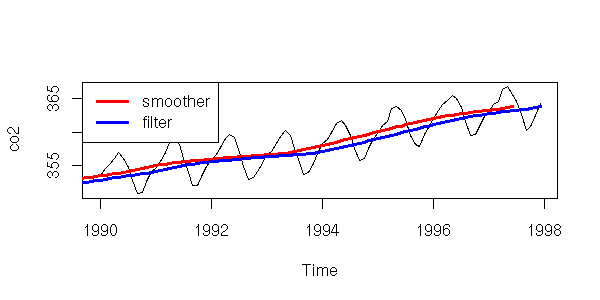
Filters are especially used in real-time systems: we want the best estimation of some quantity using all the data collected so far, and we want to update this estimate when new data comes in.
Here is a classical investment strategy (I do not claim it works): take a price time series, compute a 20-day moving average and a 50-day one; when the two curves intersect, buy or sell (finance people call the difference between those two moving averages an "oscillator" -- it is a time series that should wander around zero, that should revert to zero -- you can try to design you own oscillator: the strategy will be "buy when the oscillator is low, sell when it is high").
library(fBasics) # RMetrics
x <- yahooImport("s=IBM&a=11&b=1&c=1999&d=0&q=31&f=2000&z=IBM&x=.csv")
x <- as.numeric(as.character(x@data$Close))
x20 <- filter(x, rep(1/20,20), sides=1)
x50 <- filter(x, rep(1/50,50), sides=1)
matplot(cbind(x,x20,x50), type="l", lty=1, ylab="price", log="y")
segments(1:length(x), x[-length(x)], 1:length(x), x[-1], lwd=ifelse(x20>x50,1,5)[-1], col=ifelse(x20>x50,"black","blue")[-1])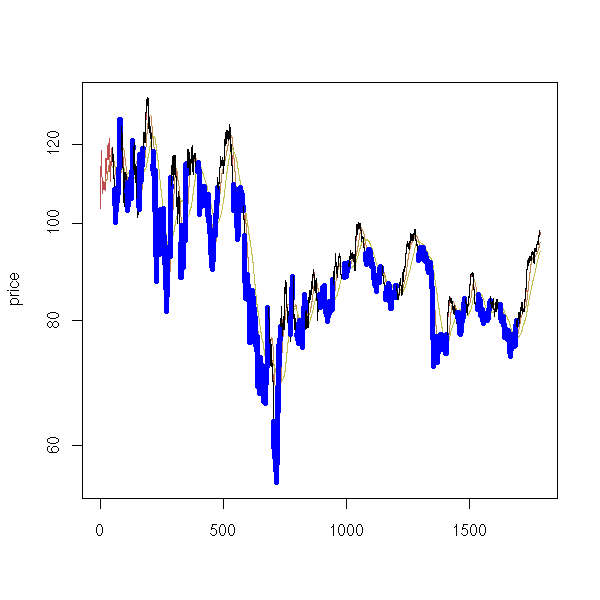
Exercise: do the same with an exponential moving average.
The moving average has a slight problem: it uses a window with sharp edges; an observation is either in the window or not. As a result, when large observations enter or leave the window, there is large jump in the moving average.
This is another moving average: instead of taking the N latest values, equally-weighted, we take all the preceding values and give a higher weight to the latest values.
exponential.moving.average <-
function (x, a) {
m <- x
for (i in 2:n) {
# Definition
# Exercise: use the "filter" function instead,
# with its "recursive" argument (that should be
# much, much faster)
m[i] <- a * x[i] + (1-a)*m[i-1]
}
m <- ts(m, start=start(x), frequency=frequency(x))
m
}
plot.exponential.moving.average <-
function (x, a=.9, ...) {
plot(exponential.moving.average(x,a), ...)
par(usr=c(0,1,0,1))
text(.02,.9, a, adj=c(0,1), cex=3)
}
op <- par(mfrow=c(4,1), mar=c(2,2,2,2)+.1)
plot(x, main="Exponential Moving Averages")
plot.exponential.moving.average(x, main="", ylab="")
plot.exponential.moving.average(x,.1, main="", ylab="")
plot.exponential.moving.average(x,.02, main="", ylab="")
par(op)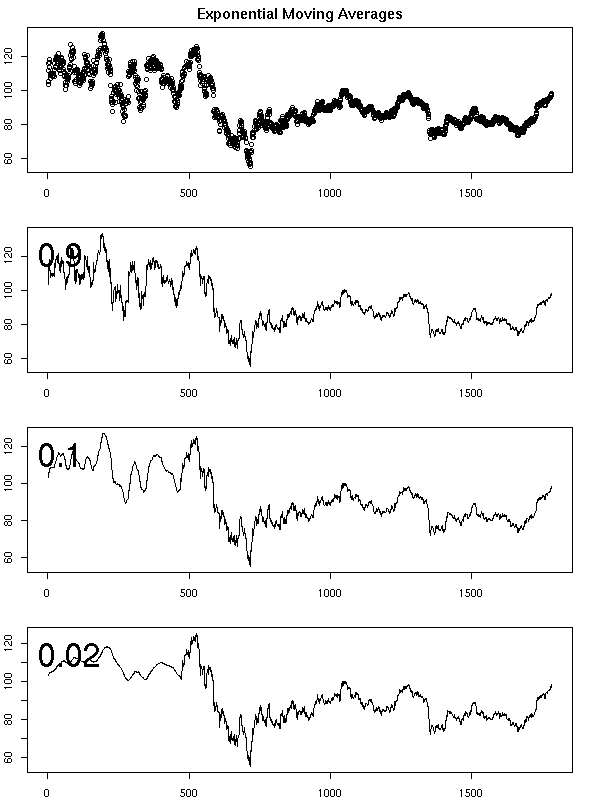
r <- x - exponential.moving.average(x,.02) op <- par(mfrow=c(4,1), mar=c(2,4,2,2)+.1) plot(r, main="Residuals of an exponential moving average") acf(r, main="") pacf(r, main="") spectrum(r, main="") abline(v=1:10,lty=3) par(op)

As with all moving average filters, there is a lag.
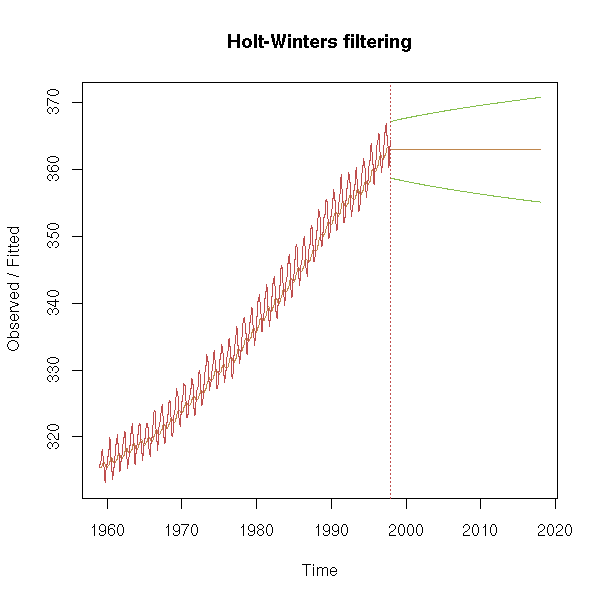
Actually, there is already a function to do this (it is a special case of the Holt-Winters filter -- we shall present the general case in a few moments):
x <- co2 m <- HoltWinters(x, alpha=.1, beta=0, gamma=0) p <- predict(m, n.ahead=240, prediction.interval=T) plot(m, predicted.values=p)
y <- x20 > x50 op <- par(mfrow=c(5,1), mar=c(0,0,0,0), oma=.1+c(0,0,0,0)) plot(y, type="l", axes=FALSE); box() plot(filter(y, 50/100, "recursive", sides=1), axes=FALSE); box() plot(filter(y, 90/100, "recursive", sides=1), axes=FALSE); box() plot(filter(y, 95/100, "recursive", sides=1), axes=FALSE); box() plot(filter(y, 99/100, "recursive", sides=1), axes=FALSE); box() par(op)
The "runing" function in the "gtools" package, the "rollFun" function in the "rollFun" in the "fMultivar" package (in RMetrics) and the "rollapply" function in the "zoo" package compute a statistic (mean, standard deviation, median, quantiles, etc.) on a moving window.
library(zoo)
op <- par(mfrow=c(3,1), mar=c(0,4,0,0), oma=.1+c(0,0,0,0))
plot(rollapply(zoo(x), 10, median, align="left"),
axes = FALSE, ylab = "median")
lines(zoo(x), col="grey")
box()
plot(rollapply(zoo(x), 50, sd, align="left"),
axes = FALSE, ylab = "sd")
box()
library(robustbase)
plot(sqrt(rollapply(zoo(x), 50, Sn, align="left")),
axes = FALSE, ylab = "Sn")
box()
par(op)
One can also find the trend of a time series by performing a Fourier transform and removing the high frequencies -- indeed, the moving averages we considered earlier are low-pass filters.
Exercise left to the reader
If a time series has a trend, if this trend is a polynomial of degree n, then you can transform this series into a trend-less one by differentiating it (using the discrete derivative) n times.
TODO: an example
To go back to the initial time series, you just have to integrate n times ("discrete integration" is just a complicated word for "cumulated sums" -- but, of course, you have to worry about the integration constants).
TODO: Explain the relations/confusions between trend, stationarity, integration, derivation.
TODO: Take a couple of (real-world) time series and apply them all the methods above, in order to compare them
The "stl" function performs a "Seasonal Decomposition of a Time Series by Loess".
In case you have forgotten, the "loess" function performs a local regression, i.e., for each value of the predictive variable, we take the neighbouring observations and perform a linear regression with them; the loess curve is the "envelope" of those regression lines.
op <- par(mfrow=c(3,1), mar=c(3,4,0,1), oma=c(0,0,2,0))
r <- stl(co2, s.window="periodic")$time.series
plot(co2)
lines(r[,2], col='blue')
lines(r[,2]+r[,1], col='red')
plot(r[,3])
acf(r[,3], main="residuals")
par(op)
mtext("STL(co2)", line=3, font=2, cex=1.2)
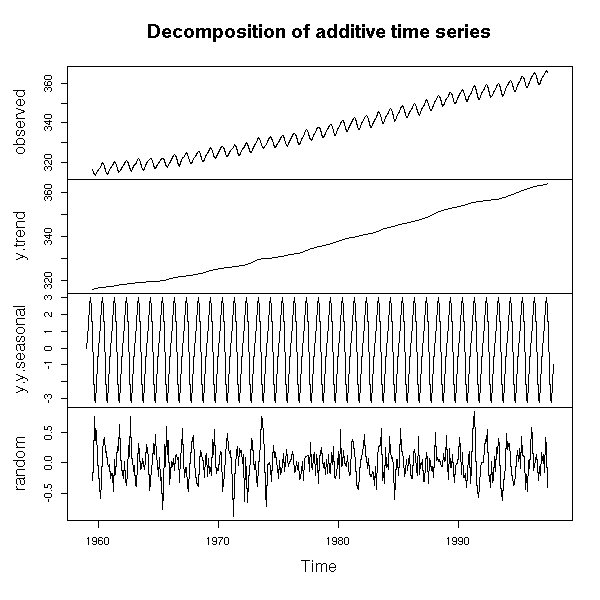
The "decompose" function has a similar purpose.
r <- decompose(co2) plot(r)
op <- par(mfrow=c(2,1), mar=c(0,2,0,2), oma=c(2,0,2,0))
acf(r$random, na.action=na.pass, axes=F, ylab="")
box(lwd=3)
mtext("PACF", side=2, line=.5)
pacf(r$random, na.action=na.pass, axes=F, ylab="")
box(lwd=3)
axis(1)
mtext("PACF", side=2, line=.5)
par(op)
mtext("stl(co2): residuals", line=2.5, font=2, cex=1.2)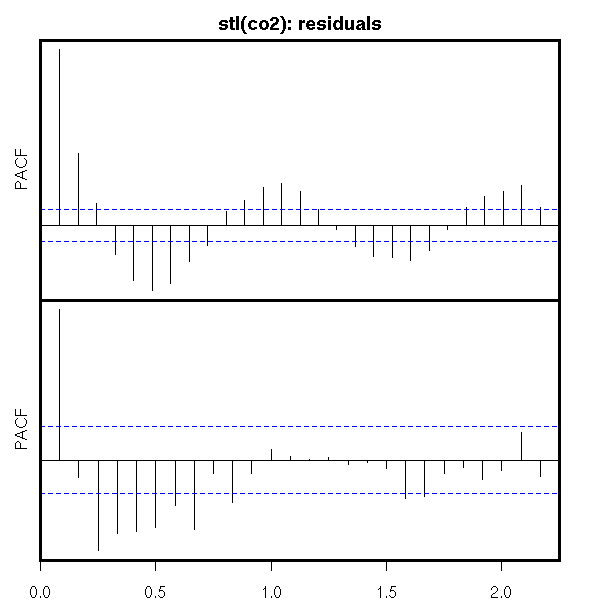
This is a generalization of exponential filtering (which assumes there is no seasonal component). It has the same advantages: it is not very sensible to (not too drastic) structural changes.
For exponential filtering, we had used
a(t) = alpha * Y(t) + (1-alpha) * a(t-1).
This is a good estimator of the future values of the time series if it is of the form Y(t) = Y_0 + noise, i.e., if the series is "a constant plus noise" (or even if it is just "locally constant").
This assumed that the series was locallly constant. Here is an example.
data(LakeHuron)
x <- LakeHuron
before <- window(x, end=1935)
after <- window(x, start=1935)
a <- .2
b <- 0
g <- 0
model <- HoltWinters(
before,
alpha=a, beta=b, gamma=g)
forecast <- predict(
model,
n.ahead=37,
prediction.interval=T)
plot(model, predicted.values=forecast,
main="Holt-Winters filtering: constant model")
lines(after)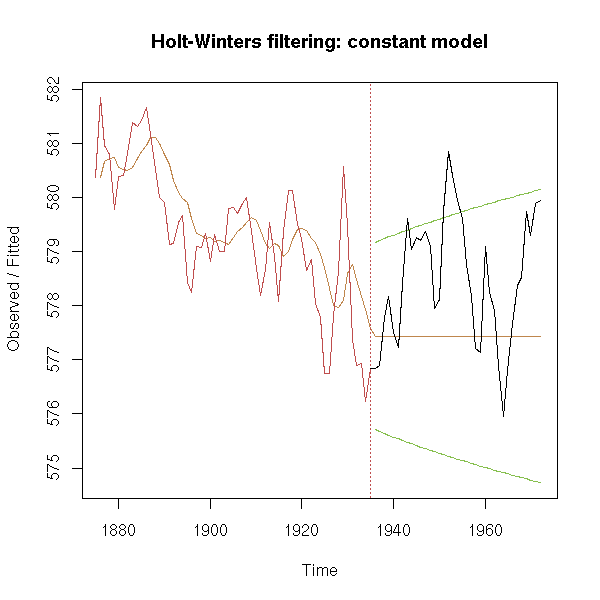
We can add a trend: we model the data as a line, from the preceding values, giving more weight to the most recent values.
data(LakeHuron)
x <- LakeHuron
before <- window(x, end=1935)
after <- window(x, start=1935)
a <- .2
b <- .2
g <- 0
model <- HoltWinters(
before,
alpha=a, beta=b, gamma=g)
forecast <- predict(
model,
n.ahead=37,
prediction.interval=T)
plot(model, predicted.values=forecast,
main="Holt-Winters filtering: trend model")
lines(after)
Depending on the choice of beta, the forecasts can be very different...
data(LakeHuron)
x <- LakeHuron
op <- par(mfrow=c(2,2),
mar=c(0,0,0,0),
oma=c(1,1,3,1))
before <- window(x, end=1935)
after <- window(x, start=1935)
a <- .2
b <- .5
g <- 0
for (b in c(.02, .04, .1, .5)) {
model <- HoltWinters(
before,
alpha=a, beta=b, gamma=g)
forecast <- predict(
model,
n.ahead=37,
prediction.interval=T)
plot(model,
predicted.values=forecast,
axes=F, xlab='', ylab='', main='')
box()
text( (4*par('usr')[1]+par('usr')[2])/5,
(par('usr')[3]+5*par('usr')[4])/6,
paste("beta =",b),
cex=2, col='blue' )
lines(after)
}
par(op)
mtext("Holt-Winters filtering: different values for beta",
line=-1.5, font=2, cex=1.2)
You can also add a seosonal component (and additive or a multiplicative one).
TODO: Example TODO: A multiplicative example
Before presenting general models whose interpretation may not be that straightforward (ARIMA, SARIMA), let us stop a moment to consider structural models, that are special cases of AR, MA, ARMA, ARIMA, SARIMA.
A random walk, with noise (a special case of ARIMA(0,1,1)):
X(t) = mu(t) + noise1
mu(t+1) = mu(t) + noise2
n <- 200
plot(ts(cumsum(rnorm(n)) + rnorm(n)),
main="Noisy random walk",
ylab="")
A random walk is simply "integrated noise" (as this is a discrete integration, we use the "cumsum" function). One can add some noise to a random walk: this is called a local level model.
We can also change the variance of those noises.
op <- par(mfrow=c(2,1),
mar=c(3,4,0,2)+.1,
oma=c(0,0,3,0))
plot(ts(cumsum(rnorm(n, sd=1))+rnorm(n,sd=.1)),
ylab="")
plot(ts(cumsum(rnorm(n, sd=.1))+rnorm(n,sd=1)),
ylab="")
par(op)
mtext("Noisy random walk", line=2, font=2, cex=1.2)
A noisy random walk, integrated, with added noise (ARIMA(0,2,2), aka local trend model):
X(t) = mu(t) + noise1
mu(t+1) = mu(t) + nu(t) + noise2 (level)
nu(t+1) = nu(t) + noise3 (slope)
n <- 200
plot(ts( cumsum( cumsum(rnorm(n))+rnorm(n) ) +
rnorm(n) ),
main = "Local trend model",
ylab="")
Here again, we can play and change the noise variances.
n <- 200
op <- par(mfrow=c(3,1),
mar=c(3,4,2,2)+.1,
oma=c(0,0,2,0))
plot(ts( cumsum( cumsum(rnorm(n,sd=1))+rnorm(n,sd=1) )
+ rnorm(n,sd=.1) ),
ylab="")
plot(ts( cumsum( cumsum(rnorm(n,sd=1))+rnorm(n,sd=.1) )
+ rnorm(n,sd=1) ),
ylab="")
plot(ts( cumsum( cumsum(rnorm(n,sd=.1))+rnorm(n,sd=1) )
+ rnorm(n,sd=1) ),
ylab="")
par(op)
mtext("Local level models", line=2, font=2, cex=1.2)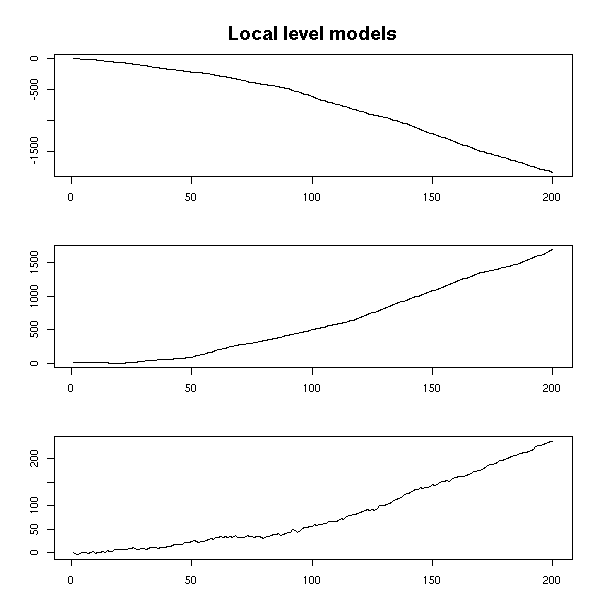
A noisy random walk, integrated, with added noise, to which we add a variable seasonal component.
X(t) = mu(t) + gamma(t) + noise1
mu(t+1) = mu(t) + nu(t) + noise2 (level)
nu(t+1) = nu(t) + noise2 (slope)
gamma(t+1) = -(gamma(t) + gamma(t-1) + gamma(t-2)) + noise4 (seasonal component)
structural.model <- function (
n=200,
sd1=1, sd2=1, sd3=1, sd4=1, sd5=200
) {
sd1 <- 1
sd2 <- 2
sd3 <- 3
sd4 <- 4
mu <- rep(rnorm(1),n)
nu <- rep(rnorm(1),n)
g <- rep(rnorm(1,sd=sd5),n)
x <- mu + g + rnorm(1,sd=sd1)
for (i in 2:n) {
if (i>3) {
g[i] <- -(g[i-1]+g[i-2]+g[i-3]) + rnorm(1,sd=sd4)
} else {
g[i] <- rnorm(1,sd=sd5)
}
nu[i] <- nu[i-1] + rnorm(1,sd=sd3)
mu[i] <- mu[i-1] + nu[i-1] + rnorm(1,sd=sd2)
x[i] <- mu[i] + g[i] + rnorm(1,sd=sd1)
}
ts(x)
}
n <- 200
op <- par(mfrow=c(3,1),
mar=c(2,2,2,2)+.1,
oma=c(0,0,2,0))
plot(structural.model(n))
plot(structural.model(n))
plot(structural.model(n))
par(op)
mtext("Structural models", line=2.5, font=2, cex=1.2)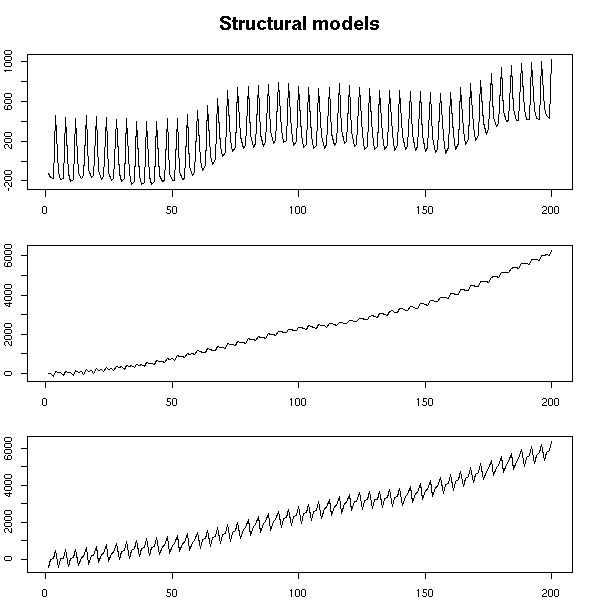
Here again, we can change the noise variance. If the seasonal component is not noisy, it is constant (but arbitrary).
n <- 200
op <- par(mfrow=c(3,1),
mar=c(2,2,2,2)+.1,
oma=c(0,0,2,0))
plot(structural.model(n,sd4=0))
plot(structural.model(n,sd4=0))
plot(structural.model(n,sd4=0))
par(op)
mtext("Structural models", line=2.5, font=2, cex=1.2)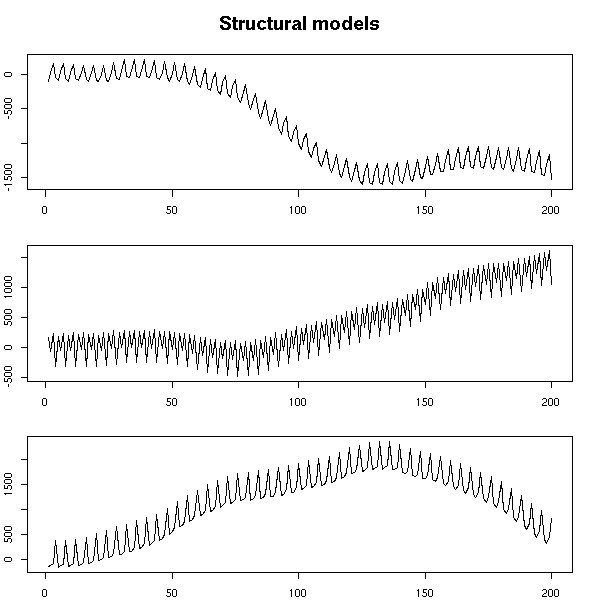
You can model a time series along those models with the "StructTS" function.
data(AirPassengers) plot(AirPassengers)

plot(log(AirPassengers))

x <- log(AirPassengers) r <- StructTS(x) plot(x, main="AirPassengers", ylab="") f <- apply(fitted(r), 1, sum) f <- ts(f, frequency=frequency(x), start=start(x)) lines(f, col='red', lty=3, lwd=3)
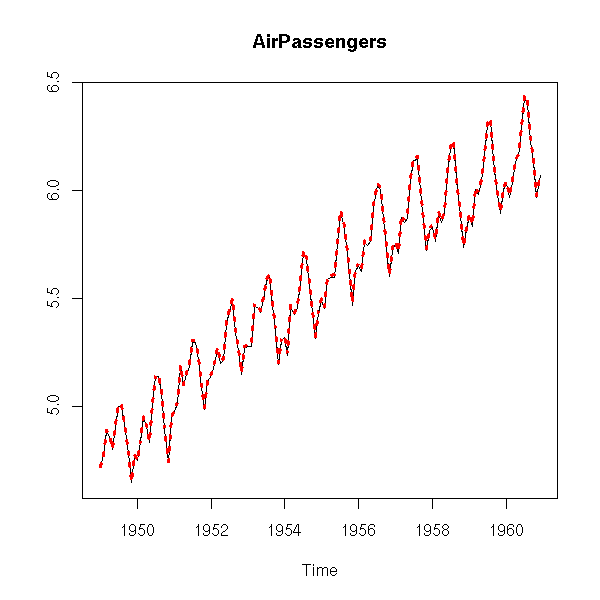
Here, the slope seems constant.
> r
Call:
StructTS(x = x)
Variances:
level slope seas epsilon
0.0007718 0.0000000 0.0013969 0.0000000
> summary(r$fitted[,"slope"])
Min. 1st Qu. Median Mean 3rd Qu. Max.
0.000000 0.009101 0.010210 0.009420 0.010560 0.011040
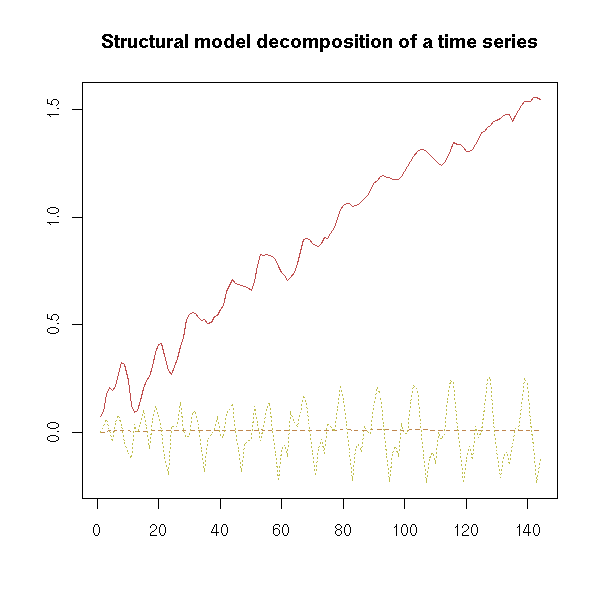
matplot(
(StructTS(x-min(x)))$fitted,
type = 'l',
ylab = "",
main = "Structural model decomposition of a time series"
)
You can also try to forecast future values (but it might not be that reliable).
l <- 1956
x <- log(AirPassengers)
x1 <- window(x, end=l)
x2 <- window(x, start=l)
r <- StructTS(x1)
plot(x)
f <- apply(fitted(r), 1, sum)
f <- ts(f, frequency=frequency(x), start=start(x))
lines(f, col='red')
p <- predict(r, n.ahead=100)
lines(p$pred, col='red')
lines(p$pred + qnorm(.025) * p$se,
col='red', lty=2)
lines(p$pred + qnorm(.975) * p$se,
col='red', lty=2)
title(main="Forecasting with a structural model (StructTS)")
TODO: put this at the end of the introduction?
# A function to look at a time series
eda.ts <- function (x, bands=FALSE) {
op <- par(no.readonly = TRUE)
par(mar=c(0,0,0,0), oma=c(1,4,2,1))
# Compute the Ljung-Box p-values
# (we only display them if needed, i.e.,
# if we have any reason of
# thinking it is white noise).
p.min <- .05
k <- 15
p <- rep(NA, k)
for (i in 1:k) {
p[i] <- Box.test(
x, i, type = "Ljung-Box"
)$p.value
}
if( max(p)>p.min ) {
par(mfrow=c(5,1))
} else {
par(mfrow=c(4,1))
}
if(!is.ts(x))
x <- ts(x)
plot(x, axes=FALSE);
axis(2); axis(3); box(lwd=2)
if(bands) {
a <- time(x)
i1 <- floor(min(a))
i2 <- ceiling(max(a))
y1 <- par('usr')[3]
y2 <- par('usr')[4]
if( par("ylog") ){
y1 <- 10^y1
y2 <- 10^y2
}
for (i in seq(from=i1, to=i2-1, by=2)) {
polygon( c(i,i+1,i+1,i), c(y1,y1,y2,y2),
col='grey', border=NA )
}
lines(x)
}
acf(x, axes=FALSE)
axis(2, las=2)
box(lwd=2)
mtext("ACF", side=2, line=2.5)
pacf(x, axes=FALSE)
axis(2, las=2)
box(lwd=2)
mtext("ACF", side=2, line=2.5)
spectrum(x, col=par('fg'), log="dB",
main="", axes=FALSE )
axis(2, las=2)
box(lwd=2)
mtext("Spectrum", side=2, line=2.5)
abline(v=1, lty=2, lwd=2)
abline(v=2:10, lty=3)
abline(v=1/2:5, lty=3)
if( max(p)>p.min ) {
main <-
plot(p, type='h', ylim=c(0,1),
lwd=3, main="", axes=F)
axis(2, las=2)
box(lwd=2)
mtext("Ljung-Box p-value", side=2, line=2.5)
abline(h=c(0,.05),lty=3)
}
par(op)
}
data(co2)
eda.ts(co2, bands=T)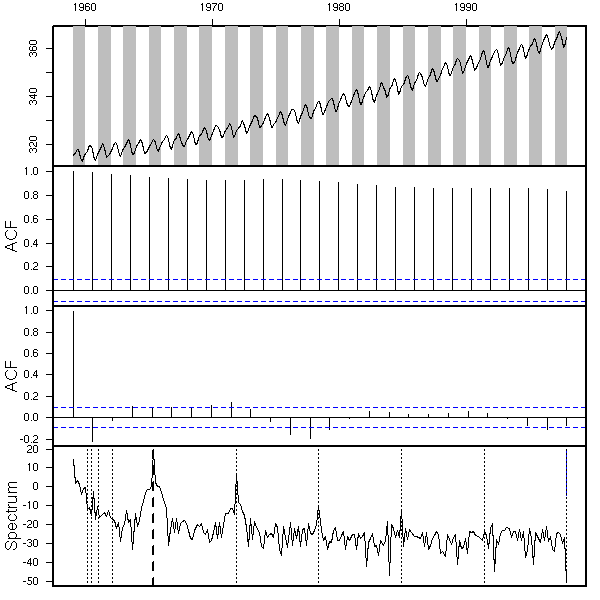
TODO: Put this section somewhere above
As for the regression, we first transform the data so that ot looks "nicer" (as usual, plot the histogram, density estimation, qqplot, etc., try a Box-Cox transformation). For instance, if you remark that the larger the value, the larger the variations, and if it is reasonable to think that the model could be "something deterministic plus noise", you can take the logarithm.
More generally, the aim of time series analysis is actually to transform the data so that it looks gaussian; the inverse of that transformation is then a model describing how the time series may have been produced from white noise.
Examples
data(AirPassengers) x <- AirPassengers plot(x)

plot(x) abline(lm(x~time(x)), col='red')
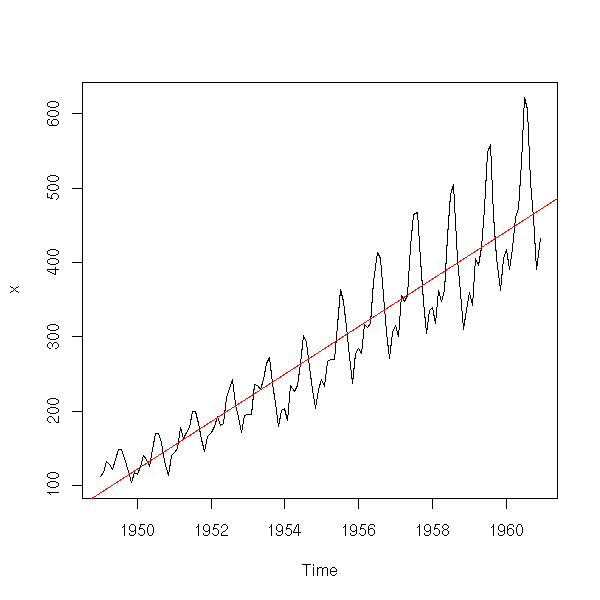
The residuals or the first derivative suggest that the amplitude of the variations increase.
plot(lm(x~time(x))$res)
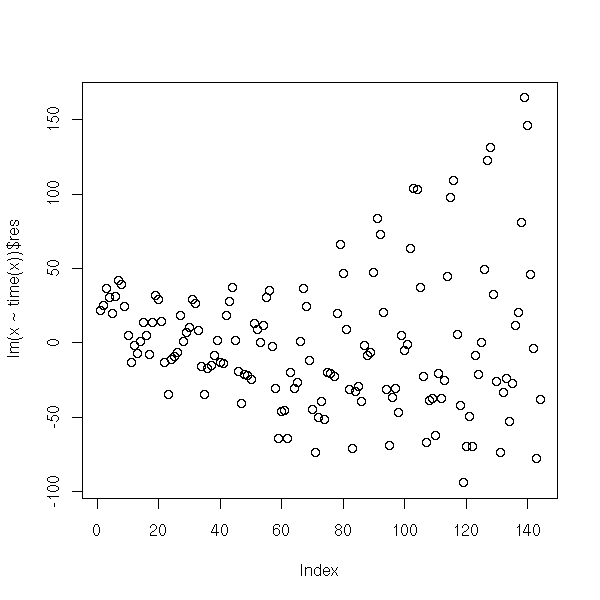
plot(diff(x))

Let us try with the logarithm.
x <- log(x) plot(x) abline(lm(x~time(x)),col='red')

plot(lm(x~time(x))$res)

plot(diff(x))
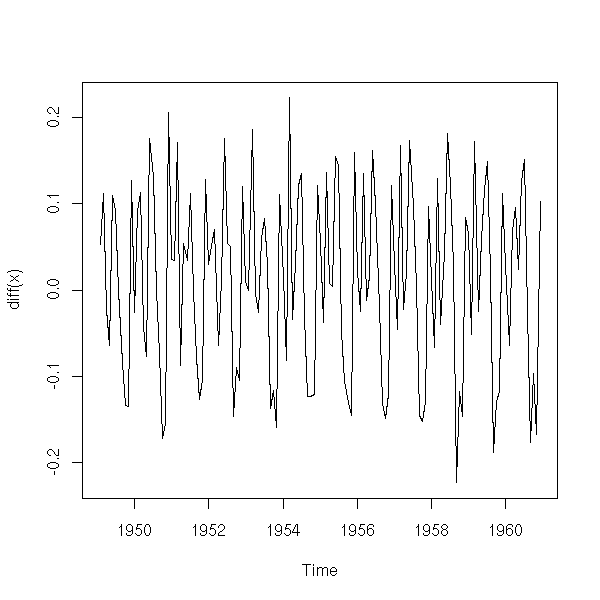
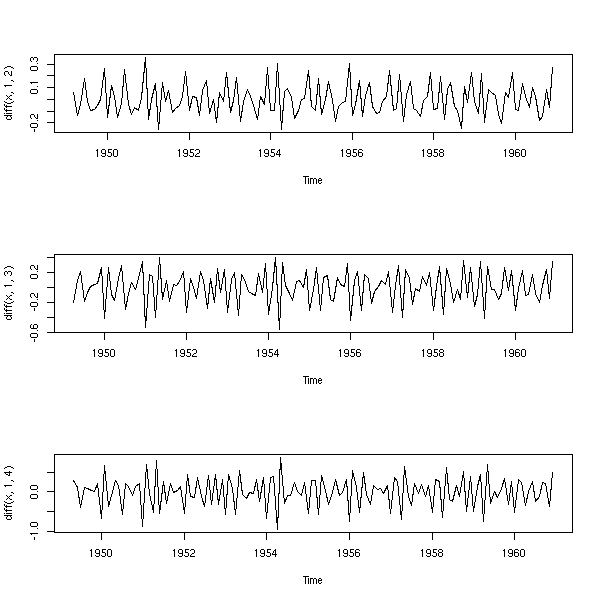
We could also have a look at the next derivatives.
op <- par(mfrow=c(3,1)) plot(diff(x,1,2)) plot(diff(x,1,3)) plot(diff(x,1,4)) par(op)
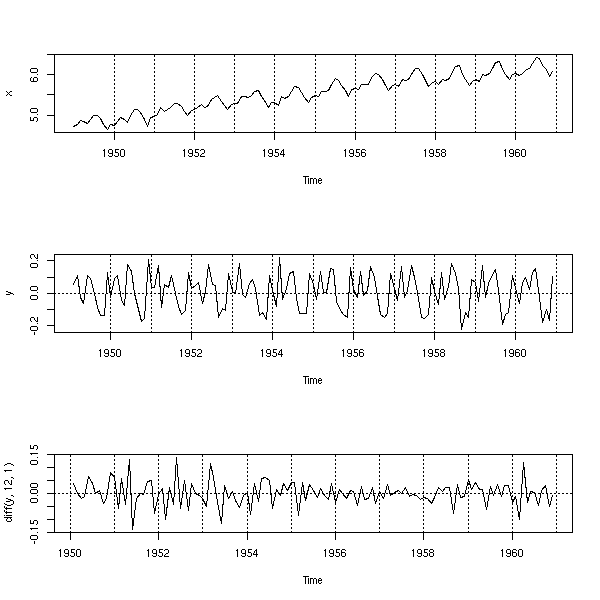
There seems to be a 12-month seasonal component.
op <- par(mfrow=c(3,1)) plot(x) abline(h=0, v=1950:1962, lty=3) y <- diff(x) plot(y) abline(h=0, v=1950:1962, lty=3) plot(diff(y, 12,1)) abline(h=0, v=1950:1962, lty=3) par(op)
You can also use a regression to get rid of the up-trend.
op <- par(mfrow=c(3,1)) plot(x) abline(lm(x~time(x)), col='red', lty=2) abline(h=0, v=1950:1962, lty=3) y <- x - predict(lm(x~time(x))) plot(y) abline(h=0, v=1950:1962, lty=3) plot(diff(y, 12,1)) abline(h=0, v=1950:1962, lty=3) par(op)

Let us look at the residuals and differentiate.
z <- diff(y,12,1) op <- par(mfrow=c(3,1)) plot(z) abline(h=0,lty=3) plot(diff(z)) abline(h=0,lty=3) plot(diff(z,1,2)) abline(h=0,lty=3) par(op)
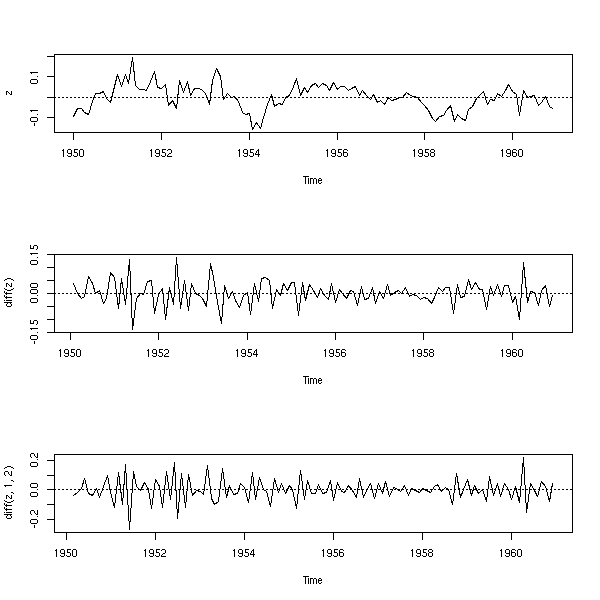
How many times should we differentiate?
k <- 3
op <- par(mfrow=c(k,2))
zz <- z
for(i in 1:k) {
acf(zz, main=i-1)
pacf(zz, main=i-1)
zz <- diff(zz)
}
par(op)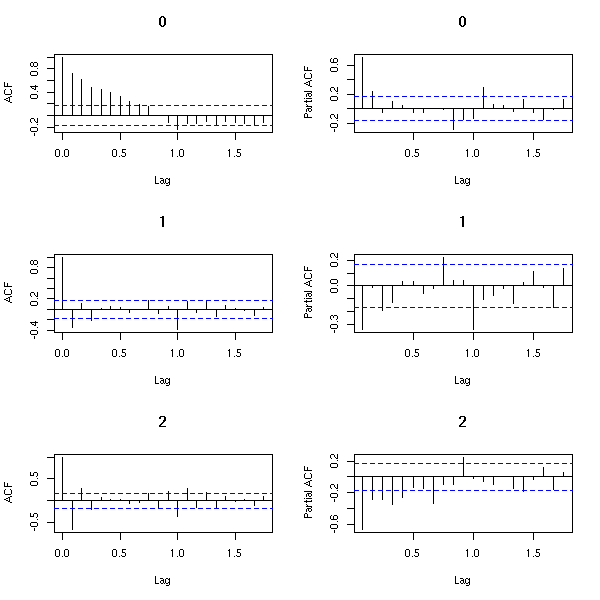
TODO: What is this?
data(sunspots)
op <- par(mfrow=c(5,1))
for (i in 10+1:5) {
plot(diff(sunspots,i))
}
par(op)
The main difference between time series and the series of iid random variables we have been playing with up to now is the lack of independance. Correlation is one means of measuring that lack of independance (if the variables are gaussian, it is even an accurate means).
The AutoCorrelation Function (ACF) is the correlation between a term and the i-th preceding term
ACF(i) = Cor( X(t), X(t-i) )
If indeed this does not depend on the position t, the time series is said to be weakly stationary -- it is said to be strongly stationary if for all t, h, the joint distributions of (X(t),X(t+1),...,X(t+n)) and (X(t+h),X(t+h+1),...,X(t+h+n)) are the same.
In the following plot, most (1/20) of the values of the ACT should be between the dashed lines -- otherwise, there might be something else than gaussian noise in your data.
Strictly speaking, one should distinguish between the theoretical ACF, computed from a model, without any data and the Sample ACF (SACF), computed from a sample. Here, we compute the SACF of a realization of a model.
op <- par(mfrow=c(2,1), mar=c(2,4,3,2)+.1)
x <- ts(rnorm(200))
plot(x, main="gaussian iidrv",
xlab="", ylab="")
acf(x, main="")
par(op)
A real example:
op <- par(mfrow=c(2,1), mar=c(2,4,3,2)+.1) data(BJsales) plot(BJsales, xlab="", ylab="", main="BJsales") acf(BJsales, main="") par(op)

f <- 24 x <- seq(0,10, by=1/f) y <- sin(2*pi*x) y <- ts(y, start=0, frequency=f) op <- par(mfrow=c(4,1), mar=c(2,4,2,2)+.1) plot(y, xlab="", ylab="") acf(y, main="") pacf(y, main="") spectrum(y, main="", xlab="") par(op)

f <- 24 x <- seq(0,10, by=1/f) y <- x + sin(2*pi*x) + rnorm(10*f) y <- ts(y, start=0, frequency=f) op <- par(mfrow=c(4,1), mar=c(2,4,2,2)+.1) plot(y, xlab="", ylab="") acf(y, main="") pacf(y, main="") spectrum(y, main="", xlab="") par(op)

The ACF plot is called an "autocorrelogram". In the case where the observations are not evenly spaced, one can plot a variogram instead: (y(t_i)-y(t_j))^2 as a function of t_i-t_j.
TODO: plot with irregularly-spaced data TODO: smooth this plot.
Often, these are (regular) time series with missing values, In this case, for a given value of k=t_i-t_j (on the horizontal axis), we have several values. You can replace them by their mean.
TODO: example Take a time series, remove some of its values, compare the correlogram and the variogram.
(There is also an analogue of the variogram for discrete-valued time series: the lorelogram, based on the LOR -- Logarithm of Odds Ratio.)
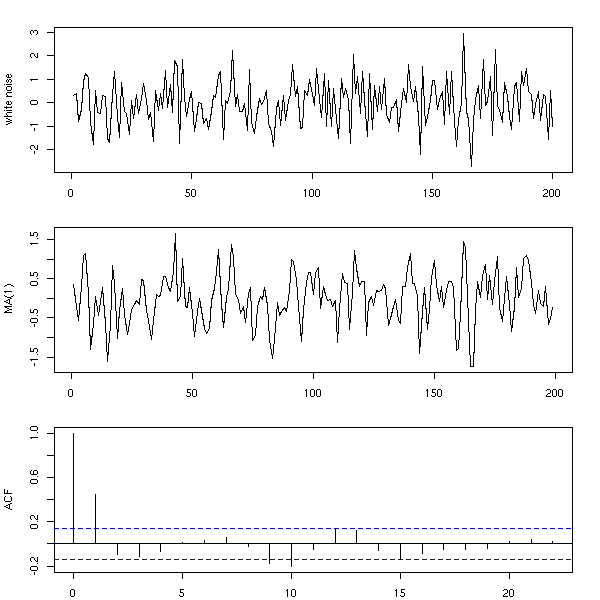
Here is a simple way of building a time series from a white noise: just perform a Moving Average (MA) of this noise.
n <- 200 x <- rnorm(n) y <- ( x[2:n] + x[2:n-1] ) / 2 op <- par(mfrow=c(3,1), mar=c(2,4,2,2)+.1) plot(ts(x), xlab="", ylab="white noise") plot(ts(y), xlab="", ylab="MA(1)") acf(y, main="") par(op)
n <- 200 x <- rnorm(n) y <- ( x[1:(n-3)] + x[2:(n-2)] + x[3:(n-1)] + x[4:n] )/4 op <- par(mfrow=c(3,1), mar=c(2,4,2,2)+.1) plot(ts(x), xlab="", ylab="white noise") plot(ts(y), xlab="", ylab="MA(3)") acf(y, main="") par(op)
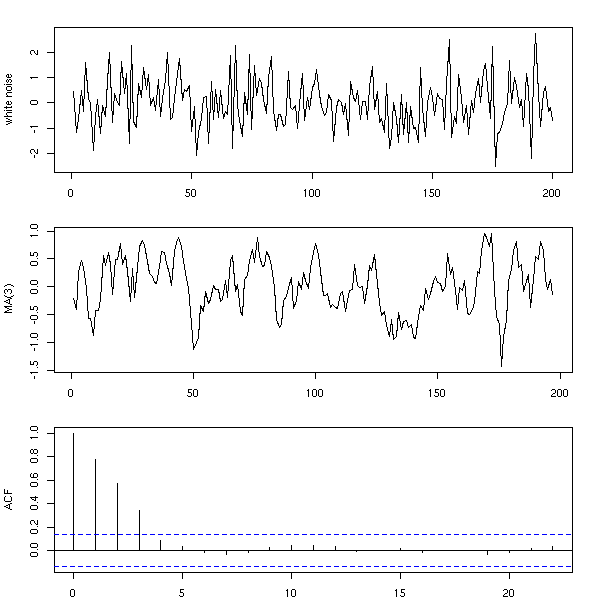
You can also compute the moving average with different coefficients.
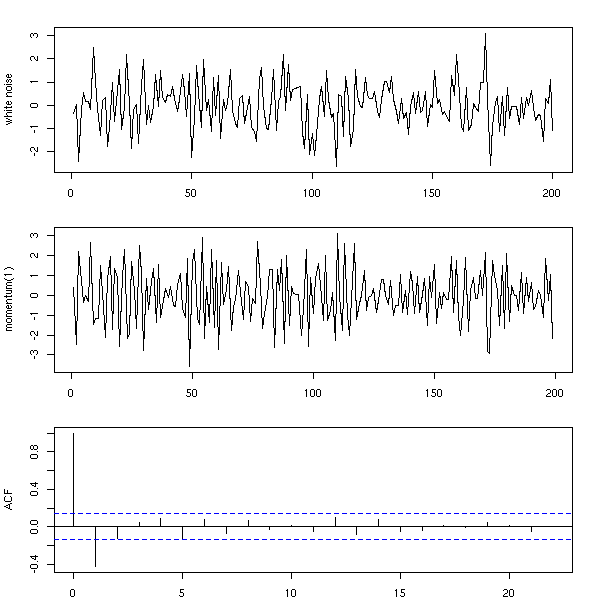
n <- 200 x <- rnorm(n) y <- x[2:n] - x[1:(n-1)] op <- par(mfrow=c(3,1), mar=c(2,4,2,2)+.1) plot(ts(x), xlab="", ylab="white noise") plot(ts(y), xlab="", ylab="momentum(1)") acf(y, main="") par(op)
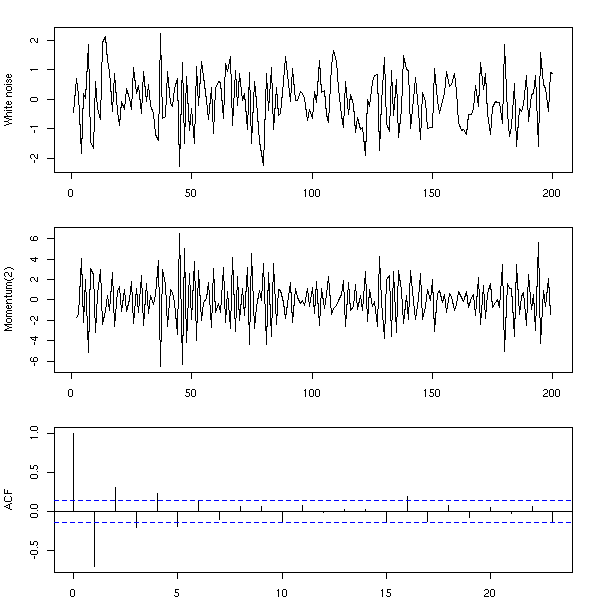
n <- 200 x <- rnorm(n) y <- x[3:n] - 2 * x[2:(n-1)] + x[1:(n-2)] op <- par(mfrow=c(3,1), mar=c(2,4,2,2)+.1) plot(ts(x), xlab="", ylab="white noise") plot(ts(y), xlab="", ylab="Momentum(2)") acf(y, main="") par(op)

Instead of computing the moving average by hand, you can use the "filter" function.
n <- 200 x <- rnorm(n) y <- filter(x, c(1,-2,1)) op <- par(mfrow=c(3,1), mar=c(2,4,2,2)+.1) plot(ts(x), xlab="", ylab="White noise") plot(ts(y), xlab="", ylab="Momentum(2)") acf(y, na.action=na.pass, main="") par(op)
TODO: the "side=1" argument.
Another means of building a time series is to compute each term by adding noise to the preceding term: this is called a random walk.
For instance,
n <- 200
x <- rep(0,n)
for (i in 2:n) {
x[i] <- x[i-1] + rnorm(1)
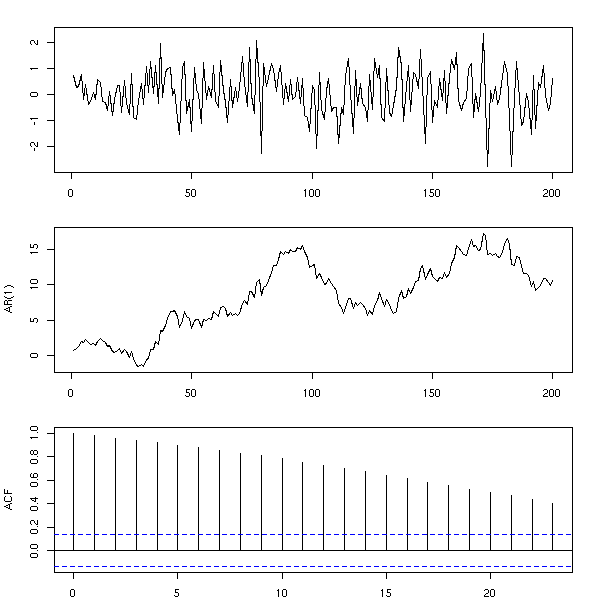
}This can be written, more simply, with the "cumsum" function.
n <- 200 x <- rnorm(n) y <- cumsum(x) op <- par(mfrow=c(3,1), mar=c(2,4,2,2)+.1) plot(ts(x), xlab="", ylab="") plot(ts(y), xlab="", ylab="AR(1)") acf(y, main="") par(op)
More generally, one can consider
X(n+1) = a X(n) + noise.
This is called an auto-regressive model, or AR(1), because one can estimate the coefficients by performing a regression of x against lag(x,1).
n <- 200
a <- .7
x <- rep(0,n)
for (i in 2:n) {
x[i] <- a*x[i-1] + rnorm(1)
}
y <- x[-1]
x <- x[-n]
r <- lm( y ~ x -1)
plot(y~x)
abline(r, col='red')
abline(0, .7, lty=2)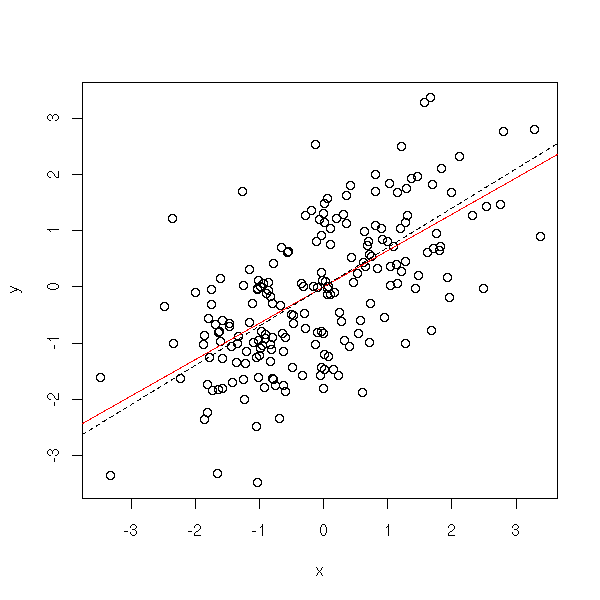
More generally, an AR(q) process is a process in which each term is a linear combination of the q preceding terms and a white noise (with fixed coefficients).
n <- 200
x <- rep(0,n)
for (i in 4:n) {
x[i] <- .3*x[i-1] -.7*x[i-2] + .5*x[i-3] + rnorm(1)
}
op <- par(mfrow=c(3,1), mar=c(2,4,2,2)+.1)
plot(ts(x), xlab="", ylab="AR(3)")
acf(x, main="", xlab="")
pacf(x, main="", xlab="")
par(op)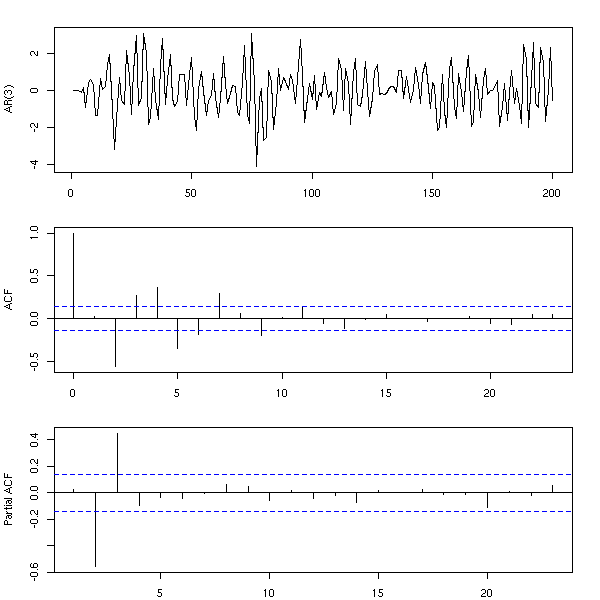
You can also simulate those models with the "arima.sim" function.
n <- 200 x <- arima.sim(list(ar=c(.3,-.7,.5)), n) op <- par(mfrow=c(3,1), mar=c(2,4,2,2)+.1) plot(ts(x), xlab="", ylab="AR(3)") acf(x, xlab="", main="") pacf(x, xlab="", main="") par(op)
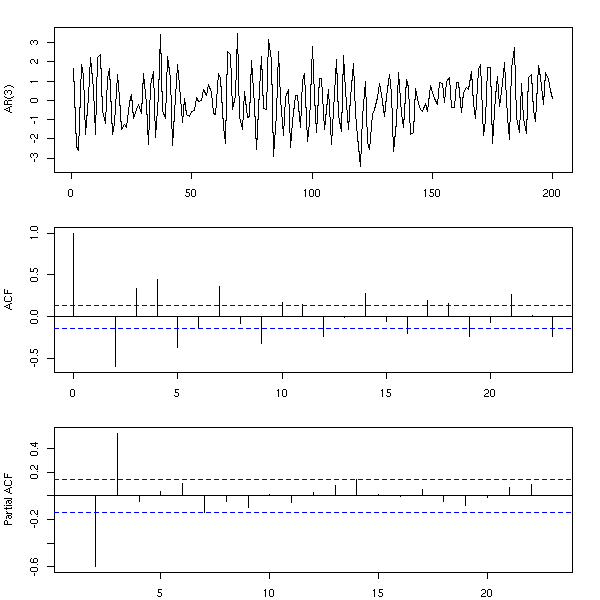
The partial AutoCorrelation Function (PACF) provides an estimation of the coefficients of an AR(infinity) model: we have already seen it on the previous examples. It can be easily computed from the autocorrelation function with the "Yule-Walker" equations.
To compute the auto-correlation function of an AR(p) process whose coefficients are known,
(1 - a1 B - a2 B^2 - ... - ap B^p) Y = Z
we just have to compute the first autocorrelations r1, r2, ..., rp, and then use the Yule-Walker equations:
r(j) = a1 r(j-1) + a2 r(j-2) + ... + ap r(j-p).
You can also use them in the other direction to compute the coefficients of an AR process from its autocorrelations.
A time series is said to be weakly stationary if the expectation of X(t) does not depend on t and if the covariance of X(t) and X(s) only depends on abs(t-s).
A time series is said to be stationary if all the X(t) have the same distribution and all the joint distribution of (X(t),X(s)) (for a given value of abs(s-t)) are the same. Thus, "weakly stationary" means "stationary up to the second order.
For instance, if your time series has a trend, i.e., if the expectation of X(t) is not constant, the series is not stationary.
n <- 200
x <- seq(0,2,length=n)
trend <- ts(sin(x))
plot(trend,
ylim=c(-.5,1.5),
lty=2, lwd=3, col='red',
ylab='')
r <- arima.sim(
list(ar = c(0.5,-.3), ma = c(.7,.1)),
n,
sd=.1
)
lines(trend+r)
Other example: a random walk is not stationary, because the variance of X(t) increases with t -- but the expectation of X(t) remains zero.
n <- 200
k <- 10
x <- 1:n
r <- matrix(nr=n,nc=k)
for (i in 1:k) {
r[,i] <- cumsum(rnorm(n))
}
matplot(x, r,
type = 'l',
lty = 1,
col = par('fg'),
main = "A random walk is not stationnary")
abline(h=0,lty=3)
Ergodicity and stationarity are two close but different notions.
Given a stochastic process X(n), (n integer), to compute the mean of X(1), we can use one of the following methods: either take several realizations of this process, each providing a value for X(1), and average those values; or take a single realization of this process and average X(1), X(2), X(3), etc.. The result we want is the first, but if we are lucky (if the process is ergodic), both will coincide.
Intuitively, a process is ergodic if, to get information that would require several realizations of the process, you can instead consider a single longer realization.
The practical interest of ergodic processes is that usually, when we study time series, we have a single realization of this time series. With an ergodic hypothesis, we can say something about it -- without it, we are helpless.
TODO: understand and explain the differences. For instance, a stationnary process need not be ergodic.
In an autoregressive (AR) process, it is reasonable to ask that past observations have less influence than more recent ones. That is why we ask, in the AR(1) model,
Y(t+1) = a * Y(t) + Z(t) (where Z is a white noise)
that abs(a)<1. This can also be written:
Y(t+1) - a Y(t) = Z(t)
or
phi(B) Y = Z (where phi(u) = 1 - a u
and B is the Backwards, operator,
aka shift, delay or lag operator)and we ask that all the roots of phi have a modulus greater than 1.
More generally, an AR process
phi(B) Y = Z where phi(u) = 1 - a_1 u - a_2 u^2 - ... - a_p u^p
is stationary if the modulus of all the roots of phi are greater that 1.
You can check that these stationary AR process are MA(infinity) processes (this is another meaning of the Yule--Walker equations).
TODO: understand and correct this.
Symetrically, for a Moving Average (MA) process, defined by
Y = psi(B) Z where psi(u) = 1 + b_1 u + b_2 u^3 + ... + b_q u^q
We shall also ask that modulus of the roots of psi be greater than 1. The process is then said to be invertible. Without this hypothesis, the autocorrelation function does not uniquely define the coefficients of the Moving Average.
For instance, for an MA(1) process,
Y(t+1) = Z(t+1) + a Z(t),
you can replace a by 1/a without changing the autocorrelation function.
n <- 200
ma <- 2
mai <- 1/ma
op <- par(mfrow=c(4,1), mar=c(2,4,1,2)+.1)
x <- arima.sim(list(ma=ma),n)
plot(x, xlab="", ylab="")
acf(x, xlab="", main="")
lines(0:n,
ARMAacf(ma=ma, lag.max=n),
lty=2, lwd=3, col='red')
x <- arima.sim(list(ma=mai),n)
plot(x, xlab="", ylab="")
acf(x, main="", xlab="")
lines(0:n,
ARMAacf(ma=mai, lag.max=n),
lty=2, lwd=3, col='red')
par(op)
TODO: an example with a higher degree polynomial (I naively thought I would just have to invert the roots of the polynomial, but apparently it is more complicated...)
sym.poly <- function (z,k) {
# Sum of the products of k
# distinct elements of the vector z
if (k==0) {
r <- 1
} else if (k==1) {
r <- sum(z)
} else {
r <- 0
for (i in 1:length(z)) {
r <- r + z[i]*sym.poly(z[-i],k-1)
}
r <- r/k # Each term appeared k times
}
r
}
sym.poly( c(1,2,3), 1 ) # 6
sym.poly( c(1,2,3), 2 ) # 11
sym.poly( c(1,2,3), 3 ) # 6
roots.to.poly <- function (z) {
n <- length(z)
p <- rep(1,n)
for (k in 1:n) {
p[n-k+1] <- (-1)^k * sym.poly(z,k)
}
p <- c(p,1)
p
}
roots.to.poly(c(1,2)) # 2 -3 1
round(
Re(polyroot( roots.to.poly(c(1,2,3)) )),
digits=1
)
# After this interlude, we can finally
# construct an MA process and one of
# its inverses
n <- 200
k <- 3
ma <- runif(k,-1,1)
# The roots
z <- polyroot(c(1,-ma))
# The inverse of the roots
zi <- 1/z
# The polynomial
p <- roots.to.poly(zi)
# The result should be real, but because
# of rounding errors, it is not.
p <- Re(p)
# We want the constant term to be 1.
p <- p/p[1]
mai <- -p[-1]
op <- par(mfrow=c(4,1), mar=c(2,4,1,2)+.1)
x <- arima.sim(list(ma=ma),n)
plot(x, xlab="")
acf(x, main="", xlab="")
lines(0:n, ARMAacf(ma=ma, lag.max=n),
lty=2, lwd=3, col='red')
x <- arima.sim(list(ma=mai),n)
plot(x, xlab="")
acf(x, main="", xlab="")
lines(0:n, ARMAacf(ma=mai, lag.max=n),
lty=2, lwd=3, col='red')
par(op)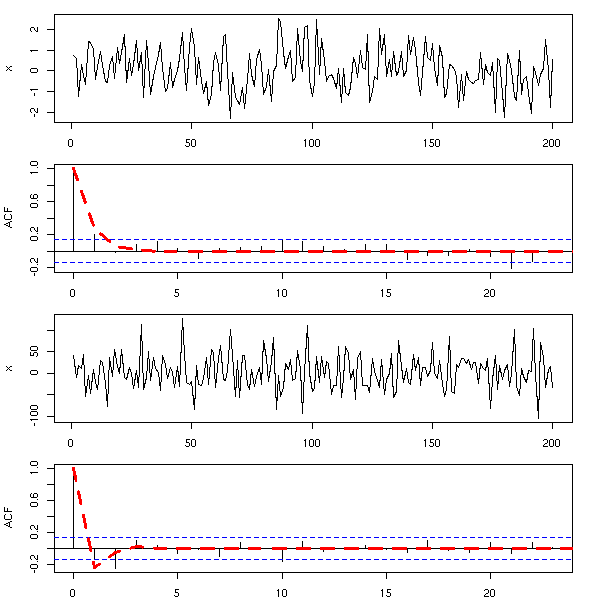
The MA(p) processes have another interesting feature: they are AR(infinity) processes.
TODO: on an example, plot the roots of those polynomials.
TODO: To check if the series we are studying has unit roots.
library(tseries) ?adf.test ?pp.tests
Of course, one can mix up MA and AR models, to get the so-called ARMA models. In the following formulas, z is a white noise and x the series we are interested in.
MA(p): x(i) = a1 z(i-1) + a2 z(i-2) + ... + ap z(i-p) AR(q): x(i) - b1 x(i-1) - b2 x(i-2) - ... - bq x(i-q) = z(i) ARMA(p,q): x(i) - b1 x(i-1) - ... - bq x(i-q) = a1 z(i-1) + ... + ap z(i-p)
Remark: AR(q) processes are also MA(infinity) processes, we could replace ARMA processes by MA(infinity) processes, but we prefer having fewer coefficients to estimate.
Remark: Wold's theorem states that any stationary process can be written as the sum of an MA(infinity) process and a deterministic one.
TODO: I have not defined what a deterministic process was.
Remark: if we let B be the shift operator, so that the derivation operator be 1-B, an ARMA process can be written as
phi(B) X(t) = theta(B) Z(t)
where theta(B) = 1 + a1 B + a2 B^2 + ... + ap B^p
phi(B) = 1 - b1 B - b2 B^2 - ... - bq B^q
Z is a white noiseARMA processes give a good approximation to most stationary processes. As a result, you can use the estimated ARMA coefficients as a statistical summary of a stationary process, exactly as the mean and the quantiles for univariate statistical series. They might be useful to forecast future values, but they provide little information as the the underlying mechanisms that produced the time series.
An ARMA(p,q) process
phi(B) Y = theta(B) Z
in which phi and theta have a root in common can be written, more simply, as an ARMA(p-1,q-1).
To model a time series as an ARMA model, it has to be stationnary. To get a stationary series (in short, to get rid of the trend), you can try to differentiate it.
The fact that the series is not stationary is usually obvious on the plot. You can also see it on the ACF: if the series is stationary, the ACF should rapidly (usually exponentially) decay to zero.
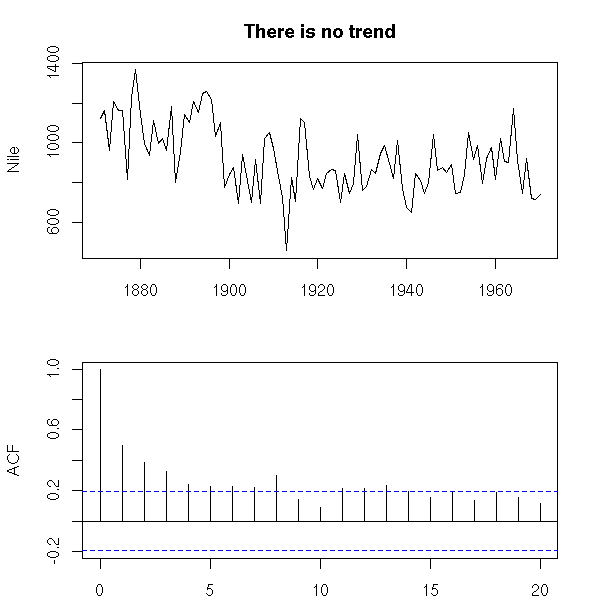
data(Nile) op <- par(mfrow=c(2,1), mar=c(2,4,3,2)+.1) plot(Nile, main="There is no trend", xlab="") acf(Nile, main="", xlab="") par(op)
data(BJsales)
op <- par(mfrow=c(3,1), mar=c(2,4,3,2)+.1)
plot(BJsales, xlab="",
main="The trend disappears if we differentiate")
acf(BJsales, xlab="", main="")
acf(diff(BJsales), xlab="", main="",
ylab="ACF(diff(BJsales)")
par(op)
n <- 2000
x <- arima.sim(
model = list(
ar = c(.3,.6),
ma = c(.8,-.5,.2),
order = c(2,1,3)),
n
)
x <- ts(x)
op <- par(mfrow=c(3,1), mar=c(2,4,3,2)+.1)
plot(x, main="It suffices to differentiate once",
xlab="", ylab="")
acf(x, xlab="", main="")
acf(diff(x), xlab="", main="",
ylab="ACF(diff(x))")
par(op)
n <- 10000
x <- arima.sim(
model = list(
ar = c(.3,.6),
ma = c(.8,-.5,.2),
order = c(2,2,3)
),
n
)
x <- ts(x)
op <- par(mfrow=c(4,1), mar=c(2,4,3,2)+.1)
plot(x, main="One has to differentiate twice",
xlab="", ylab="")
acf(x, main="", xlab="")
acf(diff(x), main="", xlab="",
ylab="ACF(diff(x))")
acf(diff(x,differences=2), main="", xlab="",
ylab="ACF(diff(diff(x)))")
par(op)
To check more precisely if the ACF decreases exponentially, one could perform a regression (but it might be overkill).
acf.exp <- function (x, lag.max=NULL, lag.max.reg=lag.max, ...) {
a <- acf(x, lag.max=lag.max.reg, plot=F)
b <- acf(x, lag.max=lag.max, ...)
r <- lm( log(a$acf) ~ a$lag -1)
lines( exp( b$lag * r$coef[1] ) ~ b$lag, lty=2 )
}
data(BJsales)
acf.exp(BJsales,
main="Exponential decay of the ACF")
acf.exp(BJsales,
lag.max=40,
main="Exponential decay of the ACF")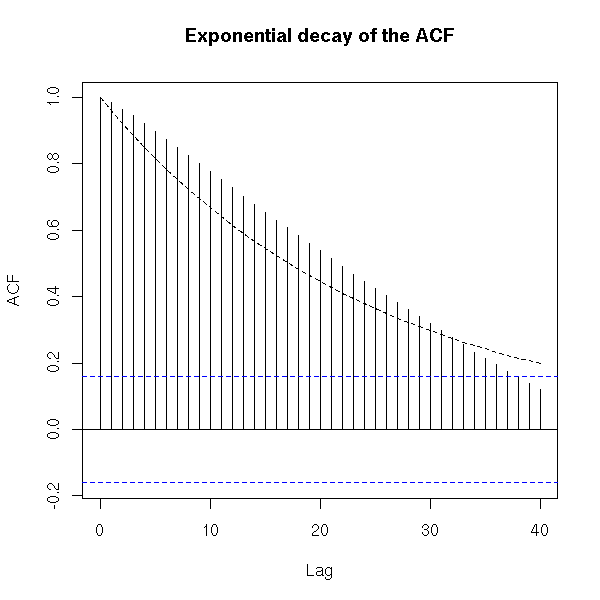
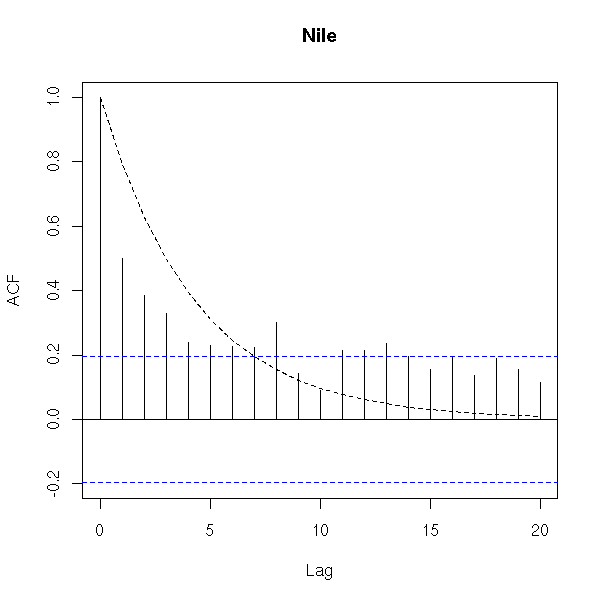
data(Nile) acf.exp(Nile, lag.max.reg=10, main="Nile")
Differentiating can also help you get rid of the seasonal component, if you differentiate with a lag: e.g., take the difference between the value today and the same value one year ago.
x <- diff(co2, lag=12)
op <- par(mfrow=c(4,1), mar=c(2,4,3,2)+.1)
plot(x, ylab="", xlab="")
acf(x, xlab="", main="")
pacf(x, xlab="", main="")
spectrum(x, xlab="", main="",
col=par('fg'))
par(op)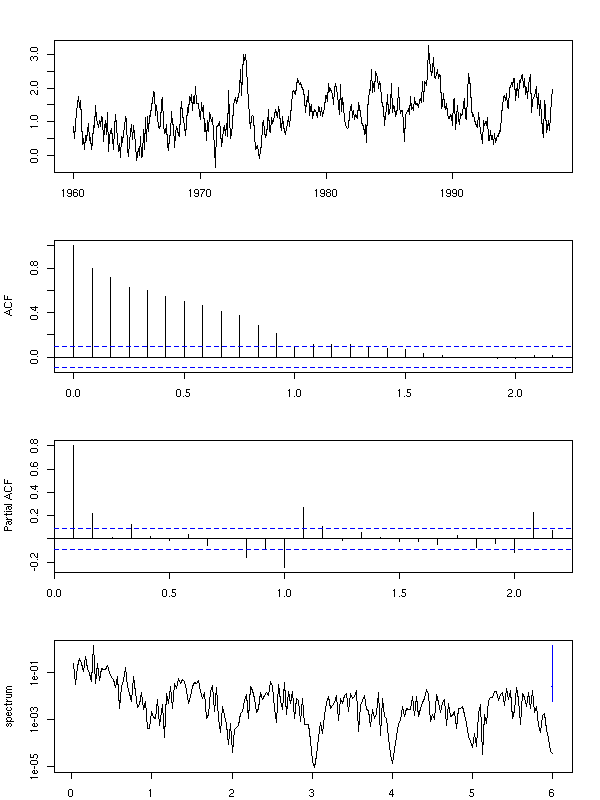
y <- diff(x)
op <- par(mfrow=c(4,1), mar=c(2,4,3,2)+.1)
plot(y, xlab="", ylab="")
acf(y, xlab="", main="")
pacf(y, xlab="", main="")
spectrum(y, col=par('fg'),
xlab="", main="")
par(op)
ARIMA processes are just integrated ARMA processes. In other words, a process is ARIMA of order d if its d-th derivative is ARMA. The model can be written
phi(B) (1-B)^d X(t) = theta(B) Z(t)
where B is the shift operator, Z a white noise, phi the polynomial defining the AR part, theta the polynomial defining the MA part of the process.
ARIMA processes are not stationary processes. We have already seen it with the random walk, which is an integrated ARMA(0,0) process, i.e., an ARIMA process of order 1: the variance of X(t) increases with t. This is the very reason why we differentiate: to get a stationary process.
TODO: Give an example of ARIMA(0,1,0) process, show that it is not stationary. Recall the tests to check if it is stationary. Quick and dirty stationarity test: cut the data into two parts, compute Cor(X(t),X(t-1)) on each, compare.
To infer the order of an ARIMA process, you can differentiate it until its ACF rapidly decreases.
n <- 200
x <- arima.sim(
list(
order=c(2,1,2),
ar=c(.5,-.8),
ma=c(.9,.6)
),
n
)
op <- par(mfrow=c(3,1), mar=c(2,4,4,2)+.1)
acf(x, main="You will have to defferentiate once")
acf(diff(x), main="First derivative")
acf(diff(x, differences=2), main="Second derivative")
par(op)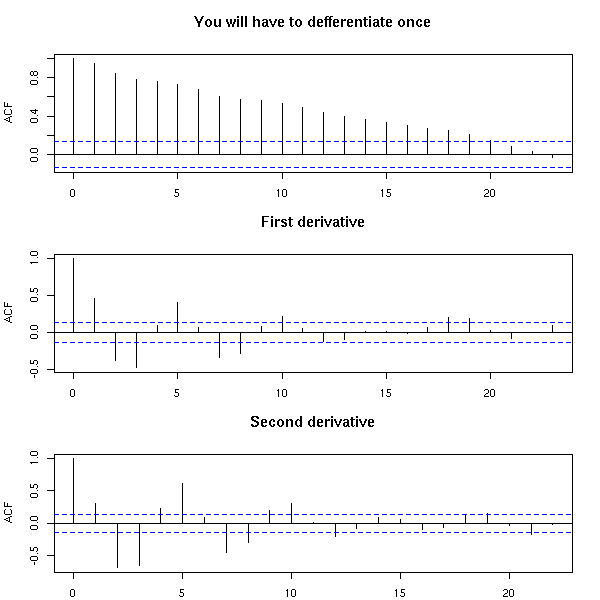
n <- 200
x <- arima.sim(
list(
order=c(2,2,2),
ar=c(.5,-.8),
ma=c(.9,.6)
),
n
)
op <- par(mfrow=c(3,1), mar=c(2,4,4,2)+.1)
acf(x, main="You will have to differentiate twice")
acf(diff(x), main="First derivative")
acf(diff(x, differences=2), main="Second derivative")
par(op)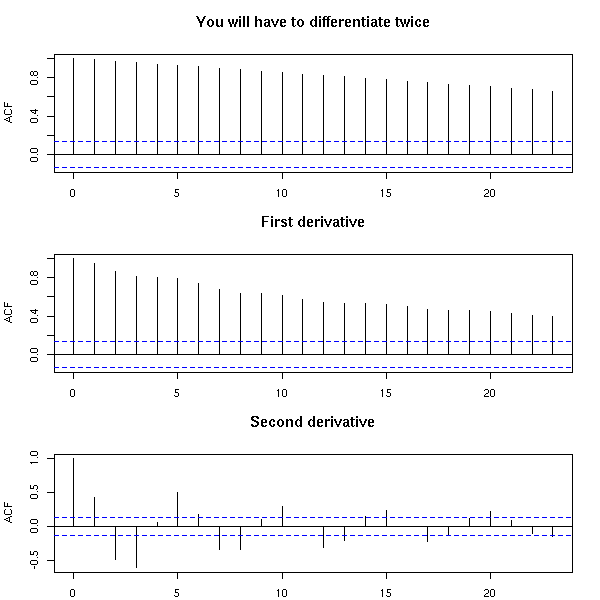
Here is a concrete example.
data(sunspot)
op <- par(mfrow=c(4,1), mar=c(2,4,3,2)+.1)
plot(sunspot.month, xlab="", ylab="sunspot")
acf(sunspot.month, xlab="", main="")
plot(diff(sunspot.month),
xlab="", ylab="diff(sunspot)")
acf(diff(sunspot.month), xlab="", main="")
par(op)
Same here (but actually, the differentiation discards the affine trend).
data(JohnsonJohnson) x <- log(JohnsonJohnson) op <- par(mfrow=c(4,1), mar=c(2,4,3,2)+.1) plot(x, xlab="", ylab="JJ") acf(x, main="") plot(diff(x), ylab="diff(JJ)") acf(diff(x), main="") par(op)
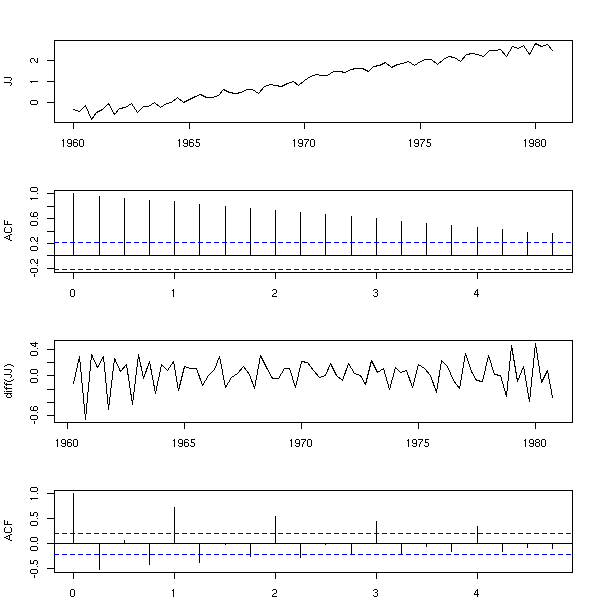
In the following examples, you might want to differentiate twice. But beware, it might not always be a good idea: if the ACF decreases exponentially, you can stop differentiating.
data(BJsales) x <- BJsales op <- par(mfrow=c(6,1), mar=c(2,4,0,2)+.1) plot(x) acf(x) plot(diff(x)) acf(diff(x)) plot(diff(x, difference=2)) acf(diff(x, difference=2)) par(op)

data(austres) x <- austres op <- par(mfrow=c(6,1), mar=c(2,4,0,2)+.1) plot(x) acf(x) plot(diff(x)) acf(diff(x)) plot(diff(x, difference=2)) acf(diff(x, difference=2)) par(op)

# In the preceding example, there was a linear trend: # let ut remove it. data(austres) x <- lm(austres ~ time(austres))$res op <- par(mfrow=c(6,1), mar=c(2,4,0,2)+.1) plot(x) acf(x) plot(diff(x)) acf(diff(x)) plot(diff(x, difference=2)) acf(diff(x, difference=2)) par(op)

These are Seasonnal ARIMA processes (the integration, the MA or the AR parts can be seasonal). They are often denoted:
(p,d,q) \times (P,D,Q) _s
and they are described by the model:
phi(B) Phi(B^s) (1-B)^d (1-B^s)^D X(t) = theta(B) Theta(B^s) Z(t)
where s is the period
theta(B) = 1 + a1 B + a2 B^2 + ... + ap B^p is the MA polynomial
phi(B) = 1 - b1 B - b2 B^2 - ... - bq B^q is the AR polynomial
Theta(B^s) = 1 + A1 B^s + A2 B^2s + ... + AP B^(P*s) is the seasonal MA polynomial
Phi(B^s) = 1 - B1 B^s - B2 B^2s - ... - BQ B^(Q*s) is the seasonal AR polynomial
Z is a white noiseThere is no function to simulate SARIMA processes -- but we can model them.
my.sarima.sim <- function (
n = 20,
period = 12,
model,
seasonal
) {
x <- arima.sim( model, n*period )
x <- x[1:(n*period)]
for (i in 1:period) {
xx <- arima.sim( seasonal, n )
xx <- xx[1:n]
x[i + period * 0:(n-1)] <-
x[i + period * 0:(n-1)] + xx
}
x <- ts(x, frequency=period)
x
}
op <- par(mfrow=c(3,1))
x <- my.sarima.sim(
20,
12,
list(ar=.6, ma=.3, order=c(1,0,1)),
list(ar=c(.5), ma=c(1,2), order=c(1,0,2))
)
eda.ts(x, bands=T)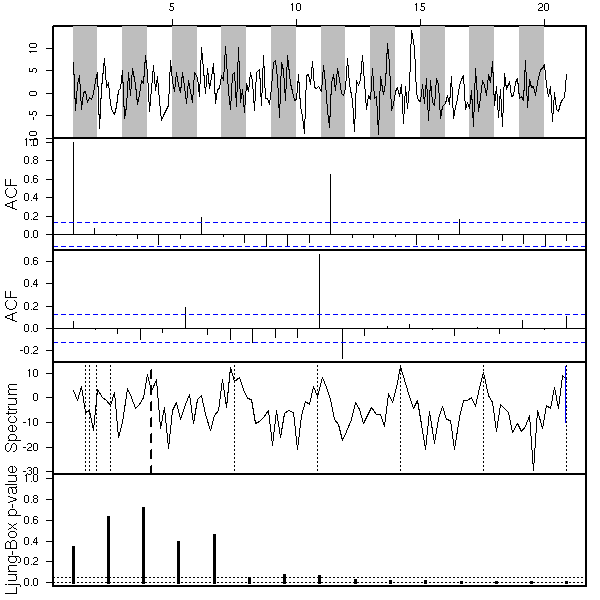
x <- my.sarima.sim( 20, 12, list(ar=c(.5,-.3), ma=c(-.8,.5,-.3), order=c(2,1,3)), list(ar=c(.5), ma=c(1,2), order=c(1,0,2)) ) eda.ts(x, bands=T)
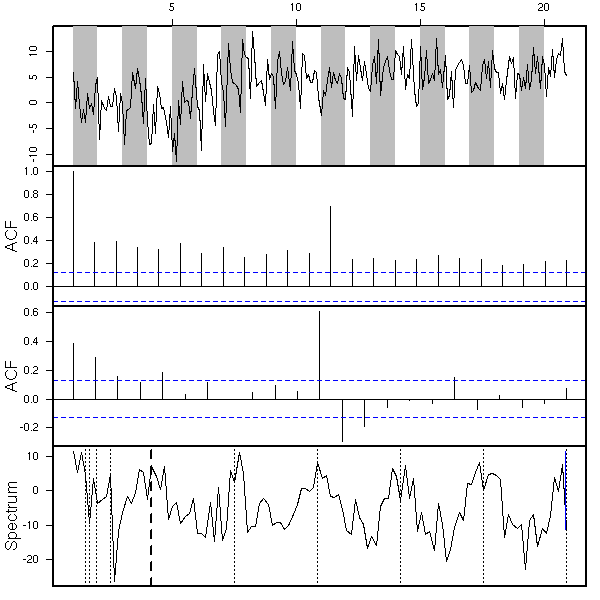
x <- my.sarima.sim( 20, 12, list(ar=c(.5,-.3), ma=c(-.8,.5,-.3), order=c(2,1,3)), list(ar=c(.5), ma=c(1,2), order=c(1,1,2)) ) eda.ts(x, bands=T)
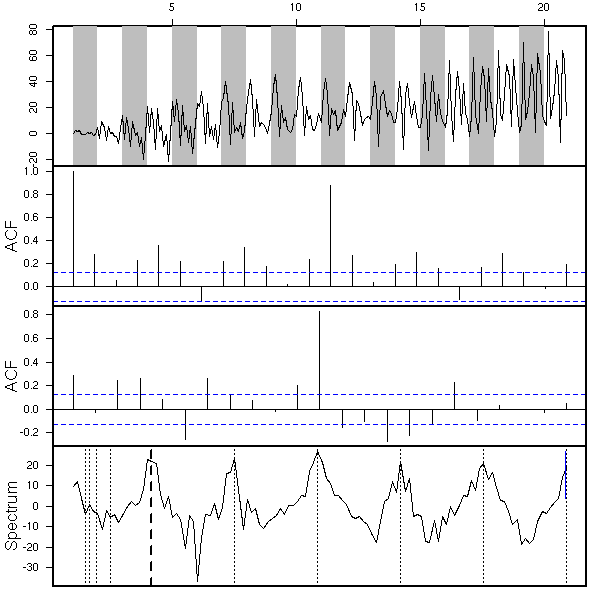
TODO
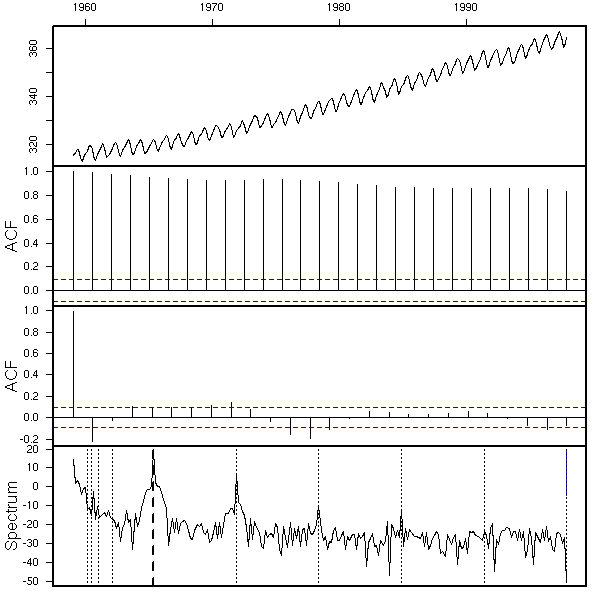
The co2 example (somewhere above) could well be modeled as an SARIMA model.
x <- co2 eda.ts(x)
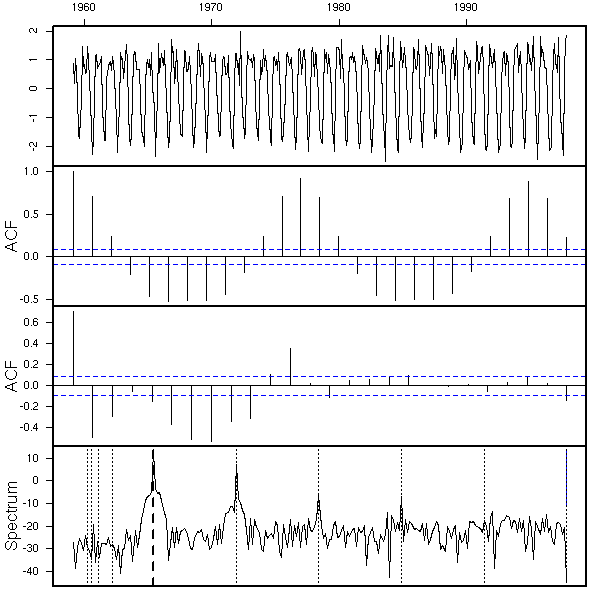
First, we see that there is a trend: we differentiate once to get rid of it.
eda.ts(diff(x))
There is also a periodic component: we differentiate, with a 12-month lag, to get rid of it.
eda.ts(diff(diff(x),lag=12))
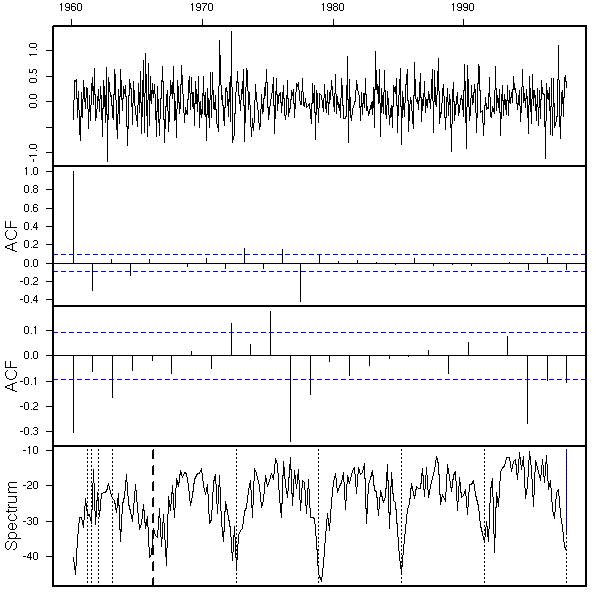
But wait! We have differentiated twice. Couldn't we get rid of both the periodic component and the trend by differentiating just once, with the 12-month lag?
eda.ts(diff(x,lag=12))
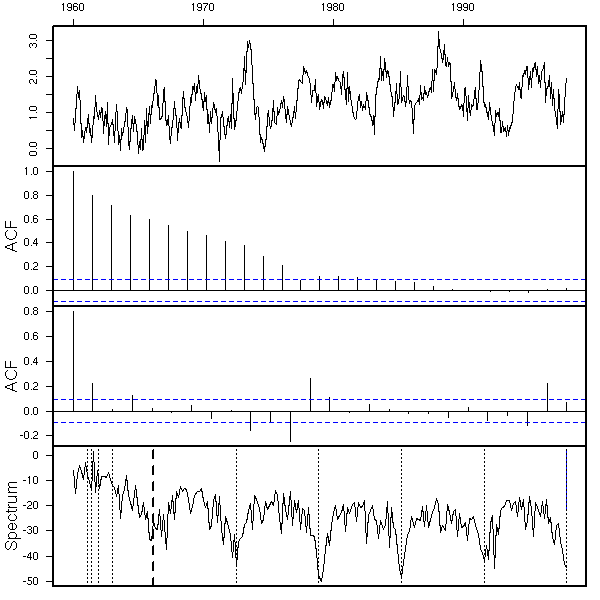
Well, perhaps. We hesitate between
SARIMA(?,1,?)(?,1,?)
and
SARIMA(?,0,?)(?,1,?).
If we look at the ACF and the PACF:
SARIMA(1,1,1)(2,1,1) SARIMA(1,1,2)(2,1,1) SARIMA(2,0,0)(1,1,0) SARIMA(2,0,0)(1,1,1)
Let us compute the coefficients of those models:
r1 <- arima(co2,
order=c(1,1,1),
list(order=c(2,1,1), period=12)
)
r2 <- arima(co2,
order=c(1,1,2),
list(order=c(2,1,1), period=12)
)
r3 <- arima(co2,
order=c(2,0,0),
list(order=c(1,1,0), period=12)
)
r4 <- arima(co2,
order=c(2,0,0),
list(order=c(1,1,1), period=12)
)This yields:
> r1
Call:
arima(x = co2, order = c(1, 1, 1), seasonal = list(order = c(2, 1, 1), period = 12))
Coefficients:
ar1 ma1 sar1 sar2 sma1
0.2595 -0.5902 0.0113 -0.0869 -0.8369
s.e. 0.1390 0.1186 0.0558 0.0539 0.0332
sigma^2 estimated as 0.08163: log likelihood = -83.6, aic = 179.2
> r2
Call:
arima(x = co2, order = c(1, 1, 2), seasonal = list(order = c(2, 1, 1), period = 12))
Coefficients:
ar1 ma1 ma2 sar1 sar2 sma1
0.5935 -0.929 0.1412 0.0141 -0.0870 -0.8398
s.e. 0.2325 0.237 0.1084 0.0557 0.0538 0.0328
sigma^2 estimated as 0.08132: log likelihood = -82.85, aic = 179.7
> r3
Call:
arima(x = co2, order = c(2, 0, 0), seasonal = list(order = c(1, 1, 0), period = 12))
Coefficients:
ar1 ar2 sar1
0.6801 0.3087 -0.4469
s.e. 0.0446 0.0446 0.0432
sigma^2 estimated as 0.1120: log likelihood = -150.65, aic = 309.3For r4, it was even:
Error in arima(co2, order = c(2, 0, 1), list(order = c(1, 1, 1), period = 12)) :
non-stationary AR part from CSSThe AIC of a3 is appallingly high (we want as low a value as possible): we really need to differentiate twice.
Let us look at the p-values:
> round(pnorm(-abs(r1$coef), sd=sqrt(diag(r1$var.coef))),5)
ar1 ma1 sar1 sar2 sma1
0.03094 0.00000 0.42007 0.05341 0.00000
> round(pnorm(-abs(r1$coef), sd=sqrt(diag(r1$var.coef))),5)
ar1 ma1 ma2 sar1 sar2 sma1
0.00535 0.00004 0.09635 0.39989 0.05275 0.00000This suggests an SARIMA(1,1,1)(0,1,1) model.
r3 <- arima( co2,
order=c(1,1,1),
list(order=c(0,1,1), period=12)
)This yields:
> r3
Call:
arima(x = co2, order = c(1, 1, 1), seasonal = list(order = c(0, 1, 1), period = 12))
Coefficients:
ar1 ma1 sma1
0.2399 -0.5710 -0.8516
s.e. 0.1430 0.1237 0.0256
sigma^2 estimated as 0.0822: log likelihood = -85.03, aic = 178.07
> round(pnorm(-abs(r3$coef), sd=sqrt(diag(r3$var.coef))),5)
ar1 ma1 sma1
0.04676 0.00000 0.00000We now look at the residuals:
r3 <- arima(
co2,
order = c(1, 1, 1),
seasonal = list(
order = c(0, 1, 1),
period = 12
)
)
eda.ts(r3$res)
Good, we can now try to use this mode to predict future values. To get an idea of the quality of those forecasts, we can use the first part of the data to estimate the model coefficients and compute the predictions and the second part to assess the quality of the predictions -- but beware, this is biased, because we chose the model by using all the data, including the data from the test sample.
x1 <- window(co2, end = 1990)
r <- arima(
x1,
order = c(1, 1, 1),
seasonal = list(
order = c(0, 1, 1),
period = 12
)
)
plot(co2)
p <- predict(r, n.ahead=100)
lines(p$pred, col='red')
lines(p$pred+qnorm(.025)*p$se, col='red', lty=3)
lines(p$pred+qnorm(.975)*p$se, col='red', lty=3)
# On the contrary, I do not know what to do with # this plots (it looks like integrated noise). eda.ts(co2-p$pred)
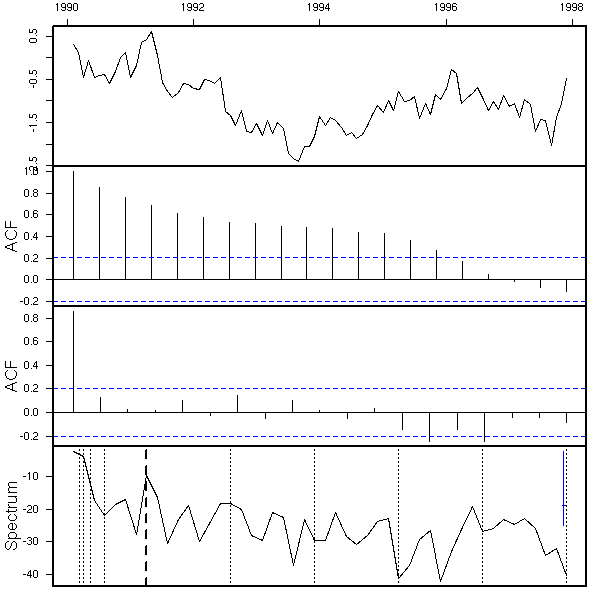
It is not that bad. Here are our forecasts.
r <- arima(
co2,
order = c(1, 1, 1),
seasonal = list(
order = c(0, 1, 1),
period = 12
)
)
p <- predict(r, n.ahead=150)
plot(co2,
xlim=c(1959,2010),
ylim=range(c(co2,p$pred)))
lines(p$pred, col='red')
lines(p$pred+qnorm(.025)*p$se, col='red', lty=3)
lines(p$pred+qnorm(.975)*p$se, col='red', lty=3)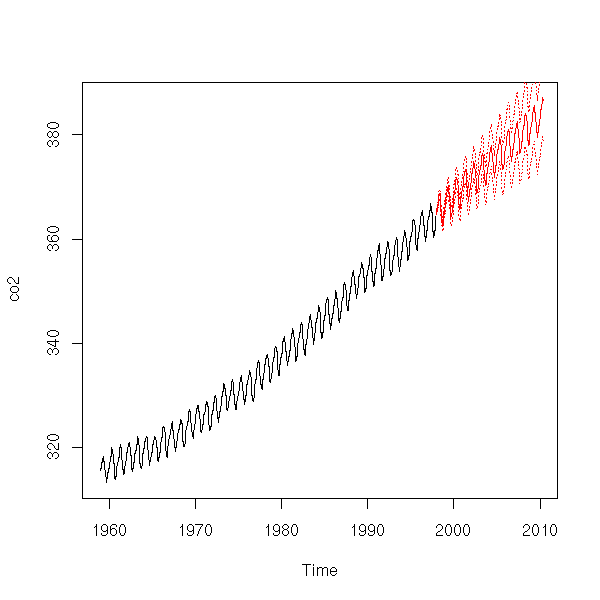
What we have done is called the Box and Jenkins method. The general case can be a little more complicated: if the residuals do not look like white noise, we have to get back to find another model.
0. Differentiate to get a stationary process. If there is a trend, the process is not stationary. If the ACF decreases slowly, try to differentiate once more. 1. Identify the model: ARMA(1,0): ACF: exponential decrease; PACF: one peak ARMA(2,0): ACF: exponential decrease or waves; PACF: two peaks ARMA(0,1): ACF: one peak; PACF: exponential decrease ARMA(0,2): ACF: two peaks; PACF: exponential decrease or waves ARMA(1,1): ACF&PACF: exponential decrease 2. Compute the coefficients 3. Diagnostics (go to 1 if they do not look like white noise) Computhe the p-values, remove unneeded coefficients (check on the residuals that they are indeed unneeded). 4. Forecasts
Here are a few examples of ARMA processes (in red: the theoretic ACF and PACF).
The ARMA(1,0) is characterized by the exponential decrease of the ACF and the single peak in the PACF.
op <- par(mfrow=c(4,2), mar=c(2,4,4,2))
n <- 200
for (i in 1:4) {
x <- NULL
while(is.null(x)) {
model <- list(ar=rnorm(1))
try( x <- arima.sim(model, n) )
}
acf(x,
main = paste(
"ARMA(1,0)",
"AR:",
round(model$ar, digits = 1)
))
points(0:50,
ARMAacf(ar=model$ar, lag.max=50),
col='red')
pacf(x, main="")
points(1:50,
ARMAacf(ar=model$ar, lag.max=50, pacf=T),
col='red')
}
par(op)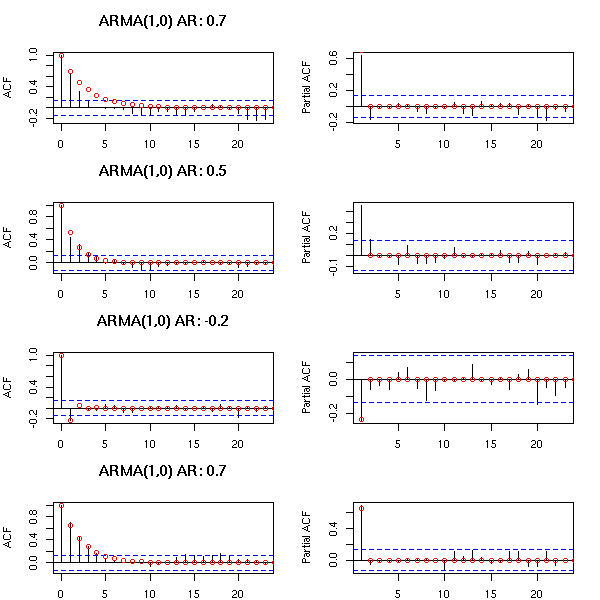
You can recognize an ARMA(2,0) from the two peaks in the PACF and the exponential decrease (or the waves) in the ACF.
op <- par(mfrow=c(4,2), mar=c(2,4,4,2))
n <- 200
for (i in 1:4) {
x <- NULL
while(is.null(x)) {
model <- list(ar=rnorm(2))
try( x <- arima.sim(model, n) )
}
acf(x,
main=paste("ARMA(2,0)","AR:",
round(model$ar[1],digits=1),
round(model$ar[2],digits=1)
))
points(0:50,
ARMAacf(ar=model$ar, lag.max=50),
col='red')
pacf(x, main="")
points(1:50,
ARMAacf(ar=model$ar, lag.max=50, pacf=T),
col='red')
}
par(op)
You can recognize an ARMA(0,1) process from its unique peak in the ACF and the exponential decrease of the PACF.
op <- par(mfrow=c(4,2), mar=c(2,4,4,2))
n <- 200
for (i in 1:4) {
x <- NULL
while(is.null(x)) {
model <- list(ma=rnorm(1))
try( x <- arima.sim(model, n) )
}
acf(x,
main = paste(
"ARMA(0,1)",
"MA:",
round(model$ma, digits=1)
))
points(0:50,
ARMAacf(ma=model$ma, lag.max=50),
col='red')
pacf(x, main="")
points(1:50,
ARMAacf(ma=model$ma, lag.max=50, pacf=T),
col='red')
}
par(op)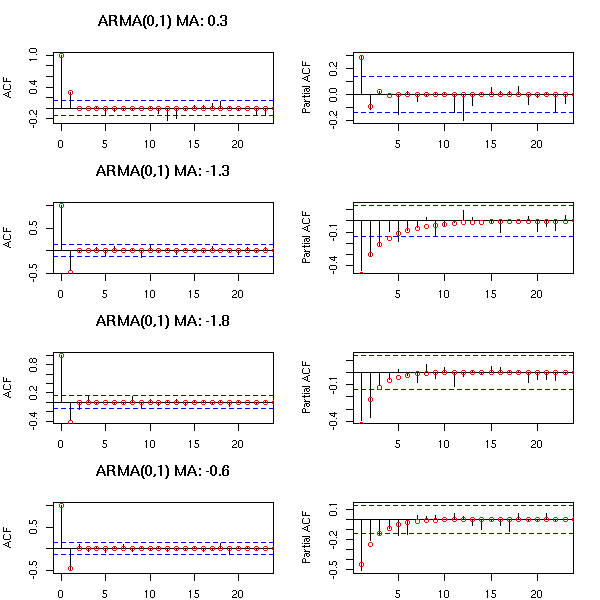
The ARMA(0,2) model has two peaks in the ACF and if PACF exponentially decreases or exhibits a pattern of waves.
op <- par(mfrow=c(4,2), mar=c(2,4,4,2))
n <- 200
for (i in 1:4) {
x <- NULL
while(is.null(x)) {
model <- list(ma=rnorm(2))
try( x <- arima.sim(model, n) )
}
acf(x, main=paste("ARMA(0,2)","MA:",
round(model$ma[1],digits=1),
round(model$ma[2],digits=1)
))
points(0:50,
ARMAacf(ma=model$ma, lag.max=50),
col='red')
pacf(x, main="")
points(1:50,
ARMAacf(ma=model$ma, lag.max=50, pacf=T),
col='red')
}
par(op)
For the ARMA(1,1), both the ACF and the PACF exponentially decrease.
op <- par(mfrow=c(4,2), mar=c(2,4,4,2))
n <- 200
for (i in 1:4) {
x <- NULL
while(is.null(x)) {
model <- list(ma=rnorm(1),ar=rnorm(1))
try( x <- arima.sim(model, n) )
}
acf(x, main=paste("ARMA(1,1)",
"AR:", round(model$ar,digits=1),
"AR:", round(model$ma,digits=1)
))
points(0:50,
ARMAacf(ar=model$ar, ma=model$ma, lag.max=50),
col='red')
pacf(x, main="")
points(1:50,
ARMAacf(ar=model$ar, ma=model$ma, lag.max=50, pacf=T),
col='red')
}
par(op)
Instead of the stepwise procedure presented, we can proceed in a more violent way, by looking at the AIC of all thereasonably complex models and retaining those whose AIC is the lowest. As this amounts to performing innumarable tests, we do not only take the single model with the lowest AIC, but several -- we shall prefer a simple model whose residuals look like white noise. You can remorselessly discard models whose AIC (or BIC: the AIC may be meaningful for nested model, but the BIC has a more general validity) is 100 units more that the lowest one, you should have remorse if you discard those 6 to 20 units from the lowest, and you should not discard those less than 6 units away.
a <- array(NA, dim=c(2,2,2,2,2,2))
for (p in 0:2) {
for (d in 0:2) {
for (q in 0:2) {
for (P in 0:2) {
for (D in 0:2) {
for (Q in 0:2) {
r <- list(aic=NA)
try(
r <- arima( co2,
order=c(p,d,q),
list(order=c(P,D,Q), period=12)
)
)
a[p,d,q,P,D,Q] <- r$aic
cat(r$aic); cat("\n")
}
}
}
}
}
}
# When I wrote this, I dod not know the "which.min" function.
argmin.vector <- function (v) {
(1:length(v)) [ v == min(v) ]
}
x <- sample(1:10)
x
argmin.vector(x)
x <- sample(1:5, 20, replace=T)
x
argmin.vector(x)
x <- array(x, dim=c(5,2,2))
index.from.vector <- function (i,d) {
res <- NULL
n <- prod(d)
i <- i-1
for (k in length(d):1) {
n <- n/d[k]
res <- c( i %/% n, res )
i <- i %% n
}
res+1
}
index.from.vector(7, c(2,2,2))
index.from.vector(29, c(5,3,2))
argmin <- function (a) {
a <- as.array(a)
d <- dim(a)
a <- as.vector(a)
res <- matrix(nr=0, nc=length(d))
for (i in (1:length(a))[ a == min(a) ]) {
j <- index.from.vector(i,d)
res <- rbind(res, j)
}
res
}
x <- array( sample(1:10,30, replace=T), dim=c(5,3,2) )
argmin(x)After a couple of hours (I am starting to worry: the computer produces a strange whistling sound when I run those computations...), this yields:
1 1 1 2 1 2
This is a rather complicated model. Let us look at models whose AIC is close to this one.
x <- as.vector(a)
d <- dim(a)
o <- order(x)
res <- matrix(nr=0, nc=6+2)
for (i in 1:30) {
p <- index.from.vector(o[i],d)
res <- rbind( res, c(p, sum(p), x[o[i]]))
}
colnames(res) <- c("p","d","q", "P","D","Q", "n", "AIC")
resThis yields:
p d q P D Q n AIC
[1,] 1 1 1 2 1 2 8 172.7083
[2,] 1 1 2 2 1 2 9 173.3215
[3,] 0 1 1 2 1 2 7 173.5009
[4,] 2 1 2 2 1 2 10 173.8748
[5,] 0 1 2 2 1 2 8 174.0323
[6,] 2 1 1 0 1 1 6 177.8278
[7,] 1 1 1 0 1 1 5 178.0672
[8,] 0 1 1 0 1 1 4 178.1557
[9,] 2 1 1 2 1 1 8 178.9373
[10,] 2 1 2 0 1 1 7 179.0768
[11,] 2 1 0 2 1 2 8 179.0776
[12,] 0 1 2 0 1 1 5 179.0924
[13,] 1 1 1 2 1 1 7 179.2043
[14,] 2 1 1 0 1 2 7 179.3557
[15,] 2 1 1 1 1 1 7 179.4335
[16,] 1 1 2 2 1 1 8 179.6950
[17,] 1 1 1 0 1 2 6 179.6995
[18,] 0 1 1 2 1 1 6 179.7224
[19,] 1 1 1 1 1 1 6 179.7612
[20,] 0 1 1 0 1 2 5 179.8808
[21,] 0 1 1 1 1 1 5 179.9235
[22,] 1 1 2 0 1 1 6 180.1146
[23,] 1 1 0 2 1 2 7 180.1713
[24,] 2 1 2 2 1 1 9 180.2019
[25,] 1 1 2 1 1 1 7 180.2686
[26,] 0 1 2 2 1 1 7 180.4483
[27,] 2 1 2 0 1 2 8 180.4797
[28,] 2 1 2 1 1 1 8 180.5757
[29,] 1 1 1 1 1 2 7 180.7777
[30,] 0 1 2 0 1 2 6 180.8024
[31,] 0 1 2 1 1 1 6 180.8495
[32,] 0 1 1 1 1 2 6 181.1830
[33,] 1 1 2 1 1 2 8 181.3127
[34,] 2 1 2 1 1 2 9 181.6425
[35,] 1 1 2 0 1 2 7 181.7322
[36,] 0 1 2 1 1 2 7 181.9859
[37,] 2 1 0 0 1 1 5 183.4687
[38,] 1 1 0 0 1 1 4 184.1817
[39,] 2 1 0 2 1 1 7 185.1404
[40,] 2 1 0 0 1 2 6 185.1918
[41,] 2 1 0 1 1 1 6 185.2337
[42,] 1 1 0 0 1 2 5 185.7290
[43,] 1 1 0 1 1 1 5 185.7909
[44,] 1 1 0 2 1 1 6 186.0117
[45,] 2 1 0 1 1 2 7 186.5521
[46,] 1 1 0 1 1 2 6 187.1703If we look at the distribution of the AICs,
plot(sort(as.vector(a))[1:100])
we see that the first bunch of values is under 200: among those, we select the simplest ones:
p d q P D Q n AIC 0 1 1 0 1 1 4 178.1557 1 1 0 0 1 1 4 184.1817 1 1 1 0 1 1 5 178.0672 0 1 2 0 1 1 5 179.0924 0 1 1 0 1 2 5 179.8808 0 1 1 1 1 1 5 179.9235 2 1 0 0 1 1 5 183.4687 1 1 0 0 1 2 5 185.7290 1 1 0 1 1 1 5 185.7909
I would be tempted to choose the first
0 1 1 0 1 1
or the third (the one we had obtained from the Box and Jenkins method).
1 1 1 0 1 1
Let us perform the computations.
> r <- arima(co2, order=c(0,1,1), list(order=c(0,1,1), period=12 ) )
> r
Call:
arima(x = co2, order = c(0, 1, 1), seasonal = list(order = c(0, 1, 1), period = T))
Coefficients:
ma1 sma1
0.1436 0.1436
s.e. 0.1068 0.1068
sigma^2 estimated as 0.7821: log likelihood = -604.01, aic = 1214.02
> r$var.coef
ma1 sma1
ma1 0.01140545 -0.01048563
sma1 -0.01048563 0.01140545
> pnorm(-abs(r$coef), sd=sqrt(diag(r$var.coef)))
ma1 sma1
0.08940721 0.08940721Let us look at the residuals.
r <- arima(co2, order=c(0,1,1), list(order=c(0,1,1), period=12 ) ) eda.ts(r$res)
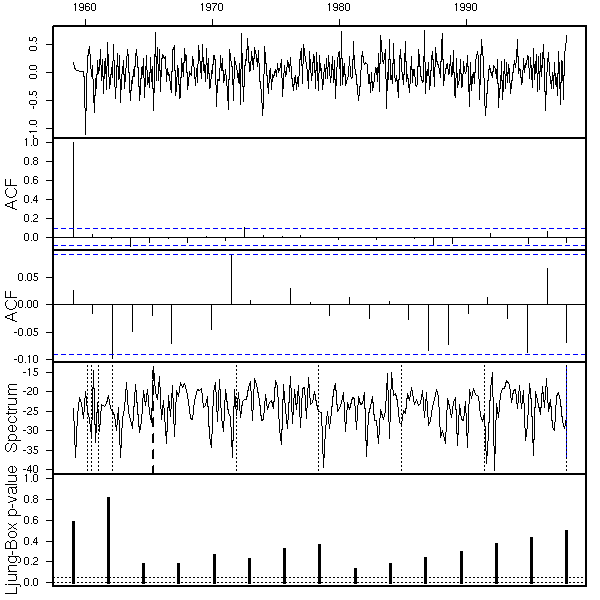
That looks fine, we can keep the model (of the residuals had not looked like a white noise, we would have investigated another model, until the residuals look fine).
As before, we can validate the model and forecast future values.
x1 <- window(co2,end=1990) r <- arima(x1, order = c(0, 1, 1), seasonal = list(order = c(0, 1, 1), period = 12)) plot(co2) p <- predict(r, n.ahead=100) lines(p$pred, col='red') lines(p$pred+qnorm(.025)*p$se, col='red', lty=3) lines(p$pred+qnorm(.975)*p$se, col='red', lty=3)
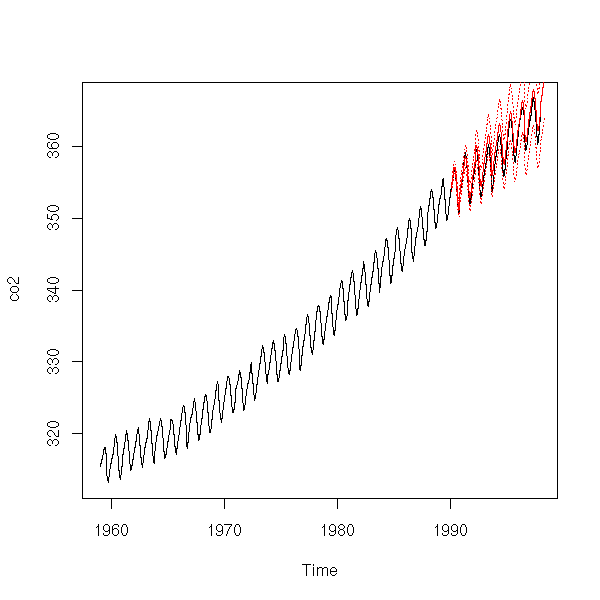
eda.ts(co2-p$pred)

r <- arima(co2, order = c(0, 1, 1), seasonal = list(order = c(0, 1, 1), period = 12)) p <- predict(r, n.ahead=150) plot(co2, xlim=c(1959,2010), ylim=range(c(co2,p$pred))) lines(p$pred, col='red') lines(p$pred+qnorm(.025)*p$se, col='red', lty=3) lines(p$pred+qnorm(.975)*p$se, col='red', lty=3)
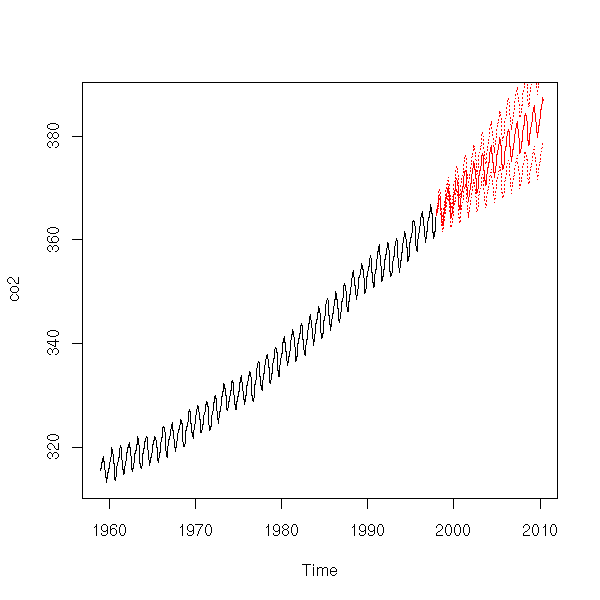
The forecasts are similar to those of the preceding model,
r1 <- arima(co2, order = c(0, 1, 1), seasonal = list(order = c(0, 1, 1), period = 12)) r2 <- arima(co2, order = c(1, 1, 1), seasonal = list(order = c(0, 1, 1), period = 12)) p1 <- predict(r1, n.ahead=150) p2 <- predict(r2, n.ahead=150) plot(co2, xlim=c(1959,2010), ylim=range(c(co2,p$pred))) lines(p1$pred, col='red') lines(p2$pred, col='green', lty=3, lwd=4)

TODO: put all this, including the study of the residuals, in a function.
TODO
TODO: put this section somewhere above
TODO: cross-validation. It is a bit limoted because, a priori, we can only do one cross-validation: we select the model with all the data, we compute the coefficients with the first half (or 90%) of the data and we check on the second half (or the remaining 10%).
TODO: bootstrap and time series (we can build a new time series by splicing pieces of the initial one: cut anywhere and splice in any order).
library(help=boot) http://cran.r-project.org/doc/Rnews/Rnews_2002-3.pdf
Some time series have a seasonal component difficult to spot, especially if you do not know the period in advance: a periodogram, also known as "sample spectrum" (simply a discrete Fourrier transform) can help you find the period.
In the following example, you get the period, 1 year, together with its harmonics (1/2 year, 1/3 year, 1/4 year, etc. -- recall that the frequency is the inverse of the period); the harmonics will always be there if the periodic function is not exactly a sine wave.
spectrum(co2) abline(v=1:10, lty=3)
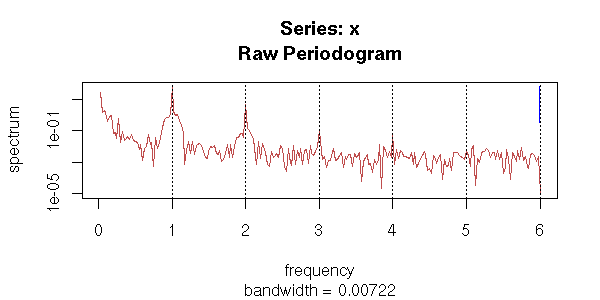
Here are a few examples of harmonics: when the signal has a given frequency f, its spectral decomposition also displays significant components at frequencies 2f, 3f, 4f, etc. -- unless the signal is a perfect sine wave.
signal.and.spectrum <- function (x, main="") {
op <- par(mfrow=c(2,1),
mar=c(2,4,2,2)+.1,
oma=c(0,0,2,0))
plot(x, type="l", main="", ylab="Signal")
spectrum(x, main="", xlab="")
abline(v=.1*1:10, lty=3)
par(op)
mtext(main, line=1.5, font=2, cex=1.2)
}
N <- 100
x <- 10 * (1:N / N)
signal.and.spectrum(sin(2*pi*x),
"Sine wave, period=10")
signal.and.spectrum(x - floor(x),
"sawtooth, period=10")
signal.and.spectrum(abs(x - floor(x)-.5),
"triangle, period=10")
signal.and.spectrum(x-floor(x)>.5,
"square, period=10")
Here is a more complicated example in which we do not know the period in advance.
data(sunspots) plot(sunspots)
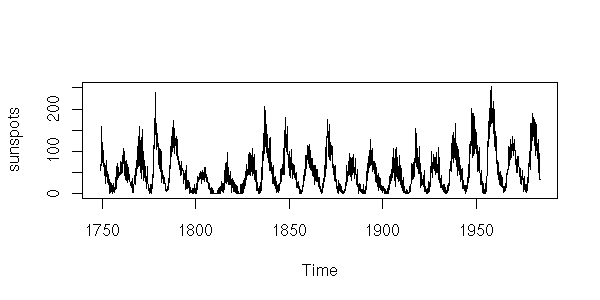
You could find the period without the periodogram:
a <- locator() # click on the local maxima b <- a$x - a$x[1] bb <- outer(b, 9:13, '/') apply(abs(bb - round(bb)), 2, mean)
This yields:
[1] 0.2278710 0.1606527 0.1545937 0.1979566 0.2106840
i.e., the most probable period is 11.
However, it will be easier with a periodogram.
spectrum(sunspots)

For the moment, we cannot see anything, so we ask R to smooth the periodogram.
spectrum(sunspots, spans=10)

Now, we can see a peak close to zero. We can estimate its value with the "locator" function, as before, then zoom in on the plot.
spectrum(sunspots, spans=10, xlim=c(0,1)) abline(v=1/1:12, lty=3)
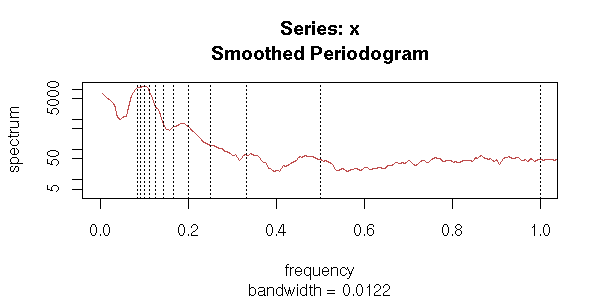
spectrum(sunspots, spans=10, xlim=c(0,1),
main="10: Not quite")
abline(v=1:3/10, lty=3)
spectrum(sunspots, spans=10, xlim=c(0,1),
main="11: Better")
abline(v=1:3/11, lty=3)
spectrum(sunspots, spans=10, xlim=c(0,1),
main="12: Not quite")
abline(v=1:3/12, lty=3)
To decompose this series, you can try to transform it (it is sometimes useful, sometime not -- here, it might not be needed).
library(car) box.cox.powers(3+sunspots) y <- box.cox(sunspots,.3) spectrum(y, spans=10, xlim=c(0,1)) abline(v=1:3/11, lty=3) # A single harmonic

Once we know the period and which harmonics are important, we can try to model the time series as a sum of sine waves.
x <- as.vector(time(y))
y <- as.vector(y)
r1 <- lm( y ~ sin(2*pi*x/11) + cos(2*pi*x/11) )
r2 <- lm( y ~ sin(2*pi*x/11) + cos(2*pi*x/11)
+ sin(2* 2*pi*x/11) + cos(2* 2*pi*x/11)
+ sin(3* 2*pi*x/11) + cos(3* 2*pi*x/11)
+ sin(4* 2*pi*x/11) + cos(4* 2*pi*x/11)
)
plot(y~x, type='l')
lines(predict(r1)~x, col='red')
lines(predict(r2)~x, col='green', lty=3, lwd=3)
More terms do not add much.
> summary(r2)
...
Estimate Std. Error t value Pr(>|t|)
(Intercept) 6.854723 0.045404 150.973 < 2e-16 ***
sin(2 * pi * x/11) 1.696287 0.064100 26.463 < 2e-16 ***
cos(2 * pi * x/11) 1.213098 0.064319 18.860 < 2e-16 ***
sin(2 * 2 * pi * x/11) 0.056443 0.064238 0.879 0.380
cos(2 * 2 * pi * x/11) 0.343087 0.064182 5.346 9.74e-08 ***
sin(3 * 2 * pi * x/11) 0.025019 0.064249 0.389 0.697
cos(3 * 2 * pi * x/11) 0.003333 0.064169 0.052 0.959
sin(4 * 2 * pi * x/11) 0.039955 0.064191 0.622 0.534
cos(4 * 2 * pi * x/11) -0.046268 0.064216 -0.721 0.471However, the analysis is far from over: the residuals do not look like white noise -- we could try an ARMA model.
z <- y - predict(r1) op <- par(mfrow=c(2,2), mar=c(2,4,3,2)+.1) hist(z, probability=T, col="light blue") lines(density(z), lwd=3, col="red") qqnorm(z) acf(z, main="") pacf(z, main="") par(op)

They are linked: if rho(k) is the lag-k autocorrelation, then the value of the spectrum at frequency omega is
+infinity
f(omega) = Sum( rho(k) * exp(- i k omega ) )
k=-infinity
TODO: A linear filter acts linearly on the spectrum. (This is linked to why the Fourrier transform is that widely used: it turns derivations into multiplications.)
The raw periodogram contains a lot of noise: you have to smooth it, as we saw in the subspot example above.
Let us come back in more details on the notion of periodogram. So far, we have only seen how to interpret it (what frequencies were "important" in the signal we are studying): we shall now see how to actually compute it.
The idea of a Fourier series is to write a (periodic) function as a sum of sines and cosines.
f(t) = a0 + a1 cos(t) + b1 sin(t) + a2 cos(2t) + b2 sin(2t) + ...
It is a bit unwieldy, because we have two sequences (a and b, for cosines and sines) that do not even start at the same index (0 for cosines, 1 for sines). It is simpler if we replace the sines and cosines by their definition in terms of complex exponentials:
f(t) = ... + c(-2) e^(-2it) + c(-1) e^-it + c(0) + c1 e^it + c2 e^2it + ...
This is not exactly what we want, because we do not start with a function, but a discrete signal, a sequence. There are actually several flavours of Fourier "transforms", according to the nature (function or discrete signal) of the input and desired output:
Fourier series decomposition: function --> sequence Fourier transform: function --> function Discrete Fourier Transform (DFT): discrete signal --> sequence
If you want formulas (I am probably forgetting some "normalizing constants"):
f(x) = Sum( c(n) exp( 2 pi i n x ) )
n in Z
f(x) = Integral \hat f ( omega ) exp( 2 pi i x omega ) d omega
x_m = Sum( c(n) exp( 2 pi i / N * n m ) )
0 <= n < NThese are not the useful formulas, because we know the left-hand side and we want c(n) of \hat f in the right hand-side. Luckily, the inversion formulas are very similar (here, I am definitely forgetting normalizing constants): the only change is the sign in the exponential.
c(n) = Integral f ( x ) exp( - 2 pi i n x ) d x
\hat f(omega) = Integral f ( x ) exp( - 2 pi i x omega ) d x
c(n) = Sum( x(m) exp( - 2 pi i / N * n m ) )
0 <= m < NThose formulas would be sufficient to compute the Discrete Fourier Transform (DFT) we are interested in, but they are not very efficient: their complexity is O(n^2), where n is the signal length -- the FFT (Fast Fourier Transform) is a way of computing this DFT in O(n log(n)).
Before presenting this algorithm, let us just play with the results.
A signal can be seen as an element of a vector space. To describe it, we can choose a basis of this vector space. If we choose the basis of "impulse signals" (i.e., the basis elements are zero everywhere except at one point), the coordinates of the signal are simply its values for each point in time. The signal is said to be described in the "time domain".
But you can choose another basis: the coordinates in the basis of sines and cosine functions are said to describe the signal in the "frequency domain".
You can choose other bases and describe the signal, say, in the "wavelet domain" -- more about this later.
Let us consider the DFT of a few signals (we take real signals: it will be easier to interpret).
n <- 8
x <- 1:n/n*2*pi
k <- 0
y <- cbind(rep(1,n),
1 + cos(x),
1 + cos(x) + sin(x),
1 + cos(x) + sin(x) + cos(2*x),
1 + cos(x) + sin(x) + cos(2*x) + sin(2*x)
)
z <- mvfft(y)
op <- par(mfrow=c(2,1))
barplot(Re(t(z)),
beside = TRUE,
col = rainbow(dim(y)[2]),
main = "Real part of the FFT")
barplot(Im(t(z)),
beside = TRUE,
col = rainbow(dim(y)[2]),
main = "Imaginary part of the FFT")
par(op)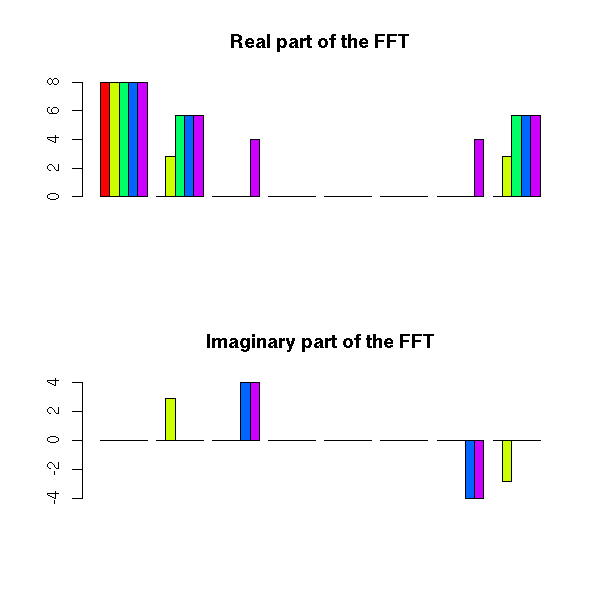
The first coefficient is the constant term, the second and last coefficients (they are conjugate) are the coefficients of cos(t) and sin(t), the third and the second from the end correspond to cos(2t) and sin(2t), etc.
As the signal we are studying is real, the last coefficients are conjugate of the first ones: we need not plot them. Besides, if we are not interested in the phase, we just have to plot the modulus of the FFT.
Here are a few examples.
x <- rep(0,256)
x[129:256] <- 1
op <- par(mfrow=c(2,1), mar=c(3,4,4,2)+.1)
plot(x, type='l', lwd=3,
main="Signal",
xlab="", ylab="")
plot(Mod(fft(x)[1: ceiling((length(x)+1)/2) ]),
type='l', lwd=3, col="blue",
xlab="", ylab="Mod(fft(x))",
main="DFT (Discrete Fourrier Transform)")
par(op)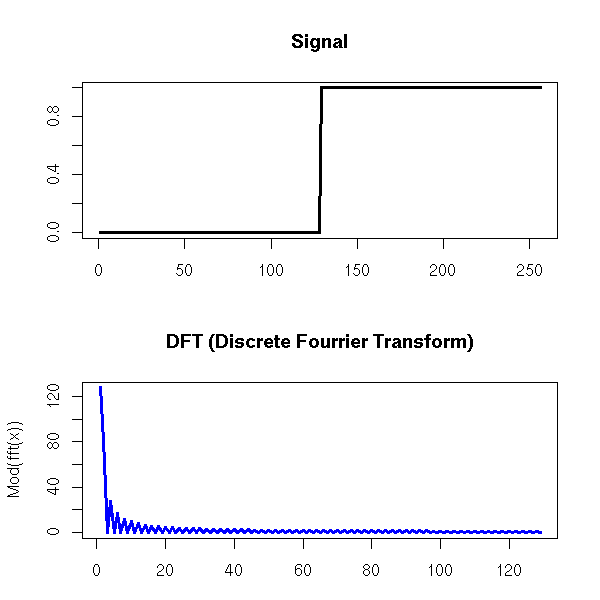
x <- rep(0,256)
x[33:64] <- 1
x[64+33:64] <- 1
x[128+33:64] <- 1
x[128+64+33:64] <- 1
op <- par(mfrow=c(2,1), mar=c(3,4,4,2)+.1)
plot(x, type='l', lwd=3,
main="Signal", xlab="", ylab="")
plot(Mod(fft(x)[1: ceiling((length(x)+1)/2) ]),
type='l', col="blue", lwd=3,
ylab="Mof(fft(x))", xlab="",
main="DTF (Discrete Fourrier Transform)")
par(op)
x <- rep( 1:32/32, 8 )
op <- par(mfrow=c(2,1), mar=c(3,4,4,2)+.1)
plot(x, type='l', lwd=3,
main="Signal", xlab="", ylab="")
plot(Mod(fft(x)[1: ceiling((length(x)+1)/2) ]),
type='l', col="blue", lwd=3,
ylab="Mof(fft(x))", xlab="",
main="DTF (Discrete Fourrier Transform)")
par(op)
x <- 1:256/256
op <- par(mfrow=c(2,1), mar=c(3,4,4,2)+.1)
plot(x, type='l', lwd=3,
main="Signal", xlab="", ylab="")
plot(Mod(fft(x)[1: ceiling((length(x)+1)/2) ]),
type='l', col="blue", lwd=3,
ylab="Mof(fft(x))", xlab="",
main="DTF (Discrete Fourrier Transform)")
par(op)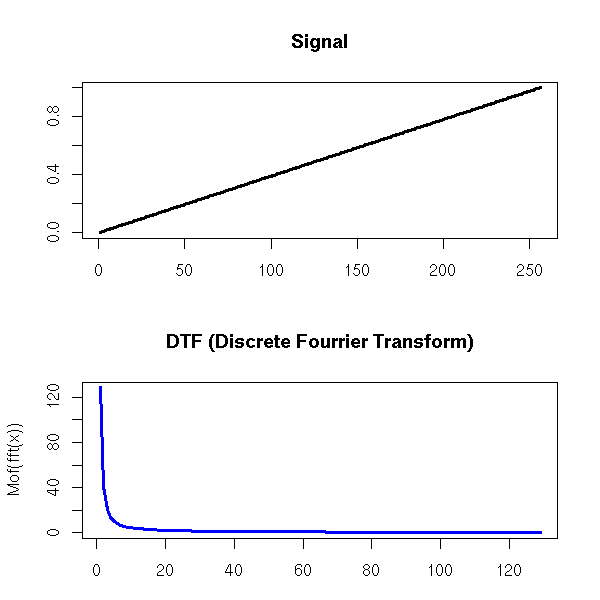
x <- abs(1:256-128)
op <- par(mfrow=c(2,1), mar=c(3,4,4,2)+.1)
plot(x, type='l', lwd=3,
main="Signal", xlab="", ylab="")
plot(Mod(fft(x)[1: ceiling((length(x)+1)/2) ]),
type='l', col="blue", lwd=3,
ylab="Mof(fft(x))", xlab="",
main="DTF (Discrete Fourrier Transform)")
par(op)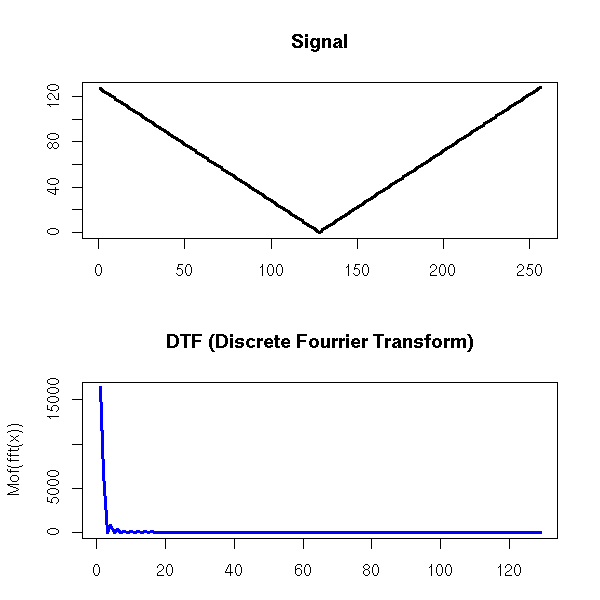
x <- 1:256/256
x <- sin(2*pi*x) + cos(3*pi*x) + sin(4*pi*x+pi/3)
op <- par(mfrow=c(2,1), mar=c(3,4,4,2)+.1)
plot(x, type='l', lwd=3,
main="Signal", xlab="", ylab="")
plot(Mod(fft(x)[1: ceiling((length(x)+1)/2) ]),
type='l', col="blue", lwd=3,
ylab="Mof(fft(x))", xlab="",
main="DTF (Discrete Fourrier Transform)")
par(op)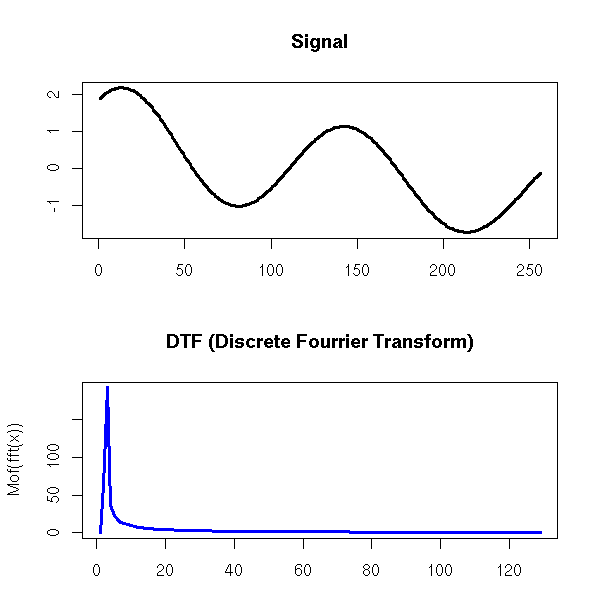
x <- 1:256/256
x <- sin(16*pi*x)
op <- par(mfrow=c(2,1), mar=c(3,4,4,2)+.1)
plot(x, type='l', lwd=3,
main="Signal", xlab="", ylab="")
plot(Mod(fft(x)[1: ceiling((length(x)+1)/2) ]),
type='l', col="blue", lwd=3,
ylab="Mof(fft(x))", xlab="",
main="DTF (Discrete Fourrier Transform)")
par(op)
x <- 1:256/256
x <- sin(16*pi*x) + .3*cos(56*pi*x)
op <- par(mfrow=c(2,1), mar=c(3,4,4,2)+.1)
plot(x, type='l', lwd=3,
main="Signal", xlab="", ylab="")
plot(Mod(fft(x)[1: ceiling((length(x)+1)/2) ]),
type='l', col="blue", lwd=3,
ylab="Mof(fft(x))", xlab="",
main="DTF (Discrete Fourrier Transform)")
par(op)
TODO http://en.wikipedia.org/wiki/Fast_Fourier_transform
Multiplying large integers Multiplying polynomials Others? PDE? DSP? TODO
We can use the FFT to filter a signal by removing the high (or the low) frequencies.
n <- 1000
x <- cumsum(rnorm(n))+rnorm(n)
y <- fft(x)
y[20:(length(y)-19)] <- 0
y <- Re(fft(y, inverse=T)/length(y))
op <- par(mfrow=c(3,1), mar=c(3,4,2,2)+.1)
plot(x, type='l',
main="FFT: Removing the high frequencies from a signal")
lines(y, col='red', lwd=3)
plot(Mod(fft(x)[1: ceiling((length(x)+1)/2) ]),
type='l', ylab="FFT")
plot(Mod(fft(y)[1: ceiling((length(y)+1)/2) ]),
type='l', ylab="Truncated FFT")
par(op)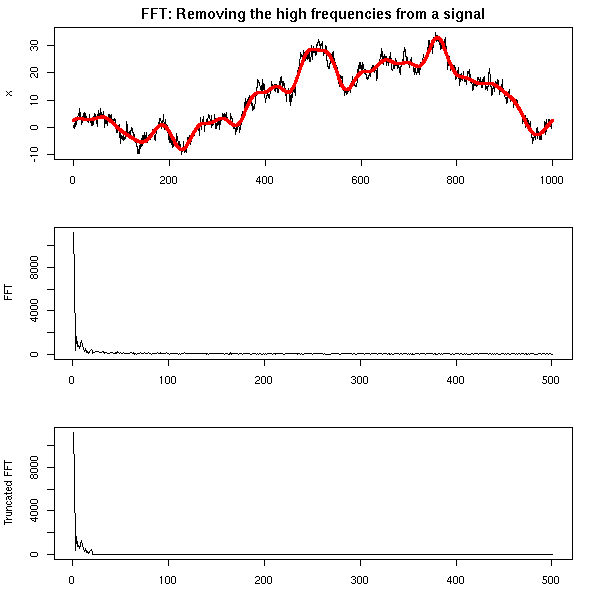
n <- 1000
x <- cumsum(rnorm(n))+rnorm(n)
plot(x, type='l', ylab="",
main="FFT: Removing more and more high frequencies")
for (i in 1:10) {
y <- fft(x)
y[(1+i):(length(y)-i)] <- 0
y <- Re(fft(y, inverse=T)/length(y))
lines(y, col=rainbow(10)[i])
}
On those examples, you should notice that, if the transform looks fine in the middle of the interval, it looks awful at both ends of the interval. This is due to the fact that we artificially build an infinite periodic signal by joining the end of the interval with the begining. This introduces a singularity in the signal: what we see at the begining or the end is a desperate attempt to equate the final level of the signal with its begining. That would be bad in its own right, but it is amplified by the "Gibbs phenomenon": the Fourier decomposition of a discontinuous function amplifies the amplifies those singularities.
n <- 1000
x <- c(129:256,1:128)/256
y <- fft(x)
y[20:(length(y)-19)] <- 0
y <- Re(fft(y, inverse=T)/length(y))
plot(x, type='l',
ylim=c(-.2,1.2),
xlab="", ylab="",
main="Gibbs phenomenon")
lines(y, col='red', lwd=3)
Here are a few ideas to overcome this effect.
Idea 1: remove the "trend" of the signal, so that the
start and the end of the signal coincide.
Idea 2: perform the DFT in a moving window and only retain
the middle of the window (yes, this sounds like
local regression)TODO: Do this on a real-life time series.
TODO: Example. Get the trend. x <- co2 y <- fft(x) y[20:(length(y)-19)] <- 0 y <- Re(fft(y, inverse=T)/length(y)) plot(x, type='l') lines(y, col='red', lwd=3)
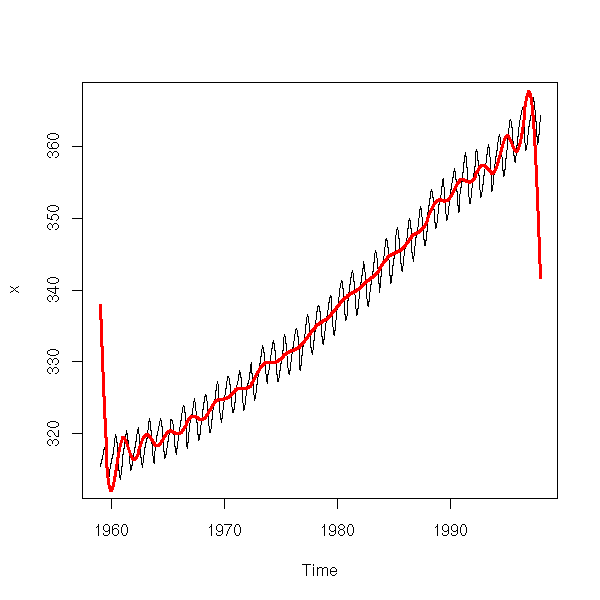
TODO: Problem: the result is a continuous periodic function, not at all what we want... TODO: We can first transform the data so that the first and last value be close, via a linear regression. (This is a bad idea: the trend need not be linear -- indeed, if it was, we could simply get it from a linear regression.) Why not simply remove a linear trend and p <- predict(lm(co2~time(co2))) x <- co2 - p y <- fft(x) y[20:(length(y)-19)] <- 0 y <- Re(fft(y, inverse=T)/length(y)) plot(x+p, type='l') lines(y+p, col='red', lwd=3) lines(x-y+mean(x+p), col='green', lwd=3)
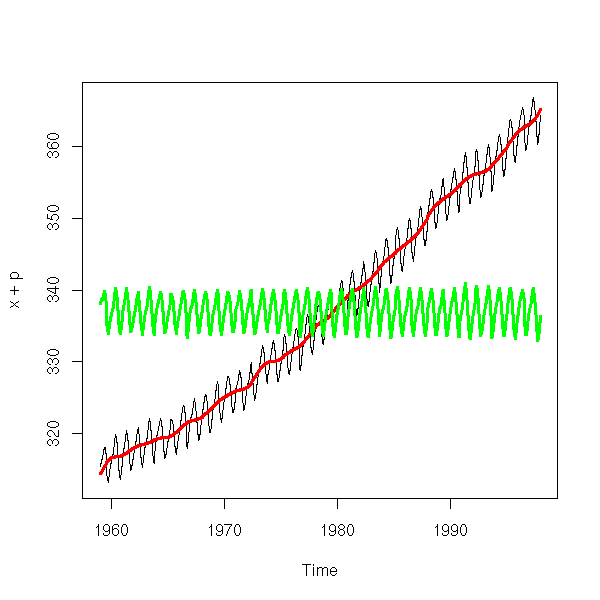
TODO: Same problem if we try to do the opposite and get the periodic component without the trend. x <- co2 y <- fft(x) k <- 20 n <- length(y) y[1:(k+1)] <- 0 y[(n-k):n] <- 0 y <- Re(fft(y, inverse=T)/length(y)) plot(x, type='l') lines(y+mean(x), col='red', lwd=3)
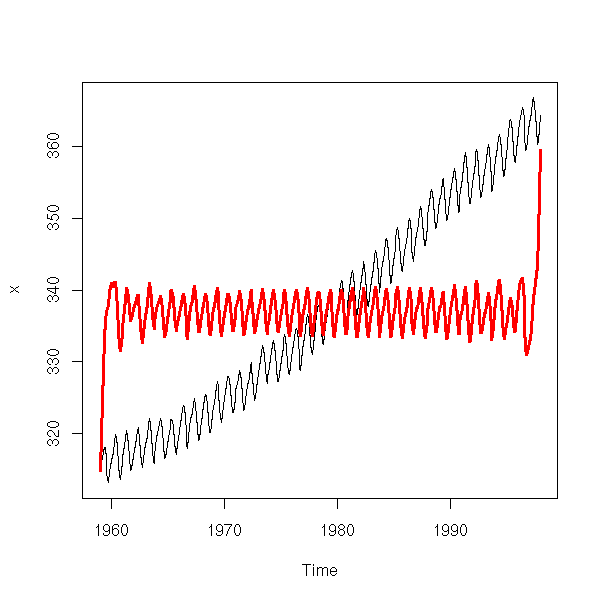
And here, we have another problem with the period: it is not the right one -- 40 years instead of 1 year.
library(sound)
x <- loadSample("sample.wav")
plot(x)
n <- length(x$sound) n <- round(n/3) y <- x$sound[ n:(n+2000) ] n <- length(y) op <- par(mfrow=c(2,1), mar=c(2,4,2,2)+.1) plot(y, type='l') #plot(Mod(fft(y)[1: ceiling((length(y)+1)/2) ]), type='l') plot(Mod(fft(y)[1:100]), type='l')
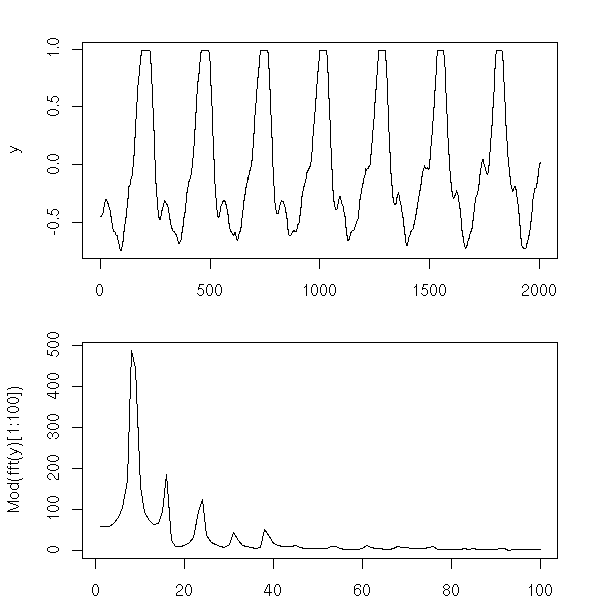
TODO: Give an example of a Fourier transform on a sound signal. (2D plot, time on the horizontal axis, FFT in a moving window along the vertical axis) TODO: give examples on sound files, with the initial *.wav (or *.ogg) file and the result. TODO: put those sound examples in a separate part.
The wavelet transform is very similar to the Fourrier transform: in both cases, we replace a function by its coordinates is some basis -- the difference is only the choice of the basis.
Fourrier analysis might be fine to study periodic phenomena, but it breaks down (Gibbs phenomenon, etc.) for non-periodic ones. This is because it expresses the characteristics of the signal only in terms of frequencies: "the signal contains this and that frequencies". On the contrary, the wavelet transforms expresses the characteristics of the signal in terms of frequencies and location, e.g., "the signal contains this frequency at the begining and that other at the end".
The basis used in the Fourrier transform was made of sine signals. You can hope to find a "wavelet" basis by cutting them into pieces: a wavelet would be a single sine wave, located at a precise location -- this is the basic idea, but it will has to be modified slightly for the basis to have good theoretical and practical properties (it has to actually be a basis; it has to be able to express most signals of interest with a few coefficients, i.e., the series decomposition of the signals we shall study should converge quickly).
The following figure represents a wavelet transform: the curve in the first plot is the signal to be described; the rectangles (or vertical segments) represent the coefficients; the lower left part tells us that in the left part of the interval, high frequencies dominate; the top right part tells us that in the right part of the interval, low frequencies dominate.
N <- 1024
k <- 6
x <- ( (1:N) - N/2 ) * 2 * pi * k / N
y <- ifelse( x>0, sin(x), sin(3*x) )
plot(y, type='l',
xlab="", ylab="")
# With the "wd" function in the "wavethresh" package library(wavethresh) y <- ifelse( x>0, sin(x), sin(10*x) ) plot(wd(y), main="")

This is very similar to the decomposition of periodic functions into Fourier series, but we have one more dimension: the frequency spectrum is replaced by a frequency-location plot (an other advantage is that there is almost no Gibbs effect -- very convenient when the signals are not periodic or stationnary...)
Fourier analysis decomposes periodic functions as sums of sine functions, each indicating what happens at a given scale.
The problem is that this assumes the signal is stationnary.
Instead, we would like to decompose the signal along two scales: first, the frequency, second, the location.
A first idea would be to cut the signal into small chunks, assume that the signal is stationnary on each chunk, and perform a Fourier decomposition.
Wavelets provide another solution.
The idea of Fourier analysis was to start with a function (the sine function), scale it (sin(x), sin(2x), sin(3x), etc.), remark that we get an orthonormal basis of some space of functions, and decompose the signals we wanto to study along this basis.
Similarly, we can start with a function, change its scale and localization (by applying both homotheties and translations), check if we get an orthonormal basis of some sufficiently large space of function (this is not always the case) and, if we are lucky, decompose our signals along this basis.
More precisely, we are looking for a function psi so that
( psi(2^j x - k), j, k \in Z )
be an orthonormal basis of L^2(R).
Here is an example:
The Haar wavelet:
H(x) = 1 if x is in [0,.5]
-1 if x is in [.5,1]
0 otherwise
TODO: Daubechies wavelets (there is a whole family of them)There is a recipe to build such wavelets: start with a "self-similar" function, i.e., satisfying an equation of the form
phi(x) = Sum( a_k phi(2x-k) ),
then consider
psi(x) = Sum( \bar a_{1-k} phi(2x-k) )For some values of a_k, psi fulfils our needs (convergence, orthogonality, etc.)
The irregular appearance of wavelets comes from this self-similarity condition.
Phi is called the father wavelet and psi the mother wavelet. (If you find your wavelets by other means, you can have a mother wavelet and no father wavelet.)
DWT: Discrete Wavelet Transform MRA: Multi-Resolution Analysis
We do not always work in L^2(R), but in smaller spaces. In particular, given a father wavelet phi, one can build a filtration of L^2(R) (i.e., an increasing sequence of subspaces of L^2(R))
... V(-2) \subset V(-1) \subset V(0) \subset V(1) \subset V(2) ...
such that
f(x) \in V(n) \ssi f(2x) \in V(n+1)
by defining V(0) as the subspace generated by the
phi(x-k), k \in Z.
In terms of mother wavelets, V(1) is generated by the
psi(2^j x - k), j <= 1, k \in Z.
One also often considers the W(n) spaces, generated by the
psi(2^n x - k), k \in Z.
One has
V(1) = V(0) \oplus W(1)
= \bigoplus _{ j \leq 1 } W(j).Example: decomposition in Haar wavelets of the function (7 5 1 9) with the "pyramidal algorithm".
Resolution Approximations Detail coefficients
----------------------------------------------
4 7 5 1 9
2 6 5 -1 4
1 5.5 -0.5
Haar(7 5 1 9) = (5.5, -.5, -1, 4)Complexity:
O(n log n) for the FFT O(n) for the wavelet decomposition
The general idea is the following: find an orthonormal basis of L^2 whose elements can be interpreted in terms of ``location'' and ``frequency''. For example (this is called the Haar basis):
father <- function (x) {
ifelse( x<0 | x>1, 0, 1 )
}
mother <- function (x) {
ifelse( x<0 | x>1,
0,
ifelse(x<.5, 1, -1))
}
jk <- function (f,x,j,k) {
f(2^j * x - k)
}
op <- par(mfrow=c(4,3), mar=c(0,0,0,0))
for (j in 1:3) {
curve(jk(father,x,0,j),
xlim=c(-.2,3.2), ylim=c(-1,1),
xlab="", ylab="",
axes=F,
lwd=3, col="blue"
)
abline(h=0,lty=3)
abline(v=0:4,lty=3)
}
for (i in 1:3) {
for (j in 1:3) {
curve(jk(mother,x,i,j),
xlim=c(-.2,3.2), ylim=c(-1,1),
xlab="", ylab="",
axes=F,
lwd=3, col="blue"
)
abline(h=0,lty=3)
abline(v=0:4,lty=3)
box()
}
}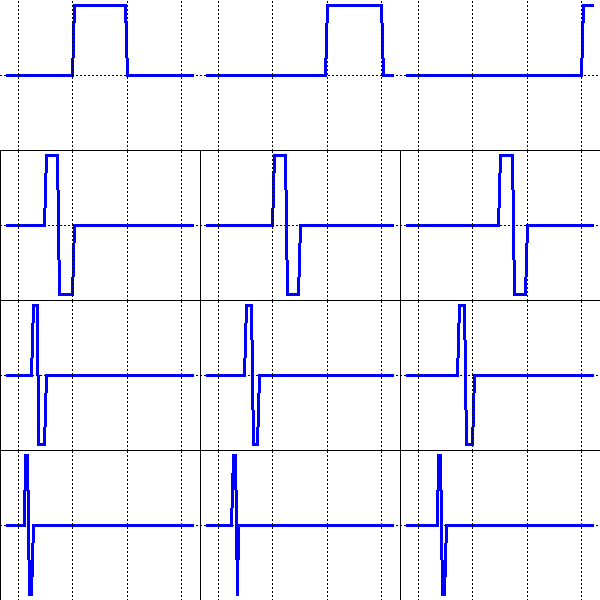
This gives a decomposition
L^2 = V_0 \oplus \bigoplus_j W_j
where V_0 is generated by the father wavelet phi and its translations and the W_j are generated by the mother wavelet psi, its translations and rescalings.
op <- par(mar=c(0,0,3,0))
curve(jk(father,x,0,1),
xlim=c(-.2,3.2),
ylim=c(-1,1),
xlab="", ylab="", axes=F,
lwd=3, col="blue",
main="phi, father wavelet")
abline(h=0,lty=3)
#abline(v=0:4,lty=3)
par(op)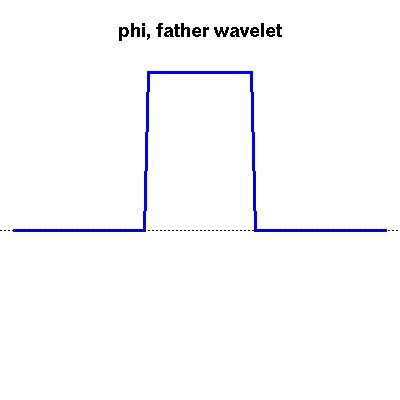
op <- par(mar=c(0,0,3,0))
curve(jk(mother,x,0,1),
xlim=c(-.2,3.2),
ylim=c(-1,1),
xlab="", ylab="", axes=F, lwd=3, col="blue",
main="psi, mother wavelet")
abline(h=0,lty=3)
#abline(v=0:4,lty=3)
par(op)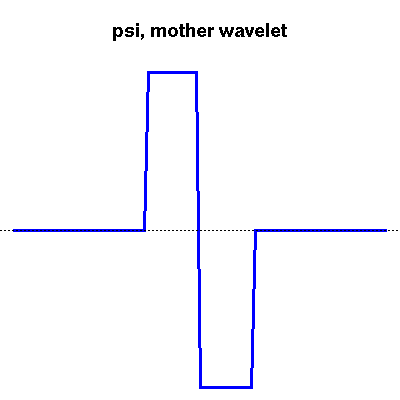
The choice of the basis depends on the applications: will you be dealing with smooth ($\mathscr{C}^\infty$) functions? continuous but non-differentiable functions, with a fractal nature? functions with jumps? The convergence speed and the parsimony of the wavelet decomposition will depend on the adequacy of the basis and the data studied.
More technically, the construction of a basis goes as follows.
1. Choose a father wavelet phi.
2. Set phi_jk(x) = 2^{j/2} phi(2^j x - k ), for all non-negative integers j and all integers k -- this is f translated by k and shrinked j times.
3. Set V_j = Vect { phi_{jk}, k in Z } and check that
4. the phi_{0k}, k in Z, form an orthonormal system (a Hilbert basis of V_0);
5. For all j in Z, V_j is included in V_{j+1};
6. The closure of the union of the V_j is L^2;
7. Then, set W_j = V_{j+1} minus V_j so that L^2 be the sum of V_0 and the W_j.
We then want to find a mother wavelet psi in W_0 such that if we set
8. psi_{jk}(x) = 2^{j/2} psi( 2^j x - k),
9. then the psi_{jk}, k in Z, for a basis of $W_j$.
10. Then (finally), we have a basis of $L^2$:
... phi_{0,-2} phi_{0,-1} phi_{0,0} phi_{0,1} phi_{0,2} ...
... phi_{1,-2} phi_{1,-1} phi_{1,0} phi_{1,1} phi_{1,2} ...
... phi_{2,-2} phi_{2,-1} phi_{2,0} phi_{2,1} phi_{2,2} ...
... ... ... ... ...When conditions 4, 5 and 6 are satisfied, we say that we have found a MultiResolution Analysis (MRA).
You can devise many recipes to construct wavelet bases, with various properties. For instance, with the Daubechies wavelets, father and mother wavelets have a compact support; the first moment of the father wavelet are vanishing.
N <- 1024 k <- 6 x <- ( (1:N) - N/2 ) * 2 * pi * k / N y <- ifelse( x>0, sin(x), sin(3*x) ) r <- wd(y) draw(r, col="blue", lwd=3, main="") abline(h=0, lty=3)
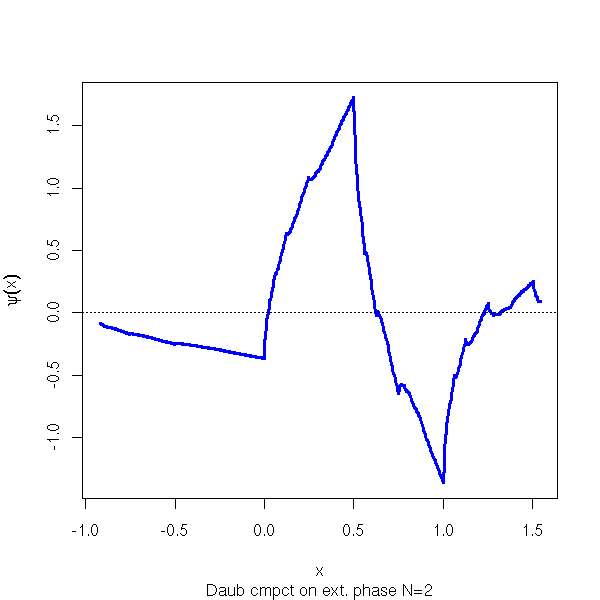
There are many other (families of) wavelets: Haar, Battle--Lemari\'e, Daubechies, Coiflets (the father wavelet has vanishing moments), Symlets (more symetric than the Daubechies wavelets), etc.
Approximation of possibly irregular functions and surfaces (there is a reduced Gibbs phenomenon, but you can circumvent it by using translation-invariant wavelets).
Smoothing.
Density estimation: just try to estimate the density as a linear combination of wavelets, then remove/threshold the wavelets whose coefficients are too small (usually, the threshold is chosen as 0.4 to 0.8 times the maximum coefficient; we also use block thresholding: we do not remove simgle coefficients but whole blocks of coefficients). For instance, density estimation of financial returns: we can clearly see the fat tails. Kernel methods do not perform that well, unless they use adaptive bandwidth.
Regression: this is very similar, we try to find a function f (linear combination of wavelets, we threshold the smaller coefficients) such that
For all i, y_i = f(x_i) + noise If x_i = i/n with n=2^k for some k in Z, it works out of the box otherwise, you have to scale and bin the data.
Gaussian White Noise Estimation: find a function f such that
dY(t) = f(t) dt + epsilon dW(t) t in [0,1]
Applications:
Jump detection. Time series. Diffusion Models (?). Image compression, indexing, reconstruction, etc.
Data management, with the help of the tree-like structure of the wavelet transforms, in particular to speed up the search for a trend change in time series, without having to retrieve the whole series (TSA, Trend and Surprise Abstraction)
You can use the same idea to index images or sound files.
More simply, you can choose to keep the first k coefficients and use them to index the data.
You can also apply a Principal Component Analysis (PCA) to the coefficients of medium resolution of a set of images (we discard the other coefficients: this speeds up the computations) in order to sort them.
One can also use wavelets to clean data (noise removal, dimension reduction) by only keeping the highest coefficients -- this is the basic idea of image compression (JPEG works like that, with a cosine transform instead of wavelets).
WaveShrink: compute the wavelet transform, reduce the coefficients (by applying a threshold (whose choice is troublesome) or something smoother) and compute the inverse transform.
One also uses wavelets to reduce the dimension of the data: after a wavelet transform (it is just a base change, like the Principal Component Analysis (PCA)), only keep the most important coefficients.
Alternatively, you can separate the coefficients in several bands (say, depending on the frequency), perform a Principal Component Analysis (PCA) in each band (you can choose to retain a different number of dimensions in each band, or even to discard some bands).
TODO: applications to regression.
Other applications, unsorted:
clustering (WaveCluster), classification (e.g.: classifying the pixels in an image)
Wavelets are also well-suited for distributed computations -- very trendy with the spread of clusters.
http://www.acm.org/sigs/sigkdd/explorations/issue4-2/li.pdf TODO (read pages 13sqq)
The main packages are
wavethresh waveslim
but you might also want to have a look at
Rwave (1-dimensional wavelets, non-free) fields ebayesthresh.wavelet in EbayesThresh (to select which coefficients to zero out when smoothing a signal with wavelets) LongMemoryModelling in fSeries rwt (not free?)
Survey on Wavelet Applications in Data Mining, SIGKDD Explorations http://www.acm.org/sigs/sigkdd/explorations/issue4-2/li.pdf Wavelets, Approximation and Statistical Applications W. Hardle et al., 1997 http://www.quantlet.com/mdstat/scripts/wav/pdf/wavpdf.pdf Pattern Recognition of Time Series Using Wavelets E. A. Mahara j http://www.quantlet.de/scripts/compstat2002_wh/paper/full/P_03_maharaj.pdf
TODO
TODO
TODO
AR(I)MA models were studying time series by modeling their autocorrelation function. (G)ARCH models do the same by modeling their variance.
The problem GARCH models tackle is the following: even if the variance is constant over time, you can only see it if you have several realizations of the process. Usually, you only have one: to estimate the variance, you can only take several continuous values. In the case of ARMA models, it gives a good approximation of the variance, in GARCH models, it does not. What happens, it that for a given realization, the apparent value of the variance will depend on time; if you had several realizations, you could consider the variance of each realization and take the mean (at a given time, across all the realizations): this mean variance could well be constant.
This is the basic problem of time series: we only have one realization of a process.
(G)ARCH models are often used in finance, where they can model the volatility.
TODO: Somewhere in this document, present the vocabulary of finance.
Volatility is a tricky notion, never defined properly. Let us have a go at it. We consider a time series (if you work in finance, think "log-returns") generated by the following process
X(n) is taken from a gaussian distribution of mean 0 and
variance v(n)where we do not know anything about v(n). This v(n) (or rather, its square root) is called the volatility. That is all. As we do not know anything about it, we cannot say much about it, let alone estimate it. So we have either to heuristically estimate it (there are many ways of doing so, yielding different results) or to make a few hypotheses about it, to assume it evolves according to a certain model.
Thus, speaking of volatility without stating which model you use, without cheking if this model fits the data, is completely meaningless.
(G)ARCH models are such models. The basic idea leading to them is that "volatility clusters": if there is a large value, the next values are likely to be large; conversely, if there is a small value, the next values are likely to be small. In other words, the volatility v(n) varies slowly.
Let us consider an example
data(EuStockMarkets) x <- EuStockMarkets[,1] x <- diff(log(x)) i <- abs(x)>median(abs(x))
and look if high values tend to cluster.
> library(tseries)
> runs.test(factor(i))
Runs Test
data: factor(i)
Standard Normal = -2.2039, p-value = 0.02753
alternative hypothesis: two.sidedIn this runs test, we look at the number of runs of sequential high values, the number of runs of sequential low values and we transform them so that it follows a gaussian distribution. Here, we get a negative value, which means that we have fewer runs that expected, i.e., longer runs than expected. As the p-value is under 5%, we shall say that the difference is statistically significant.
Here is another implementation of this test:
number.of.runs <- function (x) {
1+sum(abs(diff(as.numeric(x))))
}
my.runs.test <- function (x, R=999) {
if( is.numeric(x) )
x <- factor(sign(x), levels=c(-1,1))
if( is.logical(x) )
x <- factor(x, levels=c(FALSE,TRUE))
if(!is.factor(x))
stop("x should be a factor")
# Non-parametric (permutation) test
n <- length(x)
res <- rep(NA, R)
for (i in 1:R) {
res[i] <- number.of.runs(
x[sample(1:n,n,replace=F)]
)
}
t0 <- number.of.runs(x)
n1 <- 1+sum(t0<=res)
n2 <- 1+sum(t0>=res)
p <- min( n1/R, n2/R )*2
p <- min(1,p) # If more than half the values are identical
# Parametric test, based on a formula found on the
# internet...
# People believe that Z follows a gaussian distribution
# (this is completely wrong if the events are rare -- I
# had first used it with mutations on a DNA sequence...)
n1 <- sum(x==levels(x)[1])
n2 <- sum(x==levels(x)[2])
r <- number.of.runs(x)
mr <- 2*n1*n2/(n1+n2) + 1
sr <- sqrt( 2*n1*n2*(2*n1*n2-n1-n2)/
(n1+n2)^2/(n1+n2-1) )
z <- (r-mr)/sr
pp <- 2*min(pnorm(z), 1-pnorm(z))
r <- list(t0=t0, t=res, R=R,
p.value.boot=p,
n1=n1, n2=n2, r=r, mr=mr, sr=sr, z=z,
p.value.formula=pp)
class(r) <- "nstest"
r
}
print.nstest <- function (d) {
cat("Runs test\n");
cat(" NS = ")
cat(d$t0)
cat("\n p-value (")
cat(d$R)
cat(" samples) = ")
cat(round(d$p.value.boot,digits=3))
cat("\n")
cat(" theoretical p-value = ")
cat(d$p.value.formula)
cat("\n")
}
plot.statistic <- function (t0, t, ...) {
xlim <- range(c(t,t0))
hist(t, col='light blue', xlim=xlim, ...)
points(t0, par("usr")[4]*.8,
type='h', col='red', lwd=5)
text(t0, par("usr")[4]*.85, signif(t0,3))
}
plot.nstest <- function (
d, main="Runs test",
ylab="effectif", ...
) {
plot.statistic(d$t0, d$t, main=main,
xlab=paste("Runs, p =",signif(d$p.value.boot,3)),
...)
}
# Example
data(EuStockMarkets)
x <- EuStockMarkets[,1]
x <- diff(log(x))
i <- abs(x)>median(abs(x))
plot(my.runs.test(i))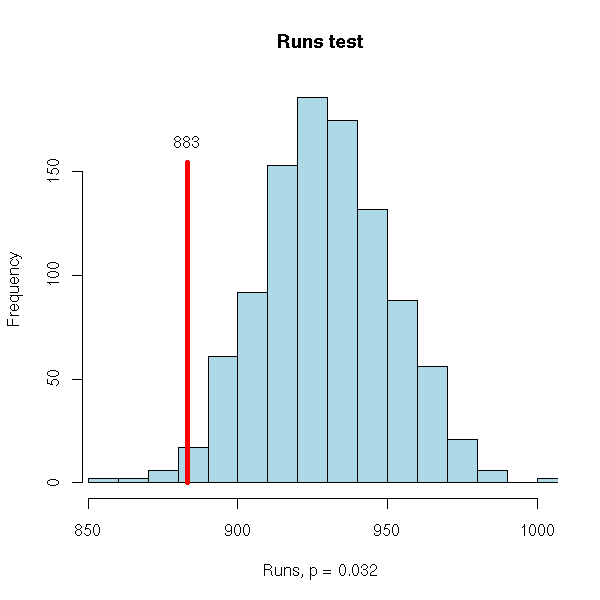
Here, we get the same p-value:
> my.runs.test(i)
Runs test
NS = 883
p-value (999 resamplings) = 0.024
p-value ("theoretical") = 0.02752902We can repeat this experiment with other financial time series.
op <- par(mfrow=c(2,2))
for (k in 1:4) {
x <- EuStockMarkets[,k]
x <- diff(log(x))
i <- abs(x)>median(abs(x))
plot(my.runs.test(i))
}
par(op)
TODO: do this with many more series...
Here are a few models of time series.
First, a few notations (these correspond to "stochastic processes" and "stochastic differential equations", i.e., the continuous-time analogue of time series -- but as far as intuition is concerned, you can stay with a discrete time).
S The quantity we want to model ("S" stands for "spot price")
dS The first derivative of S: think "dS = S(n) - S(n-1)"
t Time
dX Gaussian noise, with variance dt
s volatility
m trend
n a constantA random walk:
dS = s dX
A random walk with a trend:
dS = m dt + s dX
A logarithmic random walk:
dS = m S dt + s S dX
A mean-reverting random walk (used to model a value that will not wander too far away from zero, e.g., an interest rate):
dS = (n - m S) dt + s dX
Another mean-reverting random walk:
dS = (n - m S) dt + s S^.5 dX
We can simulate them as follows:
sde.sim <- function (t, f, ...) {
n <- length(t)
S <- rep(NA,n)
S[1] <- 1
for (i in 2:n) {
S[i] <- S[i-1] + f(S[i-1], t[i]-t[i-1], sqrt(t[i]-t[i-1])*rnorm(1), ...)
}
S
}
a <- 0
b <- 10
N <- 1000
x <- sde.sim(seq(a,b,length=N),
function (S,dt,dX,m=1,s=1) { m * S * dt + s * S * dX })
x <- ts(x, start=a, end=b, freq=(N-1)/(b-a))
op <- par(mfrow=c(4,1), mar=c(2,4,2,2))
plot(x)
plot(log(x))
plot(diff(log(x)))
acf(diff(log(x)))
par(op)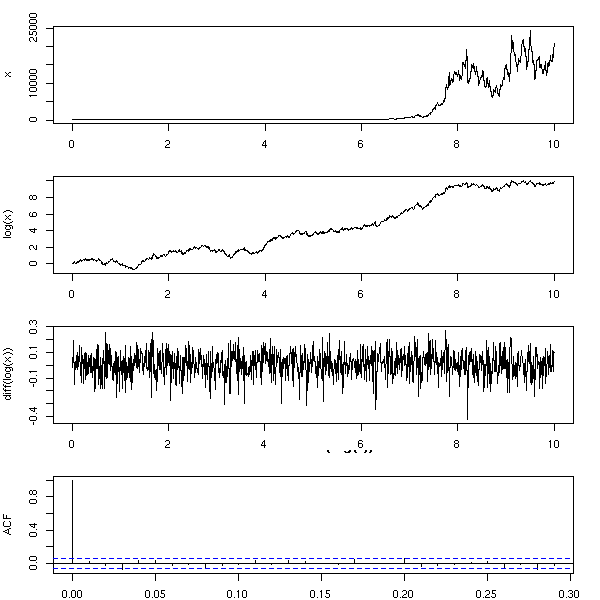
Here are similations for the previous examples:
TODO: give several examples for each model
N <- 1000
a <- 0
b <- 3
op <- par(mfrow=c(3,1))
for (i in 1:3) {
x <- sde.sim(seq(a,b,length=N),
function (S,dt,dX,m=1,s=1) { s * dX })
x <- ts(x, start=a, end=b, freq=(N-1)/(b-a))
plot(x, main="Random walk")
}
par(op)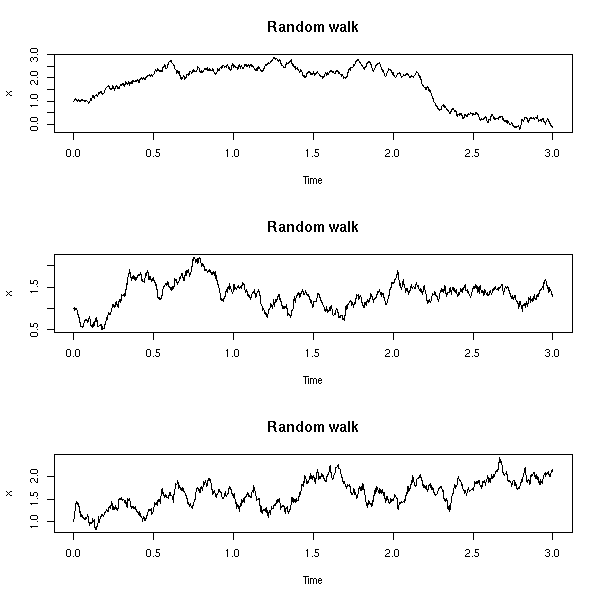
op <- par(mfrow=c(3,1))
for (i in 1:3) {
x <- sde.sim(seq(a,b,length=N),
function (S,dt,dX,m=1,s=1) { m * dt + s * dX })
x <- ts(x, start=a, end=b, freq=(N-1)/(b-a))
plot(x, main="Random walk with a trend")
}
par(op)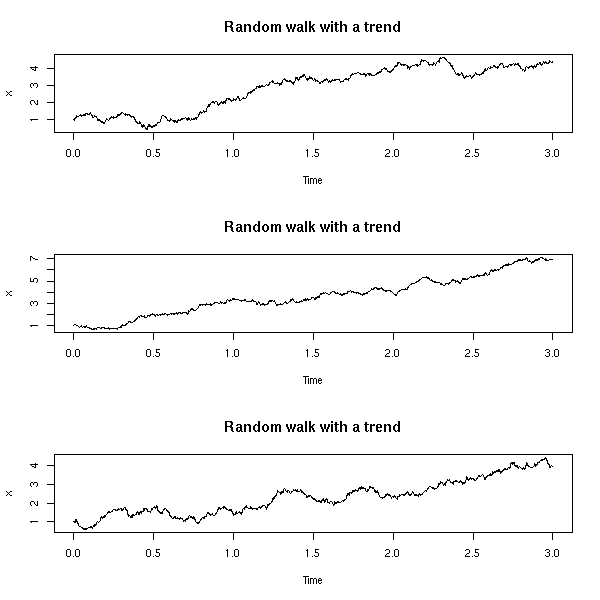
op <- par(mfrow=c(3,1))
for (i in 1:3) {
x <- sde.sim(seq(a,b,length=N),
function (S,dt,dX,m=1,s=1) { m * S * dt + s * S * dX })
x <- ts(x, start=a, end=b, freq=(N-1)/(b-a))
plot(x, main="Lognormal random walk")
}
par(op)
b <- 10
op <- par(mfrow=c(3,1))
for (i in 1:3) {
x <- sde.sim(seq(a,b,length=N),
function (S,dt,dX,m=3,s=1,n=3) { (n - m*S) * dt + s * dX })
x <- ts(x, start=a, end=b, freq=(N-1)/(b-a))
plot(x, main="Mean-reverting random walk")
abline(h=1,lty=3)
}
par(op)
op <- par(mfrow=c(3,1))
for (i in 1:3) {
x <- sde.sim(seq(a,b,length=N),
function (S,dt,dX,m=3,s=1,n=3) { (n - m*S) * dt + s * sqrt(S) * dX })
x <- ts(x, start=a, end=b, freq=(N-1)/(b-a))
plot(x, main="Mean-reverting random walk")
abline(h=1,lty=3)
}
par(op)
TODO:
Look at the volatility of the examples above.
op <- par(mfrow=c(2,1))
x <- sde.sim(seq(a,b,length=N),
function (S,dt,dX,m=1,s=1) { m * S * dt + s * S * dX })
x <- ts(x, start=a, end=b, freq=(N-1)/(b-a))
plot(x, main="Lognormal random walk")
return <- diff(x) / x[ -length(x) ]
y <- return^2
plot(y)
lines(predict(loess(y~time(y))) ~ as.vector(time(y)), col='red', lwd=3)
par(op)
Err... This has nothing to do in the chapter about GARCH models...
TODO: put this section somewhere else...
An ARCH series is a series of gaussian random variables, centered, independant, but with different variances:
u(n) ~ N(0, var=h(n)) h(n) = a0 + a1 u(n-1)^2 + a2 u(n-2)^2 + ... + aq u(n-q)^2
Example:
n <- 200
a <- c(1,.2,.8,.5)
a0 <- a[1]
a <- a[-1]
k <- length(a)
u <- rep(NA,n)
u[1:k] <- a0 * rnorm(k)
for (i in (k+1):n) {
u[i] <- sqrt( a0 + sum(a * u[(i-1):(i-k) ]^2 )) * rnorm(1)
}
u <- ts(u)
eda.ts(u)
The plots we are drawing do not allow us to spot heteroscedasticity problems; even in the most extreme casesm it really looks like iid noise.
h <- rnorm(1000)^2 x <- filter(h, rep(1,50)) x <- x[!is.na(x)] eda.ts(x)

y <- rnorm(length(x),0,sqrt(x)) eda.ts(y)
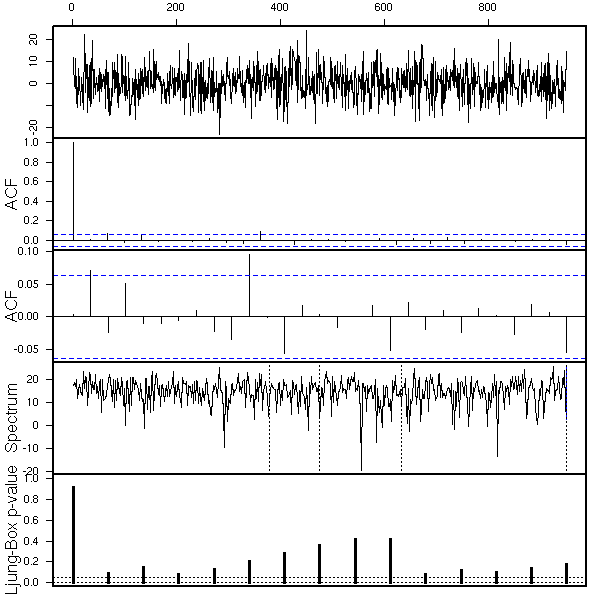
h <- c(rep(1,100), rep(2,100)) y <- ts(rnorm(length(h), 0, sd=h)) eda.ts(y)

How can we spot heteroscedasticity?
When it is obvious, as in the last example, we can perform a non-linear regression (splines or local regression, as you fancy) on the absolute value of the series.
plot(abs(y)) lines(predict(loess(abs(y)~time(y))), col='red', lwd=3) k <- 20 lines(filter(abs(y), rep(1/k,k)), col='blue', lwd=3, lty=2)

With our initial ARCH model:
plot.ma <- function (x, k=20, ...) {
plot(abs(x), ...)
a <- time(x)
b <- predict(loess(abs(x) ~ a))
lines(b ~ as.vector(a), col='red', lwd=3)
k <- 20
lines(filter(abs(x), rep(1/k,k)), col='blue', lwd=3)
}
plot.ma(u)
The ARIMA series we have seen were indeed different.
n <- 1000 op <- par(mfrow=c(4,1), mar=c(2,4,2,2)) plot.ma(ts(rnorm(n))) plot.ma(arima.sim(list(ar = c(.8,.1)), n)) plot.ma(arima.sim(list(ma = c(.8,.1)), n)) plot.ma(arima.sim(list(ma = c(.8,.4,.1), ar = c(.8,.1)), n)) par(op)
In all these models, we model the variance of a series (a series that looks like noise and whose sole problem is a heteroskedasticity one: e.g., a residuals of a regression or of an ARIMA model).
Our series is
u(n) ~ N(0, var=h(n))
and the variance, h(n) is a function if the previous u(k).
ARCH:
h(n) = a0 + a1 u(n-1)^2 + a2 u(n-2)^2 + ... + aq u(n-q)^2
For the GARCH model, we also use the previous variances:
h(n) = a0 + a1 u(n-1)^2 + a2 u(n-2)^2 + ... + aq u(n-q)^2
+ b1 h(n-1) + ... + bq h(n-q)In those models, the sign of u is not used: GARCH models are symetric. However, for some data sets (typicall, financial data), one can see that this sign is important; this is called the "leverage effect", and it calls for extensions of the GARCH model.
TODO: Find an example of this leverage effect (it is not visible here...)
op <- par(mfrow=c(1,4))
data(EuStockMarkets)
for (a in 1:4) {
x <- EuStockMarkets[,a]
x <- diff(log(x))
n <- length(x)
s <- rep(NA, n+1)
s[ which(x>0) + 1 ] <- "+"
s[ which(x<0) + 1 ] <- "-"
i <- which( !is.na(s) )
s <- factor(s[i])
x <- x[i]
boxplot(log(abs(x))~s, col='pink')
}
par(op)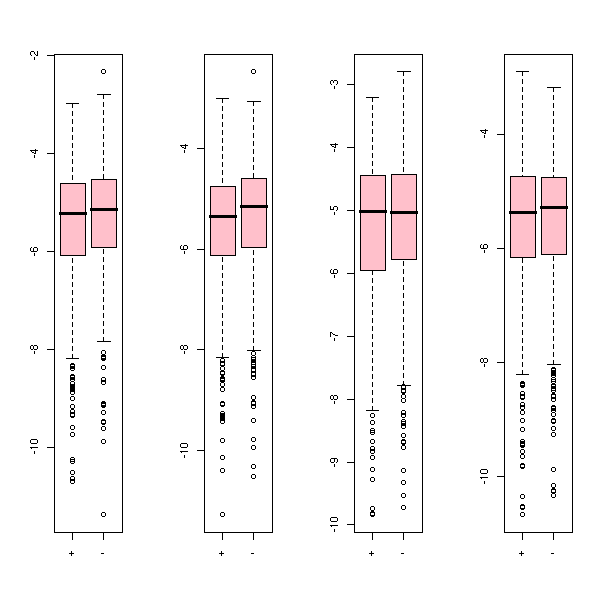
Some models account for this asymetry (you will find many others in the literature and you can roll up your own):
AGARCH1 (The effects are symetric around A, not around 0):
h(n) = a0 + a1 (A + u(n-1))^2 + ... + aq (A + u(n-q))^2
+ b1 h(n-1) + ... + bq h(n-q)AGARCH2 (Larger coefficients when u>0):
h(n) = a0 + a1 (abs(u(n-1)) + A*u(n-1))^2 + ... + aq (abs(u(n-q)) + A*u(n-q))^2
+ b1 h(n-1) + ... + bq h(n-q)GJR-GARCH (idem):
h(n) = a0 + (a1 + A * (u(n-1)>0)) * u(n-1))^2 + ... + (aq + A*(u(n-q)>0)) * u(n-q))^2
+ b1 h(n-1) + ... + bq h(n-q)EGARCH:
TODO
You can use a (G)ARCH model for the noise in a regression, when you seen that the residuals have a heteroskedasticity problem.
TODO: An example that show the effects of heteroskedasticity (bias? wrong confidence intervals? Far from optimal estimators?)
TODO
BEWARE: I have not (yet) understood what follows.
It is probably not entirely correct.
x(t+1) = x(t) * noise
log(noise) ~ N(0, var=v(t))
data(EuStockMarkets)
x <- EuStockMarkets[,1]
op <- par(mfrow=c(3,1))
plot(x, main="An index")
y <- diff(log(x))
plot(abs(y), main="Volatility")
k <- 30
z <- filter(abs(y),rep(1,k)/k)
plot(z, ylim=c(0,max(z,na.rm=T)), col='red', type='l',
main="smoothed volatility (30 days)")
par(op)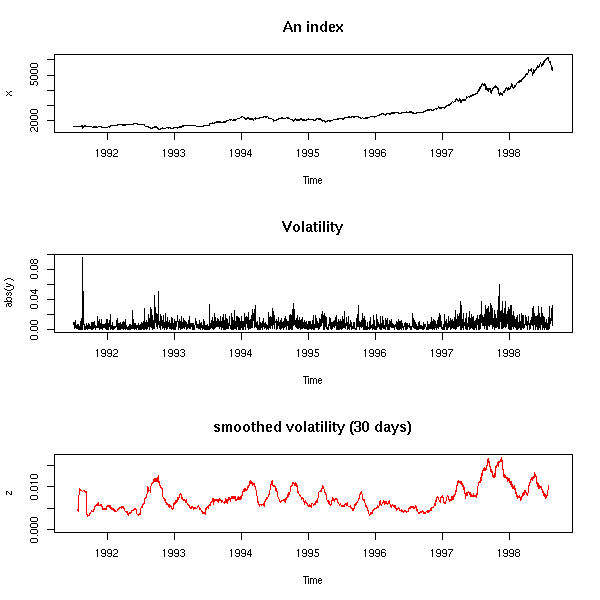
A simulation:
n <- 200
v <- function (t) { .1*(.5 + sin(t/50)^2) }
x <- 1:n
y <- rnorm(n) * v(x)
y <- ts(y)
op <- par(mfrow=c(3,1))
plot(ts(cumsum(y)), main="A simulation")
plot(abs(y), main="volatility")
plot(v(x)~x,
ylim=c(0,.3),
type='l', lty=2, main="smoothed volatility")
k <- c(5,10,20,50)
col <- rainbow(length(k))
for (i in 1:length(k)) {
z <- filter(abs(y),rep(1,k[i])/k[i])
lines(z, col=col[i])
}
par(op)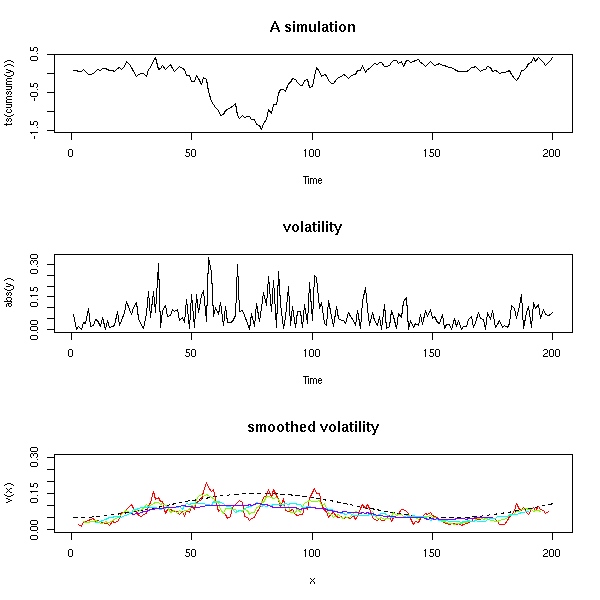
TODO: simple variant, EWMA (exponentially weighted moving average)
v[i] <- lambda * v[i-1] + (1-lambda) * u[i-1]^2 Easy, there is a simgle parameter... You can choose it empirically, lambda=0.094 TODO: Simulation, model. TODO: My likelihood is wrong. There should only be gausians, no chi^2.
you can try to estimate this variance v(t+1) as a weighted mean of: the mean variance V (e.g., obtained by an exponential moving standard deviation or an exponential moving averege of v); yesterday's forecast v(t); the square of the stock price returns u(t) = (x(t)-x(t-1))/x(t-1).
v(t+1) = gamma V + alpha v(t) + beta u(t)^2.
Rather than estimating the alpha, beta, gamma coefficients yourself, you can estimate them with the Maximum Likelihood method.
TODO: Example
ll <- function (u, gammaV, alpha, beta) {
n <- length(u)
v <- rep(NA,n)
v[1] <- u[1]^2
for (i in 2:n) {
v[i] <- gammaV + alpha * v[i-1] + beta*u[i-1]^2
}
sum(log(dchisq(u^2 / v, df=1)))
}
lll <- function (p) {
ll(y,p[1],p[2],p[3])
}
r <- nlm(lll, c(.4*mean(diff(y)^2),.3,.3))
r$estimate
res <- NULL
for (i in 1:20) {
p <- diff(c(0,sort(runif(2)),1)) *
c( mean((diff(y)/y)^2), 1, 1 )
r <- NULL
try( r <- nlm(lll, p) )
if(!is.null(r)){
res <- rbind(res, c(r$minimum, r$estimate))
print(res)
}
}
colnames(res) = c("minimum", "gammaV", "alpha", "beta")
res
TODO: I never get the same result.
gammaV is always negative: I do not like that...
minimum gammaV alpha beta
[1,] -473.3557 -2.489084e-05 0.31610437 0.23202868
[2,] -280.1692 -4.024827e-05 0.09674672 0.73230780
[3,] -266.3034 -5.859300e-05 0.23999115 0.59694235
[4,] -506.3229 -5.244953e-05 0.51160110 0.16128155
[5,] -228.9716 6.530461e-06 0.97200115 0.02253152
[6,] -516.4043 -5.520438e-05 0.85418375 0.06408601
[7,] -415.7290 -2.314525e-05 0.14884342 0.37617978
[8,] -291.3665 -1.223586e-04 0.50715120 0.36927627
[9,] -278.2773 -7.733857e-05 0.35255591 0.45927997
[10,] -310.3256 -5.888580e-05 0.17611217 0.69979118
[11,] -288.9966 -3.312234e-05 0.07831422 0.72978797
[12,] -259.3784 -1.318697e-04 0.43313467 0.46553856
[13,] -314.1510 -9.033081e-05 0.58692361 0.24131744
[14,] -210.2558 -1.020534e-05 0.22237139 0.77719951
[15,] -407.7668 -2.849821e-05 0.11921529 0.42430838
[16,] -505.7438 -1.841478e-05 0.27421749 0.22635609
[17,] -193.4423 -1.266605e-05 0.79456866 0.19993238
[18,] -426.6810 -3.046373e-05 0.26306608 0.29960224
[19,] -929.4232 -7.528851e-06 0.09520649 0.13700275This was the GARCH(1,1) model. The GARCH*p,q) is its obvious generalization:
v(t+1) = gamma V + alpha1 v(t) + alpha2 v(t-1) + ... + alphaq v(t-q+1)
+ beta1 u(t) + ... + betap u(t-p+1).
TODO: other motivation:
We do not only want a forecast of the value we are
studying but also an estimation of the forecast
error. Most models assume that the variance is constant,
so the forecast error does not change much.
But this is not realistic. The variance is not constant
and we must acocunt for it.
Question:
Among the disgnostics after modeling a time series, did I
mention heteroskedasticity?
I cursorily mentionned it in the definition of a white
noise.
You can see the problem by smoothing the squared
residualsor with the tests in the "lmtest" package.
TODO: a simulation
TODO: check
garch.sim <- function (n, gammaV, p=NULL, q=NULL) {
if(gammaV<0){ stop("gammaV should be positive") }
if (any(p)<0 || any(p)>1) {
stop("The coefficients in p should be in [0,1]")
}
if (any(q)<0 || any(q)>1 ){
stop("The coefficients in q should be in [0,1]")
}
if (sum(c(p,q))>1) {
stop("The coefficients (including gamma) should sum up to 1")
}
gamma <- 1-sum(p)-sum(q)
V <- gammaV/gamma
v <- ( sqrt(V)*rnorm(n) )^2
u <- sqrt(V)*rnorm(n)
# TODO: Initialisation
k <- max(length(p),length(q)+1)
for (i in k:n) {
v[i] <- gammaV
for (j in 1:length(q)) {
v[i] <- v[i] + q[j]*v[i-j]
}
for (j in 1:length(p)) {
v[i] <- v[i] + p[j]*u[i-j]^2
}
u[i] <- sqrt(v[i]) * rnorm(1)
}
ts(u)
}
res <- NULL
for (i in 1:20) {
x <- garch.sim(200,1,c(.3,.2),c(.2,.1))
r <- garch(x, order=c(2,2))
res <- rbind(res, r$coef)
}
res
res <- NULL
for (i in 1:200) {
x <- garch.sim(200,1,.5,.3)
r <- garch(x, order=c(1,1))
res <- rbind(res, r$coef)
}
res
apply(res, 2, mean)In R, the functions pertaining to GARCH models are in the "tseries" package.
library(tseries) x <- EuStockMarkets[,1] y <- diff(x)/x r <- garch(y) # plot(r) The plot function is only for interactive use... op <- par(mfrow=c(2,1)) plot(y, main = r$series, ylab = "Series") plot(r$residuals, main = "Residuals", ylab = "Series") par(op)
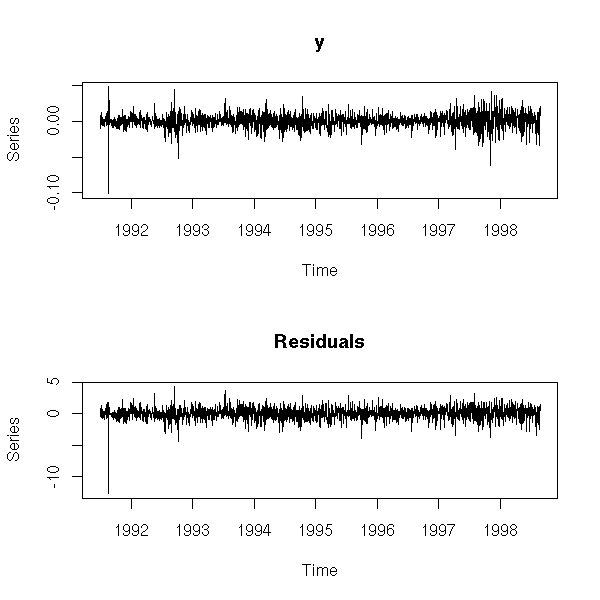
op <- par(mfrow=c(2,1))
hist(y,
main = paste("Histogram of", r$series),
xlab = "Series")
hist(r$residuals,
main = "Histogram of Residuals",
xlab = "Series")
par(op)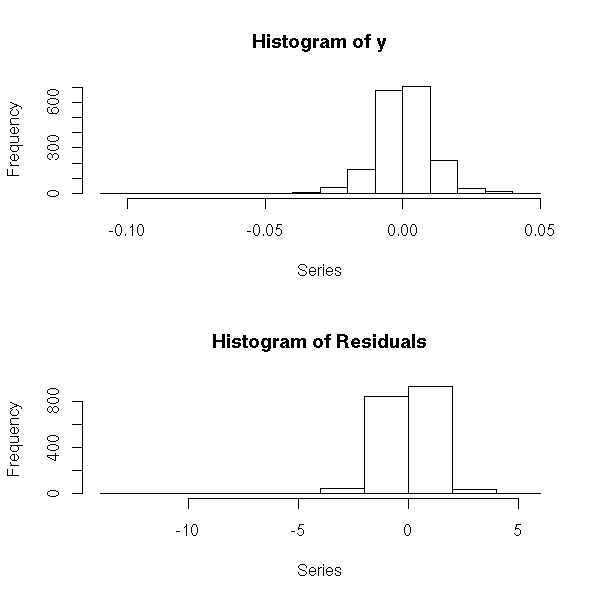
op <- par(mfrow=c(2,1))
qqnorm(y,
main = paste("Q-Q Plot of", r$series),
xlab = "Gaussian Quantiles")
qqnorm(r$residuals,
main = "Q-Q Plot of Residuals",
xlab = "Normal Quantiles")
par(op)
op <- par(mfrow=c(2,1))
acf(y^2,
main = paste("ACF of Squared", r$series))
acf(r$residuals^2,
main = "ACF of Squared Residuals",
na.action = na.remove)
par(op)
We get (The Jacques Bera test is a gaussianity test):
> r
Call:
garch(x = y)
Coefficient(s):
a0 a1 b1
5.054e-06 6.921e-02 8.847e-01
> summary(r)
Call:
garch(x = y)
Model:
GARCH(1,1)
Residuals:
Min 1Q Median 3Q Max
-12.66546 -0.47970 0.04895 0.65193 4.39506
Coefficient(s):
Estimate Std. Error t value Pr(>|t|)
a0 5.054e-06 8.103e-07 6.237 4.45e-10 ***
a1 6.921e-02 1.151e-02 6.014 1.81e-09 ***
b1 8.847e-01 1.720e-02 51.439 < 2e-16 ***
---
Signif. codes: 0 `***' 0.001 `**' 0.01 `*' 0.05 `.' 0.1 ` ' 1
Diagnostic Tests:
Jarque Bera Test
data: Residuals
X-squared = 17279.64, df = 2, p-value = < 2.2e-16
Box-Ljung test
data: Squared.Residuals
X-squared = 0.1291, df = 1, p-value = 0.7194TODO
TODO: diagnostics (look at the residuals: the are supposed to have a zero mean (or, at least, a constatn mean), a constant variance and have no autocorrelation (Ljung-Box test, with lags up to 15 days). TODO: diagnostics. Autocorrelation Autocorrelation of u/sqrt(v) TODO: forecasting the future returns??? (With the variance, you can plot the 95% confidence intervals of the forecast paths.) TODO: Generalizations TARCH (Threshold ARCH) EGARCH http://marshallinside.usc.edu/simrohoroglu/teaching/543/spring2002/garch101.pdf TODO: regression with GARCH error terms ? no (not yet in R)
TODO
TODO
TODO
We had defined the notion of auto-regressive (AR) model for 1-dimensionnal time-series,
y_{n+1} = A y_n + noise.For multidimensional time-series, i.e., vector-valued time-series, the formula is the same, but A is a matrix. As in the 1-dimensional case, we can also add in earlier terms, go get a VAR(p) process and not simply a VAR(1) process.
TODO: Example. TODO: how do we fit such a model? ?ar library(dse1) estVARXls(x) TODO: VARMA library(dse1) x <- simulate(ARMA(...)) Other packages: MSBVAR (Bayesian VAR) TODO: ARMA, VARMA, VARMAX??? correlogram data(EuStockMarkets) x <- EuStockMarkets[,1] y <- EuStockMarkets[,2] acf(ts.union(x,y),lag.max=100)
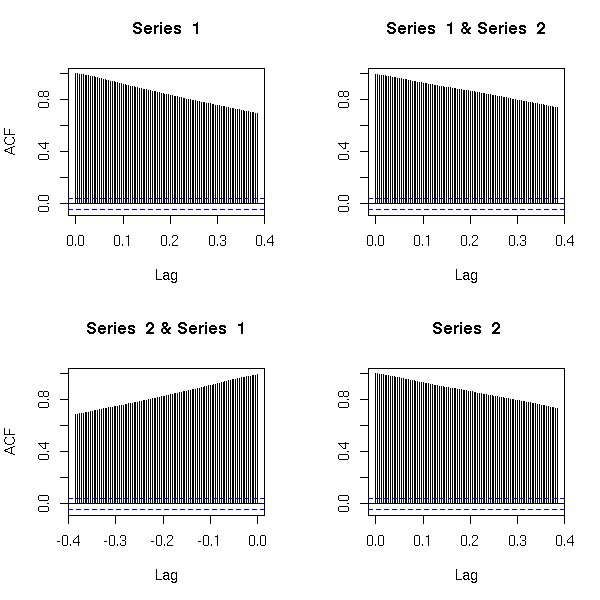
x <- diff(x) y <- diff(y) acf(ts.union(x,y),lag.max=100)

TODO
TODO
TODO
TODO
TODO: Write this section...
TODO: SSM and classical models
Motivation: For the classical model (trend, seasonal component, noise), I had used a set of equations to describe the model: this was actually a SSM. http://www.uio.no/studier/emner/matnat/biologi/BIO4040/h03/undervisningsmateriale/Lectures/lecture10.pdf
TODO (The classical example with the space probe motion)
When studying financial data, especially "return" time series (the return is the difference between today's price and yesterday's price -- some people define it as the difference of the logarithms of those prices), it is tempting to assume that the values are taken from a series of iid random variables. The volatility is the variance of those random variables. But sometimes, the assumption that the variance, aka "volatility", is constant is not reasonnable.
TODO: example (plot)
More recent models consider the volatility as a random variable: we model the evolution of two random variables, the price and its volatility -- the first is directly measurable, the second is not.
We can see this as a state space model: the phenomenom we are studying lives in a 2-dimensional space whose coordinates are the returns and the volatility. The first coordinate can be measured, the second cannot. The aim of the game is to estimate this hidden coordinate. For instance, the model could be
TODO: give the equations give the name of this model give a simulation
Given such a model, given the observed variable X_n, we want to estimate the hidden variable V_n.
Let us consider an autoregressive process S,
S(t+1) = f( S(t) ) + noise_1
that is not directly observed: we only observe a certain function of S, with noise.
X = g(S) + noise_2.
One says that
S is the unobserved state X are the observed data g is the transition function f is the measure function noise_1 is the state noise noise_2 is the measure noise
Quite often, we shall require that f and g be linear, but we will accept that the change with time.
One can consider different problems:
1. Given f, g, the variance of both noises, the first values of X, forecast the past and future values if S -- this is the Kalman filter.
2. Given the first values of X, find f, g and the variance of both noises. For this problem, we shall assume that f and g have a simple (linear) known form.
The following process
S(n) = a S(n-1) + u(n) X(n) = S(n) + v(n)
is an ARMA(1,1) process.
(Exercise for the reaser: check this.)
All ARMA(1,1) processes are actually SSM: if
X(n) = a X(n-1) + u(n) + b u(n-1),
then, if we set
/ X(n-1) \
| |
S(n) = | u(n) |
| |
\ u(n-1) /we get:
X = ( a 1 b ) * S
/ a 1 0 \ / 0 \
| | | |
S(n) = | 0 0 0 | * S(n-1) + | u(n) |
| | | |
\ 0 0 1 / \ 0 /This can be generalized: all ARA(p,q) processes are SSM.
They are very general: they contain, as a special case, ARMA models, and even ARMA models with time-changing coefficients.
They also allow us to study multivariate data: it we have several time series, we can either: study them one at a time; or consider them as independant realizations of a single process (panel data); or consider them as a single vector time series, accounting for correlations (or more complicated relations) between them -- SSM can be used in the last case.
Let us denote
x: state of the system, the hidden variables (that play a pivotal role in the evolution of the system but cannot be directly measured) y: the quantities that can actually be measured
The state of the system (i.e., the hidden variables) at time n depend on the state of the system at time n-1, but it is a stochastic process: some noise (here, epsilon) intervenes.
x_n = f ( x_{n-1}, epsilon_{n-1} )For instance, if the model states that x is "constant except that it moves a bit", we can model it as a random walk,
x_n = x_{n-1} + epsilon_{n-1}.If the variance of epsilon is small, x will indeed appear "not to move too much".
The quantities actually measures are a function of the state of the system, with some noise (here, eta),
y_n = g ( x_n, eta_n )
For instance, if we simply measure the state of the system, but if we can only do so with some imprecision, the equation would be
y_n = x_n + epsilon_n.
We now compute the probability density of the hidden variables x_n given the observed variables y_1, y_2, ..., y_n. We proceed in two steps: first, the a priori estimate,
p( x_n | y_1, ..., y_{n-1} )where we do not use (yet) the value of the observed variable at time n; and second,
p( x_n | y_1, ..., y_{n-1}, y_n ).If you really want formulas:
p( x_n | y_1, ..., y_{n-1} ) = Integral of p(x_n|x_{n-1}) p(x_{n-1}|y1,...,y_{n-1}) d x_{n-1}
p( y_n | x_n ) p( x_n | y_1,...,y_n )
p( x_n | y_1, ..., y_n ) = ---------------------------------------
p( y_n | y_1,...,y_n)
p( y_n | x_n ) p( x_n | y_1,...,y_n )
= -----------------------------------------------
Integral of p(y_n|x_n) p(x_n|y_1,...y_n) dx_nThere are too many integrals, so we do not really use those equations (but actually, we could, if the phenomena was was sufficiently non-linear and/or non-gaussian, with Monte Carlo simulations -- this would be called a Particle Filter). To simplify those formulas, let us assume that the transition and measurement function f and g are linear
x_n = f ( x_{n-1}, epsilon_{n-1} )
= A x_{n-1} + W epsilon_{n-1}
y_n = g ( x_n, eta_n )
= H x_n + U eta_nand that all the random variables are gaussian (it suffices to assume that the noises eta and epsilon are gaussian). Then, instead of estimating the whole probability distribution function of the a priori estimate
x_n | y_1,...,y_{n-1}and the a posteriori estimate
x_n | y_1,...,y_{n-1},y_nit suffices to compute the expectation and the variance of those apriori
\bar x_n = E[ x_n | y_1,...,y_{n-1} ]
\bar P = Var[ x_n | y_1,...,y_{n-1} ]and a posteriori estimates
\hat x_n = E[ x_n | y_1,...,y_n ] \hat P = Var[ x_n | y_1,...,y_n ]
The formulas become:
\bar x_n = E[ x_n | y_1,...,y_{n-1} ]
= E[ A x_{n-1} + W epsilon_{n-1} | y_1,...,y_{n-1} ]
= A E[ x_{n-1} | y_1,...,y_{n-1} ]
= A \hat x_{n-1}
\bar P_n = Var[ x_n | y_1,...,y_{n-1} ]
= Var[ A x_{n-1} + W epsilon_{n-1} | y_1,...,y_{n-1} ]
= Var[ A x_{n-1} | y_1,...,y_{n-1} ] + Var[ W epsilon_{n-1} | y_1,...,y_{n-1} ]
= A Var[ A x_{n-1} | y_1,...,y_{n-1} ] A' + W Var[ epsilon ] W'
= A \hat P_{n-1} A' + W Q W'where
Q = Var[ epsilon ].
For the second set of formulas, it is trickier. We first need to know a little more about conditionnal expectation and conditionnal variance, namely
If (X,Y) is gaussian
Then
E[X|Y] = E[X] + Cov(X,Y) (Var[Y])^-1 (Y-E[Y])
Var[X|Y] = Var[X] - Cov(X,Y) (Var[Y])^-1 Cov(X,Y)'We get
E[x1|y1] = E[x1] + Cov(x1,y1) (Var y1)^-1 (y1-E[y1])
where
y1 = H x1 + U eta
Var[eta] = R
Cov(x1,y1) = Cov( x1, H x1 + U eta )
= Cov( x1, H x1 )
= (Var x1) H'
= \bar P1 H'
Var y1 = Var[ H x1 + U eta ]
= Var[ H x1 ] + Var[ U eta ]
= H Var[x1] H' + U Var[eta] U'
= H \bar P1 H' + U R U'
E[y1] = E[ H x1 + U eta ]
= H E[x1]
= H bar x1thus (I take n=1 for readability reasons):
E[x1|y1] = \bar x1 + \bar P1 H' (H \bar P1 H' + U R U')^-1 ( y1 - H \bar x1 )
and
Var[x1|y1] = Var[x1] - Cov(x1,y1) (Var[y1])^-1 Cov(x1,y1)'
= \bar P1 - \bar P1 H' (H \bar P1 H' + U R U')^-1 (\bar P1 H)'
= \bar P1 - \bar P1 H' (H \bar P1 H' + U R U')^-1 H \bar P1 'In general,
\hat x_n = E[ x_n | y_1,...,y_n ]
= \bar x_n + \bar P_n H' (H \bar P_n H' + U R U')^-1 ( y_n - H \bar x_n )
\hat P_n = Var[ x_1 | y_1,...,y_n ]
= \bar P_n - \bar P_n H' (H \bar P_n H' + U R U')^-1 H \bar P_n 'TODO: check this formula
TODO: implement this TODO: give some simple models (LLM, LTM), mention the already available implementations TODO: CAPM regression TODO: Extended Kalman Filter (EKF) TODO: Unscented Kalman Filter (UKF) TODO: Particle Filter
The stats package contains a function StructTS that filters a 1-dimensional signal as- suming it was produced by a Local Level Model (LLM) or a Local Trend Model (LTM).
TODO
The DSE package provides a Kalman filter for a general State Space Model (the model has too many parameters for them to be reliably estimated, unless we have very long time series).
TODO: try to use it
The DSE package also contains a function to compute the likelihood of a model.
TODO: use it to estimate the parameters
Adaptive Least Squares (ALS) Regression is a non-linear Kalman filter, defined by the following State Space Model.
beta_{t+1} = beta_t + noise (hidden variables)
x_t = noise (observed variables)
y_t = beta_t x_t + noise (observed variable)This is simply a regression whose coefficient, beta, is a random walk. As we multiply two of the variables, this is a non-linear model.
TODO...
TODO If the state space model is not linear, just linearize it. This still assumes Gaussian, additive noise.
TODO
TODO
State-space models: library(dse) library(dse1) library(dse2) library(dseplus) library(tseries) (econometrics) Kalman filtering ARAR Intervention analysis (at some moment in time, the model changes) Transfer function models (?) regime switching models
A gaussian random walk (or its continuous-time equivalent, a brownian motion) is characterized by
dt is proportionnal to (dx)^2
We can use this to simulate a random walk: if we know the values of x(0) and x(N), we choose a value for x(N/2) according to a gaussian distribution of mean (x(0) + x(N)) / 2 and standard deviation (proportionnal to) N^(1/2).
f <- function (N, alpha = 2, reverting = FALSE) {
if (N <= 1) {
res <- 0
} else {
a <- rnorm(1) * (N/2)^(1/alpha)
res <- c( seq(0, a, length = N/2) + f(N/2, reverting = TRUE),
seq(a, 0, length = N/2) + f(N/2, reverting = TRUE) )
}
if (!reverting) {
final <- rnorm(1) * N^(1/alpha)
res <- res + seq(0, final, length = length(res))
}
res
}
N <- 1024
plot( f(N),
type = "l",
xlab = "time", ylab = "x",
main = "power law random walk, alpha = 2" )
do.it <- function (alpha = 2, N=1024) {
op <- par()
layout(matrix(c(1,2,3, 1,2,4), nc=2))
par(mar=c(2,4,4,2)+.1)
x <- f(N, alpha = alpha)
plot(x,
type="l",
ylab="",
main = paste("Power law random walk, alpha =", alpha))
plot(diff(x), type="l")
par(mar=c(5,4,4,2)+.1)
hist(diff(x),
col = "light blue",
probability = TRUE)
lines(density(diff(x)),
col="red", lwd=3 )
qqnorm(diff(x))
qqline(diff(x), col="red", lwd=3)
par(op)
}
do.it()
do.it(alpha = 1.5)

do.it(alpha = 1)
do.it(alpha = 2.5)

do.it(alpha = 3)
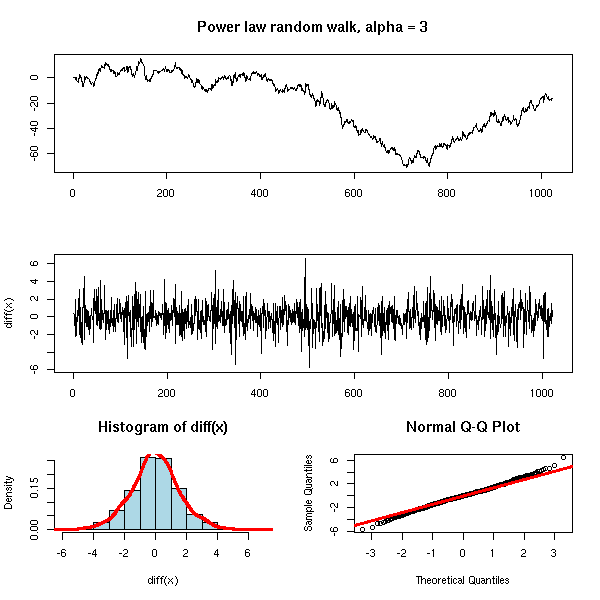
TODO: other plots, to see the exponent...
The spectrum of a random walk is very characteristic.
N <- 10000 x <- cumsum(rnorm(N)) # Random walk y <- spectrum(x)

On a logarithmic scale, it is linear.
plot(y$spec ~ y$freq,
xlab = "Frequency",
ylab = "Spectral density",
log = "xy")
in other words, there exists a real beta such that
spectral density is proportional to 1/frequency^beta
The exponent seems to be around 1.8.
N <- 1000
n <- 100
res <- rep(NA, n)
for (i in 1:n) {
x <- cumsum(rnorm(N))
y <- spectrum(x, plot = FALSE)
res[i] <- lm( log(y$spec) ~ log(y$freq) )$coef[2]
}
summary(res)
hist(res, col="light blue",
main = "Exponent of the spectral density decay")
TODO: Isn't it supposed to be 2?
TODO: More details
Noises are often classified from the decay of their spectral density:
white noise 1 pink noise 1/f brown noise (random walk) 1/f^2 black noise 1/f^p with p > 2
We can do the same thing with the AutoCorrelation Function (ACF)
N <- 10000 x <- cumsum(rnorm(N)) + rnorm(N) y <- acf(x, lag.max=N/4)

TODO...
I seem to recall that: ACF(k) is proportional to 1/k^alpha
TODO...
I seem to recall that:
the spectral density is proportional to 1/f^beta ACF(k) is proportional to 1/k^alpha E[ R/S ] is proportional to n^H (n = sample size) H = (beta - 1) / 2 = 1 - alpha / 2 H = 0.5 random H > 0.5 long-term memory H < 0.5 mean reversion I am confused: is this valid for something resembling a random walk (e.g., stock prices), or its first difference (the returns)???
Implementation:
RS <- function (x) {
diff( range( cumsum( x - mean(x)))) / sd(x)
}
hurst <- function (x) {
stopifnot( is.vector(x) )
stopifnot( is.numeric(x) )
stopifnot( length(x) >= 16 )
n <- length(x)
N <- floor( log(n/8) / log(2) ) # Number of subdivisions
size <- rep(NA, length=N)
rs <- rep(NA, length=N)
for (k in 1:N) {
l <- floor( n / 2^k ) # Subdivision length
start <- seq(1, n-l, by=floor(l/2))
y <- rep(NA, length=length(start))
for (i in seq(along=start)) {
y[i] <- RS( x[ start[i] : (start[i] + l) ] )
}
size[k] <- l
rs[k] <- mean(y)
}
size <- log(size)
rs <- log(rs)
lm(rs ~ size) $ coef [2]
}
N <- 200
n <- 100
res <- rep(NA, n)
for (i in 1:n) {
res[i] <- hurst(rnorm(N))
}
hist(res, col="light blue",
main="Hurst exponent of an iid gaussian")
%--
TODO
Look how stable its estimation is (very unstable?)
No, not that bad.
TODO: Design other examples: long-term memory, mean
reversion.
TODO: Try this with financial data (daily, weekly, monthly
returns)
TODO
TODO ( Mean abs( x(t+T) - x(t) )^q )^(1/q) ~ T ^ H_q Persistence probability (cf survival analysis): P(T) = P[ x(t) \not \in range( x(t+1), ..., x(t+T) ) ] Persistence exponent: P(T) ~ T ^ -theta
LAG <- function (x, k = 1) {
stopifnot( is.vector(x) )
n <- length(x)
stopifnot( abs(k) < n )
if (k > 0) {
x <- c( x[ -(1:k) ], rep(NA, k) )
} else if ( k < 0 ) {
k <- -k
x <- c(rep(NA,k), x[ 1:(k-n) ])
}
x
}
x <- as.vector(sunspots)
# Delay plots
op <- par(mfrow=c(3,3))
for (k in 1:9) {
plot( LAG(x, k), x )
}
par(op)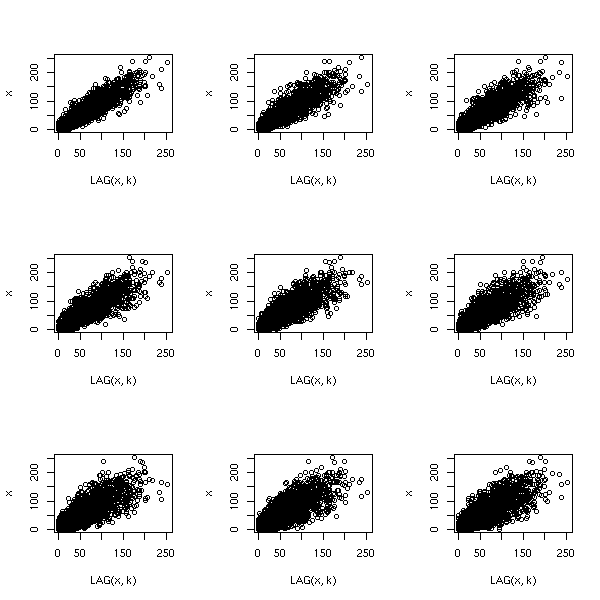
# Principal Components plots
N <- 20
d <- x
for (k in 1:N) {
d <- cbind(d, LAG(x,k))
}
d <- d[ 1:(dim(d)[1]-N), ]
r <- prcomp(d)
plot(r$x[,1:2])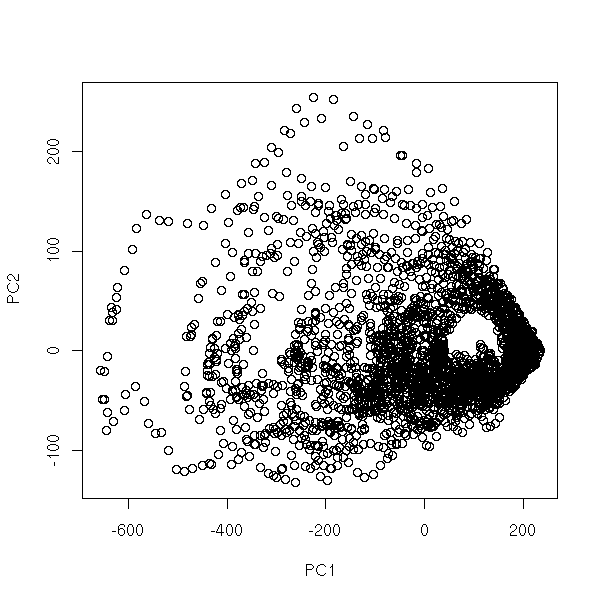
pairs(r$x[,1:4])
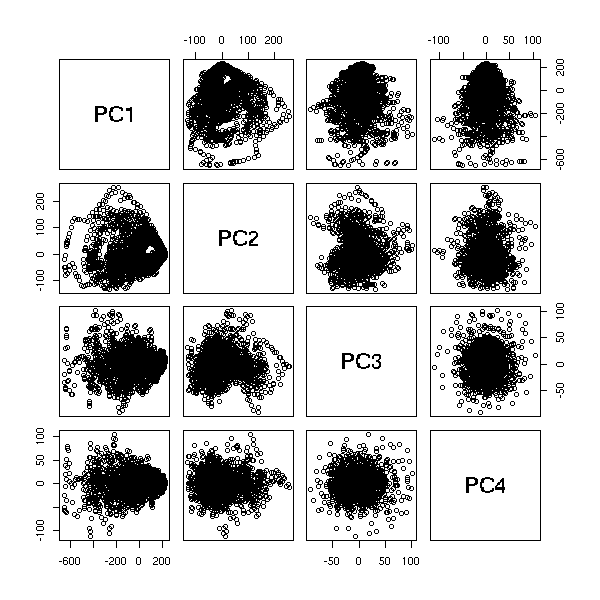
op <- par(mfrow=c(3,3))
for (i in 1 + 1:9) {
plot(r$x[,c(1,k)])
}
par(op)
# Recurrence plot
r <- outer(x, x, "-")
image(r)
image( abs(r) )
# Space-time separation plot
s <- tapply( as.vector(abs(r)),
as.vector(abs(row(r) - col(r))),
quantile, seq(.1, .9, by=.1)
)
s <- t(do.call(cbind, s))
matplot(s, type="l", lty=1,
xlab="time distance", ylab="signal distance",
main="Space-time separation plot")
# TODO: variants (moving quantiles, quantile regression)
The recurrence plot of a time series plots the distance between x(t1) and x(t2) as a function of t1 and t2.
recurrence_plot <- function (x, ...) {
image(outer(x, x, function (a, b) abs(a-b)), ...)
box()
}
N <- 500
recurrence_plot( sin(seq(0, 10*pi, length=N)),
main = "Recurrence plot: sine")
recurrence_plot( rnorm(100),
main = "Recurrence plot: noise" )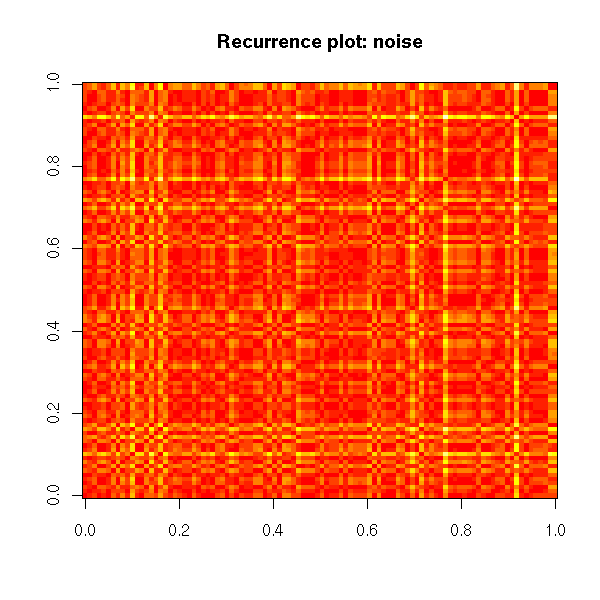
recurrence_plot( cumsum(rnorm(200)),
main = "Recurrence plot: random walk")
library(tseriesChaos)
recurrence_plot(lorenz.ts[100:200],
main = "Recurrence plot: Lorentz attractor")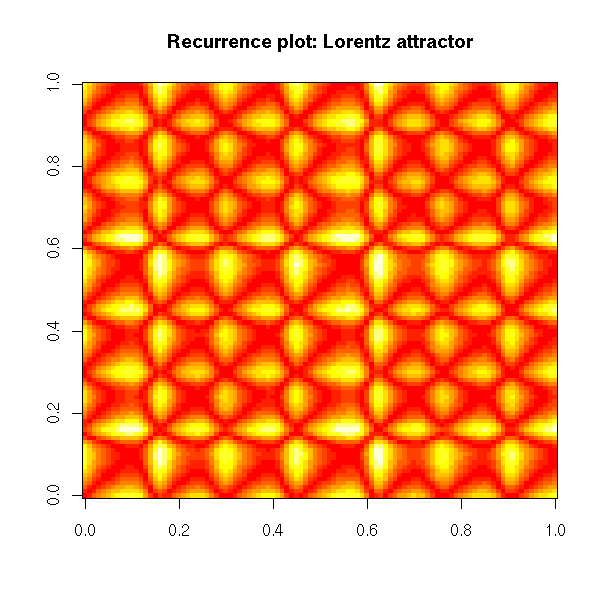
# Thresholded recurrence plot
thresholded_recurrence_plot <- function (
x,
threshold = 0,
FUN = function (x) x,
...
) {
image(-outer(
x, x,
function (a, b)
ifelse(FUN(a-b)>threshold,1,0)
),
...)
box()
}
thresholded_recurrence_plot(
lorenz.ts[1:100],
0,
main = "Thresholded recurrence plot"
)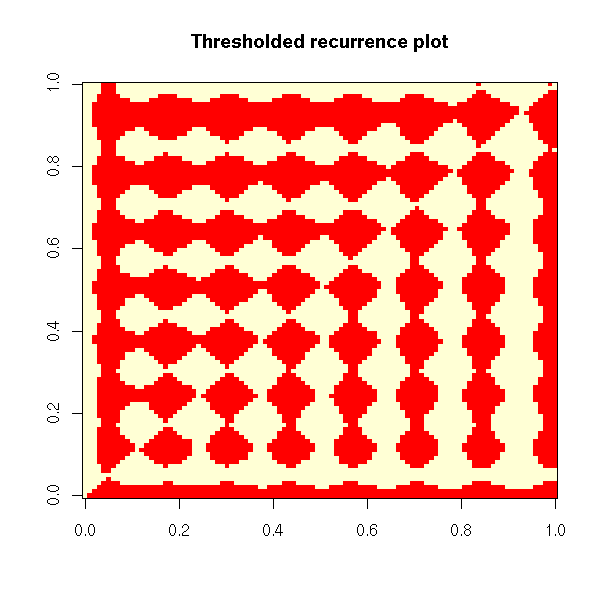
thresholded_recurrence_plot( lorenz.ts[1:100], 5, abs, main = "Thresholded recurrence plot" )

This is the "1-dimensional recurrence plot": instead of taking the distance between x(t1) and x(t2), one can compute the distance between the m-dimensional vectors (x(t1),x(t1+1),...,x(t1+m-1)) and (x(t2),x(t2+1),...,x(t2+m-1)).
# Recurrence plot
recurrence_plot <- function (x, m, ...) {
stopifnot (m >= 1, m == floor(m))
res <- outer(x, x, function (a,b) (a-b)^2)
i <- 2
LAG <- function (x, lag) {
stopifnot(lag > 0)
if (lag >= length(x)) {
rep(NA, length(x))
} else {
c(rep(NA, lag), x[1:(length(x)-lag)])
}
}
while (i <= m) {
res <- res + outer(LAG(x,i-1), LAG(x,i-1), function (a,b) (a-b)^2)
i <- i + 1
}
res <- sqrt(res)
if (m>1) {
res <- res[ - (1:(m-1)), ] [ , - (1:(m-1)) ]
}
image(res, ...)
box()
}
library(tseriesChaos)
recurrence_plot(lorenz.ts[1:200], m=1,
main = "1-dimensional recurrence plot")
recurrence_plot(lorenz.ts[1:200], m=2)
recurrence_plot(lorenz.ts[1:200], m=10)
# A more complete function
recurrence_plot <- function (
x,
m=1, # Dimension of the embedding
t=1, # Lag used to define this embedding
epsilon=NULL, # If non-NULL, threshold
box=TRUE, ...
) {
stopifnot( length(m) == 1, m >= 1, m == floor(m),
length(t) == 1, t >= 1, t == floor(t),
is.null(epsilon) || (
length(epsilon) == 1 && epsilon > 0 ) )
stopifnot( length(x) > m * t )
res <- outer(x, x, function (a,b) (a-b)^2)
i <- 2
LAG <- function (x, lag) {
stopifnot(lag > 0)
if (lag >= length(x)) {
rep(NA, length(x))
} else {
c(rep(NA, lag), x[1:(length(x)-lag)])
}
}
while (i <= m) {
y <- LAG(x,t*(i-1))
res <- res + outer(y, y, function (a,b) (a-b)^2)
i <- i + 1
}
res <- sqrt(res)
if (!is.null(epsilon)) {
res <- res > epsilon
}
if (m>1) {
# TODO: Check this...
res <- res[ - (1:(t*(m-1))), ] [ , - (1:(t*(m-1))) ]
}
image(res, ...)
if (box) {
box()
}
}
library(tseriesChaos)
recurrence_plot(lorenz.ts[1:200], m=10)
title("Recurrence plot")
op <- par(mfrow=c(5,5), mar=c(0,0,0,0), oma=c(0,0,2,0))
for (i in 1:5) {
for (j in 1:5) {
recurrence_plot(lorenz.ts[1:200], m=i, t=j,
axes=FALSE)
}
}
par(op)
mtext("Recurrence plots", line=3, font=2, cex=1.2)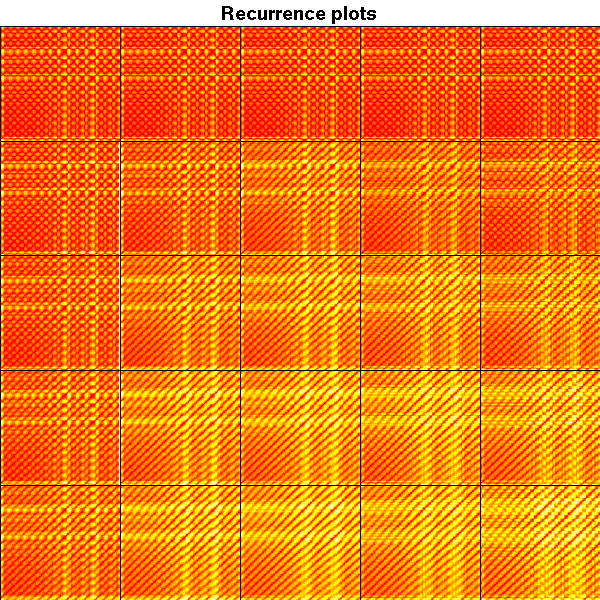
For more about recurrence plots, check
http://www.recurrence-plot.tk/
The phase plane plot of a time series (or, more generally, a dynamical system) is the plot of dx/dt versus x. If you use the time to select the colour of the points, this can highlight a regime change.
phase_plane_plot <- function (
x,
col=rainbow(length(x)-1),
xlab = "x", ylab = "dx/dt",
...) {
plot( x[-1], diff(x), col = col,
xlab = xlab, ylab = ylab, ... )
}
phase_plane_plot( sin(seq(0, 20*pi, length=200)), pch=16 )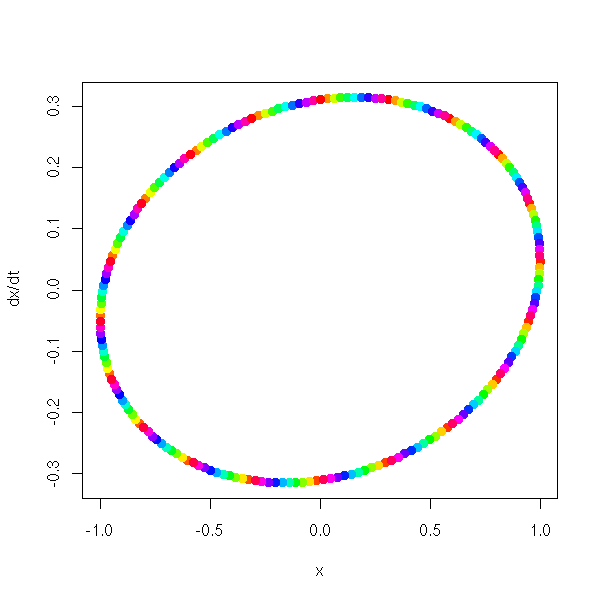
x <- c(sin(seq(0, 5*pi, length=500)),
sin(seq(0, 5*pi, length=1000)) + .2*rnorm(1000),
sin(seq(0, 2*pi, length=500)^2))
phase_plane_plot(x)
library(tseriesChaos)
phase_plane_plot(lorenz.ts, pch=16,
main = "Phase plot")
phase_plane_plot(lorenz.ts, type="l",
main = "Phase plot")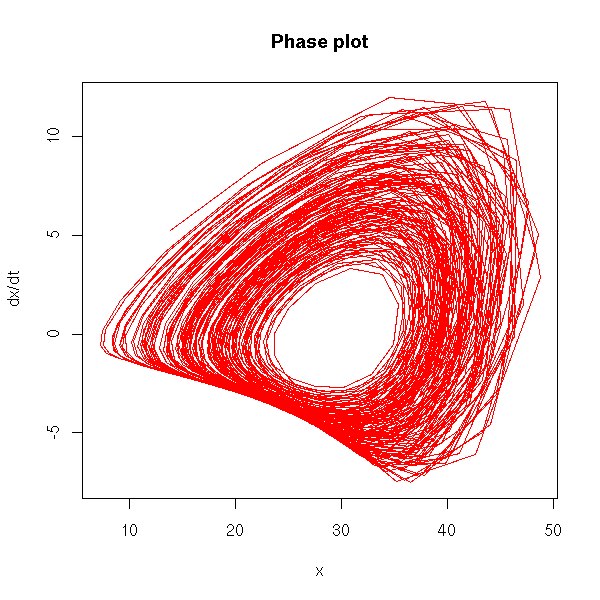
After turning a time series into a function, one can also look into Poincare sections.
http://mathworld.wolfram.com/SurfaceofSection.html http://www.maplesoft.com/applications/app_center_view.aspx?AID=5&CID=1&SCID=3 http://images.google.co.uk/images?q=poincare%20section
Phase space analysis, correlation dimension
number of i<j s.t. abs(xi-xj)<r
C(r) = -------------------------------
nomber of i<j (i.e., n(n-1))
in dimension d, C(r) sis proportional to r^d
We get the dimension of the attractor.
But the noise may be troublesome.
You may wish to zoom on part of the data, to highlight features hidden in a dense cloud of points. Traditional zooming would only display a portion of the data, without any deformation, but you can devise transformations that zoom in on part of the image and out on the rest. In the following example, some text is hidden in the cloud of points: will you be able to read it?
library(pixmap)
z <- read.pnm("2006-08-27_Hello.pgm") # Created (by hand) with The Gimp
z <- z@grey
d <- cbind(
x = col(z)[ ! z ],
y = -row(z)[ ! z ]
)
N <- 10000
d <- d[sample(1:nrow(d), N, replace = TRUE),]
d <- d + rnorm(2*N)
#plot(d)
d <- apply(d, 2, scale)
explode <- function (
d,
FUN = function (x) { rank(x, na.last="keep") / length(x) }
) {
# Convert to polar coordinates
d <- data.frame(
rho = sqrt(d[,1]^2 + d[,2]^2),
theta = atan2(d[,2], d[,1])
)
d$rho <- FUN(d$rho)
# Convert back to cartesian coordinates
d <- cbind(
x = d$rho * cos(d$theta),
y = d$rho * sin(d$theta)
)
d
}
#plot(explode(d))
d <- explode(d, FUN = function (x) x^4)
d <- apply(d, 2, function (x) (x - min(x))/diff(range(x)))
d <- rbind(d, matrix(rnorm(2*N), nc=2))
# Exercice: Find the word in the following cloud of points...
op <- par(mfrow=c(2,2), mar=c(.1,.1,.1,.1))
plot(d, axes = FALSE)
box()
plot( rank(d[,1]), rank(d[,2]), axes = FALSE )
box()
plot(explode(d), axes = FALSE)
box()
plot(explode(d, atan), axes = FALSE)
box()
par(op)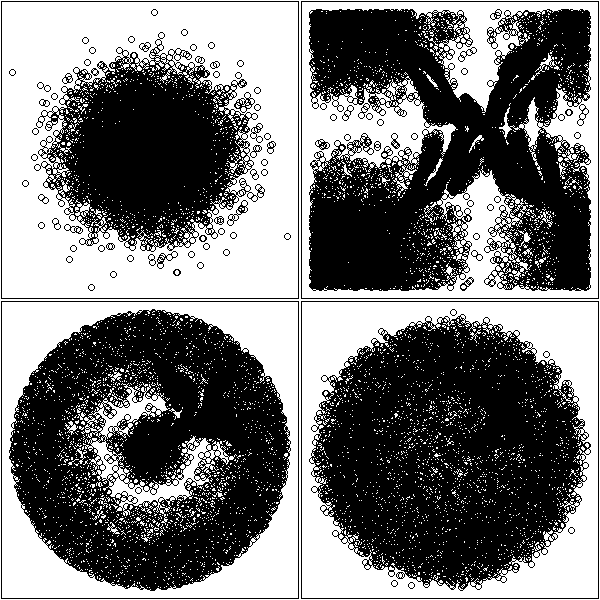
This also works with a single dimension.
one_dimensional_fish_eye <- function (x1, x2, y, method="natural") {
n <- length(y)
x <- seq(min(x1), max(x1), length=n)
x3 <- splinefun(x1, x2, method = method)(x)
if (! all(x3 == sort(x3))) {
warning("Non monotonic transformation!")
}
d <- cbind(x=x3, y=y)
op1 <- par(mar=c(.1,.1,.1,.1))
plot(d, type="l", lwd=3, axes = FALSE)
box()
abline(v=d[seq(0,length(y),by=ceiling(length(y)/50)),1])
op2 <- par(fig=c(.02,.2,.8,.98), mar=c(0,0,0,0), new=TRUE)
plot(x, x3, type = "l", lwd = 3, axes = FALSE)
polygon(rep(par("usr")[1:2], 2)[c(1,2,4,3)],
rep(par("usr")[3:4], each=2),
border = NA, col = "white")
lines(x, x3, type = "l", lwd = 3, col="blue")
box(lwd=3, col="blue")
par(op2)
par(op1)
}
library(Ecdat) # Some econometric data
data(DM)
y <- DM$s
# More details in the middle
one_dimensional_fish_eye(
seq(0, 1, length = 4),
c(0, .2, .8, 1),
y
)
# More details on the left one_dimensional_fish_eye( c(0, .33, .67, 1), c(0, .6, .9, 1), y )
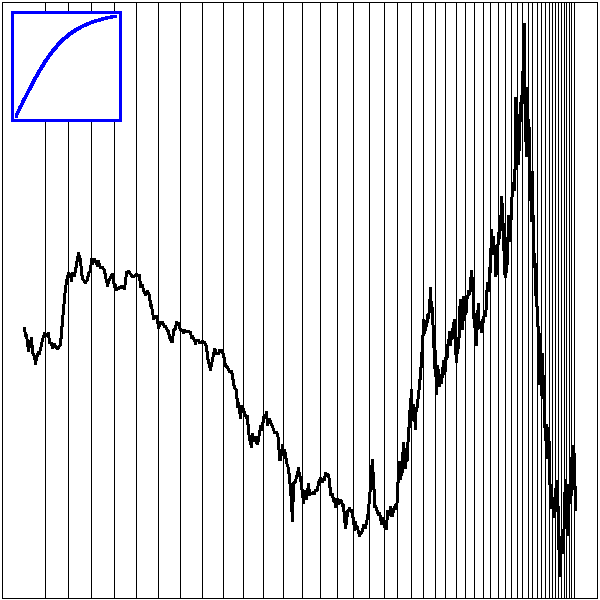
# More details on the right one_dimensional_fish_eye( seq(0, 1, length=4), c(0, .1, .4, 1), y )

TODO
When plotting time series, the time variable given by the actual, clock-on-the-wall time is not always the best way of viewing your data. If the phenomenon studied goes faster at some times of the day and slower at others, a time distortion according to this pace might be helpful. This is the case with financial data: we can plot intraday prices with respect to clock time or market time (defined, e.g., with the number of transactions or the cumulated volume of those transactions).
two_time_scales <- function (x1, x2, y) {
stopifnot( length(x1) == length(y),
length(x2) == length(y),
x1 == sort(x1),
x2 == sort(x2) )
op <- par(mfrow=c(2,1))
plot(x1, y, type="l", xlab="", axes=FALSE)
box()
axis(2, lwd=2)
mtext(side=1, "x1", line=2.5, col="blue", font=2)
mtext(side=3, "x2", line=2.5, col="red", font=2)
x2lab <- pretty(x2, 10)
axis(1, col="blue", lwd=2)
axis(3, at = approx(x2, x1, x2lab)$y, labels=x2lab,
col="red", lwd=2)
plot(x2, y, type="l", axes=FALSE,
xlab="")
box()
mtext(side=1, "x1", line=2.5, col="blue", font=2)
mtext(side=3, "x2", line=2.5, col="red", font=2)
x1lab <- pretty(x1, 10)
axis(1, at = approx(x1,x2,x1lab)$y, labels=x1lab,
col="blue", lwd=2)
axis(2, lwd=2)
axis(3, col="red", lwd=2)
par(op)
}
N <- 100
x1 <- seq(0, 2, length=N)
x2 <- x1^2
y <- x2
two_time_scales(x1,x2,y)
x <- read.csv(gzfile("2006-08-27_tick_data.csv.gz"))
op <- par(mfrow=c(3,1))
x$DateTime <- as.POSIXct(paste(as.character(x$Date),
as.character(x$Time)))
x <- x[!is.na(x$TradePrice),]
plot(TradePrice ~ DateTime,
data = x,
type = "l",
xlab = "Clock time",
main = "Is time a good choice for the X axis?")
plot(x$TradePrice,
type = "l",
ylab = "TradePrice",
xlab = "Transaction time")
coalesce <- function (x,y) ifelse(!is.na(x),x,y)
plot(cumsum(coalesce(x$TradeSize,0)),
x$TradePrice,
type = "l",
xlab = "Volume time",
ylab = "TradePrice")
par(op)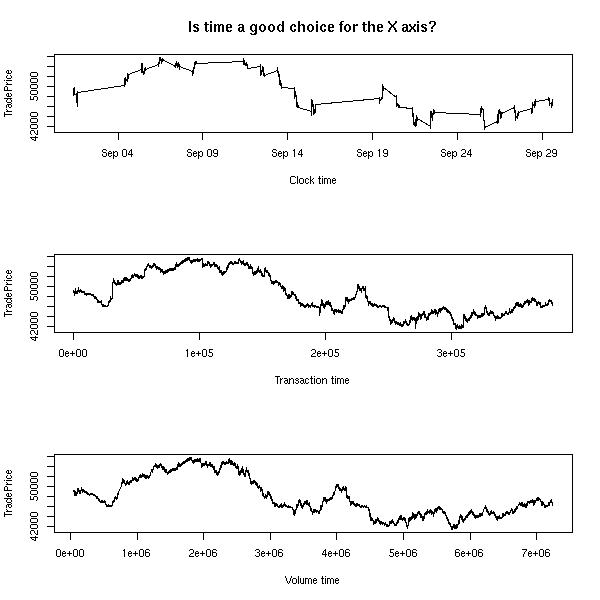
two_time_scales( cumsum(coalesce(x$TradeSize,0)), as.numeric(x$DateTime - x$DateTime[1]) / 3600, x$TradePrice )

This is especially useful when comparing two time series that should follow the same pattern, but one goes faster than the other or there is a (varying) delay between the two (this idea emerged in speech recognition problems). "Dynamic Time Warping" (DTW) refers to the algorithms used to automatically map the time of one time series to that of the other -- they were initially used in spech recognition.
http://www.cs.ucr.edu/~eamonn/
The following example is similar, but the second time is derived from the data: we want the absolute value of the slope of the curve (i.e., the amplitude of the variations) to be always the same.
data_driven_time_warp <- function (y) {
cbind(
x = cumsum(c(0, abs(diff(y)))),
y = y
)
}
library(Ecdat) # Some econometric data
data(DM)
y <- DM$s
i <- seq(1,length(y),by=10)
op <- par(mfrow=c(2,1), mar=c(.1,.1,.1,.1))
plot(y, type="l", axes = FALSE)
abline(v=i, col="grey")
lines(y, lwd=3)
box()
d <- data_driven_time_warp(y)
plot(d, type="l", axes=FALSE)
abline(v=d[i,1], col="grey")
lines(d, lwd=3)
box()
par(op)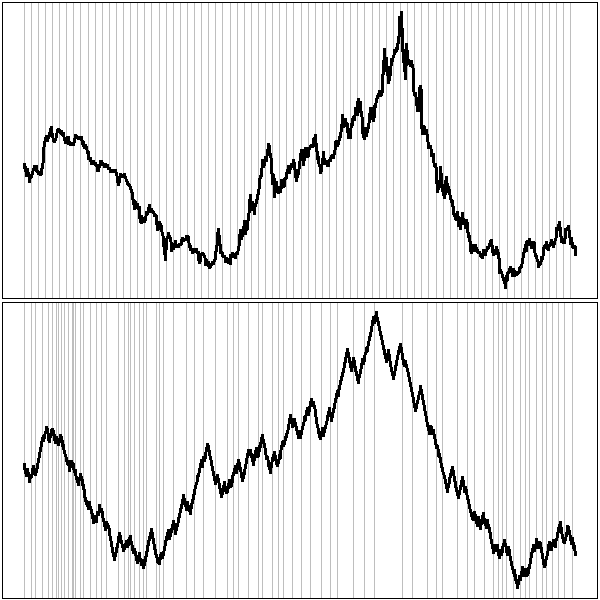
TODO
Markov chains are very similar to AR(n) processes, but they have discrete values.
TODO (The spider example) (already there, see below, put it here...)
Quite often, the vector of probabilities at time t stabilizes when t increases and does not depend on the starting vector.
TODO: example
Actually, the stationnary distribution is not always unique. For instance, if you can partition the states into two sets and if it is impossible to go from one to the other: you will get a stationnary distribution for each of those sets.
TODO: Examples (plot)
In the transition matrix, it means that we can change the ordering of the states so that it be block diagonal.
TODO: Example of such a matrix. Give an example in which we have to reorder the states.
A Markov chain is said to be irreducible if, given any two states a and b, it is always possible to go from a to b, potentially in several steps.
A return time to a state e is an integer t such that
P( X(t)=e | X(0)=e ).
A Markov chain is aperiodic if, for any state, the gcd of its return times equals 1.
For instance, if we can partition the states into two classes and, if the transitions always go from one class to the other (i.e., the Markov chain has the structure of a bipartite graph), the return times are always even: such a Markov chain is not aperiodic.
If a Markov chain is irreducible and aperiodic, then it has a unique stationnary distribution and we can use this Markov chain to integrate with respect to this distribution.
1/N * Sum( f(X_n), n=1..N ) ---> Integral( f * p )
TODO: understand
A Markov chain with transition matrix P and stationnary distribution p is reversible if
P(y|x)p(x) = P(x|y)p(y)
A Markov chain is a sequence of random variables Xn such that
P[ X(n+1)=a | X(n)=b ]
is independant of n. This property is often refered to as "short memory": if X(n+1) is a decision taken on day n+1, it only depends on what happened the previous day, not what happened before.
Let us imagine, for instance, a spider wandering on the edges of a tetrahedron, strolling from vertex to another. Let us call the vertices 1, 2, 3, 4, X(n) the location of the spider after n time units. If the spider selects the next vertex at random, we have:
P[ X(n+1) = a | X(n) = a ] = 0 P[ X(n+1) = a | X(n) = b ] = 1/3, if a <> b,
i.e., the probability that it stays on the same vertex is zero and the probability it goes to one of the three other vertices is 1/3 (for each vertex).
Such a Markov chain is often represented by a transition matrix: the columns correspond to X(n), the rows to X(n+1) and the matrix coefficients are the transition probabilities.
0 1/3 1/3 1/3 1/3 0 1/3 1/3 1/3 1/3 0 1/3 1/3 1/3 1/3 0
One can then write
P_n = M^n * P_0
where M is the transition matrix and P_k the vector containing the probability of each state (here, each vertex) at time k.
Let us make the model more interesting by adding flies on some vertices (the smell will attract the spider and entice it to stay there) or glue (when it reaches such a vertex, the spider will be stuck).
0 1/4 1/6 0
1/4 0 1/6 0
(fly) 1/2 1/2 1/2 0
(glue) 1/4 1/4 1/6 1A Markov chain can also be represented as an oriented graph: the vertices are the states (in our example, these are the vertices of the tetrahedron) and the edges are the transitions (in our example, two for each edge of the tetrahedron: one in each direction); on each edge, write the transtion probability.
TODO: plot... (using Rgraphviz?)
Exercice: simulate the path of the spider, either with a computer, or with dice. Compare those paths: in what proportion of the paths does the spider eat the fly? What is the life expectancy of the spider (before it gest glued)?
TODO: Perform this simulation...
You may notice that Markov chains are very similar to finite automata: the main difference between a Markov chain and a probabilistic finite automaton is that in the latter, the labels are on the transitions, not on the states.
Markov chain example: the extinction of smokers
Smokers' children have 60% "chances" of smoking while non-smokers' children only have 20% chances of smoking. Given that half the population currently smokes (when I wrote this, I was still living in France), can we expect that smokers will eventually disappear?
This situation can be modelled by a 2-state Markov chain, the states being "smoker" and "non-smoker" and the transitions corresponding to generation renewal (to simplify things, we assume that each individual has exactly one child). The probability vector P_k is then the proportion of smokers and non-smokers in generation k.
Exercise: write the transition matrix; compute P_100; what is the limit? Do smokers eventually dwindle and disappear?
Remark: this is very similar to the evolution of an animal population facing a predator, described by a (system of) differential equation(s): Markov chains are a discrete analogue of some evolution models.
TODO: Picture? TODO: URL?
Other Markov chain example
From an english text, one can derive transition probabilities from one word to another, e.g.,
P[ "destruction" given that the previous word was "mass" ] = 0.002,
i.e.,
P[ X(n+1) = "destruction" | X(n) = "mass" ] = 0.002
Of course, there are really many of them (if you disregard rare words and limit yourself to 2000 words, you would have 4 million probabilities -- unless your corpus is really huge, many of them would be zero).
Exercise: write a program that computes those probabilities from a set of texts (a corpus). Write another program that uses those probabilities to perform a simulation, i.e., that wrotes a text using that Markov chain. Modify those programs so that they use order 2 Markov chains, i.e., probabilities
P[ X(n+2) | X(n+1), X(n) ].
I think this example is detailed in the book "Programming pearls".
http://netlib.bell-labs.com/cm/cs/pearls/
Remark: if you consider letters (or pairs of letters, forgetting spaces -- these are called 2-grams) instead of words, you can easily and reliably recognize the manguage of a text (using the proportion of letters, regardless of the order, is less reliable).
Similarly, you can design a Markov chain to recognise a family of amino-acid sequences.
# Building a Markov chain
markov <- function (x) {
x <- strsplit(x,'')[[1]]
x <- factor(x)
aa <- strsplit("ACDEFGHIKLMNPSQRTVWY01",'')[[1]]
n <- length(aa)
m <- matrix(0, nr=n, nc=n)
colnames(m) <- aa
rownames(m) <- aa
m["1","1"] <- 1
m["0", x[1]] <- m["0", x[1]] +1
for (i in 1:(length(x)-1)) {
m[ x[i], x[i+1] ] <- m[ x[i], x[i+1] ] +1
}
m[ x[length(x)], "1" ] <- m[ x[length(x)], "1" ] +1
# This is a contingency matrix, we want a probability
# matrix, where the sum of each row is 1
m <- m +.001 # Pas n
m <- m/apply(m,1,sum)
print(round(m, digits=2))
invisible(m)
}
x <-"MAKGVAVLNSSEGVTGTIFFTQEGDGVTTVSGTVSGLKPGLHGFHVHALGDTTNGCMSTGPHFNPDGKTHGAPEDANRHAGDLGNITVGDDGTATFTITDCQIPLTGPNSIVGRAVVVHADPDDLGKGGHELSLATGNAGGRVACGIIGLQG"
m <- markov(x)
image(m)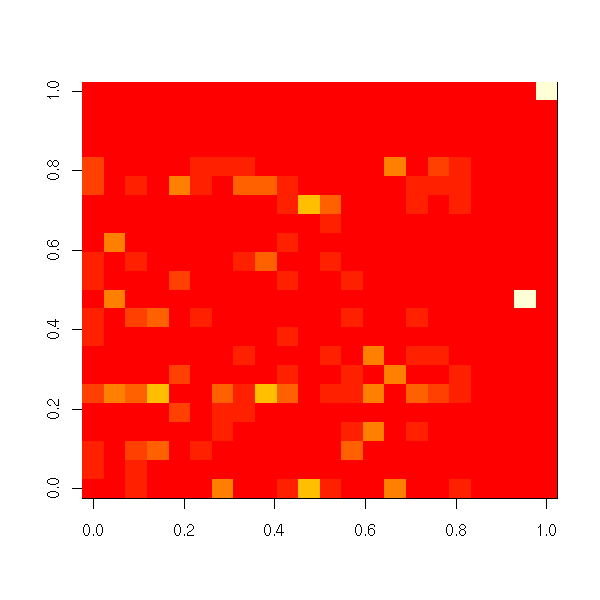
Exercise: use this Markov chain to build new sequences.
If you estimate the parameters (the transition matrix) of a Markov chain naively, by counting the number of occurrences of each transition, this may yield null probabilities: you can avoid them with Laplace pseudocounts
n_a + 1
P(a) = --------------
sum(n_i+1)or with "m-estimators"
n_a + m
P(a) = ----------------
sum(n_i) + m(one then says there are m virtual instances).
Other Markov chain example
(This example is not mine) In the Land of Oz they never have two nice days in a row. If they have a nice day they are just as likely to have snow as rain in the next . If they have snow (or rain) they have an even chance of having the same in the next day. If there is a change from snow or rain, only half of the time is this change to a nice day. You plan to arrive in the Land of Oz on a Monday, but require that it did not rain on Sunday. 1. What is the probability that Monday is a nice day? 2. What is the probability that the next Saturday is a nice day? 3. When you arrive, it is snowing. What is the probability that the next Saturday is a nice day? 4. On Tuesday, you sleep all day, and on Wednesday it is still snowing. What is the probability that the weather was nice when you were sleeping? 5. On a long span of time, what are the proportion of snowy, rainy and nice days? Is this climate description valid right away or should we wait some time for a "steady regime" to kick in?
Markov chains are merely another presentation of the notion of conditional probability, a graphical and algorithmic one.
Exercise: another Markov chain example
TODO: Translation On considere une population diploïde à deux allèles A et a, à generations non recouvrantes. Il y a trois génotypes possibles, b1=AA, b2=Aa et b3=aa. Il y a six types de couples possibles : E1 = AA × AA, E2 = AA × Aa, E3 = Aa × Aa, E4 = Aa × aa, E5 = AA × aa, E6 = aa × aa. Modéliser cette situation par une chaîne de Markov en supposant que les accouplements se font entre frêres et soeurs (i.e., entre enfants issus d'un même couple). (Indication : on pourra choisir les différents types de couples, E1, E2, ..., E6 comme états.) Quelle est la fréquence limite des divers génotypes ?
Hidden Markov chains (or Hidden Markov Models, HMM)
A hidden Markov model (HMM) is a Markov chain whose states have probabilistic labels and whose states are not observed: only the labels are. In other words, the states are hidden, but they emit labels or symbols, that are observed.
Let us come back to our wandering spider example. When it is stuck on the glue vertex, it screams for help with probability 0.8 (and remains silent, frozen by fear, with probability 0.2); when it reaches the fly vertex, it is a scream of joy with probability 0.8 (and a silent feast with probability 0.2); when it is on another vertex, there is a scream of joy with probability 0.1 (it probably dreams of the fly vertex) and a scream for help with probability 0.1 (a nightmare) and remains silent with probability 0.8.
Those probabilities can be represented by a matrix,
silence .8 .8 .2 .2 scream for help .1 .1 0 .8 scream of joy .1 .1 .8 0
Imagine that we do not see the spider but that we can only hear it: from the sound, what can we infer about its path on the tetrahedron?
Here is a summary pf the vocabulary of HMM
tetrahedron transition matrix voicing emission probability matrix spider position states spider sounds symboles, labels
Example: speech recognition. One can design a HMM for each word and, given a sequence of phonemes, one tries to find the closest HMM, i.e., the word that most likely produced this sound. (The HMM is not entirely deterministic because of pronunciation differences between people, regions).
Example: hand writing. The situation is the same as above: one designs a HMM for each character and then, given a scribble, one selects the closest HMM (i.e., letter). This is a real-world example, used by postal services to automatically read postcodes and route mail, or by PDAs, that recognize simplified letters.
TODO: In those examples, explain what the hidden states are.
Example: text analysis (the states are the PoS (parts-of-speech) of the words, the symbols are the words). This can be refined: the states are hidden and have no a priori interpretation; the PoS are classes (or "colours") of states; the symbols are the words -- we do not really want to predict the hidden states, but just the PoS.
Given a set of texts (a corpus) of an author (or of a given genre, or on a give subject), build a HMM describing it. Then, given a new text (e.g., a newly discovered manuscript, whose author is to be identified), check if it is reasonable to claim it is from the same author. This is not only yet another way of fueling the "Did Ben Johnson write Shakespeare's plays?" debate, but also a means of automatically classifying electronic documents, e.g., web pages or research articles.
Example: predicting coding and non-coding parts of a DNA sequence. The HMM has two states (coding, non-coding) and the symbols are the bases.
Algorithms around Markov chains
There are three of them
1. Given a HMM, find the probability of a sequence of symbols: forward algorithm.
This probability can be turned into an "alignment" score between the sequence of symbols and the HMM: if you have several HMMs, this can help choose the "best" (in biology, you can use this to recognize coding and non-coding DNA, CpG islands, protein families, etc.)
2. Find the most probable path (the sequence of states) given a sequence of symbols: Viterbi algorithm.
3. Find the parameters of the Markov chain (transition matrix (transition matrix, emission probability matrix -- we already know the topology of the Markov chain: forward-backward algorithm, aka Baum--Welch algorithm, aka EM algorithm.
Forward algorithm
The problem is the following: we have a hidden Markov chain and a sequence of symbols produced by it (or not). We want to know the probability of this sequence being generated by this HMM.
This can help us choose between several HMMs (for instance, the HMM can describe protein domains, or protein families) -- this probability is sometimes refered to as a score, and the pairing between a sequence and an HMM as an alignment.
If we knew the sequence of states, it would be very easy -- but we only have the symbols.
The idea is to go proceed recursively, by computing the probability of observing the first t symbols given that we reach state e.
As often, to avoid numerical instability, we replace probabilities by their logarithms and products of probabilities by sums of logarithms of probabilities.
# Not tested
# Transition matrix: mt[i,j] is P[i --> j]
mt <- matrix(c( 1/4,1/2,1/4,
1/8,3/4,1/8,
7/10,1/10,1/5),
nr=3, byrow=T)
rownames(mt) <- c('p1','p2','p3')
colnames(mt) <- rownames(mt)
mt
# Emission probability matrix
pe <- matrix(c( 1/4,1/4,1/4,1/4,
1/3,1/6,1/6,1/3,
1/5,3/10,1/4,1/4),
nr=3, byrow=T)
rownames(pe) <- rownames(mt)
colnames(pe) <- c('A','C','G','T')
pe
# Observed symbols
x <- "TTACGGATCGGGTATC"
x <- strsplit(x,'')[[1]]
# Forward algorithm: score of the alignment of an HMM and a sequence
forward <- function (mt,pe,x) {
if(length(x)==1) {
x <- strsplit(x,'')[[1]]
}
k <- length(x)
n <- dim(mt)[1]
m <- matrix(-Inf, nr=n, nc=k)
pe <- log(pe)
mt <- log(mt)
m[,1] <- pe[,x[1]]
for(i in 2:k) {
for (j in 1:n) {
m[j,i] <- sum( m[,i-1] + mt[,j] + pe[j,x[i]] )
}
}
m
}
forward(mt,pe,x)The problem of those scores is that they depend on the length of the sequence. To facilitate comparisons, we con consider the (logarithm of the) likelihood ration:
Probability of observing this sequence with this HMM
log -----------------------------------------------------------
Probability of observing this sequence with a trivial HMMBut there is no single best choice for this "trivial HMM": it can be built from the frequencies of the amino-acids in the species at hand, etc.
Quite often, this is not a real problem, because we actually want to compare two models: we just have to compute the quotient of their likelihoods.
This can be done with the Viterbi algorithm.
TODO: ???
The problem is the following: we know the Markov chain and the sequence of symbols it produced and we want the most probable sequence of states.
The idea is to proceed recursively, computing, for each time t and each state e, the most probable sequence of states producing the first t symbols and reaching state e.
You quickly realize that the problem is not recursive but requires dynamic programming (in pictorial terms: if you draw the graph of function calls required to get the result, they do not form a tree): we will store, in a table, the probability that the first t symbolswere produces by a sequence of states stopping at state e and then, once this table is filled, we just read it in the other direction to find the most probable path.
As usual, to avoid numeric instability, we replace probabilities by their logarithms and we add them instead of multiplying them.
# Not tested
# Transition matrix: mt[i,j] = P[ i --> j ]
mt <- matrix(c( 1/4,1/2,1/4,
1/8,3/4,1/8,
7/10,1/10,1/5),
nr=3, byrow=T)
rownames(mt) <- c('p1','p2','p3')
colnames(mt) <- rownames(mt)
mt
# Emssion probability matrix
pe <- matrix(c( 1/4,1/4,1/4,1/4,
1/3,1/6,1/6,1/3,
1/5,3/10,1/4,1/4),
nr=3, byrow=T)
rownames(pe) <- rownames(mt)
colnames(pe) <- c('A','C','G','T')
pe
# The observed symbols
x <- "TTACGGATCGGGTATC"
x <- strsplit(x,'')[[1]]
viterbi <- function (mt,pe,x) {
if(length(x)==1) {
x <- strsplit(x,'')[[1]]
}
pe <- log(pe)
mt <- log(mt)
n <- dim(mt)[1] # Number of states
k <- length(x) # Length of the sequence of symbols
# Building the dynamic programming matrix
m <- matrix(-Inf, nr=n, nc=k)
m[,1] <- pe[,x[1]]
for (i in 2:k) {
for (j in 1:n) {
m[j,i] <- max(m[,i-1] + mt[,j] + pe[,x[i]])
}
}
rownames(m) <- rownames(mt)
colnames(m) <- x
print(m)
# Reconstructiong the path ("chemin" is French for "path")
chemin <- rep(NA, k)
chemin[k] <- which( m[,k] == max(m[,k]) )[1]
for (i in k:2) {
j <- chemin[i]
chemin[i-1] <- which( m[j,i] == max(m[,i-1] + mt[,j] + pe[,x[i]]) )[1]
}
ch <- rownames(pe)[chemin]
print(ch)
image(t(m))
lines( seq(0,1,length=k), seq(0,1,length=n)[chemin] )
invisible(list(matrice=m, chemin=ch))
}
r <- viterbi(mt,pe,x)See, for instamce:
http://www.comp.leeds.ac.uk/roger/HiddenMarkovModels/html_dev/viterbi_algorithm/s1_pg1.html
Topology of Markov chains
Until now, we always assumed that we knew the topology of the Markov chain -- quite often, a clique: each state was reachable from each stae in a single step. Easy enough, but it does not scale well.
Depending on the nature of sequences studied and on the a priori knowledge of those sequences, people suggested ad hoc topologies.
For instance, to study proteins, one aound have pairong states, insertion states, deletion states (that do not emit any symbol), an initial state and a final state.
TODO: Picture
From a multiple protein alignment (or a PSSM), one can easily obtain the transition and emission probabilities: those Markov chains are just another way of representing a PSSM.
TODO: THe same picture as above, with probabilities, and the corresponding PSSM.
The fact that some of those probabilities can be sero can be a problem: it completely forbids you to recognize a sequence that would differ by a single character. To avoid this, we ask that the probabilities be at least equal to some threshold: this is called Markov vhain regularization.
Learning a hidden Markov model: EM (Expectation-Maximization) algorithm, Forward-Backward algorithm, Baum-Welsh algorithm.
Until now, we assumed that the Markov model was known: we shall now see how one can build it from a set of sequences and a set of states. We need to find the initial probabilities, the transition probabilities and the emission probabilities.
The idea is the following: start with random probabilities, compute the score of the sequences for this HMM, derive better estimations of the probabilities, iterate.
Since this is a local search, we might have a problem with local extrema: we might get stuck with suboptimal that can not be bettered by a small modification of the probabilities, that would need a drastic change...
This algorithm computes a HMM that maximizes the likelihood of the sequences. To increase your chances of finding a global, not local maximum, you can run the algorithm several times, with different initial guesses. Another idea would be to accept slightly suboptimal probabilities at each iteration (the tolerance would decrease with time): this is simulated annealing instead.
Bias
There is another problem: the set of sequences used to teach the HMM might contain very similar sequences, that could lead to a biased HMM. To correct this, one can compute a (rooted) phylogenetic tree on those sequences and assign a weight to each of them (the root has weight 1 and at each branching, the weight is equally divided into the two branches -- this might reming you of Kirchoff's laws, in electricity).
Another means of correcting this bias is to assign a higher weight to the sequences with a bad score -- the weights change at each iteration. This is very similar to "boosting" (the idea is to "stabilize" an estimator by computing it on many bootstrap samples, but, contrary to bagging, the bootstrap samples are not completely random: the mis-classified or mis-predicted observations have a higher probability of being chosen).
There are other ways of correcting this bias, for instance, using weights computed for each column, with lower weights for more frequent amino acids.
TODO: Dirichlet mixtures?
While learning a hidden Markov chain, instead of considering the amino acids one by one, we can group them: some are hydrophilic, some are hydrophobic, etc. Those classes can overlap: a single amino acid can be inseveral classes. We no longer look for the probability transitions from one aminoacid to another, but from one class to another -- aminoacid transition probabilities being a further step.x
This can also be seen as a form of regularization
HMM and multiple alignment
A multiple alignment can be computed as follows: build a HMM that recognizes the sequences at hand (using the "classical" topology mentionned above) and find the most probable path using Viterbi's algorithm.
Beyond HMMs
I do not know anything about what follows.
Hybrids of HMMs and neural nets
dynamic Bayesian nets
factorial HMMs
Boltzmann trees
hidden Markov random fields <-- I know this one
(example: handwritten characters)Secondary ARN structure and stochastic grammars (SCFG)
http://www.cs.tufts.edu/comp/150B/lectures/RNA2DStructureLecture.ppt
The bases of an ARN strand tend to pair, providing it with a 3-dimensional structure.
This can be described by a dotplot of the sequence with itself.
TODO (I have not presented the notion of a dotplot in this document)
You can also write the sequence on a circle and draw a chord for each pair.
TODO: picture
One usually assumes that there are no pseudo-knot, i.e., that the chords of the graphical representation do not cross.
A knot can also be represented as follows.
--------------------
| ------------------ |
|| ---------------- ||
||| -------------- |||
|||| ------------ ||||
||||| ---------- |||||
|||||| -------- ||||||
||||||| ------ |||||||
|||||||| ||||||||
GCGCGCGCATATATGCGCGCGCATATAT
|||||| ||||||
||||| -------- |||||
|||| ---------- ||||
||| ------------ |||
|| -------------- ||
| ---------------- |
------------------Algorithms
This is still dynamic programming (I skip the details).
Ussinov-Jacobson algorithm Zuker algorithm
Stochastic grammars
A language is a set of words (a word is a sequence of letters, a letter is a member of an aggreed on set). For instance "all the English words" or "any sequence of a's and b's", or "all the words made from the letters a and b and starting with aaabab" or "all the words made from the letters a and b and containing aaabab" or "all the words made from the letters a and b and containing as many a's as b's".
A grammar is a set of rules describing a language, of the form
S --> aXaab S --> X X --> aXa X --> b aX --> Xb
Here, the capitals are "non-terminal symbols", the lower case characters are the actual letters: start with the start symbol S, apply a rule, that replaces the symbol by a sequence of letters and symbols, and continue to apply rules until you have no more non-terminal symbols. The language described by this grammar is the set of words that can be obtained in this way.
Rules with the same left-hand side are usually regrouped as follows (the vertical bar reads "or"):
S --> aXaab | X X --> aXa | b aX --> Xb
Here is an example of a complete derivation of a word:
Rule Result ---------------------------------- S --> aXaab aXaab aX --> Xb Xbaab X --> aXa aXabaab X --> aXa aaXaabaab aX --> Xb aXbaabaab X --> b abbaabaab
Thus, "abbaabaab" is in the language described by the grammar above.
N. Chomsky (not a computer scientist but a linguist) distinguishes between four classes of grammars.
A grammar is regular (it is sometimes called a "regular expression" or a rational expression" -- you probably have that somewhere in your text processor) if its rules are of the form
W --> a V
or
W --> V a
where V and W are non-terminal symbols and a is one or several letters.
A regular language can be described by a finite automaton. The main counter-example is the set of well-formed parrenthesis strings -- strings of opening and closing parentheses, where each closing parenthesis corresponds to a previously openned one --, which is not regular.
A Context-Free Grammar (CFG)is a grammar whose rules are of the form
W --> S
where W is a non-terminal symbol and S any sequence of non-terminal symbols and letters. They can be be described by stack automata.
For instance, palindromes form a CFG:
S --> a S a | b S b | aa | bb
On the other hand, the language of copies (e.g., baba) are not context-free.
There are also context-sensitive grammars
a W b --> a S b
and general grammars.
a W b --> S
Stochastic grammars
Grammars are typically used when implementing compilers: they are used to describe programming languages and, given a program, to check if it is valid and to decompose it.
Grammars can also be used in a generative ways: start with the initial symbol, and apply rules at random, until all non-terminal symbols have disappeared. This can be formalized by adding a probability for each rule.
For instance, the grammar
S --> aXaab | X X --> aXa | b | Xb
can be turned into a stochastic grammar:
S --> aXaab with probability 0.7 S --> X with probability 0.3 X --> aXa with probability 0.2 X --> b with probability 0.5 X --> Xb with probability 0.3
Stochastic grammars generalize hidden Markov chains -- Markov chains are the special case of regular grammars.
Stochastic grammar and ARN secondary structure
ARN secondary structure can be described by a grammar:
S --> aS | cS | uS | gS (non-pairing) S --> Sa | Sc | Su | Sg (non-pairing) S --> aSu | uSa | cSg | gSc (pairing) S --> SS (bifurcation)
We then proceed as with hidden Markov models: start with a set of sequences whose structure is known, compute the probabilities in the model; after that learning phase, you can give a new sequence to the stochastic grammar and ask it the most probable path, i.e., the most probable secondary structure.
The learning phase still uses an EM algorithm.
The alignment of the grammar with a sequence can use the Cocke-Younger-Kasami algorithm (CYK algorith).
(As with Markiv chains, one can also focus on a third problem: compute the score of an alignment between a sequence and a stochastic grammar, in order to choose between several grammar the closest to the sequence studied.
http://www.dcs.kcl.ac.uk/teaching/units/csmacmb/DOC/lecture18b.pdf http://www.imb-jena.de/RNA.html http://scor.lbl.gov/index.html http://www.rnabase.org/metaanalysis/
Optimization algorithms
The find the secondary structure of an ARN sequence, one can start with one and try to modify it, step by step, via "elementary moves", with usual optimization algorithms (simulated annealing, genetic algorithms).
http://www.santafe.edu/%7Ewalter/Papers/kinfold.pdf
ARN sequence indexing
Usually, the bases in an ARN sequence are not well preserved, while the secondary structure is. Therefore, when searching in a database of ARN sequences, we do not really want similar sequences, but sequences whose secondary structure is similar.
TODO A Tutorial on Hidden Markov Models and selected applications in speech recognition (L.R. Rabiner) http://www.ece.ucsb.edu/Faculty/Rabiner/ece259/Reprints/tutorial%20on%20hmm%20and%20applications.pdf
TODO
TODO In each state, one can make a decision that leads to different transition probabilities. "Reinforcement learning" is the problem of finding a profitable (wrt some reward awarded to each decision) policy to make these decisions. See: Reinforcement learning, a survey, by Kaelbling, Littman and Moore. http://www.cs.cmu.edu/afs/cs/project/jair/pub/volume4/kaelbling96a.pdf
A Markov chain of order 1 is a time series with discrete values such that
P( X(n+1)=a | X(n)=b )
does not depend on n. The matrix of those probabilities is called the transition matrix. (Higher order Markov chains can be expressed as "vector-valued" Markov chains of order 1.)
TODO: Markov chains: simulation, estimating the transition matrix.
library(help=dse1) library(help=dse2) library(help=VLMC) # Variable-length Markov Chains
Hidden Markov model
(We do not directly observe the states of the Markov
chain, but other states, probabilistically related to
them (by a "confusion matrix"))
Forward algorithm: probability of observing a given
(sequence of) state(s).
Viterbo algorithm: to get an estimation of the hidden
state transitions knowing the observable state
transitions
Forward-backward algorithm: to get an estimation of the
transition matrix, the confusion matrix, and the initial
probability vector
http://www.comp.leeds.ac.uk/roger/HiddenMarkovModels/html_dev/main.html
library(msm) # Multi-state Markov models in continuous time
library(qtl) # Tools for analyzing QTL experiments --
# Analysis of experimental crosses to
# identify genes (called quantitative trait
# loci, QTLs) contributing to variation in
# quantitative traits -- see
# http://www.biostat.jhsph.edu/~kbroman/qtl
Missing values Rnews 2 2 (June 2002) library(fracdiff) Maximum likelihood estimation of the parameters of a fractionally differenced ARIMA(p,d,q) model (Haslett and Raftery, Applied Statistics, 1989).
TODO: Example with two periodic components whose ratio is not rational.
n <- 2000
x <- 1:n
y <- sin(x/10) + cos(pi*x/20) + rnorm(n)
op <- par(mfrow=c(4,1))
plot(ts(y))
acf(y)
pacf(y)
spectrum(y, col=par('fg'))
abline(v=c(1/40,1/20/pi), lty=3)
par(op)
TODO
# AR, MA, ARMA, ARIMA, etc. library(nlme) ?gls
TODO: plot() on all those examples
doit <- function (d) {
name <- deparse(substitute(d))
cat(paste(name,"\n"))
png(filename=paste(name,".png",sep=''), width=600, height=600, pointsize=12, bg="white")
try(plot(d, main=name))
dev.off()
}
source("ALL.R")
find -size 0 -exec rm {} \;
find -name "*.png" -size 444c -exec rm {} \;
(
echo '<html><head><title>R</title></head><body>'
for i in *.png
do
echo '<p>'$i'</p>'
echo '<img src="'$i'"><hr>'
done
echo '</body></html>'
) > all.htmlTODO: Plots are more informative, easier to compare, when the slope of the lines is around 45 degres.
TODO: give an example with a large unreadable plot and a smaller readable plot.
?filter (Exercice: compute Centered Moving Averages with it) help(filter) filter(y,rep(1,12),method="convolution",sides=1)[-(1:11)]
Various libraries:
The "ts" package, for ARIMA models tseries contains other models primarily of interest in economics, and GARCH models (which are better models of stock prices). It also has arma, which is subsumed by arima (and arima0) in R-devel. fracdiff handles fractionally differenced models, a very specialized topic.
(GARCH models variance, i.e., volatility)
Replicated time series
see.ts <- function (name, ma=NULL, ar=NULL, d=0, n=2000) {
order=c(length(ar), d, length(ma))
x <- arima.sim(list(ma=ma, ar=ar, order=order), n)
op <- par(mfrow=c(4,1))
plot(x, main=name)
acf(x)
pacf(x)
spectrum(x, spans=10, col=par('fg'))
par(op)
}
n <- 200
see.ts("MA(1) theta_1=.9", .9)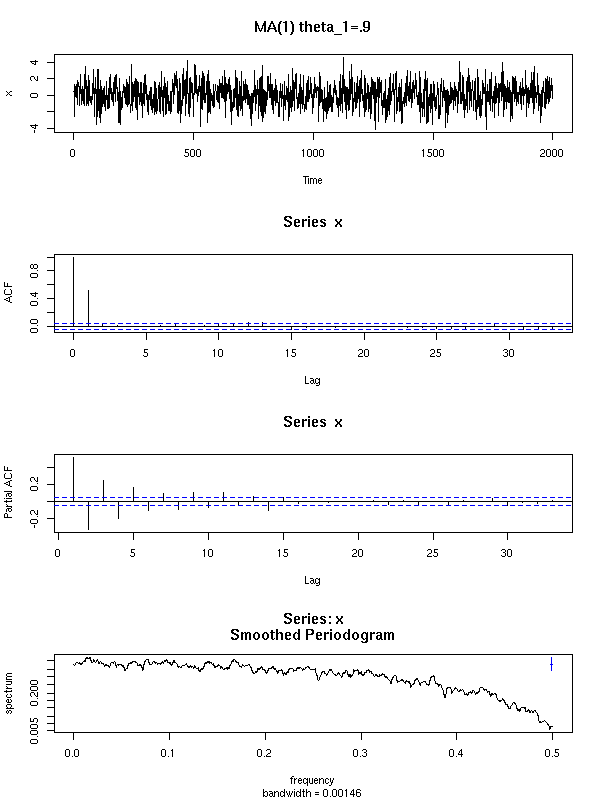
see.ts("MA(1) theta_1=.5", .5)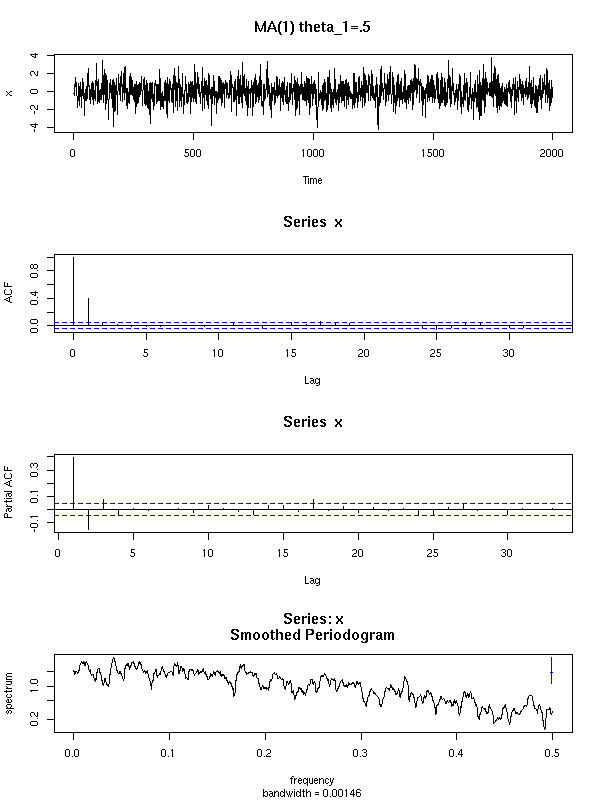
see.ts("MA(1) theta_1=.1", .1)
see.ts("MA(1) theta_1=-.9", -.9)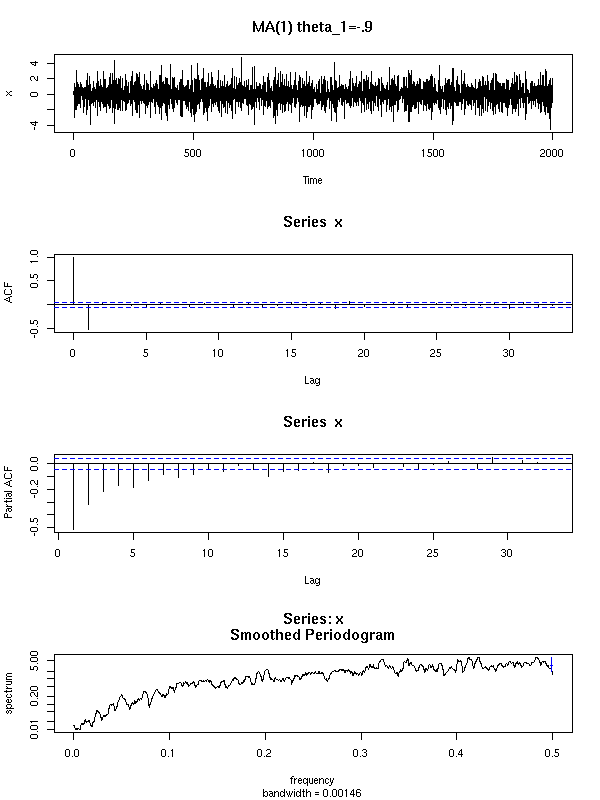
see.ts("AR(1) phi_1=.9", 0, .9)
see.ts("AR(1) phi_1=.8", 0, .9)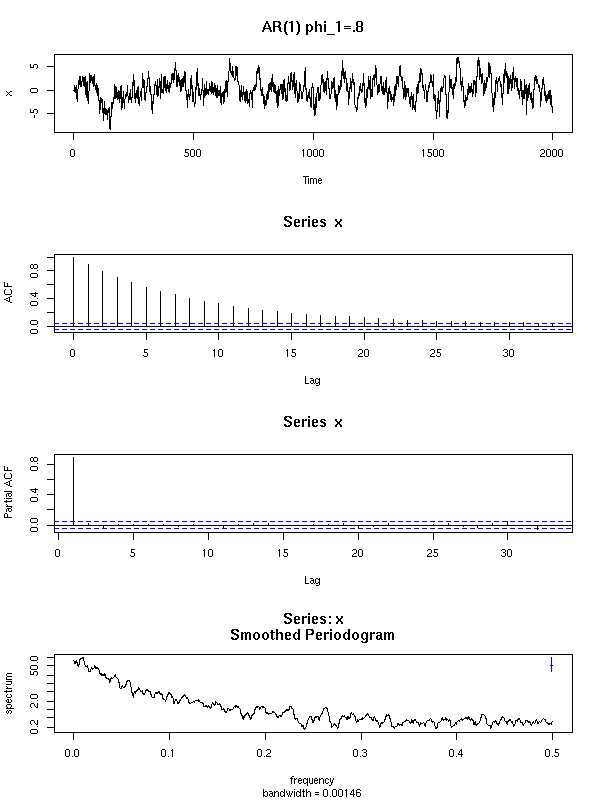
see.ts("AR(1) phi_1=.5", 0, .5)
see.ts("AR(1) phi_1=.1", 0, .1)
see.ts("AR(1) phi_1=-.9", 0, -.9)
see.ts("AR(1) phi_1=-.8", 0, -.8)
see.ts("ARMA(1,1) theta_1=.9 phi_1=.9", .9, .9)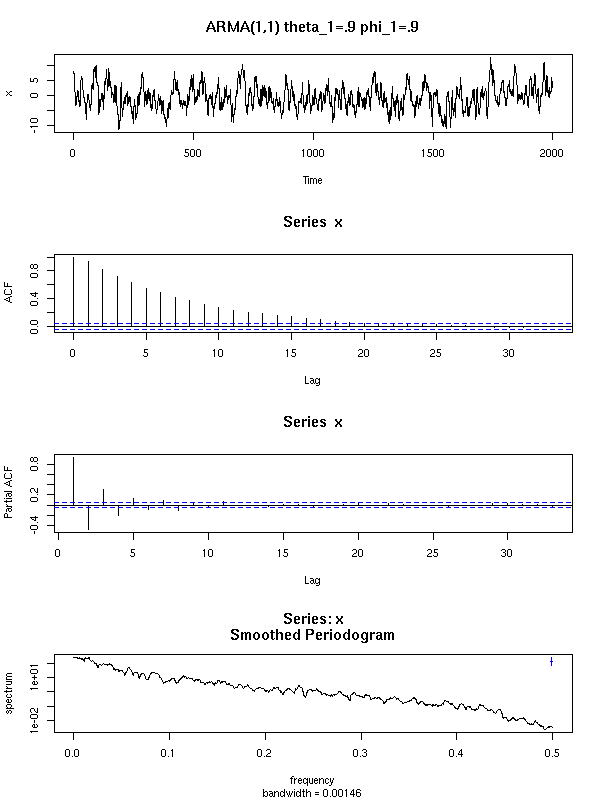
see.ts("ARMA(1,1) theta_1=.9 phi_1=-.9", .9, -.9)
see.ts("ARMA(1,1) theta_1=-.9 phi_1=.9", -.9, .9)
see.ts("ARMA(1,1) theta_1=-.9 phi_1=-.9", -.9, -.9)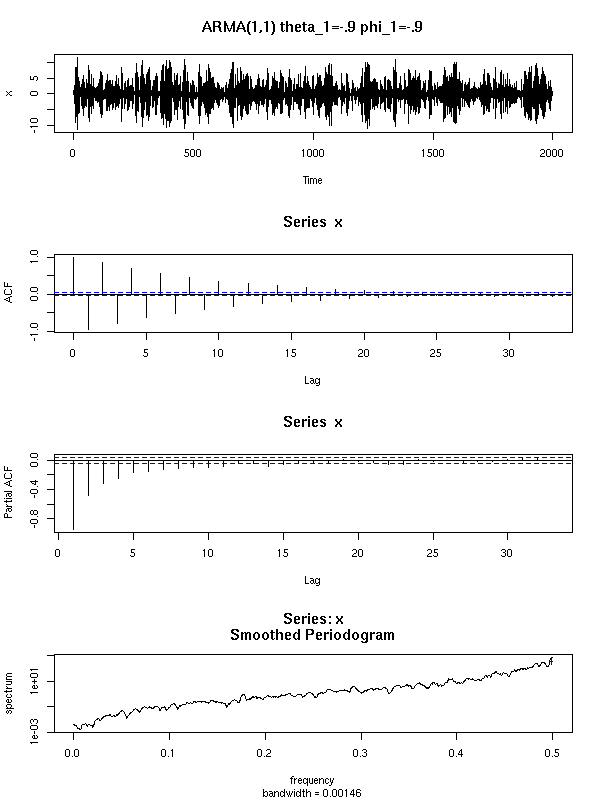
Examples from the manual.
op <- par(mfrow=c(4,1)) data(AirPassengers) plot(AirPassengers) acf(AirPassengers) pacf(AirPassengers) spectrum(AirPassengers); par(op)
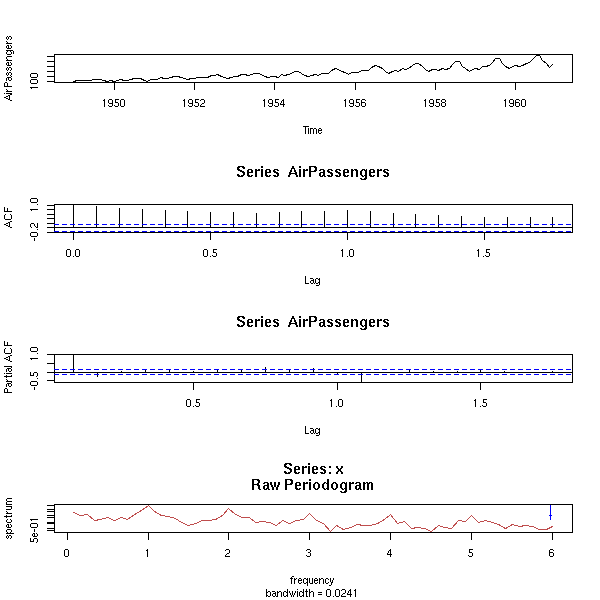
op <- par(mfrow=c(4,1)) data(austres) plot(austres) acf(austres) pacf(austres) spectrum(austres); par(op)
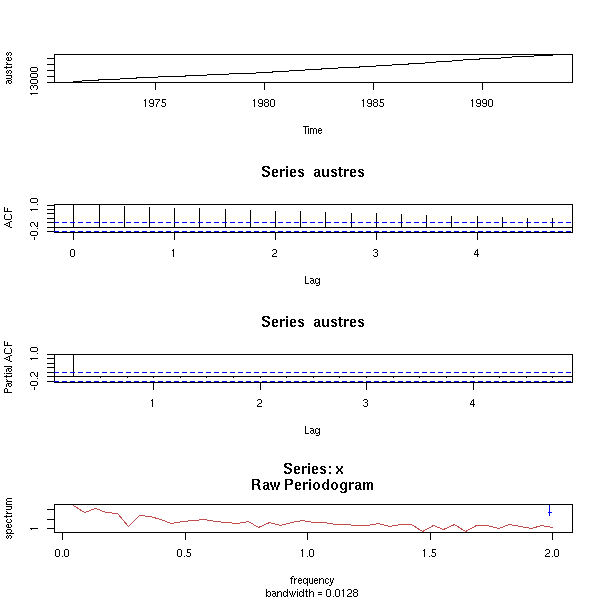
op <- par(mfrow=c(4,1)) data(beavers) plot(ts(beaver1$temp)) acf(beaver1$temp) pacf(beaver1$temp) spectrum(beaver1$temp); par(op)

op <- par(mfrow=c(4,1)) data(BJsales) plot(BJsales) acf(BJsales) pacf(BJsales) spectrum(BJsales); par(op)
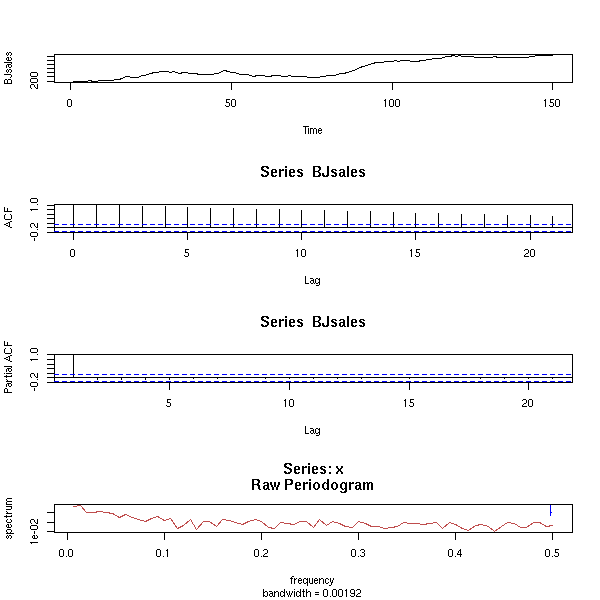
op <- par(mfrow=c(4,1)) data(EuStockMarkets) plot(EuStockMarkets[,1]) acf(EuStockMarkets[,1]) pacf(EuStockMarkets[,1]) spectrum(EuStockMarkets[,1]); par(op)
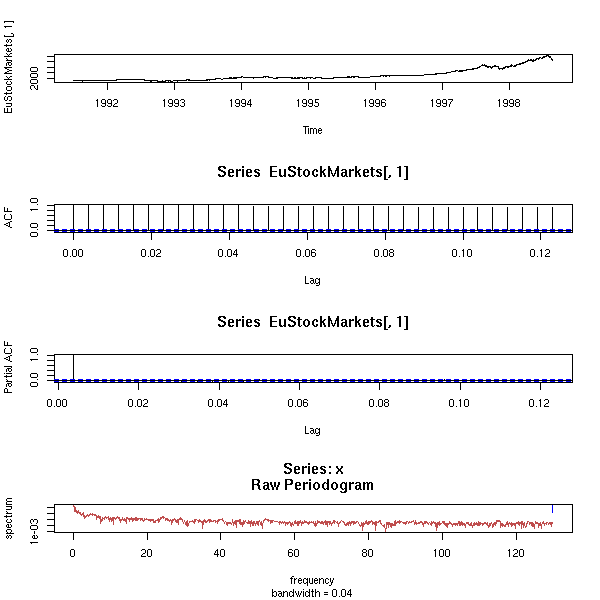
op <- par(mfrow=c(4,1)) data(JohnsonJohnson) plot(JohnsonJohnson) acf(JohnsonJohnson) pacf(JohnsonJohnson) spectrum(JohnsonJohnson); par(op)

op <- par(mfrow=c(4,1)) data(LakeHuron) plot(LakeHuron) acf(LakeHuron) pacf(LakeHuron) spectrum(LakeHuron); par(op)

op <- par(mfrow=c(4,1)) data(lh) plot(lh) acf(lh) pacf(lh) spectrum(lh); par(op)
op <- par(mfrow=c(4,1)) data(lynx) plot(lynx) acf(lynx) pacf(lynx) spectrum(lynx); par(op)

op <- par(mfrow=c(4,1)) data(Nile) plot(Nile) acf(Nile) pacf(Nile) spectrum(Nile); par(op)

op <- par(mfrow=c(4,1)) data(nottem) plot(nottem) acf(nottem) pacf(nottem) spectrum(nottem); par(op)
op <- par(mfrow=c(4,1)) #data(sunspot, package=ts) # Il y en a aussi dans "boot"... data(sunspot) plot(sunspot.month) acf(sunspot.month) pacf(sunspot.month) spectrum(sunspot.month); par(op)

op <- par(mfrow=c(4,1)) data(treering) plot(treering) acf(treering) pacf(treering) spectrum(treering); par(op)
op <- par(mfrow=c(4,1)) data(UKDriverDeaths) plot(UKDriverDeaths) acf(UKDriverDeaths) pacf(UKDriverDeaths) spectrum(UKDriverDeaths); par(op)
op <- par(mfrow=c(4,1)) data(UKLungDeaths) plot(ldeaths) acf(ldeaths) pacf(ldeaths) spectrum(ldeaths); par(op)

op <- par(mfrow=c(4,1)) data(UKgas) plot(UKgas) acf(UKgas) pacf(UKgas) spectrum(UKgas); par(op)

op <- par(mfrow=c(4,1)) data(USAccDeaths) plot(USAccDeaths) acf(USAccDeaths) pacf(USAccDeaths) spectrum(USAccDeaths); par(op)

op <- par(mfrow=c(4,1)) data(WWWusage) plot(WWWusage) acf(WWWusage) pacf(WWWusage) spectrum(WWWusage); par(op)
Nyquist theorem: you should sample you process often enough, otherwise, you will miss the highest frequencies and you may be left with artefacts.
Sampling frequency > 2 * maximum frequency
TODO: plots.
Another way of ploting a time series: y(i+1)~y(i) (plot the segments)
Example: a sine wave
TODO
Example: a sum of two sine waves
TODO
Example: a deterministic time series
x(n+1) = 4 * x(n) * ( 1 - x(n) ) TODO
Examples: AR(1)
TODO
Examples: Something completely random.
TODO
etc.
The attractor above can be written
x(n+1) = f( x(n) )
As we represent the points in a 2-dimensional space, this can be written
x(n+1) = y(n) y(n+1) = f(y(n))
If we set X = (x,y), this becomes
X = f(X).
Thus, we can consider vector-valued time series. In some cases, we have all the coordinates, but in other cases, we think that our process can be described in this way, but we only have a single variable, a single coordinate -- the others were not observed. We have a model with "hidden variables" (or "latent variables").
TODO: put this at the end of this document?
ArDec Auto-regressive decomposition

This work is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 2.5 License.
Vincent Zoonekynd
<zoonek@math.jussieu.fr>
latest modification on Sat Jan 6 10:28:25 GMT 2007