The R language
Data structures
Debugging
Object Oriented Programming: S3 Classes
Object Oriented Programming: S3 Classes
Data storage, Data import, Data export
Packages
Other languages
(Graphical) User Interface
Web interface: Rpad
Web programming: RZope
Web services
Clusters, parallel programming
Miscellaneous
Numerical optimization
Miscellaneous
Dirty Tricks
In this part, after quickly listing the main characteristics of the language, we present the basic data types, how to create them, how to explore them, how to extract pieces of them, how to modify them.
We then jump to more advanced subjects (most of which can -- should? -- be omitted by first-time readers): debugging, profiling, namespaces, objects, interface with other programs, with data bases, with other languages.
Actually, R is a programming language: as such, we have the usual control structures (loops, conditionnals, recursion, etc.)
Conditionnal statements:
if(...) {
...
} else {
...
}Conditionnals may be used inside other constructions.
x <- if(...) 3.14 else 2.71
You can also construct vectors from conditionnal expressions, with the "ifelse" function.
x <- rnorm(100) y <- ifelse(x>0, 1, -1) z <- ifelse(x>0, 1, ifelse(x<0, -1, 0))
Switch (I do not like this command -- this is probably the last time you see it in this document):
x <- letters[floor(1+runif(1,0,4))]
y <- switch(x,
a='Bonjour',
b='Gutten Tag',
c='Hello',
d='Konnichi wa',
)For loop (we loop over the elements of a vector or list):
for (i in 1:10) {
...
if(...) { next }
...
if(...) { break }
...
}While loop:
while(...) {
...
}Repeat loop:
repeat {
...
if(...) { break }
...
}
R belongs to the family of functionnal languages (Lisp, OCaML, but also Python): the notion of function is central. In particular, if you need it, you can write functions that take other functions as argument -- and in case you wonder, yes, you need it.
A function is defined as follows.
f <- function(x) {
x^2 + x + 1
}The return value is the last value computed -- but you can also use the "return" function.
f <- function(x) {
return( x^2 + x + 1 )
}Arguments can have default values.
f <- function(x, y=3) { ... }When you call a function you can use the argument names, without any regard to their order (this is very useful for functions that expect many arguments -- in particular arguments with default values).
f(y=4, x=3.14)
After the arguments, in the definition of a function, you can put three dots represented the arguments that have not been specified and that can passed through another function (very often, the "plot" function).
f <- function(x, ...) {
plot(x, ...)
}But you can also use this to write functions that take an arbitrary number of arguments:
f <- function (...) {
query <- paste(...) # Concatenate all the arguments to form a string
con <- dbConnect(dDriver("SQLite"))
dbGetQuery(con, query)
dbDisconnect(con)
}
f <- function (...) {
l <- list(...) # Put the arguments in a (named) list
for (i in seq(along=l)) {
cat("Argument name:", names(l)[i], "Value:", l[[i]], "\n")
}
}Functions have NO SIDE EFFECTS: all the modifications are local. In particular, you cannot write a function that modifies a global variable. (Well, if you really want, you can: see the "Dirty Tricks" part -- but you should not).
To get the code of a function, you can just type its name -- wit no brackets.
> IQR function (x, na.rm = FALSE) diff(quantile(as.numeric(x), c(0.25, 0.75), na.rm = na.rm, names = FALSE)) <environment: namespace:stats>
But sometimes, it does not work that well: if we want to peer inside the "predict" function that we use for predictions of linear models, we get.
> predict
function (object, ...)
UseMethod("predict")
<environment: namespace:stats>This is a generic function: we can use the same function on different objects (lm for linear regression, glm for Poisson or logistic regression, lme for mixed models, etc.). The actual function called is "predict.Foo" where "Foo" is the class of the object given as a first argument.
> methods("predict")
[1] predict.ar* predict.Arima*
[3] predict.arima0* predict.glm
[5] predict.HoltWinters* predict.lm
[7] predict.loess* predict.mlm
[9] predict.nls* predict.poly
[11] predict.ppr* predict.prcomp*
[13] predict.princomp* predict.smooth.spline*
[15] predict.smooth.spline.fit* predict.StructTS*
Non-visible functions are asteriskedAs we wanted the one for the "lm" object, we just type (I do not include all the code, it would take several pages):
> predict.lm
function (object, newdata, se.fit = FALSE, scale = NULL, df = Inf,
interval = c("none", "confidence", "prediction"), level = 0.95,
type = c("response", "terms"), terms = NULL, na.action = na.pass,
...)
{
tt <- terms(object)
if (missing(newdata) || is.null(newdata)) {
mm <- X <- model.matrix(object)
mmDone <- TRUE
offset <- object$offset
(...)
else if (se.fit)
list(fit = predictor, se.fit = se, df = df, residual.scale = sqrt(res.var))
else predictor
}
<environment: namespace:stats>But if we wanted the "predict.prcomp" function (to add new observations to a principal component analysis), it does not work:
> predict.prcomp Error: Object "predict.prcomp" not found
The problem is that the function is in a given namespace (R functions are stored in "packages" and each function is hidden in a namespace; the functions that a normal user is likely to use directly are exported and visible -- but the others, that are not supposed to be invoked directly by the user are hidden, invisible). We can get it with the "getAnywhere" function (here again, I do not include all the resulting code).
> getAnywhere("predict.prcomp")
A single object matching "predict.prcomp" was found
It was found in the following places
registered S3 method for predict from namespace stats
namespace:stats
with value
function (object, newdata, ...)
{
if (missing(newdata)) {
(...)
}
<environment: namespace:stats>Alternatively, we can use the getS3Method function.
> getS3method("predict", "prcomp")
function (object, newdata, ...)
{
(...)Alternatively, if we know in which package a function (or any object, actually is), we can access it with the "::" operator if it is exported (it can be exported but hidden by another object with the same name) or the ":::" operator if it is not.
> stats::predict.prcomp
Error: 'predict.prcomp' is not an exported object from 'namespace:stats'
> stats:::predict.prcomp
function (object, newdata, ...)
{
(...)
> lm <- 1
> lm
[1] 1
> stats::lm
function (formula, data, subset, weights, na.action, method = "qr",
model = TRUE, x = FALSE, y = FALSE, qr = TRUE, singular.ok = TRUE,
contrasts = NULL, offset, ...)
(...)Things can get even more complicated. The most common reason you want to peer into the code of a function is to extract some information that gets printed when it is run (typically, a p-value when performing a regression). Actually, quite often, this information is not printed when the function is run: the function performs some computations and returns an object, with a certain class (with our example, this would be the "lm" function and the "lm" class) which is then printed, with the "print" function.
> print
function (x, ...)
UseMethod("print")
<environment: namespace:base>As the object belong to the "lm" class:
> print.lm
function (x, digits = max(3, getOption("digits") - 3), ...)
{
cat("\nCall:\n", deparse(x$call), "\n\n", sep = "")
if (length(coef(x))) {
cat("Coefficients:\n")
print.default(format(coef(x), digits = digits), print.gap = 2,
quote = FALSE)
}
else cat("No coefficients\n")
cat("\n")
invisible(x)
}
<environment: namespace:stats>Same for the "summary" function: it takes the result of a function (say, the result of the "lm" function), builds another object (here, of class "summary.lm") on which the "print" function is called.
> class(r)
[1] "lm"
> s <- summary(r)
> class(s)
[1] "summary.lm"
> summary
function (object, ...)
UseMethod("summary")
<environment: namespace:base>
> summary.lm
function (object, correlation = FALSE, symbolic.cor = FALSE, ...)
{
z <- object
p <-
(...)
> print.summary.lm
Error: Object "print.summary.lm" not found
> getAnywhere("print.summary.lm")
A single object matching "print.summary.lm" was found
It was found in the following places
registered S3 method for print from namespace stats
namespace:stats
with value
function (x, digits = max(3, getOption("digits") - 3), symbolic.cor = x$symbolic.cor,
signif.stars = getOption("show.signif.stars"), ...)
{
cat("\nCall:\n")
cat(paste(deparse(x$cal
(...)But it does not always work... There are two object-oriented programming paradigms in R: what we have explained works for the first (old, simple, understandandable) one. Here is an example for the other.
> class(r)
[1] "lmer"
attr(,"package")
[1] "lme4"
> print.lmer
Error: Object "print.lmer" not found
> getAnywhere("print.lmer")
no object named "print.lmer" was foundThe function is no longer called "print" but "show"...
> getMethod("show", "lmer")
Method Definition:
function (object)
show(new("summary.lmer", object, useScale = TRUE, showCorrelation = FALSE))
<environment: namespace:lme4>
Signatures:
object
target "lmer"
defined "lmer"In this case, it simply calls the "summary" function (with arguments that are not the default arguments) and the "show" on the result.
> getMethod("summary", "lmer")
Method Definition:
function (object, ...)
new("summary.lmer", object, useScale = TRUE, showCorrelation = TRUE)
<environment: namespace:lme4>
Signatures:
object
target "lmer"
defined "lmer"
> getMethod("show", "summary.lmer")
Method Definition:
function (object)
{
fcoef <- fixef(object)
useScale <- object@useScale
(...)
invisible(object)
}
<environment: namespace:lme4>
Signatures:
object
target "summary.lmer"
defined "summary.lmer"
Plotting functions are used for their side effect (the plot that appears on the screen), but they can also return a value.
That value can be the result of the computations that lead to the plot. Usually, you do not want the result to be printed, because most users will to see the plot and nothing else, and those who actually want the data, want it for further processing and will store it in a variable. To this end, you can return the value as invisible(): it will not be printed.
f <- function (x, y, N=10, FUN=median, ...) {
x <- cut(x, quantile(x, seq(0,1,length=N)), include.lowest=TRUE)
y <- tapply(y, x, FUN, na.rm=TRUE)
x <- levels(x)
plot(1:length(x), y, ...)
result <- cbind(x=x, y=y)
invisible(result)
}
f(rnorm(100), rnorm(100),
type="o", pch=15, xlab="x fractiles", ylab="y median", las=1)
res <- f(rnorm(100), rnorm(100),
type="o", pch=15, xlab="x fractiles", ylab="y median", las=1)
str(res)
res # Now its gets printedSome plotting functions return a "plotting object", that can be stored, modified and later plotted, with the print() function.
r <- xyplot(rnorm(10) ~ rnorm(10)) # Does not plot anything
print(r) # Plots the data
r # Plots the data: print() is implicitely called
str(r) # An object of class "treillis", so that print(r)
# actually calls
r$panel.args.common$pch <- 15 # Modify the plot
r # Replot it
The following operators mean what you thing they mean -- but they tend to be applied to vectors.
+ * / - ^ < <= > >= == !=
The boolean operators are !, & et | (but you can write && or || instead of | and &: the result is then a scalar, even if the arguments are vectors).
The : (colon) operator creates vectors.
> -5:7 [1] -5 -4 -3 -2 -1 0 1 2 3 4 5 6 7
The [ operator retrieves one or several elements of a vector, matrix, data frame or arrow.
> x <- floor(10*runif(10)) > x [1] 3 6 5 1 0 6 7 8 5 8 > x[3] [1] 5 > x[1:3] [1] 3 6 5 > x[c(1,2,5)] [1] 3 6 0
The $ operator retrieves an element in a list, with no need to put its name between quotes, contrary to the [[ operator. The interest of the [[ operator is that is argument can be a variable.
> op <- par() > op$col [1] "black" > op[["col"]] [1] "black" > a <- "col" > op[[a]] [1] "black"
Assignment is written "<-". Some people use "=" instead: this will work most of the time, but not always (for instance, in "try" statements) -- it is easier, safer and more readable to use "<-".
x <- 1.17 y <- c(1, 2, 3, 4)
The matrix product is %*%, tensor product (aka Kronecker product) is %x%.
> A <- matrix(c(1,2,3,4), nr=2, nc=2)
> J <- matrix(c(1,0,2,1), nr=2, nc=2)
> A
[,1] [,2]
[1,] 1 3
[2,] 2 4
> J
[,1] [,2]
[1,] 1 2
[2,] 0 1
> J %x% A
[,1] [,2] [,3] [,4]
[1,] 1 3 2 6
[2,] 2 4 4 8
[3,] 0 0 1 3
[4,] 0 0 2 4The %o% operator builds multiplication tables (it calls the "outer" function with the multiplication).
> A <- 1:5 > B <- 11:15 > names(A) <- A > names(B) <- B > A %o% B 11 12 13 14 15 1 11 12 13 14 15 2 22 24 26 28 30 3 33 36 39 42 45 4 44 48 52 56 60 5 55 60 65 70 75 > outer(A,B, '*') 11 12 13 14 15 1 11 12 13 14 15 2 22 24 26 28 30 3 33 36 39 42 45 4 44 48 52 56 60 5 55 60 65 70 75
Euclidian division is written %/%, its remainder %%.
> 1234 %% 3 [1] 1 > 1234 %/% 3 [1] 411 > 411*3 + 1 [1] 1234
"Set" membership is written %in%.
> 17 %in% 1:100 [1] TRUE > 17.1 %in% 1:100 [1] FALSE
The ~ and | operators are used to describe statistical model: more about them later.
For more details (and for the operators I have not mentionned, such as <<- -> ->> @ :: ::: _ =), read the manual.
?"+" ?"<" ?"<-" ?"!" ?"[" ?Syntax ?kronecker ?match library(methods) ?slot TODO: mention <<- (and the reverse ->, ->>)
You can also define your own operators: these are just 2-arguments functions whose name starts and ends with "%". The following example comes from the manual.
> "%w/o%" <- function(x,y) x[!x %in% y] > (1:10) %w/o% c(3,7,12) [1] 1 2 4 5 6 8 9 10
Other example, to turn a 2-argument function into an operator, that can be easily used for more than two arguments:
"%i%" <- intersect intersect(x,y) # Only two arguments intersect( intersect(x,y), z ) x %i% y %i% z
TODO: See below ("dirty tricks") for actual global variables -- avoid them
TODO: options(), par()
This is a tricky bit. Object Orientation was added to R as an afterthought -- even worse, it has been added twice.
The first flavour, S3 classes, is rather simple: you add a "class" attribute to a normal object (list, vector, etc.); you then define a "generic" (C++ programmers would say "virtual" function), e.g., "plot", that looks at the class of its first argument and dispatches the call to the right function (e.g., for an object of class "Foo", the plot.Foo() function would be called).
The second flavour, S4 classes, is more intricate: it tries to copy the paradigm used in most object-oriented programming languages. For large projects, it might be a good idea, but think carefully!
More recently, several packages suggested other ways of programming with objects within R: R.oo and proto
As all Matlab-like software (remember that "Matlab" stands for "Matrix Laboratory" -- it has noting to do with Mathematics), R handles tables of numbers. Yet, there are different kinds of tables: vectors (tables of dimension 1), matrices (tables of dimension 2), arrays (tables of any dimension), "Data Frames" (tables of dimension 2, in which each column may have a different type -- for instance, a table containing the results of an experiment, with one row per subject and one column per variable). We shall now present in more detail each of these, explain how to build them, to manipulate them, to transform them, to convert them -- in the next chapter, we shall plot them.
Here are several ways to define them (here, "c" stands for "concatenate").
> c(1,2,3,4,5) [1] 1 2 3 4 5 > 1:5 [1] 1 2 3 4 5 > seq(1, 5, by=1) [1] 1 2 3 4 5 > seq(1, 5, lenth=5) [1] 1 2 3 4 5
Here are several ways to select a part of a vector.
> x <- seq(-1, 1, by=.1) > x [1] -1.0 -0.9 -0.8 -0.7 -0.6 -0.5 -0.4 -0.3 -0.2 -0.1 0.0 0.1 0.2 0.3 0.4 [16] 0.5 0.6 0.7 0.8 0.9 1.0 > x[5:10] [1] -0.6 -0.5 -0.4 -0.3 -0.2 -0.1 > x[c(5,7:10)] [1] -0.6 -0.4 -0.3 -0.2 -0.1 > x[-(5:10)] # We remove the elements whose index lies between 5 and 10 [1] -1.0 -0.9 -0.8 -0.7 0.0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1.0 > x>0 [1] FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE TRUE [13] TRUE TRUE TRUE TRUE TRUE TRUE TRUE TRUE TRUE > x[ x>0 ] [1] 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1.0
We can name the coordinates of a vector -- and then access its elements by their names.
> names(x)
NULL
> names(x) <- letters[1:length(x)] # "letters" is a vector of strings,
# containing 26 lower case letters.
# There is also LETTERS for upper
# case letters.
> x
a b c d e f g h i j k l m n o p
-1.0 -0.9 -0.8 -0.7 -0.6 -0.5 -0.4 -0.3 -0.2 -0.1 0.0 0.1 0.2 0.3 0.4 0.5
q r s t u
0.6 0.7 0.8 0.9 1.0
> x["r"]
r
0.7One can also define those names while creating the vector.
> c(a=1, b=5, c=10, d=7) a b c d 1 5 10 7
A few operations on vectors:
> x <- rnorm(10)
> sort(x)
[1] -1.4159893 -1.1159279 -1.0598020 -0.2314716 0.3117607 0.5376470
[7] 0.6922798 0.9316789 0.9761509 1.1022298
> rev(sort(x))
[1] 1.1022298 0.9761509 0.9316789 0.6922798 0.5376470 0.3117607
[7] -0.2314716 -1.0598020 -1.1159279 -1.4159893
> o <- order(x)
> o
[1] 3 1 9 6 4 7 8 10 2 5
> x[ o[1:3] ]
[1] -1.415989 -1.115928 -1.059802
> x <- sample(1:5, 10, replace=T)
> x
[1] 1 4 5 3 1 3 4 5 3 1
> sort(x)
[1] 1 1 1 3 3 3 4 4 5 5
> unique(x) # We need not sort the data before (this contrasts
# with Unix's "uniq" command)
[1] 1 4 5 3Here are still other ways of creating vectors. The "seq" command generates arithmetic sequences.
> seq(0,10, length=11) [1] 0 1 2 3 4 5 6 7 8 9 10 > seq(0,10, by=1) [1] 0 1 2 3 4 5 6 7 8 9 10
The "rep" command repeats a number or a vector.
> rep(1,10) [1] 1 1 1 1 1 1 1 1 1 1 > rep(1:5,3) [1] 1 2 3 4 5 1 2 3 4 5 1 2 3 4 5
It can also repeat each element several times.
> rep(1:5,each=3) [1] 1 1 1 2 2 2 3 3 3 4 4 4 5 5 5
We can mix the two previous operations.
> rep(1:5,2,each=3) [1] 1 1 1 2 2 2 3 3 3 4 4 4 5 5 5 1 1 1 2 2 2 3 3 3 4 4 4 5 5 5
The "gl" command serves a comparable purpose, mainly to create factors -- more about this in a few pages.
A factor is a vector coding for a qualitatitative variable (a qualitative variable is a non-numeric variable, such as gender, color, species, etc. -- or, at least, a variable whose actual numeric values are meaningless, for example, zip codes). We can create them with the "factor" command.
> x <- factor( sample(c("Yes", "No", "Perhaps"), 5, replace=T) )
> x
[1] Perhaps Perhaps Perhaps Perhaps No
Levels: No PerhapsWe can specify the list of acceptable values, or "levels" of this factor.
> l <- c("Yes", "No", "Perhaps")
> x <- factor( sample(l, 5, replace=T), levels=l )
> x
[1] No Perhaps No Yes Yes
Levels: Yes No Perhaps
> levels(x)
[1] "Yes" "No" "Perhaps"One can summarize a factor with a contingency table.
> table(x)
x
Yes No Perhaps
2 2 1We can create a factor that follows a certain pattern with the "gl" command.
> gl(1,4) [1] 1 1 1 1 Levels: 1 > gl(2,4) [1] 1 1 1 1 2 2 2 2 Levels: 1 2 > gl(2,4, labels=c(T,F)) [1] TRUE TRUE TRUE TRUE FALSE FALSE FALSE FALSE Levels: TRUE FALSE > gl(2,1,8) [1] 1 2 1 2 1 2 1 2 Levels: 1 2 > gl(2,1,8, labels=c(T,F)) [1] TRUE FALSE TRUE FALSE TRUE FALSE TRUE FALSE Levels: TRUE FALSE
The "interaction" command builds a new factor by concatenating the levels of two factors.
> x <- gl(2,4) > x [1] 1 1 1 1 2 2 2 2 Levels: 1 2 > y <- gl(2,1,8) > y [1] 1 2 1 2 1 2 1 2 Levels: 1 2 > interaction(x,y) [1] 1.1 1.2 1.1 1.2 2.1 2.2 2.1 2.2 Levels: 1.1 2.1 1.2 2.2 > data.frame(x,y, int=interaction(x,y)) x y int 1 1 1 1.1 2 1 2 1.2 3 1 1 1.1 4 1 2 1.2 5 2 1 2.1 6 2 2 2.2 7 2 1 2.1 8 2 2 2.2
The "expand.grid" computes a cartesian product (and yields a data.frame).
> x <- c("A", "B", "C")
> y <- 1:2
> z <- c("a", "b")
> expand.grid(x,y,z)
Var1 Var2 Var3
1 A 1 a
2 B 1 a
3 C 1 a
4 A 2 a
5 B 2 a
6 C 2 a
7 A 1 b
8 B 1 b
9 C 1 b
10 A 2 b
11 B 2 b
12 C 2 bWhen playing with factors, people sometimes want to turn them into numbers. This can be ambiguous and/or dangerous.
> x <- factor(c(3,4,5,1)) > as.numeric(x) # No NOT do that [1] 2 3 4 1 > x [1] 3 4 5 1 Levels: 1 3 4 5
What you get is the numbers internally used to code the various levels of the factor -- and it depends on the order of the factors...
Instead, try one of the following:
> x [1] 3 4 5 1 Levels: 1 3 4 5 > levels(x)[ x ] [1] "3" "4" "5" "1" > as.numeric( levels(x)[ x ] ) [1] 3 4 5 1 > as.numeric( as.character(x) ) # probably slower [1] 3 4 5 1
TODO
The missing values are coded as "NA" (it stands for "Not Available").
> x <- c(1,5,9,NA,2) > x [1] 1 5 9 NA 2
The default behaviour of many functions is to reject data containing missing values -- this is natural when the result would depend on the missing value, were it not missing.
> mean(x) [1] NA
But of course, you can ask R to first remove the missing values.
> mean(x, na.rm=T) [1] 4.25
You can do that yourself with the "na.omit" function.
> x [1] 1 5 9 NA 2 > na.omit(x) [1] 1 5 9 2 attr(,"na.action") [1] 4 attr(,"class") [1] "omit"
This also works with data.frames -- it discards the rows containing at least one missing value.
> d <- data.frame(x, y=rev(x)) > d x y 1 1 2 2 5 NA 3 9 9 4 NA 5 5 2 1 > na.omit(d) x y 1 1 2 3 9 9 5 2 1
You should NOT use missing values in boolean tests: if you test wether two numbers are equal, and if one (or both) is (are) missing, then you cannot conclude: the result will be NA.
> x
[1] 1 5 9 NA 2
> x == 5
[1] FALSE TRUE FALSE NA FALSE
> x == NA # If we compare with something unknown, the
# result is unknown.
[1] NA NA NA NA NATo test if a value is missing, use the "is.na" function.
> is.na(x) [1] FALSE FALSE FALSE TRUE FALSE
This is not the only way of getting non-numeric values in a numeric vector: you can also get +Inf, -Inf (positive and negative infinites), and NaN (Not a Number).
> x <- c(-1, 0,1,2,NA)
> cbind(X=x, LogX=log(x))
X LogX
[1,] -1 NaN
[2,] 0 -Inf
[3,] 1 0.0000000
[4,] 2 0.6931472
[5,] NA NA
Warning message:
NaNs produced in: log(x)You can check wether a numeric value is actually numeric with the "is.finite" function.
> is.finite(log(x)) [1] FALSE FALSE TRUE TRUE FALSE
A data frame may be seen as a list of vectors, each with the same length. Usually, the table has one row for each subject in the experiment, and one column for each variable measured in the experiement -- as the different variables measure different things, they maight have different types: some will be quantitative (numbers; each column may contain a measurement in a different unit), others will be qualitative (i.e., factors).
> n <- 10 > df <- data.frame( x=rnorm(n), y=sample(c(T,F),n,replace=T) )
The "str" command prints out the structure of an object (any object) and display a part of the data it contains.
> str(df) `data.frame': 10 obs. of 2 variables: $ x: num 0.515 -1.174 -0.523 -0.146 0.410 ... $ y: logi FALSE TRUE FALSE FALSE FALSE TRUE FALSE FALSE FALSE FALSE
The "summary" command print concise information about an object (here, a data.frame, but it could be anything).
> summary(df)
x y
Min. :-1.17351 Length:10
1st Qu.:-0.42901 Mode :logical
Median : 0.13737
Mean : 0.09217
3rd Qu.: 0.48867
Max. : 1.34213
> df
x y
1 0.51481130 FALSE
2 -1.17350867 TRUE
3 -0.52338041 FALSE
4 -0.14589347 FALSE
5 0.41022626 FALSE
6 1.34213009 TRUE
7 0.77715729 FALSE
8 -0.55460889 FALSE
9 -0.03843468 FALSE
10 0.31318467 FALSEDifferent ways to access the columns of a data.frame.
> df$x [1] 0.51481130 -1.17350867 -0.52338041 -0.14589347 0.41022626 1.34213009 [7] 0.77715729 -0.55460889 -0.03843468 0.31318467 > df[,1] [1] 0.51481130 -1.17350867 -0.52338041 -0.14589347 0.41022626 1.34213009 [7] 0.77715729 -0.55460889 -0.03843468 0.31318467 > df[["x"]] [1] 0.51481130 -1.17350867 -0.52338041 -0.14589347 0.41022626 1.34213009 [7] 0.77715729 -0.55460889 -0.03843468 0.31318467 > dim(df) [1] 10 2 > names(df) [1] "x" "y" > row.names(df) [1] "1" "2" "3" "4" "5" "6" "7" "8" "9" "10"
One may change the colomn/row names.
> names(df) <- c("a", "b")
> row.names(df) <- LETTERS[1:10]
> names(df)
[1] "a" "b"
> row.names(df)
[1] "A" "B" "C" "D" "E" "F" "G" "H" "I" "J"
> str(df)
`data.frame': 10 obs. of 2 variables:
$ a: num 0.515 -1.174 -0.523 -0.146 0.410 ...
$ b: logi FALSE TRUE FALSE FALSE FALSE TRUE FALSE FALSE FALSE FALSEWe can turn the columns the data.frame into actual variables with the "attach" command (it is the same principle as namespaces in C++). Do not forget to "detach" the data.frame after use.
> data(faithful) > str(faithful) `data.frame': 272 obs. of 2 variables: $ eruptions: num 3.60 1.80 3.33 2.28 4.53 ... $ waiting : num 79 54 74 62 85 55 88 85 51 85 ... > attach(faithful) > str(eruptions) num [1:272] 3.60 1.80 3.33 2.28 4.53 ... > detach()
The "merge" command joins two data frames -- it is the same JOIN as in Databases. More precisely you have two data frames a (with columns x, y, z) and b (with columns x1, x2, y,z) and certain observations (rows) of a correspond to certain observations of b: the command merges them to yield a data frame with columns x, x1, x2, y, z. In this example, the command
merge(a,b)
is equivalent to the SQL command
SELECT * FROM a,b WHERE a.y = b.y AND a.z = b.z
In SQL, this is called an inner join can also be written as
SELECT * FROM a INNER JOIN b ON a.y = b.y AND a.z = b.z
There are several types of SQL JOINs: in an INNER JOIN, we only get the rows that are present in both tables; in a LEFT JOIN, we get all the elements of the first table and the corresponding elements of the second (if any); a RIGHT JOIN is the opposite; an OUTER JOIN is the union of the LEFT and RIGHT JOINs. In R, you can get the other types of JOIN with the "all", "all.x" and "all.y" arguments.
merge(x, y, all.x = TRUE) # LEFT JOIN merge(x, y, all.y = TRUE) # RIGHT JOIN merge(x, y, all = TRUE) # OUTER JOIN
By default, the join is over the columns common present in both data frames, but you can restrict it to a subset of them, with the "by" argument.
merge(a, b, by=c("y", "z"))Data frames are often used to store data to be analyzed. We shall detail those examples later -- do not be frightened if you have never heard of "regression", we shall shortly demystify this notion.
# Regression data(cars) # load the "cars" data frame lm( dist ~ speed, data=cars) # Polynomial regression lm( dist ~ poly(speed,3), data=cars) # Regression with splines library(Design) lm( y ~ rcs(x) ) # TODO: Find some data # Logistic regression glm(y ~ x1 + x2, family=binomial, data=...) # TODO: Find some data library(Design) lrm(death ~ blood.presure + age) # TODO: Find some data # Non linear regression nls( y ~ a + b * exp(c * x), start = c(a=1, b=1, c=-1) ) # TODO: Find some data ?selfStart # Principal Component Analysis data(USArrest) princomp( ~ Murder + Assault + UrbanPop, data=USArrest) # Treillis graphics xyplot( x ~ y | group ) # TODO: Find some data
We shall see in a separate section how to transform data frames, because there are several ways of putting the result of an experiment in a table -- but usually, we shall prefer the one with the most rows and the fewer columns.
Some people may advise you to use the "subset" command to extract subsets of a data.frame. Actually, you can do the same thing with the basic subsetting syntax -- which is more general: the "subset" function is but a convenience wrapper around it.
d[ d$subject == "laika", ] d[ d$day %in% c(1, 3, 9, 10, 11), ] d[ d$value < .1 | d$value > .9, ] d[ d$x < d$y, ]
TODO
d <- data.frame(...) as.matrix(d) data.matrix(d)
Vectors only contain simple types (numbers, booleans or strings); lists, on the contrary, may contain anything, for instance sata frames or other lists. They can be used to store complex data, for instamce, trees. They can also be used, simply, as hash tables.
> h <- list()
> h[["foo"]] <- 1
> h[["bar"]] <- c("a", "b", "c")
> str(h)
List of 2
$ foo: num 1
$ bar: chr [1:3] "a" "b" "c"You can access one element with the "[[" operator, you can access several elements with the "[" operator.
> h[["bar"]]
[1] "a" "b" "c"
> h[[2]]
[1] "a" "b" "c"
> h[1:2]
$foo
[1] 1
$bar
[1] "a" "b" "c"
> h[2] # Beware, the result is not the second element, but a
# list containing this second element.
$bar
[1] "a" "b" "c"
> str(h[2])
List of 1
$ bar: chr [1:3] "a" "b" "c"For instance, the graphic parameters are stored in a list, used as a hash table.
> str( par() ) List of 68 $ adj : num 0.5 $ ann : logi TRUE $ ask : logi FALSE $ bg : chr "transparent" $ bty : chr "o" $ cex : num 1 $ cex.axis : num 1 $ cex.lab : num 1 $ cex.main : num 1.2 $ cex.sub : num 1 $ cin : num [1:2] 0.147 0.200 ... $ xpd : logi FALSE $ yaxp : num [1:3] 0 1 5 $ yaxs : chr "r" $ yaxt : chr "s" $ ylog : logi FALSE
The results of most statistical analyses is not a simple number or array, but a list containing all the relevant values.
> n <- 100 > x <- rnorm(n) > y <- 1 - 2 * x + rnorm(n) > r <- lm(y~x) > str(r) List of 12 $ coefficients : Named num [1:2] 0.887 -2.128 ..- attr(*, "names")= chr [1:2] "(Intercept)" "x" $ residuals : Named num [1:100] 0.000503 0.472182 -1.079153 -2.423841 0.168424 ... ..- attr(*, "names")= chr [1:100] "1" "2" "3" "4" ... $ effects : Named num [1:100] -9.5845 -19.5361 -1.0983 -2.5001 0.0866 ... ..- attr(*, "names")= chr [1:100] "(Intercept)" "x" "" "" ... $ rank : int 2 $ fitted.values: Named num [1:100] 0.67 1.65 1.75 4.20 4.44 ... ..- attr(*, "names")= chr [1:100] "1" "2" "3" "4" ... $ assign : int [1:2] 0 1 $ qr :List of 5 ..$ qr : num [1:100, 1:2] -10 0.1 0.1 0.1 0.1 0.1 0.1 0.1 0.1 0.1 ... .. ..- attr(*, "dimnames")=List of 2 .. .. ..$ : chr [1:100] "1" "2" "3" "4" ... .. .. ..$ : chr [1:2] "(Intercept)" "x" .. ..- attr(*, "assign")= int [1:2] 0 1 ..$ qraux: num [1:2] 1.10 1.04 ..$ pivot: int [1:2] 1 2 ..$ tol : num 1e-07 ..$ rank : int 2 ..- attr(*, "class")= chr "qr" ... > str( summary(r) ) List of 11 $ call : language lm(formula = y ~ x) $ terms :Classes 'terms', 'formula' length 3 y ~ x .. ..- attr(*, "variables")= language list(y, x) .. ..- attr(*, "factors")= int [1:2, 1] 0 1 .. .. ..- attr(*, "dimnames")=List of 2 .. .. .. ..$ : chr [1:2] "y" "x" .. .. .. ..$ : chr "x" .. ..- attr(*, "term.labels")= chr "x" .. ..- attr(*, "order")= int 1 .. ..- attr(*, "intercept")= int 1 .. ..- attr(*, "response")= int 1 .. ..- attr(*, ".Environment")=length 6 <environment> .. ..- attr(*, "predvars")= language list(y, x) .. ..- attr(*, "dataClasses")= Named chr [1:2] "numeric" "numeric" .. .. ..- attr(*, "names")= chr [1:2] "y" "x" $ residuals : Named num [1:100] 0.000503 0.472182 -1.079153 -2.423841 0.168424 ... ..- attr(*, "names")= chr [1:100] "1" "2" "3" "4" ... ...
To delete an element from a list:
> h[["bar"]] <- NULL > str(h) List of 1 $ foo: num 1
Matrices are 2-dimensional tables, but contrary to data frames (whose type may vary from one column to the next), their elements all have the same type.
A matrix:
> m <- matrix( c(1,2,3,4), nrow=2 )
> m
[,1] [,2]
[1,] 1 3
[2,] 2 4Caution: by default, the elements of a matrix are given vertically, column after column.
> matrix( 1:3, nrow=3, ncol=3 )
[,1] [,2] [,3]
[1,] 1 1 1
[2,] 2 2 2
[3,] 3 3 3
> matrix( 1:3, nrow=3, ncol=3, byrow=T )
[,1] [,2] [,3]
[1,] 1 2 3
[2,] 1 2 3
[3,] 1 2 3
> t(matrix( 1:3, nrow=3, ncol=3 ))
[,1] [,2] [,3]
[1,] 1 2 3
[2,] 1 2 3
[3,] 1 2 3Matrix product (beware: A * B is an element-by-element product):
> x <- matrix( c(6,7), nrow=2 )
> x
[,1]
[1,] 6
[2,] 7
> m %*% x
[,1]
[1,] 27
[2,] 40Determinant:
> det(m) [1] -2
Transpose:
> t(m)
[,1] [,2]
[1,] 1 2
[2,] 3 4A diagonal matrix:
> diag(c(1,2))
[,1] [,2]
[1,] 1 0
[2,] 0 2Identity matrix (or, more generally, a scalar matrix, i.e., the matrix of a homothety):
> diag(1,2)
[,1] [,2]
[1,] 1 0
[2,] 0 1
> diag(rep(1,2))
[,1] [,2]
[1,] 1 0
[2,] 0 1
> diag(2)
[,1] [,2]
[1,] 1 0
[2,] 0 1There is also a "Matrix" package, in case you prefer a full object-oriented framework and/or you need other operations on matrices.
library(help=Matrix)
We have already seen the "cbind" and "rbind" functions that put data frames side by side or on top of each other: they also work with matrices.
> cbind( c(1,2), c(3,4) )
[,1] [,2]
[1,] 1 3
[2,] 2 4
> rbind( c(1,3), c(2,4) )
[,1] [,2]
[1,] 1 3
[2,] 2 4The trace of a matrix:
> sum(diag(m)) [1] 5
The inverse of a matrix:
> solve(m)
[,1] [,2]
[1,] -2 1.5
[2,] 1 -0.5Actually, one rarely need the inverse of a matrix -- we usually just want to multiply a given vector by this inverse: this operation is simpler, faster and numerically more stable.
> solve(m, x)
[,1]
[1,] -1.5
[2,] 2.5
> solve(m) %*% x
[,1]
[1,] -1.5
[2,] 2.5Eigenvalues:
> eigen(m)$values [1] 5.3722813 -0.3722813
Eigenvectors:
> eigen(m)$vectors
[,1] [,2]
[1,] -0.5742757 -0.9093767
[2,] -0.8369650 0.4159736Let us check that the matrix has actually been diagonalized:
> p <- eigen(m)$vectors
> d <- diag(eigen(m)$values)
> p %*% d %*% solve(p)
[,1] [,2]
[1,] 1 3
[2,] 2 4It might be the good moment to recall the main matrix decompositions.
The LU decomposition, or more precisely, the PA = LDU decomposition (P: permutation matrix; L, U: lower (or upper) triangular matrix, with 1's on the diagonal) expresses the result of Gauss's Pivot Algorithm (L contains the operations on the lines; D contains the pivots).
We do not really need it, because the Pivot Algorithm is already implemented in the "solve" command.
The Choleski decomposition is a particular case of the LU decomposition: if A is real symetric definite positive matrix, it can be written as B * B' where B is upper triangular. It is used to solve linear systems AX=Y where A is symetric positive -- this is the case for the equations defining least squares estimators.
We shall see later another application to the simulation of non independant normal variables, with a given variance-covariance matrix.
When you look at them, matrices are rather complicated (there are a lot of coefficients). However, if you look at the way they act on vectors, it looks rather simple: they often seem to extend or shrink the vectors, depending on their direction. A matrix M of size n is said to be diagonalizable if there exists a basis e_1,...,e_n of R^n so that M e_i = lambda_i e_i for all i, for some (real or sometimes complex) numbers. Geometrically, it means that, in the direction of each e_i, the matrix acts like a homothety. The e_i are said to be eigen vectors of the matrix M, the lambda_i are said to be its eigen values. in matrix terms, this means that there exists an invertible matrix P (whose columns will be the eigen vectors) and a diagonal matrix D (whose elements will be the corresponding eigen values) such that
M = P D P^-1.
Diagonalizable matrices sound good, but there may still be a few problems. First, the eigen values (and the eigen vectors) can be complex -- if you want to interpret them as a real-world quantity, it is a bad start. However, the matrices you will want to diagonalize are often symetric real matrices: they are diagonalizable with real eigen values (and eigen vectors). Second, not all matrices are diagonalizable. For instance,
1 1 0 1
is not diagonalizable. However, the set of non-diagonalizable matrices has zero measure: in particular, if you take a matrix at random, in some "reasonable" way ("reasonable" means "along a probability measure absolutely continuous with respect to the Lebesgue measure on the set of square matrices of size n), the probability that it be diagonalizable (over the complex numbers) is 1 -- we say that matrices are almost surely diagonalizable.
Should you be interested in the rare cases when the matrices are not diagonalizable (for instance, if you are interested in matrices with integer, bounded coefficients), you can look into the Jordan decomposition, that generalizes the diagonalization and works with any matrix.
There are also many decompositions based on the matrix t(A)*A.
The A=QR decomposition (R: upper triangular, Q: unitary) expresses the Gram-Schmidt orthonormalization of the columns of A -- we can compute it from the LU decomposition of t(A)*A.
?qr
It may be used to do a regression:
Model: Y = b X + noise X = QR \hat Y = Q Q' Y b = R^-1 Q' Y
The Singular Value Decomposition (SVD) A=Q1*S*Q2 (Q1, Q2: matrices containing the eigenvectors of A*t(A) and t(A)*A; S: diagonal matrix containing the square roots of the eigenvalues of A*t(A) or t(A)*A (they are the same)) which yields, when A is symetrix, its diagonalization in an orthonormal basis; it also used in the computation of the pseudo inverse. This decomposition may also be seen as a sum of matrices of rank 1, such that the first matrices in this sum approximate "best" the initial matrix.
?svd
The polar decomposition, A=QR (Q: orthogonal, R: symetric positive definite) is an analogue of the polar decomposition of a complex number: it decomposes the correspondiong linear transformation into rotation and "stretching". We can meet this decomposition in Least Squares Estimates: when we try to minimize the absolute value of Ax-b, this amounts to solve
t(A) A x = t(A) b
(Usually, t(A)*A is invertible, otherwise we would use pseudo-inverses.)
TODO: speak a bit more about pseudo-inverses.
There is also an "array" type, that generalizes matrices in higher dimensions.
> d <- array(rnorm(3*3*2), dim=c(3,3,2))
> d
, , 1
[,1] [,2] [,3]
[1,] 0.97323599 -0.7319138 -0.7355852
[2,] 0.06624588 -0.5732781 -0.4133584
[3,] 1.65808464 -1.3011671 -0.4556735
, , 2
[,1] [,2] [,3]
[1,] 0.6314685 0.6263645 1.2429024
[2,] -0.2562622 -1.5338054 0.9634999
[3,] 0.1652014 -0.9791350 -0.2040375
> str(d)
num [1:3, 1:3, 1:2] 0.9732 0.0662 1.6581 -0.7319 -0.5733 ...Contigency tables are arrays (computed with the "table" function), when there are more than two variables.
> data(HairEyeColor)
> HairEyeColor
, , Sex = Male
Eye
Hair Brown Blue Hazel Green
Black 32 11 10 3
Brown 38 50 25 15
Red 10 10 7 7
Blond 3 30 5 8
, , Sex = Female
Eye
Hair Brown Blue Hazel Green
Black 36 9 5 2
Brown 81 34 29 14
Red 16 7 7 7
Blond 4 64 5 8
> str(HairEyeColor)
table [1:4, 1:4, 1:2] 32 38 10 3 11 50 10 30 10 25 ...
- attr(*, "dimnames")=List of 3
..$ Hair: chr [1:4] "Black" "Brown" "Red" "Blond"
..$ Eye : chr [1:4] "Brown" "Blue" "Hazel" "Green"
..$ Sex : chr [1:2] "Male" "Female"
- attr(*, "class")= chr "table"It says "table", but a "table" is an "array":
> is.array(HairEyeColor) [1] TRUE
One may attach meta-data to an object: these are called "attributes". For instance, names of the elements of a list are in an attribute.
> l <- list(a=1, b=2, c=3) > str(l) List of 3 $ a: num 1 $ b: num 2 $ c: num 3 > attributes(l) $names [1] "a" "b" "c"
Similarly, the row and columns names of a data.frame
> a <- data.frame(a=1:2, b=3:4) > str(a) `data.frame': 2 obs. of 2 variables: $ a: int 1 2 $ b: int 3 4 > attributes(a) $names [1] "a" "b" $row.names [1] "1" "2" $class [1] "data.frame" > a <- matrix(1:4, nr=2) > rownames(a) <- letters[1:2] > colnames(a) <- LETTERS[1:2] > str(a) int [1:2, 1:2] 1 2 3 4 - attr(*, "dimnames")=List of 2 ..$ : chr [1:2] "a" "b" ..$ : chr [1:2] "A" "B" > attributes(a) $dim [1] 2 2 $dimnames $dimnames[[1]] [1] "a" "b" $dimnames[[2]] [1] "A" "B" > data(HairEyeColor) > str(HairEyeColor) table [1:4, 1:4, 1:2] 32 38 10 3 11 50 10 30 10 25 ... - attr(*, "dimnames")=List of 3 ..$ Hair: chr [1:4] "Black" "Brown" "Red" "Blond" ..$ Eye : chr [1:4] "Brown" "Blue" "Hazel" "Green" ..$ Sex : chr [1:2] "Male" "Female" - attr(*, "class")= chr "table"
It is also used to hold the code of a function if you want to keep the comments.
> f <- function (x) {
+ # Useless function
+ x + 1
+ }
> f
function (x) {
# Useless function
x + 1
}
> str(f)
function (x)
- attr(*, "source")= chr [1:4] "function (x) {" ...
> attr(f, "source") <- NULL
> str(f)
function (x)
> f
function (x)
{
x + 1
}Some people even suggest to use this to "hide" code -- but choosing an interpreted language is a very bad idea if you want to hide your code.
> attr(f, "source") <- "Forbidden" > f Forbidden > attr(f, "source") <- "Remember to use brackets to call a function, e.g., f()" > f Remember to use brackets to call a function, e.g., f()
Typically, when the data has a complex structure, you use a list; but when the bulk of the data has a very simple, table-like structure, you store it in an array or data frame and put the rest in the attributes. For instance, here is a chunk of an "lm" object (the result of a regression):
> str(r$model) `data.frame': 100 obs. of 2 variables: $ y: num 5.087 -1.587 -0.637 2.023 2.207 ... $ x: num -1.359 0.993 0.587 -0.627 -0.853 ... - attr(*, "terms")=Classes 'terms', 'formula' length 3 y ~ x .. ..- attr(*, "variables")= language list(y, x) .. ..- attr(*, "factors")= int [1:2, 1] 0 1 .. .. ..- attr(*, "dimnames")=List of 2 .. .. .. ..$ : chr [1:2] "y" "x" .. .. .. ..$ : chr "x" .. ..- attr(*, "term.labels")= chr "x" .. ..- attr(*, "order")= int 1 .. ..- attr(*, "intercept")= int 1 .. ..- attr(*, "response")= int 1 .. ..- attr(*, ".Environment")=length 149 <environment> .. ..- attr(*, "predvars")= language list(y, x) .. ..- attr(*, "dataClasses")= Named chr [1:2] "numeric" "numeric" .. .. ..- attr(*, "names")= chr [1:2] "y" "x"
We shall soon see another application of attributes: the notion of class -- the class of an object is just the value of its "class" attribute, if any.
If you want to use a complex object, obtained as the result of a certain command, by extracting some of its elements, or if you want to browse through it, the printing command is not enough: we need other means to peer inside an object.
The "unclass" command removes the class of an object: only remains the underlying type (usually, "list"). As a result, it is printed by the "print.default" function that displays its actual contents.
> data(USArrests)
> r <- princomp(USArrests)$loadings
> r
Loadings:
Comp.1 Comp.2 Comp.3 Comp.4
Murder 0.995
Assault -0.995
UrbanPop -0.977 -0.201
Rape -0.201 0.974
Comp.1 Comp.2 Comp.3 Comp.4
SS loadings 1.00 1.00 1.00 1.00
Proportion Var 0.25 0.25 0.25 0.25
Cumulative Var 0.25 0.50 0.75 1.00
> class(r)
[1] "loadings"
> unclass(r)
Comp.1 Comp.2 Comp.3 Comp.4
Murder -0.04170432 0.04482166 0.07989066 0.99492173
Assault -0.99522128 0.05876003 -0.06756974 -0.03893830
UrbanPop -0.04633575 -0.97685748 -0.20054629 0.05816914
Rape -0.07515550 -0.20071807 0.97408059 -0.07232502You cound also directly use the "print.default" function.
> print.default(r)
Comp.1 Comp.2 Comp.3 Comp.4
Murder -0.04170432 0.04482166 0.07989066 0.99492173
Assault -0.99522128 0.05876003 -0.06756974 -0.03893830
UrbanPop -0.04633575 -0.97685748 -0.20054629 0.05816914
Rape -0.07515550 -0.20071807 0.97408059 -0.07232502
attr(,"class")
[1] "loadings"The "str" function prints the contents of an objects and truncates all the vectors it encounters: thus, you can peer into large objects.
> str(r) loadings [1:4, 1:4] -0.0417 -0.9952 -0.0463 -0.0752 0.0448 ... - attr(*, "dimnames")=List of 2 ..$ : chr [1:4] "Murder" "Assault" "UrbanPop" "Rape" ..$ : chr [1:4] "Comp.1" "Comp.2" "Comp.3" "Comp.4" - attr(*, "class")= chr "loadings" > str(USArrests) `data.frame': 50 obs. of 4 variables: $ Murder : num 13.2 10 8.1 8.8 9 7.9 3.3 5.9 15.4 17.4 ... $ Assault : int 236 263 294 190 276 204 110 238 335 211 ... $ UrbanPop: int 58 48 80 50 91 78 77 72 80 60 ... $ Rape : num 21.2 44.5 31 19.5 40.6 38.7 11.1 15.8 31.9 25.8 ...
Finally, to get an idea of what you can do with an object, you can always look the code of its "print" or "summary" methods.
> print.lm
function (x, digits = max(3, getOption("digits") - 3), ...)
{
cat("\nCall:\n", deparse(x$call), "\n\n", sep = "")
if (length(coef(x))) {
cat("Coefficients:\n")
print.default(format(coef(x), digits = digits), print.gap = 2,
quote = FALSE)
}
else cat("No coefficients\n")
cat("\n")
invisible(x)
}
<environment: namespace:base>
> summary.lm
function (object, correlation = FALSE, symbolic.cor = FALSE,
...)
{
z <- object
p <- z$rank
if (p == 0) {
r <- z$residuals
n <- length(r)
etc.
> print.summary.lm
function (x, digits = max(3, getOption("digits") - 3), symbolic.cor = x$symbolic.cor,
signif.stars = getOption("show.signif.stars"), ...)
{
cat("\nCall:\n")
cat(paste(deparse(x$call), sep = "\n", collapse = "\n"),
"\n\n", sep = "")
resid <- x$residuals
df <- x$df
rdf <- df[2]
cat(if (!is.null(x$w) && diff(range(x$w)))
"Weighted ", "Residuals:\n", sep = "")
if (rdf > 5) {
etc.The "deparse" command produces a character string whose evaluation will yield the initial object (the resulting syntax is a bit strange: if you were to build such an object from scratch, you would not proceed that way).
> deparse(r)
[1] "structure(c(-0.0417043206282872, -0.995221281426497, -0.0463357461197109, "
[2] "-0.075155500585547, 0.0448216562696701, 0.058760027857223, -0.97685747990989, "
[3] "-0.200718066450337, 0.0798906594208107, -0.0675697350838044, "
[4] "-0.200546287353865, 0.974080592182492, 0.994921731246978, -0.0389382976351601, "
[5] "0.0581691430589318, -0.0723250196376096), .Dim = c(4, 4), .Dimnames = list("
[6] " c(\"Murder\", \"Assault\", \"UrbanPop\", \"Rape\"), c(\"Comp.1\", \"Comp.2\", "
[7] " \"Comp.3\", \"Comp.4\")), class = \"loadings\")"
> cat(deparse(r)); cat("\n")
structure(c(-0.0417043206282872, -0.995221281426497,
-0.0463357461197109, -0.075155500585547, 0.0448216562696701,
0.058760027857223, -0.97685747990989, -0.200718066450337,
0.0798906594208107, -0.0675697350838044, -0.200546287353865,
0.974080592182492, 0.994921731246978, -0.0389382976351601,
0.0581691430589318, -0.0723250196376096), .Dim = c(4, 4),
.Dimnames = list( c("Murder", "Assault", "UrbanPop", "Rape"),
c("Comp.1", "Comp.2", "Comp.3", "Comp.4")), class = "loadings")
TODO: Check that I mention apply, sapply, lapply,
rapply (recursive apply), rollapply (zoo)
TODO: Mention the "reshape" packageThere are several ways to code the results of an experiment.
First example: we have measured several qualitative variables on several (hundred) subjects. The data may be written down as a table, one line per subject, one column per variable. We can also use a contingency table (it is only a good idea of there are few variables, otherwise the array would mainly contain zeroes; if there are k variables the array would hane k dimensions).
How can we switch from one formulation to the next.
In one direction, the "table" function computes a contingency table.
n <- 1000 x1 <- factor( sample(1:3, n, replace=T), levels=1:3 ) x2 <- factor( sample(LETTERS[1:5], n, replace=T), levels=LETTERS[1:5] ) x3 <- factor( sample(c(F,T),n,replace=T), levels=c(F,T) ) d <- data.frame(x1,x2,x3) r <- table(d)
This yields:
> r , , x3 = FALSE x2 x1 A B C D E 1 27 45 31 38 25 2 41 33 30 35 33 3 33 30 28 35 39 , , x3 = TRUE x2 x1 A B C D E 1 26 30 28 42 29 2 35 33 22 37 40 3 42 31 31 36 35
The "ftable" command presents the result in a slightly different way (more readable if there are more variables).
> ftable(d)
x3 FALSE TRUE
x1 x2
1 A 27 26
B 45 30
C 31 28
D 38 42
E 25 29
2 A 41 35
B 33 33
C 30 22
D 35 37
E 33 40
3 A 33 42
B 30 31
C 28 31
D 35 36
E 39 35Let us now see how to turn a contingency table into a data.frame.
Case 1: 1-dimensional table
n <- 100 k <- 10 x <- factor( sample(LETTERS[1:k], n, replace=T), levels=LETTERS[1:k] ) d <- table(x) factor( rep(names(d),d), levels=names(d) )
Case 2: 2-dimensional table
n <- 100
k <- 4
x1 <- factor( sample(LETTERS[1:k], n, replace=T), levels=LETTERS[1:k] )
x2 <- factor( sample(c('x','y','z'),n,replace=T), levels=c('x','y','z') )
d <- data.frame(x1,x2)
d <- table(d)
y2 <- rep(colnames(d)[col(d)], d)
y1 <- rep(rownames(d)[row(d)], d)
dd <- data.frame(y1,y2)General case:
n <- 1000
x1 <- factor( sample(1:3, n, replace=T), levels=1:3 )
x2 <- factor( sample(LETTERS[1:5], n, replace=T), levels=LETTERS[1:5] )
x3 <- factor( sample(c(F,T),n,replace=T), levels=c(F,T) )
d <- data.frame(x1,x2,x3)
r <- table(d)
# A function generalizing "row" and "col" in higher dimensions
foo <- function (r,i) {
d <- dim(r)
rep(
rep(1:d[i], each=prod(d[0:(i-1)])),
prod(d[(i+1):(length(d)+1)], na.rm=T)
)
}
k <- length(dimnames(r))
y <- list()
for (i in 1:k) {
y[[i]] <- rep( dimnames(r)[[i]][foo(r,i)], r )
}
d <- data.frame(y)
colnames(d) <- LETTERS[1:k]
# Test
r - table(d)
Other example: we made the same experiment, with the same subject, three times. We can represent the data with one row per subject, with several results for each
subject, result1, result2, result3
We can also use one row per experiment, with the number of the subject, the number of the experiment (1, 2 or 3) and the result.
subject, retry, result
Exercice: Write function to turn one representation into the other. (Hint: you may use the "split" command that separates data along a factor).
Other example: Same situation, but this time, the numner or experiments per subject is not constant. The first representation can no longer be a data frame: it can be a list of vectors (one vector for each subject). The second representation is unchanged.
n <- 100 k <- 10 subject <- factor( sample(1:k,n,replace=T), levels=1:k ) x <- rnorm(n) d1 <- data.frame(subject, x) # Data.frame to vector list d2 <- split(d1$x, d1$subject) # vector list to data.frame rep(names(d2), sapply(d2, length))
(I never use those functions: fell free to skip to the next section that present more general and powerful alternatives.)
In SQL (this is the language spoken by databases -- to simplify things, you can consider that a database is a (set of) data.frame(s)), we often want to apply a function (sum, mean, sd, etc.) to groups of records ("record" is the database word for "line in a data.frame). For instance, if you store you personnal accounting in a database, giving, for each expense, the amount and the nature (rent, food, transortation, taxes, books, cinema, etc.),
amount nature ------------------ 390 rent 4.90 cinema 6.61 food 10.67 food 6.40 books 14.07 food 73.12 books 4.90 cinema
you might want to compute the total expenses for each type of expense. In SQL, you would say:
SELECT nature, SUM(amount) FROM expenses GROUP BY nature;
You can do the same in R:
nature <- c("rent", "cinema", "books", "food")
p <- length(nature):1
p <- sum(p)/p
n <- 10
d <- data.frame(
nature = sample( nature, n, replace=T, prob=p ),
amount = 10*round(rlnorm(n),2)
)
by(d$amount, d$nature, sum)This yields:
> d nature amount 1 books 59.9 2 rent 3.0 3 books 6.7 4 cinema 4.7 5 food 7.3 6 books 11.3 7 rent 12.2 8 cinema 6.5 9 food 3.2 10 food 4.7 > by(d$amount, d$nature, sum) INDICES: books [1] 77.9 ------------------------------------------------------------ INDICES: cinema [1] 11.2 ------------------------------------------------------------ INDICES: food [1] 15.2 ------------------------------------------------------------ INDICES: rent [1] 15.2
The "by" function assumes that you have a vector, that you want to cut into pieces and on whose pieces you want to apply a function. Sometimes, it is not a vector, but several: all the columns in a data.frame. You can then replace the "by" function by "aggregate".
> N <- 50 > k1 <- 4 > g1 <- sample(1:k1, N, replace=TRUE) > k2 <- 3 > g2 <- sample(1:k2, N, replace=TRUE) > d <- data.frame(x=rnorm(N), y=rnorm(N), z=rnorm(N)) > aggregate(d, list(g1, g2), mean) Group.1 Group.2 x y z 1 1 1 -0.5765 0.07474 -0.01558 2 2 1 0.4246 0.12450 -0.05569 3 3 1 -0.3418 0.30908 -0.32289 4 4 1 0.7405 -0.79703 0.18489 5 1 2 -0.5855 -0.07166 -0.16581 6 2 2 -0.4230 -0.15215 0.24693 7 3 2 0.4329 0.32154 -0.82883 8 4 2 -1.0167 -0.18424 0.12709 9 1 3 0.3961 -0.86940 0.68552 10 2 3 -0.8808 0.62404 0.79728 11 3 3 -0.4884 -0.67295 0.03346 12 4 3 0.1605 -0.68522 -0.35144 TODO: Replace this example by real data...
These two functions, "by" and "aggregate", are actually special cases of the apply/tapply/lapply/sapply/mapply functions, that are more general and that we shall now present.
> by.data.frame
function (data, INDICES, FUN, ...) {
(...)
ans <- eval(substitute(tapply(1:nd, IND, FUNx)), data)
(...)
}
> aggregate.data.frame
function (x, by, FUN, ...) {
(...)
y <- lapply(x, tapply, by, FUN, ..., simplify = FALSE)
(...)
}
The "apply" function applies a function (mean, quartile, etc.) to each column or row of a data.frame, matrix or array.
> options(digits=4)
> df <- data.frame(x=rnorm(20),y=rnorm(20),z=rnorm(20))
> apply(df,2,mean)
x y z
0.04937 -0.11279 -0.02171
> apply(df,2,range)
x y z
[1,] -1.564 -1.985 -1.721
[2,] 1.496 1.846 1.107It also works in higher dimensions. The second argument indicates the indices along which the program should loop, i.e., the dimensions used to slice the data, i.e., the dimensions that will remain after the computation.
> options(digits=2)
> m <- array(rnorm(10^3), dim=c(10,10,10))
> a <- apply(m, 1, mean)
> a
[1] 0.060 -0.027 0.037 0.160 0.054 0.012 -0.039 -0.064 -0.013 0.061
> b <- apply(m, c(1,2), mean)
> b
[,1] [,2] [,3] [,4] [,5] [,6] [,7] [,8] [,9] [,10]
[1,] -0.083 -0.7297 0.547 0.283 0.182 -0.409 -0.0029 0.170 -0.131 0.7699
[2,] -0.044 0.3618 -0.206 -0.095 0.062 -0.568 -0.4841 0.334 0.362 0.0056
[3,] 0.255 0.2359 -0.331 0.040 0.213 -0.547 -0.1852 0.492 -0.257 0.4525
[4,] -0.028 0.7422 0.417 -0.088 0.205 -0.521 -0.1981 0.042 0.604 0.4244
[5,] -0.085 0.3461 0.047 0.683 -0.018 -0.173 0.1825 -0.826 -0.037 0.4153
[6,] -0.139 -0.4761 0.276 0.174 0.145 0.232 -0.1194 -0.010 0.176 -0.1414
[7,] -0.139 0.0054 -0.328 -0.264 0.078 0.496 0.2812 -0.336 0.124 -0.3110
[8,] -0.060 0.1291 0.313 -0.199 -0.325 0.338 -0.2703 0.166 -0.133 -0.5998
[9,] 0.091 0.2250 0.155 -0.277 0.075 -0.044 -0.4169 0.050 0.200 -0.1849
[10,] -0.157 -0.3316 -0.103 0.373 -0.034 0.116 0.0660 0.249 -0.040 0.4689
> apply(b, 1, mean)
[1] 0.060 -0.027 0.037 0.160 0.054 0.012 -0.039 -0.064 -0.013 0.061The "tapply" function groups the observations along the value of one (or several) factors and applies a function (mean, etc.) to the resulting groups. The "by" command is similar.
> tapply(1:20, gl(2,10,20), sum) 1 2 55 155 > by(1:20, gl(2,10,20), sum) INDICES: 1 [1] 55 ------------------------------------------------------------ INDICES: 2 [1] 155
The "sapply" function applies a function to each element of a list (or vector, etc.) and returns, if possible, a vector. The "lapply" function is similar but returns a list.
> x <- list(a=rnorm(10), b=runif(100), c=rgamma(50,1))
> lapply(x,sd)
$a
[1] 1.041
$b
[1] 0.294
$c
[1] 1.462
> sapply(x,sd)
a b c
1.041 0.294 1.462In particular, the "sapply" function can apply a function to each column of a data.frame without specifying the dimension numbers required by the "apply" command (at the beginning, you never know if it sould be 1 or 2 and you end up trying both to retain the one whose result has the expected dimension).
The "split" command cuts the data, as the "tapply" function, but does not apply any function afterwards.
> str(InsectSprays)
`data.frame': 72 obs. of 2 variables:
$ count: num 10 7 20 14 14 12 10 23 17 20 ...
$ spray: Factor w/ 6 levels "A","B","C","D",..: 1 1 1 1 1 1 1 1 1 1 ...
> str( split(InsectSprays$count, InsectSprays$spray) )
List of 6
$ A: num [1:12] 10 7 20 14 14 12 10 23 17 20 ...
$ B: num [1:12] 11 17 21 11 16 14 17 17 19 21 ...
$ C: num [1:12] 0 1 7 2 3 1 2 1 3 0 ...
$ D: num [1:12] 3 5 12 6 4 3 5 5 5 5 ...
$ E: num [1:12] 3 5 3 5 3 6 1 1 3 2 ...
$ F: num [1:12] 11 9 15 22 15 16 13 10 26 26 ...
> sapply( split(InsectSprays$count, InsectSprays$spray), mean )
A B C D E F
14.500 15.333 2.083 4.917 3.500 16.667
> tapply( InsectSprays$count, InsectSprays$spray, mean )
A B C D E F
14.500 15.333 2.083 4.917 3.500 16.667
TODO: This is a VERY important section.
At the begining of this document, list the most important sections, list what the reader is expected to be able to do after reading this document.
In R, many commands handle vectors or tables, allowing an (almost) loop-less programming style -- parallel programming. Thus, the computations are faster than with an explicitely written loop (because R is an interpreted language). The resulting programming style is very different from what you may be used to: here are a few exercises to warm you up. We shall need the table functions we have just introduced, in particular "apply".
Many people consider the "apply" function as a loop: in the current implementation of R, it might be implemented as a loop, if if you run R on a parallel machine, it could be different -- all the operations could be run at once. This really is parallelization.
Exercice: Let x be a table. Compute the sum of its rows, the sum of each of its columns. If x is the contingency table of two qualitative variables, compute the theoretical contingency table under the hypothesis that the two variables are independant. If you already know what it is, computhe the corresponding Chi^2.
# To avoid any row/column confusion, I choose a non-square table n <- 4 m <- 5 x <- matrix( rpois(n*m,10), nr=n, nc=m ) rownames(x) <- 1:n colnames(x) <- LETTERS[1:m] x apply(x,1,sum) # Actually, there is already a "rowSums" function apply(x,2,sum) # Actually, there is already a "colSums" function # Theoretical contingency table y <- matrix(apply(x,1,sum),nr=n,nc=m) * matrix(apply(x,2,sum),nr=n,nc=m,byrow=T) / sum(x) # Theoretical contingency table y <- apply(x,1,sum) %*% t(apply(x,2,sum)) / sum(x) # Computing the Chi^2 by hand sum((x-y)^2/y) # Let us check... chisq.test(x)$statistic
Exercice: Let x be a boolean vector. Count the number of sequences ("runs") of zeros (for instance, in 00101001010110, there are 6 runs: 00 0 00 0 0 0). Count the number of sequences of 1. Counth the total number of sequences. Same question for a factor with more tham two levels.
n <- 50
x <- sample(0:1, n, replace=T, p=c(.2,.8))
# Number of runs
sum(abs(diff(x)))+1
# Number of runs of 1's.
f <- function (x, v=1) { # If someone has a simpler idea...
x <- diff(x==v)
x <- x[x!=0]
if(x[1]==1)
sum(x==1)
else
1+sum(x==1)
}
f(x,1)
# Number of runs of 0's.
f(x,0)
n <- 50
k <- 4
x <- sample(1:k, n, replace=T)
# With a loop
s <- 0
for (i in 1:4) {
s <- s + f(x,i)
}
s
# With no loop (less readable)
a <- apply(matrix(1:k,nr=1,nc=k), 2, function (i) { f(x,i) } )
a
sum(a)In a binary vector of length n, find the position of the runs of 1's of length greater than k.
n <- 100 k <- 10 M <- sample(0:1, n, replace=T, p=c(.2,.8)) x <- c(0,M,0) # Start of the runs of 1's deb <- which( diff(x) == 1 ) # End of the runs of 1's fin <- which( diff(x) == -1 ) -1 # Length of those runs long <- fin - deb # Location of those whose lengths exceed k cbind(deb,fin)[ fin-deb > k, ]
Exercise: same question, but we are looking for runs of 1's of length at least k in an n*m matrix. Present the result as a table.
foo <- function (M,k) {
x <- c(0,M,0)
deb <- which( diff(x) == 1 )
fin <- which( diff(x) == -1 ) -1
cbind(deb,fin)[ fin-deb >= k, ]
}
n <- 50
m <- 50
M <- matrix( sample(0:1, n*m, replace=T, prob=c(.2,.8)), nr=n, nc=m )
res <- apply(M, 1, foo, k=10)
# Add the line number (not very pretty -- if someone has a better idea)
i <- 0
res <- lapply(res, function (x) {
x <- matrix(x, nc=2)
i <<- i+1
#if (length(x)) {
cbind(ligne=rep(i,length(x)/2), deb=x[,1], fin=x[,2])
#} else {
# x
#}
})
# Present the result as a table
do.call('rbind', res) # The line numbers are still missingTODO: check that I mention the "do.call" function somewhere in this document...
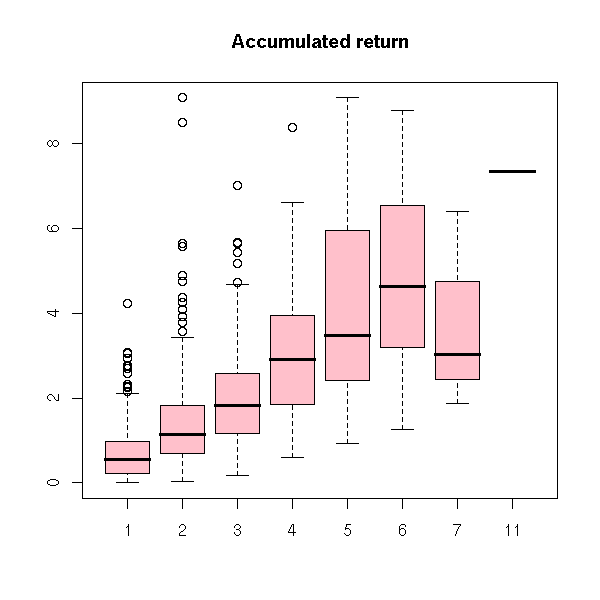
Let r be the return of a financial asset. The clustered return is the accumulated return for a sequence of returns of the same sign. The trend number is the number of steps in such a sequence. The average return is their ratio. Compute these quantities.
data(EuStockMarkets)
x <- EuStockMarkets
# We aren't interested in the spot prices, but in the returns
# return[i] = ( price[i] - price[i-1] ) / price[i-1]
y <- apply(x, 2, function (x) { diff(x)/x[-length(x)] })
# We normalize the data
z <- apply(y, 2, function (x) { (x-mean(x))/sd(x) })
# A single time series
r <- z[,1]
# The runs
f <- factor(cumsum(abs(diff(sign(r))))/2)
r <- r[-1]
accumulated.return <- tapply(r, f, sum)
trend.number <- table(f)
boxplot(abs(accumulated.return) ~ trend.number, col='pink',
main="Accumulated return")
boxplot(abs(accumulated.return)/trend.number ~ trend.number,
col='pink', main="Average return")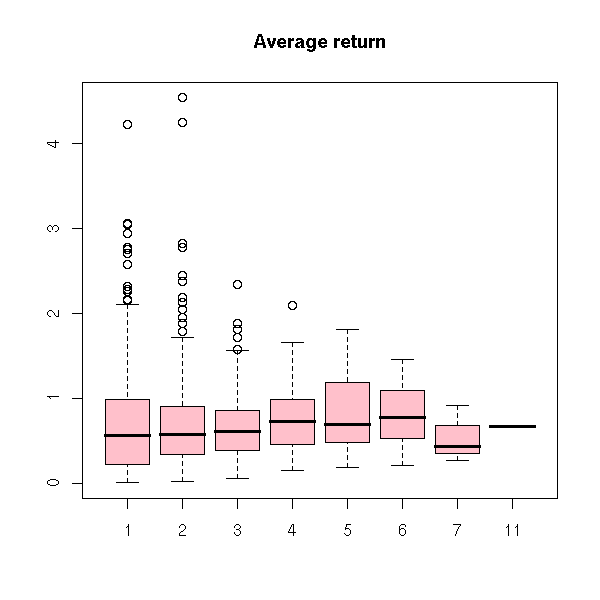
op <- par(mfrow=c(2,2))
for (i in 1:4) {
r <- z[,i]
f <- factor(cumsum(abs(diff(sign(r))))/2)
r <- r[-1]
accumulated.return <- tapply(r, f, sum)
trend.number <- table(f)
boxplot(abs(accumulated.return) ~ trend.number, col='pink')
}
par(op)
op <- par(mfrow=c(2,2))
for (i in 1:4) {
r <- z[,i]
f <- factor(cumsum(abs(diff(sign(r))))/2)
r <- r[-1]
accumulated.return <- tapply(r, f, sum)
trend.number <- table(f)
boxplot(abs(accumulated.return)/trend.number ~ trend.number, col='pink')
}
par(op)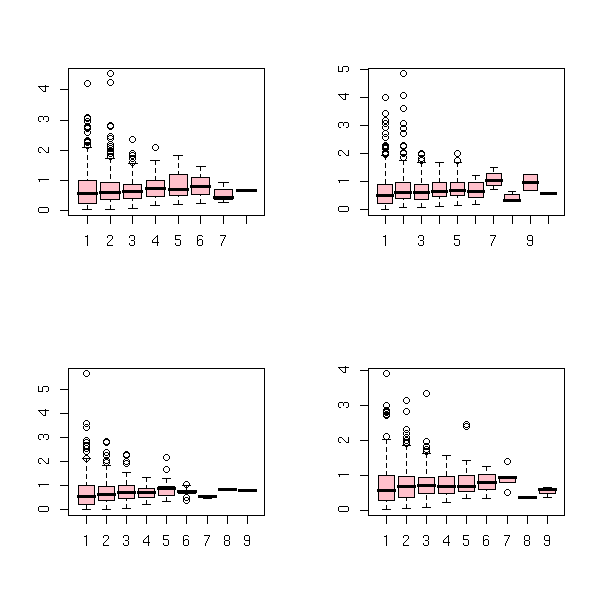
Let M be an n*m matrix (representing a grayscale image); compute the mean value of each quadripixel.
data(volcano) M <- volcano n <- dim(M)[1] m <- dim(M)[2] M1 <- M [1:(n-1),] [,1:(m-1)] M2 <- M [2:n,] [,1:(m-1)] M3 <- M [1:(n-1),] [,2:m] M4 <- M [2:n,] [,2:m] # Overlapping quadripixels M0 <- (M1+M2+M3+M4)/4 # Non-overlapping quadripixels nn <- floor((n-1)/2) mm <- floor((m-1)/2) M00 <- M0 [2*(1:nn),] [,2*(1:mm)] op <- par(mfrow=c(2,2)) image(M, main="Initial image") image(M0, main="Overlapping Quadripixels") image(M00, main="Non Overlapping Quadripixels") par(op)
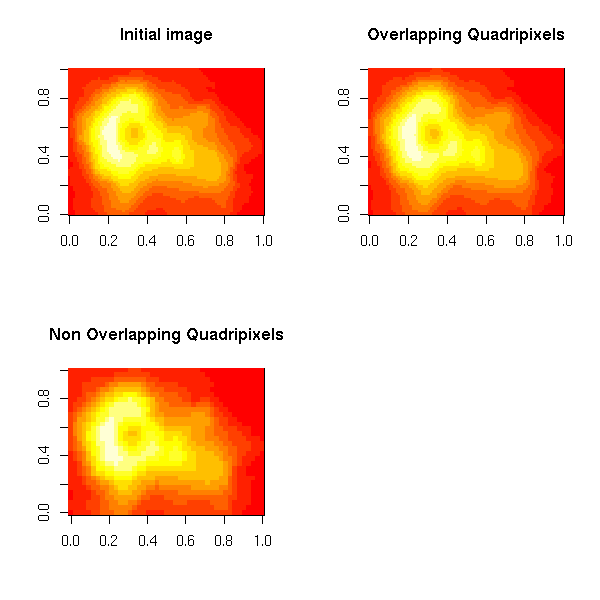
Construct a Van der Monde matrix.
outer(x, 0:n, '^')
Draw a graph from its indicence matrix.
n <- 100
m <- matrix(runif(2*n),nc=2)
library(ape)
r <- mst(dist(m)) # The incidence matrix (of the minimum spanning
# tree of the points)
plot(m)
n <- dim(r)[1]
w <- which(r!=0)
i <- as.vector(row(r))[w]
j <- as.vector(col(r))[w]
segments( m[i,1], m[i,2], m[j,1], m[j,2], col='red' )
TODO: Find other exercises.
R is not the best tool to process strings, but you sometimes have to do it.
Strings are delimited by double or single quotes.
> "Hello" == 'Hello' [1] TRUE
You do not print a string with the "print" function but with the "cat" function. The "print" function only gives you the representation of the string.
> print("Hello\n")
[1] "Hello\n"
> cat("Hello\n")
Hello
> s <- "C:\\Program Files\\" # At work, I am compelled to use Windows...
> print(s)
[1] "C:\\Program Files\\"
> cat(s, "\n")
C:\Program Files\You can concatenate strings with the "paste" function. To get the desired result, you may have to play with the "sep" argument.
> paste("Hello", "World", "!")
[1] "Hello World !"
> paste("Hello", "World", "!", sep="")
[1] "HelloWorld!"
> paste("Hello", " World", "!", sep="")
[1] "Hello World!"
> x <- 5
> paste("x=", x)
[1] "x= 5"
> paste("x=", x, paste="")
[1] "x= 5 "The "cat" function also accepts a "sep" argument.
> cat("x=", x, "\n")
x= 5
> cat("x=", x, "\n", sep="")
x=5Sometimes, you do not want to concatenate strings stored in different variables, but the elements of a vector of strings. If you want the result to be a single string, and not a vector of strings, you must add a "collapse" argument.
> s <- c("Hello", " ", "World", "!")
> paste(s)
[1] "Hello" " " "World" "!"
> paste(s, sep="")
[1] "Hello" " " "World" "!"
> paste(s, collapse="")
[1] "Hello World!"In some circumstances, you can even need both (the "cat" function does not accept this "collapse" argument).
> s <- c("Hello", "World!")
> paste(1:3, "Hello World!")
[1] "1 Hello World!" "2 Hello World!" "3 Hello World!"
> paste(1:3, "Hello World!", sep=":")
[1] "1:Hello World!" "2:Hello World!" "3:Hello World!"
> paste(1:3, "Hello World!", sep=":", collapse="\n")
[1] "1:Hello World!\n2:Hello World!\n3:Hello World!"
> cat(paste(1:3, "Hello World!", sep=":", collapse="\n"), "\n")
1:Hello World!
2:Hello World!
3:Hello World!The "nchar" function gives the length of a string (I am often looking for a "strlen" function: there it is).
> nchar("Hello World!")
[1] 12The "substring" function extract part of a string (the second argument is the starting position, the third argument is 1 + the end position).
> s <- "Hello World" > substring(s, 4, 6) [1] "lo "
The "strsplit" function splits a string into chunks, at each occurrence of a given "string".
> s <- "foo, bar, baz" > strsplit(s, ", ") [[1]] [1] "foo" "bar" "baz" > s <- "foo-->bar-->baz" > strsplit(s, "-->") [[1]] [1] "foo" "bar" "baz"
Actually, it is not a string, but a regular expression.
> s <- "foo, bar, baz" > strsplit(s, ", *") [[1]] [1] "foo" "bar" "baz"
You can also use it to get the individual characters of a string.
> strsplit(s, "") [[1]] [1] "f" "o" "o" "," " " "b" "a" "r" "," " " "b" "a" "z" > str(strsplit(s, "")) List of 1 $ : chr [1:13] "f" "o" "o" "," ...
The grep function looks for a "string" in a vector of strings.
> s <- apply(matrix(LETTERS[1:24], nr=4), 2, paste, collapse="")
> s
[1] "ABCD" "EFGH" "IJKL" "MNOP" "QRST" "UVWX"
> grep("O", s)
[1] 4
> grep("O", s, value=T)
[1] "MNOP"Actually, it does not look for a string, but for a regular expression.
If Perl is installed on your machine, you can simply type (to the shell)
man perlretut
and read its Regular Expression TUTorial.
(It may seem out of place to speak of regular expressions in a document about statistics: it is not. We shall see (well, not in the current version of this document, but soon -- I hope) that stochastic regular expressions are a generalization of Hidden Markov Models (HMM), which are the analogue of State Space Models for qualitative time series. If you understood the last sentence, you probably should not be reading this.)
The "regexpr" performs the same task as the "grep" function, but gives a different result: the position and length of the first match (or -1 if there is none)
> regexpr("o", "Hello")
[1] 5
attr(,"match.length")
[1] 1
> regexpr("o", c("Hello", "World!"))
[1] 5 2
attr(,"match.length")
[1] 1 1
> s <- c("Hello", "World!")
> i <- regexpr("o", s)
> i
[1] 5 2
attr(,"match.length")
[1] 1 1
> attr(i, "match.length")
[1] 1 1Sometimes, you want an "approximate" matches, not exact matches, accounting for potential spelling or typing mistakes: the "agrep" function provides suc a "fuzzy" matching. It is used by the "help.search" function.
> grep ("abc", c("abbc", "jdfja", "cba"))
numeric(0)
> agrep ("abc", c("abbc", "jdfja", "cba"))
[1] 1The "gsub" function replaces each occurrence of a string (a regular expression, actually) by a strin.
> s <- "foo bar baz"
> gsub(" ", "", s) # Remove all the spaces
[1] "foobarbaz"
> s <- "foo bar baz"
> gsub(" ", "", s)
[1] "foobarbaz"
> gsub(" ", " ", s)
[1] "foo bar baz"
> gsub(" +", "", s)
[1] "foobarbaz"
> gsub(" +", " ", s) # Remove multiple spaces and replace them by single spaces
[1] "foo bar baz"The "sub" is similar to "gsub" but only replaces the first occurrence.
> s <- "foo bar baz"
> sub(" ", "", s)
[1] "foobar baz"
When you read data from various sources, you often run into date format problem: different people, different software use different formats, different conventions. For instance, 01/02/03 can mean the first of february 2003 for some and the second of january 2003 for others -- and perhaps even the third of february 2001 for some. The only unambiguous, universal format is the ISO 8601 one, not really used by people but rather by programmers: dates are coded as
2005-15-05
The main rationale for this format is that when you write a numeric quantity you start with the largest units and end with the smallest; e.g., when you write "123", everyone understands "a hundred and twenty three": you start with the hundreds, proceed with the tens, and end with the units. Why should it be different for dates? We should start with the largest unit, the years, procedd with the next largest the months, and end with the smallest, the days.
This format has an advantage: if you want to sort data according to the date, your program just has to be able to sort strings, it need not be aware of dates.
You can extend the format with a time, but it becomes ambiguous:
2005-05-15 21:34:10.03
It does not look ambiguous (hours, minutes, seconds, hundredths of seconds -- for some applications, you may even need thousandths of seconds), but the time zone is missing. Most of the problems you have with times comes from those time zones.
To convert a string into a Date object:
> as.Date("2005-05-15")
[1] "2005-05-15"If you convert from an ambiguous format, you must specify the format:
> as.Date("15/05/2005", format="%d/%m/%Y")
[1] "2005-05-15"
> as.Date("15/05/05", format="%d/%m/%y")
[1] "2005-05-15"
> as.Date("01/02/03", format="%y/%m/%d")
[1] "2001-02-03"
> as.Date("01/02/03", format="%y/%d/%m")
[1] "2001-03-02"You can compute the difference between two dates -- it is a number of days.
> a <- as.Date("01/02/03", format="%y/%m/%d")
> b <- as.Date("01/02/03", format="%y/%d/%m")
> a - b
Time difference of -27 daysToday's date:
> Sys.Date() [1] "2005-05-16"
You can add a Date and a number (a number of days).
> Sys.Date() + 21 [1] "2005-06-06"
You can format the date to produce one of those ambiguous formats your clients like.
> format(Sys.Date(), format="%d%m%y") [1] "160505" > format(Sys.Date(), format="%A, %d %B %Y") [1] "Monday, 16 May 2005"
The format is described in the manpage of the "strftime" function.
If you want to extract part of a date, you can use the format" function. For instance, if I want to aggregate my data by month, I can use
d$month <- format( d$date, format="%Y-%m" )
For looping purposes, you might need series of dates: you may want to use the "seq" function.
?seq.Date
> seq(as.Date("2005-01-01"), as.Date("2005-07-01"), by="month")
[1] "2005-01-01" "2005-02-01" "2005-03-01" "2005-04-01" "2005-05-01"
[6] "2005-06-01" "2005-07-01"
# A month is not always 31 days...
> seq(as.Date("2005-01-01"), as.Date("2005-07-01"), by=31)
[1] "2005-01-01" "2005-02-01" "2005-03-04" "2005-04-04" "2005-05-05"
[6] "2005-06-05"
> seq(as.Date("2005-01-01"), as.Date("2005-03-01"), by="2 weeks")
[1] "2005-01-01" "2005-01-15" "2005-01-29" "2005-02-12" "2005-02-26"However, you should be aware that loops tend to turn Dates into numbers.
> a <- seq(as.Date("2005-01-01"), as.Date("2005-03-01"), by="2 weeks")
> str(a)
Class 'Date' num [1:5] 12784 12798 12812 12826 12840
> for (i in a) {
+ str(i)
+ }
num 12784
num 12798
num 12812
num 12826
num 12840Inside the loop, you may want to add
for (i in dates) {
i <- as.Date(i)
...
}There is another caveat about the use of dates as indices to arrays: as a date is actually a number, if you use it as an index, R will understand the number used to code the date (say 12784 for 2005-01-01) as a row or column number, nor a row or column name. When using dates as indices, always convert them into strings.
a <- matrix(NA, nr=10, nc=12)
rownames(a) <- LETTERS[1:10]
dates <- seq(as.Date("2004-01-01"), as.Date("2004-12-01"),
by="month"))
colnames(a) <- as.character( dates )
for (i in dates) {
i <- as.Date(i)
a[, as.character(i)] <- 1
}There are other methods:
> methods(class="Date") [1] as.character.Date as.data.frame.Date as.POSIXct.Date c.Date [5] cut.Date -.Date [<-.Date [.Date [9] [[.Date +.Date diff.Date format.Date [13] hist.Date* julian.Date Math.Date mean.Date [17] months.Date Ops.Date plot.Date* print.Date [21] quarters.Date rep.Date round.Date seq.Date [25] summary.Date Summary.Date trunc.Date weekdays.Date
For the time (up to the second, only):
> as.POSIXct("2005-05-15 21:45:17")
[1] "2005-05-15 21:45:17 BST"
> as.POSIXlt("2005-05-15 21:45:17")
[1] "2005-05-15 21:45:17"The two classes are interchangeable, only the internal representation changes (use the first, more compact, one in data.frames).
> unclass(as.POSIXct("2005-05-15 21:45:17"))
[1] 1116189917
attr(,"tzone")
[1] ""
> unclass(as.POSIXlt("2005-05-15 21:45:17"))
$sec
[1] 17
$min
[1] 45
$hour
[1] 21
$mday
[1] 15
$mon
[1] 4
$year
[1] 105
$wday
[1] 0
$yday
[1] 134
$isdst
[1] 1You can also perform a few computations
> as.POSIXlt("2005-05-15 21:45:17") - Sys.time()
Time difference of -1.007523 daysThis is actually a call to the "difftime" function (the unit is automatically chose so that the result be readable).
> difftime(as.POSIXlt("2005-05-15 21:45:17"), Sys.time(), units="secs")
Time difference of -87246 secsShould you be unhappy with those date and time classes, there is host of packages that provide replacements for them.
date (only dates, not times; rather limited, probably old,
ignores ISO 8601)
chron (no timezones or daylight saving times: this is a
limitation, but as many problems come from timezones, it
may be an advantage)
zoo (Important)When reading a data.frame containing dates in a column, from a file, you can either read the column as strings and convert it afterwards,
d <- read.table("foo.txt")
d$Date <- as.Date( as.character( d$Date ) )or explicitely state it is a Date
read.table("foo.txt", colClasses=c("Date", "character", rep(10, "numeric")))If the format is not the international one, it may be trickier. One solution is to create your own class, that inherits from Date, but with a different method to convert from strings.
setClass("Date")
setClass("USDate", contains="Date")
setAs("character", "USDate",
function (from) { as.Date(from, format="%m/%d/%Y") })
read.table("foo.txt", colClasses=c("USDate", "character", rep(10, "numeric")))TODO: and if we need hundredths or thousandths of seconds?
There is an R-News article about date anhd time handling in R:
http://cran.r-project.org/doc/Rnews/Rnews_2004-1.pdf
Some of the intricacies of time and date handling are well known (some months are 30-day long, others 31-day long, one 28-day long -- or 29, every fourth year), others are not. But actually, every hundredth year, the year that should be leap is not: 1700, 1800, 1900 were not leap years. And this exception has exceptions: every fourth century, the would-be leap year that should not be leap actually is -- 2000 was a leap year, 2400 will be one.
But this was just for dates: there are similar problems with time. We have, from time to time, to add a second to the day. This has already happened 18 times.
> .leap.seconds [1] "1972-07-01 01:00:00 BST" "1973-01-01 00:00:00 GMT" [3] "1974-01-01 00:00:00 GMT" "1975-01-01 00:00:00 GMT" [5] "1976-01-01 00:00:00 GMT" "1977-01-01 00:00:00 GMT" [7] "1978-01-01 00:00:00 GMT" "1979-01-01 00:00:00 GMT" [9] "1980-01-01 00:00:00 GMT" "1981-07-01 01:00:00 BST" [11] "1983-07-01 01:00:00 BST" "1985-07-01 01:00:00 BST" [13] "1986-07-01 01:00:00 BST" "1988-01-01 00:00:00 GMT" [15] "1990-01-01 00:00:00 GMT" "1991-01-01 00:00:00 GMT" [17] "1992-07-01 01:00:00 BST" "1993-07-01 01:00:00 BST" [19] "1994-07-01 01:00:00 BST" "1996-01-01 00:00:00 GMT" [21] "1997-07-01 01:00:00 BST" "1999-01-01 00:00:00 GMT"
The next one will be in december 2005.
Leap years are due to the fact that there is not a whole number of days in a year; similarly, leap secons are due to the fact that there is not a whole number of seconds in a day.
http://en.wikipedia.org/wiki/Leap_second http://hpiers.obspm.fr/eop-pc/earthor/utc/leapsecond.html http://www.ucolick.org/~sla/leapsecs/onlinebib.html
Actually, I have never used this function: let me just list a few uncommented examples.
?match # Get the 2's and 4's x[as.logical( match(x, c(2,4), nomatch=0) )]
There are a few function written with "match":
> setdiff
function (x, y)
unique(if (length(x) || length(y)) x[match(x, y, 0) == 0] else x)
<environment: namespace:base>
> match.fun("%in%")
function (x, table)
match(x, table, nomatch = 0) > 0
<environment: namespace:base>
> intersect
function (x, y)
unique(y[match(x, y, 0)])
<environment: namespace:base>
> is.element
function (el, set)
match(el, set, 0) > 0
<environment: namespace:base>
> setequal
function (x, y)
all(c(match(x, y, 0) > 0, match(y, x, 0) > 0))
<environment: namespace:base>Exercice: How would we find ALL the functions whose definition uses "match"?
TODO: simplify the following code and state its limitations (limited
to visible loaded functions)
a <- lapply(search(), ls)
names(a) <- search()
a <- unlist(a)
names(a) <- a
a <- a[ sapply(a,
function (x) {
try( x <- match.fun(x) )
is.function(x)
}) ]
a <- lapply(a, match.fun)
b <- lapply(a, deparse)
b <- lapply(b, length)
b <- order(unlist(b))
a <- a[b]
i <- lapply(a, function(x) { length(grep("match\\(", deparse(x)))>0 })
i <- unlist(i)
a[i]
If you know (or even simply if you suspect) problems in your code, you can ask the R interpreter to be more rigorous, by saying
options(warn=1)
which prints the warning messages when they appear (and not at the end on the execution, as usual), or even
options(warn=2)
which turns the warning messages into real errors, that stop the execution.
One of the simplest ways to find the location of a bug in a program (once we have witnessed an abnormal behaviour) is to add "print" statement at the problematic locations, to see if the code breaks before that point, or to have a look at the data the functions are playing with (quite often, you have a number or NULL while you would expect a vector, or you have a vector instead of a matrix, or you have a vector of strings instead of a vector of numbers, or complex numbers have appeared, unnoticed, at some way in you code).
TODO: detail the functions
print cat str unclass
TODO: log4R (no, it does not exist).
The "debug" command tags a function so that, when run, it be executed step by step.
> debug(f)
> f(3)
debugging in: f(3)
debug: {
x^2 + x + 1
}
Browse[1]>
debug: x^2 + x + 1
Browse[1]>
exiting from: f(3)
[1] 13
> undebug(f)
The "browser" function adds a breakpoint in the code.
For instance, if we run the following function,
f <- function () {
x <- rnorm(10)
y <- rnorm(11)
browser()
x + y
}R will stop when it encounters the "browser()" call.
> f() Called from: f() Browse[1]>
You can then type in expressions, functions, to examine the environment where it stopped.
> f()
Called from: f()
Browse[1]> x
[1] -1.6684445 -1.4662686 -1.3792824 0.1103995 0.7431116 -1.9117947
[7] 0.5333812 -0.6695517 -1.2382940 -0.3560036
Browse[1]> str(x)
num [1:10] -1.668 -1.466 -1.379 0.110 0.743 ...
Browse[1]> str(y)
num [1:11] 0.247 -0.505 0.197 -0.468 1.446 ...
Browse[1]> x + y
[1] -1.42137599 -1.97117326 -1.18208672 -0.35809903 2.18871467 -2.16168749
[7] 0.88886591 -2.85428126 -0.85448640 0.37425241 -0.02050070
Warning message:
longer object length
is not a multiple of shorter object length in: x + yYou can type "n" to execute the next instruction (and stop again) or "c" to resume the execution, until the next stop.
The "traceback" command prints the callstack, i.e., the list of functions that were called when the latest error occurred.
?traceback
The "dump.frames" command yields the equivalent of a "core" file (the state of the interpretor at a given moment, typically, just after an error), we can then examine with the "debugger" command.
?dump.frames
The "sys.calls" function gives the list of the functions that have been called, with all their arguments.
f <- function () { g(1) }
g <- function (...) { h(17^2) }
h <- function (x) {
print( sqrt(x) )
sys.calls()
}This yields:
> str( f() ) [1] 17 Dotted pair list of 4 $ : language str(f()) $ : language f() $ : language g(1) $ : language h(17^2)
Here is an application of this "sys.calls" function: when you write a new function, especially a function that will be implicitely called (typically, a function of the form "[.foo", which is the overloaded "[" operator for an S3 class "foo"), you might want to know from where it was called. To this end, you can call the following "function.print" at the start of your function.
function.print <- function () {
l <- sys.calls()
s <- lapply(l, function (x) { as.character(x[[1]]) })
s <- unlist(s)
s <- s[-length(s)]
cat("Stack: ", paste(s, collapse="/"), "(", sep="")
cat(paste(as.character(l[[ length(l)-1 ]][-1]), collapse=","))
cat(")\n")
}
f <- function (...) { g(17) }
g <- function (...) { function.print() }This yields:
> f(2,11) Stack: f/g(17)
To check that your functions behave as expected (one could say, "to check that they respect their contracts"), people sometimes add comments saying "this should be so and so". This is a bad practice, because the computer does not read the comments. Instead, you can actually check that "this is so and so". This is called an assertion.
Typically, assertions check thigs that should always be true: if they are broken, they reveal there is problem in the code, that should be fixed. And the program stops, often violently.
As R is an interpreted environment, one often uses assertions to check both the internal consistency of the code (the "things that should always be true") and how the code is used (if the arguments you give to a function are not those expected, the function should not return anything, and the computations should be halted until the problem is corrected).
The "assert" function is not called "assert", but "stopifnot".
TODO: An example
If you want to be less violent when you check the arguments given to a function, you can decide to return NULL or NA (as appropriate) a give a warning. For instance:
> mean.default
function (x, trim = 0, na.rm = FALSE, ...)
{
if (!is.numeric(x) && !is.complex(x) && !is.logical(x)) {
warning("argument is not numeric or logical: returning NA")
return(as.numeric(NA))
}
...I am not very happy with the "assert" function: it tells me something is wrong, it tells me where, but neither does it tell me how we got there, nor offers me to examine what happenned. This suggests to use the "sys.calls" and "browser" functions, to print the calling stack and to insert a break point where the problem occurred.
assert <- function (condition, ...) {
mc <- match.call()
if (!is.logical(eval(condition)) || ! all(condition)) {
cat("Assertion failled:",
deparse(mc[[2]]), "is not TRUE\n")
ll <- list(...)
for (i in seq(along=ll)) {
cat(" ", deparse(mc[[i+2]]), ": ", ll[[i]], "\n", sep="")
}
ca <- sys.calls()
cat(paste(length(ca):1, ": ", rev(ca), sep="", collapse="\n"), "\n")
cat("BROWSER (type 'c' to quit):\n")
browser()
stop(paste(deparse(mc[[2]]), "is not TRUE"), call.=FALSE)
}
}TODO: test this function TODO: is "browser" called in the right environment?
TODO
"Profiling" means "finding where the program we have just written spends most of its time, in order to rethink, rewrite or rewrite in C those time-consuming parts. It is very useful when R is used for prototyping (i.e., to test algorithms, to see if they actually work, before using them in real applications).
The "system.time" tells you how much time was spent inside a command.
several.times <- function (n, f, ...) {
for (i in 1:n) {
f(...)
}
}
matrix.multiplication <- function (s) {
A <- matrix(1:(s*s), nr=s, nc=s)
B <- matrix(1:(s*s), nr=s, nc=s)
C <- A %*% B
}
v <- NULL
for (i in 2:10) {
v <- append(
v,
system.time(
several.times(
10000,
matrix.multiplication,
i
)
) [1]
)
}
plot(v, type = 'b', pch = 15,
main = "Matrix product computation time")
But this is too coarse: we can compare the spped of two functions, but given a slow function, we still need to find the parts of the functions responsible for this. Here comes the "Rprof" command.
?Rprof
Example:
Rprof() n <- 200 m <- matrix(rnorm(n*n), nr=n, nc=n) eigen(m)$vectors[,c(1,2)] Rprof(NULL)
We then look at the result (we are no longer under R; we call R from the shell, with other options):
% R CMD Rprof Rprof.out Each sample represents 0.02 seconds. Total run time: 0.9 seconds. Total seconds: time spent in function and callees. Self seconds: time spent in function alone. % total % self total seconds self seconds name 95.56 0.86 2.22 0.02 "eigen" 82.22 0.74 82.22 0.74 ".Fortran" 11.11 0.10 4.44 0.04 "all.equal.numeric" 4.44 0.04 0.00 0.00 "matrix" 4.44 0.04 0.00 0.00 "as.vector" 4.44 0.04 4.44 0.04 "rnorm" 2.22 0.02 2.22 0.02 "<Anonymous>" 2.22 0.02 2.22 0.02 "|" 2.22 0.02 2.22 0.02 "t.default" 2.22 0.02 0.00 0.00 "mean" 2.22 0.02 0.00 0.00 "t" % self % total self seconds total seconds name 82.22 0.74 82.22 0.74 ".Fortran" 4.44 0.04 11.11 0.10 "all.equal.numeric" 4.44 0.04 4.44 0.04 "rnorm" 2.22 0.02 2.22 0.02 "<Anonymous>" 2.22 0.02 2.22 0.02 "|" 2.22 0.02 2.22 0.02 "t.default" 2.22 0.02 95.56 0.86 "eigen"
The easiest (not the cleanest) way of defining classes in R is simply to attach a "class" attribute to an object and to define functions that look up this attribute and act accordingly.
TODO: rewrite this section, stressing the difference between those two paradigms. Introduction: the "print" method Other common methods: print, str, summary, predict, plot, List of all the methods of all classes Writing your own classes and methods More complex examples: Overloading [, [<-, etc. (a simple "panel data" class?)
When we print certain objects, they do not look like the simple types we have described (vector, array, data.frame). This is the case for the results of a regression.
n <- 200 x <- rnorm(n) y <- 1 - 2 * x + rnorm(n) r1 <- lm(y~x) r2 <- summary(r1)
This yields
> r1
Call:
lm(formula = y ~ x)
Coefficients:
(Intercept) x
0.924 -2.042
> r2
Call:
lm(formula = y ~ x)
Residuals:
Min 1Q Median 3Q Max
-2.85364 -0.66754 -0.04169 0.61238 2.78004
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 0.92395 0.07345 12.58 <2e-16 ***
x -2.04152 0.07613 -26.82 <2e-16 ***
---
Signif. codes: 0 `***' 0.001 `**' 0.01 `*' 0.05 `.' 0.1 ` ' 1
Residual standard error: 1.038 on 198 degrees of freedom
Multiple R-Squared: 0.7841, Adjusted R-squared: 0.783
F-statistic: 719.1 on 1 and 198 DF, p-value: < 2.2e-16Yet, the "str" command tells us this is truly one of the simple types we have already seen, often, a list -- here, I removed a part of it -- it was too huge.
> str(r2) List of 11 $ call : language lm(formula = y ~ x) $ terms :Classes 'terms', 'formula' length 3 y ~ x .. ..- attr(*, "variables")= language list(y, x) .. ..- attr(*, "factors")= int [1:2, 1] 0 1 .. .. ..- attr(*, "dimnames")=List of 2 .. .. .. ..$ : chr [1:2] "y" "x" .. .. .. ..$ : chr "x" (...) - attr(*, "class")= chr "summary.lm"
There is one difference between the lists we created earlier: the "class" attribute. The "r1" and "r2" objects we have just created belong the the "lm" and "summary.lm" classes. As a result, certain "generic" functions we apply to these objects are changed: this is the case for the "print", "summary" and "plot" functions -- let us focus on "print".
> print
function (x, ...)
UseMethod("print")
<environment: namespace:base>
> print.lm
function (x, digits = max(3, getOption("digits") - 3), ...)
{
cat("\nCall:\n", deparse(x$call), "\n\n", sep = "")
if (length(coef(x))) {
cat("Coefficients:\n")
print.default(format(coef(x), digits = digits), print.gap = 2,
quote = FALSE)
}
else cat("No coefficients\n")
cat("\n")
invisible(x)
}
<environment: namespace:base>The "print" function, in this case, is called a "generic method": the function actually called will depend on the class of the object we apply it to.
The "methods" command gives the list of all the implementations of this method.
> methods(plot)
[1] plot.acf* plot.ACF* plot.augPred*
[4] plot.compareFits* plot.data.frame plot.decomposed.ts*
[7] plot.default plot.dendrogram* plot.density
[10] plot.factor plot.formula plot.function
[13] plot.gls* plot.hclust* plot.histogram
[16] plot.HoltWinters* plot.intervals.lmList* plot.isoreg*
[19] plot.lm plot.lme plot.lme1*
[22] plot.lmList* plot.mlm plot.nffGroupedData*
[25] plot.nfnGroupedData* plot.nls* plot.nmGroupedData*
[28] plot.pdMat* plot.POSIXct plot.POSIXlt
[31] plot.ppr* plot.prcomp* plot.princomp*
[34] plot.profile.nls* plot.ranef.lme* plot.ranef.lmList*
[37] plot.shingle* plot.simulate.lme* plot.spec
[40] plot.spec1* plot.spec.coherency plot.spec.phase
[43] plot.stl* plot.table plot.ts
[46] plot.tskernel* plot.TukeyHSD plot.Variogram*
Non-visible functions are asteriskedIf you want to see the code of one of the non-visible functions, you can use the "getAnywhere" of the "getS3method" function.
> plot.Date
Error: Object "plot.Date" not found
> getAnywhere("plot.Date")
A single object matching `plot.Date' was found
It was found in the following places
registered S3 method for plot from namespace graphics
namespace:graphics
with value
function (x, y, xlab = "", axes = TRUE, frame.plot = axes, xaxt = par("xaxt"),
...)
{
axisInt <- function(x, main, sub, xlab, ylab, col, lty, lwd,
xlim, ylim, bg, pch, log, asp, ...) axis.Date(1, x, ...)
plot.default(x, y, xaxt = "n", xlab = xlab, axes = axes,
frame.plot = frame.plot, ...)
if (axes && xaxt != "n")
axisInt(x, ...)
}
<environment: namespace:graphics>
> getS3method("plot", "Date")
function (x, y, xlab = "", axes = TRUE, frame.plot = axes, xaxt = par("xaxt"),
...)
{
axisInt <- function(x, main, sub, xlab, ylab, col, lty, lwd,
xlim, ylim, bg, pch, log, asp, ...) axis.Date(1, x, ...)
plot.default(x, y, xaxt = "n", xlab = xlab, axes = axes,
frame.plot = frame.plot, ...)
if (axes && xaxt != "n")
axisInt(x, ...)
}
<environment: namespace:graphics>Let us remark that an object may have several types: the "class" attribute may contain a string or a vector of strings -- when we call the function, the computer tries all the types specified in this vector, until it finds a method. If it finds none, it uses the "default" class. In object-oriented parlance, this is called "inheritance".
For instance, the result of the "aov" command
n <- 500 x <- rnorm(n) y <- 1 - x + rnorm(n) r <- aov(y~x)
belongs to the classes "aov" and "lm" (in object-oriented programming, the "aov" class inherits from "lm", i.e., an "aov" object is an "lm" object -- the relation is sometimes called the "is a" (or "ISA") relation).
> class(r) [1] "aov" "lm" > attr(r,"class") [1] "aov" "lm"
There are many things one can want to do with an object that, from the user's point of view should work for any object -- but that, from the programmer's point of view, require completely different implementations: for instance, displaying all the contents of an object (with the "print" function -- this function is automatically called when R prints a result -- for the Java programmers among you, this is the analogue of the toString method), plotting an object (with the "plot") function or displaying its structure (with the "str" function).
All this seems to be done from a single function.
But actually, the sole role of that function is to check the type of its argument and call the (type-dependant) function that actually does the job.
> print
function (x, ...)
UseMethod("print")
<environment: namespace:base>
> methods("print")
[1] print.Arima* print.AsIs
[3] print.Bibtex* print.DLLInfo
[5] print.DLLInfoList print.DLLRegisteredRoutines
[7] print.Date print.HoltWinters*
[9] print.Latex* print.MethodsFunction*
[11] print.MethodsList* print.NativeRoutineList
[13] print.POSIXct print.POSIXlt
[15] print.RGBcolorConverter* print.StructTS*
[17] print.TukeyHSD* print.acf*
[19] print.anova print.anova.gam
[21] print.aov* print.aovlist*
[23] print.ar* print.arima0*
[25] print.by print.checkDocFiles*
[27] print.checkDocStyle* print.checkFF*
[29] print.checkReplaceFuns* print.checkS3methods*
[31] print.checkTnF* print.checkVignettes*
[33] print.check_Rd_files_in_Rd_db* print.check_Rd_xrefs*
[35] print.check_code_usage_in_package* print.check_demo_index*
[37] print.check_make_vars* print.check_package_depends*
[39] print.check_package_description* print.check_vignette_index*
[41] print.citation* print.citationList*
[43] print.classRepresentation* print.codoc*
[45] print.codocClasses* print.codocData*
[47] print.colorConverter* print.condition
[49] print.connection print.data.frame
[51] print.default print.dendrogram*
[53] print.density print.difftime
[55] print.dist* print.dummy_coef*
[57] print.dummy_coef_list* print.ecdf*
[59] print.factanal* print.factor
[61] print.family print.formula
[63] print.ftable print.gam
[65] print.getAnywhere* print.glm
[67] print.hclust* print.help_files_with_topic*
[69] print.hexmode print.hsearch*
[71] print.htest* print.infl
[73] print.integrate print.isoreg*
[75] print.kmeans* print.libraryIQR
[77] print.listof print.lm
[79] print.loadings* print.loess*
[81] print.logLik print.ls_str*
[83] print.medpolish* print.mtable*
[85] print.nls* print.noquote
[87] print.octmode print.packageDescription*
[89] print.packageIQR* print.packageInfo
[91] print.packageStatus* print.package_version
[93] print.pairwise.htest* print.power.htest*
[95] print.ppr* print.prcomp*
[97] print.princomp* print.recordedplot*
[99] print.restart print.rle
[101] print.sessionInfo* print.simple.list
[103] print.smooth.spline* print.socket*
[105] print.stepfun* print.stl*
[107] print.subdir_tests* print.summary.aov*
[109] print.summary.aovlist* print.summary.gam
[111] print.summary.glm* print.summary.lm*
[113] print.summary.loess* print.summary.manova*
[115] print.summary.nls* print.summary.ppr*
[117] print.summary.prcomp* print.summary.princomp*
[119] print.summary.table print.table
[121] print.tables_aov* print.terms
[123] print.ts print.tskernel*
[125] print.tukeyline* print.tukeysmooth*
[127] print.undoc* print.vignette*
[129] print.xgettext* print.xngettext*
[131] print.xtabs*
Non-visible functions are asterisked(The exact list you get will depend on the packages you have loaded: you can have much more than that.)
To get the actual code, just type the name of the function (the method, dot, the type):
> print.lm
function (x, digits = max(3, getOption("digits") - 3), ...)
{
cat("\nCall:\n", deparse(x$call), "\n\n", sep = "")
if (length(coef(x))) {
cat("Coefficients:\n")
print.default(format(coef(x), digits = digits), print.gap = 2,
quote = FALSE)
}
else cat("No coefficients\n")
cat("\n")
invisible(x)
}
<environment: namespace:stats>For hidden objects, you can obtain the code with the getAnywhere function.
> print.acf
Error: object "print.acf" not found
> getAnywhere("print.acf")
A single object matching 'print.acf' was found
It was found in the following places
registered S3 method for print from namespace stats
namespace:stats
with value
function (x, digits = 3, ...)
{
type <- match(x$type, c("correlation", "covariance", "partial"))
msg <- c("Autocorrelations", "Autocovariances", "Partial autocorrelations")
cat("\n", msg[type], " of series ", sQuote(x$series), ", by lag\n\n",
sep = "")
nser <- ncol(x$lag)
if (type != 2)
x$acf <- round(x$acf, digits)
if (nser == 1) {
acfs <- drop(x$acf)
names(acfs) <- format(drop(x$lag), digits = 3)
print(acfs, digits = digits, ...)
}
else {
acfs <- format(x$acf, ...)
lags <- format(x$lag, digits = 3)
acfs <- array(paste(acfs, " (", lags, ")", sep = ""),
dim = dim(x$acf))
dimnames(acfs) <- list(rep("", nrow(x$lag)), x$snames,
x$snames)
print(acfs, quote = FALSE, ...)
}
invisible(x)
}
<environment: namespace:stats>If you know the namespace of your function, you can also obtain it with the ::: operator (twice for non-hidden functions, thrice for hidden ones).
> stats:::print.acf
function (x, digits = 3, ...)
{
type <- match(x$type, c("correlation", "covariance", "partial"))
...
The class of an object is just a string attribute, attached to it -- if you want to add information to an object, typically metadata, just put it in the attributes.
> class(x) [1] "numeric" > mode(x) # The class the object would have were there no attribute [1] "numeric" > r <- lm(y ~ x) > class(r) [1] "lm" > mode(r) [1] "list" > attributes(r) $names [1] "coefficients" "residuals" "effects" "rank" [5] "fitted.values" "assign" "qr" "df.residual" [9] "xlevels" "call" "terms" "model" $class [1] "lm" > attr(r, "class") [1] "lm"
Here are a few examples of generic functions, that can be used with a large number of classes:
print str plot predict seq anova
If you want more:
> methods(class="default") [1] AIC.default* Axis.default* add1.default* [4] aggregate.default all.equal.default ansari.test.default* [7] ar.burg.default* ar.yw.default* as.Date.default [10] as.POSIXct.default as.character.default as.complex.default [13] as.data.frame.default as.dist.default* as.double.default [16] as.expression.default as.function.default as.hclust.default* [19] as.integer.default as.list.default as.logical.default [22] as.matrix.default as.null.default as.person.default* [25] as.personList.default* as.single.default as.stepfun.default* [28] as.table.default as.ts.default* barplot.default [31] bartlett.test.default* biplot.default* boxplot.default [34] by.default case.names.default* cdplot.default* [37] coef.default* confint.default contour.default [40] cophenetic.default* cor.test.default* cut.default [43] cycle.default* deltat.default* density.default [46] deriv.default deriv3.default deviance.default* [49] df.residual.default* diff.default diffinv.default* [52] drop1.default* duplicated.default edit.default* [55] end.default* fitted.default* fligner.test.default* [58] format.default formula.default* frequency.default* [61] friedman.test.default* ftable.default* getInitial.default* [64] head.default* hist.default identify.default* [67] image.default is.na<-.default kappa.default [70] kernapply.default* kruskal.test.default* labels.default [73] lag.default* levels<-.default lines.default [76] makepredictcall.default* mean.default merge.default [79] model.frame.default model.matrix.default monthplot.default* [82] mood.test.default* mosaicplot.default* na.action.default* [85] na.contiguous.default* na.exclude.default* na.fail.default* [88] na.omit.default* names.default names<-.default [91] napredict.default* naprint.default* naresid.default* [94] pacf.default* pairs.default persp.default* [97] plot.default points.default ppr.default* [100] prcomp.default* princomp.default* print.default [103] proj.default* prompt.default* qqnorm.default [106] quade.test.default* quantile.default range.default [109] relevel.default* rep.default residuals.default [112] rev.default row.names.default row.names<-.default [115] rowsum.default scale.default selfStart.default* [118] seq.default solve.default sortedXyData.default* [121] spineplot.default* split.default split<-.default [124] stack.default start.default* str.default* [127] subset.default summary.default t.default [130] t.test.default* tail.default* terms.default [133] text.default time.default* toString.default [136] transform.default unique.default unstack.default [139] update.default var.test.default* variable.names.default* [142] weights.default* wilcox.test.default* window.default* [145] with.default > methods(class="lm") [1] add1.lm* alias.lm* anova.lm case.names.lm* [5] confint.lm* cooks.distance.lm* deviance.lm* dfbeta.lm* [9] dfbetas.lm* drop1.lm* dummy.coef.lm* effects.lm* [13] extractAIC.lm* family.lm* formula.lm* hatvalues.lm [17] influence.lm* kappa.lm labels.lm* logLik.lm* [21] model.frame.lm model.matrix.lm plot.lm predict.lm [25] print.lm proj.lm* residuals.lm rstandard.lm [29] rstudent.lm simulate.lm* summary.lm variable.names.lm* [33] vcov.lm*
Here is another way of getting all the methods (the functions in whose code the string "UseMethod" appears, in any loaded namespace, whether they are visible or not).
res <- character(0)
env <- append(
lapply(search(), function (x) as.environment(x)),
lapply(loadedNamespaces(), function (x) asNamespace(x))
)
for (e in env) {
n <- ls(envir=e)
l <- lapply(n, function (x) {
x <- get(x, envir=e)
x <- deparse(x)
x <- paste(x, collapse="")
length(grep("UseMethod", x)) > 0
})
l <- unlist(l)
res <- c(res, n[l])
}
res <- unique(res)
resHere are the most often used.
names(res) <- res res <- lapply(res, function (x) try(length(methods(x)))) res <- res[unlist(lapply(res, is.numeric))] res <- unlist(res) head(sort(res, dec=TRUE), 40)
This yields:
> length(res)
[1] 211
> head(sort(res, dec=TRUE), 40)
print plot summary predict
168 53 50 32
as.data.frame resid residuals format
26 13 13 12
coef coefficients vcov fitted
11 11 10 9
fitted.values anova formula all.equal
9 8 8 8
extractAIC head tail as.Date
7 7 7 7
Predict.matrix smooth.construct logLik image
6 6 6 6
lines as.POSIXct as.matrix mean
6 6 6 6
add1 confint deviance drop1
5 5 5 5
model.frame str diff duplicated
5 5 5 5
labels unique kurtosis skewness
5 5 4 4
You can define your own "classes" and overload the "plot", "print" and "summary" functions.
> print.foo <- function (x,...) {
print.default(x)
print.default(min(x))
print.default(median(x))
print.default(max(x))
}
> x <- matrix( rnorm(20), nrow=4 )
> print(x)
[,1] [,2] [,3] [,4] [,5]
[1,] 0.05858332 -0.3082483 1.08259617 -0.10539949 -0.3734017
[2,] 0.23264808 -0.4763760 -0.01989608 -0.07837898 2.3640196
[3,] 0.05239833 -0.6764430 -0.76649216 0.76078938 0.2715206
[4,] 0.27780672 -0.5458009 -0.96929622 0.90089157 1.7325063
> class(x)
[1] "matrix"
> class(x) <- c("foo", class(x))
> print(x)
[,1] [,2] [,3] [,4] [,5]
[1,] 0.05858332 -0.3082483 1.08259617 -0.10539949 -0.3734017
[2,] 0.23264808 -0.4763760 -0.01989608 -0.07837898 2.3640196
[3,] 0.05239833 -0.6764430 -0.76649216 0.76078938 0.2715206
[4,] 0.27780672 -0.5458009 -0.96929622 0.90089157 1.7325063
attr(,"class")
[1] "foo"
[1] -0.9692962
[1] 0.01625113
[1] 2.364020Actually, you might want to use cat() instead of print().
print.foo <- function (x,...) {
cat("foo: ", length(x), " values between ",
min(x), " and ", max(x), "\n", sep="")
cat(" ", "mean: ", mean(x),
" median: ", median(x), "\n", sep="")
print(x)
}
You can define your own overloadable functions as:
print <- function (x, ...) UseMethod("print")
The "getS3method" starts with
> getS3method
function (f, class, optional = FALSE)
{
knownGenerics <- c(tools:::.get_internal_S3_generics(), names(.knownS3Generics))
...So we can get all the gemeric methods as follows (these are only the methods currently loaded):
> tools:::.get_internal_S3_generics(); names(.knownS3Generics) [1] "[" "[[" "$" "[<-" [5] "[[<-" "$<-" "length" "dimnames<-" [9] "dimnames" "dim<-" "dim" "c" [13] "unlist" "as.character" "as.vector" "is.array" [17] "is.atomic" "is.call" "is.character" "is.complex" [21] "is.double" "is.environment" "is.function" "is.integer" [25] "is.language" "is.logical" "is.list" "is.matrix" [29] "is.na" "is.nan" "is.null" "is.numeric" [33] "is.object" "is.pairlist" "is.recursive" "is.single" [37] "is.symbol" "abs" "sign" "sqrt" [41] "floor" "ceiling" "trunc" "round" [45] "signif" "exp" "log" "cos" [49] "sin" "tan" "acos" "asin" [53] "atan" "cosh" "sinh" "tanh" [57] "acosh" "asinh" "atanh" "lgamma" [61] "gamma" "gammaCody" "digamma" "trigamma" [65] "tetragamma" "pentagamma" "cumsum" "cumprod" [69] "cummax" "cummin" "+" "-" [73] "*" "/" "^" "%%" [77] "%/%" "&" "|" "!" [81] "==" "!=" "<" "<=" [85] ">=" ">" "all" "any" [89] "sum" "prod" "max" "min" [93] "range" "Arg" "Conj" "Im" [97] "Mod" "Re" [1] "Math" "Ops" "Summary" "Complex" [5] "as.character" "as.data.frame" "as.matrix" "as.vector" [9] "labels" "print" "solve" "summary" [13] "t" "edit" "str" "contour" [17] "hist" "identify" "image" "lines" [21] "pairs" "plot" "points" "text" [25] "add1" "AIC" "anova" "biplot" [29] "coef" "confint" "deviance" "df.residual" [33] "drop1" "extractAIC" "fitted" "formula" [37] "logLik" "model.frame" "model.matrix" "predict" [41] "profile" "qqnorm" "residuals" "se.contrast" [45] "terms" "update" "vcov"
You can get all the classes (only those currently loaded, actually), as follows.
> g <- c(tools:::.get_internal_S3_generics(), names(.knownS3Generics))
> r <- sapply(g[1:3], methods)
> r[[ which.max(sapply(r, length)) ]] <- NULL # This was not a class
> r <- sort(unique(gsub("^[^\\.]+\\.", "", unlist(r))))
> r
[1] "acf" "anova"
[3] "aov" "aovlist"
[5] "ar" "Arima"
[7] "arima0" "AsIs"
[9] "Bibtex" "by"
[11] "character.condition" "character.Date"
[13] "character.default" "character.error"
[15] "character.factor" "character.octmode"
[17] "character.package_version" "character.person"
[19] "character.personList" "character.POSIXt"
[21] "check_demo_index" "checkDocFiles"
[23] "checkDocStyle" "checkFF"
[25] "check_make_vars" "check_package_depends"
[27] "check_package_description" "check_Rd_files_in_Rd_db"
[29] "checkReplaceFuns" "checkS3methods"
[31] "checkTnF" "check_vignette_index"
[33] "checkVignettes" "citation"
[35] "citationList" "classRepresentation"
[37] "codoc" "codocClasses"
[39] "codocData" "colorConverter"
[41] "condition" "connection"
[43] "contrast.aov" "contrast.aovlist"
[45] "coxph" "data.frame"
[47] "data.frame.array" "data.frame.AsIs"
[49] "data.frame.character" "data.frame.complex"
[51] "data.frame.data.frame" "data.frame.Date"
[53] "data.frame.default" "data.frame.factor"
[55] "data.frame.integer" "data.frame.list"
[57] "data.frame.logical" "data.frame.logLik"
[59] "data.frame.matrix" "data.frame.model.matrix"
[61] "data.frame.numeric" "data.frame.ordered"
[63] "data.frame.package_version" "data.frame.POSIXct"
[65] "data.frame.POSIXlt" "data.frame.raw"
[67] "data.frame.table" "data.frame.ts"
[69] "data.frame.vector" "Date"
[71] "decomposed.ts" "default"
[73] "dendrogram" "density"
[75] "difftime" "dist"
[77] "DLLInfo" "DLLInfoList"
[79] "DLLRegisteredRoutines" "dummy_coef"
[81] "dummy_coef_list" "ecdf"
[83] "factanal" "factor"
[85] "family" "formula"
[87] "frame.aovlist" "frame.default"
[89] "frame.glm" "frame.lm"
[91] "ftable" "getAnywhere"
[93] "glm" "glmlist"
[95] "gls" "hclust"
[97] "help_files_with_topic" "histogram"
[99] "HoltWinters" "hsearch"
[101] "htest" "infl"
[103] "integer.factor" "integrate"
[105] "isoreg" "kmeans"
[107] "Latex" "libraryIQR"
[109] "listof" "lm"
[111] "lme" "loadings"
[113] "loess" "logLik"
[115] "ls_str" "manova"
[117] "matrix" "matrix.data.frame"
[119] "matrix.default" "matrix.dist"
[121] "matrix.lm" "matrix.noquote"
[123] "matrix.POSIXlt" "medpolish"
[125] "MethodsFunction" "MethodsList"
[127] "mlm" "mtable"
[129] "na.data.frame" "na.POSIXlt"
[131] "NativeRoutineList" "negbin"
[133] "nls" "noquote"
[135] "numeric.factor" "octmode"
[137] "ordered" "packageDescription"
[139] "packageInfo" "packageIQR"
[141] "packageStatus" "package_version"
[143] "pairwise.htest" "poly"
[145] "POSIXct" "POSIXlt"
[147] "POSIXt" "power.htest"
[149] "ppr" "prcomp"
[151] "princomp" "profile.nls"
[153] "qr" "recordedplot"
[155] "residual.default" "residual.nls"
[157] "restart" "RGBcolorConverter"
[159] "rle" "sessionInfo"
[161] "simple.list" "smooth.spline"
[163] "smooth.spline.fit" "socket"
[165] "spec" "spec.coherency"
[167] "spec.phase" "stepfun"
[169] "stl" "StructTS"
[171] "summary.aov" "summary.aovlist"
[173] "summary.glm" "summary.lm"
[175] "summary.loess" "summary.manova"
[177] "summary.nls" "summary.ppr"
[179] "summary.prcomp" "summary.princomp"
[181] "summary.table" "survreg"
[183] "table" "tables_aov"
[185] "terms" "ts"
[187] "tskernel" "TukeyHSD"
[189] "tukeyline" "tukeysmooth"
[191] "undoc" "vector.factor"
[193] "vignette" "xgettext"
[195] "xngettext" "xtabs"
One may write one's own classes: it suffices to add a "class" attribute" to an object and to define the corresponding method.
x <- pi
attr(x, 'class') <- "number"
print.number <- function (x) {
cat("(number) ")
cat(signif(x))
cat("\n")s
}This gives:
> x (number) 3.14159
We can also define our own methods.
affiche <- function (x,...) {
UseMethod("affiche")
}
affiche.default <- print
affiche.number <- function (x) {
cat("(number) ")
cat(signif(x))
cat("\n")
}This gives:
> affiche(x) (number) 3.14159 > affiche(pi) [1] 3.141593
Let us write a class to store panel data, i.e., something like a data.frame, but in which ecah variable is an array, one row per subject, one column per data, instead of a vector.
TODO...
is.panel.data <- function (x) {
# A panel data object should be a (non-empty) list, all of whose
# elements are matrices of the same size and with the same row and
# column names.
# The attributes should be as follows:
# class: contains "panel.data"
# rownames (subjects)
# colnames (dates)
# names (variables)
if( is.null(x) ) return(FALSE)
if( ! is.list(x) ) return(FALSE)
if( ! inherits(x, "panel.data") ) return(FALSE)
# Here, the object claims to be a "panel.data" object.
# If one of the following conditions is not satisfied, it is
# corrupted -- this is a bug.
x <- unclass(x)
stopifnot(!is.null(attr(x, "names")))
stopifnot(!is.null(attr(x, "rownames")))
stopifnot(!is.null(attr(x, "colnames")))
d1 <- attr(x, "rownames")
d2 <- attr(x, "colnames")
for (k in 1:length(x)) {
stopifnot( is.array(x[[k]]) )
stopifnot( length(dim(x[[k]])) == 2 )
stopifnot( dimnames(x[[k]])[[1]] == d1 )
stopifnot( dimnames(x[[k]])[[2]] == d2 )
}
return(TRUE)
}
panel.data <- function(...) {
r <- list(...) ############ TODO: flatten this list and remove the NULL elements
if (is.null(r)) return(NULL)
cat("Checking elements\n")
for (i in seq(along=r)) {
stopifnot( is.matrix(r[[i]]) )
stopifnot( dim(r[[1]]) == dim(r[[i]]) )
stopifnot( dimnames(r[[1]])[[1]] == dimnames(r[[i]])[[1]] )
stopifnot( dimnames(r[[1]])[[2]] == dimnames(r[[i]])[[2]] )
}
cat("Checking attributes\n")
stopifnot(!is.null(dimnames(r[[1]])))
stopifnot(!is.null(names(r)))
cat("Setting attributes\n")
attr(r, "rownames") <- dimnames(r[[1]])[[1]]
attr(r, "colnames") <- dimnames(r[[1]])[[2]]
attr(r, "class") <- "panel.data"
r
}
dim.panel.data <- function (x) {
c( length(attr(r,"rownames")),
length(attr(r,"colnames")),
length(attr(r,"names")) )
}
n1 <- 2
n2 <- 3
n3 <- 4
x <- matrix(rnorm(n1*n2), nr=n1, nc=n2)
rownames(x) <- paste("Subject", 1:n1, sep="")
colnames(x) <- paste("Date", 1:n2, sep="")
r <- list(a=x, b=x, c=x, d=x)
is.panel.data(x)
is.panel.data(r)
r <- panel.data(a=x, b=1+x, c=2+x, d=3+x)
is.panel.data(r)
dim(r)
"[.panel.data" <- function (x, i=1:dim(x)[1], j=1:dim(x)[2], k=1:dim(x)[3], drop=T) {
if (length(i) == 0 | length(j) == 0 | length(k) == 0) return(NULL)
a <- attributes(x)
x <- unclass(x) # It is now a list
x <- lapply(x, function (y) { y[i,j, drop=F] }) # The first two indices
if (is.logical(k)) k <- which(k)
if (is.numeric(k)) k <- a$names[k]
r <- NULL
for (ind in k) {
r[[ ind ]] <- x[[ ind ]]
}
if (drop) {
if (is.list(r) & length(r) == 1) r <- r[[1]]
r <- drop(r)
}
r
}
"[<-.panel.data" <- function(x,
i=rownames(x), j=colnames(x), k=names(x),
value) {
# Make sure that the arguments contain the names of the rows, columns, etc.
if (is.logical(i)) { stopifnot(length(i)==length(rownames(x))); i <- rownames(x)[i] }
if (is.logical(j)) { stopifnot(length(j)==length(colnames(x))); j <- colnames(x)[i] }
if (is.logical(k)) { stopifnot(length(k)==length(names(x))); k <- names(x)[i] }
if (is.numeric(i)) { i <- rownames(x)[i] }
if (is.numeric(j)) { i <- colnames(x)[i] }
if (is.numeric(k)) { i <- names(x)[i] }
if (!is.panel.data(value)) {
stop("Not implemented: non-panel.data argument") ################## TODO
}
for (a in 1:length(k)) {
x[[ k[a] ]] <- value[[a]]
}
}
# "$.panel.data" <- ... # Unchanged
"$<-.panel.data" <- function (x, key, value) {
x[[key]] <- value
}
# "[[.panel.data" <- ... # Unchanged
"[[<-.panel.data" <- function (x, key, value) {
cl <- class(x)
d <- dim(x)
x <- unclass(x)
stopifnot(is.character(key), length(key) == 1)
stopifnot(is.array(value))
stopifnot(dim(value) == d[1:2])
if (!is.null(rownames(value))) {
stopifnot( rownames(value) == attr(x, "rownames") )
} else {
rownames(value) <- attr(x, "rownames") )
}
if (!is.null(colnames(value))) {
stopifnot( colnames(value) == attr(x, "colnames") )
} else {
colnames(value) <- attr(x, "colnames") )
}
x[[key]] <- value
class(x) <- cl
x
}
"dimnames.panel.data" <- function (x) {
list(subject = attr(x, "rownames"),
dates = attr(x, "colnames"),
variables = attr(x, "names") )
}
"dimnames<-.panel.data" <- function (x, l) {
stopifnot( is.list(l) )
stopifnot( length(l) == 3 )
stopifnot( is.character(l[[1]]) )
stopifnot( length(l[[1]]) == dim(x)[1] )
stopifnot( length(l[[2]]) == dim(x)[2] )
stopifnot( length(l[[3]]) == dim(x)[3] )
attr(x, "rownames") <- l[[1]]
attr(x, "colnames") <- l[[2]]
attr(x, "names") <- l[[3]]
x
}
TODO
The central notion is that of method, not that of object...
There is no encapsulation...
But they are very easy to use...
TODO: this section should be (re)written
Here is the new way of defining objects and function:
library(help=methods) http://www.omegahat.org/RSMethods/Intro.ps
TODO: comment the following example (from BioConductor).
library('methods')
setClass('microarray', ## the class definition
representation( ## its slots
qua = 'matrix',
samples = 'character',
probes = 'vector'),
prototype = list( ## and default values
qua = matrix(nrow=0, ncol=0),
samples = character(0),
probes = character(0)))
dat = read.delim('../data/alizadeh/lc7b017rex.DAT')
z = cbind(dat$CH1I, dat$CH2I)
setMethod('plot', ## overload generic function `plot'
signature(x='microarray'), ## for this new class
function(x, ...)
plot(x@qua, xlab=x@samples[1], ylab=x@samples[2], pch='.', log='xy'))
ma = new('microarray', ## instantiate (construct)
qua = z,
samples = c('brain','foot'))
plot(ma)To understand object oriented programming in R, the easiest is probably to look at the libraries that use it, such as "pixmap".
less /usr/lib/R/library/pixmap/R/pixmap.R
Other examples (in 2003):
MASS/scripts/ch03.R DBI gpclib pixmap SparseM
Two years later (2005), I update this list:
arules boolean CoCo coin colorspace DBI deal distr dynamicGraph fBasics flexmix fSeries gpclib gRbase its kernlab kinship limma lme4 matlab Matrix orientlib pamr pixmap R2HTML rgdal rmetasim RMySQL ROCR R.oo ROracle RSQLite rstream SciViews SparseM tuneR urca XML
For a larger example, check BioConductor or Rmetrics.
http://www.bioconductor.org/ http://www.itp.phys.ethz.ch/econophysics/R/
For more details abour how to import or export data to and from sensible or less sensible formats, check the R data import export manual:
http://cran.r-project.org/doc/manuals/R-data.pdf
To import data from readable formats, you can use one of the following commands:
d <- read.table("foo.txt", header=T, sep=",")
d <- read.csv("txt.csv")
d <- read.csv2("txt.csv") # semicolon-separated file, with a
# comma instead of the decimal point.
d <- read.delim("foo.txt") # Tab-delimited file
d <- read.fwf("txt.fwf") # Fixed width fieldsIn case your file comes from Excel, this may be trickier: the missing values often appear as "#N/A!" and are mistaken for the start of a comment... You can try
d <- read.table("foo.csv", header = TRUE, sep = ",",
na.strings = c("#N/A!", "NA", "@NA"),
quote = '"',
comment.char = "")
For simple and short examples, you can type in the data by hand. In this document, we shall use a lot of simulated data: they are larger, but a couple of lines suffice to produce them.
On the contrary, in real situations, the data are large and stored in files or data bases: how to import them into R?
Personnaly, I often use the "source" command, even though it was not designed for that purpose: it reads in code, not data -- you have to process the data via external tools. In one situation, the data I had to process had a rather non standard format (multiple alignment of DNA sequences): thus, I wrote a small Perl program to convert this format into R code (not "R data", but actual code).
More precisely, the data looked like
CLUSTAL W (1.83) multiple sequence alignment
AB020905 ATGACCAACATCCGAAAAACCCACCCATTAGCTAAAATCATCAACAACTCATTTATTGAC
AB020906 ATGACCAACATCCGAAAAACCCACCCATTAGCTAAAATCATCAACAACTCATTTATTGAC
AB020907 ATGACCAACATCCGAAAAACCCACCCATTAGCTAAAATCATCAACAACTCACTTATTGAC
AB020908 ATGACCAACATCCGAAAAACCCACCCATTAGCTAAAATCATCAACAACTCATTTATTGAC
AB020909 ATGACCAACATCCGAAAAACCCACCCATTAGCTAAAATCATCAACAACTCATTTATTGAC
*************************************************** ********
AB020905 CTTCCAACACCATCAAACATCTCGGCATGATGAAACTTTGGATCCCTCCTTGGAGTATGT
AB020906 CTTCCAACACCATCAAACATCTCAGCATGATGAAACTTTGGATCCCTCCTTGGAGTATGT
AB020907 CTTCCAACACCATCAAACATCTCAGCATGATGAAACTTTGGATCCCTCCTTGGAGTATGT
AB020908 CTTCCAACACCATCAAACATCTCAGCATGATGAAACTTTGGATCCCTCCTCGGAGTATGT
AB020909 CTTCCAACACCATCAAACATCTCAGCATGATGAAACTTTGGATCCCTCCTCGGAGTATGT
*********************** ************************** *********the program was
#! perl -w
use strict;
my @seq;
my @names;
my $i=0;
# Go just after the first empty line
while (<>) {
chomp;
print STDERR "Skipping $. ($_)\n";
last if m/^\s*$/;
}
while (<>) {
chomp;
if( m/^\s*$/ ){
$i=0;
print STDERR "Skipping $. ($_)\n";
next;
}
print STDERR "Reading $. ($i) ($_)\n";
if (m/^([^\s]+?)\s+(.*)/) {
print STDERR "Remembering $.\n";
$names[$i] = $1;
$seq[$i] .= $2;
}
$i++;
}
# foreach my $s (@seq) { print "$s\n"; }
print "d <- matrix( c(\n";
foreach my $s (@seq) {
print '"'. join('", "', split('', $s)) .'",' ."\n";
}
print "), nr=". (scalar @seq) .", byrow=T)\n";
print "rownames(d) <- c('". join("', '", @names) ."')\n"and the result looked like
d <- matrix( c( "A", "T", "G", "A", "C", "C", "A", "A", "C", "A",
"T", "C", "C", "G", "A", "A", "A", "A", "A", "C", "C", "C", "A",
...
), nr=5, byrow=T)
rownames(d) <- c('AB020905', 'AB020906', 'AB020907', 'AB020908', 'AB020909')The problem, with this method (yes, it is a bad method), is that these are not data but code. If you just want to use it with R and ignore all other software, that is fine, but otherwise, a more portable format would be welcome.
The "read.table" can read data frames, i.e., (rectangular) tables, whose columns may have different types (but the type of the data does not change inside a column -- and all the columns have the same length). With the preceeding example, the file could look like
AB020905 "T" "T" "A" "A" "A" "G" "T" "G" ... AB020906 "T" "T" "A" "A" "A" "G" "T" "G" ... AB020907 "T" "T" "A" "A" "A" "G" "T" "G" ... AB020908 "T" "T" "A" "A" "A" "G" "T" "G" ... AB020909 "T" "T" "A" "A" "T" "G" "T" "G" ...
(with very, very long lines).
Often, the "read.table" command works fine, but sometimes, problems occur (usually because one has not read the manual of the "read.table" function).
Let us consider first the simple case of a file containing only numeric data, with no row or column name. It could look like
2 7 3 9 2 8 7 3 2 2 6 2 8 8 1
We try:
> d <- read.table('A.txt')
> d
V1 V2 V3 V4 V5
1 2 7 3 9 2
2 8 7 3 2 2
3 6 2 8 8 1R has give names to the columns. If we do not like them, we may change them.
> names(d) [1] "V1" "V2" "V3" "V4" "V5" > length(d) [1] 5 > names(d) <- 1:length(d) > d 1 2 3 4 5 1 2 7 3 9 2 2 8 7 3 2 2 3 6 2 8 8 1 > names(d) <- LETTERS[1:length(d)] > d A B C D E 1 2 7 3 9 2 2 8 7 3 2 2 3 6 2 8 8 1
The file could be more complex and contain row names.
x1 2 7 3 9 2 x2 8 7 3 2 2 x3 6 2 8 8 1
Here, it does not work as well, because the computer has no way of knowing that the first column contains the name of the rows and not a qualitative variable.
> read.table('A.txt')
V1 V2 V3 V4 V5 V6
1 x1 2 7 3 9 2
2 x2 8 7 3 2 2
3 x3 6 2 8 8 1We can ask it to remove the first column an use it as row names (this is a good exercise: try to do it yourself).
> d <- read.table('A.txt')
> row.names(d) <- d[,1]
> d <- d[,-1]
> d
V2 V3 V4 V5 V6
x1 2 7 3 9 2
x2 8 7 3 2 2
x3 6 2 8 8 1
> names(d) <- LETTERS[1:length(d)]
> d
A B C D E
x1 2 7 3 9 2
x2 8 7 3 2 2
x3 6 2 8 8 1Other situation: we have both column and row names. The file looks like:
A B C D E x1 2 7 3 9 2 x2 8 7 3 2 2 x3 6 2 8 8 1
Now, R understands that the first row contains the variable names and that the first column contains the observation names, because the first line in the file has one fewer element that the others.
> read.table('A')
A B C D E
x1 2 7 3 9 2
x2 8 7 3 2 2
x3 6 2 8 8 1Last situation: The columns have names, but not the rows. The file looks like
A B C D E 2 7 3 9 2 8 7 3 2 2 6 2 8 8 1
If we try, naively:
> d <- read.table('A.txt')
> d
V1 V2 V3 V4 V5
1 A B C D E
2 2 7 3 9 2
3 8 7 3 2 2
4 6 2 8 8 1
> str(d)
`data.frame': 4 obs. of 5 variables:
$ V1: Factor w/ 4 levels "2","6","8","A": 4 1 3 2
$ V2: Factor w/ 3 levels "2","7","B": 3 2 2 1
$ V3: Factor w/ 3 levels "3","8","C": 3 1 1 2
$ V4: Factor w/ 4 levels "2","8","9","D": 4 3 1 2
$ V5: Factor w/ 3 levels "1","2","E": 3 2 2 1First, the computer had no way of guessing that the first line contained the column names, Second, it thought that each column containes character strings (before of the first element)... We can avoid the problem by adding an argument to the "read.table" command.
> read.table('A.txt', header=T)
A B C D E
1 2 7 3 9 2
2 8 7 3 2 2
3 6 2 8 8 1Have weexhausted the problems one may encounter while using the "read.table" command? Well, not quite. Let us look again at our first example, the file containing our nucleis sequences.
> read.table('A.txt')
V1 V2 V3 V4 V5 V6 V7 V8 V9
1 AB020905 TRUE TRUE A A A G TRUE G
2 AB020906 TRUE TRUE A A A G TRUE G
3 AB020907 TRUE TRUE A A A G TRUE G
4 AB020908 TRUE TRUE A A A G TRUE G
5 AB020909 TRUE TRUE A A T G TRUE GEach column contained characters (the four letters A, C, G, T), but the computer misunderstood the "T" as a boolean value. To avoid the problem, it suffices to state the column types (here, it is always the same, we just give it once).
> read.table('A', colClasses=c('character'))
V1 V2 V3 V4 V5 V6 V7 V8 V9
1 AB020905 T T A A A G T G
2 AB020906 T T A A A G T G
3 AB020907 T T A A A G T G
4 AB020908 T T A A A G T G
5 AB020909 T T A A T G T GTODO: What if the file is not on the local disc but given by its URL?
TODO: What if the file comes from a well-known spreadsheet program?
TODO: ?scan
To know more about all this, you might want to reaf the man page of the "read.table" command and the "Data Import-Export manual".
http://cran.r-project.org/doc/manuals/R-data.pdf
For large files, it might be faster to explicitely give the type of each column: otherwise, R would have to read the whole file to check that the numeric columns are indeed numeric -- the begining of the file could contain numbers and later rows strings...
# All the columns contain strings
read.table("foo.txt", colClasses = "character")
# the fist column is numeric, the others contain strings
read.table("foo.txt",
colClasses = c("numeric", rep("character", 10)))If your file only contains number, or only strings, it is wiser to store it in a matrix, not a data.frame. This is what the "scan" function does.
# A numeric matrix
x <- scan("foo.txt", sep=",") # Gives a numeric vector
n <- scan("foo.txt", sep=",", nlines=1)
x <- matrix(x, nc=n)
# A vector of strings
x <- scan("foo.txt", what=character(0))If you file is really large, you should consider storing your data in a database (MySQL, PostgreSQL, or even simply SQLite, that requires no configuration whatsoever), as explained in a few pages.
This is a big problem: only Microsoft knows what is inside those files -- all we can do is try to guess from the outside, what they contain. The easiest solution is to ask the person providing you with the files to save them (with Excel) as "text files" or as "CSV files" (Comma-Separated Values).
If this is impossible, you can try to convert the files yourself, either with Excel (if you have it) or with any software that tries to recognize this format, e.g., Open Office.
http://www.openoffice.org/
If this is also impossible, for instance if you want to automate this process, you can turn to the Spreadsheet::ParseExcel Perl module.
http://www-106.ibm.com/developerworks/linux/library/l-pexcel/
Actually, you do not have to know about Perl (it is an eclectic language, designed to process text, used by computer hackers in the early 1990s for its network capabilities and its tight interaction with the operating system, in the mid-1990s for the first web-based applications, later as a scripting language for games
http://www.frozen-bubble.org/
scientific computations
http://pdl.perl.org/index_en.html
more ambitious web-based applications thanks to its tight interaction with the Apache web-server
http://perl.apache.org/ http://www.modperl.com/ http://modperlbook.org/ http://www.perl.com/pub/a/2002/02/26/whatismodperl.html http://www.perl.com/pub/a/2002/03/22/modperl.html ...
etc.): there there is an R function to call this Perl module to convert an Excel file to a CSV file and read it into R.
library(gdata) ?read.xls (there is a bug in the current version: they use "dquote" instead of "shQuote", which has a disastrous effect if your string contains symbols such as $ or " -- it also crashes in an UTF8 locale).
The sink() function diverts the output to a file: all the messages that would normally end up on the screen are instead written to the file. To have them back on the screen, call sink() once again, with no arguments.
The caputure.output() function does the same thing, but takes the code whole result is to be retrieved as an argument. Instead of a file, it can return a string -- for instance, you may want to escape some characters that would otherwise be interpreted further down in the pipeline, or you can add formatting information (colours, fonts, etc.).
At the end of each session, R asks if you want to save the the environment to continue to work with the same data and functions next time: he saves functions and variables in a file in the current directory; if you work on several R projects at the same time, simply use several directories.
It might be a good idea to clean the variables of the current directory from time to time, with the "ls" and "rm" commands.
ls() rm(x, y, z)
You can also store code in a file (especially if the code is rather long: you will prefer typing it with a decent text editor, such as Emacs) and call it back with the "source" command.
source("MyCode.R")Sometimes, you also want to see the code being executed (inparticular if some parts of it are time-consuming):
source("MyCode.R", echo=TRUE)
One of the differences between R and other statistical systems, such as SAS, is that R stores all the data in memory: this prevents it from dealing with datasets that do not fit in memory. This is less ans less true. One way around that problem is to check wheter you need the whole dataset or if you can split your computations into chunks that each deal with a slice of it (for instance, just a couple of variables at a time insteal of hundreds of them) and store and retrieve the data in a database (see below). Depending on the algorithms you are using, this may not be straightforward: your problem may require a new implementation of the algorithm that does not take memory allocation for granted and that sparinggly, explicitely uses the disk -- these are called out-of-memory algorithms.
Should you want it, there is already an out-of-memory linear regression function, in the biglm package.
When dealing with large amounts of data, you do not really need all the data at once in memory: quite often, your computations only require one chunk of it at a time. It makes sens to store the data in a database and only extract what you need.
R can talk to most databases (SQLite, MySQL, PostgreSQL, Oracle), either through a generic API, such as ODBC, or through database-specific interfaces).
And it works both ways: you can fetch data in a database from R, but you can also use R as a language for stored procedures in some of them (e.g., PostgreSQL).
http://linuxfr.org/2003/02/20/11415.html http://archives.postgresql.org/pgsql-general/2003-02/msg00989.php http://www.joeconway.com/plr/
Installing a DataBase Management System (DBMS) is often daunting: you must start the server, create a new user and create a new database. If you plan to use this database in a networked environment, from a different machine, if you plan to access the same data from different applications or machines at the same time, if you want to prevent inconsistencies when two different people try to modify the same data at the same time, a real DBMS is worth the trouble.
But if you just want to play with the data, from a single application, from a single machine, this is a overkill.
Instead, you can use SQLite: you do not have to install anything, you do not have to configure anything. It is just a library that stores data in a file, and allows you to access and modify it with SQL commands. It is just an elaborated binary file format.
http://www.sqlite.org/
It is becoming more and more popular: when you write an application that has to store some data, in some structured way (for instance, the configuration, the logs, etc.), when you want to be able to search through those data -- SQLite is a light and efficient choice.
http://www.linuxjournal.com/print.php?sid=7803 http://linuxgazette.net/109/chirico1.html http://conferences.oreillynet.com/cs/os2004/view/e_sess/5701
Back to R. As I said, there is nothing to install. More precisely, if you tried to install all the packages from CRAN, it is already there.
TODO: a better example...
library(RSQLite)
# First, connect to to the database.
con <- dbConnect(dbDriver("SQLite"), dbname="tmp.dbms")
# As we currently have no data, we create a new table (poetically
# named "foo") and put a data.frame in it.
r <- data.frame(...)
dbWriteTable(con, "Foo", r)
# We can retrieve the whole data frame
r2 <- dbReadTable(con, "foo")
# We can also perform a few queries on the table
x <- dbGetQuery(con, "SELECT ...")
# When you are finished, you MUST close the connection.
dbDisconnect(con)Other tasks you might want to do:
# List all the tables in this database
dbListTables(con)
# List the fields of a table
dbListFields(con, "Foo")
# Delete a table
dbSendQuery("DROP TABLE Foo")Remember to close your connections once you no longer need them. Otherwise:
> for (i in 1:200) {
+ con <- dbConnect(dbDriver("SQLite"), dbname="tmp.dbms")
+ }
Error in sqliteNewConnection(drv, ...) : RS-DBI driver: (1cannot
allocate a new connection -- maximum of 16 connections already
opened)Let us check how fast it is:
TODO...
Actually, we can speed this up. Up to now, we have just used SQLite as a binary file -- but it is actually a real data base, so we can define the tables in the usual SQL way, in particular stating which columns should be UNIQUE, we can use indices, we can use transactions, etc.
http://web.utk.edu/~jplyon/sqlite/SQLite_optimization_FAQ.html TODO
Caveat: If you are still using version 2, the data are not typed: everything is stored as strings. But version 3 is out.
Caveat: All the data are stored in the same file (if your file system has a 2Gb limit, beware)...
Caveat: I am very suspicious of the efficiency when the data becomes very large -- but when I think "very large", I am probably not very reasonnable.
When you handle a lot of data, you do not really need all the data all the time: quote often, each step in your computations only requires a slice of the data. In those situations in can be helpful to only keep in memory the data you need: to rest being stored in a database for later use.
You might object that doing so requires a DataBase Management System (DBMS), which is very cumbersome to install and administer. This is not the case: if your needs are reasonable (a few GB of data, a single user and process accessing the data), SQLite might be a good solution: it is not a client-server DBMS, but merely a library to access, with SQL commands a file containing the data.
It is as if you were retrieving data from a CSV file with SQL commands -- only faster.
library(RSQLite)
con <- dbConnect(dbDriver("SQLite"), "myData.dbms")
x <- dbGetQuery(con, "SELECT * FROM Foo WHERE date > '2005-01-01';")
...
dbDisconnect(con)Actually, I use it as follows.
# Parameters: the name of the database (this is actually
# the name of the file containing the data) and the name
# of the database driver (here, SQLite, but the same code
# would work with other, more robust DBMS).
global_dbDriver <<- "SQLite"
global_dbname <<- "myData.dbms"
# Connect to the database
try(
library(RSQLite)
)
if (exists("global_SQL_con")) {
try( dbDisconnect(global_SQL_con) )
}
global_SQL_con <- dbConnect(
dbDriver(global_dbDriver),
dbname = global_dbname
)
# The function I use to retrieve the data
# I use a single database connection, so I do not want to
# give the connection argument each time.
# Furthermore, when the result has a single column, I want
# a vector, not a data.frame.
sql <- function (s) {
res <- dbGetQuery(global_SQL_con, s)
if (!is.null(res)) {
if (is.data.frame(res) & ncol(res) == 1) {
res <- res[,1]
}
}
drop(res)
}
# Function to quote strings
as.sql.character <- function (x) {
x <- as.character(x)
x <- gsub("'", " ", x) # DANGER: you probably do not
# want to do that!
x <- ifelse(is.na(x), "NULL", paste("'", x, "'", sep=""))
x
}
# This should speed things up a bit
sql("PRAGMA cache_size = 500000;")
TODO: sync?
cat(sprintf("Price table
%d rows
%d stocks
%d dates from %s to %s
",
sql("SELECT COUNT(*) FROM Price;"),
sql("SELECT COUNT(DISTINCT sedol) FROM Price;"),
sql("SELECT COUNT(DISTINCT date) FROM Price;"),
sql("SELECT MIN(date) FROM Price;"),
sql("SELECT MAX(date) FROM Price;")
))There are a few problems, though.
First, the SQL understood by SQLite is a bit limited; for instance, you have LEFT OUTER JOINs but no FULL OUTER JOINs -- SQLite does understand the syntax of the latter, but replaces it by the former, which can lead to surprising and incorrect results.
Second, the query optimizer is also very limited. You do have indices, but all the joins are nested loop joins (TODO: EXPLAIN).
Third, it is a 1-user, 1-process DBMS. It may look fine at first, but you might end up willing to have a process write the data and another read it, or you might want to give read access to the database to your colleagues -- this is not possible.
Fourth, it is unreliable. I sometimes end up with a database that contains duplicated data, in spite of the UNIQUE constraints I added. I routinely end up with a corrupted and/or locked database, when I violently kill SQLite.
Worse, when dealing with large amounts of data with SQLite, R crashes: the cause of the problem is unclear (it does not necessarily crash inside the SQLite functions: I first suspected R, then some of the packages I was using, but the problems only stopped when I removed SQLite -- the problem seems to be due to large numbers of large INSERTs in a large (5GB) database: if you only read from the database, if you only write data once or twice per session, if your database is small (say, under 2GB), you might be fine).
As a conclusion, SQLite is a very good replacement for CSV files, especially if you have many CSV files, but if you start using it, you will get more ambitious and will end up needing a full-fledge DBMS, such as PostgreSQL, MySQL or Firebird (there are also commercial alternatives, such as Oracle or Microsoft SQL Server -- but even commercial software proponents do not view MS SQL Server as a serious product and suggest MySQL as a better alternative).
If you are new to SQL, here are a few sample queries. The syntax is often that of SQLite, but not always: if in doubt, check the documentation of your DBMS.
Extractting information from a table:
-- Get all the contents of a table SELECT * FROM JPE3_ret; -- Only the first 10 rows of a table SELECT * FROM JPE3_ret LIMIT 10; -- Only a few columns SELECT date, jcode, return_ FROM JPE3_ret LIMIT 10; -- Create a new column SELECT date, sed_cus, loc_price / loc_capt * usd_capt FROM GEMF_rsk LIMIT 10; -- Create a new column, with a new name SELECT date, sed_cus, loc_price / loc_capt * usd_capt AS usd_price FROM GEMF_rsk LIMIT 10;
Extracting information from a table:
-- Select a given row (or set of rows)
SELECT * FROM JPE3_ret
WHERE name = "TOYOTA MOTOR" AND date = "2005-12";
-- Order the results
SELECT * FROM JPE3_ret
WHERE name = "TOYOTA MOTOR" AND date >= "2000-01"
ORDER BY date;
-- Idem, descending order
SELECT * FROM JPE3_ret
WHERE name = "TOYOTA MOTOR"
ORDER BY date DESC;
-- Rows for which a given column is NULL
SELECT * FROM GEMF_rsk WHERE sed_cus ISNULL;
-- Remove duplicates
SELECT DISTINCT isocurr FROM GEMF_rsk;
-- The values of a columns are in a given set
SELECT DISTINCT barrid, sed_cus, isocurr, name
FROM GEMF_rsk
WHERE isocurr IN ("JPY", "THB","HKD", "SGD", "KRW")
ORDER BY isocurr, name;Extracting information from several tables ("joining" several tables):
-- Inner join
SELECT * FROM JPE3_ret, JPE3_rsk
WHERE JPE3_ret.date = JPE3_rsk.date
AND JPE3_ret.barrid = JPE3_rsk.barrid
LIMIT 10;
-- Inner join (query equivalent to the previous one)
SELECT * FROM JPE3_ret JOIN JPE3_rsk USING (date, barrid)
LIMIT 10;
-- Inner join (query equivalent to the previous ones)
SELECT * FROM JPE3_ret JOIN JPE3_rsk
ON JPE3_ret.date = JPE3_rsk.date
AND JPE3_ret.barrid = JPE3_rsk.barrid
LIMIT 10;
-- Outer join (if there are rows in the first table with no
-- corresponding row in the second, they are discarded in an inner
-- join; with an outer join, they are preserved and paired with
-- empty ("NULL") rows)
SELECT * FROM JPE3_ret OUTER JOIN JPE3_rsk USING (date, barrid)
LIMIT 10;Aggregate operations:
-- Count the number of rows in a table
SELECT COUNT(*) FROM JPE3_ret;
-- Partition the rows of a table and count the number of rows in
-- each group
SELECT date, COUNT(*) FROM JPE3_ret GROUP BY date;
-- Minimum
SELECT MIN(return_) FROM JPE3_ret;
-- Minumum, maximum, mean, median, etc.
SELECT date,
COUNT(*) AS number,
MIN(return_) AS minimum,
AVG(return_) AS mean,
MAX(return_) AS maximum
FROM JPE3_ret
GROUP BY date
ORDER BY date;
-- Add a condition to be evaluated after the groups are formed
SELECT COUNT(*) AS number, isocurr
FROM GEMF_rsk
WHERE date = "2006-01"
GROUP BY isocurr
HAVING number < 100
ORDER BY number;
-- Embedded queries
-- (You can probably reformulate this one with DISTINCT and
-- GROUP BY, but combining those two usually leads to hard-to-find
-- bugs.)
SELECT date, COUNT(*) AS number_of_currencies
FROM (SELECT date, isocurr, COUNT(*) AS number
FROM GEMF_rsk
GROUP BY date, isocurr
)
GROUP BY date
ORDER BY date;For performance reasons, it is pivotal to index the columns (or groups of columns) you will use in your queries -- otherwise, the DBMS would have to scan the whole table for the rows you want.
CREATE INDEX idx_foo_id_date ON Foo (id, date); CREATE INDEX idx_foo_id_date ON Foo (id); CREATE INDEX idx_foo_id_date ON Foo (date);
For performance reasons (and data integrity), you should group related changes to the database into a single transaction (e.g., updating several tables at the same time; inserting interconnected data at the same time and make sure the database is never in an incoherent state; or inserting a lot of data at once).
BEGIN TRANSACTION; INSERT INTO Foo (id, date, value) VALUES (1, "2006-01-02", 1.4); INSERT INTO Foo (id, date, value) VALUES (2, "2006-01-05", 1.1); INSERT INTO Foo (id, date, value) VALUES (3, "2006-01-09", 0.7); ... END TRANSACTION;
Creating your own tables
-- Remember two data types: NUMERIC and VARCHAR(255) DROP TABLE Foo; CREATE TABLE Foo ( date VARCHAR(255), id NUMERIC, value NUMERIC ); -- When values are supposed to be non missing (typically, -- identifiers), explicitely state them. DROP TABLE Foo; CREATE TABLE Foo ( date VARCHAR(255) NOT NULL, id NUMERIC NOT NULL, value NUMERIC ); -- When values or tuples are supposed to be unique, -- explicitely state that constraint DROP TABLE Foo; CREATE TABLE Foo ( date VARCHAR(255) NOT NULL, id NUMERIC NOT NULL, value NUMERIC, UNIQUE (date, id) ); -- Some DBMS allow you to specify a polocy to follow when someone -- tries to breach this constraint. DROP TABLE Foo; CREATE TABLE Foo ( date VARCHAR(255) NOT NULL, id NUMERIC NOT NULL, value NUMERIC, UNIQUE (date, id) ON CONFLICT REPLACE ); -- When a column of a table references a key of another table, -- explicitely state it. This is called a "foreign key constraint". -- SQLite does not enfore foreign key constraints DROP TABLE Foo; DROP TABLE Bar; CREATE TABLE Bar ( id NUMERIC NOT NULL, name VARCHAR(255), UNIQUE (id) ON CONFLICT REPLACE ); CREATE TABLE Foo ( date VARCHAR(255) NOT NULL, id NUMERIC NOT NULL REFERENCES Bar(id), value NUMERIC, UNIQUE (date, id) ON CONFLICT REPLACE ); -- It is possible to add or remove columns to an already-created -- table. ALTER TABLE Foo ADD COLUMN other_value NUMERIC;
Populating your tables:
-- Inserting a row INSERT INTO Foo (id, date, value) VALUES (17, "2006-04-05", 3.14); -- Changing one (or several) row(s) UPDATE Foo WHERE id=17 AND date="2006-04-05" SET value = 6.28; -- Deleting one (or several) rows DELETE FROM Foo WHERE id=17 AND date="2006-04-05";
NULL:
-- Missing values are coded as NULL in SQL INSERT INTO Foo (id, date, value) VALUES (19, "2006-12-25", NULL); -- Beware: in some contexts, NULL has other meanings... -- This is due to the fact that most DBMS (PostgreSQL is a notable -- exception) do not allow for user-defined types.
Unsorted code samples:
-- Set operations
SELECT DISTINCT sedol FROM Price WHERE date="2004-01-19"
EXCEPT
SELECT DISTINCT sedol FROM Price WHERE date="2004-01-20";
-- Merging two tables and putting the result in one of them
UPDATE Alpha_Europe
SET forward_returns_1W_7 = (
SELECT forward_returns_1W_7
FROM Foo
WHERE Foo.sedol = Alpha_Europe.sedol
AND Foo.date = Alpha_Europe.date7d
) WHERE EXISTS (
-- I do not like that syntax: we have to repeat
-- the same query twice...
SELECT forward_returns_1W_7
FROM Foo
WHERE Foo.sedol = Alpha_Europe.sedol
AND Foo.date = Alpha_Europe.date7d
);
-- Merging two tables
CREATE TABLE Result AS
SELECT * FROM A LEFT OUTER JOIN B USING (id, date);
-- Merging two tables
INSERT INTO Result
SELECT * FROM A LEFT OUTER JOIN B USING (id, date);
-- Negations and double negations
-- select the elements that are not in category 1, 2 or 3
-- (each element can be in several categories)
SELECT DISTINCT id FROM A WHERE id NOT IN (
SELECT id FROM A WHERE category IN (1, 2, 3)
); -- not tested
-- Other solution
SELECT DISTINCT id FROM A
EXCEPT
SELECT id FROM A WHERE category IN (1, 2, 3); -- not testedTODO:
-- -- More specialized SQL notions -- Embedded SELECTs, EXISTS(SELECT...) -- LIKE, REGEXP -- String operations -- Functions -- Triggers -- Views -- Temporary tables -- Optimization (EXPLAIN) -- -- A few words on database design and normalization could be useful. -- -- Other SQL details -- ANALYZE (computes statistics on tables and indices, used to -- find the "best" way of running a query) -- VACUUM (defragmentation) -- COPY (to read data from a file) -- DEFAULT -- AUTOINCREMENT -- PRIMARY KEY (UNIQUE and NOT NULL) -- CHECK (for more complicated constraints) -- COLLATE (and other locale problems) -- UNION, UNION ALL, INTERSECT, EXCEPT --
For more information, check the manual of the DBMS you chose.
http://www.sqlite.org/lang.html http://dev.mysql.com/doc/ http://www.postgresql.org/docs/ http://otn.oracle.com/pls/db10g/portal.portal_demo3?selected=1
There is one more pivotal detail: getting the data in the database in the first place. This is called ETL (Extraction, Transformation, Loading) and most DBMS provide at least a crude form if it.
With PostgreSQL, this would be the COPY command or psql's \copy (psql is the command-line client to PostgreSQL and its non-SQL command all start with a backslash).
I once needed something along those lines, but a litte more complicated: I wanted the table to be created if it did not exist, I wanted the column types to be automatically inferred (either VARCHAR or NUMERIC), I wanted new columns to be added if they were missing, I wanted column types to be converted if they were wrong. Here is what I was using -- use at your own risk, but bug reports are welcome.
#! perl -w
##
## (c) 2006 Vincent Zoonekynd <zoonek@gmail.com>
##
## Load a CSV file into a database, creating or extening the
## table schema if needed.
## You should be aware that the result will not be very
## clean, in particular, the database will usually not be in
## third normal form and referencial integrity will not be
## enforced.
##
## It should not replace a database with a schema upon which
## you would have pondered for a long time, but it allows
## the schema to be altered automatically when new columns
## are added -- and the data will be more accessible than in
## a bunch of CSV files.
##
## (Incomplete) bug list
## - Missing trailing commas are not handled
## - problem while inferring the type of bps.csv
##
############################################################
##
## Modules
##
############################################################
use strict;
use warnings;
use Getopt::Simple qw/$switch/;
use Text::CSV_XS;
use Data::Dumper;
use IO::File; # Needed to use Text::CSV_XS
use POSIX; # For strtod(), to infer the type of the columns
use constant TRUE => 0==0;
use constant FALSE => 0==1;
############################################################
##
## A few functions
##
############################################################
##
## In case two columns have the same name (this can be due
## to them genuinely having the same name, or having the
## same name up to capitalization, or the same name up to
## non-alphanumeric characters), we change the name of the
## second by adding "_X1", "_X2", etc. to it.
## This function creates those new names.
##
sub alter_duplicate_column_names {
my %a = ();
my @result = ();
foreach (@_) {
if (exists $a{$_}) {
my $i=0;
$i++ while exists $a{ $_ . "_X" . $i };
$_ .= "_X" . $i;
}
$a{$_} = 1;
push @result, $_;
}
@result;
}
##
## The values to be inserted into the database have to be
## slightly modified:
## - They are quoted
## - Missing values (as described by the --NA command line
## option) are replaced by NULL
## - To avoid other problems, dangerous characters (double
## quote (") and backslash (\)) are replaced by a space.
##
## There are two versions of this function: one that
## produces unquoted results, useful to infer the type of
## the columns, and a quoted one, for the actual generation
## of SQL code.
##
sub process_values_unquoted {
my @a = map { $a = $_; # Do not modify $_: it would
# change the elements of
# @extra_values...
$a =~ s/\'/_/g;
$a = "" if $a =~ m/$$switch{"NA"}/o;
$a;
} @_;
return @a;
}
sub process_values_quoted {
my @a = map { $a = $_; # Do not modify $_: it would
# change the elements of
# @extra_values...
$a =~ s/\'/_/g;
if ($a =~ m/$$switch{"NA"}/o) {
$a = "NULL";
} else {
$a = "\'$a\'";
}
$a;
} @_;
return @a;
}
##
## Some command line options expect comma-seperated lists of
## column names or numbers: this function transforms them
## into lists of column names.
##
sub get_column_names ($@) {
my ($col, @column_names) = @_;
my @col = split(",", $col);
# Convert the column numbers to column names
for (my $i=0; $i<=$#col; $i++) {
if ( (POSIX::strtod($col[$i])) [1] == 0 ){
$col[$i] = $column_names[ $col[$i] - 1 ];
}
}
return @col;
}
############################################################
##
## Parameters: how does the CSV file(s) look like?
##
############################################################
my $option = Getopt::Simple -> new();
$option -> getOptions({
quote_char => { type => "=s",
default => q/"/, # Usually NOT ', because it
# appears in some French names...
verbose => "quote character" },
sep_char => { type => "=s",
default => q/,/, # Could also be | or \t
verbose => "field separator" },
header => { type => "=i",
default => 1,
verbose => "number of the line containing the headers" },
data => { type => "=i",
default => 2,
verbose => "number of the first line after the headers" },
table_name => { type => "=s",
default => "Foo",
verbose => "Name of the SQL table to create and populate" },
NA => { type => "=s",
default => '^\s*(|\.|NA|NULL|Null|Default|-999(.0*)?|[#@]?N/?A\!?)\s*$',
verbose => 'Regular expression to match missing values, e.g., ^NA$' },
"add-column" => { type => "=s@",
default => [],
verbose => "Columns missing in the CSV file, usually because they are constant and can be inferred from the file name; e.g., date=2006-03-27"
},
"index" => { type => "=s@",
default => [],
verbose => "Columns on which to create an INDEX, e.g. '1,2,3' or 'id,date'"
},
"unique" => { type => "=s@",
default => [],
verbose => "UNIQUE constraints to impose"
},
"not-null" => { type => "=s@",
default => [],
verbose => "NOT NULL constraints to impose"
},
"no-column-type-check" => { type => "",
default => "",
verbose => "Should we try to guess the type of all the columns or set them all to VARCHAR(255)?"
},
"wide" => { type => "=i",
default => -1,
verbose => "If the file contains wide data, number of the column where these data start; e.g., if the columns are factor1,factor2,2000,2001,2002,etc., this would be 3"
},
"wide-name" => { type => "=s",
default => "Wide_column_name",
verbose => "If the file contains wide data, name of the (SQL) column that will identify those data, e.g., if the file header is factor1,factor2,2000,2001,2002,etc., this could be 'date'"
},
"wide-value" => { type => "=s",
default => "Wide_value",
verbose => "If the file contains wide data, name of the (SQL) column that will contain those data, e.g., if the file header is factor1,factor2,2000,2001,2002,etc., this could be 'date'"
}
}, "usage: $0 [options] file.csv");
my @extra_headers = map { $a = $_; $a =~ s/=.*//; $a; }
@{ $$switch{"add-column"} };
my @extra_values = map { $a = $_; $a =~ s/^.*?=//; $a; }
@{ $$switch{"add-column"} };
if ($$switch{"data"} <= $$switch{"header"}) {
$$switch{"data"} = $$switch{"header"} + 1;
}
#print STDERR "Options:\n";
#print STDERR Dumper($switch);
if (@extra_headers) {
print STDERR "Extra headers: " . join(", ", @extra_headers) . "\n";
print STDERR " values: " . join(", ", @extra_values) . "\n";
}
if ($$switch{"sep_char"} eq "TAB") {
$$switch{"sep_char"} = "\t";
}
my $csv = new Text::CSV_XS({
quote_char => $$switch{"quote_char"},
sep_char => $$switch{"sep_char"},
binary => TRUE
});
my $file = shift @ARGV or die "usage: $0 file.csv";
my $fh = new IO::File;
############################################################
##
## Trying to infer the type of the columns
##
############################################################
my @types;
{
print STDERR "Reading file $file to get the number of columns and their types\n";
open($fh, "<", $file) || die "Cannot open $file for reading: $!";
my $line = 0;
while(1) {
my $fields = $csv->getline($fh);
last unless $fields;
last unless @$fields;
next if $#$fields == 0 and $$fields[0] =~ m/^\s*$/; # Skip blank lines
$line++;
if ($line == $$switch{"header"}) {
if ($$switch{"no-column-type-check"}) {
@types = map { FALSE } (@extra_headers, @$fields);
last;
} else {
@types = map { TRUE } (@extra_headers, @$fields);
}
} elsif ($line >= $$switch{"data"}) {
#print STDERR $line . " " . join(", ", @$fields) . "\n";
my @values = process_values_unquoted(@extra_values, @$fields);
#print STDERR $line . " " . join(", ", @values) . "\n";
#print STDERR $line . " " . join(", ", map { (POSIX::strtod($_))[1] > 0 ? "VARCHAR(255)" : "NUMERIC" } @values) . "\n";
@values = map { (POSIX::strtod($_))[1] == 0 } @values;
for (my $i=0; $i<=$#values; $i++) {
$types[$i] &&= $values[$i];
}
#print STDERR $line . " " . join(", ", map { $_ ? "NUMERIC" : "VARCHAR(255)" } @types) . "\n";
}
}
close($fh);
if ($$switch{"wide"} > 0) {
for (my $i = $#extra_headers + 1 + $$switch{"wide"}; $i <= $#types; $i++) {
$types[ $#extra_headers + 1 + $$switch{"wide"} ] =
$types[ $#extra_headers + 1 + $$switch{"wide"} ] && $types[$i];
}
$types[ $#extra_headers + 1 + $$switch{"wide"} - 1 ] = FALSE;
@types = @types[0..($#extra_headers + 1 + $$switch{"wide"})];
}
@types = map { $_ ? "NUMERIC" : "VARCHAR(255)" } @types;
print STDERR "Column types: ";
print STDERR join(", ", @types) . "\n";
}
############################################################
print STDERR "Reading file $file\n";
open($fh, "<", $file) || die "Cannot open $file for reading: $!";
my @column_names;
my @wide_values;
my $line = 0;
while(1) {
my $fields = $csv->getline($fh);
last unless $fields;
last unless @$fields;
next if $#$fields == 0 and $$fields[0] =~ m/^\s*$/; # Skip blank lines
$line++;
if ($line == $$switch{"header"}) {
@column_names = @$fields;
if ($$switch{"wide"} > 0) {
@wide_values = @column_names[ ($$switch{"wide"}-1) .. ($#column_names) ];
map { s/^\s+//; s/\s+$//; } @wide_values;
@column_names = @column_names[ 0 .. ($$switch{"wide"}-1) ];
$column_names[ $$switch{"wide"} - 1 ] = $$switch{"wide-name"};
$column_names[ $$switch{"wide"} ] = $$switch{"wide-value"};
}
@column_names = (@extra_headers, @column_names);
@column_names = map { y/A-Z/a-z/; # Only lower case
s/\s+$//; # No trailing spaces
s/^\s+//; # No leading spaces
s/[^a-z0-9]/_/g; # Only alphanumeric characters
s/^([0-9])/x$1/; # First character is a letter
s/^$/nameless_column/; # At least one character
$_; } @column_names;
@column_names = alter_duplicate_column_names(@column_names);
@column_names = map { "\"$_\"" } @column_names;
my %not_null = ();
foreach my $i (@{$$switch{"not-null"}}) {
foreach my $j (get_column_names($i, @column_names)) {
$not_null{$j} = 1;
}
}
print "-- Table schema\n";
print "CREATE TABLE " . $$switch{"table_name"} . " (\n";
for (my $i=0; $i <= $#column_names; $i++) {
print " " . $column_names[$i] . " " . $types[$i];
print " NOT NULL" if exists $not_null{ $column_names[$i] };
print "," if $i < $#column_names or @{$$switch{"unique"}};
print "\n";
}
foreach (my $j=0; $j <= $#{ $$switch{"unique"} }; $j++) {
my $col = ${ $$switch{"unique"} }[$j];
my @col = get_column_names($col, @column_names);
print " UNIQUE (" . join(", ", @col) . ")";
# ." ON CONFLICT REPLACE";
print "," unless $j == $#{ $$switch{"unique"} };
print "\n";
}
print ");\n";
print "-- In case the table already exists, we make sure it has enough columns...\n";
for (my $i=0; $i<=$#column_names; $i++) {
print "ALTER TABLE " . $$switch{"table_name"} .
" ADD COLUMN " . $column_names[$i] . " " .
$types[$i] . ";\n";
}
if (@{ $$switch{"index"} }) {
print "-- Indices\n";
foreach my $col (@{ $$switch{"index"} }) {
my @col = get_column_names($col, @column_names);
print "CREATE INDEX " .
"idx_" . $$switch{"table_name"} . "_" .
join("_", @col) .
" ON " .
$$switch{"table_name"} .
" (".
join(", ", @col) .
");\n";
}
}
print "-- The data from $file\n";
print "BEGIN TRANSACTION;\n";
print "PRAGMA cache_size = 500000;\n";
} elsif ($line >= $$switch{"data"}) {
map { s/^\s+//; s/\s+$//; } @$fields;
if ($$switch{"wide"} > 0) {
for (my $i=0; $i <= $#wide_values; $i++) {
print "INSERT INTO " . $$switch{"table_name"} . " (" .
join(", ", @column_names) .
")\n";
print " VALUES (" .
join(",", process_values_quoted(
@extra_values,
@$fields[ 0 .. ($$switch{"wide"}-2) ],
$wide_values[$i],
$$fields[$$switch{"wide"} - 1 + $i]) ) .
");\n";
}
} else {
print "INSERT INTO " . $$switch{"table_name"} . " (" .
join(", ", @column_names) .
")\n";
print " VALUES (" .
join(",", process_values_quoted(@extra_values, @$fields)) .
");\n";
}
}
}
print "COMMIT TRANSACTION;\n";
close($fh);
Database specialists often distinguish between two uses of databases.
In OLTP (On-Line Transaction Processes) applications, very small amounts of data (usually one record at a time) are read and written to the database: this is the case for most web applications (e-commerce, forums, etc.).
At the other end of the spectrum, OLAP (On-Line Analytical Processing) applications or Decision Support Systems (DSS) or Business Intelligence (BI) applications, only use the database as a data repository, as a data warehouse (DW) or as an operational datastore (ODS) (to be read from, not written to), extract large amounts of data (several gigabytes) and try to summarize them, in as interactive a way as possible.
The main example is sales data: you know the value of each transaction, what item it was, which customer it was, which sales clerk it was. You can summarize all the transactions in a large 3-dimensional cube: one dimension for the customers, one for the items, one for the sales clerk. But that cube is too large to be presented to the end user. To get a more amenable data cube, the elements in each dimension can be grouped: customers grouped by city, state, age, value of past purchases, number of past purchases, gender, etc.; items by category, price, etc.; sales clerks by gender, religion, shop, city, state, proximity of public transportations, etc. Typically, OLAP applications are interactive: they first present the user with the coarsest grouping (all the customers, all the items, all the sales clerks -- the corresponding cube has a single element) and then allow to "drill-down", i.e., to chose finer and finer groupings. But three dimensions may be too much: you may prefer to select a 2-dimensional slice of the data (e.g., "only a given sales clerk") or project the data cube onto one dimension (i.e., consider "all the sales clerks").
Building a Data Warehouse (DW) is often a prerequisite to OLAP operations: it refers to the nightmare of combining several databases into one -- the problem being that the databases may contain incoherencies, may use different identifiers, may use different naming schemes, may lack some of the data needed.
If you need a free OLAP tool, have a look at Mondrian.
http://mondrian.pentaho.org/
Most Database Management Systems (DBMS) are relational DBMS: they store relations, usually represented as SQL tables.
Some databases are not relational but simply store associations or hash tables, i.e., key-value pairs: they are mere presistence engines, that provide a random access to the data (in this context, the word "random" loses its statistical meaning: it means that to access a data item, we do not have to scan the whole database, we just go directly where it is supposed to be). They are often used to store directories and are optimized for fast read access (e.g., the information associated to an employee (name, social security number, phone, address, login, password, email address, etc.; the information associated to computers in a network (name, IP address, etc. -- those directories are called DNS)). BerkelyDB is such a DBMS.
Some databases are targeted at large applications and implement a client-server architecture (the DBMS is a program (the server), the applications using the database (the clients) are other programs, that run at the same time, on the same machine or on a different machine, and they all talk to each other). Most databases fall into this category: MySQL, PostgreSQL, Interbase, Oracle, DB2, Microsoft SQL Server, etc.
At the other end of the spectrum, some databases are designed for small ("embedded") applications: they require very few ressources, but lack some features, such as concurrency. You can find some of them, for instance, in mobile phones. SQLite is designed for embedded applications. Some client-server DBMS have a light, embeddable version -- most notably MySQL -- I think it is their main source of revenue.
Some databases advertise their ability to store complex datatypes (e.g., time series) as easily as basic, "atomic" types and to provide enhanced performance when accessing them. Those products are called "multi-value databases" or "post-relational databases" or "non-1NF DBMS" and are usually commercial: Vision, Cache (formerly known as Mumps or M), KSQL. Unkess you really know what you are doing, you should stay away from those: from my experience in the domain, it is very hard to find expertise with these products, the schema of the database is rarely documented, there are no established best practices (such as "put your data in third normalized form" with relational databases -- here, the followed rule is to ignore those best practives), the promised performance is rarely there (unless you manage to find an expert on this product), the syntaxe is arcane and does not allow end users to actually use the product.
The algorithms used in conventional databases do not always scale well; furthermore, the principles underlying conventional databases often fail for Very Large DataBases (VLDB). For instance, one cannot be sure that large databases contain "the truth" -- large databases do contain mistakes -- the algorithms used must be "robust", in some sense, to those mistakes. Furthermore, computing the exact result to a query can be very time-consuming while an approximate result would be as useful: approximate joining algorithms are starting to emerge. Another desirable feature of VLDB systems is to provide "the best result so far", and to update that result as time passes -- when the user is bored, she can stop the computations.
http://www.vldb.org/ http://www.acm.org/sigs/sigkdd/explorations/issue.php?issue=current TODO: URLs approximate matching
Real-time databases (RTDB), flow-programming langages, streaming data are closely-related subjects.
TODO: URL?
Databases often contain personal information (e.g., medical information about patients in a hospital, bank details, etc.) and mining those databases, let alone combining them, poses confidentiality problems. To this end, privacy-enhanced data-mining techniques are starting to emerge.
http://www.wired.com/news/wireservice/0,71184-0.html Mentionned in Cryptogram 2006-07: http://www.schneier.com/crypto-gram-0607.html
TODO:
Temporal databases
Other types of databases: relational (SQL: MySQL, PostgreSQL, Interbase, Oracle, DB2, MSSQL, Derby, HSQL) persistence (berkeleyDB) embedded (SQLite, MySQL, berkeleyDB) ORM post-relational = non-1NF = multi-value Vocabulary: DDL (Data Definition Language) DML (Data Manipulation Language) MDX: a Microsoft language for OLAP ACID bitemporality
TODO:
OLTP; OLAP, Data cube, OLAP system, drill-down Other types: Temporal data and the relational model (C. Date et al.) Time series databases (Vision, Cache (Mumps)) VLDB, Approximate querying JOIN, approximate join and statistical matching
Last time I used MySQL from R, I proceeded as follows (after installing what was needed):
library(RMySQL)
con <- dbConnect(dbDriver("MySQL"), dbname = "MySQL_Test_1")
dbListTables(con)
d <- dbGetQuery(con, "SELECT * FROM Foo")
d
dbDisconnect(con)
TODO: Some explanations
# Not tested library(RODBC) ?ODBC DSN <- "foobar" channel <- odbcConnect(DSN, "zoonek", "azerty", believeNRows=FALSE) sqlQuery(channel, "SELECT foo, bar, baz FROM FooBar WHERE foo > bar") close(channel)
First, install PostgreSQL and configure it. If you are using Gentoo/Linux, just type (the first command actually asks you to type the second).
emerge postgresql emerge --config =postgresql-8.0.4
If not, you can install it by hand and type
# Choose a directory to put the data DB=$HOME/Data initdb -D $DB # Launch the server postmaster -D $DB >logfile 2>&1 & # Create an empty "database" (you can think of a # "database" as a "namespace": it will be a set of tables, # isolated from the rest of the data, so as to avoid name # clashes). createdb test # Use it! (This is the command-line interface, you might # prefer a more graphical application.) psql test
But we want to use it from R.
Install Rdbi and RdbiPgSQL, from Bioconductor.
source("http://www.bioconductor.org/biocLite.R")
biocLite("RdbiPgSQL")
biocLite()
biocLite(c("graph", "Rgraphviz"))
I had to alter the .FirstLib function in RdbiPgSQL
and remove the autoloading of the chron.
library(Rdbi)
# We connect via a UNIX socket (in the default PostgreSQL
# installation, there are no INET sockets) and there is
# no password.
pcon <- dbConnect(PgSQL(), dbname="zoonek", user="zoonek")
res <- dbGetQuery(pcon, "SELECT * FROM TickData LIMIT 10")
dbDisconnect(pcon)
Look on CRAN (Complete R Archive Network)
http://cran.r-project.org/
You can install them as:
R CMD INSTALL vcd_0.1-3.tar.gz
It you realize they do not work (it could happen a couple of years ago, but it should now be exceptionnal), you can remove them with:
R CMD REMOVE vcd
You have written some nifty functions and would like to share them with your colleagues, with the world, you would like to see them on CRAN. For this, you have to put all your functions in a "package".
There is often a confusion between "package" and "library". A "library" is a directory, usually containing one or several packages. A "package" is a set of functions, data sets and manual pages, contained in a directory ("library") or a *.tar.gz file (for Windows users, it can also be a *.zip file, but you must find the one corresponding to your version of R). A "bundle" is a set of packages contained in the same "*.tar.gz" file. To increase the confusion, the function to load a package is called "library"...
Let us assume you have written three functions, "foo", "bar" and "baz", one data.frame, "fbz", and that you have put their definitions in a file "foobar.R". You can create a package as follows.
source("foobar.R")
package.skeleton("foobar", c("foo", "bar", "baz", "fbz"))This creates the files
foobar foobar/man foobar/man/README foobar/man/foo.Rd foobar/man/bar.Rd foobar/man/baz.Rd foobar/src foobar/src/README foobar/R foobar/R/foo.R foobar/R/bar.R foobar/R/baz.R foobar/data foobar/data/fbz.rda foobar/DESCRIPTION foobar/README
We can leave the *.R files untouched -- they contain the code of our functions. We need to modify the DESCRIPTION file. It currently contains
Package: foobarType: Package Title: What the package does (short line) Version: 1.0 Date: 2005-05-04 Author: Who wrote it Maintainer: Who to complain to <yourfault@somewhere.net> Description: More about what it does (maybe more than one line) License: What license is it under?
We change this to
Package: foobar Type: Package Title: Almost empty package Version: 1.0 Date: 2005-05-04 Author: Vincent Zoonekynd <zoonek@example.com> Maintainer: Vincent Zoonekynd <zoonek@example.com> Description: Example package, containing silly functions, such as addition or multiplication. License: GPL
We also have to read and alter the documentation files *.Rd. They look like this:
\name{foo}
\alias{foo}
%- Also NEED an '\alias' for EACH other topic documented here.
\title{ ~~function to do ... ~~ }
\description{
~~ A concise (1-5 lines) description of what the function does. ~~
}
\usage{
foo(x)
}
%- maybe also 'usage' for other objects documented here.
\arguments{
\item{x}{ ~~Describe \code{x} here~~ }
}
\details{
~~ If necessary, more details than the __description__ above ~~
}
\value{
~Describe the value returned
If it is a LIST, use
\item{comp1 }{Description of 'comp1'}
\item{comp2 }{Description of 'comp2'}
...
}
\references{ ~put references to the literature/web site here ~ }
\author{ ~~who you are~~ }
\note{ ~~further notes~~ }
~Make other sections like Warning with \section{Warning }{....} ~
\seealso{ ~~objects to See Also as \code{\link{~~fun~~}}, ~~~ }
\examples{
##---- Should be DIRECTLY executable !! ----
##-- ==> Define data, use random,
##-- or do help(data=index) for the standard data sets.
## The function is currently defined as
function (x) { x + 1 }
}
\keyword{ ~kwd1 }% at least one, from doc/KEYWORDS
\keyword{ ~kwd2 }% __ONLY ONE__ keyword per lineIt is not really a LaTeX file. Let us read this file line by line. First is the name of the manual page -- usually the name of the function currently described.
\name{foo}Then, all the functions that will be described in this manual page. If you have several functions that perform a similar task, it is wise to "refactor" them into a single function -- the user will only have to remember a single function name, you will have a single manual page to write, a single set of tests. If it is not possible, you can still document the functions together, in the same manual page. Here, let us document the three functions in the same page.
\alias{foo}
\alias{bar}
\alias{baz}Then, a short (less than one line) description of the function.
\title{Arithmetic operations}Then, a longer (but still short) description.
\description{
Very simple functions that perform elementary arithmetic
operations such as adding one, multiplying by two or squaring.
}Then the "usage" of the function, i.e., how we should call it, with all the arguments, with their default values, if any.
\usage{
foo(x)
}
\usage{
bar(x)
}
\usage{
baz(x)
}Then, a description of the arguments, one by one (there can be many arguments and the description can, of course, be much longer than that).
\arguments{
\item{x}{A number}
}Then, a more detailed description of the functions, of the algorithms involved, of the common mistakes, etc.
\details{
The \code{foo} function returns its argument incremented by 1.
The \code{bar} function returns its argument multiplied by 2.
The \code{baz} function returns its argument squared.
}Then, the description of the value of the functions, especially if the value is a list.
\value{
Result of the operation.
}A reference to articles, books, web sites that present the algorithms or ideas behind the package.
\references{The four operations for dummies}Your name and email address.
\author{Vincent Zoonekynd <zoonek@math.jussieu.fr>}Links to other manual pages of interest: functions the user may want to use in conjunction with your code -- or instead of your code.
\seealso{\code{\link{sum}}, \code{\link{prod}}}The most important part: the examples. The code must run without any problem, and must not take too long: it will be run to check that everything went fine when downloading and installing the package -- it will also serve as regression tests: do use "stopifnot".
\examples{
foo(1) + bar(2) + baz(3)
(1+1) + (2*2) + (3*3)
stopifnot( foo(5) == 6 }
stopifnot( bar(5) == 10 }
stopifnot( baz(5) == 25 }
}You should also include keywords (one at a time).
\keyword{arith}% at least one, from doc/KEYWORDS
\keyword{increment}
\keyword{double}
\keyword{square}That is all for this first manual page. As we have documented the three functions, we can remove the (empty) manual pages of "bar" and "baz".
rm foobar/man/bar.Rd rm foobar/man/baz.Rd
I let you document the data set, man/fbz.Rd.
We can now build the package (we are still in the shell):
R CMD build foobar
If there are no errors (in particular in the DESCRIPTION file), this yields
* checking for file 'foobar/DESCRIPTION' ... OK * preparing 'foobar': * checking DESCRIPTION meta-information ... OK * cleaning src * removing junk files * checking for LF line-endings in source files * checking for empty directories * building 'foobar_1.0.tar.gz'
We can check it (this runs the examples of the manual pages),
R CMD check foobar
This yields
* checking for working latex ... OK
* using log directory '/tmp/foobar.Rcheck'
* using R version 2.1.0, 2005-04-18
* checking for file 'foobar/DESCRIPTION' ... OK
* checking extension type ... Package
* this is package 'foobar' version '1.0'
* checking if this is a source package ... OK
* Installing *source* package 'foobar' ...
** libs
WARNING: no source files found
chmod: cannot access `/tmp/foobar.Rcheck/foobar/libs/*': No such file or directory
** R
** data
** help
>>> Building/Updating help pages for package 'foobar'
Formats: text html latex example
fbz text html latex example
foo text html latex example
missing link(s): ~~fun~~
** building package indices ...
* DONE (foobar)
* checking package directory ... OK
* checking for portable file names ... OK
* checking for sufficient/correct file permissions ... OK
* checking DESCRIPTION meta-information ... OK
* checking package dependencies ... OK
* checking index information ... OK
* checking package subdirectories ... WARNING
Subdirectory 'src' contains no source files.
* checking R files for syntax errors ... OK
* checking R files for library.dynam ... OK
* checking S3 generic/method consistency ... OK
* checking replacement functions ... OK
* checking foreign function calls ... OK
* checking Rd files ... WARNING
Rd files with likely Rd problems:
Unaccounted top-level text in file "/tmp/foobar/man/foo.Rd":
Following section "note":
"\n\n ~Make other sections like Warning with \\section{Warning }{....} ~\n\n"
Rd files with duplicate "usage":
/tmp/foobar/man/foo.Rd
These entries must be unique in an Rd file.
Rd files with non-standard keywords:
/tmp/foobar/man/foo.Rd: ~kwd1 ~kwd2
Each "\keyword" entry should specify one of the standard keywords (as
listed in file "KEYWORDS.db" in the "doc" subdirectory of the R home
directory).
See chapter 'Writing R documentation files' in manual 'Writing R
Extensions'.
* checking for missing documentation entries ... WARNING
Undocumented code objects:
baz
All user-level objects in a package should have documentation entries.
See chapter 'Writing R documentation files' in manual 'Writing R
Extensions'.
* checking for code/documentation mismatches ... OK
* checking Rd \usage sections ... WARNING
Objects in \usage without \alias in documentation object "foo":
baz
Functions with \usage entries need to have the appropriate \alias entries,
and all their arguments documented.
See chapter 'Writing R documentation files' in manual 'Writing R
Extensions'.
* checking for CRLF line endings in C/C++/Fortran sources/headers ... OK
* creating foobar-Ex.R ... OK
* checking examples ... OK
* creating foobar-manual.tex ... OK
* checking foobar-manual.tex ... ERROR
LaTeX errors when creating DVI version.
This typically indicates Rd problems.Then, you can start the bug squashing: typically, you have forgotten to document a function, to delete a file, to delete an unwanted line in a manual page (the LaTeX errors above are due to this) or you have deleted too much, etc..
Then, when there are no bugs left, you can install the package and distribute the *.tar.gz file to the world.
R CMD build foobar R CMD check foobar R CMD install foobar
Windows people are usually very inhappy with source packages (they lack the appropriate tools to install everything -- some people even say it is easier and faster to install Linux that to install all the missing software) so you can provide them with a "binary" package -- this will not work if your package contains C code or if they have a different version of R -- and I have not tested it either -- I do not have Windows.
cd /usr/local/R/library/ zip -r /tmp/foobar foobar/
TODO:
Understand the problems with the keywords. Read the documentation for all the bells and whistles I am not aware of...
TODO
TODO Namespaces (there can be a "NAMESPACE" file in the root directory of the package)
Lyx is a user-friendly WYSIWYM (What You See Is What You Mean) interface to LaTeX.
http://www.troubleshooters.com/lpm/200210/200210.htm
It can be made Sweave-aware.
http://www.mail-archive.com/r-help%40stat.math.ethz.ch/msg46946.html http://www.ci.tuwien.ac.at/~leisch/Sweave/LyX
TODO
For efficientcy reasons, all the code in a package will not be written in R: the parts of the program that require the most time or the most memory will be written in a faster language (often C, but I think there are still some people using Fortran -- in this 21st century...).
The procedure is detailes in "Writing R extensions". I simply reproduce their example:
In a "foobar.c" file:
void convolve(double *a, int *na, double *b, int *nb, double *ab)
{
int i, j, nab = *na + *nb - 1;
for(i = 0; i < nab; i++)
ab[i] = 0.0;
for(i = 0; i < *na; i++)
for(j = 0; j < *nb; j++)
ab[i + j] += a[i] * b[j];
}
Build a shared library (if it is for a package, it is automatic):
R CMD SHLIBS foobar.c
Load the shared library: for a package, you would use
.First.lib <- function(lib, pkg) {
library.dynam("foobar",pkg,lib)
cat("...")
}
but for an isolated use:
dyn.load("foobar")
You can then use it as:
conv <- function(a, b)
.C("convolve",
as.double(a),
as.integer(length(a)),
as.double(b),
as.integer(length(b)),
ab = double(length(a) + length(b) - 1))$abLet us also mention the ".Call" function that allows you to use more complex data types (the code would use R.h and Rinternals.h or Rdefines.h; the C function expects SEXP objects as arguments and returns a SEXP object) and the ".External" function (with a simgle argument, that contains the list of arguments -- useful if the function has a variable number of arguments).
I do not give any more details: do read "Writing R extensions", do check how libraries are implemented.
I almost forgot: you may also call R code from C.
Here, it also works both ways: you can call Perl from R (for instance, to use the network or regular expressions) or call R from Perl.
TODO: give an example where one calls R from Perl.
R::initR("--silent", "--vanilla");
my @x = 1..100;
R::callWithNames("plot", { x => \@x, ylab => 'foo bar' });
R::eval("plot(1:10)");But it might be easier, instead of calling Perl from R, to write a small perl script you would call with the "system" command.
> library(gdata)
> read.xls
function (xls, sheet = 1, verbose = FALSE, ...)
{
package.dir <- .path.package("gregmisc")
perl.dir <- file.path(package.dir, "perl")
xls <- shQuote(xls)
xls2csv <- file.path(perl.dir, "xls2csv.pl")
csv <- paste(tempfile(), "csv", sep = ".")
cmd <- paste("perl", xls2csv, xls, dQuote(csv), sheet, sep = " ")
if (verbose)
cat("Executing ", cmd, "... \n")
results <- system(cmd, intern = !verbose)
if (verbose)
cat("done.\n")
out <- read.csv(csv, ...)
file.remove(csv)
return(out)
}
When you play with very large data (R becomes less efficient when the data sizes grows unwieldy), you can store them in a database: then, you just have to fetch the data you need at a given moment (typically, a small part of the whole data).
TODO: give a more complete example...
TODO See also iPlots: http://rosuda.org/iPlots/
I first heard about Tcl (pronounce "tickle") in the early 1990s: it was used to build GUI on Unix systems: at the time, it was quite a feat, and as Tcl was an interpreted language, as easy to learn as a shell, all it required was a couple of lines of code. Later, Tk, the library used to build those GUI, has been incorporated into other scripting languages, such as Perl or Python -- and now, R.
TODO: URLs http://www.math.jussieu.fr/~zoonek/UNIX/10_ptk/1.html
Tcl is still used now:
http://www.macdevcenter.com/pub/a/mac/2005/08/12/tcl.html http://www.macdevcenter.com/pub/a/mac/2005/01/28/tcl.html http://www.macdevcenter.com/pub/a/mac/2004/11/09/weblog.html http://www.macdevcenter.com/pub/a/mac/2004/08/27/blitting.html http://www.vhayu.com/faq.html
As R is a real programming language, it is already very powerful as is, but there are two situations where you will need a GUI.
The first one is when you want some interactive graphics, while exploring the data. When you want to see what happens when you change a parameter, you can write a loop and display a plot for each iteration, but it is a bit clumsy: you would probably prefer
The second situation is when you want other people to use the software, without knowing R (yet): either scientists, statistics users, or students, learning statistics. They will prefer a menu-driven application.
One may easily build graphical interfaces under R with Tcl/Tk.
library(tcltk) library(help=tcltk)
The widgets are not documented -- but they are the standard Tk widgets, that have been used from Tcl, Perl, Python for ages.
http://www.math.jussieu.fr/~zoonek/UNIX/10_ptk/1.html
TODO: The problem with variables...
A small calculator.
tkdestroy(wtop)
wtop <- tktoplevel()
w.titre <- tklabel(wtop, text="Additions")
w.un <- tkentry(wtop)
w.deux <- tkentry(wtop)
w.resultat <- tklabel(wtop, text=0)
tkpack(w.titre, w.un, w.deux, w.resultat)
on.key.press <- function () {
# How complicated it os!
a <- tclvalue(tkget(w.un))
a <- eval(parse(text=a))
if(!is.numeric(a)) a <- 0
b <- eval(parse(text=b))
b <- tclvalue(tkget(w.deux))
if(!is.numeric(b)) b <- 0
tkconfigure(w.resultat, text=a+b)
}
tkbind(wtop, "<KeyPress>", on.key.press)
Here is an example from the manual.
tkdestroy(tt) tt <- tktoplevel() tkpack(txt.w <- tktext(tt)) tkinsert(txt.w, "0.0", "plot(1:10)") eval.txt <- function() eval(parse(text=tclvalue(tkget(txt.w, "0.0", "end")))) tkpack(but.w <- tkbutton(tt,text="Submit", command=eval.txt))
The interested reader will especially look into the "tkrplot" package, to include an R graphic inside a widget. The example from the manual shows a curve, depending on a parameter that you can fix with a slider.
Here is a more general function whose arguments are: a function that draws a picture depending on a real parameter; the limits of this parameter.
library(tkrplot)
animate <- function (plot.function, limits) {
bb <- mean(limits)
tt <- tktoplevel()
img <-tkrplot(tt, function () { plot.function(bb) } )
f <- function (...) {
b <- as.numeric(tclvalue("bb"))
if (b != bb) {
bb <<- b
tkrreplot(img)
}
}
s <- tkscale(tt, command=f, from=limits[1], to=limits[2],
variable="bb", showvalue=TRUE,
resolution=diff(range(limits))/100, orient="horiz")
tkpack(img,s)
}
animate( function (a) { hist(abs(rnorm(200))^a) }, c(.1,2) )Example: find the transformation to apply to a variable so that it looks normal.
n <- 200
k <- runif(1, 0,2)
x <- (5+rnorm(n))^k
animate( function (a) { x <- x^(1/a); qqnorm(x); qqline(x,col='red') },
c(.01,2) )Example: watch the effects of bin width in a histogram.
n <- 200
x <- rnorm(n)
animate( function (a) {
a <- ceiling(a)
print(a)
hist(x, breaks=a, col='light blue', probability=T);
lines(density(x), col='red', lwd=3)
},
c(2,102) )Example: the central limit theorem, presented with an interactive animation.
N <- 1000
n <- 102
m <- .5
s <- 1/sqrt(12)
x <- matrix(runif(n*N), nc=n)
animate( function (a) {
x <- (apply(x[,1:a],1,sum) - a*m)/(sqrt(a)*s)
hist(x, col='light blue', probability=T,
main=paste("n =",a), ylim=c(0,.4),
xlim=c(-4,4))
lines(density(x), col='red', lwd=3)
curve(dnorm(x), col='blue', lwd=3, lty=3, add=T)
if( N>100 ) {
rug(sample(x,100))
} else {
rug(x)
}
},
c(2,102)
)
# Idem, with a bimodal distribution
N <- 1000
n <- 101
m <- 0
s <- sqrt(10)
x <- rnorm(n*N, sample(c(-3,3),n*N,replace=T))
x <- matrix(x, nc=n)
animate( function (a) {
x <- (apply(x[,1:a],1,sum) - a*m)/(sqrt(a)*s)
hist(x, col='light blue', probability=T,
main=paste("n =",a), ylim=c(0,.4),
xlim=c(-4,4))
lines(density(x), col='red', lwd=3)
curve(dnorm(x), col='blue', lwd=3, lty=3, add=T)
if( N>100 ) {
rug(sample(x,100))
} else {
rug(x)
}
},
c(1,101)
)
# Idem, with an asymetric distribution
N <- 1000
n <- 102
m <- 1
s <- 1
x <- rexp(n*N)
x <- matrix(x, nc=n)
animate( function (a) {
x <- (apply(x[,1:a],1,sum) - a*m)/(sqrt(a)*s)
hist(x, col='light blue', probability=T,
main=paste("n =",a), ylim=c(0,.4),
xlim=c(-4,4))
lines(density(x), col='red', lwd=3)
curve(dnorm(x), col='blue', lwd=3, lty=3, add=T)
if( N>100 ) {
rug(sample(x,100))
} else {
rug(x)
}
},
c(1,101)
)Exercice: draw the density function of a distribution depending on a parameter.
TODO: other examples (to be written...)
Write a generic function to modify a graphic depending on one or several parameters. Application: - density of a distribution depending on several parameters. - qqnorm and variable transformations - histogram: interactively change "bw" and "offset" Do the same with several graphics that simultaneously change. Example: density + repartition function + qqnorm + boxplot for a probability distribution depending on several parameters. or a sample to which you apply a transformation depending on one parameter.
TODO: Screenshots
library(fBasics) symstbSlider() TODO: screenshot...
TODO: screenshots, examples
First, install it (check the latest version number):
wget http://www.rpad.org/downloads/Rpad_0.9.2.tar.gz R CMD INSTALL Rpad_0.9.2.tar.gz
If the pages are already written, if a server is already running, it works as follows: you fill in the forms, you click on the "Calculate" button
and you get the result, that contains both numeric results and plots.

So we have to see several things: how do we create the pages? How do we run the server? There are two ways of creating the pages: either with the "wysiwyg" editor (some Javascript can turn a web browser into an HTML editor) or with a normal text editor that will not hide the HTML. There are also two ways of running the server: either a tiny HTTP server (in Tcl) run from within R, or a full-fledged HTTP server (typically, Apache with php and mod_perl).
For the moment, let us simply run the tiny HTTP server
library(Rpad) Rpad()

(this should launch your default web browser -- it works with firefox but not with Konqueror) and have a look at the contents of the pages. They are normal XHTML pages, with some R code in the middle.
Let us quickly list some of the idiosyncrasies of this HTML.
The calculate button, that runs the computations:
<span contentEditable="false">
<input onClick="javascript:top.Rpad_calculate()"
value="Calculate"
type="button"
/>
</span>You can also run the computations when the user clicks on link:
href=javascript:R_run_commands('source("foo.bar")', 'Rpad_calculate()')Some computations (yes, you have to add "<br/>" to indicate the end of the lines and to replace the "<" by ">":
<div class="Rpad_input"
rpad_type="R">
source("myMacros.R") <br/>
x >- foo.bar() <br/>
</div>Sometimes, you want the computations to be performed when the page is loaded:
<div class="Rpad_input" rpad_type="R" Rpad_run="init"> ... </div>
A plot:
plot(...) ... HTMLon() showgraph()
Another plot:
graphoptions(width=4, height=4) newgraph() plot(...) ... HTMLon() showgraph()
Displaying a data frame in HTML:
HTMLon() d <- data.frame(...) HTML(d)
Forms to fill in:
<span contentEditable="false">
<input class="Rpad_input"
name="foo"
rpad_type="Rvariable"
value="2*pi"
/>
</span>The "Rvariable" type corresponds to numbers or any R expression. If you want a string (and do not want the user to enter the quotes), use "Rstring" instead.
For larger data (say, copy-pasted from another application), you can use a <textarea>.
<textarea class="Rpad_input"
rpad_type="file"
name="data.csv"
rows=10 cols="60">
</textarea>
...
<div class="Rpad_input" rpad_type="R">
x = read.csv("data.csv")
...
</div>For choices from a dropdown menu:
HTMLon()
HTMLselect("foo", myList)
...
cat("You have chosen ", foo, ".\n", sep="")
plot(get(foo))
...You can ask the browser to colour the R code:
<style>
.Rpad_input {
behavior: url(js/R_highlight.htc)
-moz-bindings: url(js/moz-behaviors.xml#R-highlight.htc)
}
</style>Sometimes, you want to hide parts of the code (uninteresting code, such as loading your functions, your data, or creating the HTML buttons or menus):
(not tested)
<div contentEditable="false">
<span class="Rpad_input" rpad_type="R"
style="display:none">
...
</span>
</div>
I have really tried hard to use Rpad, but the results were unsatisfactory. There are speed and stability problems, and we never know where they come from: is it a browser-related problem (if the server seems dead and if you are using Internet Explorer, just restart IE -- the problem does not come from the server), is it a network problem, a server problem, an R problem, an HTML problem (the documentation examples contain incorrect HTML (<div> inside of <span>) and suggests to use browsers known not to respect the standards (IE)), a javascript problem? There are simply too many software components -- and they interact in too many ways.
If you just want a "speciallized calculator", with which you would perform a single simple task, Rpad may be a good choice. If you want anything more complex, in particular if you want several pages linked together, it is not a good solution.
TODO:
The Mozille extension How to use a "true" web server Give an example.
TODO
A web service is like a web page with a form on it, for the user to fill in, except that it is not designed to be used by a human user, but by another machine. As a result, the various fields to fill in and the results are not hidden in the HTML but presented in a more directly accessible way -- if you want to extract the information from the result, you do not have to trim down the HTML response.
Here are a few examples. You can access Google as a web service: you send the search terms and you get an XML file that contains the first 10 results with, for each of them, the URL, the tile, the date and an extract containing the serach terms.
TODO: an example of the actual XML received
Amazon.com also provides a web service: you send an ISBN (this is the reference number, on the back of every book) and you get all the book details (author, title, publisher, date, price, availability, etc.) in an XML file.
TODO: other examples Amazon
Some data centers also provide API: for instrance, in Finance, you can imagine a web service to which you send a list of company names or identifiers, a list of dates, a list of items of interest about the company (say, price, volume, book value, earnings, sales, cash flow, etc. -- well, numbers hopefully describing the company) and that gives you the corresponding items, for the corresponding companies and the corresponding dates. It would be as simple as retrieving a URL
http://.../getData.pl?ids=IBM,RHAT&dates=2005-06-01,2005-07-01&items=price,volume
With more spaces:
http://.../getData.pl ? ids = IBM, RHAT
& dates = 2005-06-01, 2005-07-01
& items = price, volumeThe result could be, say, a CSV file such as
TODO: give an example.
The technologies used range from the utterly obvious (a URL that ends in foo.cgi?search=bar) to the very complex (SOAP: the request is an XML file, send via HTTP POST, the answer, in XML, is contained in an XML "enveloppe").
TODO http://www.google.com/apis/
Actually, I have never used a cluster, so the following lines might not be the most reliable source of information.
SIMD (Simple Instruction Multiple Data): this is an architecture in which we have several processors, that process different data, according to the same program. This is the ideal architecture if you want to parallelize the operations that, in R, already appear parallelized, such as vector addition or multiplication.
MIMD (Multiple Instruction Multiple Data): this is another kind of architecture, in which different data are processed in different ways. You can think of it as several machines (or several processors in the same machine) that perform different tasks, independantly.
A problem is said to be "embarassingly parallel" if it is easy to solve, provided we have a lot of machines: we can cut it into many small pieces, write a program to solve a single piece of the problem, send those pieces to our different machines, and finally gather and combine the results. In particular, if the problem is data-intensive, in order to solve a part of the problem, you only need a part of the data.
There is often a distinction between parallel programming (everything is done on the same processor, that can do several things at the same time, in a SIMD or MIMD fashion -- but the different tasks are perfectly timed) and distributed programming. With distributed programming, the processors are often on different machines, communication between those machines takes time, the machines do not run at the same speed -- so that we do not know if all the computations will end at the same time, nor even which one will end first --, there can be network problems (one or several machines can become inaccessible), the machines can break (so that if we do not receive the results from a machine, we have to send the data again, to another machine) and even the main machine (the "master"), that controls the others, may break (so that the other machines have to choose, themselves, someone to replace it).
A cluster is a set of machines used for parallel programming. Typically, the operating system provides the distributed programming layer, so that the programmer (or user) sees the cluster as a parallel programming (or computing) environment.
A node is a machine (or a processor) in a cluster.
The use of clusters is sometimes refered to as High Performance Computing (HPC) or, nore recently, Grid Computing.
A lot of parallel (or non-parallel, actually) computations require vector or matrix computations: processor vendors (Intel, IBM, Sun, etc.) can provide libraries that take advantage of the peculiarities of their processors to speed up those operations. For the most trivial operations, such as adding or multiplying two vectors, the libraries ask the processor to do several operations at the same time (with very old processors, it was not possible, but recent processors can do that, to a certain extent); for more complicated operations, such as multiplying two matrices, the libraries can, on top of that, use non-trivial algorithms that have a lower complexity.
If you do not have a BLAS library (usually, you have to pay extra for it), you can use ATLAS (Automatically Tuned Linear Algebra Software).
http://math-atlas.sourceforge.net/
When you search the internet about BLAS, you will run into LinPack (an old linear algebra library, whose function names are as readable as the 2-letter basic Unix commands -- but with five letters), LaPack (a more recent replacement for LinPack -- BLAS is a part of LaPack) and the LinPack benchmark (a series of computations used to gauge the speed of a computer for numeric computations). ScaLaPack is a parallel implementation of LaPack.
http://en.wikipedia.org/wiki/LAPACK
These are protocols for parallel programming. You will use them if you want to program yourself the parallelization of your application, if this paralelization is not trivial. It is used, internally, by the user-level alternatives such as OpenMosix.
LAM/MPI and MPICH are different implementations of MPI.
This is a first kind of cluster, that uses MPI or PVM. The programs running on a Beowulf cluster have to be specifically written (or modified) for this architecture: the programmer has to know about PVM and/or MPI.
This is another type of cluster that turns a bunch of machines into a single SMP machine (i.e., a multi-processor machine).
You can use normal programs on an SSI cluster: each program will run on a single machine (but you do not know which one: the cluster will choose an idle machine and, if the load increases, it may even move the process to another machine). You can take advantage of such an architecture by either forking your program (if you write it yourself) or by running several programs at the same time -- in Perl, I would use the Parallel::ForkManager module.
#!perl -w
use strict;
my $MAX_PROCESSES = shift || 10; # Number of processes to run simultaneously
use Parallel::ForkManager;
my $pm = new Parallel::ForkManager($MAX_PROCESSES);
while(<>){ # The processes (shell commands) are read from stdin
my $pid = $pm->start and next;
system($_);
$pm->finish; # Terminates the child process
}
This is a free (GPL) SSI implementation.
An R package for parallel computations. It can be used as follows.
library(pR)
StartPE(2) # Either 2 processors on the same machine
# or 2 nodes in an MPI cluster
PE( a <- some.function(some.argument) )
PE( b <- some.function(some.other.argument) )
PE( y <- f(a, b) )
An R package to use ScaLaPack, a parallel implementation of LaPack -- if you have really large matrices: the computations must take longer than the time required to send and receive the data.
An R package that provides a parallelized version of the "lapply" function -- but, if I understand correctly, there must be at least as many machines as elements in the list.
A new package, that provides seamless parallelism.
TODO
R packages if you want to use MPI or PVM yourself, i.e., if you want to control very finely how your algorithm is parallelized.
R package that provides a parallelized random number generator -- otherwise, random numbers generated on different machines may fail to look independant (indeed, they are generated by the same algorithm...).
http://www.aspect-sdm.org/
TODO
?D Explain where those derivatives could be used (optimization algorithms) ?integrate library(help=adpat) library(help=odesolve)
Some functions (lm, prcomp, plot, xyplot, lme) accept a formula as argument. You might want to do the same with your own functions.
TODO # To turn a formula into a data.frame model.frame(y ~ x1 + x2) # If you have several variables on the left hand-side of the ~ # operator, you get a data.frame whose first component is not a # vector but a matrix -- yes, this is possible. model.frame( cbind(y1, y2) ~ x1 + x2 ) # For formulas that contain the | operator TODO
Exercise: Take the code of a function using the "model.frame" function and understand it.
getAnywhere("plot.formula")
When computing with large matrices, you tend to keep the whole matrices in memory. But this is not always needed: in particular, if the matrix contains a lot of zeros, it can be a waste of memory -- and a waste of time when you multiply with it. A sparse matrix is such a matrix, with a lot of zeros -- and we can ask the computer to efficiently deal with it.
TODO
library(help=Matrix) library(help=SparseM)
Sometimes, to check if a new computation software works well, people give it a few simple computations, such as
> 1 + 1 [1] 2
or
> .3 - .2 - .1 [1] -2.775558e-17 > 0.3 / 0.1 [1] 3 > 0.3 / 0.1 == 3 [1] FALSE > 0.3 / 0.1 - 3 [1] -4.440892e-16
Er...
This might not be the result you were expecting, but it should not be surprising. Most computers and numerical software use the so-called "floating point numbers". Broadly speaking, it means that numbers like 121 are not stored as "121", but rather as "1.21 * 10 ^2". The first number, "1.21", is called the mantissa (or significand), the second, "2", the exponent.
Well, you easily guess, from the result above, that this is not the whole story: computers do not like decimal arithmetics -- they prefer binary arithmetics. As a result, the mantissa is written as a binary number, and we do not use a power of 10 but a power of 2.
1.21 = 1 * 2^0 +
0 * 2^-1 +
0 * 2^-2 +
1 * 2^-3 +
1 * 2^-4 +
0 * 2^-5 +
1 * 2^-6 +
0 * 2^-7 +
1 * 2^-8 +
1 * 2^-9 +
1 * 2^-10 +
0 * 2^-11 +
0 * 2^-12 +
0 * 2^-13 +
...In other words,
1.21 (decimal) = 1.00110101110000101... (binary)
You can compute this as follows:
x <- 1.21
for (i in 1:20) {
cat(floor(x))
x <- x - floor(x)
x <- x * 2
}; cat("\n")The problem is that this decimal number is not a round number in binary arithmetics: it has to be rounded, it cannot be represented exactly in base 2.
This was the case with the numbers at the begining of this note (I add spaces to underline the periodicity of the binary expansion):
.1 (decimal) = 0.0 0011 0011 0011 0011... (binary) .2 (decimal) = 0.0011 0011 0011 0011 0011... (binary) .3 (decimal) = 0.01 0011 0011 0011 0011... (binary)
(You may notice that the binary expansion of .2 is the same as that of .1, shifted by one digit -- it simply means that .2 is the double of .1.)
As none of those numbers are whole binary numbers, they have to be rounded. When you compute, some of those rounding errors cancel, but others accumulate.
To know more about IEEE 754 arithmetics:
http://babbage.cs.qc.edu/courses/cs341/IEEE-754references.html http://grouper.ieee.org/groups/754/ http://stevehollasch.com/cgindex/coding/ieeefloat.html
If you want those unequal numbers to be equal (one usually needs this to write tests for one's code), use the "all.equal" function.
> all.equal(0.3 / 0.1, 3) [1] TRUE > all.equal(0.3 - 0.2 - 0.1, 0) [1] TRUE
In actual regression tests, it should be
> stopifnot( all.equal(0.3 / 0.1, 3) ) > stopifnot( all.equal(0.3 - 0.2 - 0.1, 0) )
Many numerical statistical problems can be phrased as "find the values of the parameters that minimize some quantity -- some error term". We now present a few algorithms to numerically solve such problems.
TODO
TODO
Some of those optimization problems can be stated as "minimize some linear function of x1, x2, ..., xn, subject to a few linear constraints". For historical reasons, such an optimization problem is called a "program" -- this dates back to the pre-computer era. As the constraints are linear, they define a "simplex", i.e., a higher-dimensional analogue of a (convex) polygon or polyhedron. It can be shown that, as the function to be minimized is linear, the solution is on a vertex of this simplex.
The simplex algorithm starts at one vertex and hops to a nearby vertex where the function to be minimized is lower -- when we have nowhere to hop, we are done.
TODO: give more details about the algorithm
TODO: in R?
library(help=lpSolve) library(help=linprog) library(help=glpk)
Sometimes, the constraints state that some of the variables have to be integral or binary.
TODO: explain the algorithm in the case of binary constraints.
TODO: give an example (the Travelling Salesman Problem)
TODO: In R?
TODO
One sometimes stumbles upon a generalization of a linear program: the constraints are still linear, but the function to optimize is a degree-2 polynomial. This is called a quadratic program.
TODO: Give an example (portfolio optimization)
TODO: In R
library(help=quadprog)
In the same way as Newton's method solves f(x) = 0 by approximating the function f with its first-order Taylor expansion, one can minimize a function f, iteratively, by apploximating it by its second-order Taylor expansion.
One can even add linear constraints (equalities and inequalities): the problem to solve at each iteration is then a Quadratic Program (QP). In high dimensions, that way of solving non-linear (and even non-convex) optimization problems is actually faster than other methods (e.g., interior-point (IP) methods).
SQP also applies to non-linear constraints: replace the constraints by their first-order Taylor expansion and use the second-order derivative of those constraints as a penalty to the function to optimize.
TODO: understand
Replace the inequalities in Min f(x) g(x) = 0 h(x) >= 0 by a penalty Min f(x) - mu sum log(s_i) g(x) = 0 h(x) = s
TODO
Tricky, but check the genalg and DEoptim packages.
TODO (I am not sure it really belongs here) Examples: - matrix multiplication - order of the JOINs - portfolio optimization (?)
The most common memory problem strikes Windows users with a 2Gb machine: their operating software does not allow them to use more than 1Gb of memory. If you are in this situation, the R windows FAQ details all the new problems that appear if you are stuck on this platform. In particular, it explains how to increase this memory limit -- but Windows specialists tell me that this operating system becomes unstable when a process uses more than 1Gb: you might reach 1.5Gb without any problem, but do not hope to access those 2Gb...
http://cran.r-project.org/bin/windows/base/rw-FAQ.html
But you should really consider installing Linux instead: you can use those 2Gb (problems may appear when a process uses more that 2Gb if the machine only has 2Gb, though).
> library(fortunes)
> fortune("install")
Benjamin Lloyd-Hughes: Has anyone had any joy getting the
rgdal package to compile under windows?
Roger Bivand: The closest anyone has got so far is Hisaji
Ono, who used MSYS (http://www.mingw.org/) to build
PROJ.4 and GDAL (GDAL depends on PROJ.4, PROJ.4 needs a
PATH to metadata files for projection and
transformation), and then hand-pasted the paths to the
GDAL headers and library into src/Makevars, running Rcmd
INSTALL rgdal at the Windows command prompt as
usual. All of this can be repeated, but is not portable,
and does not suit the very valuable standard binary
package build system for Windows. Roughly: [points 1 to
5 etc omitted]
Barry Rowlingson: At some point the complexity of
installing things like this for Windows will cross the
complexity of installing Linux... (PS excepting
live-Linux installs like Knoppix)
-- Benjamin Lloyd-Hughes, Roger Bivand and Barry Rowlingson
R-help (August 2004)Actually, even on Linux, you can run into memory problems: when R needs more memory, it asks the operating system for more and, from time to time, redeems the memory it no longer needs to the operating system (this is called "garbage collection"). The problem is that (when you get near the maximum physically available memory) the memory can become fragmented. A simple solution, if it only happens once (not in the middle of a huge loop), is to save the current, fragmented session (it is fragmented in memory, but the fragmentation will be lost when it is written to disc), quit R, launch it again and read in the previous session.
?save.image
If it happens in the middle of a loop, you can try to explicitely delete the large objects (with the "rm" function) when you no longer need them and explicitely call the garbage collector (with the "gc" function).
for (...) {
r1 <- lmer(...)
...
rm(r1)
gc()
...
rm(r2)
gc()
}If you do not know where the memory is used, the "object.size" function is your friend.
all.object.sizes <- function () {
res <- unlist(lapply( ls(1), function (x) { object.size(get(x)) } ))
names(res) <- ls(1)
sort(res)
}
all.object.sizes.everywhere <- function () {
res <- NULL
for (a in search()) {
r <- unlist(lapply( ls(a), function (x) { object.size(get(x)) } ))
if (!is.null(r)) {
names(r) <- paste(a, ls(a), sep="::")
res <- c(res, r)
}
}
sort(res)
}But these are just workarounds: a better solution is to look if you really need all this data at once. Usually, you do not: if this is your case, you can store your data in a database and only retrieve the chunks you need. The word "database" may sound daunting, but for simple data, SQLite (discussed somewhere in this document) requires no server, no configuration, no installation -- it stores the data in a conventionnal file and provides an SQL interface to it.
If you really need more memory, you should know that: 32-bit machines are limited to 4Gb per processor; the Windows operating system cannot reliably grant more that 1Gb to a single process; on Linux, problems may appear if a simgle process requires more than 3Gb (if you have that much memory). You can turn to 64-bit machines, but then again, you should know that: on these machines, the Windows operating system runs in 32-bit emulation mode, so you are still limited to 4Gb per processor; most Unix-like operating systems (MacOS X.4, Linux, FreeBSD, etc.) are available for 64-bit machines and can take advantage of them.
It is usually meaningless to express the result of a statistical computation with a lot of significant digits. For instance, if you compute the average height of 10 people, you need not be as precise as "1.718937283m": "1.72m" will do.
You can round numbers with the "floor" (round below), "ceiling" (round above), "round" (round to the nearest), "signif" (round to the nearest, not with a prespecified number of decimal places, as with the previous function, but with a prespecified number of significant digits).
> f <- function (x) {
+ c(x=x, floor=floor(x), ceiling=ceiling(x), round=round(x,2), signif=signif(x,2))
+ }
> t(apply(t(rt(10,4)),2,f))
x floor ceiling round signif
[1,] 0.3209408 0 1 0.32 0.32
[2,] -3.2453803 -4 -3 -3.25 -3.20
[3,] -0.8474375 -1 0 -0.85 -0.85
[4,] 1.7481940 1 2 1.75 1.70
[5,] -1.1009298 -2 -1 -1.10 -1.10
[6,] 0.5767945 0 1 0.58 0.58
[7,] 0.9479906 0 1 0.95 0.95
[8,] 0.6373905 0 1 0.64 0.64
[9,] -2.1388324 -3 -2 -2.14 -2.10
[10,] -0.5720559 -1 0 -0.57 -0.57Sometimes, you do not want to round the numbers but merely control the way they are printed. The "digits" option specifies the number of digits to be displayed (but, in memory, for the computations, the numbers retain all their digits).
> pi [1] 3.141593 > options()$digits [1] 7 > options(digits=4) > pi [1] 3.142 > options(digits=7)
Sometimes, the numbers get printed in scientific notation, while you would prefer a more classical notation.
> x <- as.data.frame(t(t(rcauchy(10)^2)))
> x
V1
1 1.869630e+00
2 5.909726e-01
3 6.114153e-01
4 5.320118e-01
5 5.699883e+00
6 2.616534e+04
7 2.019110e-02
8 1.910365e-01
9 2.384527e-03
10 7.097835e-02The computer tries to choose between the standard notation and the scientific one by comparing the length of the various numbers. In this example, we want at least 7 significant digits (the "digits" option): for this, because one value is around 2e-3, we need 10 decimal places. But as we also 2e+4, we end up using as much as 16 characters to display some of the numbers. On the contrary, in scientific notation, we only use 12 characters: by parsimony, the computer chooses the scientific notation.
But we can alter this by adding a penalty to the scientific notation, with the "scipen" option: here, we add a 5-character penalty to the scientific notation; as 16 <= 12 + 5, we keep the standard notation.
> options(scipen=5)
> x
V1
1 1.869630292
2 0.590972584
3 0.611415260
4 0.532011822
5 5.699882601
6 26165.335966629
7 0.020191104
8 0.191036531
9 0.002384527
10 0.070978346Sometimes, when we want a greater control on the way the numbers are printed (typically when you are writing the "print" method of an object you have just defined), you can resort to the lower-level "formatC" function, that transforms numbers into strings, allows you to choose between integer, standard or scientific notation, that allows you to add marks between thousands, millions, etc., that allows you to change the symbol used as decimal point, that allows you to align the numbers on the left or on the right.
> formatC(pi, digits=2, width=8, format="f") [1] " 3.14" > formatC(pi, digits=4, width=8, format="f") [1] " 3.1416" > formatC(pi, digits=4, width=8, format="f", flag="-") # Flush left [1] "3.1416 " > formatC(1e6, digits=4, width=20, format="f", big.mark=",") [1] " 1,000,000.0000" > formatC(1e6, digits=0, width=20, format="f", big.mark=",") [1] " 1,000,000" > formatC(pi * 1e6, digits=9, width=20, format="f", big.mark=",", small.mark=" ") [1] " 3,141,592.65358 9793" > formatC(pi * 1e6, digits=9, width=20, format="f", big.mark=" ", + small.mark=" ", small.interval=3, decimal.mark=",") # in France... [1] " 3 141 592,653 589 793 "
There is also a "format" function (slightly less powerful), a "prettyNum" function (a variant of "format"), a "format.pval" function (for p-values).
There is a "try" command, to run functions that might crash.
try(...)
We shall use it later in this document, usually on the form
x <- NA
try( x <- ... )
if( is.na(x) ) {
...
} else {
...
}or even, sometimes,
done <- FALSE
while (!done) {
r <- try( ... )
done <- !inherits(r, "try-error")
}Actually, the manual tells us that we are not supposed to use "try" (I use it a lot) but "tryCatch" (which I have never used).
?tryCatch
TODO
?on.exit ?reg.finalizer # When I speak about memory and garbage collection ?setHook # AOP...
As functions have NO side effect, we should not be able to change global variables from within a function. However,
x <<- 1+2+3+4+5
modifies the "x" variable where it lives or, if it does not exist yet, defines it as a global variable.
Other way of doing it:
set.global <- function (x, value) {
x <- deparse(substitute(x))
assign(x, value, pos=.GlobalEnv)
}And it works:
> set.global(a,3) > a [1] 3 > set.global(a,1:10) > a [1] 1 2 3 4 5 6 7 8 9 10
This can be generalized to write methods that modify the object to which they are atteched. Instead of using pos=.GlobalEnv, you can try -2: a variable local to the environment that called the function (I think).
You can explicitely create "environments" and use them as hash tables.
> x <- new.env(hash=T)
> assign('foo', 3, env=x)
> assign('bar', list('a'=3, 'b'=list('c'=1, d='foo')), env=x)
> assign('baz', data.frame(rnorm(10),rnorm(10)), env=x)
> x
<environment: 0x8bb97bc>
> ls(env=x)
[1] "bar" "baz" "foo"
> get('foo', env=x)
[1] 3
We can ask R to perform certain actions when it is launched (for instance, load a certain library) or when we close it (for instance, save some of the data under a certain format) by redefining the ".First" and ".Last" functions.
> ?Startup
> .First
function() {
require("ctest", quietly = TRUE)
}
TODO
The "system" command can launch any Unix command.
system("top")If you want to launch the command in the background, you just add an "&" at the end, as usual. If the command expects arguments (in particular the name of a file containing the data to process), it might be useful to print the command that will be used (R is not good/intuitive at string processing). For instance, in xgobi's code (xgobi or ggobi is an external program to visualize data in dimension 3 of higher), we find
...
args <- paste("-title", paste("'", title, "'", sep = ""),
args)
command <- paste("xgobi", args, dfile, "&")
cat(command, "\n")
s <- system(command, FALSE)
invisible(s)
}This is mainly used to transfer the data we are working with to another program, often to visualize them. We shall see how to call xgobi/ggobi (to visualize high-dimensional data, dynamically and interactively) from R. We can also use it to produce "pretty" pictures, for instance to add a background to a graphic (with ImageMagick) or to ask PoVRay to produce a picture (such as the one used as title of this document) or an animation.
TODO: URL of the Linux Journal article about data visualization with PoVRay.
You can also use it to automatically launch LaTeX (them xdvi, dvips, lpr) on a file, previously created (with SWeave, that allows one to add R code, results of computations made with R, graphics made with R, in a LaTeX document).
The "deparse" command shows the contents of an object, as a string (you can then play with the string -- you would want to do that, for instance, if you wanted to create a LaTeX file by hand, from R) -- if you just want to see it, just give the object name to the interpreter or use the "print.defaut" function.
> print
function (x, ...)
UseMethod("print")
> deparse(print)
[1] "function (x, ...) " "UseMethod(\"print\")"The "substitute" command performs substitutions in an expression (the result is an unevaluated expression).
> substitute(x+1, list(x=3)) 3 + 1
We have also seen that the "substitute" command (often together with the "deparse" command) could allow a function to see where its arguments came from.
my.arg <- function (x, ...) {
cat("My first argument was: ")
cat(deparse(substitute(x)))
cat("\n")
}
> my.arg(3)
My first argument was: 3
> my.arg(x)
My first argument was: x
> my.arg(x+1)
My first argument was: x + 1
The "get" command turns a string containing the name of a variable into the contents of the variable.
> get("plot")
function (x, ...)
{
if (is.null(attr(x, "class")) && is.function(x)) {
if ("ylab" %in% names(list(...)))
plot.function(x, ...)
else plot.function(x, ylab = paste(deparse(substitute(x)),
"(x)"), ...)
}
else UseMethod("plot")
}
The "ls" command gives the list of the variables currently defined. You can specify in which environment to look (as a result, you can browse through the global variables, even if they are masked by the local variables). You can also search a variable name from a regural expression.
> ls() [1] "a" "my.arg" "set.global" "x" "y" > ls(pos=.GlobalEnv) [1] "a" "my.arg" "set.global" "x" "y"
In a Unix fashion, variables whose name start with a dot are "hidden": you must explicitely ask to see them.
> ls(all=T) [1] "a" "my.arg" ".Random.seed" "set.global" [5] ".Traceback" "x" "y"
The "rm" command deletes variables.
The "search" command shows the "path" (i.e., the list of environments) in which R looks for the variables.
> library(MASS) > search() [1] ".GlobalEnv" "package:MASS" "package:ctest" "Autoloads" [5] "package:base" > ls(pos="package:MASS") [1] "addterm" "addterm.default" "addterm.glm" [4] "addterm.lm" "addterm.mlm" "addterm.negbin" [7] "addterm.survreg" "anova.loglm" "anova.negbin" ... [175] "update.loglm" "vcov" "vcov.glm" [178] "vcov.lm" "vcov.nls" "vcov.polr" [181] "width.SJ" "write.matrix"
The "apropos" (or "find") command helps us find a variable (or function) name.
> apropos('exp')
[1] "negexp.SSival" "as.expression" "as.expression.default"
[4] "char.expand" "dexp" "exp"
[7] "expand.grid" "expand.model.frame" "expm1"
[10] "expression" "is.expression" "path.expand"
[13] "pexp" "qexp" "regexpr"
[16] "rexp"
> apropos('.')
[1] "x" "boxcox"
[3] "boxcox.default" "boxcox.formula"
[5] "boxcox.lm" "corresp.matrix"
...
[1767] "xyinch" "xyz.coords"
[1769] "yinch" "zapsmall"
[1771] "zip.file.extract"
The "stop" function stops a function when a problem is spotted (for example, when there is a type problem with its arguments).
do.it <- function (x) {
if( !is.numeric(x) )
stop("Expecting a NUMERIC vector!")
if( !is.vector(x) )
stop("Expecting a numeric VECTOR!")
if( length(x)<2 )
stop("Expecting a numeric vector of length at least 2")
return("Well done.")
}
> do.it("abc")
Error in do.it("abc") : Expecting a NUMERIC vector!
> do.it(3)
Error in do.it(3) : Expecting a numeric vector of length at least 2
> do.it(data.frame(a=1:3,b=3:1))
Error in do.it(data.frame(a = 1:3, b = 3:1)) :
Expecting a NUMERIC vector!
> do.it(matrix(1:4,nc=2,nr=2))
Error in do.it(matrix(1:4, nc = 2, nr = 2)) :
Expecting a numeric VECTOR!
> do.it(1:26)
[1] "Well done."The "stopifnot" function is similar -- it is an assertion mechanism, as the "assert" mechanism in C -- is is a VERY good idea to use a lot of assertions in your code: it helps you spot bugs before they appear.
The warning() function is similar but emits a (usually non-fatal) warning.
TODO: Example
You can control whether a warning is fatal or not with
options(warn=-1) # Do not print warnings
options(warn=0) # Print warnings at the end of the function, not when
# they are emitted; if there are too many of them,
# just say there are too many
options(warn=1) # Print the warnings when they occur
options(warn=2) # Make the warnings fatal
The "parse" command transforms a string into an unevaluated expression. You can then evaluate the expression with the "eval" command.
> parse(text="0==1") expression(0 == 1) > eval(parse(text="0==1")) [1] FALSE
Expressions may also be used as labels, in graphics.
x <- seq(0,4, length=100) y <- sqrt(x) plot(y~x, type='l', lwd=3, main=expression(y == sqrt(x)) )
There are more details in the manual:
?plotmath

This work is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 2.5 License.
Vincent Zoonekynd
<zoonek@math.jussieu.fr>
latest modification on Sat Jan 6 10:28:16 GMT 2007